Selective ensemble of doubly weighted fuzzy extreme learning machine for tumor classification

Abstract

Malignant epithelial cell tumor also known as cancer is a deadly disease requiring a very costly and complex treatment. Early and accurate diagnosis of tumor plays an important role in reducing the mortality rate. With the rapid development of gene chip technology, gene expression data based tumor classification is helpful for accurate decision-making and has achieved great attention of researchers. Due to gene expression data having the properties of multi-class imbalance, high noise and high-dimensional small samples, in this paper, selective ensemble of doubly weighted fuzzy extreme learning machine (SEN-DWFELM) is presented for tumor classification. In view of good generalization performance of extreme learning machine (ELM), feature weighted fuzzy membership is embedded in ELM for eliminating classification error from noise samples. It considers the influence of feature importance on classification to acquire more accurate fuzzy membership. Simultaneously, by removing features with smaller weights it reduces the dimensionality of samples to improve training efficiency. Considering imbalanced learning, the weighted scheme is also introduced to enhance the effect of minority class samples on classification. Furthermore, doubly weighted fuzzy extreme learning machine (DWFELM) based selective ensemble algorithm is proposed to make classification performance more robust. Partial-based DWFELMs are selected using binary version of an improved whale optimization algorithm, and the selected base DWFELMs are integrated by majority voting. Finally, the proposed SEN-DWFELM is compared with conventional ensemble methods and variants of SEN-DWFELM on various gene expression data. Experimental results show that SEN-DWFELM remarkably outperforms other competitors in accordance with classification performance and can effectively deal with tumor diagnosis problems.

1 Introduction

Tumor includes malignant and benign tumor, where malignant epithelial cell tumor also known as cancer is a hazard to human health [1]. So accurate and timely treatment of cancer is of vital importance in reducing the mortality rate. Nevertheless, the same cancer caused by many factors can have different symptoms, and it is difficult for traditional methods to identify cancer precisely [2]. With the rapid development of gene chip technology, gene expression data based tumor classification can acquire more accurate results and has drawn a lot of research interests [3]. In virtue of gene expression data having the properties of multi-class imbalance, high noise and high-dimensional small samples, it is indispensable to carry out research on gene expression classification.

Extreme learning machine (ELM) proposed by Huang et al. [4] is a new type of single hidden layer feedforward neural networks (SLFNs). In virtue of good generalization performance with a fast learning speed, ELM has been successfully applied to various practical application [5,6,7,8]. Inspired by the ensemble idea [9, 10], the stability along with generalization performance of single ELM can be further improved. AdaBoost constructed a serial ensemble model. The weight distributed for every training sample is updated in the light of classification performance of the former classifiers before every iteration [11]. Li et al. [12] proposed that weighted ELM is put into the amended AdaBoost framework, namely boosting weighted ELM. The weight distributed for every training sample from different class is updated apart. Cao et al. [13] proposed V-ELM that completes ensemble of ELMs and then reaches the decision by majority voting. Lu et al. [14] proposed DF-D-ELM and D-D-ELM that select some base ELMs by the dissimilarity measure and then integrate the selected ELMs by majority voting.

Nowadays, gene expression classification brings extreme challenge. Existing methods usually ignore the influence of noises and outliers on classification and are extremely sensitive to noises and outliers. Zhang and Ji [15] introduced a fuzzy membership to solve the problem. The fuzzy membership can be flexibly set on different applications. Moreover, existing methods usually assume balanced class distribution and are unfit for handling data with complex class distribution. Data processing approach and algorithmic approach are two strategies handling imbalanced dataset [16]. In data processing approach, there is mainly undersampling and oversampling studied for balancing the size of every class [17, 18]. Data processing approach changes samples distribution and probably brings about losing crucial information, whereas algorithmic approach has come into wide use in handling imbalanced dataset without changing samples distribution [19, 20]. Gupta [21] proposed weighted twin support vector regression based on K-nearest neighbor (KNN), which decreases the effect of outliers and achieves better generalization performance. Hazarika et al. [22] proposed density-weighted twin support vector machine (SVM) considering 2-norm of slack variables and equality constraints, which validate the usability and efficacy of the proposed model for binary class imbalance learning.

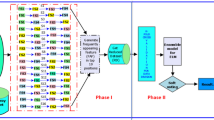
This paper takes an interest in algorithmic approach, and presents selective ensemble of doubly weighted fuzzy extreme learning machine (SEN-DWFELM) for tumor classification. Firstly, doubly weighted fuzzy extreme learning machine (DWFELM) is constructed. ReliefF is a high-efficiency feature optimization algorithm, which can effectively cope with noisy data and missing data without limiting data types [23]. ReliefF-based feature weighted fuzzy membership is developed to eliminate classification error from noises and outliers. It not only considers the decrease in the dimensionality of samples but also considers the impact of feature importance on classification. Simultaneously, the weighted scheme is introduced to enhance the relative influence of minority class samples and lessen the bias against performance from imbalanced dataset.

Furthermore, binary version of an improved whale optimization algorithm (IWOA) is put forward for selecting some base DWFELMs integrated by majority voting. Whale optimization algorithm (WOA) is a new meta-heuristic method imitating hunting behaviors of humpback whales [24]. With good search capability and simplicity property, WOA has been widely used for tackling various optimization problems [25,26,27,28,29]. However, the property of WOA has still much room for improving as described by Mafarja et al. [30]. Therefore, in this paper, population initialization based on quasi-opposition learning strategy is adopted to accelerate convergence. The dynamic weight and nonlinear control parameter are proposed for coordinating the exploitation and exploration ability. By various experiments, comparison results show the proposed SEN-DWFELM can acquire better classification performance and is suited for coping with gene expression data.

The remaining section of this paper is arranged below. Section 2 discusses related works based on gene expression classification. Section 3 presents the description of preliminaries. In Sect. 4, the proposed method is explained in detail. In Sect. 5, the experimental design and comparative results of related algorithms are presented. Finally, Sect. 6 states conclusions of the paper.

2 Related works

Recently, many methods have been developed for tackling gene expression classification problems. Gao et al. [31] presented a hybrid gene selection method, where information gain (IG) is initially used for filtering redundant and irrelevant genes, then SVM is used for further removing redundant genes and eliminating noises. Selected genes are again served as input for SVM classifier, and the proposed method achieves superior classification performance. Rani et al. [32] presented a two-stage gene selection method, where mutual information (MI) is firstly employed for selecting genes having higher information relevant to cancers, then genetic algorithm (GA) is again employed for identifying the optimal set of genes in the second stage. Besides, SVM is employed for classification and the proposed method acquires higher classification accuracy. Tavasoli et al. [33] introduced an optimized gene selection method, where Wilcoxon, two-sample T-test, entropy, receiver operating characteristic curve, and Bhattacharyya distance are employed in the ensemble soft weighted approach. Moreover, parameter optimization of SVM is performed by a modified water cycle algorithm and the proposed method shows its robustness in terms of accuracy. Lu et al. [34] presented an efficient gene selection method combining the adaptive GA and the mutual information maximization (MIM), which remarkably removed the redundancies of genes. Four different classifiers are used for classification, then the proposed method shows reduced genes provide higher classification accuracy. Mondal et al. [35] used entropy-based method for differentiating between breast tumor and normal tissue. In addition, random forest, naive Bayes, KNN and SVM are used for breast cancer prediction. Experimental results show SVM obtains better accuracy. Shukla et al. [36] introduced a new wrapper gene selection method, where minimum redundancy maximum relevance (mRMR) is firstly used for selecting relevant genes from gene expression data, then teaching learning-based algorithm in combination with gravitational search algorithm is employed to select the informative genes from data reduced by mRMR. Naive Bayes classifier is again employed to classify cancer, and experimental results demonstrate its effectiveness regarding optimal number of genes and classification accuracy. Dabba et al. [37] incorporated modified moth flame algorithm in MIM to evolve gene subsets and used SVM for detecting cancer. The proposed method provides greater classification accuracy. All these algorithms have focused on solving gene selection problem. However, confronted with the properties of multi-class imbalance, high noise and high-dimensional small samples of gene expression data, it is crucial to find an appropriate classifier for addressing these problems.

3 Preliminaries

3.1 Weighted extreme learning machine (WELM)

Given a training dataset comprising N different samples ($x_j,z_j$), where $x_j=[x_{j1},x_{j2},\ldots ,x_{jm}]^T\in R^m$ is an m$\times$1 feature vector and $z_j=[z_{j1},z_{j2},\ldots ,z_{jn}]^T\in R^n$ is an n$\times$1 target vector. With activation function G(x) and hidden nodes L, the mathematical pattern of SLFNs can be expressed as follows.

$$\begin{aligned} \sum \limits _{k=1}^L\beta _kG(a_k\cdot x_j+b_k)=z_j\qquad j=1,2,\ldots ,N \end{aligned}$$

(1)

where $a_k=[a_{k1},a_{k2},\ldots ,a_{km}]^T$ means the input weight vector for the link between the kth hidden node and input nodes, $a_k\cdot x_j$ means the inner product for $a_k$ and $x_j$, $b_k$ means the bias for the kth hidden node, and $\beta _k=[\beta _{k1},\beta _{k2},\ldots ,\beta _{kn}]^T$ means the output weight vector for the link between output nodes and the kth hidden node.

Training samples can be approximated with zero error in SLFNs if L is identical with N. Then the formula (1) can also be given as follows.

$$\begin{aligned} H\beta =Z \end{aligned}$$

(2)

$$\begin{aligned} H= & {} \begin{bmatrix} h(x_1)\\ \vdots \\ h(x_N) \end{bmatrix}\\= & {} \begin{bmatrix} G(a_1\cdot x_1+b_1)&{} \quad \ldots &{} \quad G(a_L\cdot x_1+b_L)\\ \vdots &{} \quad \ldots &{} \quad \vdots \\ G(a_1\cdot x_N+b_1)&{} \quad \ldots &{} \quad G(a_L\cdot x_N+b_L) \end{bmatrix}_{N\times L} \end{aligned}$$

$$\begin{aligned} \beta =\begin{bmatrix} \beta ^T_1\\ \vdots \\ \beta ^T_L \end{bmatrix}_{L\times n}, \hbox {and} \quad Z=\begin{bmatrix} z^T_1\\ \vdots \\ z^T_N \end{bmatrix}_{N\times n} \end{aligned}$$

(3)

where $\beta$ means the output weight matrix, and Z means the output matrix. H means the output matrix for hidden layer, and the kth column for H indicates the output vector for the kth hidden node concerning all of the inputs.

Nevertheless, Eq. (2) can not be fulfilled owing to L$<<$N in most cases. The output weights are just calculated through the Least Square solution $\beta =H^+Z$ using the Moore-Penrose generalized inverse $H^+$ of H [38, 39]. ELM algorithm is described briefly in Fig. 1.

Fig. 1

Algorithm for ELM

In light of Bartlett’s theory [40], the aim of ELM is to minimize training errors and the norm of output weights. Then an especial weight is also assigned for every sample to better handle imbalanced dataset. Consequently, the classification problem of weighted extreme learning machine (WELM) is defined below.

$$\begin{aligned} \begin{aligned}&\hbox {min}:L=\frac{1}{2}||\beta ||^2+CW\frac{1}{2}\sum \limits _{j=1}^N\xi ^2_j\\&\hbox {s.t}:h(x_j)\beta =z_j-\xi _j \end{aligned} \end{aligned}$$

(4)

where C is penalty parameter, and $\xi _j=[\xi _{j1},\xi _{j2},\ldots ,\xi _{jn}]^T$ is the training error vector of all the output nodes on the training sample $x_j$. As a diagonal matrix, W is associated with every training sample and can be assigned below [41].

$$\begin{aligned} \begin{aligned}&W1:w_{jj}=\frac{1}{\#(z_j)}\\&W2:w_{jj}=\left\{ \begin{array}{cc} \frac{0.618}{\#(z_j)}\quad if\ \#(z_j)> \hbox {avg}\\ \frac{1}{\#(z_j)}\quad if\ \#(z_j)\le { \hbox {avg}} \end{array}\right. \end{aligned} \end{aligned}$$

(5)

where avg is the average of the samples number of all the classes, and $\#(z_j)$ is the samples number of class $z_j$. Based on KKT theorem, the output weight of WELM is calculated as

$$\begin{aligned} \beta =\left\{ \begin{array}{ll} H^T\left( \frac{I}{C}+WHH^T\right) ^{-1}WZ &{} \quad \hbox {when} \ N < L\\ \left( \frac{I}{C}+H^TWH\right) ^{-1}H^TWZ &{} \quad \hbox {when} \ N>> L \end{array}\right. \end{aligned}$$

(6)

3.2 Whale optimization algorithm (WOA)

WOA simulates hunting behaviors of humpback whales, namely bubble-net feeding approach. There are mainly three stages including searching for prey, encircling prey and bubble-net attacking in WOA [24]. The mathematical model is described as follows.

3.2.1 Searching for prey

In the exploration stage of searching for prey, whales seek randomly according to respective position to perform a global search. This behavior is written as

$$\begin{aligned}{} & {} \overrightarrow{D}=|\overrightarrow{F}\cdot \overrightarrow{U}_\textrm{rand}-\overrightarrow{U}(t)| \end{aligned}$$

(7)

$$\begin{aligned}{} & {} \overrightarrow{U}(t+1)=\overrightarrow{U}_\textrm{rand}-\overrightarrow{A}\cdot \overrightarrow{D} \end{aligned}$$

(8)

where $\overrightarrow{U}_\textrm{rand}$ is a whale position of random selection from the present population, $\overrightarrow{U}$ is the present position for a whale, t is the present iteration, $\overrightarrow{D}$ is the distance kept by the random position and the present position, then the coefficient vectors $\overrightarrow{F}$ and $\overrightarrow{A}$ are defined as

$$\begin{aligned}{} & {} \overrightarrow{F}=2\cdot \overrightarrow{r} \end{aligned}$$

(9)

$$\begin{aligned}{} & {} \overrightarrow{A}=2\overrightarrow{a}\cdot \overrightarrow{r}-\overrightarrow{a} \end{aligned}$$

(10)

where $\overrightarrow{r}$ is a random vector in [0,1], $\overrightarrow{a}=2-t*(2/MN)$ is decreasing linearly from 2 to 0, and MN is the maximum iteration number.

3.2.2 Encircling prey

In the exploitation stage of encircling prey, the target prey is just the present best solution, which offers guidance on other solutions updating their positions. This behavior is expressed as

$$\begin{aligned}{} & {} \overrightarrow{D}=|\overrightarrow{F}\cdot \overrightarrow{U}_\textrm{best}-\overrightarrow{U}(t)| \end{aligned}$$

(11)

$$\begin{aligned}{} & {} \overrightarrow{U}(t+1)=\overrightarrow{U}_\textrm{best}-\overrightarrow{A}\cdot \overrightarrow{D} \end{aligned}$$

(12)

where $\overrightarrow{U}_\textrm{best}$ is the present best solution. If a better solution is acquired after every iteration, $\overrightarrow{U}_{best}$ is also updated accordingly.

3.2.3 Bubble-net attacking

Bubble-net attacking approach performs the entire exploitation stage. In this stage, WOA uses a spiral-shaped path of bubble nets to simulate attacking behaviors of humpback whales, and this behavior is shown below.

$$\begin{aligned}{} & {} \overrightarrow{D'}=|\overrightarrow{U}_\textrm{best}-\overrightarrow{U}(t)| \end{aligned}$$

(13)

$$\begin{aligned}{} & {} \overrightarrow{U}(t+1)=\overrightarrow{D'}\cdot e^{bl}\cdot \cos (2\pi l)+\overrightarrow{U}_\textrm{best} \end{aligned}$$

(14)

where $\overrightarrow{D'}$ is the distance kept by the prey and the whale, l is a random number in $[-1,1]$, and b is a constant indicating the logarithmic spiral shape.

WOA starts with a group of random solutions. |A| determines whether WOA emphasizes the exploitation or exploration ability. Whales update their positions by Eq. (8) if $|A|\ge$1, and the exploration capability is emphasized. Whales update their positions relying on p by Eqs. (12) or (14) if $|A|<$1, and the exploitation capability is emphasized. It is assumed that there is 50% probability to move between bubble-net attacking and encircling prey behavior. So this behavior is formulated as

$$\begin{aligned} \overrightarrow{U}(t+1)=\left\{ \begin{array}{ll} \overrightarrow{U}_\textrm{best}-\overrightarrow{A}\cdot \overrightarrow{D} &{} \quad \hbox {if} \ p<0.5\\ \overrightarrow{D'}\cdot e^{bl}\cdot \cos (2\pi l)+\overrightarrow{U}_\textrm{best} &{} \quad \hbox {if} \ p\ge 0.5 \end{array}\right. \nonumber \\ \end{aligned}$$

(15)

where p is a random number in [0, 1]. The flowchart of WOA is shown in Fig. 2.

Fig. 2

The flowchart of WOA

4 Proposed SEN-DWFELM model

4.1 ReliefF algorithm

Recently, ReliefF algorithm is widely applied in feature optimization [42, 43]. It selects randomly a sample $x_i$, then searches for k-nearest neighbor samples of $x_i$ from the same class called $H_j$ and the different classes called $M_j$(e). The initial weights assigned for all the features are 0. These weights are again calculated by the between-class and within-class distances kept by the nearest neighbor samples. The formula of adjusting the weights is expressed as

$$\begin{aligned} \begin{aligned} f_v&= \, f_v-\sum \limits _{j=1}^{k}\frac{\hbox {diff}(v,x_i,H_j)}{q\cdot k}\\&\quad + \sum \limits _{e\ne \textrm{class}(x_i)}\frac{P(e)}{1-P(\textrm{class}(x_i))}\cdot \sum \limits _{j=1}^{k}\frac{\hbox {diff}\left( v,x_i,M_j(e) \right) }{q\cdot k} \end{aligned}\nonumber \\ \end{aligned}$$

(16)

where P(e) is the ratio of samples in the eth class to the total samples, $P(\hbox {class}(x_i))$ is the ratio of samples in the same class as $x_i$ to the total samples, $\hbox {diff}(v,x_i,H_j )$ is the distance between $x_i$ and $H_j$ on the vth feature, $\hbox {diff}(v,x_i,M_j (e))$ is the distance between $x_i$ and $M_j (e)$ on the vth feature, then q and k are respectively the amount of the sampling and the nearest neighbor samples.

ReliefF algorithm aims at repeating q times of the above procedure. Finally, the weights of all the features are calculated, and then feature optimization is completed by the features with higher weights.

4.2 Doubly weighted fuzzy extreme learning machine (DWFELM)

Feature weighted fuzzy membership and the weighted scheme are introduced into ELM in this paper. Feature weighted fuzzy membership is proposed for eliminating classification error from noises and outliers. In [15], all the features are used for calculating fuzzy membership and are regarded as having the same contribution to classification. However, this method can assign high fuzzy membership for noises and outliers to result in reducing classification performance. Therefore, based on the feature set obtained by ReliefF algorithm, the weighted distance between training sample and class center is developed for analyzing the impact of feature importance to improve classification performance.

First, the samples center for every class is expressed as

$$\begin{aligned} d_t^v=\frac{1}{N_t}\sum \limits _{j=1}^{N_t}x_j^v\qquad t=1,\ldots ,c \end{aligned}$$

(17)

where $x_j^v$ is the vth feature of the jth sample, c is the classes number, $N_t$ is the samples number for the tth class, and $d_t^v$ is the samples center for the tth class. Feature weighted distance $fd_t$ for the tth class from samples to center is expressed below.

$$\begin{aligned} fd_t=\sqrt{\sum \limits _{v=1}^{m}{f_v \left( x_j^v-d_t^v \right) ^2}}\qquad j=1,\ldots ,N_t \end{aligned}$$

(18)

where $f_v$ is the weight of the vth feature, and m is the amount of feature. Accordingly, feature weighted fuzzy membership is presented below.

$$\begin{aligned} R:r_{jj}=1-\frac{fd_t}{\max (fd_t)+\epsilon } \end{aligned}$$

(19)

where $\epsilon$ is very small and positive. As a diagonal matrix, R is closely associated with every training sample. From Eqs. (18) and (19), it can be found that feature weighted fuzzy membership avoids being dominated by some uncorrelated or weakly correlated features. In order to reduce the effect of noises and outliers, the approach will exert a minimum fuzzy membership over them.

On the other hand, the weighted scheme is designed for enhancing the relative influence of minority class samples, and it is presented as

$$\begin{aligned} W:w_{jj}=\frac{\#(c-z_j+1)}{\max (\#z_j)} \end{aligned}$$

(20)

where $\max (\#z_j)$ is the maximum samples number for all the classes, and $\#(c-z_j+1)$ is the samples number for class $c-z_j+1$. The samples number for class 1,2,$\ldots$,c is arranged in the order of rising.

In contrast, W-based weighted scheme has much stronger influence on classification performance, and the reason is explained below for binary classification problem.

$$\begin{aligned} \varDelta W= & {} \left( \frac{\#{\hbox {majority}}}{\max (\#z_j)}\right) -\left( \frac{\#\hbox {minority}}{\max (\#z_j)}\right) \\= & {} \frac{\#\hbox {majority}-\#\hbox {minority}}{\max (\#z_j)}\\ \varDelta W1= & {} \left( \frac{1}{\#\hbox {minority}}\right) -\left( \frac{1}{\#\hbox {majority}}\right) \\= & {} \frac{\#\hbox {majority}-\#\hbox {minority}}{\#\hbox {majority}\times \#\hbox {minority}} \end{aligned}$$

where $\#\hbox {majority}$ and $\#\hbox {minority}$ denote respectively the amount of majority class and minority class samples. Due to $\#\hbox {majority}>2$ and $\#\hbox {minority}>2$, $\#\hbox {majority}\times \#\hbox {minority}>\max (\#z_j)$. So $\varDelta W>\varDelta W1$ and W-based weighted scheme is superior to W1-based weighted scheme.

$$\begin{aligned} \begin{aligned} \varDelta W2&=\left( \frac{1}{\#\hbox {minority}}\right) -\left( \frac{0.618}{\#\hbox {majority}}\right) \\&=\frac{\#\hbox {majority}-0.618\times \#\hbox {minority}}{\#\hbox {majority}\times \#\hbox {minority}} \end{aligned} \end{aligned}$$

Due to $\#\hbox {majority}>2$ and $\#\hbox {minority}>2$, $\#\hbox {majority}\times \#\hbox {minority}-\max (\#z_j)>(\#\hbox {majority}-0.618\times \#\hbox {minority})-(\#\hbox {majority}-\#\hbox {minority})$. So $\varDelta W>\varDelta W2$ and W-based weighted scheme is superior to W2-based weighted scheme. Consequently, the classification problem of DWFELM is expressed below.

$$\begin{aligned} \begin{aligned}&L_\textrm{DWFELM}=\frac{1}{2}||\beta ||^2+CW\frac{1}{2}\sum \limits _{j=1}^{N}r_{jj}\xi ^2_j\\&\hbox {s.t}:h(x_j)\beta =z_j-\xi _j \end{aligned} \end{aligned}$$

(21)

Relative constraint conditions are deduced below on the grounds of KKT theorem.

$$\begin{aligned}{} & {} \frac{\partial {L_\textrm{DWFELM}}}{\partial {\beta }}=0\rightarrow \beta =\sum \limits _{j=1}^N{\alpha _jh(x_j)^T}=H^T\alpha \end{aligned}$$

(22)

$$\begin{aligned}{} & {} \frac{\partial {L_\textrm{DWFELM}}}{\partial {\xi _j}}=0\rightarrow \alpha _j=CWr_{jj}\xi _j \end{aligned}$$

(23)

$$\begin{aligned}{} & {} \frac{\partial {L_\textrm{DWFELM}}}{\partial {\alpha _j}}=0\rightarrow h(x_j)\beta -z_j+\xi _j=0 \end{aligned}$$

(24)

If $N<L$, by substituting Eqs. (23) and (22) into (24), the output weight of DWFELM is calculated as

$$\begin{aligned} \beta =H^T\left( \frac{R^{-1}}{C}+WHH^T\right) ^{-1}WZ \end{aligned}$$

(25)

If $N\gg L$, by substituting Eqs. (23) and (24) into (22), the output weight of DWFELM is calculated as

$$\begin{aligned} \beta =\left( \frac{I}{C}+H^TWRH\right) ^{-1}H^TWRZ \end{aligned}$$

(26)

4.3 Improved Whale optimization algorithm (IWOA)

WOA has the risk of poor convergence because of diverse exploration and less exploitation [24]. In this paper, it is indispensable for searching for a well improved WOA (IWOA).

4.3.1 Population initialization based on quasi-opposition learning strategy

WOA does not guarantee the diversity of initialization population because it uses the approach of random initialization. Opposition-based learning (OBL) adopts the notion of opposite point [44], and then adds opposite search to random search for accelerating search speed. In general, OBL considers both initial solutions and opposite solutions to find the best solution faster.

In initialization phase, IWOA generates an initial population randomly, and every solution $U_j=\{u_{j,1},u_{j,2},\ldots ,u_{j,D}\}$ is expressed as

$$\begin{aligned} \begin{aligned}&u_{j,k}=u_{\textrm{min},k}+\hbox {rand}(0,1)(u_{\textrm{max},k}-u_{\textrm{min},k})\\&j=1,2,\ldots ,PN\qquad k=1,2,\ldots ,D \end{aligned} \end{aligned}$$

(27)

where $u_{\min ,k}$ and $u_{\max ,k}$ are lower and upper bound for the kth parameter, D is the amount of optimization parameters, and PN is the size of population. Then the opposite solution $OU_j=\{ou_{j,1},ou_{j,2},\ldots ,ou_{j,D}\}$ of $U_j$ is expressed as

$$\begin{aligned} ou_{j,k}=u_{\min ,k}+u_{\max ,k}-u_{j,k} \end{aligned}$$

(28)

with the research going on, Rahnamayan et al. [45] found a new method called quasi-opposition-based learning (QOBL). Compared with OBL, solutions of QOBL acquired are better. The quasi-opposition solution $QU_j=\{qu_{j,1},qu_{j,2},\ldots ,qu_{j,D}\}$ of $U_j$ is the point between the opposite point and the center of search space.

$$\begin{aligned} \begin{aligned} qu_{j,k}=\left\{ \begin{array}{ll} \hbox {rand}(y_k,ou_{j,k}) &{}\quad u_{j,k}\le y_k\\ \hbox {rand}(ou_{j,k},y_k) &{} \quad u_{j,k}>y_k \end{array}\right. \end{aligned} \end{aligned}$$

(29)

where $y_k=\frac{u_{\min ,k}+u_{\max ,k}}{2}$, rand$(y_k,ou_{j,k})$ stands for a random number in $[y_k,ou_{j,k}]$, and rand$(ou_{j,k},y_k)$ stands for a random number in $[ou_{j,k},y_k]$. Finally, the initial population retains PN individuals having better solutions from $\{U_j\cup QU_j\}$.

4.3.2 The dynamic weight and nonlinear control parameter

The balance of the exploitation and exploration ability in WOA mostly lies on the coefficient A. The search range is extended for finding better solution if $|A|\ge$1, which determines the exploration capability of WOA. The search range is narrowed for carrying out more careful search if $|A|<$1, which determines the exploitation capability of WOA. By observing Eq. (10), it can be found that control parameter $\overrightarrow{a}$ affects $\overrightarrow{A}$ directly. However, $\overrightarrow{a}$ decreases from 2 to 0 linearly during the course of iterations, which can not fully reflect the entire search process. Therefore, in this paper, nonlinear control parameter is proposed to improve convergence performance of WOA, and it is formulated as

$$\begin{aligned} \overrightarrow{a}=1+ \cos \left( \pi \times \frac{t}{MN}\right) \end{aligned}$$

(30)

Figure 3 shows the changing trend of $\overrightarrow{a}$ with the increase of the iteration number. It can be seen that nonlinear control parameter $\overrightarrow{a}$ in the early stage is larger than original control parameter. It begins by the wide search range provided with high exploration ability. Moreover, nonlinear control parameter $\overrightarrow{a}$ in the later stage is smaller than original control parameter, which makes the search range getting smaller provided with high exploitation ability. In this way, IWOA may keep an effective balance between the exploration and exploitation ability.

From Eq. (15), it can be seen that in the later local exploitation stage WOA can stay near the optima and not find the optima well. Inspired by particle swarm optimization (PSO) [46], the dynamic weight is proposed to perform a fine search near the optima, and it is formulated as

$$\begin{aligned} S= \left( 1-\frac{t}{MN} \right) ^\mu \end{aligned}$$

(31)

where $\mu>$0, and $\mu$ is a constant coefficient used to adjust the decay extent of the dynamic weight. Correspondingly, mathematical expressions are updated below.

$$\begin{aligned}{} & {} \overrightarrow{U}(t+1)=S\cdot \overrightarrow{U}_\textrm{best}-\overrightarrow{A}\cdot \overrightarrow{D} \end{aligned}$$

(32)

$$\begin{aligned}{} & {} \overrightarrow{U}(t+1)=\overrightarrow{D'}\cdot e^{bl}\cdot \cos (2\pi l)+S\cdot \overrightarrow{U}_\textrm{best} \end{aligned}$$

(33)

From Eqs. (32) and (33), it can be seen that in the later stage the optima is more and more attractive to the whales. The dynamic weight is getting smaller and smaller so that the whales can find the optima more accurately, which can effectively improve optimization accuracy of WOA.

Fig. 3

The changing trend of control parameter

4.4 Selective ensemble

In this paper, selective ensemble based on binary version of IWOA is used for handling imbalanced dataset. All the base DWFELMs are expressed as binary strings by using a binary encoding form $(\alpha _1,\alpha _2,\ldots ,\alpha _i,\ldots ,\alpha _k)$, where k is the amount of base classifiers, $\alpha _i=1$ means the ith base classifier is selected, and $\alpha _i=0$ means the ith base classifier is discarded. Motivated by discrete PSO [47], binary IWOA is presented for selective ensemble of base classifier. In binary IWOA, the solution is transformed below.

$$\begin{aligned} \hbox {sigmoid}(u_{j,k})= & {} \frac{1}{1+exp(-u_{j,k})} \end{aligned}$$

(34)

$$\begin{aligned} u_{j,k}'= & {} \left\{ \begin{array}{ll} 1 &{}\quad \hbox {if} \ \hbox {rand}(0,1)< \hbox {sigmoid}(u_{j,k})\\ 0 &{} \quad \hbox {otherwise} \end{array}\right. \end{aligned}$$

(35)

where $u_{j,k}'$ is the discretization solution. Then the integration by majority voting is adopted for the selected base DWFELMs.

Furthermore, the fitness of selective ensemble is formulated as

$$\begin{aligned} \begin{aligned} \hbox {fitness}=\frac{1}{s}\sum \limits _{j=1}^s\aleph (\hat{z_j},z_j),\aleph (\hat{z_j},z_j)=\left\{ \begin{array}{ll} 1 &{}\quad \hbox {if} \ \hat{z_j}=z_j\\ 0 &{} \quad \hbox {if} \ \hat{z_j}\ne z_j \end{array}\right. \end{aligned}\nonumber \\ \end{aligned}$$

(36)

where $\hat{z_j}$ is the target predicted concerning the jth testing sample, $z_j$ is the target expected concerning the jth testing sample, and s is testing samples number. The ensemble performance is proportional to the fitness. The pseudo-code of IWOA is described in Fig. 4.

Fig. 4

The pseudo-code of IWOA

5 Experiments

5.1 Experimental datasets and experimental setting

To confirm the effectiveness of the proposed model, a number of comparative experiments are conducted on various gene expression data from GEMS repository [48]. The description of these datasets is listed in detail in Table 1.

The variation of these datasets attributes is quantitatively from 2000 to 12533, which are normalized into $\left[ 0,1\right]$. The variation of these datasets classes is quantitatively from 2 to 11. The imbalance ratio (IR) is defined as

$$\begin{aligned} \begin{aligned}&{\text {Multi-class}}:IR=\frac{\max (\#z_j)}{\min (\#z_j)}\\&\hbox {Binary}\,\hbox {class}:IR=\frac{\#\hbox {majority}}{\#\hbox {minority}} \end{aligned} \end{aligned}$$

(37)

All the datasets are randomly divided into training–testing set. Based on a series of experiments, the results of classification performance are evaluated by the average of individually repeated 10 runs.

Experimental comparison of various approaches are made for evaluating the performance of SEN-DWFELM. All the experiments are test by using MATLAB platform and windows 10 OS with 8 GB of RAM. For an impartial comparison purpose, population size, the maximum iteration number and searching ranges for hidden nodes L, penalty parameter C are set the same for all the approaches. Set 40 for population size and 100 for the maximum iteration. Among comparative approaches, a grid search of hidden nodes L on $\{100,110,\ldots ,990,1000\}$ and penalty parameter C on $\{2^{-18},2^{-16},\ldots ,2^{48},2^{50}\}$ is conducted, and $G(x)=\frac{1}{1+\hbox {exp}(-(a\cdot x+b))}$ is used as activation function.

Table 1 Description of these datasets

5.2 Measure metrics

Accuracy is the overall classification accuracy, which means the proportion of the correctly classified samples to all the samples. G-mean means the geometric mean of the proportion of the correct classification of all the classes. The higher G-mean is, the better classification performance of every class is. F-measure is commonly used for evaluating class imbalanced problems, and F-score is the average of F-measure in all the classes. Based on above analysis, these measure metrics are expressed as follows.

Table 2 Parameters setting

Table 3 Performance results (Mean±SD) of different approaches

$$\begin{aligned} \hbox {Accuracy}= & {} \frac{\sum _{j=1}^c \hbox {TP}_j}{\sum _{j=1}^c \hbox {TP}_j+ \hbox {FN}_j} \end{aligned}$$

(38)

$$\begin{aligned} \hbox {SP}_j= & {} \frac{\hbox {TP}_j}{\hbox {TP}_j+\hbox {FP}_j} \end{aligned}$$

(39)

$$\begin{aligned} \hbox {SR}_j= & {} \frac{\hbox {TP}_j}{\hbox {TP}_j+\hbox {FN}_j} \end{aligned}$$

(40)

$$\begin{aligned} G{\text {-mean}}= & {} \left( \prod \nolimits _{j=1}^c \hbox {SR}_j\right) ^\frac{1}{c} \end{aligned}$$

(41)

$$\begin{aligned} F{\text {-measure}}_j= & {} \frac{2SR_j\times \hbox {SP}_j}{\hbox {SR}_j+SP_j} \end{aligned}$$

(42)

$$\begin{aligned} F{\text {-score}}= & {} \frac{\sum _{j=1}^c F{\text {-measure}}_j}{c} \end{aligned}$$

(43)

where $\hbox {TP}_j$ is the number of the jth class samples correctly classified as the jth class samples, $\hbox {FN}_j$ is the number of the jth class samples wrongly classified as other class samples, $\hbox {FP}_j$ is the number of other class samples wrongly classified as the jth class samples, $\hbox {SP}_j$ is precision ratio of the jth class samples, and $SR_j$ is recall ratio of the jth class samples. Obviously, G-mean makes a more impartial comparison in that G-mean is 0 if classification accuracy of a certain class is 0 [49].

5.3 Comparison with variants of SEN-DWFELM

To evaluate classification performance of SEN-DWFELM, it is respectively compared with ELM, learning algorithm applying W1- weighted scheme (WELM1), learning algorithm applying W2-weighted scheme (WELM2) in this experiment. Meanwhile, SEN-DWFELM is also compared with its variants, namely learning algorithm applying W- weighted scheme (WELM) and DWFELM built to discuss the importance of different sections in SEN-DWFELM.

Fig. 5

F-measure of every class on all the datasets by using different approaches

Fig. 6

Comparison of performance results

Fig. 7

The best and average fitness obtained by WEN-DWFELM and SEN-DWFELM for run #1 on Leukemia1 dataset

The detailed results of parameters setting for comparative algorithms are shown in Table 2, then the best parameters with regard to C and L are specified for correspinding datasets. The detailed results of G-mean, F-score, Accuracy and training time for comparative algorithms are shown in Table 3, then the best results are indicated in bold. From Table 3, it can be observed that SEN-DWFELM obtains better G-mean and F-score compared with other approaches. On Leukemia2, Colon, SRBCT, DLBCL, Leukemia1 and 11_Tumors datasets, compared with ELM, G-mean is improved by about 8.67%, 8.52%, 4.54%, 7.55%, 7.97% and 8.49%, then F-score is improved by about 8.45%, 7.63%, 4.32%, 7.28%, 7.20% and 8.10%. The reason is because ELM ignores minority class samples due to the premise that the size of every class is relatively balanced. Compared with WELM1, WELM2 and WELM, G-mean obtained by SEN-DWFELM is improved by about 5.45%, 5.09% and 4.34% on average on all the datasets, then F-score obtained by SEN-DWFELM is improved by about 5.61%, 5.65% and 4.82% on average on all the datasets. The reason is because DWFELM is proposed by amending WELM in the study. In DWFELM, feature weighted fuzzy membership is presented to eliminate classification error from noise samples and improve generalization performance of ELM. Meanwhile, the weighted scheme is also presented to strengthen the impact of minority class samples on classification. Furthermore, DWFELM-based selective ensemble algorithm is proposed to improve classification performance and the stability of single DWFELM.

By observing Table 3, it can be found that SEN-DWFELM improves Accuracy remarkably on all the datasets. Accuracy is improved by about 6.70%, 5.25%, 5.24%, 4.28% and 3.31% on average compared with ELM, WELM1, WELM2, WELM and DWFELM. The standard deviation (SD) obtained by SEN-DWFELM is also much smaller than other comparative algorithms. It illustrates that SEN-DWFELM can maintain classification accuracy of majority class samples and improve classification accuracy of minority class samples. In short, generalization performance of SEN-DWFELM is superior to other competitors. Table 3 also shows training time obtained by measuring the average of 10 runs for different approach, which is used for evaluating the computation cost of comparative algorithms. From Table 3, it can be seen that SEN-DWFELM consumes more training time by learning multiple classifiers compared with other variants. It is acceptable because the proposed SEN-DWFELM is based on WELM with faster learning speed.

In order to analyze thoroughly the performance, F-measure of different approach for all the datasets is shown in Fig. 5, whose x-axis indicates the abbreviation for every class name to observe the results more distinctly. From the results, it can be observed that F-measure of BL class obtained by SEN-DWFELM on SRBCT dataset is worse than some other approaches. The reason is because F-measure of a certain class is on increase at the expense of a sharp decline in F-measures of other classes. From Fig. 5, it can be concluded that SEN-DWFELM can actually strengthen classification performance of minority class samples, and SEN-DWFELM is suitable for not only binary classification but also multi-class classification problems.

5.4 Comparison with other ensemble learning methods

SEN-DWFELM is also compared with other ensemble algorithms, namely V-ELM [13], DF-D-ELM, D-D-ELM [14], AdaBoost [11], Boosting [12] and WOA-based selective ensemble algorithm of DWFELM (WEN-DWFELM). Performance results in terms of G-mean, Accuracy, F-score and SD are shown in Fig. 6. From Fig. 6, it can be observed that performance results acquired by SEN-DWFELM outperforms other comparative ensemble algorithms. Based on the dissimilarity measure, classification performance of DF-D-ELM and D-D-ELM is superior to V-ELM, and then classification performance of above approaches is also comparatively low. Especially on Colon and 11_Tumors dataset affected by complex data distribution, G-mean is significantly in decline. The reason is because D-D-ELM, V-ELM, and DF-D-ELM are all based on ELM algorithm in no consideration of weighted schemes. Therefore, these algorithms neglect minority class samples and then lead to the decline of G-mean. In AdaBoost, the importance of samples is indicated by the weight distributed for every training sample. When samples are misclassified, the weights distributed for them are larger. On the contrary, the weights distributed for samples correctly classified are smaller. In Boosting, the weight distributed for every training sample from different class is updated apart in the light of classification performance of the former classifiers. Based on the weights distributed, classification performance of AdaBoost and Boosting is superior to D-D-ELM, V-ELM and DF-D-ELM. Compared to above comparative approaches, WEN-DWFELM performs better in terms of G-mean, Accuracy and F-score. It indicates the superiority of meta-heuristics algorithms based selective ensemble of classifiers. In all the circumstances, SEN-DWFELM obtains the best G-mean, Accuracy and F-score. The reason is because samples number of every class, feature weighted fuzzy membership and IWOA-based selective ensemble of classifiers are all taken into consideration for enhancing generalization performance of SEN-DWFELM. As shown in Fig. 6, dispersion degree of SEN-DWFELM in terms of G-mean, Accuracy and F-score is relatively lower, which illustrates the stability and robustness of the proposed model. From the analyses, it can be concluded that SEN-DWFELM is suitable for both imbalanced dataset and relatively balanced dataset.

To catch on the variation procedure of IWOA and WOA, Fig. 7 shows the evolution of the best and average fitness obtained by WEN-DWFELM and SEN-DWFELM for run #1 on Leukemia1 dataset. From this figure, it can be seen that the best fitness has no fluctuates during the evolution and the best fitness for SEN-DWFELM is larger than that for WEN-DWFELM. The average fitness has significant variation from iteration 1 to 100. The average fitness for SEN-DWFELM is close to the best fitness, and the average fitness for WEN-DWFELM is smaller than that for SEN-DWFELM. This phenomenon illustrates that the proposed IWOA can significantly improve the convergence rate and the quality of solution compared to WOA. The confusion matrix obtained by SEN-DWFELM on DLBCL dataset is shown in Fig. 8, where DLBCL denotes diffuse large B-cell lymphoma, and FL denotes follicular lymphoma. As observed from Fig. 8, SEN-DWFELM can classify 75 samples correctly in all 77 samples, where 1 DLBCL sample is misclassified as FL and 1 FL sample is misclassified as DLBCL. From the above results, it can be concluded that SEN-DWFELM can effectively improve diagnostic performance of tumor.

Fig. 8

The confusion matrix obtained by SEN-DWFELM on DLBCL dataset

To further compare the performance, the paired t-test as the statistical testing method is utilized to study the difference among these comparative algorithms. Generally, the threshold is set as 0.05, and that the p value is less than 0.05 means the two methods are remarkably different. Then the p value results based on classification accuracy are shown in Table 4. As shown in Table 4, SEN-DWFELM exists evident difference with other comparative algorithms. Meanwhile, it can be seen that SEN-DWFELM is effective in coping with gene expression data.

Table 4 Results of the paired t-test

6 Conclusions

Tumor classification is a complex task, which is closely related to the properties of multi-class imbalance, high noise and high-dimensional small samples of gene expression data. An effective SEN-DWFELM model is proposed for tumor classification using gene expression data in this paper. Feature weighted fuzzy membership is presented to eliminate classification error from noise samples, and then it reduces the dimensionality of sample by removing features with smaller weights to improve training efficiency. The weighted scheme is also designed to strengthen the relative impact of minority class samples and lessen the bias against performance from imbalanced dataset. Furthermore, meta-heuristic method based selective ensemble concept is developed for making classification performance more robust. The experiments are conducted on gene expression data of binary class and multi-class. Compared with its variants and conventional ensemble methods, experimental results prove that SEN-DWFELM significantly outperforms other competitors in terms of G-mean, Accuracy and F-score. In future, the proposed SEN-DWFELM model may help in practical medical diagnosis, and neural network in combination with machine learning techniques can be applied to achieve better classification performance.