Ensemble based fuzzy weighted extreme learning machine for gene expression classification

Abstract

Multi-class imbalance is one of the challenging problems in many real-world applications, from medical diagnosis to intrusion detection, etc. Existing methods for gene expression classification usually assume relatively balanced class distribution. However, the assumption is invalid for imbalanced data learning. This paper presents an effective method named EN-FWELM for class imbalance learning. First, based on a fast classifier extreme learning machine (ELM), fuzzy membership of sample is proposed in order to eliminate classification error coming from noise and outlier samples, and balance factor is introduced in combination with sample distribution and sample number associated with class to alleviate the bias against performance caused by imbalanced data. Furthermore, ensemble of ELMs is used for making classification performance more stable and accurate. A number of base ELMs are removed based on dissimilarity measure, and the remaining base ELMs are integrated by majority voting. Finally, experimental results on various gene expression classification and real-world classification demonstrate that the proposed EN-FWELM remarkably outperforms other approaches in the literature.

1 Introduction

Generally, the type of cancer being identified early on can improve the health of people. Because the same cancer resulting from many factors may have different symptoms, traditional diagnostic methods can fail to identify cancer exactly [1]. However, gene expression data based on the microarray technology can achieve more accurate results. Therefore, the relevant research based on gene expression classification attracted more and more attention [2,3,4].

Extreme learning machine (ELM) was proposed for the single-hidden layer feed-forward networks (SLFNs). It has good generalization performance and fast learning speed by generating randomly input weights and biases of hidden nodes instead of adjusting network parameters iteratively [5, 6]. With the advantages, ELM has been widely applied in various areas [7,8,9,10,11,12]. Inspired by the ensemble idea [13], the stability and classification performance of single ELM can be improved. For example, Bagging takes different bootstrap samples from training data to construct a parallel ensemble model. AdaBoost runs repeatedly a learning machine on different distribution of training data to construct a serial ensemble model [14]. Cao et al. [15] proposed V-ELM that performs ensemble of ELMs and makes the final decision by majority voting. Li et al. [16] proposed boosting weighted ELM. Weighted ELM is embedded into a modified AdaBoost framework, and the distribution weights can be used as training sample weights. Zhang et al. [17] presented ensemble learning strategy based on differential evolution (DE) that performs ensemble of WELMs with different activation functions and employs DE to optimize the weight of each base classifier. Xu et al. [18] proposed WELM-Ada based on fusion optimization of weighted ELM and AdaBoost. Lu et al. [19] proposed D-D-ELM and DF-D-ELM, which remove some base ELMs based on the dissimilarity and group the remaining ELMs by majority voting on gene expression data.

One is often confronted with multi-class imbalance problem on gene expression data, and this issue brings extreme challenge. On one hand, existing methods for gene expression classification usually ignore the influence of samples distribution on classification, which can incur classification error coming from noise and outlier samples and reduce generalization performance of ELM. Furthermore, existing methods usually assume relatively balanced class distribution and are more concerned with overall accuracy, which can ignore the minority class and tend to be biased against the majority class in dealing with imbalanced data [20, 21]. In other words, they may achieve higher misclassification accuracy of the minority class than that of the majority class.

There are two methods dealing with imbalanced data i.e. resampling technique and algorithmic technique [22]. Resampling technique includes oversampling which duplicates some minority class samples randomly or creates new samples in the neighborhood of minority class samples and undersampling which removes some majority class samples randomly to balance the size of each class [23, 24]. Moreover, resampling technique modifies samples distribution and can lose some useful information. However, algorithmic technique does not change sample distribution and is widely used to cope with imbalanced data [25].

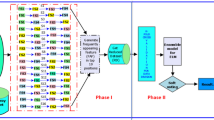
In this study, algorithmic technique is of particular interest, and ensemble based fuzzy weighted extreme learning machine is presented to perform gene expression classification. First, different fuzzy membership is assigned for each sample. Fuzzy membership indicates the importance of sample on classification, and the bigger fuzzy membership is, the greater the influence of sample on classification is. Therefore, noise and outlier samples are assigned low fuzzy membership to improve classification performance. In addition, balance factor is used to alleviate the bias against performance caused by imbalanced data. An extra balance factor, relevant to samples distribution and samples number of each class, is designed for each sample to strengthen the relative impact of the minority class, and G-mean is taken as evaluation measure to monitor classification ability. Furthermore, some base ELMs are removed based on the dissimilarity and the remaining ELMs are integrated by majority voting. Finally, experimental results illustrate that the proposed method named EN-FWELM is effective and robust.

The rest of this paper is organized as follows. Section 2 presents a brief review of relevant preliminary knowledge. In Section 3, the detailed implementations of the proposed method are explained. In Section 4, the experimental design is described and many experiments are completed to demonstrate that the proposed method presents better classification performance than that achieved by some existing methods. Finally, conclusions are summarized in Section 5.

2 Related work

2.1 Extreme learning machine (ELM)

Given a training dataset consisting of N arbitrary samples (x_j,t_j), where t_j = [t_j1,t_j2,⋯ ,t_jm]^T ∈ R^m and x_j = [x_j1,x_j2,⋯ ,x_jn]^T ∈ Rⁿ. The j th sample t_j is an m × 1 target vector, and x_j is an n × 1 feature vector. Given hidden nodes L << N and activation function g(x), then the standard mathematical model of SLFNs is as follows:

$$ \sum\limits_{i = 1}^{L}\beta_{i}g(a_{i}\cdot x_{j}+b_{i})=t_{j}\qquad j = 1,2,\cdots,N $$

(1)

where β_i = [β_i1,β_i2,⋯ ,β_im]^T is the output weight vector connecting the i th hidden node and output nodes, a_i = [a_i1,a_i2,⋯ ,a_in]^T is the input weight vector connecting input nodes and the i th hidden node, a_i ⋅ x_j is the inner product of a_i and x_j, and b_i is the bias of the i th hidden node.

SLFNs can approximate the training samples with zero error if the number of hidden nodes L is equal to the number of training samples N. The formula (1) can compactly be rewritten as (2).

$$ H\beta=T $$

(2)

$$H=\left[\begin{array}{l} h(x_{1})\\ {\vdots} \\h(x_{N}) \end{array}\right]= \left[\begin{array}{lll} g(a_{1}\cdot x_{1}+b_{1})&\cdots&g(a_{L}\cdot x_{1}+b_{L})\\ \vdots&\cdots&\vdots\\g(a_{1}\cdot x_{N}+b_{1})&\cdots&g(a_{L}\cdot x_{N}+b_{L}) \end{array}\right]_{N\times L} $$

$$ \beta=\left[\begin{array}{l} {\beta^{T}_{1}}\\ \vdots\\ {\beta^{T}_{L}} \end{array}\right]_{L\times m}, and \quad T=\left[\begin{array}{l} {t^{T}_{1}}\\ \vdots\\t^{T}_{N} \end{array}\right]_{N\times m} $$

(3)

where H is the hidden layer output matrix, and the j th column of H represents the j th hidden node output vector on all the inputs. T is the output matrix, and β is the output weight matrix.

However, in most cases, it is L << N and there may not exist a β that satisfies (2). The hidden layer biases and input weights need not be tuned at all and can be randomly generated, so the output weights can be determined by finding the Least Square solution β = H⁺T of Hβ = T, where H⁺ is the Moore-Penrose generalized inverse of matrix H. In short, ELM algorithm is summarized as follows.

• 1) Generate randomly input weights a_i and biases b_i, i = 1,2,⋯ ,L.

• 2) Calculate the hidden layer output matrix H.

• 3) Calculate the output weight β = H⁺T.

2.2 Weighted extreme learning machine (WELM)

According to Bartlett’s theory [26], ELM is not only to minimize the training error but also to minimize the norm of the output weights. Meanwhile, an extra weight is designed for each sample to better deal with imbalanced data, so the classification problem can be formulated as (4).

$$\begin{array}{@{}rcl@{}} min\left( \frac{1}{2}||\beta||^{2}+CW\frac{1}{2}\sum\limits_{j = 1}^{N}{\xi^{2}_{j}}\right)\\ s.t.\sum\limits_{j = 1}^{N}\beta_{i}g(a_{i}\cdot x_{j}+b_{i})=t_{j}-\xi_{j} \end{array} $$

(4)

The equivalent dual optimization problem in regard to (4) based on KKT theorem is

$$\begin{array}{@{}rcl@{}} L_{ELM}&=&\frac{1}{2}||\beta||^{2}+CW\frac{1}{2}\sum\limits_{j = 1}^{N}{\xi^{2}_{j}}\\ &&-\sum\limits_{j = 1}^{N}\alpha_{j}(\beta_{i}g(a_{i}\cdot x_{j}+b_{i})-t_{j}+\xi_{j}) \end{array} $$

(5)

where ξ_j is the training error, C is penalty parameter, and α_j is Lagrange multiplier. W is diagonal matrix relevant to each training sample, namely W = diag(w_jj),j = 1,2,⋯ ,N. For instance, weighted strategy associated with the number of samples in each class can be assigned as follows [20]:

$$\begin{array}{@{}rcl@{}} W1:w_{jj}&=&\frac{1}{N(t_{j})}\\ W2:w_{jj}&=&\left\{\begin{array}{cc} \frac{0.618}{N(t_{j})}\quad if\ N(t_{j})>AVG\\ \frac{1}{N(t_{j})}\quad if\ N(t_{j})\leq{AVG} \end{array}\right. \end{array} $$

(6)

where N(t_j) is the number of samples in class t_j, and AVG is the average samples number of each class. Then solution of (5) can be formulated as (7).

$$ \beta=\left\{\begin{array}{cc} H^{T}\left( \frac{I}{C}+WHH^{T}\right)^{-1}WT\quad when\ N < L\\ \left( \frac{I}{C}+H^{T}WH\right)^{-1}H^{T}WT\quad when\ N>> L \end{array}\right. $$

(7)

3 Proposed EN-FWELM model

In this study, construction of the optimal model comprises three main procedures: fuzzy weighted extreme learning machine (FWELM), ensemble learning based on the dissimilarity and performance evaluation.

3.1 FWELM

In this study, balance factor and fuzzy membership are introduced into ELM. WELM is a widely used method dealing with imbalance data. However, it only considers the imbalance of sample numbers in each class. In fact, not only does the imbalance of samples lies in the imbalance of the number of samples but also lies in the imbalance of sample distribution. Therefore, it is crucial that sample number and sample distribution are both considered as balance factors. In this study, sample density, as the important index to measure sample distribution, is used for representing sample distribution [21, 27]. Center of samples in each class can be formulated as (8).

$$ d_{k}=\frac{1}{N_{k}}\sum\limits_{j = 1}^{N_{k}}x_{j}\quad k = 1,\cdots,c $$

(8)

where c is the number of class, N_k is the number of samples in the k th class, x_j is the j th sample, and d_k is center of samples in the k th class. Accordingly, sample density in each class is defined as (9).

$$ p_{k}=\frac{\sum\limits_{j = 1}^{N_{k}}||x_{j}-d_{k}||}{N_{k}}\quad k = 1,\cdots,c $$

(9)

where p_k is sample density in the k th class. In addition, weighted strategy is also designed for each sample to better deal with imbalanced data, and it can be presented as (10).

$$ W:w_{jj}=\frac{N(c-t_{j}+ 1)}{N} $$

(10)

where N(c − t_j + 1) is the number of samples in class c − t_j + 1. The number of samples in class 1,⋯ ,c is ranked in the ascending order. Therefore, in this study, balance factor R is diagonal matrix relevant to each training sample and is defined as (11).

$$ R:r_{jj}=w_{jj}\times p_{c-t_{j}+ 1} $$

(11)

Weight W has more enormous influence than weight W 1 and weight W 2 on the classification performance. For example, for binary classification problem the reason is as follows.

$$\begin{array}{@{}rcl@{}} {\Delta} W&=&\left( \frac{N^{-}}{N}\right)-\left( \frac{N^{+}}{N}\right)=\frac{N^{-}-N^{+}}{N}\\ &=&\frac{N^{-}-N^{+}}{N^{-}+N^{+}}\\ 1)\ {\Delta} W1&=&\left( \frac{1}{N^{+}}\right)-\left( \frac{1}{N^{-}}\right)\\ &=&\frac{N^{-}-N^{+}}{N^{-}\times N^{+}} \end{array} $$

where N⁻,N⁺ stand for the number of negative and positive samples, respectively. Moreover, N⁻× N⁺ − (N⁻ + N⁺) = (N⁻− 1) × (N⁺ − 1) − 1. For N⁻ > 2, N⁺ > 2, so N⁻− 1 > 1 and N⁺ − 1 > 1, namely (N⁻− 1) × (N⁺ − 1) > 1. Therefore, ΔW > ΔW1 and weight W has better performance than weight W 1.

$$\begin{array}{@{}rcl@{}} 2)\ {\Delta} W2&=&\left( \frac{1}{N^{+}}\right)-\left( \frac{0.618}{N^{-}}\right)\\ &=&\frac{N^{-}-0.618\times N^{+}}{N^{-}\times N^{+}} \end{array} $$

for N⁻ > 2, N⁺ > 2, so (N⁻ + N⁺) − N⁻× N⁺ < (N⁻− N⁺) − (N⁻− 0.618 × N⁺), namely ΔW > ΔW2 and weight W has better performance than weight W 2.

On the other hand, fuzzy membership of sample is proposed in order to eliminate classification error coming from noise and outlier samples [21]. The radius from all samples to center in each class is defined as (12).

$$ rd_{k}=max||x_{j}-d_{k}||\quad j = 1,\cdots,N_{k} $$

(12)

where rd_k is the radius from samples to center in the k th class. Then fuzzy membership is defined as (13).

$$ S:s_{jj}= 1-\frac{||x_{j}-d_{k}||}{rd_{k}+\delta}\quad j = 1,2,\cdots,N_{k} $$

(13)

where S is diagonal matrix relevant to each training sample, and δ is an arbitrary small positive number. From (13), it can be seen that noise and outlier samples are usually far away from center of the class, and they will be given a minimum fuzzy membership to reduce the influence on classification. Therefore, in this study, the classification problem can be formulated as (14).

$$\begin{array}{@{}rcl@{}} &&L_{ELM}=\frac{1}{2}||\beta||^{2}+CR\frac{1}{2}\sum\limits_{j = 1}^{N}s_{jj}{\xi^{2}_{j}}\\ &&s.t.\quad h(x_{j})\beta=t_{j}-\xi_{j} \end{array} $$

(14)

Based on KKT theorem, KKT constraint conditions can be formulated as:

$$ \frac{\partial{L_{ELM}}}{\partial{\xi_{j}}}= 0\to\alpha_{j}=CRs_{jj}\xi_{j}\quad j = 1,2,\cdots,N $$

(15)

$$ \frac{\partial{L_{ELM}}}{\partial{\beta}}= 0\to\beta=\sum\limits_{j = 1}^{N}{\alpha_{j}h(x_{j})^{T}}=H^{T}\alpha $$

(16)

$$ \frac{\partial{L_{ELM}}}{\partial{\alpha_{j}}}= 0\to h(x_{j})\beta-t_{j}+\xi_{j}= 0 $$

(17)

By substituting (15) and (16) into (17), the output weight of FWELM can be formulated as (18).

$$ \beta=H^{T}\left( \frac{(S)^{-1}}{C}+RHH^{T}\right)^{-1}RT $$

(18)

If the number of training samples is large, the output weight of FWELM can be formulated as (19) by substituting (15) and (17) into (16).

$$ \beta=\left( \frac{I}{C}+H^{T}RSH\right)^{-1}H^{T}RST $$

(19)

3.2 Ensemble learning

In this study, ensemble learning [28] based on the dissimilarity is used for handling class imbalance, and the dissimilarity between the i th ELM and the j th ELM is defined as (20).

$$ df_{i,j}=\frac{P^{01}+P^{10}+P^{11}}{P^{01}+P^{10}+P^{11}+P^{00}} $$

(20)

where P^yz is the number of samples for which samples are separately classified as y by the i th ELM and classified as z by the j th ELM. 0 denotes samples are wrongly classified, while 1 denotes samples are correctly classified. Moreover, the dissimilarity between the i th ELM and other ELMs is defined as (21).

$$ D_{i}=\sum\limits_{j = 1}^{K}{df_{i,j}} $$

(21)

where K is the number of classifiers. Inspired by [19], ELMs with larger dissimilarity are selected based on D = {D₁,D₂,⋯ ,D_K}. The one-sided confidence interval of D is calculated to select ELMs whose D_i belong to the confidence interval, and the t distribution with no arguments is constructed to calculate the confidence interval.

The mean value of D is

$$ \overline{D}=\frac{1}{K}\sum\limits_{i = 1}^{K}{D_{i}} $$

(22)

The standard deviation of D is

$$ SD=\sqrt{\frac{1}{K-1}\sum\limits_{i = 1}^{K}{(D_{i}-\overline{D})}^{2}} $$

(23)

$$ \frac{\overline{D}-\mu}{SD/\sqrt{K}}\sim{t(K-1)} $$

(24)

The one-side confidence interval at 95% confidence level of μ is

$$ \left[\overline{D}-\frac{t_{0.05}(K-1)SD}{\sqrt{K}},\infty\right) $$

(25)

This study starts with selecting ELMs whose D_i belong to the one-sided confidence interval, and then integrates them by majority voting.

3.3 Measure metrics

In this study, Accuracy, G-mean and F-score are used for evaluating the performance of proposed EN-FWELM model. These measure metrics are defined below.

$$ Accuracy=\frac{{\sum}_{i = 1}^{c}TP_{i}}{{\sum}_{i = 1}^{c}TP_{i}+FN_{i}} $$

(26)

$$ Precision_{i}=\frac{TP_{i}}{TP_{i}+FP_{i}} $$

(27)

$$ Recall_{i}=\frac{TP_{i}}{TP_{i}+FN_{i}} $$

(28)

$$ F-measure_{i}=\frac{2Recall_{i}Precision_{i}}{Recall_{i}+Precision_{i}} $$

(29)

$$ F-score=\frac{{\sum}_{i = 1}^{c}F-measure_{i}}{c} $$

(30)

$$ G-mean=\left( {\prod}_{i = 1}^{c}Recall_{i}\right)^{\frac{1}{c}} $$

(31)

where TP, FP, TN, FN stand for the number of true positive, false positive, true negative and false negative, respectively.

Accuracy is the evaluation measure for correctly classified samples over all samples. F-measure is usually used to assess the performance of imbalanced data classification, and F-score is the average over F-measure. Obviously, G-mean is 0 when the classification accuracy for the i th class is 0 [17]. Therefore, G-mean is also used to evaluate classification performance of imbalanced data and makes a more fair comparison.

4 Experiments

4.1 Experiment datasets

To compare proposed EN-FWELM with other learning algorithms, a variety of datasets from GEMS and KEEL repository are used for classification [29, 30]. The detailed information about these datasets is listed in Table 1 and these datasets are ordered according to IR. The imbalance degree measured by the imbalance ratio (IR) is defined as

$$\begin{array}{@{}rcl@{}} &&Binary:IR=\frac{\#majority}{\#minority}\\ &&Multi-class:IR=\frac{max(\#i)}{min(\#i)}, i = 1,2,\cdots,c \end{array} $$

(32)

Table 1 Description of imbalanced datasets

The number of these datasets attributes varies from 5 to 12600. The number of these datasets classes varies from 2 to 11, and IR varies from 1.4 to 23.17.

4.2 Experimental setting

To evaluate the performance of the proposed approach, it is compared against variants of EN-FWELM and other ensemble learning methods [14,15,16,17,18,19]. The whole experiment is conducted on MATLAB platform, which runs on windows 8 OS with Intel(R) Core(TM) i5-4460 CPU (3.2 GHz) and 8 GB of RAM. The parameters setting is given as follows. A grid search of penalty parameter C on {2^− 18,2^− 16,⋯ ,2⁴⁸,2⁵⁰} and hidden nodes L on {10,20,⋯ ,990,1000} is used to find the optimal G-mean, and ${g}({x})=\frac {1}{1+exp(-(a\cdot x+b))}$ is applied as activation function.

The attributes of these datasets are normalized into [0,1]. Each dataset is randomly divided into a training-testing set. Then each experiment is individually repeated 10 times, and the average of 10 runs is used as the final results.

4.3 Comparison with variants of EN-FWELM

In these experiments, the classification performance of ELM, W1-based weighted learning algorithm (WELM1) and W2-based weighted learning algorithm (WELM2) [20] is evaluated, respectively. To show the effectiveness of EN-FWELM, it is also compared against its variants i.e. WELM and FWELM, which are built to analyze the importance of different parts in EN-FWELM. Meanwhile, the dimension of gene expression data is reduced by information gain (IG) [31] before training the classifier.

Tables 2, 3, 4, 5 and 6 show the detailed results of parameters setting, Accuracy, G-mean, F-score and training time, where the bold indicates the best results. From Tables 4 and 5, we can see that EN-FWELM achieves better G-mean and F-score than other algorithms. In particular, the performance results show that our EN-FWELM can improve significantly G-mean and F-score when datasets are sensitive to class imbalance, such as Lung_cancer, new-thyroid, 11_Tumors, ecoli-0-1-4-6_vs_5 and glass2. On these datasets, G-mean is respectively improved by about 18.43%, 14.18%, 8.46%, 8.39% and 24.32% compared with ELM, then F-score is respectively improved by about 11.53%, 8.24%, 8.23%, 7.83% and 19.35% compared with ELM. The reason is that ELM is based on the assumption that the size of each class is relatively balanced. Therefore, ELM has the bias against the majority class and ignores the minority class. From Tables 4 and 5, it can also be seen that G-mean and F-score of EN-FWELM outperforms WELM1, WELM2 and WELM. G-mean is respectively improved by about 3.01%, 2.67% and 2.53% on average compared with WELM1, WELM2 and WELM. F-score is respectively improved by about 4.43%, 4.65% and 3.43% on average compared with WELM1, WELM2 and WELM. The reason is that in this study FWELM is proposed by modifying WELM, in which balance factor and fuzzy membership are respectively presented. Balance factor is designed for each sample to strengthen the relative impact of the minority class, and fuzzy membership is designed for each sample to improve generalization performance of ELM. On the other hand, multiple FWELMs are trained and FWELMs with high dissimilarity are retained to improve the stability and classification performance of single FWELM. From the results, it can be concluded that it can be better to ensemble some base classifiers instead of all of base classifiers.

Table 2 Parameters setting

Table 3 Performance results (Mean ± SD) in terms of Accuracy(%)

Table 4 Performance results (Mean ± SD) in terms of G-mean(%)

Table 5 Performance results (Mean ± SD) in terms of F-score(%)

Table 6 Comparison (Mean ± SD) of training time(s)

To further analyze the results, F-measure of each class on all the datasets is shown in Fig. 1, and the abbreviation of each class name is shown in x-axis to visualize the results more clearly. F-score is the average result over F-measures of each class on a dataset. From Fig. 1, we can see that F-measure of hypo class on new-thyroid acquired by EN-FWELM is worse than that acquired by some other variants. The reason is that F-measures of some classes are improved at the cost of relatively slight decrease in F-measures of other classes. From Fig. 1, it can be concluded that EN-FWELM can improve the classification accuracy of the minority class on the multi-class imbalanced data.

Fig. 1

F-measure of each class on all the datasets by using different methods

Performance results in terms of Accuracy is shown in Table 3. We can see that EN-FWELM obtains more than 90% classification accuracy on most of the datasets, and improves significantly the classification accuracy. In particularly, on glass2 dataset, sensitive to class imbalance, Accuracy is improved by about 18.91%, 9.69% and 8.59% compared with ELM, WELM1 and WELM2, respectively. It illustrates that not only can EN-FWELM improve the classification accuracy of the minority class but also can maintain the classification accuracy of the majority class. Moreover, EN-FWELM is applicable to not only imbalanced data, but also relatively balanced data. The standard deviation (SD) acquired by EN-FWELM is also relatively much smaller than that acquired by other variants. From the results, it can be concluded that generalization performance of EN-FWELM outperforms other algorithms.

The computation cost of each method is evaluated by measuring training time. Training time averaged over 10 runs of each method is shown in Table 6. From Table 6, we can see that EN-FWELM learns multiple classifiers and consumes more training time than other variants, which is acceptable because the proposed EN-FWELM is based on ELM algorithm and ELM is fast in learning speed.

4.4 Comparison with other ensemble learning methods

To validate its effectiveness, EN-FWELM is also compared against other ensemble learning methods, including V-ELM [15], D-D-ELM, DF-D-ELM [19], AdaBoost, Boosting [16], DE-WELM [17] and WELM-Ada [18]. Performance results of above methods are shown in Fig. 2.

Fig. 2

Comparison of Performance results

From Fig. 2, it can be seen that the classification performance of EN-FWELM outperforms other ensemble learning algorithms. Among these ensemble learning algorithms, the classification performance of D-D-ELM and DF-D-ELM based on the dissimilarity measure is better than V-ELM, but the classification results of V-ELM, D-D-ELM and DF-D-ELM are also relatively low. In particular, G-mean is remarkably on the decrease on the datasets sensitive to class imbalance, such as new-thyroid and glass2. The reason is that they are based on ELM algorithm and are more applicable to balanced data. Therefore, these methods ignore the minority class and result in relatively decrease in G-mean. In AdaBoost, multiple classifiers are trained serially. The distribution weights of training samples reflect their relative importance and the samples that are often misclassified will obtain larger distribution weights than the correctly classified samples. In Boosting, the distribution weights of training samples are adjusted according to the performance of the previous classifiers and updated separately for samples coming from different classes. Based on the distribution weights, they perform better than V-ELM, D-D-ELM, and DF-D-ELM. But in some cases, their G-mean is improved at the cost of relatively slight decrease in Accuracy, for instance, Leukemia1 and ecoli-0-1-4-6_vs_5. In DE-WELM, ensemble of WELMs based on W 1 weighted strategy with different activation functions is constructed and DE is employed to optimize the weight of each WELM. In WELM-Ada, W 2 weighted strategy is used as initial weight, then the fusion optimization of weighted ELM and AdaBoost is constructed. Similarly, in some cases, their G-mean is also improved at the cost of relatively slight decrease in Accuracy, such as new-thyroid and glass2. However, in all the cases, EN-FWELM achieves the best Accuracy, G-mean, and F-score. The reason is that samples distribution, samples number of each class and the dissimilarity of classifiers are all taken into account to strengthen the classification performance of EN-FWELM. In addition, the results of Lung_cancer are not given, because SMCL class has only 6 samples and there is always no sample in training-testing set.

Based on the above analysis, the box plot is used to show G-mean results of different algorithms in Fig. 3. From the results, it can be seen that dispersion degree of EN-FWELM is relatively low, which indicates the robustness and stability of the proposed model. Furthermore, statistical testing is a meaningful way to study the difference between EN-FWELM and other algorithms. In this study, the paired t-test at a significance level of 0.05 is used to judge the difference based on the classification accuracy. It illustrates that the difference between two methods is significant if the p-value is less than 0.05. In fact, the p-value results are shown in Table 7. From Table 7, it can be seen that EN-FWELM exists significant difference with other algorithms.

Fig. 3

The box plot representation using different methods

Table 7 Results of the paired t-test

5 Conclusion

In this study, an effective method named EN-FWELM is proposed to handle multi-class imbalance problem. The core components of EN-FWELM are FWELM, ensemble learning based on the dissimilarity and performance evaluation. In FWELM, balance factor is devised in combination with sample distribution and sample number associated with class to alleviate the bias against performance caused by imbalanced data, and fuzzy membership of sample is proposed to eliminate classification error coming from noise and outlier samples. Ensemble of FWELMs is used for making classification results more stable and accurate. Then some base FWELMs are removed based on dissimilarity measure, and the remaining base FWELMs are integrated by majority voting. Experiments are conducted on gene expression classification and real-world classification, and the proposed EN-FWELM is compared against its variants and other ensemble learning methods, respectively. It is proven that EN-FWELM remarkably outperforms other approaches in the literature, and it is applicable to not only imbalanced data, but also relatively balanced data. The future work is that the proposed method is to be evaluated in other medical diagnosis areas.