Bifurcation and Quasiperiodic Behaviors of Ion Acoustic Waves in Magnetoplasmas with Nonthermal Electrons Featuring Tsallis Distribution

Abstract

Bifurcation and quasiperiodic behaviors of ion acoustic waves in electron-ion magnetoplasmas with nonthermal electrons featuring Cairns-Tsallis distribution have been investigated on the frameworks of non-perturbed and perturbed Kadomtsev-Petviashvili (KP) equations, respectively. Employing the reductive perturbation technique (RPT), we have derived the KP equation in electron-ion magnetoplasmas with nonthermal electrons featuring Cairns-Tsallis distribution. Bifurcations of ion acoustic traveling waves of the KP equation have been presented. Using the bifurcation theory of planar dynamical systems, the existence of solitary wave solutions and periodic traveling wave solutions has been established. Three analytical solutions of these waves have been derived depending on the system parameters. Considering an external periodic perturbation, we have presented the quasiperiodic behavior of ion acoustic waves in electron-ion magnetoplasmas.

1 Introduction

During the last few decades, the study of nonlinear wave dynamics, which is referred to as nonlinear science or chaos theory, is rapidly growing in many areas, and plasma physics has gained a wild support from the scientific research community. The investigations on nonlinear wave propagations in space plasma environments and laboratory plasmas in the form of solitons and double layers have been of remarkable interest because of their huge applications in different areas. It is important to note that the mathematical formalism of soliton dynamics was initiated by Korteweg-de Vries [1] (KdV) which has been followed by many profound advances in finding the salient features of the robust solitons. Washimi and Taniuti [2] derived the KdV equation in plasma dynamics for the first time using the reductive perturbation technique (RPT). During that period, Sagdeev [3] investigated the nonlinear propagation of waves in plasmas that helped to highlight many more interesting phenomena of plasma acoustic modes. These two methods become the main tool to obtain the formation of solitons of different types in laboratory plasmas as well as in space plasma environments. As a result, there is an uneven competition in bridging the gap between theory and experiments in laboratory [4, 5] and space plasma environments [6]. Recently, several investigations have been performed which helped to develop the subject of evolution of nonlinear solitary waves [7, 8], shock waves, as well as double layers [9, 10] in plasmas.

There are some astrophysical and space plasmas environments containing particles with distribution functions which are quasi-Maxwellian up to the mean thermal velocities and present non-Maxwellian tails when the particles gain high velocities and energies [11–13]. These types of plasmas are known as nonthermal plasmas, which are observed in Mercury, in the solar winds, Saturn, and in the magnetosphere of the Earth [13, 14].

The nonextensive nonthermal velocity distribution [15] function is given by:

$$f_{e}(v_{x})=C_{q,\alpha}\left(1+\alpha \frac{{v_{x}^{4}}}{v_{te}^{4}}\right)\left\{1-(q-1)\frac{{v_{x}^{2}}}{2v_{te}^{2}}\right\}^{\frac{1}{q-1}}, $$

where v _{t e} =(T _e /m _e )^1/2 is the electron thermal velocity, T _e is the electron temperature, m _e is its mass, and C _{q, α} is the constant of normalization which is given by the following expressions:

$$C_{q,\alpha} = n_{e0} \sqrt{\frac{m_{e}}{2\pi T_{e}}} \frac{\Gamma\left(\frac{1}{1-q}\right)\left(1-q\right)^{5/2}}{\Gamma\left(\frac{1}{1-q} -\frac{5}{2}\right)\left[3\alpha+\left(\frac{1}{1-q} -\frac{3}{2}\right)\left(\frac{1}{1-q} -\frac{5}{2}\right)\left(1-q\right)^{2}\right]} \text{for} -1<q<1, $$

and

$$C_{q,\alpha} = n_{e0} \sqrt{\frac{m_{e}}{2\pi T_{e}}} \frac{\Gamma\left(\frac{1}{q-1}+\frac{3}{2}\right)(q-1)^{5/2}\left(\frac{1}{q-1}+\frac{3}{2}\right)\left(\frac{1}{q-1}+\frac{5}{2}\right)}{\Gamma\left(\frac{1}{q-1}+1\right)\left[3\alpha+\left(\frac{1}{q-1} +\frac{3}{2}\right)\left(\frac{1}{q-1}+\frac{5}{2}\right)(q-1)^{2}\right]} \text{for} q>1. $$

Here, α is a parameter determining the number of nonthermal electrons present in the model, q stands for the strength of nonextensivity, and Γ is the standard Gamma function. For q > 1, the distribution function exhibits a thermal cutoff on the maximum value allowed for the velocity of the electrons, given by

$$v_{\text{max}}=\sqrt{\frac{2T_{e}}{m_{e}(q-1)}}, $$

beyond which no probable states exist.

Integrating the nonthermal velocity distributed function f _e (v _x ) over all velocity space, one can obtain the electron density [15] as:

$$n_{e}=n_{e0}\left(1+M\left(\frac{e\phi}{T_{e}}\right)+N\left(\frac{e\phi}{T_{e}}\right)^{2}\right)\left\{1+(q-1)\left(\frac{e\phi}{T_{e}}\right)\right\}^{\frac{1}{q-1}+\frac{1}{2}}, $$

where $M=-\frac {16\alpha q}{(5q-3)(3q-1)+12\alpha }$ and $N=\frac {16\alpha q(2q-1)}{(5q-3)(3q-1)+12\alpha }$.

In the limiting case, when q→1, the above electron density reduces to the nonthermal electron density of Cairns et al. [16] as

$$n_{e}=n_{e0}\bigg(1-\frac{4\alpha}{1+3\alpha}\left(\frac{e\phi}{T_{e}}\right)+\frac{4\alpha}{1+3\alpha}\left(\frac{e\phi}{T_{e}}\right)^{2}\bigg)\times \text{exp}\left(\frac{e\phi}{T_{e}}\right), $$

and in the case, when α = 0, the electron density reduces to the nonextensive electron density [17] as

$$n_{e}=n_{e0}\left\{1+(q-1)\left(\frac{e\phi}{T_{e}}\right)\right\}^{\frac{1}{q-1}+\frac{1}{2}}. $$

There are some standard nonlinear evolution equations, for example, Sine-Gordon, KdV and nonlinear Schrodinger equations, which describe many physical phenomena, and these evolution equations are Hamiltonian integrable [18, 19]. It is well known that the integrability could be destroyed due to the effect of external periodic perturbations occurring in some real physical environments [20–22]. The type of this external periodic perturbation may be different depending on different physical situations. A significant attention is recently paid to the study of nonlinear evolution equations in the presence of external periodic perturbations since a completely integrable nonlinear wave equation can not describe quasi-periodic or chaotic behaviors. But the presence of an external periodic perturbation to a nonlinear integrable wave equation may lead to quasi-periodic or chaotic dynamics. In 2012, Saha [25] investigated the generalized Kadomtsev-Petviashvili modified equal width equation (KP-MEW) employing the bifurcation theory of planar dynamical systems and obtained some analytical traveling wave solutions such as solitary wave solutions, periodic wave solutions, and compactons. Using bifurcation theory of planar dynamical systems, some works [26–34] have been reported on bifurcations of nonlinear traveling waves in unmagnetized and magnetized plasmas through perturbative and non-perturbative approaches. Recently, Sahu et al. [35] studied the quasiperiodic behavior in quantum plasmas due to the presence of Bohm potential. Very recently, Zhen et al. [36] studied dynamic behavior of the quantum Zakharov-Kuznetsov equation (ZK) in dense quantum magnetoplasma, and Saha et al. [37] studied dynamic behavior of ion acoustic waves in e-p-i magnetoplasmas with kappa distributed electrons and positrons. Zhen et al. [38] also studied soliton solution and chaotic motion of the extended ZK equations in a magnetized dusty plasma with Maxwellian hot and cold ions. But there is no attempt to the study of quasiperiodic behavior of nonlinear traveling waves in electron-ion plasmas on the frameworks of KdV, KP, and ZK equations considering external periodic perturbation, to the best of our knowledge. Also, there is no work in literature to study the quasi-periodic and chaotic behaviors of nonlinear waves in plasmas with nonthermal electrons featuring Tsallis distribution. The works on quasiperiodic and chaotic behaviors [37, 38] which have been reported are only related to kappa-distributed electrons and positrons and Maxwellian hot and cold ions but not with nonthermal particles featuring Tsallis distribution. It is important to note that q-nonextensive distribution and Maxwellian distribution are special cases of Tsallis distribution.

So, in this work, our aim is to investigate the bifurcation behavior of ion acoustic traveling waves in electron-ion magnetoplasmas with nonthermal electrons featuring Cairns-Tsallis distribution on the framework of KP equation using bifurcation theory of planar dynamical systems. We obtain solitary and periodic wave solution of the KP equation. Considering an external periodic perturbation, we study the quasiperiodic behavior of the perturbed KP equation in the mentioned plasmas.

The remaining part of the paper is organized as follows: In Section 2, we consider model equations. We derive the KP equation in Section 3. In Section 4, we obtain traveling wave system of this KP equation. Bifurcations of phase portraits are obtained in Section 5. Some exact traveling wave solutions of the KP equation are derived in Section 6. We discuss the quasiperiodic behavior of the perturbed system in Section 7, and Section 8 is kept for conclusions.

2 Model Equations

We consider a plasma model whose constituents are cold ions and nonthermal electrons featuring Cairns-Tsallis distribution in the presence of an external static magnetic field $M_{0}=\hat {x}M_{0}$ acting along the x-axis, where $\hat {x}$ is the unit vector along the x-axis. The normalized continuity, momentum, and Poisson’s equations are given by:

$$\begin{array}{@{}rcl@{}} \frac{\partial n}{\partial t}+\nabla.(n\tilde{U}) &=& 0, \end{array} $$

(1)

$$\begin{array}{@{}rcl@{}} \frac{\partial \tilde{U}}{\partial t}+(\tilde{U}.\nabla)\tilde{U} &=&-\nabla \phi+\tilde{U}\times\hat{x}, \end{array} $$

(2)

$$\begin{array}{@{}rcl@{}} \nabla^{2} \phi &=& \alpha_{1}(n_{e}-n). \end{array} $$

(3)

The normalized electron density [15] is given by

$$n_{e}=\left(1+M\phi+N\phi^{2}\right)\{1+(q-1)\phi\}^{\frac{1}{q-1}+\frac{1}{2}}, $$

where $M=-\frac {16\alpha q}{(5q-3)(3q-1)+12\alpha }$ and $N=\frac {16\alpha q(2q-1)}{(5q-3)(3q-1)+12\alpha }$.

Here, $\alpha _{1}=\frac {r^{2}}{\lambda ^{2}}$, $r=\frac {C_{s}}{\Omega }$ is the ion gyroradius, $\lambda =\sqrt {T_{e}/4\pi e^{2} n_{0}}$ is the electron Debye length, $C_{s}=(T_{e}/m)^{1/2}$ C _s =(T _e /m)^1/2 is the ion acoustic velocity, and ${\Omega }=\frac {eM_{0}}{m c}$ is the ion gyrofrequency, where c is the speed of the light and m is the mass of ions. ϕ is the electrostatic potential. n and $\tilde {U}$ denote number density and velocity of ions, respectively. We assume that the wave is propagating in the xy-plane. Here, n _e0, and n ₀ are, respectively, unperturbed number densities of electrons, and ions. The ion velocity $\tilde {U}=(u,v,w)$ is normalized to ion acoustic speed $C_{s}=\sqrt {\frac {T_{e}}{m}}$, and electrostatic potential ϕ is normalized to T _e /e, where e denotes the electron’s charge. Space variables and time are normalized to the ion gyroradius r and inverse of the ion gyrofrequency Ω, respectively.

Equations (1)–(3) can be written in components form:

$$\begin{array}{@{}rcl@{}} \frac{\partial n}{\partial t}+\frac{\partial (nu)}{\partial x}+\frac{\partial (nv)} {\partial y}&=& 0, \end{array} $$

(4)

$$\begin{array}{@{}rcl@{}} \frac{\partial u}{\partial t}+\left(u\frac{\partial}{\partial x}+v\frac{\partial} {\partial y}\right)u&=&-\frac{\partial \phi}{\partial x}, \end{array} $$

(5)

$$\begin{array}{@{}rcl@{}} \frac{\partial v}{\partial t}+\left(u\frac{\partial}{\partial x}+v\frac{\partial} {\partial y}\right)v&=& -\frac{\partial \phi}{\partial y}+w, \end{array} $$

(6)

$$\begin{array}{@{}rcl@{}} \frac{\partial w}{\partial t}+\left(u\frac{\partial}{\partial x}+v\frac{\partial} {\partial y}\right)w&=& -v, \end{array} $$

(7)

$$\begin{array}{@{}rcl@{}} \left(\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}\right)\phi =\alpha_{1}\left[\left(1+M\phi+N\phi^{2}\right)\{1+(q-1)\}^{\frac{1}{q-1}+\frac{1}{2}}-n\right]. \end{array} $$

(8)

3 KP Equation

We employ the reductive perturbation technique (RPT) to derive the KP equation. According to the RPT, the independent variables are stretched as:

$$\begin{array}{@{}rcl@{}} Y &=& \epsilon^{2} y, \end{array} $$

(9)

$$\begin{array}{@{}rcl@{}} \eta &=& \epsilon(x-Vt), \end{array} $$

(10)

$$\begin{array}{@{}rcl@{}} \tau &=& \epsilon^{3} t, \end{array} $$

(11)

where V denotes the phase velocity of ion acoustic wave along the x-axis in electron-ion magnetoplasmas with nonthermal electrons featuring Cairns-Tsallis distribution, and 𝜖 is a small parameter which characterizes the strength of the nonlinearity. The dependent variables in the above relations are expanded as:

$$\begin{array}{@{}rcl@{}} n &=& 1+\epsilon^{2} n_{1}+\epsilon^{4} n_{2}+\ldots \end{array} $$

(12)

$$\begin{array}{@{}rcl@{}} u &=& \epsilon^{2} u_{1}+\epsilon^{4} u_{2}+\ldots \end{array} $$

(13)

$$\begin{array}{@{}rcl@{}} v &=& \epsilon^{3} v_{1}+\epsilon^{5} v_{2}+\ldots \end{array} $$

(14)

$$\begin{array}{@{}rcl@{}} w &=& \epsilon^{3} w_{1}+\epsilon^{5} w_{2}+\ldots \end{array} $$

(15)

$$\begin{array}{@{}rcl@{}} \phi &=& \epsilon^{2}\phi_{1}+\epsilon^{4}\phi_{2}+\ldots \end{array} $$

(16)

Substituting equations (9)–(16) into the system of (4)–(8) and equating the coefficient of lowest order of 𝜖, one can obtain the dispersion relation as

$$\begin{array}{@{}rcl@{}} V^{2}&=&\frac{1}{(a+M)}, \end{array} $$

(17)

where $a=\frac {q+1}{2}$.

Considering the coefficient of next order of 𝜖, we obtain the KP equation as

$$\begin{array}{@{}rcl@{}} \frac{\partial}{\partial \eta} \left[\frac{\partial \phi_{1}}{\partial \tau}+A \phi_{1}\frac{\partial \phi_{1}} {\partial \eta}+B \frac{\partial^{3} \phi_{1}}{\partial \eta^{3}}\right] +C\frac{\partial^{2} \phi_{1}}{\partial Y^{2}} &=& 0, \end{array} $$

(18)

where $A=\frac {V}{2P}[3P^{2}-2Q],\quad B=\frac {V} {2P\alpha _{1}},\quad C=\frac {V}{2},$with P = a+M, $b=\frac {(q+1)(3-q)}{8}$ and Q = b+N+a M.

4 Traveling Wave System

To investigate all traveling wave solutions of (18), we transform the KP (18) to the traveling wave system. We introduce a new variable χ as:

$$\begin{array}{@{}rcl@{}} \chi = \beta(l\eta+mY-U\tau ), \end{array} $$

(19)

where l and m are the direction cosines of the angles made by the wave propagation with x-axis and y-axis, respectively. Here, U is the speed of the traveling wave and β is a constant. Substituting ψ(χ)=ϕ ₁(η, Y, τ) into (18) and then integrating twice, the KP (18) takes the form

$$\begin{array}{@{}rcl@{}} B\beta^{2}l^{4} \frac{d^{2}\psi}{d \chi^{2}} + (Cm^{2} - lU)\psi + \frac{Al^{2}}{2}\psi^{2} = 0. \end{array} $$

(20)

Then (20) can be written as the following dynamical system:

$$ \left\{ \begin{array}{ll} \frac{d\psi}{d \chi}=z, \\ \frac{dz}{d \chi}=\frac{\left(lU-Cm^{2}-\frac{Al^{2}}{2}\psi\right)\psi}{B\beta^{2}l^{4}}. \end{array} \right. $$

(21)

Equation (21) represents a planar Hamiltonian system with the following Hamiltonian function:

$$ H(\psi,z)=\frac{z^{2}}{2}-\frac{1}{6 B\beta^{2}l^{4}}\left(3(lU-Cm^{2})-Al^{2}\psi\right)\psi^{2}=h,\text{say}. $$

(22)

The system (21) is a planar dynamical system with parameters α, β, α ₁,q, l, m, and U. It is interesting to note that the phase orbits defined by the vector fields of (21) determine all traveling wave solutions of (18). So, we investigate the bifurcations of phase portraits of (21) in the (ψ, z) phase plane as the parameters α, β, α ₁,q, l, m, and U are changed. In this case, we consider a physical system for which only bounded traveling wave solutions are meaningful. So, we need to pay our attention to the bounded traveling wave solutions of (18). It is known that a solitary wave solution of (18) corresponds to a homoclinic orbit of (21). A periodic orbit of (21) corresponds to a periodic traveling wave solution of (18). The bifurcation theory of planar dynamical systems ([23, 24]) plays an important role in this study.

5 Bifurcations of Phase Portraits

In this section, we investigate the bifurcations of phase portraits of (21). When A B β l ≠ 0 and l U ≠ C(1−l ²), then there are two equilibrium points at E ₀(ψ ₀, 0) and E ₁(ψ ₁, 0), where ψ ₀=0 and $\psi _{1}=\frac {2(lU-C(1-l^{2}))}{Al^{2}}$. Let M(ψ _i , 0) be the coefficient matrix of the linearized system of (21) at an equilibrium point E _i (ψ _i , 0). Then we have

$$ J=detM(\psi_{i},0)=\frac{\left(C\left(1-l^{2}\right)-lU\right)}{B\beta^{2}l^{4}}+\frac{A}{B\beta^{2}l^{2}}\psi_{i}. $$

(23)

By the theory of planar dynamical systems ([23, 24]), we know that the equilibrium point E _i (ψ _i , 0) of the planar dynamical system (21) is a saddle point when J < 0 and the equilibrium point E _i (ψ _i , 0) of the planar dynamical system (21) is a center when J > 0.

We consider 0<l < 1 and β ≠ 0. Then we have the following cases:

Case 1

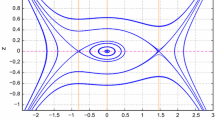
When 2l U < V(1−l ²),3P ²>2Q,−1<q < 0,α > 0, and α ₁>0, then the system (21) has two equilibrium points at E ₀(ψ ₀, 0) and E ₁(ψ ₁, 0), where ψ ₀=0 and ψ ₁>0. Here, E ₀(ψ ₀, 0) is a center and E ₁(ψ ₁, 0) is a saddle point. There is a homoclinic orbit to E ₁(ψ ₁, 0) enclosing the center at E ₀(ψ ₀, 0) (see Fig. 1).

Fig. 1

Phase portrait of (21) for l = 0.5,α = 0.3,α ₁=0.2,β = 3,q = −0.6, and U = 2

Case 2

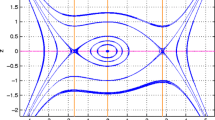
When 2l U > V(1−l ²),3P ²<2Q,0<q < 1,α > 0, and α ₁>0, then the system (21) has two equilibrium points at E ₀(ψ ₀, 0) and E ₁(ψ ₁, 0), where ψ ₀=0 and ψ ₁>0. Here, E ₀(ψ ₀, 0) is a saddle point and E ₁(ψ ₁, 0) is a center. There is a homoclinic orbit to E ₀(ψ ₀, 0) enclosing the center at E ₁(ψ ₁, 0) (see Fig. 2).

Fig. 2

Phase portrait of (21) for l = 0.1,α = 0.3,α ₁=0.2,β = 3,q = 0.8, and U = 2.

Case 3

When 2l U < V(1−l ²),3P ²>2Q, q > 1,α > 0, and α ₁>0, then the system (21) has two equilibrium points at E ₀(ψ ₀, 0) and E ₁(ψ ₁, 0), where ψ ₀=0 and ψ ₁<0. Here, E ₀(ψ ₀, 0) is a center and E ₁(ψ ₁, 0) is a saddle point. There is a homoclinic orbit to E ₁(ψ ₁, 0) enclosing the center at E ₀(ψ ₀, 0) (see Fig. 3).

Fig. 3

Phase portrait of (21) for l = 0.1,α = 0.3,α ₁=0.2,β = 3,q = 1.6, and U = 2

Using the above analysis, we have shown different phase portraits of (21) in Figs. 1, 2, and 3 depending on some special values of the parameters.

6 Analytical Solutions

In this section, using the planar dynamical system (21) and the Hamiltonian function (22) with h = 0, we derive the solitary wave solution and periodic traveling wave solution of (18) depending on the system parameters.

(1) When 2l U < V(1−l ²),3P ²>2Q,−1<q < 0,α > 0, and α ₁>0, (see Figs. 1 and 4), the KP (18) has the solitary wave solution:

$$ \phi_{1}=\frac{3(lU-C(1-l^{2}))}{Al^{2}}\mathrm{sech}^{2}\left(\frac{1}{2\beta l^{2}}\sqrt{\frac{lU-C(1-l^{2})}{B}} \chi\right). $$

(24)

(2)When 2l U > V(1−l ²),3P ²<2Q,0<q < 1,α > 0, and α ₁>0, (see Figs. 2 and 5), the KP (18) has the periodic traveling wave solution:

$$ \phi_{1}=\frac{3(lU-C(1-l^{2}))}{Al^{2}}\mathrm{sec}^{2}\left(\frac{1}{2\beta l^{2}}\sqrt{-\frac{[lU-C(1-l^{2})]}{B}} \chi\right). $$

(25)

(3) When 2l U < V(1−l ²),3P ²>2Q, q > 1,α > 0, and α ₁>0, (see Figs. 3 and 6), the KP (18) has the periodic traveling wave solution:

$$ \phi_{1}=\frac{3(lU-C(1-l^{2}))}{Al^{2}}\mathrm{cosec}^{2}\left(\frac{1}{2\beta l^{2}}\sqrt{-\frac{[lU-C(1-l^{2})]}{B}} \chi\right). $$

(26)

Using numerical simulations, we obtain some graphs of these solitary wave solution and periodic traveling wave solutions of (18) depending on some special values of the system parameters, shown in Figs. 4, 5, and 6.

Fig. 4

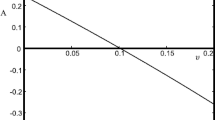
Variation of the solitary wave profiles of (18) for different values of q with α = 0.3,α ₁=0.2,l = 0.5,β = 3, and U = 2

Fig. 5

Variation of the periodic wave profiles of (18) for different values of q with α = 0.3,α ₁=0.2,l = 0.1,β = 3, and U = 2

Fig. 6

Variation of the periodic wave profiles of (18) for different values of q with α = 0.3,α ₁=0.2,l = 0.1,β = 3, and U = 2

In Fig. 3, we have presented the variation of the solitary wave profiles for different values of q(−0.5(black dashed curve),−0.6(blue solid curve),−0.7(red dotted curve)) with fixed values of the other parameters. It is important to note that when q increases, the amplitude of the solitary wave increases and the width of the solitary wave decreases and it becomes more spiky.

In Fig. 4, we have presented the variation of periodic wave profiles for different values of q(0.8(black dashed curve),0.84(blue solid curve),0.88(reddotted curve)) with fixed values of the other parameters. It is clear that when q increases, the amplitude and width of the periodic wave decrease.

In Fig. 5, we have presented the variation of periodic wave profiles for different values of q(1.4(black dashed curve),1.6(blue solid curve), 1.8(red dottedcurve)) with fixed values of the other parameters. It is clear that when q increases, the amplitude and width of the periodic wave increase.

7 Quasiperiodic Behavior

In this section, we present the quasiperiodic behavior of the perturbed system given by:

$$ \left\{ \begin{array}{ll} \frac{d\psi}{d \chi}=z, \\ \frac{dz}{d \chi}=\frac{\left(lU-Cm^{2}-\frac{Al^{2}}{2}\psi\right)\psi}{B\beta^{2}l^{4}}+f_{0} \mathrm{cos}(\omega \chi), \end{array} \right. $$

(27)

where f ₀ cos(ω χ) is the external periodic perturbation, f ₀ is the strength of the periodic perturbation and ω is the frequency. It is to be noted that the difference between the system (21) and the system (27) is that only external periodic perturbation is added with the system (27).

In Fig. 7(a)-7(b), we have presented the phase portraits of the perturbed system (27) for different values of q(−0.5, −0.7) with fixed values of the other parameters l = 0.1,α = 0.3,α ₁=0.2,β = 3,f ₀=1.2,ω = 1.3, and U = 2. When q is decreasing with −1<q < 0, a quasi periodic motion of the system (27) is found with incommensurable periodic motions and the trajectory in the phase space winds around a torus filling its surface densely.

Fig. 7

Phase portrait of the perturbed system (27) for l = 0.1,U = 2,β = 3,α ₁=0.2,α = 0.3,f ₀=1.2, ω = 1.3, (a) q = −0.5, and (b) q = −0.7

In Fig. 8(a)-8(b), we have shown the phase portraits of the perturbed system (27) for different values of q(0.7, 0.9) with fixed values of the other parameters l = 0.1,α = 0.3,α ₁=0.2,β = 3,f ₀=0.2,ω = 1.3, and U = 2. When q is increasing with 0<q < 1, a quasi periodic motion of the system (27) is found with incommensurable periodic motions and the trajectory in the phase space winds around a torus filling its surface sparsely. Hence, the parameter q affects significantly on the quasiperiodic behavior of the perturbed system (27).

Fig. 8

Phase portrait of the perturbed system (27) for l = 0.1,U = 2,β = 3,α ₁=0.2,α = 0.3,f ₀=0.2, ω = 1.3, (a) q = 0.7, and (b) q = 0.9

In Fig. 9a, b, we have presented the phase portraits of the perturbed system (27) for different values of q(1.4, 1.8) with fixed values of the other parameters l = 0.1,α = 0.3,α ₁=0.2,β = 3,f ₀=1.2,ω = 1.3, and U = 2. When q is increasing with q > 1, a quasi periodic motion of the system (27) is found with incommensurable periodic motions and the trajectory in the phase space winds around a torus filling its surface densely.

Fig. 9

Phase portrait of the perturbed system (27) for l = 0.1,U = 2,β = 3,α ₁=0.2,α = 0.3,f ₀=1.2, ω = 1.3, (a) q = 1.4, and (b) q = 1.8

In Fig. 10(a)-10(b), we have plotted z vs. χ for the perturbed system (27) for different values of q(−0.5, −0.7) with fixed values of the other parameters same as Fig. 7. In Fig. 11(a)-11(b), we have plotted z vs. χ for the perturbed system (27) for different values of q(0.7, 0.9) with fixed values of the other parameters same as Fig. 8. In Fig 12(a)-12(b), we have plotted z vs. χ for the perturbed system (27) for different values of q(1.4, 1.8) with fixed values of the other parameters same as Fig. 7. It is easily seen that stable oscillatory behavior is possible in the system (27) for different values of q. The presence of slow and fast frequency components is visible in the time evolution of the state variable.

Fig. 10

Plot of z vs. χ for l = 0.1,U = 2,β = 3,α ₁=0.2,α = 0.3,f ₀=1.2, ω = 1.3, (a) q = −0.5, and (b) q = −0.7

Fig. 11

Plot of z vs. χ for l = 0.1,U = 2,β = 3,α ₁=0.2,α = 0.3,f ₀=0.2, ω = 1.3, (a) q = 0.7, and (b) q = 0.9

Fig. 12

Plot of z vs. χ for l = 0.1,U = 2,β = 3,α ₁=0.2,α = 0.3,f ₀=1.2, ω = 1.3, (a) q = −1.4, and (b) q = −1.8

8 Conclusions

In this work, we have obtained the KP equation for ion acoustic waves in magnetoplasmas with nonthermal electrons featuring Cairns-Tsallis distribution. Applying the bifurcation theory of planar dynamical systems to the KP equation, we have presented the existence of solitary and periodic traveling waves. Three exact solutions of the solitary and periodic waves are obtained depending on the parameters α, β, α ₁,q, l, m, and U. Considering an external periodic perturbation, the quasi-periodic behavior of the ion acoustic waves is studied with the help of numerical simulations. The presence of the parameters q, α, α ₁, and β affects significantly the bifurcations of traveling wave solutions of the KP equation and the quasi-periodic behavior of the perturbed KP equation. Our study may be helpful to understand the salient features of bifurcation and quasi-periodic behaviors of nonlinear traveling waves observed in Mercury, Saturn, and in the magnetospheres of the Earth [13, 14] where nonthermal electrons featuring Cairns-Tsallis distribution are present.