1 Introduction

Multicomponent plasmas, which contain both negative and positive ion species as well as electrons, have a great significance to various fields of plasma science and technology. In astrophysical environments, the presence of heavy negative ions in the upper region of Titan atmosphere has been confirmed by Cassini spacecraft (Coates et al. 2007). These particles may act as organic building blocks for even more complicated molecules. Moreover, the existence of a considerable number of negative ions in the Earth’s ionosphere (Massey 1976) and cometary comae (Chaizy et al. 1991) is observed. In addition, positive-negative ion plasmas are found in neutral beam sources (Bacal and Hamilton 1979), plasma processing reactors (Gottscho and Gaebe 1986), and in low-temperature laboratory plasma experiments (Jacquinot et al. 1977; Ichiki et al. 2002). Therefore, the importance of positive-negative ion to the field of plasma physics is growing day by day.

Actually, most research work of ion acoustic (IA) waves are based on electrons and ions with Maxwell-Boltzmann distributions. Nevertheless, numerous observations in space and astrophysical plasma environments, viz., the ionosphere, auroral zones, mesosphere, lower thermosphere, etc. are not often of Boltzmann distribution feature. They really have distributions with more complicated shapes exhibiting long tails which strongly deviate from the simple Maxwellians. Also, non-Maxwellian particles can precisely model various astrophysical plasmas, such as solar wind, magnetosphere, interstellar medium, and auroral zone plasma (Lundin et al. 1987; Sahu 2010; Cairns et al. 1995; Gill et al. 2007). In fact, there are many regions in space and laboratory plasmas in which high energetic particles (thermal and supper thermal) are present. The superthermal particles may arise from the effect of external force acting on the natural space environment plasmas or to wave-particle interactions. Hence, kappa distribution (the generalized Lorentzian distribution) has been found to be more appropriate rather than the other distributions (Saha and Chatterjee 2014d; Samanta et al. 2013a, 2013c). It has been utilized to analyze and interpret spacecraft data on the Earth’s magnetospheric plasma sheet, Jupiter (Leubner 1982) and Saturn (Armstrong et al. 1983) and it is found that many space plasmas can be modeled more effectively by kappa distribution than by superposition of the Maxwellian distribution. However, Kappa distribution reduces to the Maxwellian distribution for very large values of the spectral index symbol; kappa (i.e., \(\kappa\rightarrow\infty\)).

While much literatures are concentrated on finding the solitary, shock, and periodic solutions of plasma evolution equations by traditional methods, the dynamical system approach is proved to be crucial in initiating new conceptual and theoretical tools. In this sense, the bifurcation theory is one of the most famous and important theories to study the dynamical behaviour for any plasma system (Chow and Hale 1981). Till now, a few work has been done in the field of plasma dynamics. For instance, Samanta et al. (2013b, 2013c, 2013d) have used the bifurcation theory of planar dynamical systems to investigate nonlinear travelling waves in plasmas in the frameworks of Kadomtsev-Petviashili (KP) and Zkharov-Kuznetsov (ZK) equations. Thereafter, Saha and Chatterjee (2014a) have used the bifurcation theory to study nonlinear electron acoustic travelling waves in an unmagnetized quantum plasma with cold and hot electrons in the framework of KdV equation obtained by the reductive perturbation technique (RPT). Later, they have generalized this model to study nonlinear dust ion acoustic travelling waves in the framework of MKP equation in a magnetized dusty plasma with superthermal electrons (Saha and Chatterjee 2014b) and with q-nonextensive velocity distributed ions (Saha and Chatterjee 2014c). Furthermore, Saha and Chatterjee (2014d) have used the bifurcation theory to investigate the propagation of dust acoustic solitary waves and periodic waves in an unmagnetized dusty plasma with kappa distributed electrons and ions through non-perturbative approach. Cairns et al. (1995) investigated the effect of the superthermal electrons population on the ion-acoustic structures observed by the FREJA satellite. In addition, the simultaneous existence of negative and positive ions with non-Maxwellian electron distribution in a plasma introduces a new aspect of the nonlinear ion-acoustic travelling waves. Indeed, \((H_{+},O_{2}^{-})\) and \((H_{+},H_{-})\) plasmas composition occur in the D and F-regions of the Earth’s ionosphere, where negative ions and superthermal electrons are found (Swider 1988). To the best of our knowledge, the basic features of nonlinear ion-acoustic travelling waves in a three-dimensional multicomponent magnetoplasma system through the bifurcation analysis are untouched before. It therefore seems interesting to study the nonlinear ion-acoustic travelling waves in a multicomponent magnetoplasma with kappa distributed electrons. So, the aim of the present study is discussing bifurcations of solitary wave and periodic wave solutions, with the help of bifurcation theory of planar dynamical systems. Furthermore, we investigate the combined effects of kappa distributed electron, magnetic field, and the density ratios of the positive and negative ions on the basic features of nonlinear ion-acoustic travelling waves. This paper is organized as follows; In Sect. 2 we present the basic equations of our model and a ZK equation is derived using the RPT (Washimi and Taniuti 1966). The nonlinear propagation of solitary wave solutions and periodic travelling wave solutions is described by the bifurcation theory. Section 3 is allocated to present numerical results and conclusions

2 Basic equations

We consider a multicomponent magnetoplasma whose constituents are positive ions, negative ions, and superthermal electrons. A uniform external static magnetic field \(B=B_{0}\widehat{x}\) is applied in the \(x\)-axis direction, where \(\widehat{x}\) is the unit vector along the \(x\)-axis, and \(B_{0}\) is the intensity of the magnetic field. In 3D geometry, our plasma system is governed by the following normalized equations.

$$\begin{aligned} &\frac{\partial n_{j}}{\partial t}+\mathbf{\nabla}\cdot(n_{j} \mathbf{u}_{j})=0, \end{aligned}$$
(1)
$$\begin{aligned} &\biggl( \frac{\partial}{\partial t}+\mathbf{u}_{j}\cdot\mathbf{ \nabla} \biggr) \mathbf{u}_{j}\mp Q_{j}\mathbf{\nabla}\phi+ \frac{5}{3}Q_{j}\sigma_{j}n_{j}^{\frac{-1}{3}} \mathbf{\nabla}n_{j} \\ &\quad{}+\varOmega_{j}\mathbf{u}_{j} \times\widehat{x}=0, \end{aligned}$$
(2)
$$\begin{aligned} &\mathbf{\nabla}^{2}\phi=n_{-}-n_{+}+n_{e}, \end{aligned}$$
(3)

where, \(j=(+,-)\) for positive and negative ions, respectively. The upper sign in Eq. (2), and in the remaining equations, is assigned for negative ions, while the lower one is allocated for positive ions. \(n_{j}\) and \(\mathbf{u}_{j}\ [\equiv(u_{j},v_{j},w_{j})]\) are the densities and velocities with \((u_{j},v_{j},w_{j})\) represent the velocity components in the Cartesian coordinates, respectively. \(\phi\) is the electrostatic wave potential. \(Q_{+}=1\) and \(Q_{-}\equiv Q=\frac{m_{+}}{m_{-}}\), where, \(m_{+}\) and \(m_{-}\) are the positive and negative ion masses, respectively. \(\sigma_{j}=T_{j}/T_{e}\) is the temperature ratio of the positive/negative ion to the electron. The number density for electrons is expressed as

$$ n_{e}=\mu \biggl( 1-\frac{\phi}{\kappa-\frac{3}{2}} \biggr) ^{-\kappa+\frac{1}{2}}, $$
(4)

where \(\kappa\) is the spectral index, which determines the hardness of the energy spectrum corresponding to the presence of excess superthermal electrons in the tail of the distribution function. \(\mu=\frac{n_{e0}}{n_{+0}}\) is the ratio between the unperturbed electron-to-positive ion density.

The density \(n_{j}\) has been scaled in terms of the unperturbed positive ion density, \(n_{0+}\) and \(\mathbf{u}_{j}\) is scaled in the ion sound speed, \(C_{s}=(k_{B}T_{e}/m_{+})^{1/2}\), the potential \(\phi\) is normalized by the thermal potential, \(k_{B}T_{e}/e\). The space and time variables are scaled in the positive ion Debye radius, \(\lambda_{Di}= (k_{B}T_{e}/4\pi e^{2}n_{+0} ) ^{1/2}\), and the negative ion plasma period, \(\omega _{pi}^{-1}=(4\pi e^{2}n_{+0}/m_{+})^{-1/2}\), respectively. We have defined \(\varOmega_{\pm}=\frac{\omega_{c\pm}}{\omega_{pi}}\) where \(\omega_{c\pm}=\frac{eB_{0}}{m_{\pm}c}\). The neutrality condition implies \(\mu +\upsilon=1\), where \(\upsilon=\frac{n_{-0}}{n_{+0}}\).

To investigate the propagation of the nonlinear ion-acoustic travelling waves, we employ the RPT (Washimi and Taniuti 1966). According to this method, we stretch the independent variables into a moving frame in which the nonlinear wave moves at a phase speed, \(\lambda\), as:

$$ \begin{aligned} &X=\epsilon^{1/2}(x-\lambda t),\qquad Y= \epsilon^{1/2}y,\\ &Z=\epsilon^{1/2}z\quad \text{and}\quad T= \epsilon^{3/2}t \end{aligned} $$
(5)

where \(\epsilon\) is a small (real) parameter measuring the weakness of the nonlinearity. The dependent variables are expanded as

$$\begin{aligned} \begin{aligned} &n_{j} =\rho+\epsilon n_{j}^{(1)}+\epsilon^{2}n_{j}^{(2)}+\cdots,\\ &u_{j} =\epsilon u_{j}^{(1)}+\epsilon^{2}u_{j}^{(2)}+\cdots,\\ &v_{j} =\epsilon^{3/2}v_{j}^{(1)}+\epsilon^{2}v_{j}^{(2)}+\cdots,\\ &w_{j} =\epsilon^{3/2}w_{j}^{(1)}+\epsilon^{2}w_{j}^{(2)}+\cdots,\\ &\phi =\epsilon\phi^{(1)}+\epsilon^{2}\phi^{(2)}+\cdots, \end{aligned} \end{aligned}$$
(6)

where \(\rho=\upsilon\) for negative ions and \(\rho=1\) for positive ions. Substituting the stretching (5) and the expansions (6) into the basic Eqs. (1)–(3) we obtain the lowest-order in \(\epsilon\)

$$\begin{aligned} \begin{aligned} &n_{j}^{(1)}=\frac{\mp\rho Q_{j}}{\frac{5}{3}Q_{j}\sigma_{j}\rho^{\frac{2}{3}}\upsilon-\lambda^{2}}\phi^{(1)},\\ &u_{j}^{(1)}=\frac{\mp\lambda Q_{j}}{\frac{5}{3}Q_{j}\sigma_{j}\rho^{\frac{2}{3}}-\lambda^{2}} \phi^{(1)}, \end{aligned} \end{aligned}$$
(7)
$$\begin{aligned} \begin{aligned} &w_{j}^{(1)}=\mp\frac{1}{\varOmega_{j}} \biggl( \frac{Q_{j}\lambda^{2}}{\frac{5}{3}Q\sigma_{j}\upsilon^{\frac{2}{3}}-\lambda^{2}} \biggr) \frac{\partial \phi^{(1)}}{\partial Y},\\ &v_{j}^{(1)}=\mp\frac{1}{\varOmega_{j}} \biggl( \frac{Q_{j}\lambda^{2}}{\frac{5}{3}Q\sigma_{j}\upsilon^{\frac{2}{3}}-\lambda^{2}} \biggr) \frac{\partial\phi^{(1)}}{\partial Z}, \end{aligned} \end{aligned}$$
(8)

and

$$\begin{aligned} &\bigl( \lambda^{2} \bigr) ^{2}- \lambda^{2} \biggl[ \biggl( \frac{5}{3}Q\sigma_{-} \upsilon^{\frac{2}{3}}+\frac{5}{3}\sigma_{+} \biggr) + \frac {1+\upsilon Q}{\mu ( \frac{2\kappa-1}{2\kappa-3} ) } \biggr] \\ &\quad{}+\frac{5}{3}\upsilon Q \biggl[ \frac{\sigma_{+}+\sigma_{-}\upsilon^{\frac {-1}{3}}}{\mu ( \frac{2\kappa-1}{2\kappa-3} ) }+ \frac{5}{3}\upsilon^{\frac{-1}{3}}\sigma_{-} \sigma_{+} \biggr] =0, \end{aligned}$$
(9)

where, Eq. (9) is the compatibility condition. Apparently, the modes are further significantly modified by the superthermal electron distribution parameter \(\kappa\). The phase velocities of the two modes are given by the following expression:

$$ \lambda_{\pm}^{2}=\frac{5}{6} \bigl( Q \sigma_{-}\upsilon^{\frac{2}{3}}+\sigma_{+} \bigr) + \frac{1+\upsilon Q}{2\mu ( \frac{2\kappa-1}{2\kappa-3} ) }\pm\delta, $$
(10)

where

$$\begin{aligned} \delta =&\biggl\{ \biggl[ \frac{5}{6} \bigl( Q \sigma_{-}\upsilon^{\frac{2}{3}}+\sigma_{+} \bigr) + \frac{1+\upsilon Q}{2\mu ( \frac{2\kappa-1}{2\kappa-3} ) } \biggr] ^{2} \\ &{}-\frac{5}{3}\upsilon Q \biggl[ \frac {\sigma_{+}+\sigma_{-}\upsilon^{\frac{-1}{3}}}{\mu ( \frac{2\kappa -1}{2\kappa-3} ) }+\frac{5}{3}\upsilon^{\frac{-1}{3}}\sigma_{+} \sigma_{-} \biggr]\biggr\} ^{1/2}. \end{aligned}$$
(11)

\(\lambda_{+}\) stands for the fast ion-acoustic mode, while \(\lambda_{-}\) stands for the slow one.

The next order in \(\epsilon\) gives the following system of equations in the second-order perturbed quantities

$$\begin{aligned} &\frac{\partial n_{j}^{(1)}}{\partial T}-\lambda\frac{\partial n_{j}^{(2)}}{\partial X} +\rho \frac{\partial u_{j}^{(2)}}{\partial X}+n_{j}^{(1)}\frac{\partial u_{j}^{(1)}}{\partial X}+u_{j}^{(1)} \frac{\partial n_{j}^{(1)}}{\partial X} \\ &\quad{}+\rho\frac{\partial v_{j}^{(2)}}{\partial Y}+\rho\frac{\partial w_{j}^{(2)}}{\partial Z}=0, \end{aligned}$$
(12)
$$\begin{aligned} &\frac{\partial u_{j}^{(1)}}{\partial T}-\lambda\frac{\partial u_{j}^{(2)}}{\partial X} +u_{j}^{(1)} \frac{\partial u_{j}^{(1)}}{\partial X}\mp Q_{j}\frac{\partial\phi^{(2)}}{\partial X} \\ &\quad{}+\frac{5}{3}Q_{j} \sigma_{j}\rho ^{\frac{-1}{3}} \biggl( \frac{\partial n_{j}^{(2)}}{\partial X}- \frac {n_{j}^{(1)}}{3\upsilon}\frac{\partial n_{j}^{(1)}}{\partial X} \biggr) =0. \end{aligned}$$
(13)

Eliminating the second-order perturbed quantities in Eqs. (12) and (13), making use of the first-order results, Eqs. (7) to (9), we obtain a ZK nonlinear partial-differential equation in the form

$$ \frac{\partial\phi}{\partial T}+A\phi\frac{\partial\phi}{\partial X}+B\frac{\partial^{3}\phi}{\partial X^{3}} +C \frac{\partial}{\partial X} \biggl( \frac{\partial^{2}\phi}{\partial Y^{2}}+\frac{\partial^{2}\phi}{\partial Z^{2}} \biggr) =0, $$
(14)

where, \(\phi=\phi^{(1)}\), and

$$\begin{aligned} A =& B \biggl( \frac{\upsilon Q^{2} ( 3\lambda^{2}-\frac{5}{3}Q\sigma_{-}\upsilon^{\frac{5}{3}} ) }{ ( \frac{5}{3}Q\sigma _{-}\upsilon^{\frac{2}{3}}-\lambda^{2} ) ^{3}}-\frac{ ( 3\lambda^{2}-\frac{5}{3}\sigma_{+} ) }{ ( \frac{5}{3}\sigma _{+}-\lambda^{2} ) ^{3}} \\ &{}-2 \biggl(\frac{4\kappa^{2}-1/4}{2\kappa -3} \biggr) \mu \biggr), \end{aligned}$$
(15)
$$\begin{aligned} B =& \frac{ ( \frac{5}{3}Q\sigma_{-}\upsilon^{\frac{2}{3}}-\lambda ^{2} ) ^{2} ( \frac{5}{3}\sigma_{+}-\lambda^{2} ) ^{2}}{2\lambda\upsilon Q ( \frac{5}{3}\sigma_{+}-\lambda^{2} ) ^{2}+2\lambda ( \frac{5}{3}Q\sigma_{-}\upsilon^{\frac{2}{3}}-\lambda ^{2} ) ^{2}}, \end{aligned}$$
(16)

and

$$\begin{aligned} C=B \biggl[ \frac{1}{\varOmega_{-}^{2}}\frac{\upsilon Q\lambda^{4}}{ ( \frac{5}{3}Q\sigma_{-}\upsilon^{\frac{2}{3}}-\lambda^{2} ) ^{2}}+ \frac{1}{\varOmega_{+}^{2}}\frac{\lambda^{4}}{ ( \frac{5}{3}\sigma _{+}-\lambda^{2} ) ^{2}}+1 \biggr]. \end{aligned}$$
(17)

3 Bifurcation of phase portraits of ZK equation

To transform the ZK equation, Eq. (14), into the corresponding ordinary differential equation, we introduce the transformation \(\xi=\alpha ( LX+MY+NZ-u_{0}T )\), where \(L\), \(M\), and \(N\) are the directions cosines of the wave propagation vector, \(\mathbf{k}\), with respect to \(X\), \(Y\), and \(Z\) axes, respectively and \(\alpha\) is a constant. \(u_{0}\) is the velocity of the moving frame normalized by ion acoustic speed. Considering \(U(\xi )=\phi(X,Y,Z,T)\), one can integrate Eq. (14) with respect to \(\xi\) and neglect the integration constant. Therefore, Eq. (14) takes the following form

$$ \frac{d^{2}U}{d^{2}\xi}=aU-bU^{2} $$
(18)

where \(a=\frac{u_{0}}{\alpha^{2}L [ L^{2}(B-C)+C ]}\) and \(b=\frac{A}{2\alpha^{2} [ L^{2} ( B-C ) +C ]}\). Now we can express Eq. (18) in the following dynamical system of travelling wave equations

$$ \left\{ \textstyle\begin{array}{l} \frac{dU}{d\xi}=\psi, \\ \frac{d\psi}{d\xi}= ( a-bU ) U. \end{array}\displaystyle \right. $$
(19)

The phase orbits defined by the vector fields of Eqs. (19) determine all travelling wave solutions of Eq. (14), which is a planar Hamiltonian system with Hamiltonian function:

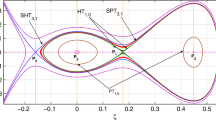
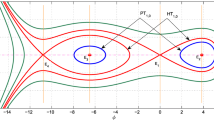
$$ H(U,\psi)=\frac{\psi^{2}}{2}- \biggl( \frac{a}{2}- \frac{b}{3}U \biggr) U^{2}=h_{1}. $$
(20)

According to the bifurcation theory (Chow and Hale 1981) of phase portraits of Eqs. (19), there are two equilibrium points, \(P_{0}(U_{0},0)\) and \(P_{1}(U_{1},0)\) at \(a\neq0\) and \(b\neq0\), where \(U_{0}=0\) and \(U_{1}=\frac{2u_{0}}{LA}\). We will investigate the bifurcations of phase portraits of Eqs. (19) in the \((U,\psi)\) phase plane as the parameters, \(\kappa\), \(\upsilon\), \(\sigma_{+}\), \(\sigma_{-}\) and \(u_{0}\) varies. Now let us consider

$$ J=\det M(U_{i},0)=-a+2bU_{i}, $$
(21)

where \(M(U_{i},0)\) is the coefficient matrix of the linearized system of Eqs. (19) at an equilibrium point \(P_{i}(U_{i},0)\). It is well known that (Chow and Hale 1981), if \(J<0\), the equilibrium point \(P_{i}(U_{i},0)\) of the Hamiltonian system will be a saddle point, while it will be a center if \(J>0\). At \(J=0\) the poincare index of the equilibrium point becomes 0, then the equilibrium point \(P_{i}(U_{i},0)\) will be a cusp.

4 Numerical results and discussions

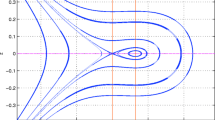
To validate the results found in this manuscript, we make use of the typical parameters relevant to the observed situations (El-Labany et al. 2010; Mehdipoor 2013). For example, \((H_{+},O_{2}^{-})\) and \((H_{+},H_{-})\) plasmas have been found in the D and F-regions of the Earth’s ionosphere. Particularly, we analyze the effect of the spectral index, \(\kappa\), the unperturbed density ratio of negative-to-positive ions, \(\upsilon\), the temperature ratio of positive/negative ions-to-electron, \(\sigma_{\pm}\), and the direction cosines of the wave vector along the \(x\)-axis, \(L\), on the nonlinear ion-acoustic travelling waves in the \((H_{+},O_{2}^{-})\) plasmas (\(Q=0.03\)). Before going into details, let us first investigate numerically the existence of compressive ion-acoustic travelling waves (i.e., pulse at \(\upsilon<0.1\)) and rarefactive ones (i.e., cavity at \(\upsilon>0.1\)). It is worth to notice that the pulse is satisfied at the nonlinear coefficient \(A>0\), whereas the cavity exists for \(A<0\), as depicted in Fig. 1. Now, in Figs. 2 to 7, we study the exact explicit travelling wave solutions of Eq. (14). For \(\upsilon>0.1\) (\(\upsilon<0.1\)) and \(u_{0}>0\), the travelling wave system, Eqs. (19), has a homoclinic orbit at the equilibrium point \(P_{0}\) \((U_{0},0)\) realized by Eq. (20) as shown in Fig. 2 (Fig. 3). According to the above-mentioned condition, \(A>0\) (\(A<0\)), as illustrated in Fig. 4 (Fig. 5), Eq. (14) gives a compressive (rarefactive) solitary wave solution of the form (Saha et al. 2015)

$$ \phi(\xi)=\phi_{A}\operatorname{sech}^{2} \biggl[ \frac{\xi}{W} \biggr], $$
(22)

where \(\phi_{A} ( =3u_{0}/AL ) \) and \(W ( =\sqrt{\frac {4\alpha^{2}L [ L^{2}(B-C)+C ] }{u_{0}}} ) \) are the amplitude and the width of ion-acoustic solitary wave, respectively.

Fig. 1
figure 1

The variation of the nonlinear coefficient \(A\) against \(\upsilon\) for \(\sigma_{+}=0.1\), \(\sigma_{-}=0.01\), and \(\kappa=4\)

Full size image
Fig. 2
figure 2

Phase curves with \(\upsilon=0.005\), \(L=0.7\), \(u_{0}=1.1\), \(\sigma_{+}=0.1\), \(\sigma_{-}=0.01\), and \(\kappa=4\)

Full size image
Fig. 3
figure 3

Phase curves with \(\upsilon=0.16\), \(L=0.7\), \(u_{0}=1.1\), \(\sigma_{+}=0.1\), \(\sigma_{-}=0.01\), and \(\kappa=4\)

Full size image
Fig. 4
figure 4

Solitary wave for \(\upsilon=0.005\), \(L=0.7\), \(u_{0}=1.1\), \(\sigma_{+}=0.1\), \(\sigma_{-}=0.01\), and \(\kappa =1.6\)

Full size image
Fig. 5
figure 5

Solitary wave for \(\upsilon=0.16\), \(L=0.7\), \(u_{0}=1.1\), \(\sigma_{+}=0.1\), \(\sigma_{-}=0.01\), and \(\kappa=8\)

Full size image

Now, let us discuss the possibility of the propagation of periodic travelling wave in the system under consideration. For \(\upsilon<0.1\), the travelling wave system, Eqs. (19), has a family of periodic orbits about the equilibrium point \(P_{1}\) \((U_{1},0)\) defined by Eq. (20) (see Fig. 2). Furthermore, at \(U_{1}=2u_{0}/AL\), we obtain

$$ -\frac{AL}{u_{0}}\phi_{n}^{3}+3 \phi_{n}^{2}-\frac{4u_{0}^{2}}{A^{2}L^{2}}=0, $$
(23)

where \(n=1,2\) and 3. The three real zeros of Eq. (23) are \(\phi_{1}\), \(\phi_{2}\) and \(\phi_{3}\). It should be mentioned here that the conditions for the existence of a periodic travelling wave solution of Eq. (14) require that \(\phi_{1}>\phi_{2}> \phi_{3}\). Accordingly, the periodic wave solution of Eq. (14) is given by (El-Shamy 2015)

$$ \phi(\xi)=\phi_{3}+(\phi_{2}-\phi_{3}) \operatorname{sn}^{2} [ D\xi,k ], $$
(24)

where sn is the Jacobian elliptic function. For the nonlinear coefficient \(A>0\), the amplitude of the periodic travelling wave is given by \((\phi_{2}-\phi_{3})>0\). The elliptic parameter \(k=\sqrt{\frac{\phi_{2}-\phi_{3}}{\phi_{1}-\phi_{3}}}\) refers physically to the nonlinearity with the linear limit corresponds to \(k\rightarrow0\) and the extreme nonlinear limit corresponds to \(k\rightarrow1\). The parameter \(D\) is given by

$$ D=\sqrt{\frac{u_{0} ( \phi_{1}-\phi_{3} ) }{12\alpha^{2}L [ L^{2}(B-C)+C ] }}. $$
(25)

For this case, the periodic travelling wave solution of Eq. (14) is represented in Fig. 6. On the other side, for \(\upsilon>0.1\), the travelling wave system, Eqs. (19), has a family of periodic orbits about the equilibrium point \(P_{1}\) \((U_{1},0)\) realized by Eq. (20) (see Fig. 3). Moreover, at \(U_{1}=2u_{0}/AL\), we have

$$ -\frac{AL}{u_{0}}\phi_{i}^{3}+3 \phi_{i}^{2}-\frac{4u_{0}^{2}}{A^{2}L^{2}}=0, $$
(26)

where \(i=1,2\) and 3. The three real zeros of Eq. (26) are \(\phi_{1}\), \(\phi_{2}\) and \(\phi_{3}\). The conditions for the presence of a periodic travelling wave solution of Eq. (14) require that \(\phi_{1}>\phi_{2}> \phi_{3}\). Therefore, the periodic wave solution of Eq. (14) is given by (Samanta et al. 2013b)

$$ \phi(\xi)=\phi_{1}-(\phi_{1}-\phi_{2}) \operatorname{sn}^{2} [D\xi,m_{1} ], $$
(27)

where the modulus \(m_{1}=\sqrt{\frac{\phi_{1}-\phi_{2}}{\phi_{1}-\phi_{3}}}\) may be considered as a fair indicator of the nonlinearity; with the linear limit being \(m_{1}\rightarrow0\) and the extreme nonlinear limit being \(m_{1}\rightarrow1\). For the nonlinear coefficient \(A<0\), the amplitude of the periodic travelling wave is given by \(-(\phi_{1}-\phi _{2})<0\). In this case, Fig. 7 demonstrates the periodic travelling wave solution of Eq. (14). Here, we will study the impacts of the spectral index, \(\kappa\), the direction cosine, \(L\), and the intensity of the magnetic field, \(B_{0}\), on the basic properties of periodic travelling waves. Numerically, the results are displayed in Figs. 8 to 10 (Figs. 11 to 13) for \(\upsilon<0.1\) (\(\upsilon>0.1\)). In Fig. 8 (Fig. 11), the effect of the spectral index \(\kappa\) on the profile of the periodic travelling waves against the space coordinate \(\xi\) is studied. It is clear that the amplitude of the periodic travelling waves increases (decreases) due to the increase of \(\kappa\). This behavior, shown in Fig. 8, can be explained as follows: for certain values of \(\kappa\), the thermal energy is not sufficient enough to increase the nonlinearity of the system, so the amplitude of nonlinear periodic travelling wave shrinks. However, the situation in Fig. 11 is different. This means physically that for lower values of \(\kappa\), the restoring force of nonlinear periodic travelling wave is provided by the electron pressure, which increases due to the increase of the energetic superthermal electrons in positive ion-negative ion-superthermal electron plasma system. Therefore, the enhancement in the restoring force leads to an increase in the amplitude of nonlinear periodic travelling wave, which makes it taller. In Figs. 9 and 12, the variation of the profile of the periodic travelling waves with \(L\) is examined. It is obvious that both of the amplitude and the width increase as \(L\) decreases. Physically, one can predict that as the nonlinear periodic travelling wave approaches the direction perpendicular to the magnetic field, the amplitude and the width of it become extremely large, and from this point, the nonlinear periodic travelling wave disappears.

Fig. 6
figure 6

Periodic travelling wave for \(\upsilon=0.005\), \(L=0.7\), \(u_{0}=1.1\), \(\sigma_{+}=0.1\), \(\sigma_{-}=0.01\), and \(\kappa=4\)

Full size image
Fig. 7
figure 7

Periodic travelling wave for \(\upsilon=0.16\), \(L=0.7\), \(u_{0}=1.1\), \(\sigma_{+}=0.1\), \(\sigma_{-}=0.01\), and \(\kappa=4\)

Full size image
Fig. 8
figure 8

Variation of periodic travelling wave for \(L=0.7\), \(\upsilon=0.005\), \(u_{0}=1.1\), \(\sigma_{+}=0.1\), \(\sigma_{-}=0.01\), and \(\kappa=3.8\) (dashed curve) and \(\kappa=4\) (solid curve)

Full size image
Fig. 9
figure 9

Variation of periodic travelling wave for \(\kappa=4\), \(\upsilon=0.005\), \(u_{0}=1.1\), \(\sigma_{+}=0.1\), \(\sigma_{-}=0.01\), \(L=0.7\) (solid curve) and \(L=0.6\) (dashed curve)

Full size image
Fig. 10
figure 10

Variation of periodic travelling wave for \(L=0.7\), \(\upsilon=0.005\), \(u_{0}=1.1\), \(\sigma_{+}=0.1\), \(\sigma_{-}=0.01\), \(\kappa =4\), \(B_{0}=0.5\) (solid curve) and \(B_{0}=0.4~\mbox{G}\) (dashed curve)

Full size image
Fig. 11
figure 11

Variation of periodic travelling wave for \(L=0.7\), \(\upsilon=0.16\), \(u_{0}=1.1\), \(\sigma_{+}=0.1\), \(\sigma_{-}=0.01\), \(\kappa=4\) (solid curve) and \(\kappa=4.2\) (dashed curve)

Full size image
Fig. 12
figure 12

Variation of periodic travelling wave for \(\kappa=4\), \(\upsilon=0.16\), \(u_{0}=1.1\), \(\sigma_{+}=0.1\), \(\sigma_{-}=0.01\), \(L=0.7\) (solid curve) and \(L=0.6\) (dashed curve)

Full size image
Fig. 13
figure 13

Variation of periodic travelling wave for \(L=0.7\), \(\upsilon=0.16\), \(u_{0}=1.1\), \(\sigma_{+}=0.1\), \(\sigma_{-}=0.01\), \(\kappa=4\), \(B_{0}=0.5\) (solid curve) and \(B_{0}=0.4~\mbox{G}\) (dashed curve)

Full size image

The impacts of intensity of the magnetic field \(B_{0}\) on the periodic travelling waves is exhibited in Figs. 10 and 13. It is seen that the width of the periodic travelling waves increases as \(B_{0}\) decreases. On the other hand, \(B_{0}\) has no effect on the amplitude of the periodic travelling waves. This means that the magnetic field acts to bind the particles tightly to the lines of force so that, in the motion of a fluid element, the transverse movements of the particles are constrained within the element. It is worth to notice that the considered plasma may be contained entirely by the magnetic force, an arrangement referred to as magnetic confinement (i.e., the magnetic field makes the nonlinear periodic travelling wave structures more spiky) (El-Shamy 2014).

Finally, we studied the nonlinear propagation of ion-acoustic travelling waves in a three-dimensional magnetoplasma system composed of positive ions, negative ions and superthermal electrons. Using the reductive perturbation technique, a ZK equation is derived. The nonlinear propagation of solitary waves and periodic travelling waves are described by the bifurcation theory. The compressive and rarefactive structures of solitary waves and periodic travelling waves are formed. In details, we have discussed the effects of the negative-to-positive ions density ratio, \(\upsilon\), the spectral index, \(\kappa\), the direction cosines, \(L\), and the intensity of the magnetic field, \(B_{0}\), on the nonlinear propagation of ion-acoustic travelling waves. These parameters have strong effects on the propagation of ion-acoustic travelling waves. These results are found to be helpful to understand the propagation and the formation of ion-acoustic travelling waves in certain astrophysical scenarios, especially in the D and F-regions of the Earth’s ionosphere.