1 Introduction

In last few decades, the study of nonlinear evolution of electrostatic waves in quantum plasma is growing and it becomes an interesting research topic in the area of plasma physics. The electron acoustic waves (EAWs) is an electrostatic wave with high frequency in comparison with the ion plasma frequency. Electron acoustic waves (EAWs) have been observed in the laboratory for the plasma consisting of hot and cold electrons (Derfler and Simonen 1969; Ikezawa and Nakamura 1981) and in an electron ion plasma consisting of ions hotter than electrons (Fried and Gould 1961). The propagation of EAWs plays a significant role in laboratory as well as in space plasma. Several authors have carried out investigations on linear (Yu and Shukla 1983; Gary and Tokar 1985; Dell et al. 1987) as well as nonlinear (Dubouloz et al. 1991; Mace et al. 1991; Berthomier et al. 2000; Ghosh et al. 2002; Masood and Shah H. A 2003) properties of EAWs in unmagnetized plasma. Dubouloz et al. (1991) have investigated the one dimensional electron acoustic solitary waves (EASWs) in the present of two-electron population and motionless ions in unmagnetized and collisionless plasma. Mace et al. (1991) have investigated the EASWs in unmagnetized plasma consisting of ions with finite temperature. Furthermore, many investigations have been presented on the nonlinear features of EAWs in magnetized plasma (Mace and Hellberg 2001; Dubouloz et al. 1993; Mamun et al. 2002). Since the two-electron populations (one hot and one cold) take place frequently in fusion devices and in the auroral ionosphere (Bezzerides et al. 1978), EAWs may exist in such a two-electron temperature plasma. It is well known that EAWs can also describe the electrostatic component of the broadband electrostatic noise (BEN) which is observed in magnetosphere (Tokar and Gary 1984) and in the geomagnetic tail (Schriver and Ashour-Abdalla 1989).

The study on the investigation of quantum plasma is growing day by day because of its huge applications in many areas of laboratory plasma and astrophysics. Most of them include the fabrication of semiconductor devices (Markowhich et al. 1990), quantum dots and quantum wires (Shpatakovskaya 2006), carbon nanotubes and quantum diodes (Ang et al. 2006; Ang and Zhang 2007; Shukla and Eliasson 2008), ultracold plasmas (Killian 2006), microplasma (Becker et al. 2005) etc. Mahmood and Masood (2008) investigated EAWs in an unmagnetized quantum plasma with two population electrons with the help of Sagdeev potential approach and found hot electron density hump structures in the subsonic region of the mentioned plasmas. Sah and Manta (2009) considered one dimensional quantum hydrodynamical model and studied electron acoustic solitary waves in an unmagnetized dense quantum plasma consisting of two types of electrons which are inertial cold electron, inertialess hot electrons and immobile ions. By applying RPT they obtained KdV equation governing the dynamics of EAWs. They derived both compressive and rarefactive solitons along with periodical structures. Sahu et al. (2012) investigated the nonlinear wave structures of electron acoustic waves in an unmagnetized quantum plasma consisting of cold electrons, hot electrons and ions. Mahmood et al. (2010) studied acoustic solitons and double layers in an unmagnetized quantum electron-positron plasma in the presence of stationary ions. They used quantum hydrodynamic model and by applying RPT they derived KdV equation and modified KdV equation for solitons and double layers. In 2012, Abdelsalam et al. studied linear and nonlinear properties of low frequency electrostatic excitations of charge dust particles in a dense collisionless, unmagnetized Thomas–Fermi plasma. Hass et al. (2003) have investigated the linear and nonlinear ion acoustic waves in unmagnetized quantum plasma by using quantum hydro-dynamic (QHD) model. Masood and Mushtaq (2008) have carried out a theoretical investigation for the first time to understand the linear and nonlinear properties of obliquely propagating EASWs in a two-electron quantum magnetoplasma. Several authors (Roy et al. 2011; Ghosh et al. 2012; Pakzad 2010; Chatterjee et al. 2012) have devoted their attention to understand and to investigate the nonlinear propagation of waves in plasmas over the last few years.

Some authors (Chatterjee et al. 2008; Ghorui et al. 2013; Saha and Chatterjee 2009) studied nonlinear solitary waves in different angles in magnetized plasma. Using quantum hydrodynamic model, Misraa et al. (2007) investigated the propagation characteristics of nonlinear electron-acoustic solitary waves (EASWs) in a dense quantum plasma whose constituents are inertial cold electrons and inertialess hot electrons, and the stationary ions which form the neutralizing background. Chatterjee et al. (2013) studied the nonlinear propagation of electron-acoustic waves in three components unmagnetized dense quantum plasma consisting of inertially cold electrons, inertia-less hot electrons and immobile ions using a one dimensional quantum hydrodynamic model. Sahu and Ghosh (2013) studied different properties of IAWs deriving KP equation in quantum dusty plasma. Recently, Samanta et al. (2013a) studied dust ion acoustic travelling waves in the framework of a KP equation in magnetized dusty plasma with a q-nonextensive electron velocity distribution using the bifurcation theory of planar dynamical systems and derived exact solitary wave solutions and periodic travelling wave solutions depending on the values of the parameters. By applying bifurcation theory and methods of planar dynamical systems, Samanta et al. (2013b) investigated nonlinear propagation of ion acoustic waves (IAWs) in the framework of a ZK equation in a magnetized plasma whose constituents are cold ions and kappa distributed electron using a two component plasma model. The existence of solitary wave solutions and periodic travelling wave solutions was established. They also have obtained all exact explicit solutions of these travelling waves. Very recently, Samanta et al. (2013c) studied bifurcation behavior of nonlinear dust ion acoustic travelling waves of KP equation in a magnetized quantum dusty plasma with the help of the bifurcation theory of planar dynamical systems depending on the parameters.

But, no work has been reported in the study of nonlinear waves in plasmas in the framework of a KdV equation by using the bifurcation theory of planar dynamical systems to the best of our knowledge. In the present work, our aim is to study the bifurcation behavior of electron acoustic traveling waves in a three-component unmagnetized quantum plasma with cold and hot electrons and ions in the framework of a KdV equation depending on the system parameters.

The remaining part of the paper is organized as follows: In Sect. 2, we consider one dimensional hydrodynamic model equations. We obtain the KdV equation in Sect. 3 using reductive perturbation technique (RPT). In Sect. 4, we find the traveling wave system of this KdV equation. Bifurcations of phase portraits are considered in Sect. 5. Two exact traveling wave solutions (solitary and periodic wave solutions) of the KdV equation are derived in Sect. 6. Section 7 is kept for conclusions.

2 Model equations

In this work, we consider an unmagnetized and collisionless quantum plasma whose constituents are cold electrons, hot electrons and ions. We consider the dynamics of cold electrons in the background of hot electrons and ions. The phase speed of EAWs lies in between v Fc and v Fh , i.e., v Fc ≪ω/k≪v Fh , where v Fc and v Fh are Fermi velocities of cold and hot electrons, respectively. The model equations (Mahmood and Masood 2008) in normalized form are as follows:

$$\begin{aligned} &\frac{\partial n}{\partial t}+\frac{\partial (nu)}{\partial x}= 0, \end{aligned}$$
(1)
$$\begin{aligned} &\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}= \alpha \frac{\partial \phi}{\partial x}, \end{aligned}$$
(2)
$$\begin{aligned} &\frac{\partial^2 \phi}{\partial x^2}= n_h+\frac{1}{\alpha}n-\biggl(1+ \frac{1}{\alpha}\biggr), \end{aligned}$$
(3)
$$\begin{aligned} &\phi=-\frac{1}{2}+\frac{n^2_h}{2}-\frac{H^2}{2\sqrt{n_h}} \frac{\partial^2 \sqrt{n_h}}{\partial x^2}, \end{aligned}$$
(4)

where n is the cold electron number density normalized by n 0, n h is the hot electron number density normalized by n h0, u is the cold electron velocity normalized by \(\sqrt{2k_{B}T_{Fh}/\alpha m_{e}}\), α=n h0/n 0>1, m e is the electron mass, T Fh is the Fermi temperature of hot electron, e is the electron charge, k B is the Boltzman constant, ϕ is the electrostatic wave potential normalized by 2k B T Fh /e, H is nondimensional quantum parameter due to hot electron defined by \(H= \bar{h} \omega_{ph}/2k_{B}T_{Fh}\), \(\omega_{ph}=\sqrt{4\pi n_{h0}e^{2}/m_{e}}\) is the hot electron plasma frequency, \(\bar{h}\) is the Planck’s constant, space variables are normalized by Fermi wave length of hot electron \(\lambda_{Fh}=\sqrt{2k_{B}T_{Fh}/4\pi n_{h0}e^{2}}\) and time is normalized by the inverse of cold electron plasma frequency \(\omega^{-1}_{pc}=\sqrt{m_{e}/4\pi n_{0}e^{2}}\). In unperturbed state n 0+n h0=n i0. The Fermi temperature of hot electrons is given by the relation \(m_{e}v^{2}_{Fh}/2=k_{B}T_{Fh}\).

3 Derivation of KdV equation

we apply the reductive perturbation technique (RPT) to derive KdV equation which describes the behavior of small amplitude electron acoustic waves in quantum plasma. According to RPT, stretched coordinates are as follows:

$$\begin{aligned} &\xi = \epsilon^{\frac{1}{2}}(x-vt), \end{aligned}$$
(5)
$$\begin{aligned} &\tau = \epsilon^{\frac{3}{2}} t, \end{aligned}$$
(6)

where v is the phase velocity of electron acoustic wave in quantum plasma and ϵ is a small parameter which characterizes the strength of the nonlinearity. Expanding the dependent quantities in a power series, we have

$$\begin{aligned} &n = 1+\epsilon n_1+\epsilon^2 n_2+\cdots \end{aligned}$$
(7)
$$\begin{aligned} &n_h = 1+\epsilon n_h^{(1)}+ \epsilon^2 n_h^{(2)}+\cdots \end{aligned}$$
(8)
$$\begin{aligned} &u = \epsilon u_1+\epsilon^2 u_2+\cdots \end{aligned}$$
(9)
$$\begin{aligned} &\phi = \epsilon \phi_1+\epsilon^2 \phi_2+\cdots \end{aligned}$$
(10)

Substituting the Eqs. (5)–(10) into the system of Eqs. (1)–(4) and equating the coefficients of lowest power of ϵ, we have

$$\begin{aligned} &n_1 = \frac{1}{v}u_1, \end{aligned}$$
(11)
$$\begin{aligned} &u_1 = -\frac{\alpha}{v} \phi_1, \end{aligned}$$
(12)
$$\begin{aligned} &n^{(1)}_h = -\frac{1}{\alpha}n_1, \end{aligned}$$
(13)
$$\begin{aligned} &\phi_1 = n^{(1)}_h. \end{aligned}$$
(14)

Equating the coefficients of next power of ϵ, we have

$$\begin{aligned} &\frac{\partial n_1}{\partial \tau} - v\frac{\partial n_2}{\partial \xi}+\frac{\partial }{\partial \xi}(n_1u_1) +\frac{\partial u_2}{\partial \xi}=0, \end{aligned}$$
(15)
$$\begin{aligned} &\frac{\partial u_1}{\partial \tau}-v\frac{\partial u_2}{\partial \xi}+u_1 \frac{\partial u_1}{\partial \xi} = \alpha\frac{\partial \phi_2}{\partial \xi}, \end{aligned}$$
(16)
$$\begin{aligned} &\frac{\partial^{2}\phi_1}{\partial \xi^{2}} =n^{(2)}_h+ \frac{1}{\alpha}n_2, \end{aligned}$$
(17)
$$\begin{aligned} &n^{(2)}_h =\phi_2+ \frac{H^2}{4}\frac{\partial^2 n^{(1)}_h}{\partial \xi^2}-\frac{(n^{(1)}_h)^2}{2}. \end{aligned}$$
(18)

From the relations (11)–(14), we get

$$\begin{aligned} &v^2=1. \end{aligned}$$
(19)

From the relations (11)–(19), we obtain KdV equation as

$$\begin{aligned} \frac{\partial \phi_1}{\partial \tau}+\frac{v}{2}(1-3\alpha)\phi_1 \frac{\partial \phi_1}{\partial \xi}+\frac{v}{2}\biggl(1-\frac{H^2}{4}\biggr) \frac{\partial^3\phi_1}{\partial \xi^3} = 0. \end{aligned}$$
(20)

4 Travelling wave system of Eq. (20)

We transform the obtained KdV Eq. (20) to travelling wave system defining a variable as

$$\begin{aligned} \chi =(\xi-c\tau ), \end{aligned}$$
(21)

where c is the velocity of the travelling wave. Substituting ψ(χ)=ϕ 1(ξ,τ) into the kdV Eq. (20), we have

$$ -c\frac{d\psi}{d \chi}+\frac{v}{2}(1-3\alpha)\psi \frac{d\psi}{d \chi}+\frac{v}{2}\biggl(1-\frac{H^2}{4}\biggr) \frac{d^3\psi}{d \chi^3}=0. $$
(22)

Integrating Eq. (22) with respect to χ and neglecting integrating constant, we have

$$ -c\psi+\frac{v}{4}(1-3\alpha)\psi^2+ \frac{v}{2}\biggl(1-\frac{H^2}{4}\biggr)\frac{d^2\psi}{d \chi^2}=0. $$
(23)

Then Eq. (23) is equivalent to the following dynamical system:

$$ \left\{ \begin{aligned} &\frac{d\psi}{d \chi}=z,\\ &\frac{dz}{d \chi}=\frac{1}{v(1-\frac{H^2}{4})}\biggl(2c-\frac{v}{2}(1-3\alpha) \psi\biggr)\psi. \end{aligned} \right. $$
(24)

The Eq. (24) is a planar dynamical system with Hamiltonian function:

$$\begin{aligned} H_m(\psi,z) =&\frac{z^2}{2}-\frac{1}{3v(1-\frac{H^2}{4})} \biggl(3c-\frac{v}{2}(1-3\alpha)\psi\biggr)\psi^2 \\ =&h,\quad\mbox{say}. \end{aligned}$$
(25)

The system Eq. (24) is a planar dynamical system with four parameters α, v, H and c. It is clear that the phase orbits defined by the vector fields of Eq. (24) will represent all traveling wave solutions of the KdV Eq. (20). we will search the bifurcations of phase portraits of Eq. (24) in the (ψ,z) phase plane when the parameters α,v,H and c change. We want to point out that we are considering a physical system for which only bounded traveling wave solutions are meaningful. So, we only concentrate to the bounded traveling wave solutions of Eq. (20). A solitary wave solution of Eq. (20) corresponds to a homoclinic orbit of Eq. (24). A periodic orbit of Eq. (24) corresponds to a periodic traveling wave solution of Eq. (20). The bifurcation theory and methods of planar dynamical systems play a significant role in this work (Samanta et al. 2013a; Guckenheimer and Holmes 1983).

5 Bifurcations of phase portraits of Eq. (24)

In this section, we investigate the bifurcations of phase portraits of the dynamical system Eq. (24). When H 2≠4 and α>1, then there are two fixed points at E 0(ψ 0,0) and E 1(ψ 1,0), where ψ 0=0 and \(\psi_{1}=\frac{4c}{v(1-3\alpha)}\). Let M(ψ i ,0) be the coefficient matrix of the linearized system of the dynamical system Eq. (24) at a fixed point E i (ψ i ,0). Then we have

$$ J=\operatorname{det}M(\psi_i,0)=-\frac{2c}{v(1-\frac{H^2}{4})}+ \frac{1-3\alpha}{(1-\frac{H^2}{4})}\psi_i. $$
(26)

By the theory of planar dynamical systems (Samanta et al. 2013a; Guckenheimer and Holmes 1983), it is well known that the fixed point E i (ψ i ,0) of the planar dynamical system is a saddle point when J<0 and the fixed point E i (ψ i ,0) of the planar dynamical system is a center when J>0.

Then we have the following cases:

Case 1::

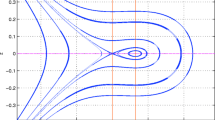
When v=1,c>0,α>1 and H 2<4, then the dynamical system Eq. (24) has two fixed points at E 0(ψ 0,0) and E 1(ψ 1,0), where ψ 0=0 and ψ 1<0. Here E 0(ψ 0,0) is a saddle point and E 1(ψ 1,0) is a center. There is a homoclinic orbit to E 0(ψ 0,0) surrounding the center E 1(ψ 1,0) (see Fig. 1).

Fig. 1
figure 1

Phase portrait of Eq. (24) for α=1.2,v=1,H=1.001 and c=0.808

Full size image
Case 2::

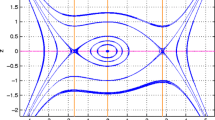
When v=1, c>0, α>1 and H 2>4, then the system (24) has two fixed points at E 0(ψ 0,0) and E 1(ψ 1,0), where ψ 0=0 and ψ 1<0. Here E 0(ψ 0,0) is a centre and E 1(ψ 1,0) is a saddle point. There is a homoclinic orbit to E 1(ψ 1,0) surrounding the center E 0(ψ 0,0) (see Fig. 2).

Fig. 2
figure 2

Phase portrait of Eq. (24) for α=1.302,v=1,H=2.81 and c=1.2594

Full size image

Applying the systematic analysis, we obtain the different phase portraits of Eq. (24) depending on both cases, shown in Figs. 1–2.

6 Exact explicit travelling wave solutions of Eq. (20)

By using the planar dynamical system Eq. (24) and the Hamiltonian function Eq. (25) with h=0, we derive two exact traveling wave solutions of Eq. (20) depending on different parameters which are the blow up solitary wave solution and periodic traveling wave solution.

  1. (1)

    When v=1,c>0,α>1 and H 2<4, (see Figs. 1 and 3), the system Eq. (20) has the blow up solitary wave solution given by

    $$ \phi_1=-\frac{6c}{v(1-3\alpha)}\operatorname{cosech}^2 \biggl(\frac{1}{2}\sqrt{\frac{2c}{v(1-\frac{H^2}{4})}} \chi\biggr). $$
    (27)
    Fig. 3
    figure 3

    Graph of the blow up solitary wave solution of Eq. (20) for α=1.2,v=1,H=1.001 and c=0.808

    Full size image
  2. (2)

    When v=1,c>0,α>1 and H 2>4, (see Figs. 2 and 4), the system Eq. (20) has periodic traveling wave solution given by

    $$ \phi_1=\frac{6c}{v(1-3\alpha)}\operatorname{cosec}^2 \biggl(\frac{1}{2}\sqrt{-\frac{2c}{v(1-\frac{H^2}{4})}} \chi\biggr). $$
    (28)
    Fig. 4
    figure 4

    Graph of the periodic traveling wave solution of Eq. (20) for α=1.302,v=1,H=2.81 and c=1.2594

    Full size image

By using symbolic computations, we obtain two graphs of these exact explicit solitary wave solution and periodic traveling wave solution of Eq. (20) depending on some particular values of the system parameters, shown in Figs. 3–4.

In the Fig. 3, we have presented the graph for the blow up solitary wave solution (27) in which ϕ 1 is ploted against χ for α=1.2,v=1,H=1.001 and c=0.808 satisfying the conditions of case 1. The amplitude of the blow up solitary wave solution is dependent on α, c, v but not on H. The width of the blow up solitary wave solution is dependent on c, v, H but not on α.

In the Fig. 4, we have presented the graph for the periodic traveling wave solution (28) in which ϕ 1 is ploted against χ for α=1.302,v=1,H=2.81 and c=1.2594 satisfying the conditions of case 2. The amplitude of the periodic wave solution is dependent on α, c, v but not on H. The width of the periodic traveling wave solution is dependent on c, v, H but not on α.

7 Conclusions

By using the bifurcation theory of planar dynamical systems, we have studied electron acoustic traveling waves in an unmagnetized quantum plasma in the (ψ,z) phase plane depending on the systematic analysis of the parameters α,c,H and v. With the help of well known RPT, the KdV equation is derived for our model equations. By applying the bifurcation theory and methods of planar dynamical systems, we have established that our system has the blow up solitary wave solution and periodic traveling wave solution. All possible cases of the system parameters are considered and the effect of different situations are shown in detail. We have obtained the blow up solitary wave solution and periodic traveling wave solution depending on the parameters α,c,H and v. From these exact traveling wave solutions, it is clear that the amplitude of these solitary and periodic wave solutions depends on α,c and v and width of these exact solutions depends on c,H and v. This work may help one to understand the salient features in laboratory plasma and space plasma.