1 Introduction

Nonlinear wave propagation in dusty plasma is one of the most interesting research topics of modern plasma physics because of its huge existence in different areas such as planetary rings, asteroid zones, magnetosphere, coating of thin films (Selwyn 1993), plasma crystals (Thomas et al. 1994), cometary tails and atmosphere of lower part of the earth (Goertz 1989). Due to the presence of different types of dust charged grains in a plasma, a number of different wave modes are introduced, for examples, dust acoustic mode (Rao et al. 1990), dust ion acoustic mode (Kourakis and Shukla 2004), dust lattice mode (Melandso 1996), shukla-varma mode (Shukla and Varma 1993), dust Berstain-Green-Kruskal mode (Tribeche and Zerguini 2004) and dust drift mode (Shukla et al. 1991). Rao et al. (1990) investigated the existence of a new extremely low-phase velocity dust acoustic waves (DAW) in an unmagnetized dusty plasma. Shukla and Silin (1992) studied the nonlinear dust-ion acoustic waves (DIAW) in a dusty plasma. Many experimental and theoretical observations performed by D’Angelo (1995), Barkan et al. (1995, 1996), Nakamura et al. (1999), Duan et al. (2001) have confirmed the linear and nonlinear phenomena of both DAW and DIAW. Recently, Saini and Kohli (2013) studied dust-acoustic solitary waves and double layers with two temperature ions in a nonextensive dusty plasma. Bains et al. (2013) investigated dust-acoustic wave modulation in the presence of q-nonextensive electrons and ions in dusty plasma. More recently, Ali Shan and Akhtar (2014) studied large amplitude acoustic solitons in a warm electronegative dusty plasma with q-nonextensive distributed electrons.

It is important to note that Maxwell distribution is valid for the macroscopic ergodic equilibrium state. However, Maxwell distribution may not be adequate to describe the long range interactions in unmagnetized collision less plasma in which the non-equilibrium stationary state exists. This state may occur because of a number of physical mechanisms such as external force field present in natural space plasma environments, wave-particle interaction, turbulence, etc. Space plasma observations clearly indicate the presence of ion and electron populations that are far away from their thermodynamic equilibrium (Shukla et al. 1986; Pakzad 2009). Renyi proposed a new statistical approach (Renyi 1955), namely non-extensive statistics or Tsallis statistics based on the derivation of Boltzmann-Gibbs-Shannon (BGS) ex tropic measure (Tsallis 1988) to study the cases where Maxwell distribution is not suitable. This was first acknowledged by Renyi (1955) and afterward proposed by Tsallis (1988), where the entropic index q that characterized the degree of non extensivity of the considered system. The Tsallis distribution is also known as q-Gaussian which is a probability distribution arising from the optimization of the Tsallis entropy. Tsallis (1988) has modeled nonextensivity by considering a composition law in the sense that the entropy of the composition (A+B) of two independent systems A and B is equal to \(S^{(A+B)}_{q}=S_{q}^{(A)}+S_{q}^{(B)}+(1-q)S_{q}^{(A)}S_{q}^{(B)}\), where the parameter q which underpins the generalized entropy of Tsallis is linked to the underlying dynamics of the system and gives a measure of the degree of its correlation. In statistical mechanics and thermodynamics, systems which are characterized by the property of nonextensivity, are systems for which the entropy of the whole is different from the sum of the entropies of the respective parts. In other words, the generalized entropy of the whole is greater than the sum of the entropies of the parts if q<1 which is known as superextensivity, whereas the generalized entropy of the system is smaller than the sum of the entropies of the parts if q>1 which is known as subextensivity. The q-entropy may represent a suitable frame for the analysis of many astrophysical scenarios (Amour and Tribeche 2010; Bains et al. 2011), for examples, stellar polytropes, solar neutrino problem, and peculiar velocity distribution of galaxy cluster. It should be noted that the q-distribution is unnormalizable when q<−1. In the extensive limiting case when q→1, the q-distribution reduces to the best known Maxwell-Boltzmann velocity distribution.

Recently, by using bifurcation theory of planar dynamical systems, Samanta et al. (2013a, 2013b, 2013c) investigated nonlinear traveling waves in plasmas in the frameworks of KP and ZK equations obtained by reductive perturbation technique (RPT). Saha and Chatterjee (2013a) studied nonlinear electron acoustic traveling waves in an unmagnetized quantum plasma with cold and hot electrons in the framework of KdV equation obtained by reductive perturbation technique (RPT) by using bifurcation theory of planar dynamical systems. Very recently, Saha and Chatterjee (2013b) studied nonlinear dust ion acoustic traveling waves in the framework of MKP equation obtained by reductive perturbation technique (RPT) in a magnetized dusty plasma with superthermal electrons by using bifurcation theory of planar dynamical systems.

In the present work, our intention is to study dust acoustic solitary and periodic waves in an unmagnetized plasma with q-nonextensive velocity distributed ions through non-perturbative approach by applying the bifurcation theory of planar dynamical systems. Two exact solutions of the dust acoustic solitary and periodic waves are obtained depending on the system parameters q and v. From the dust acoustic solitary wave and periodic wave solutions, we have presented the significant effect of the parameter q on the characteristics of dust acoustic solitary and periodic waves.

The remaining part of the paper is organized as follows: In Sect. 2, we consider basic equations. In Sect. 3, we study bifurcations of phase portraits. Two exact solutions are derived in Sect. 4. We present the parametric effect in Sect. 5 and Sect. 6 is kept for conclusions.

2 Basic model equations

In this paper, we consider a two component unmagnetized dusty plasma whose constituents are dust particles and q-nonextensive velocity distributed ions. The normalized model equations for one-dimensional low velocity dust acoustic oscillations (Tribeche and Merriche 2011) are given by

$$\begin{aligned}& \frac{\partial n_d}{\partial t}+\frac{\partial(n_du_d)}{\partial x} = 0, \end{aligned}$$
(1)
$$\begin{aligned}& \frac{\partial u_d}{\partial t}+u_d\frac{\partial u_d}{\partial x} = \frac{\partial\phi}{\partial x}, \end{aligned}$$
(2)
$$\begin{aligned}& \frac{\partial^2 \phi}{\partial x^2} =n_d-n_i. \end{aligned}$$
(3)

In order to model ions, we use the following distribution function (Ghosh et al. 2012):

$$f_i(v)=C_q\biggl\{ 1+(q-1)\biggl[\frac{m_iv^2}{2T_i}- \frac{e\phi}{T_i}\biggr]\biggr\} ^{\frac{1}{(q-1)}}, $$

where ϕ denotes the electrostatic potential and the remaining variables or parameters obey their usual meaning. It is really important to note that f i (v) is the particular distribution which maximizes the Tsallis entropy and, thus, conforms to the laws of thermodynamics. In this case, the constant of normalization is given by

$$C_q = n_{i0} \frac{\varGamma(\frac{1}{1-q})}{\varGamma(\frac{1}{1-q} -\frac {1}{2})} \sqrt{\frac{m_i(1-q)}{2\pi T_i}} \quad\mbox{for }-1<q<1, $$

and

$$C_q = n_{i0} \frac{1+q}{2} \frac{\varGamma(\frac{1}{q-1}+\frac {1}{2})}{\varGamma(\frac{1}{q-1})} \sqrt{ \frac{m_i(q-1)}{2\pi T_i}}\quad \mbox{for }q>1. $$

Integrating f i (v) over all velocity space, we obtain the following nonextensive ion number density as:

$$n_i(\phi)=n_{i0}\biggl\{ {1-(q-1)\frac{e\phi}{T_i}}\biggr\} ^{1/(q-1)+1/2}. $$

Therefore, the normalized ion number density (Ghosh et al. 2012) is given by

$$ n_i(\phi)=\bigl\{ {1-(q-1)\phi}\bigr\} ^{1/(q-1)+1/2}. $$
(4)

where the parameter q is a real number greater than −1, and it stands for the strength of nonextensivity.

Here n d and n i denote the number densities of the dust particles and ions, respectively, normalized by their unperturbed densities n d0 and n i0. In this case, u d and ϕ are the dust fluid velocity and electrostatic wave potential, respectively, normalized by the dust acoustic speed C d =(Z d T i /m d )1/2 and T i /e, where e is the electron charge, m d is the mass of dust particles and Z d is the number of the charge residing on the dust grains. The time t and space variable x are normalized by the dust plasma frequency \(\omega_{pd}^{-1}=(m_{d}/4\pi e^{2} n_{d0}Z_{d})^{1/2}\) and the Debye length λ d =(T i /4πe 2 n d0 Z d )1/2, respectively, by using the charge neutrality condition n i0=n d0 Z d .

To investigate all traveling wave solutions of our system, we consider the traveling wave transformation ξ=x−vt, where v is the speed of the traveling wave. Using this transformation and the initial condition u d =0,n d =1 and ϕ=0 in Eqs. (1) and (2), we obtain

$$\begin{aligned} n_d= \frac{v}{\sqrt{v^2+2\phi}}. \end{aligned}$$
(5)

Substituting Eqs. (4) and (5) into Eq. (3) and considering the terms of ϕ up to second degree, we have

$$\begin{aligned} \frac{d^2 \phi}{d\xi^2} =&\biggl[\frac{(1+q)}{2}-\frac{1}{v^2}\biggr]\phi \\ &{}- \biggl[\frac {(1+q)(3-q)}{8}-\frac{3}{2v^4}\biggr]\phi^2. \end{aligned}$$
(6)

Then Eq. (6) is equivalent to the following dynamical system:

$$ \begin{cases} \frac{d\phi}{d \xi}=z, \\ \frac{dz}{d \xi}=[\frac{(1+q)}{2}-\frac{1}{v^2}]\phi-[\frac{(1+q)(3-q)}{8}-\frac{3}{2v^4}]\phi^2. \end{cases} $$
(7)

The system Eq. (7) is a planar Hamiltonian system and integrating the system (7) we obtain the Hamiltonian function:

$$\begin{aligned} H(\phi,z) =&\frac{z^2}{2}+\biggl[\frac{(1+q)(3-q)}{8}-\frac{3}{2v^4}\biggr] \frac{\phi ^3}{3} \\ &{}-\biggl[\frac{(1+q)}{2}-\frac{1}{v^2}\biggr] \frac{\phi^2}{2}=h. \end{aligned}$$
(8)

The system Eq. (7) is a planar dynamical system with parameters q and v. It is really important to note that the phase orbits defined by the vector fields of Eq. (7) will determine all traveling wave solutions of Eq. (6). We investigate the bifurcations of phase portraits of Eq. (7) in the (ϕ,z) phase plane depending on the parameters q and v. A solitary wave solution of Eq. (6) corresponds to a homoclinic orbit of Eq. (7). A periodic orbit of Eq. (7) corresponds to a periodic traveling wave solution of Eq. (6).

3 Bifurcations of phase portraits of Eq. (7)

In this section, we search for all possible periodic orbits and homoclinic orbits defined by the vector field Eq. (7) when the parameters q and v are changed. When a≠0, and b≠0, the dynamical system (7) has two equilibrium points at E 0(ϕ 0,0) and E 1(ϕ 1,0), with ϕ 0=0 and \(\phi_{1}=\frac{b}{a}\), where \(a=[\frac{(1+q)(3-q)}{8}-\frac{3}{2v^{4}}]\) and \(b=[\frac {(1+q)}{2}-\frac{1}{v^{2}}]\). Let M(ϕ i ,0) be the coefficient matrix of the linearized system of Eq. (7) at an equilibrium point E i (ϕ i ,0). Then we obtain

$$ J=\operatorname{det} M(\phi_i,0)=-b+2a\phi_i. $$
(9)

By applying the theory of planar dynamical systems (Saha 2012; Guckenheimer and Holmes 1983), it should be noted that an equilibrium point E i (ϕ i ,0) of the planar dynamical system (7) is a saddle point for J<0 and the equilibrium point E i (ϕ i ,0) of the planar dynamical system (7) is a center for J>0.

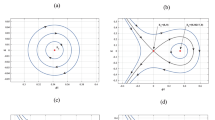
With the help of systematic analysis, we have shown the different phase portraits of Eq. (7) depending on the parameters q and v, shown in Figs. 1 and 2.

Fig. 1
figure 1

Phase portrait of Eq. (7) for q=1.723 and v=3.5 (here “phi” denotes “ϕ”)

Full size image
Fig. 2
figure 2

Phase portrait of Eq. (7) for q=−0.81 and v=0.8 (here “phi” denotes “ϕ”)

Full size image

For the phase portrait given by Fig. 1, the parameters q and v are connected with the relations \(\frac{(1+q)(3-q)}{8}>\frac{3}{2v^{4}}\) and \(\frac{(1+q)}{2}>\frac{1}{v^{2}}\). Figure 1 shows that there exist a homoclinic orbit at the equilibrium point E 0(ϕ 0,0) and a family of periodic orbits at E 1(ϕ 1,0). In this case, equilibrium point E 0(ϕ 0,0) is a saddle point and equilibrium point E 1(ϕ 1,0) is a center. For the phase portrait given by Fig. 2, the parameters q and v are connected with the relations \(\frac{(1+q)(3-q)}{8}<\frac{3}{2v^{4}}\) and \(\frac{(1+q)}{2}<\frac{1}{v^{2}}\). We get homoclinic orbit at the equilibrium point E 1(ϕ 1,0) and a family of periodic orbits at E 0(ϕ 0,0). Here E 0(ϕ 0,0) is a center and E 1(ϕ 1,0) is a saddle point.

4 Exact traveling wave solutions of Eq. (6)

In this section, applying the planar dynamical system given by Eq. (7) and the Hamiltonian function given by Eq. (8) with h=0, we derive solitary wave solution and periodic traveling wave solution of Eq. (6) depending on different parameters.

(1) When the parameters q and v satisfy the conditions \(\frac {(1+q)(3-q)}{8}>\frac{3}{2v^{4}}\) and \(\frac{(1+q)}{2}>\frac{1}{v^{2}}\) (see Figs. 1 and 3), the system Eq. (6) has compressive solitary wave solution given by

$$ \phi=\frac{3[\frac{(1+q)}{2}-\frac{1}{v^2}]}{2[\frac {(1+q)(3-q)}{8}-\frac{3}{2v^4}]} sech^2\biggl(\frac{1}{2}\sqrt{\biggl[ \frac{(1+q)}{2}-\frac{1}{v^2}\biggr]} \xi\biggr). $$
(10)

(2) When the parameters q and v satisfy the conditions \(\frac {(1+q)(3-q)}{8}<\frac{3}{2v^{4}}\) and \(\frac{(1+q)}{2}<\frac{1}{v^{2}}\) (see Figs. 2 and 4), the system Eq. (6) has periodic traveling wave solution given by

$$ \phi=\frac{3[\frac{(1+q)}{2}-\frac{1}{v^2}]}{2[\frac {(1+q)(3-q)}{8}-\frac{3}{2v^4}]} sec^2\biggl(\frac{1}{2}\sqrt{-\biggl[ \frac{(1+q)}{2}-\frac{1}{v^2}\biggr]} \xi\biggr). $$
(11)
Fig. 3
figure 3

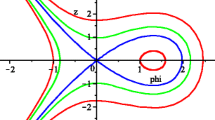
Solitary wave solutions of Eq. (6) have been plotted for v=0.35 with q=1.723 (black dashed curve), q=1.923 (blue solid curve) and q=2.123 (long dashed red curve)

Full size image
Fig. 4
figure 4

Periodic traveling wave solutions of Eq. (6) have been plotted for v=0.8 with q=−0.81 (black dashed curve), q=−0.51 (blue solid curve) and q=−0.11 (long dashed red curve)

Full size image

5 Parametric effect

In this section, we have presented the effect of the nonextensive parameter q on the characteristics of dust acoustic solitary and periodic waves.

Figure 3 shows the variation of solitary wave profile for different values of the nonextensive parameter q with fixed value of v. Here ϕ is ploted against ξ for v=0.35 with q=1.723 (black dashed curve), q=1.923 (blue solid curve) and q=2.123 (long dashed red curve). In this case, we choose parameters in such a way that they satisfy the conditions \(\frac{(1+q)(3-q)}{8}>\frac{3}{2v^{4}}\) and \(\frac{(1+q)}{2}>\frac {1}{v^{2}}\). The amplitude and width of the solitary waves increase with increase in q. Then we can conclude that the dust acoustic solitary waves are flourished as the electrons evolve far away from their Maxwell-Boltzmann equilibrium.

In the Fig. 4, we have shown the variation of periodic traveling wave profile for different values of the nonextensive parameter q with fixed value of v. Here ϕ is ploted against ξ for v=0.8 with q=−0.81 (black dashed curve), q=−0.51 (blue solid curve) and q=−0.11 (long dashed red curve). In this case, we choose parameters in such a way that they satisfy the conditions \(\frac{(1+q)(3-q)}{8}<\frac{3}{2v^{4}}\) and \(\frac{(1+q)}{2}<\frac {1}{v^{2}}\). The amplitude and width of periodic traveling waves increase with increase in q. Then we can conclude that the dust acoustic periodic waves are diminished as the electrons evolve far away from their Maxwell-Boltzmann equilibrium.

6 Conclusions

We have investigated dust acoustic solitary waves and periodic waves in an unmagnetized dusty plasma with nonextensive ions through non-perturbative approach. By applying the bifurcation theory of planar dynamical systems, we have shown that our model has dust acoustic solitary and periodic wave solutions. Two exact solutions for dust acoustic solitary and periodic waves have been derived with the help of Hamiltonian function given by Eq. (8) and the traveling wave system given by Eq. (7). From these exact traveling wave solutions, the effect of nonextensive parameter (q) on the characteristics of dust acoustic solitary and periodic waves has been shown. Our present study may be helpful in understanding the salient features of the nonlinear solitary and periodic structures in mercury, solar wind and in magnetosphere of the Earth.