1 Introduction

Studies of nonlinear wave phenomena in collisionless plasmas provide a firm basis not only for exploring fundamental properties of the nonlinear physics but also for developing practical application in controlled nuclear fusion technologies. About 37 years ago, Watanabe and Taniuti [1] have first shown the existence of the electron-acoustic (EA) mode in a plasma of two-temperature (cold and hot) electrons. This is basically an electro-acoustic wave in which the inertia is provided by the mass of the cold electron, and the restoring force comes from the pressure of the hot electrons. The ions play the role of a neutralizing background, i.e., the ion dynamics does not influence the EA waves, since the EA wave frequency is much larger than the ion plasma frequency. The propagation of the EA waves has received a great deal of renewed interest, not only because the two electron temperature plasma is very common in laboratory experiments [2–6], and in space [7–12] but also because of the potential importance of the EA waves in interpreting electrostatic component of the broadband electrostatic noise (BEN) observed in the cusp of the terrestrial magnetosphere [13], in the geomagnetic tail [14], in white dwarfs and neutron stars [15], etc.

In the present days, there is a great deal of interest in understanding the basic properties of matter under extreme conditions [16–23]. A white dwarf is an example of matter under extreme condition. In a white dwarf, the matter compresses to an enormous density (one cubic meter of material from a white dwarf core weighs about one billion tonnes). The core is also very hot as it was once the active core of a star, but is now exposed to outer space and will slowly cool over billions of years, as it no longer burns fuel by nuclear fusion to generate heat. The material inside the white dwarf is rather like a very dense gaseous metal, initially, with electrons tripped from the nuclei and nuclei vibrating due to their thermal energy. When this happens, the white dwarf will contract slightly, until the electrons are squeezed together as tightly as quantum mechanics will allow. At this point, the gas of electrons which permeates the solid ion lattice becomes a degenerate electron gas (which although extremely hot behaves as if it was cold). This is a purely (and somewhat mysterious) quantum mechanical phenomenon, but the degeneracy pressure produced by these tightly packed electrons stops the core from collapsing under its own gravity. In case of such a compact object, the degenerate electron number density is so high (in white dwarfs it can be of the order of 10 30 cm −3, even more) [24–27] that the electron Fermi energy is comparable to the electron mass energy and the electron speed is comparable to the speed of light in a vacuum. Chandrasekhar [16, 17] presented a general expression for the relativistic ion and electron pressures in his classical papers. The pressure for cold electron fluid can be given by the following equation

$$ P_{c}=K_{c}n_{c}^{\alpha}, $$
(1)

where n c is the cold electron number density and

$$ \alpha=\frac{5}{3};\quad K_{c}=\frac{3}{5}\left(\frac{\pi}{3}\right)^{\frac{1}{3}} \frac{\pi\hbar^{2}}{m}\simeq\frac{3}{5}\Lambda_{c}\hbar c, $$
(2)

for the non-relativistic limit (where \(\varLambda _{c}=\pi \hbar /mc=1.2\times 10^{-10}\) cm, and \(\hbar \) is the Planck constant divided by 2π). And for hot electron fluids

$$ P_{h}=K_{h}n_{h}^{\gamma}, $$
(3)

where

$$\begin{array}{@{}rcl@{}} \gamma=\frac{4}{3};\quad K_{h}=\frac{3}{4}\left(\frac{\pi^{2}}{9}\right)^{\frac{1}{3}} \hbar c\simeq\frac{3}{4} \hbar c, \end{array} $$
(4)

for the ultra-relativistic limit [16–18].

There has been an enormous interest in understanding a quantum plasma physics (i.e., a plasma which has a very high electron number density in comparison with classical plasmas where the plasma particle number density is relatively low) because it is a new emerging and a rapidly growing subfield of plasma physics [28–34]. By considering a quantum plasma physics, Shukla et al. [32] investigated the basic properties of EASWs. They derived Kadomtsev-Petviashvili equation and found that the angular dependence of the physical quantities and the presence of cold electrons in a quantum plasma lead to the coexistence of some new interesting novel solitary structures quite distinctive from the classical ones. Sah and Manta [33] investigated in a three component unmagnetized dense quantum plasma consisting of two distinct groups of electrons and examined numerically on the profiles of the amplitude and the width of EA solitary waves. El-Labany et al. [35] considered a quantum plasma system and rigorously investigated the effects of Bohm potential on the head-on collision between two quantum electron-acoustic solitary waves using the extended Poincaré-Lighthill-Kuo method.

Recently, Chandra et al. [36, 37] considered both unmagnetized and magnetized relativistic quantum plasma and rigorously investigated the basic properties of solitary excitations by using the quantum hydrodynamic model. The formation of electrostatic shocks in a super-dense plasma composed of relativistically degenerate electrons and fully ionized ions is theoretically investigated by Eliasson and Shukla [38]. Masood and Eliasson [39] considered a model for nonlinear ion waves in an unmagnetized plasma with relativistically degenerate electrons and cold fluid ions and studied the properties of localized ion acoustic solitons for parameters relevant for dense astrophysical objects such as white dwarf stars. By using a Sagdeev pseudo-potential method, the propagation of nonlinear ion waves in relativistically degenerate electron-ion plasmas has been investigated theoretically by Akbari-Moghanjoughi [40]. He found that the electron relativistic degeneracy parameter has significant effects on nonlinear wave dynamics in superdense degenerate plasmas such as those encountered in white dwarfs and the cores of massive planets.

Moreover, quantum EA solitary wave (QEASWs) represents one of the most important aspects of nonlinear waves in modern quantum plasma researches. The QEASWs can exist in a quantum plasma consisting of two different types of electrons (i.e., hot and cold electrons). Typically, QEASWs are high frequency in comparison with the quantum ion plasma frequency. It is important to mention here that in quantum plasmas, two population electrons, i.e., densely and sparsely populated electrons, can exist because, according to the Fermi gas model, Fermi temperature is directly related to number density of fermionic particles. In astrophysical dense compact objects, the electron Fermi temperature is usually greater than the electron thermal temperature. Therefore, plasma becomes degenerate and quantum mechanical effects can no longer be ignored. Elwakil et al. [41] considered a four-component relativistic degenerate plasma whose constituents are cold relativistic electron fluid, non-thermal hot electrons obeying a non-thermal distribution, a relativistic electron beam, and stationary ions, and studied the nonlinear characteristics of EASWs. Sahu and Roychoudhurya [42] derived the exact Sagdeev pseudopotential for EAWs in a two electron temperature plasma (cold and hot electrons) in the presence of relativistic electron beam plasma using a vortex-like distribution for trapped electrons. All of the authors did not consider the effects of relativistic limits (i.e., both non-relativistic and ultra-relativistic) and degenerate plasma pressure which can significantly modify the propagation of solitary and shock waves. As far as we know, no theoretical investigation has been made to study the extreme conditions of matter for both non-relativistic and ultra-relativistic limits, and considering the effects of relativistic parameter and degenerate pressure in a one-dimensional EA mode. Therefore, in our present work, we attempt to study the basic features of EASWs by deriving the Korteweg-de Vries equation in a degenerate quantum plasma containing degenerate cold and hot electrons and static positive ion fluids.

2 Governing Equations

We consider a nonlinear propagation of EA waves in an unmagnetized, collisionless, homogeneous dense plasma system. The plasma system is assumed to be composed of non-relativistic inertial cold electrons, both non-relativistic and ultra-relativistic degenerate hot electron fluids, and static positive ions. Thus at equilibrium, we have n i0 = n c0+n h0, where n s0 is the equilibrium number density of the species s (s = c, h, i for cold electrons, hot electrons, positive ions, respectively). The nonlinear dynamics of the electrostatic waves propagating in such a degenerate quantum plasma system is governed by the following normalized equations

$$\begin{array}{@{}rcl@{}} &&\frac{\partial n_{s}}{\partial t} +\frac{\partial}{\partial x} (n_{s}u_{s}) = 0, \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} &&\frac{\partial u_{c}}{\partial t} + u_{c} \frac{\partial u_{c}} {\partial x}-\frac{\partial \phi} {\partial x}+\frac{K_{1}}{n_{c}}\frac{\partial n_{c}^{\alpha}}{\partial x} =0, \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} &&n_{h} \frac{\partial \phi}{\partial x}-K_{2}\frac{\partial n_{h}^{\gamma}}{\partial x}=0, \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} &&\frac{\partial^{2} \phi}{\partial x^{2}}=-\rho, \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} &&\rho = \upmu-n_{c}-(\upmu-1)n_{h}, \end{array} $$
(9)

where n s (s =c, h, i) is the plasma species number density normalized by its equilibrium value n s0, u s is the plasma fluid speed normalized by C c = (m h c 2/m c )1/2 with m h and m c being the hot electron and the cold electron masses, c is the speed of light in vacuum, ϕ is the electrostatic wave potential normalized by m h c 2/e. Here, μ (=n i0/n c0) is the ratio of ion-to-cold electron number density. The time variable (t) is normalized by \({\omega _{pi}}=\left (4 \pi n_{c0}e^{2}/m_{c}\right )^{1/2}\), and the space variable (x) is normalized by \(\lambda _{s}=\left (m_{h}c^{2}/4 \pi n_{c0}e^{2}\right )^{1/2}\). We have defined \(K_{1} = n_{c0}^{\alpha-1}K_i/m_c c^2\) and \(K_2 = n_{h0}^{\gamma-1}K_e/m_h c^2\).

3 Derivation of K-dV Equation

Now, we derive K-dV equation by employing the reductive perturbation technique in order to examine the characteristics of the electrostatic solitary waves propagating in a dense plasma system. We introduce the stretched coordinates [43, 44] as follows:

$$ \xi=-{\epsilon}^{1/2}(x + V_{p}t), \quad \tau={\epsilon}^{3/2}t, $$
(10)

where V p is the wave phase speed (ω/k with ω being the angular frequency and k being the wave number), and 𝜖 is a smallness parameter measuring the weakness of the dispersion (0<𝜖<1). We then expand the parameters n c , n h , u c , ϕ, and ρ in power series of 𝜖 as:

$$\begin{array}{@{}rcl@{}} n_{c}&=&1+\epsilon n_{c}^{(1)}+\epsilon^{2}n_{c}^{(2)}+ {\cdots} , \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} n_{h}&=&1+\epsilon n_{h}^{(1)}+\epsilon^{2}n_{h}^{(2)}+ {\cdots} , \end{array} $$
(12)
$$\begin{array}{@{}rcl@{}} u_{c}&=&\epsilon u_{c}^{(1)}+\epsilon^{2}u_{c}^{(2)}+{\cdots} , \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} \phi&=&\epsilon\phi^{(1)}+\epsilon^{2}\phi^{(2)}+{\cdots} , \end{array} $$
(14)
$$\begin{array}{@{}rcl@{}} \rho&=&\epsilon\rho^{(1)}+\epsilon^{2}\rho^{(2)}+{\cdots} , \end{array} $$
(15)

Now, expressing (5–9) (using (10), in terms of ξ and τ, and substituting (11–15), one can easily develop different sets of equations in various powers of 𝜖. To the lowest order in 𝜖, we have: \(u_{c}^{(1)}=V_{p}\phi ^{(1)}/({V_{p}^{2}}-K_{1}^{\prime })\), \(n_{c}^{(1)}=-\phi ^{(1)}/({V_{p}^{2}}-K_{1}^{\prime })\), \(n_{h}^{(1)}=\phi ^{(1)}/K_{2}^{\prime }\), \(V_{p}=\sqrt {\frac {K_{2}^{\prime }}{\upmu -1}+K_{1}^{\prime }}\), where \(K_{1}^{\prime }=\alpha K_{1}\) and \(K_{2}^{\prime }=\gamma K_{2}\). The relation \(V_{p}=\sqrt {\frac {K_{2}^{\prime }}{\upmu -1}+K_{1}^{\prime }}\) represents the dispersion relation as well as the phase speed for the EA type electrostatic waves in the degenerate quantum plasma under consideration.

To the next higher order in 𝜖, we obtain a set of equations

$$\begin{array}{@{}rcl@{}} \frac{\partial n_{c}^{(1)}}{\partial \tau} -V_{p}\frac{\partial n_{c}^{(2)}}{\partial \xi} -\frac{\partial}{\partial \xi}\left[u_{c}^{(2)}+n_{c}^{(1)}u_{c}^{(1)}\right]=0, \end{array} $$
(16)
$$\begin{array}{@{}rcl@{}} \frac{\partial u_{c}^{(1)}}{\partial \tau} &-&V_{p}\frac{\partial u_{c}^{(2)}}{\partial \xi} -u_{c}^{(1)}\frac{\partial u_{c}^{(1)}}{\partial \xi}+\frac{\partial \phi^{(2)}}{\partial \xi}\\ &-&K_{1}^{\prime}\frac{\partial}{\partial \xi}\left[n_{c}^{(2)}+\frac{(\alpha-2)}{2}{\left(n_{c}^{(1)}\right)}^{2}\right] =0, \end{array} $$
(17)
$$\begin{array}{@{}rcl@{}} \frac{\partial \phi^{(2)}}{\partial \xi} &-&K_{2}^{\prime} \frac{\partial}{\partial \xi}\left[n_{h}^{(2)}+\frac{(\gamma-2)}{2}{\left(n_{h}^{(1)}\right)}^{2}\right]=0, \end{array} $$
(18)
$$\begin{array}{@{}rcl@{}} \frac{\partial^{2} \phi^{(1)}}{\partial \xi^{2}} &= &- {\rho^{(1)}}, \end{array} $$
(19)
$$\begin{array}{@{}rcl@{}} \rho^{(1)} &=&-n_{c}^{(2)}-(\upmu-1)n_{h}^{(2)}, \end{array} $$
(20)

Now, combining Eqs. (16–20), we deduce Korteweg-de Vries (K-dV) equation

$$ \frac{\partial\phi^{(1)}}{\partial \tau} + A \phi^{(1)} \frac{\partial \phi^{(1)}}{\partial \xi} + B \frac{\partial^{3} \phi^{(1)}}{\partial \xi^{3}}= 0, $$
(21)

where

$$\begin{array}{@{}rcl@{}} A&=&\frac{{\left({V_{p}^{2}}\,-\,K_{1}^{\prime}\right)}^{2}}{2V_{p}}\!\left[\!\frac{(\gamma\,-\,2)(\upmu\,-\,1)}{{K_{2}^{\prime}}^{2}}\,-\,\frac{3{V_{p}^{2}}\,+\,K_{1}^{\prime}\!(\alpha\!\,-\,\!2)}{{\left({V_{p}^{2}}\,-\,K_{1}^{\prime}\right)}^{3}}\!\right], \end{array} $$
(22)
$$\begin{array}{@{}rcl@{}} B&=&\frac{{\left({V_{p}^{2}}-K_{1}^{\prime}\right)}^{2}}{2V_{p}}. \end{array} $$
(23)

4 Numerical Analysis

Our aim is now to numerically analyze the K-dV equation. However, for clear understanding, we first briefly discuss the stationary solitary wave solution for (21). The stationary solitary wave solution of standard K-dV equation is obtained by considering a frame ζ = ξ−u 0 τ (u 0 is the small increment of wave speed above sound speed) and the solution is,

$$\begin{array}{@{}rcl@{}} \phi^{(1)}=\mathrm \phi_{m}\text{sech}^{2}(\xi/{\Delta}), \end{array} $$
(24)

where the amplitude, ϕ m = 3u 0/A, and the width, Δ = (4B/u 0)1/2.

The conditions for the existence of one-dimensional solitary waves, and their basic features are found to be significantly modified in the presence of non-relativistic cold electrons, both non-relativistic and ultra-relativistic hot electrons and positively charged static ions. The EA waves are seen to be modified when ions are non-relativistic degenerate (α = 5/3) and electrons are ultra-relativistic degenerate (γ = 4/3), compared to when electrons and ions are non-relativistic degenerate (α = γ = 5/3). It is important to mention that our present work deals with the properties of one-dimensional EASWs in a relativistic degenerate quantum plasma (containing degenerate cold electron and hot electron fluids, and positively charged static ions), and that we have derived the K-dV equation. We have then analyzed the basic features of the one-dimensional EASWs. It is also important to note that for μ>μ c (μ c =0.89), rarefactive solitary waves are found but no compressive solitary waves exist at μ<μ c . We have considered u 0 = 0.01 for our numerical analysis of EASWs for the plasma system under investigation here.

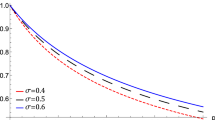
Figure 1 shows the variation of phase speed (V P ) with ion to cold electron number density ratio μ. It is found that the phase speed decreases with the increasing values of μ. It is expected as the phase speed V p (derived from this considered plasma) is higher for lower values of μ (see the expression of V p in Section 3). The variation of the amplitude of EASWs for both non-relativistic and ultra-relativistic limits is shown in Fig. 2. Figures 3, 4, 5, 6, 7, and 8 shows the variation of amplitude with μ, u0, and Δ for both non-relativistic and ultra-relativistic limits.

Fig. 1
figure 1

Showing the variation of phase speed V p with ion-to-cold electron number density ratio μ for u 0 = 0.01. The dashed blue line represents the ultra-relativistic case and the red one represents the non-relativistic case (color online)

Full size image
Fig. 2
figure 2

Showing the variation of amplitude of EASWs. The dashed blue line represents the ultra-relativistic case and the red one represents the non-relativistic case (color online)

Full size image
Fig. 3
figure 3

Showing the variation of the amplitude of the EA rarefactive solitary waves with μ when both cold electrons and hot electrons are non-relativistic degenerate (color online)

Full size image
Fig. 4
figure 4

Showing the variation of the amplitude of the EA rarefactive solitary waves with μ when cold electrons are non-relativistic degenerate and hot electrons are ultra-relativistic degenerate (color online)

Full size image
Fig. 5
figure 5

Showing the variation of the amplitude of the EA rarefactive solitary waves with u0 when both cold electron and hot electron being non-relativistic degenerate (color online)

Full size image
Fig. 6
figure 6

Showing the variation of the amplitude of the EA rarefactive solitary waves with u0 when cold electrons are non-relativistic degenerate and hot electrons are ultra-relativistic degenerate (color online)

Full size image
Fig. 7
figure 7

Showing the variation of the amplitude of the EA rarefactive solitary waves with Δ when both cold electrons and hot electrons are non-relativistic degenerate (color online)

Full size image
Fig. 8
figure 8

Showing the variation of the amplitude of the EA rarefactive solitary waves with Δ when cold electrons are non-relativistic degenerate and hot electrons are ultra-relativistic degenerate (color online)

Full size image

5 Discussion and Results

We have studied the nonlinear propagation of EASWs in an unmagnetized, collisionless dense plasma (containing non-relativistic or ultra-relativistic degenerate hot electrons, non-relativistic degenerate cold electrons, and positively charged static ions). The degenerate pressure is provided by the hot electrons whereas the inertia is provided by the cold electrons. The positively charged static ions participate only in maintaining the quasi-neutrality condition at equilibrium. We derived a nonlinear K-dV equation and numerically analyzed the basic features of EASWs in a degenerate quantum plasma. Finally, the results that we have found in this investigation can be summarized as follows:

  1. 1.

    The basic properties (speed, amplitude, and width) of EASWs are found to be significantly modified due to the relativistic parameters and plasma particle number densities.

  2. 2.

    We observed that the plasma system under consideration supports only rarefactive solitary waves with negative potential, but no compressive solitary waves exist.

  3. 3.

    The phase speed (V p ) of EASWs decreases with the increasing values of μ (see Figs. 1).

  4. 4.

    The amplitude of EA rarefactive solitary waves increases with the increasing values of μ, u0, and Δ (see Figs. 3, 4, 5, 6, 7, and 8).

  5. 5.

    We also compare the non-relativistic and ultra-relativistic limits in Figs. 3, 4, 5, 6, 7, and 8. We found that the magnitude of the amplitude of the EA rarefactive solitary waves is lower for ultra-relativistic case than for non-relativistic case.

To conclude, the results of the present investigation should be useful in understanding the salient features of localized EA excitation in dense (degenerate) plasmas [7–12, 45–48] as well as laboratory devices [2–6] where the degenerate plasma pressure and relativistic effect are taken into account.