1 Introduction

Electron acoustic waves (EAWs) occur in plasmas containing two distinct groups of electrons. These are high frequency (in comparison with ion plasma frequency) electrostatic modes in which cold electrons provide the inertia and the restoring force comes from the hot electron pressure. The phase speed of EAWs is much larger than the thermal speed of cold electrons but much smaller than the thermal speed of hot electrons. Here ions may be regarded as forming a uniform neutralizing background. Since plasmas with two groups of electrons are known to occur in both space plasmas (Ang and Zhang 2007; Barnes et al. 2003; Feldman et al. 1975, 1983a, 1983b) and laboratory experiments Defler and Simonen (1969), Henry and Trguier (1972), Kadomtsev and Pogutse (1971), Armstrong et al. (1979), Sheridan et al. (1991), Ditmire et al. (1998) the EAWs play an important role in these environments. EAWs have been used to explain the source of broad band electrostatic noise, wave emission in different regions of earth’s magnetosphere and also the hiss observed in the polar cusp region. For this the study of EAWs has become one of the important areas of research in plasma physics. In recent years the study on the nonlinear evolution of EAWs has gained momentum (Bains et al. 2011; Kourakis and Shukla 2004; Singh and Lakhina 2001; Sultana and Kourakis 2011) with a view to explain the observation of moving EAW related structures reported by various space-craft missions, e.g. the FAST at the auroral region (Ergun et al. 1998a, 1998b; Delory et al. 1998; Pottelette et al. 1999) as well as the GEOTAIL and POLAR missions in the magnetosphere (Matsumoto et al. 1994; Franz et al. 1998; Cattell et al. 1999, 2003). However most of the works on EAWs are for classical nonrelativistic plasmas. The matter in some compact astrophysical objects (e.g. white dwarfs, neutron stars, magnetars etc.) exists in extreme conditions of density. In such situation the average inter-Fermion distance is comparable to or less than the thermal de Broglie wavelength and hence quantum degeneracy effects become important. At extreme high densities the thermal pressure of electrons may be negligible as compared to the Fermi degeneracy pressure which arises due to implications of Pauli’s exclusion principle. In such extreme conditions of density the electron Fermi energy E Fe [=ħ 2(3π 2 n e )3/2/2m e ] may become comparable to the electron rest mass energy [m e c 2] and the electron speed can approach the speed of light in vacuum. So the plasma in the interior of such compact astrophysical objects is both degenerate and relativistic. Such a plasma is also likely to be produced in the next generation laser based plasma compression schemes. Under such conditions quantum and relativistic effects are unavoidable. Recently a large number of theoretical investigations have been made of the linear and nonlinear propagation of various electrostatic modes in degenerate quantum plasmas by using the quantum hydrodynamic model (Manfredi 2005; Haas et al. 2003; Gardner and Ringhofer 1996; Shukla and Eliasson 2006; Khan and Mushtaq 2007; Sahu and Roychoudhury 2006, 2007; Ali and Shukla 2006; Shukla and Ali 2005). Recent reviews of quantum plasma physics can be obtained Manfredi (2005), Shukla and Eliasson (2010). However regarding the electron-acoustic waves in degenerate quantum plasmas only a few works have been reported (Misra et al. 2007; Bhowmik et al. 2007; Sah and Manta 2009; Masood and Mushtaq 2008). Misra et al. (2007) have investigated the modulational instability of EAWs in a quantum plasma consisting of two distinct groups of electrons and immobile ions. Bhowmik et al. (2007) studied the oblique modulational instability of EAWs in quantum plasmas. Sah and Manta (2009) considered quantum plasma consisting of inertial cold electrons, inertia less hot electrons and immobile ions and studied the effect of quantum parameter on the formation and properties of electron-acoustic KdV solitary waves. The propagation of electron-acoustic solitary waves in a two-electron temperature quantum magneto plasma has also been reported by Masood and Mushtaq (2008).

All these works use quantum hydrodynamic models and consider only the nonrelativistic cases. But in extreme conditions of density such as in a typical white dwarf where the electron density can be as high as 1028 cm−3 the degeneracy can be relativistic and both quantum and relativistic effects should be taken into account. Recently the nonlinear propagation of ion-acoustic waves in relativistically degenerate quantum plasma has been studied by a few authors (Akbari-Moghanjoughi 2011; Mamun and Shukla 2010; Masood and Eliasson 2011). But to the best of our knowledge no investigation has been made of the nonlinear properties of electron-acoustic waves in degenerate quantum-relativistic plasmas. The purpose of the present paper is to investigate the linear and nonlinear properties of EAWs in relativistically degenerate dense quantum plasma consisting of two distinct groups of electrons and stationary ions. The paper is organized in the following way: in Sect. 2 the basic set of quantum hydrodynamic equations are presented; in Sect. 3 the linear dispersion characteristics is investigated; in Sect. 4 the Korteweg-deVries equation is derived by using the standard perturbation techniques; in Sect. 5 we discuss the dependence of soliton properties on different plasma parameters. The paper ends up with some concluding remarks.

2 Basic equations

We consider the propagation of electron-acoustic waves in an unmagnetized three component completely degenerate dense plasma consisting of two groups of relativistic electrons at different temperatures and stationary cold ions forming a uniform neutralizing background. For electrons the thermal pressure is assumed to be negligible as compared to the degeneracy pressure which arises due to the implications of Pauli Exclusion Principle. In degenerate plasmas the rate of electron-ion collisions is limited due to the Pauli blocking mechanism which allows only degenerate particles with energies limited to a narrow range around the Fermi energy to interact, hence the plasma may be considered to be almost collision-less. The dynamics of such a plasma is governed by the following quantum hydrodynamic equations:

(1)
(2)
(3)

where the subscript j is used to denote hot (eh) and cold (ec) electrons. u j and p j are respectively the fluid velocity and degeneracy pressure of the jth species, ħ is the Planck’s constant divided by 2π, ϕ is the electrostatic wave potential and Z i e is the charge of an ion. Following Chandrasekhar (1939) the electron degeneracy pressure in fully degenerate and relativistic configuration can be expressed in the following form:

(4)

in which

$$ R_{j} = p_{F_j} / m_{e}c = \bigl[ 3h^{3}n_{j} / 8\pi m_{e}^{3}c^{3} \bigr]^{\frac{1}{3}} = R_{j0}n_{j}^{\frac{1}{3}} $$
(5)

where R j0=(n j0/n 0)1/3 with \(n_{0} = 8\pi m_{e}^{3}c^{3} / 3h^{3} \approx5.9 \times10^{29}\ \mbox{cm}^{ - 3}\), ‘c’ being the speed of light in vacuum. \(p_{F_{j}}\) is the electron Fermi relativistic momentum. It is to be noted that in the limits of very small and very large values of relativity parameter R j , we obtain:

(6)
(7)

Note that the degenerate electron pressure depends only on the electron number density but not on the electron temperature. Now considering the fact that \(\frac{1}{n_{j}}\frac{\partial P_{j}}{\partial x} = \frac{\partial\sqrt{1 + R_{j}^{2}}}{\partial x}\) the basic Eqs. (1)–(5) can be written in the following normalized form:

(8)
(9)
(10)

where \(F_{j} = ( \chi/ 3 )( R_{j0}^{2} / \sqrt{1 + R_{j0}^{2}} )\) is the term arising from relativistic pressure in weakly relativistic case, whereas for ultra relativistic case F j =χR j0/3 where χ=m e c 2/2k B T Feh ; H is the non-dimensional quantum diffraction parameter defined as H=ħω ec /2k B T Feh , where T Feh is the Fermi temperatures for hot electrons; δ=n ec0/n eh0 and δ 1=Z i n i0/n eh0, in which n ec0, n eh0 and n i0 are the equilibrium number densities of cold electrons, hot electrons and ions respectively.

The normalization has been carried out in the following manner:

in which \(\omega_{\mathit{ec}} = \sqrt{4\pi n_{\mathit {ec}0}e^{2}/m_{e}}\) is the cold electron plasma frequency, \(c_{\mathit{sh}} = \sqrt{2k_{B}T_{\mathit {Feh}}/m_{e}}\) is the electron-acoustic speed. The charge neutrality at equilibrium reads δ=δ 1−1. It is to be noted that the parameter R j0 is a measure of the relativistic effects and may be called relativistic degeneracy parameter. For ultra relativistic case R j0≫1 and for weakly relativistic case R j0≪1. The parameter R j0 can also be related to mass density as \(\rho(\mathrm{gr}/\mathrm{cm}^{3}) = 1.97 \times10^{6} \cdot R_{j0}^{3}\) (Akbari-Moghanjoughi 2011). The density of white dwarfs can be in the range 105<ρ<109. So in this case the relativity parameter R j0 can be in the range 0.37<R j0<8.

3 Dispersion characteristics

In order to investigate the nonlinear behaviour of electron-acoustic waves we make the following perturbation expansion for the field quantities n eh , u eh , n ec , u ec and ϕ about their equilibrium values:

$$ \begin{bmatrix} n_{j} \\ u_{j} \\ \phi \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} + \varepsilon \begin{bmatrix} n_{j}^{(1)} \\ \noalign{\vspace{3pt}} u_{j}^{(1)} \\ \noalign{\vspace{3pt}} \phi^{(1)} \end{bmatrix} + \varepsilon^{2} \begin{bmatrix} n_{j}^{(2)} \\\noalign{\vspace{3pt}} u_{j}^{(2)} \\ \noalign{\vspace{3pt}} \phi^{(2)} \end{bmatrix} + \cdots{} $$
(11)

Substituting the expansion (11) in Eqs. (8)–(10) and then linearizing and assuming that all the field quantities vary as e i(kx−ωt), we get for normalized wave frequency ω and wave number k, the following linear dispersion relation:

$$ 1 = \frac{1 / \delta}{\omega^{2} - k^{2}F_{\mathit{eh}} - H^{2}k^{4}/4} + \frac{1}{\omega^{2} - k^{2}F_{\mathit{ec}} - H^{2}k^{4}/4} $$
(12)

where \(F_{\mathit{eh}} = ( \chi R_{\mathit{eh}0}^{2} / \sqrt{1 + R_{\mathit{eh}0}^{2}} ) / 3\) and \(F_{\mathit{ec}} = ( \chi\delta^{2 / 3}R_{\mathit{eh}0}^{2} / \allowbreak\sqrt{1 + \delta^{2 / 3}R_{\mathit{eh}0}^{2}} ) / 3\) in the weakly relativistic limit and F eh =χR eh0/3 and F ec =χδ 1/3 R eh0/3 in the ultra relativistic case.

Equation (12) represents the dispersion relation for EAWs in fully degenerate relativistic plasma. It is a quadratic equation in ω 2 and has the solutions:

$$ \begin{aligned}[c] \omega_{1}^{2} &= [ B + \sqrt{B^{2} - 4C} ] / 2 \\ \omega_{2}^{2} &= [ B - \sqrt{B^{2} - 4C} ] / 2 \end{aligned} $$
(13)

where

(14)

It indicates that two stable linear modes for EAWs are possible when one considers inertial and relativistic effects of both groups of electrons.

EAWs are high frequency electrostatic electron oscillations where the restoring force comes from the hot electron pressure and the cold electrons provide the inertia. If we neglect the inertia of hot electrons and assume that the pressure is solely due to the ultra relativistic hot electrons then the dispersion relation (12) reduces to:

$$ \omega^{2} = \frac{\delta k^{2}(\chi R_{\mathit{eh}0} / 3 + H^{2}k^{2} / 4)}{1 + \delta k^{2}(\chi R_{\mathit{eh}0} / 3 + H^{2}k^{2} / 4)} + \frac {H^{2}k^{4}}{4} $$
(15)

In the long wavelength limit (i.e. k→0)

$$ \omega= k\sqrt{\delta\chi R_{\mathit{eh}0} / 3} $$
(16)

The long wave phase speed is:

$$ V_{0} = \omega/k = \sqrt{\delta\chi R_{\mathit{eh}0} / 3} $$
(17)

It represents the long wave dispersion character of EAWs in a quantum-relativistic plasma composed of inertia less hot electrons, inertial cold electrons and stationary ions.

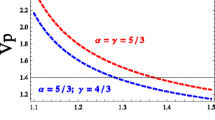
We numerically examine the behaviour of the dispersion relation (15) with respect to the variations of R eh0, δ and H. Figure 1a shows the variation of ω with k for different values of the relativity parameter R eh0. It shows that the wave frequency ω increases with increase in the value of R eh0. Figures 1b and 1c show the ω–k curves for different values of δ and H respectively. Obviously, the wave frequency ω also increases with increase in both δ and H.

Fig. 1a
figure 1

Dispersion curves for different values of the relativity parameter R eh0 keeping δ and H constant

Full size image
Fig. 1b
figure 2

Dispersion curves for different values of the equilibrium cold to hot electron density δ keeping R eh0 and H constant

Full size image
Fig. 1c
figure 3

Dispersion curves for different values of the quantum diffraction parameter H keeping δ and R eh0 constant

Full size image

4 Derivation of the KdV equation

In order to study the nonlinear behaviour of electron acoustic waves we consider inertia less hot ultra relativistic electrons, inertial cold electrons and stationary ions. The pressure effect is assumed to be only due to the hot electrons. This type of consideration has been made by many previous authors (Sah and Manta 2009; Sahu and Roychoudhury 2006, 2007). Following the standard reductive perturbation technique we use the usual stretching of the space and time variables:

$$ \xi= \varepsilon^{1 / 2}(x - V_{0}t)\quad \mbox{and}\quad \tau= \varepsilon^{3 / 2}t $$
(18)

where V 0 is the normalized linear long wave phase velocity given by Eq. (17) and ε is the smallness parameter measuring the dispersion and nonlinear effects. Now writing the Eqs. (8)–(12) in terms of these stretched co-ordinates ξ and τ and then applying the perturbation expansion (11) and solving for the lowest order equation with the boundary condition that \(n_{\mathit{eh}}^{(1)}\), \(u_{\mathit {eh}}^{(1)}\), \(n_{\mathit{ec}}^{(1)}\), \(u_{\mathit{ec}}^{(1)}\) and ϕ (1)→0 as |ξ|→∞, the following solutions are obtained:

$$ \lefteqn{\! \begin{aligned}[c] &n_{\mathit{eh}}^{(1)} = \frac{\delta\phi^{(1)}}{V_{0}^{2}}, \quad u_{\mathit{eh}}^{(1)} = \frac{\delta\phi^{(1)}}{V_{0}}, \\ &n_{\mathit{ec}}^{(1)} = - \frac{\phi^{(1)}}{V_{0}^{2}}, \quad u_{\mathit{ec}}^{(1)} = - \frac{\phi^{(1)}}{V_{0}}. \end{aligned} } $$
(19)

Going for the next higher order terms in ε and following the usual method we obtain the desired Korteweg-de Vries (KdV) equation:

$$ \frac{\partial\phi}{\partial\tau} + A\phi\frac {\partial\phi}{ \partial\xi} + B\frac{\partial^{3}\phi}{\partial\xi^{3}} = 0 $$
(20)

where

(21a)
(21b)

To find the solution of Eq. (20) we transform the independent variables ξ and τ into one variable η=ξ−Mτ where M is the normalized constant speed of the wave frame. Applying the boundary conditions that as η→±∞; \(\phi,\frac{\partial \phi}{\partial\eta} ,\frac{\partial^{2}\phi}{\partial^{2}\eta} \rightarrow0\) the possible stationary solution of Eq. (20) is obtained as:

$$ \phi= \phi_{m}\operatorname{sec} h^{2} \biggl( \frac{\eta}{ \varDelta } \biggr) $$
(22)

where the amplitude ϕ m and width Δ of the soliton are given by:

$$ \phi_{m} = 3\frac{M}{A} $$
(23)

and

$$ \varDelta = \sqrt{\frac{4B}{M}} $$
(24)

The solitary wave structure is formed due to a delicate balance between dispersive and nonlinear effects. Relative strength of these two effects determines the characteristic of such solitary wave structure. The coefficients A and B, corresponding to the nonlinear effect and dispersive effect play a crucial role in determining the solitary wave structure. So it is important to study the dependence of these coefficients on different physical parameters. From Eqs. (17) and (21a)–(21b) it is clear that both the nonlinear and dispersion coefficients get modified due to the inclusion of relativistic effect whereas the quantum effect enters only into the dispersion coefficient. Both these coefficients depend on δ, the equilibrium cold-to-hot electron concentration ratio. For a given H and δ there exists a critical value of the relativity parameter R eh0 at which the dispersion coefficient vanishes. This critical value of R eh0 is given by:

$$ ( R_{\mathit{eh}0} )_{c} = \bigl( 3H\sqrt{1 + \delta} \bigr) / 2 \chi\delta $$
(25)

No solitary structure is possible for R eh0<(R eh0) c . Note that the critical value of the relativity parameter depends on both δ and H.

5 Results and discussion

Using the one-dimensional quantum hydrodynamic model and the standard reductive perturbation technique both the linear and nonlinear properties of electron-acoustic waves have been investigated in three-component relativistically degenerate plasma consisting of two distinct groups of electrons and stationary ions. A general type dispersion relation has been obtained including inertia and quantum relativistic effects of both groups of electrons. It is shown that two stable linear modes of propagation are possible for electron-acoustic waves when one considers the inertia effect of both groups of electrons. The wave frequency is shown to increase with the increase in the values of relativity parameter R eh0, the equilibrium cold-to-hot electron density ratio δ and also the quantum diffraction parameter H.

To study the nonlinear behaviour of the wave a KdV equation has been derived in which the coefficients of the nonlinear and dispersive terms are found to get modified due to the inclusion of quantum relativistic effects. There exists a critical value of the relativistic degeneracy parameter R eh0 such that for R eh0<(R eh0) c no soliton solution is possible. This critical value of the degeneracy parameter is determined by the values of δ and H. From Eqs. (21a), (21b)–(24) it is obvious that the degenerate plasma under consideration supports only rarefactive solitary wave structures which are associated with negative potentials. Figure 2a shows electron-acoustic solitary profiles for different values of the relativistic degeneracy parameter R eh0 (which is directly proportional to the plasma number density) for fixed values of M, δ and H. It shows that both the amplitude and width of the soliton increase with increase of R eh0. Figure 2b shows solitary structures for different values of δ keeping R eh0, M and H constant. It is observed that with increase in δ both the amplitude and width of the soliton increase. Figure 2c shows solitary structures for different values of H keeping other parameters fixed. It shows that the soliton width increases with increase in the value of H but its amplitude is independent of H. The amplitude of electron-acoustic solitary structure increases with increase in R eh0 and δ, but it is independent of H. On the other hand the width of the soliton increases with increase in R eh0, δ or H.

Fig. 2a
figure 4

Electron-acoustic solitary profiles for different values of the relativistic degeneracy parameter R eh0 for fixed values of M, δ and H

Full size image
Fig. 2b
figure 5

Electron-acoustic solitary profiles for different values of the equilibrium cold-to-hot electron concentration ratio δ for fixed values of R eh0, M and H

Full size image
Fig. 2c
figure 6

Electron-acoustic solitary profiles for different values of the quantum diffraction parameter H for fixed values of M, δ and R eh0

Full size image

6 Concluding remarks

Linear and nonlinear propagation characteristics of EAWs are investigated in a relativistic degenerate dense plasma consisting of two distinct groups of electrons and stationary ions. It is shown that the plasma under consideration can support only rarefactive solitary waves under certain restricted regions of plasma parameters. The soliton properties are shown to depend significantly on the relativistic degeneracy parameter R eh0, the equilibrium cold-to-hot electron density ratio δ and also the quantum diffraction parameter H. The present investigation may be helpful in understanding the basic features of electron-acoustic waves in super dense astrophysical objects like white dwarfs, neutron stars as well as in the future intense laser-solid plasma experiments where the relativistic electron degeneracy effects become important.