1 Introduction

The overhead crane is an indispensable manipulation system. It offers heavy cargo transportation services in areas such as the transportation sector, automated assembly lines, shipping yards, automotive industries, mining sector, power plants, and marine industries. Traditionally, the crane is controlled manually. However, due to the human operator’s incompetence in handling the crane, flexibility of the system, and the presence of unexpected endogenous and exogenous disturbances, it may suffer from excessive payload sway. Thus, crane manufacturers devote colossal efforts to build fully automated cranes that meet particular safety and performance criteria. Besides the effects of extraneous perturbations (such as winds, collisions), the hoisting rope’s flexibility makes the system lightly damped. Thus, the trolley motion induces undesirable oscillations that make fast and precise payload positioning time-consuming. Additionally, its operation may even be risky, especially when the payload is of a hazardous type. It should be understood that the crane system is highly nonlinear, under-actuated (primarily when DP phenomenon exists). Stabilization of under-actuated mechanical systems is challenging since it is difficult to evaluate the complex nonlinear behaviour of the uncontrolled dynamics with traditional analysis methods [1,2,3].

As control scheme developments have progressed, efforts have been devoted to the control of under-actuated overhead cranes in recent decades [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. The similarity in these works is that they all consider the payload’s sway as a simple pendulum. That is, compared with the payload, the hook’s mass is wholly ignored. Additionally, the payload is treated as a point mass. However, in practical operations, the payload size is usually large, and the hook mass cannot be neglected. Consequently, as the trolley accelerates/decelerates, the hook oscillates around the trolley. The payload oscillates around the hook simultaneously, producing rather complex DP swing dynamics. The appearance of DP effects further complicates the control problem due to the increased under-actuation degree. Furthermore, the system dynamics are entirely different, consequently deteriorating the performances of traditional control algorithms that are developed without considering the DP effects. Hence, considering this common scenario in real-world applications alongside the effects of parasitic dynamics, nonzero initial conditions, frictions, and external disturbances (such as noise and wind), the effectiveness of the proposed feed-forward techniques such as [7,8,9,10,11,12,13] may not always be reliable since they are susceptible to perturbations. That being said, the merits of these techniques, such as design simplicity (since no feedback sensors are required), cannot be suppressed. On the other hand, the effectiveness of the proposed classical feedback control algorithms, such as pole placement [14], proportional integral derivative control [15,16,17], linear quadratic regulator [18], and model predictive control [19], designed using small-angle approximation is limited to the closeness of this approximation to the real crane system.

A feedback strategy observed to be the most robust in dealing with uncertainties and external disturbances for single-pendulum cranes is the sliding mode control (SMC) [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. The SMC is a variable structure control system characterized by a discontinuous control structure that switches as the system crosses a specific manifold in the state space. It drives the system trajectory to reach and subsequently slide along the manifold along which the system is entirely insensitive to the so-called matched perturbations. However, during this transient reaching phase, the tracking error is difficult to control since the sliding mode is yet to be reached, and the crane may be sensitive to perturbations. One would ideally like to shorten the reaching duration or even eliminate it. One easy way to shorten the reaching duration is to employ more considerable control gains. Using higher gains could increase robustness when one is dealing with large perturbations. However, using higher gains may result in extreme crane sensitivity to parasitic dynamics, actuator saturation, and higher unwanted chattering (a well-known drawback of first-order SMC). It is worth noting that the switching gain should be small for SMC to be practically realizable. Nevertheless, small gains may result in SMC’s performance degradation. Nevertheless, small gains may result in SMC’s performance degradation. To eliminate the reaching phase for cranes with actuator nonlinearities, Defoort et al. [31] proposed a control solution based on integral SMC (ISMC). To circumvent the unwanted chattering, second-order twisting control was proposed by [29]. However, the use of twisting algorithms increases design complexity since the sliding variable’s time derivative is needed. To improve robustness to perturbations, have finite time convergence, and suppress the chattering without the need of sliding variable time derivative, the most preferred second-order SMC algorithm is the super-twisting control (STC) [37].

Considering the highlighted DP problem in actual cranes, it is crucial to design an effective controller that considers the DP effects. Regarding this DP topic, fewer works on SMC were reported in the literature compared to those for traditional single-pendulum cranes, for instance, in [38,39,40,41]. The majority of the available control algorithms for DP cranes are using nonlinear Lyapunov-based energy methods [42,43,44,45,46,47,48] with complex control algorithms. Elsewhere, the PID [49] and feed-forward strategies like input shaping technique [50,51,52] and trajectory planning techniques (TP) [53, 54] have been proposed. Although input shaping technology or other trajectory planning control techniques have been used to tackle the DP problem in cranes and good results achieved, as classic feed-forward control techniques, they primarily rely on the crane’s linear model. Input shaping only deals with sway suppression of the payload, neglecting the positioning accuracy and trolley speed. Elsewhere, in TP control, the crane trajectory planning problem is not fully solved yet, but only provides reasonable solutions for many practical problems. More so, using these feed-forward methods, the control effectiveness might deteriorate when external disturbance or parameter variations occurred. Hence, it is needed to include state feedback into the control strategy for better robustness.

Many studies were without simultaneous regards to the DP effect (a common scenario in practice due to large hook mass or irregular payload), friction, model uncertainties, and disturbances. However, these perturbations’ effects could induce DP effects and positioning error in practice, increasing the difficulty to guarantee control effectiveness. Concerning the highlighted research gap, these problems are simultaneously considered in this paper to work with a more practical crane case. Also, an event that occurs in practice is that when the target position is issued to the controller, the initial control effort may be enormous to overdrive the trolley. In this work, a novel smooth super-twisting control algorithm (NSSTC) is proposed. We will show that using the proposed NSSTC algorithm, the initial peaking of the control effort and the overshoot in the sliding surface variable that may be obtained using a recently proposed modified super-twisting algorithms (MSTC) in [55] and [56] may be alleviated. Additionally, the proposed NSSTC technique can achieve some superior performance than the MSTC technique. The stability of the closed-loop system is proved using a strict quadratic Lyapunov function. Lastly, the effectiveness of the proposed control technique is demonstrated by numerical simulations and tracking error analysis.

The paper’s contribution is summarized as follows.

  1. (1)

    The mathematical model of a perturbed overhead crane that considers the DP effect, actuator dynamics, and friction is presented.

  2. (2)

    The paper proposes a hybrid control strategy using ISMC and novel smooth super-twisting control (NSSTC) for position tracking and sway regulation for DP cranes.

  3. (3)

    It will be shown that the novel algorithm mitigates the sliding surface overshoot and the initial peaking of the control effort, as well as improved performance compared to the MSTC algorithm.

  4. (4)

    To our best knowledge, it will be the first time the algorithm is tested on overhead cranes subject to DP effect, parasitic dynamics, disturbances, and various frictions. To our best knowledge, few works have been reported in control of these effects simultaneously.

  5. (5)

    The proposed algorithm is simple, and sufficient closed-loop stability analysis is proved, implying the proposed algorithm’s effectiveness.

In this paper, \(\mathfrak {R},\mathfrak {R}^{+}\), and \(\mathfrak {R}^{\mathrm{n}}\) refer to the spaces of real numbers, positive real numbers, and real n-vectors, respectively. \(\Vert {\mathbf {X}}\Vert \) is the Frobenius norm of \({\mathbf {X}}\), \(\sigma \) is a stable manifold in space with boundary \(\omega \), while \(x\in \mathfrak {R}, r \in \mathfrak {R}^{+},{\mathbf {X}}\in \mathfrak {R}^{\mathrm{n}}\), and \(\mathrm{n}\) is a natural number.

Paper organization is as follows. Section 2 presents the model of the nominal and perturbed overhead crane. Section 3 is devoted to the design of the proposed NSSTC-ISMC hybrid strategy and the stability analysis of the closed-loop system from a mathematical perspective. In Sect. 4, control experiments, performance evaluation, and comparative analysis of the obtained results based on mean absolute error (MAE) and mean squared error (MSE) criteria are presented. Section 5 concludes the paper.

2 Problem Formulation

2.1 Nominal Crane Dynamics

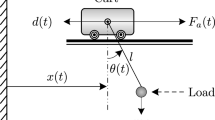
The schematic diagram of the system under study is shown in Fig. 1: a three-degree-of-freedom, 2D overhead crane. The parameters of the system are defined in Table 1. Derivation of the model of the overhead crane system is based on the Euler–Lagrange method. For simplicity, the following assumptions are considered: (1) hoisting cable is massless; (2) all joints are well lubricated; (3) hoisting is only needed for obstacle avoidance; and (4) information about the mass of the payload, cart position, payload and hook sways, and hoisting height is available through sensors.

Fig. 1
figure 1

Overhead crane schematic diagram

Full size image
Table 1 Model parameters and variables
Full size table

By defining independent generalized coordinates as \({\mathbf {q}}\triangleq \left[ \begin{array}{l l l}{q_{\mathrm{1}}}&{q_{\mathrm{2}}}&{q_{\mathrm{3}}}\end{array}\right] ^{\mathrm{T}}=\left[ \begin{array}{l l l}{x}&{\theta _\mathrm{h}}&{\theta _{\mathrm{p}}}\end{array}\right] ^{\mathrm{T}}\), and non-conservative forces as \({\mathbf {Q}}_\mathrm{c}\triangleq \left[ \begin{array}{l l l}{Q_{1}}&{Q_{2}}&{Q_{3}}\end{array}\right] ^{\mathrm{T}}=\left[ \begin{array}{l l l}{F_{\mathrm{c}}}&{0}&{0}\end{array}\right] ^{\mathrm{T}}\), using the Euler–Lagrange method, the system’s equations of motion (EOM) can easily be obtained in matrix compact as

$$\begin{aligned} {\mathbf {M}}_{\mathrm{c}}({\mathbf {q}}){\ddot{{\mathbf {q}}}} + {\mathbf {C}}_{\mathrm{c}}({\mathbf {q}}, \dot{{\mathbf {q}}})\dot{{\mathbf {q}}} + {\mathbf {G}}_{\mathrm{c}}({\mathbf {q}})= {\mathbf {Q}}_{\mathrm{c}}; \end{aligned}$$
(1)

where the acceleration-related inertia matrix \({\mathbf {M}}_{\mathrm{c}}({\mathbf {q}})\in \mathfrak {R}^{3 \times 3}\), the velocity-related Coriolis–centrifugal matrix \({\mathbf {C}}_{\mathrm{c}}({\mathbf {q}}, \dot{{\mathbf {q}}})\in \mathfrak {R}^{3\times 3}\), and the gravity vector \({\mathbf {G}}_{\mathrm{c}}({\mathbf {q}})\in \mathfrak {R}^{3}\) are defined as:

$$\begin{aligned}&{\mathbf {M}}_{\mathrm{c}}({\mathbf {q}})=\left[ \begin{array}{ccc}{{M}_{\mathrm{chp}}} &{}\quad {{M}_{\mathrm{hp}} {L}_{{1}} \cos \theta _{\mathrm{h}}} &{}\quad {{m}_{\mathrm{p}} {L}_{{2}} \cos \theta _{\mathrm{p}}} \\ {{M}_{\mathrm{hp}} {L}_{{1}} \cos \theta _{\mathrm{h}}} &{}\quad {{M}_{\mathrm{hp}} {L}_{{1}}^{2}} &{}\quad {{m}_{\mathrm{p}} {L}_{{1}} {L}_{{2}} \cos \theta _{\mathrm{hp}}} \\ {{m}_{\mathrm{p}} {L}_{{2}} \cos \theta _{\mathrm{p}}} &{}\quad {{m}_{\mathrm{p}} {L}_{{1}} {L}_{{2}} \cos \theta _{\mathrm{hp}}} &{}\quad {\mathrm{m}_{\mathrm{p}} {L}_{{2}}^{2}}\end{array}\right] ;\\&{\mathbf {C}}_\mathrm{c}({\mathbf {q}},{\dot{\mathbf {q}}})=\left[ \begin{array}{ccc}{0} &{}\quad {-{M}_{\mathrm{chp}} {L}_{1} {\dot{\theta }}_{\mathrm{h}} \sin \theta _{\mathrm{h}}} &{}\quad {-{m}_{\mathrm{p}} {L}_{{2}} {\dot{\theta }}_{\mathrm{p}} \sin \theta _{\mathrm{p}}} \\ {0} &{}\quad {0} &{}\quad {{m}_{\mathrm{p}} {L}_{{1}} {L}_{{2}} {\dot{\theta }}_{\mathrm{p}} \sin \theta _{\mathrm{hp}}} \\ {0} &{}\quad {-{m}_{\mathrm{p}} {L}_{{1}} {L}_{{2}} {\dot{\theta }}_{\mathrm{h}} \sin \theta _{\mathrm{hp}}} &{}\quad {0}\end{array}\right] ;\\&{\mathbf {G}}_{\mathrm{c}}({\mathbf {q}})=\left[ \begin{array}{lll}{0}&\quad {{M}_{\mathrm{chp}} {g} {L}_{{1}} \sin \theta _{\mathrm{h}}}&\quad {{m}_{\mathrm{p}} {g} {L}_{{2}} \sin \theta _{\mathrm{p}}}\end{array}\right] ^{\mathrm{T}}; \end{aligned}$$

where \({M}_{\mathrm{chp}}=({m}_{\mathrm{c}}+{m}_{\mathrm{h}}+{m}_{\mathrm{p}})\), \({M}_{\mathrm{hp}}=({m}_{\mathrm{h}}+{m}_{\mathrm{p}})\) and \(\theta _{\mathrm{hp}}=(\theta _{\mathrm{h}}-\theta _{\mathrm{p}})\).

A form more suitable for control design is to separate the EOM into actuated and non-actuated subsystems. Isolating \({\ddot{x}}\), \(\ddot{\theta }_\mathrm{h}\) and \({\ddot{\theta }}_\mathrm{p}\) from (1) and using the notation \({\mathbf {X}}=\left[ \begin{array} {l l l l l l} {x_{\mathrm{1}}}&{x_{\mathrm{2}}}&{x_{\mathrm{3}}}&{x_{\mathrm{4}}}&{x_{\mathrm{5}}}&{x_{\mathrm{6}}}\end{array}\right] ^{\mathrm{T}}\), where \(x_{\mathrm{1}}=x\), \(x_{\mathrm{2}}={\dot{x}}\), \(x_{\mathrm{3}}=\theta _{\mathrm{h}}\), \(x_{\mathrm{4}}={\dot{\theta }}_{\mathrm{h}}\), \(x_{\mathrm{5}}=\theta _{\mathrm{p}}\) and \(x_{\mathrm{6}}={\dot{\theta }}_{\mathrm{p}}\). The state-space representation for the nominal crane model is obtained as:

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}}_{1}=x_{2}};\\ {{\dot{x}}_{2}=g_{1}({\mathbf {X}}) + b_{1}({\mathbf {X}})F_{{\mathrm{c}}}};\\ {{\dot{x}}_{3}=x_{4}};\\ {{\dot{x}}_{4}=g_{2}({\mathbf {X}}) + b_{2}({\mathbf {X}})F_{{\mathrm{c}}}};\\ {{\dot{x}}_{5}=x_{6}};\\ {{\dot{x}}_{6}=g_{3}({\mathbf {X}}) + b_{3}({\mathbf {X}})F_{{\mathrm{c}}}}.\end{array}\right. \end{aligned}$$
(2)

In (2), \(g_{{{i}}}({\mathbf {X}})\) and \(b_{{i}}({\mathbf {X}})\) are smooth nonlinear functions of the state vector \({\mathbf {X}}\), given by \(g_{{i}}({\mathbf {X}})=G_{{i}}({\mathbf {X}})/D({\mathbf {X}})\) and \(b_{{i}}({\mathbf {X}})=B_{{i}}({\mathbf {X}})/D({\mathbf {X}})\). After dropping the state dependency notations, \(G_{{i}}({\mathbf {X}})\), \(B_{{i}}({\mathbf {X}})\) and \(D({\mathbf {X}})\), \(({i}=1,2,3)\) are, respectively, defined as:

$$\begin{aligned} G_{1}= \,&[{M}_{\mathrm{hp}} {m}_{\mathrm{p}} {L}_{1}^{2} {L}_{2}^{2}-{m}_{\mathrm{p}}^{2} {L}_{1}^{2} {L}_{2}^{2} \cos ^{2} x_{35}][ {M}_{\mathrm{hp}}{L}_{1} x_{4}^{2} \sin x_{3}\\&+{m}_{\mathrm{p}} {L}_{2} x_{6}^{2} \sin x_{5} ]+[ {M}_{\mathrm{hp}}{m}_{\mathrm{p}} {L}_{1} {L}_{2}^{2} \cos x_{3}-{m}_{\mathrm{p}}^{2} {L}_{1} {L}_{2}^{2} \\&\times \cos x_{5} \cos x_{35} ] [ {m}_{\mathrm{p}} {L}_{1}{L}_{2} x_{6}^{2} \sin x_{35}+{M}_{\mathrm{hp}} {g} {L}_{1} \sin x_{3} ]\\&+[ {M}_{\mathrm{hp}}{m}_{\mathrm{p}} {L}_{1}^{2} {L}_{2} \cos x_{5}-{m_\mathrm{p}} {L}_{1}^{2} {L}_{2} \cos x_{3} \cos x_{35} ]\\&\times [{m}_{\mathrm{p}} {g} {L}_{2} \sin x_{5}-{m}_{\mathrm{p}} {L}_{1} {L}_{2} x_{4}^{2} \sin x_{35}];\\ G_{2}=\,&[{m}_{\mathrm{p}}^{2} {L}_{1} {L}_{2}^{2} \cos x_{5} \cos x_{35}-{M}_{\mathrm{hp}} {m}_{\mathrm{p}} {L}_{1} {L}_{2}^{2} \cos x_{3}][ {M}_{\mathrm{hp}} {L}_{1} x_{4}^{2}\\&\times \sin x_{3}+{m}_{\mathrm{p}} {L}_{2} x_{6}^{2} \sin x_{5} ]+[ {m}_{\mathrm{p}}^{2} {L}_{2}^{2} \cos ^{2} x_{5} -{M}_{\mathrm{thp}} {m}_{\mathrm{p}} \\&\times {L}_{2}^{2} ] [ {m}_{\mathrm{p}} {L}_{1} {L}_{2} x_{6}^{2} \sin x_{35}+{M}_{\mathrm{hp}} {g} {L}_{1} \sin x_{3}] +{M}_{\mathrm{thp}} {m}_{\mathrm{p}} \\&\times {L}_{1} {L}_{2} \cos x_{35}- {M}_{\mathrm {hp}} {m}_{\mathrm {p}} {L}_{1} {L}_{2}\cos x_{3} \cos x_{5} ][{m}_{\mathrm {p}} {g} {L}_{2}\\&\times \sin x_{5}- {m}_{\mathrm {p}} {L}_{1} {L}_{2} x_{4}^{2} \sin x_{35})];\\ G_{3}= \,&[{M}_{\mathrm {hp}} {m}_{\mathrm {p}} {L}_{1}^{2} {L}_{2}\left( \cos x_{3} \cos x_{35}-\cos x_{5} \right) ][{M}_{\mathrm {hp}} {L}_{1} x_{4}^{2} \sin x_{3}\\&+{m}_{\mathrm {p}} {L}_{2} x_{6}^{2} \sin x_{5} ]+[{M}_{\mathrm {thp}} {m}_{\mathrm {p}} {L}_{1} {L}_{2} \cos x_{35}- {M}_{\mathrm {hp}} {m}_{\mathrm {p}} \\&\times {L}_{1} {L}_{2} \cos x_{3} \cos x_{5} ][{m}_{\mathrm {p}} {L}_{1} {L}_{2} x_{6}^{2} \sin x_{35}+ {M}_{\mathrm {hp}} {g} {L}_{1} \sin x_{3} ] \\&+[{M}_{\mathrm {hp}}^{2} {L}_{1}^{2} \cos ^{2} x_{3}- {M}_{\mathrm {thp}} {M}_{\mathrm {hp}} {L}_{1}^{2}] [{m}_{\mathrm {p}} {g} {L}_{2} \sin x_{5}\\&-{m}_{\mathrm {p}} {L}_{1} {L}_{2} x_{4}^{2} \sin x_{35} ];\\ B_{1}=\,&{M}_{\mathrm {hp}} {m}_{\mathrm {p}} {L}_{1}^{2} {L}_{2}^{2}- {m}_{\mathrm {p}}^{2} {L}_{1}^{2} {L}_{2}^{2} \cos ^{2}x_{35};\\ B_{2} = \,&{m}_{\mathrm {p}}^{2} {L}_{1}^{2} {L}_{2}^{2} \cos x_{5} \cos x_{35}- {M}_{\mathrm {hp}} {m}_{\mathrm {p}} {L}_{1} {L}_{2}^{2} \cos x_{3};\\ B_{3}= \,&{M}_{\mathrm {hp}} {m}_{\mathrm {p}} {L}_{1}^{2} {L}_{2} \cos x_{3} \cos x_{35}- {M}_{\mathrm {hp}} {m}_{\mathrm {p}} {L}_{1}^{2} \mathrm {L}_{2} \cos x_{5};\\ D= \,&{M}_{\mathrm {hp}} {m}_{\mathrm {p}} {L}_{1}^{2} {L}_{2}^{2}[{M}_{\mathrm {thp}}-{M}_{\mathrm {hp}}\cos ^{2}x_{3}]- {m}_{\mathrm {p}}^{2} {L}_{1}^{2} {L}_{2}^{2}[ {M}_{\mathrm {hp}} \\&\times \cos ^{2}x_{5}+ {M}_{\mathrm {thp}}\cos ^{2}x_{35}-2 {M}_{\mathrm {hp}} \cos x_{3} \cos x_{5} \cos x_{35}]; \end{aligned}$$

where \(x_{35}=x_{3}-x_{5}=\theta _{\mathrm {h}}-\theta _{\mathrm {p}}\).

2.2 Perturbed Crane Dynamics

In practice, cranes are with un-modelled dynamics, various frictions, and external disturbances. When matched and unmatched uncertainties are considered, the uncertain system can be represented as:

$$\begin{aligned} \left\{ \begin{array}{l}{{\dot{x}}_{1}=x_{2}};\\ {{\dot{x}}_{2}=\left\{ g_{1}({\mathbf {X}})+\delta g_{1}({\mathbf {X}})\right\} +\left\{ b_{1}({\mathbf {X}})+\delta b_{1}({\mathbf {X}})\right\} F_{\mathrm {c}}^{\prime }+\varDelta _{1}({\mathbf {X}})};\\ {{\dot{x}}_{3}=x_{4}};\\ {{\dot{x}}_{4}=\left\{ g_{2}({\mathbf {X}})+\delta g_{2}({\mathbf {X}})\right\} +\left\{ b_{2}({\mathbf {X}})+\delta b_{2}({\mathbf {X}})\right\} F_{\mathrm {c}}^{\prime }+\varDelta _{2}({\mathbf {X}})};\\ {{\dot{x}}_{5}=x_{6}};\\ {{\dot{x}}_{6}=\left\{ g_{3}({\mathbf {X}})+\delta g_{3}({\mathbf {X}})\right\} +\left\{ b_{3}({\mathbf {X}})+\delta b_{3}({\mathbf {X}})\right\} F_{\mathrm {c}}^{\prime }+\varDelta _{3}(\mathrm {X})}.\end{array} \right. \end{aligned}$$
(3)

The terms \(\delta g_{{i}}({\mathbf {X}})\) and \(\delta b_{{i}}({\mathbf {X}})\)   \((i =1,2,3)\) depict matched uncertainties due to parametric variations, un-modelled dynamics, neglected nonlinearities, and external disturbances. The so-called matched uncertainties mean that the perturbations \(\delta g_{{i0}}({\mathbf {X}})\), \(\delta b_{{i0}}({\mathbf {X}}) \in {\text {span}}\left\{ b_{{i}}({\mathbf {X}})\right\} \); and enter the same channel as the control \(F_\mathrm {c}\). This statement can be explicitly expressed as:

$$\begin{aligned} \left\{ \begin{array}{l}{\delta g_{{i}}({\mathbf {X}})=b_{{i}}({\mathbf {X}})\delta {\tilde{g}}_{{i}}({\mathbf {X}})};\\ {\delta b_{{i}}({\mathbf {X}})=b_{{i}}({\mathbf {X}})\delta {\widetilde{b}}_{{i}}({\mathbf {X}})}.\end{array}\right. \end{aligned}$$
(4)

On the other hand, the terms \(\varDelta _{{i}}({\mathbf {X}})\, (i = 1,2,3)\) depict unmatched uncertainties (due to friction, measurement noise, for example) and can be expressed as:

$$\begin{aligned} \varDelta _{{i}}({\mathbf {X}})=\varDelta g_{{i}}({\mathbf {X}})+\varDelta b_{{i}}({\mathbf {X}}). \end{aligned}$$
(5)

Moreover, \(F_{\mathrm {c}}^{\prime }=F_{\mathrm {c}}-F_{\mathrm {f}}\), where \(F_{\mathrm {f}}\) denotes the trolley friction along x-axis that opposes the trolley force \(F_{\mathrm {c}}\). When (4) and (5) apply, in (3) we have the following modifications:

$$\begin{aligned}&{\dot{x}}_{{2i}}=g_{{i}}({\mathbf {X}})+b_{{i}}({\mathbf {X}})\left[ \delta g_{{i}}({\mathbf {X}})+\delta {\tilde{b}}_{{i}}({\mathbf {X}}) F_{\mathrm {c}}^{\prime }+F_{\mathrm {c}}^{\prime }\right]&\nonumber \\&\qquad \quad +\left[ \varDelta g_{{i}}({\mathbf {X}})+\varDelta b_{{i}}({\mathbf {X}})\right] , \, (i=1,2,3).&\end{aligned}$$
(6)

In practice, friction model parameter identification is not trivial. Also, traditional discontinuous friction models like [57] may not be suitable for smooth control efforts. Since using discontinuous models in the analysis is rather challenging, this study adopted a recently developed continuously differentiable model given as [58]:

$$\begin{aligned} F_{\mathrm {f}}={\alpha }_{1}\left( \tanh \left( {\beta }_{1} {\dot{x}}\right) -\tanh \left( {\beta }_{2} {\dot{x}}\right) \right) +{\alpha }_{2} \tanh \left( {\beta }_{3} {\dot{x}}\right) +{\alpha }_{3} {\dot{x}}; \end{aligned}$$
(7)

where \({\alpha }_{1}\), \({\alpha }_{2}\), \({\alpha }_{3}\), \({\beta }_{1}\), \({\beta }_{2}\), and \({\beta }_{3}\) are positive constants. In (7), the terms \(\left[ \tanh \left( {\beta }_{1} {\dot{x}}\right) -\tanh \left( {\beta }_{2} {\dot{x}}\right) \right] \) captured Stribeck friction, the term \({\alpha }_{2} \tanh \left( {\beta }_{3} {\dot{x}}\right) \) captured Coulomb friction, \({\alpha }_{3} {\dot{x}}\) captured Viscous friction, while \({\alpha }_{1}\) and \({\alpha }_{2}\) are stiction friction coefficients. By selecting \({\alpha }_1=3.9\), \(\alpha _2=2.2\), \({\alpha }_3=0.15\), \({\beta }_1=50\), \({\beta }_2=0.9\), and \(\beta _3=70\), the friction uncertainties described by the model (7) are as shown in Fig. 2.

Fig. 2
figure 2

Friction uncertainty profile

Full size image

Remark 1

In practice, the payload is always suspended below the trolley; hence, \({L}_1\in \mathfrak {R}^{+}\) and \({L}_2\in \mathfrak {R}^{+}\), \(\forall t\). Moreover, for safe operation, sway angles \(\theta _\mathrm {h}\) and \(\theta _\mathrm {p}\) satisfy the range \(-\frac{\pi }{2}<(\theta _\mathrm {h},\theta _\mathrm {p})< \frac{\pi }{2}\), \(\forall t\).

The below assumptions will be invoked for the design and stability analysis of the control system presented in Sect. 3.

Assumption 1

The drifting terms, \(g_{{i}}({\mathbf {X}})\); and the control channel terms, \(b_{{i}}({\mathbf {X}})\); for \(i =1,2,3\), are smooth nonlinear functions. Additionally, along Remark 1, the terms \(b_{{i}}({\mathbf {X}})\), are invertible \(\forall {\mathbf {X}}.\)

Assumption 2

The uncertainties are Lipschitz continuous and bounded such that \(\left| \delta {\tilde{g}}_{{i}}({\mathbf {X}})\right| \le \) \(\delta _{\mathrm {g}},|\delta \tilde{{b}}_{{i}}({\mathbf {X}})|\le \delta _{\mathrm {b}},\left| \varDelta g_{{i}}\right. \)\(\left. ({\mathbf {X}})\right| \le \varDelta _{\mathrm {g}}\) and \(\left| \varDelta b_{{i}}({\mathbf {X}})\right| \le \varDelta _{\mathrm {b}}, \, (i =1,2,3)\), where \(\delta _{\mathrm {g}}\in \mathfrak {R}^{+}\), \(\delta _{\mathrm {b}}\in \mathfrak {R}^{+}\), \(\varDelta _{\mathrm {g}}\in \mathfrak {R}^{+}\), and \(\varDelta _{\mathrm {b}}\in \mathfrak {R}^{+}\) are known upper bounds.

2.3 DC Actuator Dynamics

Since the cart’s physical force (\(F_\mathrm {c}\)), in (2) is generated by a DC motor, actuator dynamic is taken into account. The following equation set relates the linear force, \(F_\mathrm {c}\); with motor torque, \(T_\mathrm {m}\); and motor input voltage, \(V_{\mathrm {DC}}\):

$$\begin{aligned} \left\{ \begin{array}{l}{T_{\mathrm {m}}={r_\mathrm{p}}F_{\mathrm {c}}=\frac{{K}_{\mathrm {m}}}{{R}}V_{\mathrm {DC}}-\frac{{K}_{\mathrm {m}} {K}_{\mathrm {E}}}{{R}} \omega _{\mathrm {m}}};\\ {\omega _{\mathrm {m}}=\frac{x_{2}}{{r_\mathrm{p}}}},\end{array}\right. \end{aligned}$$
(8)

where \({r_\mathrm{p}}\), \({K}_\mathrm {m}\), \(V_{\mathrm {DC}}\), \({K}_\mathrm {E}\), and R have been earlier defined in Table 1, while \(\omega _\mathrm {m}\) is the angular velocity of the DC motor. From (8), one can easily obtain \(F_\mathrm {c}\) as

$$\begin{aligned} F_{\mathrm {c}}=\frac{{K}_{\mathrm {m}}}{\mathrm {R r}_{\mathrm {p}}}V_{\mathrm {DC}}-\frac{{K}_{\mathrm {m}}{K}_{\mathrm {E}}}{\mathrm {Rr}_{\mathrm {p}}^{2}}x_{2}. \end{aligned}$$
(9)

3 Control Design and Stability Analysis

3.1 Controller Design

The control objective is to design a controller that drives the states of the system, \({\mathbf {X}} \in \mathfrak {R}^{6}\), to their respective desired trajectories, \({\mathbf {X}}^\mathrm {d} \in \mathfrak {R}^{6}\), in the presence of the perturbations (4) and (5), and friction (7). The controller is required to maintain robust stability and robust performance despite the perturbations.

In conventional SMC, the system’s motion under sliding mode has a dimension less than the state space. In the ISMC developed by Utkin and Shi [59], the integral term breaks out of this point and increases sliding mode dimension to equal that of the state space and system trajectory emanates from the sliding manifold. Hence, the reaching phase is eliminated, and robustness against matched uncertainties is guaranteed throughout the state space.

When (6) applies, the perturbed crane model (3) can be rewritten in compact form given by:

$$\begin{aligned} \dot{{\mathbf {X}}}=\mathbf {A X}+{\mathbf {B}}\left( F_{\mathrm {c}}^{\prime }+\varvec{\delta }\right) +{\mathbf {G}}+\varvec{\varDelta }; \end{aligned}$$
(10)

where \({\mathbf {X}}\in \mathfrak {R}^{6}\) is the state vector, \(F_\mathrm {c}^{\prime }\) is the perturbed control input, \(\varvec{\delta }\in {\mathfrak {R}}^{6}\) is the vector of matched uncertainties, and \(\varDelta \in \mathfrak {R}^{6}\) is the vector of unmatched uncertainties. When we, for simplicity, drop the state and time dependency notations, the vectors \(\varvec{\delta }\) and \(\varvec{\varDelta }\), and the matrices \({\mathbf {A}}\in \mathfrak {R}^{6\times 6}, {\mathbf {B}}\in \mathfrak {R}^{6}\) and \({\mathbf {G}}\in \mathfrak {R}^{6}\) are here defined as:

$$\begin{aligned}&{\mathbf {A}}=\left[ \begin{array}{cccccc}{0} &{} {1} &{} {0} &{} {0} &{} {0} &{} {0} \\ {0} &{} {0} &{} {0} &{} {0} &{} {0} &{} {0} \\ {0} &{} {0} &{} {0} &{} {1} &{} {0} &{} {0} \\ {0} &{} {0} &{} {0} &{} {0} &{} {0} &{} {0}\\ {0} &{} {0} &{} {0} &{} {0} &{} {0} &{} {1}\\ {0} &{} {0} &{} {0} &{} {0} &{} {0} &{} {0}\end{array}\right] ; \quad {\mathbf {B}}=\left[ \begin{array}{c}{0} \\ {b_{1}} \\ {0} \\ {b_{2}}\\ {0} \\ {b_{3}}\end{array}\right] ; \quad {\mathbf {G}}=\left[ \begin{array}{c}{0} \\ {g_{1}} \\ {0} \\ {g_{2}} \\ {0} \\ {g_{3}}\end{array}\right] ;&\\&\varvec{\delta }=\left[ \begin{array}{c}{0} \\ {\delta g_{1}+\delta {\tilde{b}}_{1} F_{\mathrm {c}}} \\ {0} \\ {\delta {\tilde{g}}_{2}+\delta {\tilde{b}}_{2} F_{\mathrm {c}}} \\ {0} \\ {\delta {\tilde{g}}_{3}+\delta {\tilde{b}}_{3} F_{\mathrm {c}}}\end{array}\right] ; \quad \varvec{\varDelta }=\left[ \begin{array}{c}{0} \\ {\varDelta g_{1}+\varDelta b_{1}} \\ {0} \\ {\varDelta g_{2}+\varDelta b_{2}} \\ {0} \\ {\varDelta g_{3}+\varDelta b_{3}}\end{array}\right] .&\end{aligned}$$

Define the state tracking error as \({\mathbf {e}}(t)={\mathbf {X}}-{\mathbf {X}}^{\mathrm {d}}\), where \({\mathbf {e}}(t)\in \mathfrak {R}^{6}\) is the error between the actual states trajectories \(({\mathbf {X}}\in \mathfrak {R}^{6})\), and the desired states trajectories \(({\mathbf {X}}^{\mathrm {d}}\in \mathfrak {R}^{6})\). Design the integral ISMC surface as:

$$\begin{aligned} \xi ({\mathbf {e}},t)={\varvec{\Gamma }} \left[ {\mathbf {e}}(t)-{\mathbf {e}}(0)\right] -\int _{0}^{t} {\varvec{\Gamma }}({\mathbf {A}}-{{\mathbf {B}}}{{\mathbf {F}}}){\mathbf {e}}(\tau ) \mathrm {d}\tau ; \end{aligned}$$
(11)

where \({\varvec{\Gamma }} \in \mathfrak {R}^{6}\), and \({\mathbf {F}} \in \mathfrak {R}^{6}\) are design parameters that characterize the sliding surface.

Assumption 3

The input distribution matrix, \({\mathbf {B}}\), has full rank \(\forall {\mathbf {X}} \in \mathfrak {R}^{6}\).

Remark 2

The vector \({\varvec{\Gamma }}\) is designed to ensure that the product \({\varvec{\Gamma } {\mathbf {B}}}\) is non-singular. It is easy to achieved this since matrix \({\mathbf {B}}\) has full rank and \({\varvec{\Gamma }}\) is a free parameter. On the other hand, \({\mathbf {F}}\) is designed using pole placement technique such that \(({\mathbf {A}}-{{\mathbf {B}}}{{\mathbf {F}}})\) is Hurwitz.

Due to its merits, we adopt the equivalent control (12), where \(u_{\mathrm {eq}}\), and \(u_{\mathrm {sw}}\) (to be designed) are known as the equivalent control, and the switching control, respectively.

$$\begin{aligned} F_{\mathrm {c}}=u_{\mathrm {eq}}+u_{\mathrm {sw}}. \end{aligned}$$
(12)

Only \(u_{\mathrm {eq}}\) is applied during the sliding phase to maintain the variables sliding along the manifold \(\xi ({\mathbf {e}},t)=0\) and eventually converge to the origin. For the reaching phase, both \(u_{\mathrm {eq}}\) and \(u_{\mathrm {sw}}\) are applied. The time derivative of (11) is given by:

$$\begin{aligned} {\dot{\xi }}({\mathbf {e}},t)={\varvec{\Gamma }}\dot{{\mathbf {X}}}-{\varvec{\Gamma }}({\mathbf {A}}-{{\mathbf {B}}}{{\mathbf {F}}}){\mathbf {e}}(t). \end{aligned}$$
(13)

When (10) applies, and argument notation henceforth dropped, \({\dot{\xi }}({\mathbf {e}},t)\) can be expressed as:

$$\begin{aligned} {\dot{\xi }}={\varvec{\Gamma }}\left[ {{\mathbf {A}}}{{\mathbf {X}}}+{\mathbf {B}}\left( F_{\mathrm {c}}^{\prime }+\varvec{\delta }\right) +{\mathbf {G}}+{\varvec{\varDelta }}\right] -{\varvec{\Gamma }} {\mathbf {A}}{\mathbf {X}}+{\varvec{\Gamma }}{{\mathbf {B}}}{{\mathbf {F}}} {\mathbf {e}}(t); \end{aligned}$$
(14)

which by invoking (12), and simplifying; one obtains:

$$\begin{aligned} {\dot{\xi }}={\varvec{\Gamma }}{\mathbf {B}}\left( u_{\mathrm {eq}} + u_{\mathrm {sw}}\right) +{\varvec{\Gamma }}{\mathbf {B}} {\varvec{\delta }}+{\varvec{\Gamma }}{\mathbf {G}}+{\varvec{\Gamma \varDelta }} + {\varvec{\Gamma }}\mathbf {BFe}(t). \end{aligned}$$
(15)

One’s objective is to have \(\xi ={\dot{\xi }}=0\) in finite time (i.e., sliding motion along \(\xi =0 )\). Hence, considering (15) and Assumption 1, \(u_{\mathrm {eq}}\) is here designed as:

$$\begin{aligned} u_{\mathrm {eq}}=-({\varvec{\Gamma }}\mathbf {B)}^{-1} {\varvec{\Gamma }}{\mathbf {G}}-{{\mathbf {F}}}{{\mathbf {e}}}(t). \end{aligned}$$
(16)

Applying (16) to (15), one easily obtains \({\dot{\xi }}\) as:

$$\begin{aligned} {\dot{\xi }}={\varvec{\Gamma }}{\mathbf {B}} u_{\mathrm {sw}}+{\varvec{\Gamma }}{\mathbf {B}} {\varvec{\delta }}+{\varvec{\Gamma \varDelta }}. \end{aligned}$$
(17)

Remark 3

In conventional SMC, the law \(u_{\mathrm {sw}}\) makes the control effort to suffer from high-frequency switching (i.e., the chattering issue). Chattering makes control effort difficult to track by most practical actuators. One solution is boundary layer control. However, the boundary method may result in the degradation of tracking and robustness. Chattering can be significantly attenuated using STC (a second-order SMC) that ensures a continuous control effort.

3.1.1 The STC and MSTC Algorithms

The second-order STC algorithm has been defined as [37]:

$$\begin{aligned} \left\{ \begin{array}{l}{u_{\mathrm {STC}}=-{\lambda }_1|\xi |^{1/2} {\text {sgn}}(\xi )+w};\\ { {\dot{w}}=-{\lambda }_3{\text {sgn}}(\xi )},\end{array}\right. \end{aligned}$$
(18)

where \(\lambda _1\), and \(\lambda _3\) are the controller design parameters. The signum function \({\text {sgn}}\,(\cdot )\) is defined as:

$$\begin{aligned} {\text {sgn}}(\xi ):=\left\{ \begin{array}{ll}-1, &{}\quad \text {if} \, \xi <0;\\ 0, &{}\quad \text {if} \, \xi =0;\\ 1, &{}\quad \text {if} \, \xi >0.\end{array}\right. \end{aligned}$$
(19)

The controller gains \(\lambda _1\) and \(\lambda _3\) in (18) are usually required to be high in order to accelerate the convergence of the sling variable \(\xi ({\mathbf {e}},t)\) to the origin. However, for chattering to have low amplitudes, it is required that these gains have small values. To circumvent this problem, researchers such as [55] and [56] proposed the following modified algorithm, here referred to as the MSTC:

$$\begin{aligned} \left\{ \begin{array}{l}{u_{\mathrm {MSTC}}=-{\lambda }_1 |\xi |^{1/2} {\text {sgn}}(\xi ) - {\lambda }_2 \xi + w};\\ {{\dot{w}}=-{\lambda }_3 {\text {sgn}}(\xi ) - {\lambda }_4 \xi },\end{array}\right. \end{aligned}$$
(20)

where \(\lambda _1\), \(\lambda _2\), \(\lambda _3\), and \(\lambda _4\) are the controller parameters, with \(\lambda _1\), and \(\lambda _3\) as in (18).

3.1.2 The Proposed NSSTC Algorithm and Its Application

Using (20), one can achieve faster convergence of \(\xi \) to the origin. However, when the auxiliary variable \({\dot{w}}\) increases and consequently w increases, a longer settling time and larger overshoot of \(\xi \) is produced. These result in higher control effort amplitude. To address this issue, we propose the following novel NSSTC algorithm:

$$\begin{aligned} \left\{ \begin{array}{l}{u_{\mathrm {NSSTC}}=-{\lambda }_1 |\xi |^{\mathrm {y}} {\text {sgn}}(\xi ) - {\lambda }_2 \xi {\text {e}}^{-{\gamma } t} + w};\\ {{\dot{w}}=-{\lambda }_3 |\xi |^{\mathrm {M}} {\text {sgn}}(\xi ) - {\lambda }_4 \xi };\\ {\mathrm {y}=\frac{{\theta }-1}{{\theta }}, {M}=\frac{{\theta }-2}{{\theta }}}.\end{array}\right. \end{aligned}$$
(21)

The parameter \(\theta \ge 2\) in (21) is referred to as the ‘smoothness factor,’ while \(\lambda _1\), \(\lambda _2\), \(\lambda _3\) and \(\lambda _4\) are the controller parameters, with \(\lambda _1\) and \(\lambda _3\) as in (18) and (20), and \({\gamma }\) is a small positive constant used to penalize the sliding surface overshoot and settling time. We will show that the control structure in (21) does not suffer, severely, the problems of (20) and relatively has some improved performance.

In summary, the objective here is to improve the classical STC algorithm (18) so as to improve the convergence speed of the sliding variable \(\xi \) while avoiding the earlier highlighted problems of (20).

Remark 4

The ‘smoothness factor,’ \({\theta }\) can be exploited to improve the control effort’s smoothness. Also, the design parameter \({\gamma }\) can be used to penalize the sliding surface and the control force peaks. Intelligent turning algorithms like neural networks or fuzzy logic may be employed to obtain these parameters’ optimal values online.

Considering (17) and the proposed NSSTC algorithm (21), we design the switching control law, \(u_{\mathrm {sw}}\), as:

$$\begin{aligned} u_{\mathrm {sw}}=&-({\varvec{\Gamma }}{\mathbf {B}})^{-1}\left[ {\lambda }_1 |\xi |^{\mathrm {y}} {\text {sgn}}(\xi ) + {\lambda }_2 \xi {\text {e}}^{-\gamma t}\right.&\nonumber \\&\left. + \int _{0}^{t} \left( {\lambda }_3 |\xi |^{\mathrm {M}} {\text {sgn}}(\xi ) + {\lambda }_4 \xi \right) \mathrm {d} \tau \right] .&\end{aligned}$$
(22)

And by submitting the foregoing into (17), one gets \({\dot{\xi }}\) as:

$$\begin{aligned} {\dot{\xi }}({\mathbf {e}},t)=&-{\lambda }_1 |\xi |^{\mathrm {y}} {\text {sgn}}(\xi ) - {\lambda }_2 \xi {\text {e}}^{-\gamma t}&\nonumber \\&-\int _{0}^{t} \left( {\lambda }_3 |\xi |^{\mathrm {M}} {\text {sgn}}(\xi ) + {\lambda }_4 \xi \right) \mathrm {d} \tau + {\varvec{\Gamma }} {\mathbf {B}}\varvec{\delta }+{\varvec{\Gamma \varDelta }}. \end{aligned}$$
(23)

Set the uncertainty in (23) to be represented by \(({\varvec{\Gamma }}{\mathbf {B}} \varvec{\delta }+{\varvec{\Gamma \varDelta })}=\phi \). In this connection, the \(\xi \)-dynamics (23) can be represented by the following closed-loop system.

$$\begin{aligned} \left\{ \begin{array}{l}{{\dot{z}}_1=-{\lambda }_1 |z_1|^{\mathrm {y}} {\text {sgn}}(z_1) - {\lambda }_2 z_1 {\text {e}}^{-\gamma t} + z_2+\phi };\\ {{\dot{z}}_2=-{\lambda }_3 |z_1|^{\mathrm {M}} {\text {sgn}}(z_1) - {\lambda }_4 z_1},\end{array}\right. \end{aligned}$$
(24)

where \([\xi \quad w]^{\mathrm {T}} \triangleq [z_1 \quad z_2]^{\mathrm {T}}=z\).

To simplify the subsequent analysis, we let

$$\begin{aligned} |\phi | \le \varrho _1 + \varrho _2 ||{h}||, \end{aligned}$$
(25)

where \(\varrho _1 \in \mathfrak {R}^{+}\), \(\varrho _2 \in \mathfrak {R}^{+}\), \(\varrho _1\ne 0\), and h as in (29), where \(\varrho _2\) is sufficiently small.

Remark 5

It may have been noticed that the lumped uncertainty, \(\phi \), in (24) does not vanish at the origin since \(\varrho _1 \ne 0\) in (25). As a result, the trajectories will not converge to the origin but will be ultimately bounded [60].

To this length, the control objective has been narrowed to steering to zero the sliding variable \(\xi \) and its time derivative \({\dot{\xi }}\) (or equivalently, dynamics (24)) in finite time with perturbations satisfying (24). Hence, the design of the NSSTC controller is formulated in the following theorem.

Theorem 1

Consider system (24) with perturbation term satisfying (25) and controller parameters \(\lambda _1\), \(\lambda _2\), \(\lambda _3\), \(\lambda _4\), \(\gamma \), and y designed in a way that matrix \({\mathbf {A}}_\mathrm {L}\) is Hurwitz, then the trajectories of the system are globally ultimately bounded by:

$$\begin{aligned} {b}=\sqrt{\frac{\lambda _{\max }({\mathbf {P}})}{\lambda _{\min }({\mathbf {P}})}} \frac{2 \varrho _{1} \varepsilon }{(1-\tau )\left[ \lambda _{\min }\left( {\mathbf {Q}}\right) -2 \varrho _{2} \varepsilon \right] }, \end{aligned}$$
(26)

for \(\varrho _1 \in \mathfrak {R}^{+}\), \(\varrho _2 \le \lambda _{\min }\left( {\mathbf {Q}}\right) /2 \varepsilon \) with a positive definite (PD) symmetric matrix \({\mathbf {P}}\), and \(\tau \in \left( 0,1\right) \). Also, the trajectories will enter the manifold \(\sigma _{\omega }=\left\{ z \in \mathfrak {R}^{2} \quad | \quad V(t, z) \le \lambda _{\max }({\mathbf {P}}) \omega ^{2}\right\} \) containing the origin in a time less than \(T_r\), given by:

$$\begin{aligned} T_\mathrm {r}={\theta } \frac{\lambda _{\max }^{\mathrm {y}}({\mathbf {P}})}{\tau \left( \lambda _{\min }\left( {\mathbf {Q}}\right) -2 \varrho _{2} \varepsilon \right) }\left( V_{0}^{\frac{1}{{\theta }}}-\lambda _{\max }^{\frac{1}{{\theta }}}({\mathbf {P}}) \omega ^{\frac{2}{{\theta }}}\right) , \end{aligned}$$
(27)

where

$$\begin{aligned} \omega \triangleq \frac{2 \varrho _{1} \varepsilon }{(1-\tau )\left( \lambda _{\min }\left( {\mathbf {Q}}\right) -2 \varrho _{2} \varepsilon \right) }. \end{aligned}$$

The proof of Theorem 1 is presented in Sect. 3.2.

3.2 Stability Analysis

At this juncture, the proof for Theorem 1 is presented. Like in Moreno’s work [55], we examine a PD and radially unbounded Lyapunov function candidate given by:

$$\begin{aligned} V(t, z)={h}^{\mathrm {T}} {\mathbf {P}} {h}. \end{aligned}$$
(28)

For the system to be globally stable, \({\dot{V}}(t, z)\) needs to be ND [61]. In (28), \({h} \in \mathfrak {R}^{2}\) is a new state vector introduced representing system (24), which is defined as:

$$\begin{aligned} {h}=[h_1 \quad h_2]^{\mathrm {T}}=\left[ \left| z_{1}\right| ^{\mathrm {y}} {\text {sign}}\left( z_{1}\right) \quad z_{2}\right] ^{\mathrm {T}}, \end{aligned}$$
(29)

while \({\mathbf {P}} \in \mathfrak {R}^{2 \times 2}\) is a PD symmetric matrix, and is the solution to the algebraic Lyapunov equation given by:

$$\begin{aligned} {\mathbf {A}}_{\mathrm {L}}^{\mathrm {T}}{\mathbf {P}}+{\mathbf {P}}{\mathbf {A}}_{\mathrm {L}}=-{\mathbf {Q}}. \end{aligned}$$
(30)

Since the matrix \({\mathbf {A}}_{\mathrm {L}}\) is Hurwitz, a PD matrix \({\mathbf {Q}}\) exists such that the foregoing is satisfied.

The time derivative of (29) is given by:

$$\begin{aligned} \dot{{h}}&=\left[ \frac{\partial }{\partial t}\left| z_{1}\right| ^{\mathrm {y}} {\text {sign}}\left( z_{1}\right) \quad \frac{\partial }{\partial t} z_{2}\right] ^{\mathrm {T}}=\left[ \mathrm {y}|z_{1}|^{\mathrm {y}-1}{\dot{z}}_{1} \quad {\dot{z}}_{2}\right] ^{\mathrm {T}} \nonumber \\&=\left[ \begin{array}{c}{\mathrm {y}\left| z_{1}\right| ^{\mathrm {y}-1}\left( -{\lambda }_1 |z_1|^{\mathrm {y}} {\text {sgn}}(z_1) - {\lambda }_2 z_1 {\text {e}}^{-\gamma t} + z_2+\phi \right) } \\ {-{\lambda }_3 |z_1|^{\mathrm {M}} {\text {sgn}}(z_1) - {\lambda }_4 z_1}\end{array}\right] \nonumber \\&=\frac{1}{\left| z_{1}\right| ^{\frac{1}{\theta }}}\left[ \begin{array}{c} {\mathrm {y}\left( -{\lambda }_1 |z_1|^{\mathrm {y}} {\text {sgn}}(z_1) - {\lambda }_2 z_1 {\text {e}}^{-\gamma t} + z_2+\phi \right) } \\ {-{\lambda }_3 |z_1|^{\mathrm {y}} {\text {sgn}}(z_1) - {\lambda }_4 \left| z_{1}\right| ^{1 / \theta }z_1} \end{array}\right] \nonumber \\&=\frac{1}{\left| z_{1}\right| ^{\frac{1}{\theta }}}\left\{ \left[ \begin{array}{cc} {-\mathrm {y}( \lambda _{1}+\lambda _{2}\frac{ \left| z_{1}\right| ^{\frac{1}{\theta }}}{{\text {e}}^{\gamma t}}} ) &{} {\mathrm {y}} \\ {-\lambda _{3}-\lambda _4 \left| z_{1}\right| ^{\frac{2}{\theta }}} &{} {0} \end{array}\right] \left[ \begin{array}{c} {h_1} \\ {h_{2}} \end{array}\right] +\left[ \begin{array}{c} {\mathrm {y} \phi } \\ {0} \end{array}\right] \right\} \nonumber \\&=\left| z_{1}\right| ^{-\frac{1}{\theta }} \left( {\mathbf {A}}_\mathrm {L} {h}+{\Phi } \right) , \end{aligned}$$
(31)

where \({\Phi }=\left[ \mathrm {y}\phi \quad 0\right] ^{\mathrm {T}}\). Hence, the transpose of (31) can be expressed as:

$$\begin{aligned} \dot{{h}}^{\mathrm {T}}=\left| z_{1}\right| ^{-\frac{1}{\theta }} \left( {h}^{\mathrm {T}} {{\mathbf {A}}^{\mathrm {T}}_\mathrm {L}}+{\Phi }^{\mathrm {T}} \right) . \end{aligned}$$
(32)

The total time derivative of (28) is given by:

$$\begin{aligned} {\dot{V}}(t, z)=\dot{{h}}^{\mathrm {T}} {\mathbf {P}} {h}+{h}^{\mathrm {T}} {\mathbf {P}} \dot{{h}}. \end{aligned}$$
(33)

Invoking (31) and (32), the foregoing can be expressed as:

$$\begin{aligned} {\dot{V}}(t, z)=\left| z_{1}\right| ^{-\frac{1}{\theta }}\left[ {h}^{\mathrm {T}} {\mathbf {A}}^{\mathrm {T}}_\mathrm {L} {\mathbf {P}} {h}+\mathrm {h}^{\mathrm {T}} {\mathbf {P}} {\mathbf {A}}_\mathrm {L} {h}+2{\Phi }^{\mathrm {T}} {\mathbf {P}} {h}\right] , \end{aligned}$$
(34)

where the fact that \({\Phi }^{\mathrm {T}} {\mathbf {P}} {h}=\mathrm {h}^{\mathrm {T}} {\mathbf {P}} {\Phi }\) has been applied. The term \({\Phi }^{\mathrm {T}} {\mathbf {P}} {h}\) can further be simplified as follows:

$$\begin{aligned} {\Phi }^{\mathrm {T}} {\mathbf {P}} {h}&= \left[ \begin{array}{cc} {\mathrm {y} \phi }&{0} \end{array}\right] \left[ \begin{array}{cc} {P_{11}} &{} {P_{12}} \\ {P_{12}} &{} {P_{22}} \end{array}\right] \left[ \begin{array}{c} {\left| z_{1}\right| ^{\mathrm {y}} {\text {sign}}\left( z_{1}\right) } \nonumber \\ {z_{2}} \end{array}\right] \nonumber \\&=\mathrm {y}\phi \mathrm {h}^{\mathrm {T}}\left[ \begin{array}{c} {P_{11}} \\ {P_{12}} \end{array}\right] . \end{aligned}$$
(35)

Hence, considering (30) and (35) one can represent (34) as:

$$\begin{aligned} {\dot{V}}(t,z)=-\left| z_{1}\right| ^{-\frac{1}{\theta }}\left[ {h}^{\mathrm {T}} {\mathbf {Q}} {h}-2 \phi {h}^{\mathrm {T}} \varepsilon \right] , \end{aligned}$$
(36)

where \(\varepsilon =[\mathrm {y} P_{11} \quad \mathrm {y} P_{12}]^{\mathrm {T}}\).

One can easily show that the candidate Lyapunov function (28) can be both sides bounded as follows:

$$\begin{aligned} \lambda _{{\min }}({\mathbf {P}})\Vert \mathrm {h}\Vert ^{2} \le V(t, z) \le \lambda _{{\max }}({\mathbf {P}})\Vert \mathrm {h}\Vert ^{2}, \end{aligned}$$
(37)

where \(\lambda _{{\min }}\) and \(\lambda _{{\mathrm {\max }}}\) are, respectively, the smallest and the largest eigenvalues of the matrix \({\mathbf {P}}\) and \(\Vert {h}\Vert \) is the Frobenius norm of h. From (37), the below inequalities also hold.

$$\begin{aligned} \left\{ \begin{aligned}&\Vert {h}\Vert ^{2} \ge \frac{V(t, z)}{\lambda _{{\max }}({\mathbf {P}})}; \\&\Vert {h}\Vert ^{2} \le \frac{V(t, z)}{\lambda _{{\min }}({\mathbf {P}})}. \end{aligned}\right. \end{aligned}$$
(38)

Similarly, it can easily be shown that the following inequality set holds for \({\dot{V}}(t, z)\).

$$\begin{aligned} \left\{ \begin{aligned}&-\frac{1}{\left| z_{1}\right| ^{\frac{1}{\theta }}}\lambda _{{\max }}({\mathbf {Q}})\Vert {h}\Vert ^{2} \le {\dot{V}}(t, z) \le -\frac{1}{\left| z_{1}\right| ^{\frac{1}{\theta }}} \lambda _{{\min }}({\mathbf {Q}})\Vert {h}\Vert ^{2};\\&\Vert {h}\Vert ^{2} \ge \frac{-{\dot{V}}(t,z)}{\left| z_{1}\right| ^{-\frac{1}{\theta }} \lambda _{{\max }}({\mathbf {Q}})}; \\&\Vert {h}\Vert ^{2} \le \frac{-{\dot{V}}(t,z)}{\left| z_{1}\right| ^{-\frac{1}{\theta }} \lambda _{{\min }}({\mathbf {Q}})}. \end{aligned}\right. \end{aligned}$$
(39)

Along (25), it is easy to show that (36) is given by:

$$\begin{aligned} {\dot{V}}(t, z)\le -\left| z_{1}\right| ^{-\frac{1}{\theta }}\left[ {h}^{\mathrm {T}} {\mathbf {Q}} {h}-2\left( \varrho _{1}+\varrho _{2}\Vert {h}\Vert \right) \Vert {h}\Vert \varepsilon \right] , \end{aligned}$$
(40)

which along inequality (39) and using the fact that \(\left| z_{1}\right| ^{\frac{1}{\theta }} \le \Vert {h}\Vert \) and \({\mathbf {Q}}\) is PD and symmetric, can be expressed as:

$$\begin{aligned} {\dot{V}}(t, z)&\le -\left| z_{1}\right| ^{-\frac{1}{\theta }}\left[ \lambda _{{\min }}({\mathbf {Q}}) \Vert {h}\Vert -2\left( \varrho _{1}+\varrho _{2}\Vert {h}\Vert \right) \Vert {h}\Vert \varepsilon \right] \nonumber \\&\le -\left| z_{1}\right| ^{-\frac{1}{\theta }}\Vert {h}\Vert \left[ \left( \lambda _{{\min }}({\mathbf {Q}})-2\varrho _2 \varepsilon \right) \Vert {h}\Vert -2\varrho _{1}\varepsilon \right] . \end{aligned}$$
(41)
Fig. 3
figure 3

Control system configuration

Full size image

If we set \(\Vert {h}\Vert =\tau \Vert {h}\Vert +(1-\tau )\Vert {h}\Vert \) (which is true \(\forall \tau \in \left( 0,1\right) \)), then for small enough \(\varrho _2\) such that the following holds:

$$\begin{aligned} \varrho _2 \le \frac{\lambda _{\mathrm {min}}({Q})}{2\varepsilon }; \end{aligned}$$
(42)

then for every \(\varrho _1>0\), and \(\tau \in \left( 0,1\right) \), it can be obtained, from (41), that

$$\begin{aligned} {\dot{V}}(t,z) \le -\sqrt{\frac{V^{\mathrm {M}}(\cdot )}{\lambda _{{\max }}^{\mathrm {M}}({\mathbf {P}})}} \left[ \beta \tau \Vert {h}\Vert +\beta (1-\tau )\Vert {h}\Vert -2\varrho _{1}\varepsilon \right] , \end{aligned}$$
(43)

where \(\beta =\left( \lambda _{\mathrm {min}}({\mathbf {Q}})-2\varrho _2 \varepsilon \right) \).

Remark 6

In the preceding equation, whether or not \({\dot{V}}(t,z)\) is negative definite (ND) depends on whether or not the following two conditions are satisfied:

C1. :

\(\lambda _{{\min }}\left( {\mathbf {Q}}\right) \ge 2 \varrho _{2} \varepsilon \);

C2. :

\(\beta (1-\tau )\Vert {h}\Vert \ge 2\varrho _{1}\varepsilon \).

Along (38), condition C2 can be equivalently expressed as:

$$\begin{aligned} \Vert {h}\Vert \ge \frac{2 \varrho _{1} \varepsilon }{\beta (1-\tau )}\ge \sqrt{\frac{V(\cdot )}{\lambda _{{\max }}({\mathbf {P}})}}=\omega , \end{aligned}$$
(44)
Table 2 Simulation model parameters
Full size table

where \(\omega \) denotes the boundary of the manifold \(\sigma \). Hence, one gets the systems stable manifold as \(V(\cdot ) \le \lambda _{\mathrm {max}}({\mathbf {P}}) \omega ^2\), describing the interior of the manifold. When condition (44) applies, along the boundary of \(\sigma \), (43) reduces to:

$$\begin{aligned} {\dot{V}}(t,z)&\le -\sqrt{\frac{V^{\mathrm {M}}(\cdot )}{\lambda _{{\max }}^{\mathrm {M}}({\mathbf {P}})}} \beta \tau \sqrt{\frac{V(\cdot )}{\lambda _{{\max }}({\mathbf {P}})}}, \forall \Vert {h}\Vert \ge \omega \nonumber \\&\le -\tau \left( \lambda _{{\min }}\left( {\mathbf {Q}}\right) -2 \varrho _{2} \varepsilon \right) \frac{V^{\mathrm {y}}(t,{h})}{\lambda _{{\max }}^{\mathrm {y}}({\mathbf {P}})}, \forall \Vert {h}\Vert \ge \omega . \end{aligned}$$
(45)

Ultimately, any trajectory starting from initial state \(z_0\) will converge to the set \(\sigma ={z \in \mathfrak {R}^2 | V(t,z) \le \lambda _{\mathrm {max}} \omega ^2}\) in finite time, \(T_\mathrm {r}\), which by using Bihari’s inequality [60] and the separation principle can be computed as:

$$\begin{aligned} T_{\mathrm {r}}=\theta \frac{\lambda _{{\max }}^{\mathrm {y}}({\mathbf {P}})}{\tau \left( \lambda _{{\min }}({\mathbf {Q}})-2 \varrho _{2} \varepsilon \right) }\left( V_{0}^{\frac{1}{\theta }}-\lambda _{{\max }}^{\frac{1}{\theta }}({\mathbf {P}}) \omega ^{\frac{2}{\theta }}\right) , \end{aligned}$$
(46)

and remain in \(\sigma \) such that \(\Vert z\Vert \le \omega \) for all future times \(t \ge {t_0}+T_\mathrm {r}\) with b as in (26).

Remark 7

Since \(\varrho _1 \ne 0\), trajectories will not converge to the origin, but may converge to the set \(\sigma \) which may contain the origin, and will be globally ultimately bounded. This means that \(\exists {b}>0\) and for every \({a}>0\), \(\exists T=T({a,b}) \ge 0 \, | \, \Vert z({t_0})\Vert \le {a} \rightarrow \Vert z\Vert \le {b}, \, \forall t \ge {t_0}+T_\mathrm {r}\).

The following assumption is considered for the purpose of the control applications in Sect. 4.

Assumption 4

For the purpose of simulation, the matched uncertainties due to un-modelled dynamics, parametric variations, and external disturbance that enter the system through the same channel as the control force, \(F_\mathrm {c}\), are taken as \(\delta {\tilde{g}}_{{i}}({\mathbf {X}})+\delta {\tilde{b}}_{{i}}({\mathbf {X}})=2 \sin 3 t+\cos t+2\). Additionally, the unmatched uncertainties are taken as \(\varDelta g_{{i}}({\mathbf {X}})+\varDelta b_{{i}}({\mathbf {X}}), \, (i =1,2,3)\), representing some random fluctuations in the range \({[-0.1 0.1]}\).

Figure 3 shows the configuration of the overall system with the proposed NSSTC-ISMC strategy. The error vector, \({\mathbf {e}}(t) \in \mathfrak {R}^6\), is obtained as the discrepancy between the actual states, \({\mathbf {X}}(t) \in \mathfrak {R}^6\), and their corresponding set points, \({\mathbf {X}}^\mathrm {d}(t) \in \mathfrak {R}^6\). This error vector is taken as an input by the equivalent control and sliding variable blocks. As it can also be seen, the sliding variable \(\xi (t)\) is taken as an input by the switching control block to generate the \(u_{\mathrm {sw}}(t)\). As the sum of \(u_{\mathrm {sw}}(t)\) and \(u_{\mathrm {eq}}(t)\), the input to the trolley actuator is then obtained. The actuator physical force \(F_{\mathrm {c}}(t)\) minus the frictional force \(F_{\mathrm {f}}(t)\) is used to drive the perturbed system (3).

4 Results and Discussion

Below this section, the effectiveness of the proposed NSSTC-ISMC algorithm will be demonstrated. The NSSTC-ISMC is compared with those obtained using the existing MSTC algorithm in the literature. For fair comparative analysis, the ISMC method is used to design the sliding surface for the existing MSTC algorithm (forming a hybrid MSTC-ISMC control scheme). Simulations experiments were conducted within the MATLAB software using the Runge–Kutta numerical solver with an iteration step size of 0.001. It is to be noted that Assumption 4 applies. Crane and control parameters are accepted as in Tables 2 and 3, respectively.

Table 3 Control design parameters
Full size table

The performances of the NSSTC-ISMC is also compared against those of MSTC-ISMC and the classical ISMC algorithms. The ISMC is designed based on the exponential reaching law given by:

$$\begin{aligned} F_{\mathrm {c(ISMC)}}=u_{\mathrm {eq}}-{\varvec{\Gamma }} {\mathbf {B}}[\mathrm {k}\xi ({\mathbf {e}},t)+\eta {\text {sgn}}\{\xi ({\mathbf {e}},t)\}], \end{aligned}$$
(47)

where \({k}\xi ({\mathbf {e}},t)\) is the exponential term and \({k}, \eta >0 .\) For the purpose of comparison, \(u_{\mathrm {eq}}\) in (47) is the same as in (16).

Fig. 4
figure 4

Tracking responses, a cart position, b cart velocity, c hook sway, d hook sway velocity, e load sway, f load sway velocity

Full size image

Figure 4 shows the responses obtained when the proposed NSSTC-ISMC control strategy’s efficacy is compared against those of the MSTC-ISMC and the conventional ISMC methods. Zero initial conditions for the crane states were assumed. Moreover, for comparison, the same model parameters and sliding manifold parameters are used.

One can see from the responses that the cart tracked the desired 1 m position in about 4 s, and the controllers effectively suppress both hook and payload sways. Additionally, as respectively shown in Fig. 4c and e, the performance of the proposed NSSTC-ISMC is slightly more effective with regards to hook sway and payload sway suppression as compared to the other two controllers.

Fig. 5
figure 5

Zero initial conditions tracking responses, a control effort, b sliding variable, c matched uncertainty, d unmatched uncertainty

Full size image
Fig. 6
figure 6

Error analysis for the ISMC, MSTC-ISMC and NSSTC-ISMC controllers from zero initial states, a MSE, b MAE

Full size image
Fig. 7
figure 7

Tracking responses for nonzero initial states, a cart position, b cart velocity, c hook sway, d hook velocity, e load sway, f load velocity

Full size image
Fig. 8
figure 8

Nonzero initial conditions tracking responses, a control effort, b sliding variable, c matched uncertainty, d unmatched uncertainty

Full size image
Fig. 9
figure 9

Error analysis for ISMC, MSTC-ISMC, and NSSTC-ISMC controllers from nonzero initial states, a MSE, b MAE

Full size image

In Fig. 5a and b, the control efforts and the sliding surfaces for the three controllers are compared, respectively. It may have been noted that the control effort for the conventional ISMC chatters, while no chattering was observed for the case using the MSTC-ISMC. However, a much greater control effort is required, and the sliding variable overshoots. Similar to the MSTC-ISMC, the proposed NSSTC-ISMC has no chattering. However, a relatively much lower control effort is required, and the sliding variable overshoot is suppressed. The profiles for the matched and unmatched uncertainties are depicted in Fig. 5c and d, respectively. It is to be noted that, until otherwise expressed, below this section, all horizontal axes represent time in seconds.

To further investigate the claims of improvements in the control effort and the sliding variable achieved using the proposed NSSTC-ISMC algorithm, like in the works of [32,33,34,35,36, 62] we employ the MAE and the MSE criteria computed using (48) and (49), respectively.

$$\begin{aligned} \mathrm {MAE}= & {} \frac{\sum _{{i}=1}^{\mathrm {N}}\left| {S}(\tau )\right| }{\mathrm {N}}; \end{aligned}$$
(48)
$$\begin{aligned} \mathrm {MSE}= & {} \frac{\sum _{{i}=1}^{\mathrm {N}}{S}(\tau )^{2}}{\mathrm {N}}, \end{aligned}$$
(49)

where \({S}(\tau )\) is signal sampled at the \(\tau \)th instance, while N represents total samples count. The MAE and MSE values for the control application in Figs. 4 and 5 are depicted in Fig. 6. One can argue that the MAE and MSE analysis results further support the claims in the preceding paragraph.

Zero initial conditions were taken for the previous control application. Nevertheless, in real cranes, this is not always the scenario. Control application was repeated to test the effectiveness of the three control strategies for nonzero initial conditions given by \({\mathbf {X}}_0=\left[ \begin{array} {l l l l l l} {1.5}&{0.4}&{0.1}&{0}&{0.1}&{0.1}\end{array}\right] ^{\mathrm {T}}\), i.e., the driving cart was assumed to be at an initial position of 1.5 m from the datum point. The payload and the hook angles were at an angle of about \(6^0\) from the vertical reference of \(0^0\) when the command to track a 1 m position was applied. Figure 7 shows the evolution of the state trajectories from nonzero initial conditions. From the figure, one can see that the cart tracked the desired 1 m position in about 7 s, and the controllers effectively suppress both hook and payload sways. Like in the previous control application, the performance of the proposed NSSTC-ISMC is slightly more effective when compared to the other two controllers. It is worth pointing out that the driving cart reached the desired position in about 7 s, slower than the case where zero initial conditions are assumed (see Fig. 4). This is because, since the payload and hook sways are non-actuated state variables, the controllers used the driving cart’s motion (i.e., the actuated state variable) to regulate or suppress the initial and residual sways indirectly. The reader may refer to the cart’s velocity (Fig. 7b) to see how the cart’s direction of travel changed while the driving cart tracked the desired trajectory, and at the same time, attenuated the pendulum-like motions of the payload and hook.

In Fig. 8a and b, the control efforts and the sliding surfaces for the three controllers are compared. It may have been noticed that the control effort for the conventional ISMC chatters, while no chattering is observed for the case using the MSTC-ISMC, but a greater control effort is required, and the sliding variable overshoots. Similar to the MSTC-ISMC, the proposed NSSTC-ISMC has no chattering; however, a relatively lesser control effort is required, and the sliding variable overshoot is suppressed. The profiles for the matched and unmatched uncertainties are depicted in Fig. 8c and d, respectively.

Like in the previous control application, the MAE and MSE values for the control application in Figs. 7 and 8 (for nonzero initial conditions) are depicted in Fig. 9. Based on the MAE and MSE results, one can argue that the proposed NSSTC-ISMC algorithm’s effectiveness is better compared to the two other controllers.

Remark 8

The chattering problem affects the fatigue life of actuators. Besides that, driving a system with such a high-frequency signal may excite the system’s parasitic dynamics (which are of high frequencies). Nevertheless, one may employ boundary layer control to circumvent this problem when using conventional first-order SMC algorithms. However, studies have shown that using boundary layer control may reduce control resilience. This robustness reduction is attributed to the fact that the sliding variable is no longer confined to the sliding manifold but the neighbourhood around the manifold. Hence, control strategies (such as second-order STC) that attenuate chattering without compromising robustness are always preferred in practice.

5 Conclusions and Future Works

In overhead cranes, the presence of the double-pendulum effect, disturbances, and frictions make control more challenging. The paper devised a novel structure of a super-twisting algorithm that ensured the desired performance of a sixth-order nonlinear perturbed overhead crane. A hybrid control strategy formed by blending NSSTC and ISMC is proposed. The proposed method’s efficacy has been investigated compared to those of a hybrid MSTC-ISMC and conventional ISMC control algorithms. The proposed NSSTC algorithm has been found to mitigate the sliding surface overshoot and alleviate the initial peak of the trolley control effort that can be encountered using the existing MSTC algorithm. By using a strict quadratic Lyapunov function, the closed-loop system has been shown to be finite-time stable.

In future work, the assumption that crane states are available for full-state feedback design may be addressed using a state observer. In this way, the efficacy of the proposed control method could be investigated on an industrial crane. Additionally, the ‘smoothness factor,’ \({\theta }\) and the design parameter \({\gamma }\) may be optimally obtained by exploiting intelligent turning algorithms like neural networks or fuzzy logic.