1 Introduction

Overhead cranes are used in factories and industries for the transport of heavy cargoes, nuclear wastes and loading and unloading of ship cargoes at ports. Especially, in order to be able to minimize the service period during loading and unloading of ship containers, faster carriage of cargoes is needed. Control of crane movement is needed for optimization of dynamic performance. In a plenary operation, load is lifted from a given point and usually transferred to the required position with a fast car and the load is unloaded at the end of the transfer. The problem here is to minimize the oscillation of the load while carrying it as fast as possible to the desired position [1].

However, some problems are faced while ensuring these requirements. Acceleration of crane car always causes some unwanted oscillations which can lead to the damage of the load and even accidents. This situation has led to an increase in the interest of the crane control system as a beneficial application [2].

Studies conducted thus far have addressed some examinations on cranes, and two- and three-dimensional dynamic models have been formed. Developed control algorithms have been applied to the crane models which were designed at different scale [3–5]. Studies conducted for optimum orbit control of cranes in loaded and unloaded situations utilized genetic algorithm techniques. In addition, different control techniques have been developed and applied for perfect positioning of cranes and minimization of load oscillation. Artificial neural networks were resorted for this effect, and successful results have been obtained [6–14].

The susceptibility of sliding mode control to external effects and parametric changes is one of its biggest advantages. The fact that developed technology forms a basis for the applicability of such control methods makes this method even more attractive [15, 16]. Provided that an ideal sliding mode switching in real world has to be at infinite speed. In practice, this is impossible to succeed. A boundary layer is applied on sliding surface in order to get rid of this problem. However, such approaches decrease the performance of the controller [17].

In speed trajectory control, sliding surface is kept moving during control period by rotating or by sliding. Quick damping, decrease in switching effect and increase in performance have been examined in the studies when sliding mode controller with moving sliding surface is used [18].

The motion equations of the system investigated in this study are obtained mathematically. Subsequently, sliding mode control with moving sliding surface is designed and applied to the system. The slope of the sliding surface is determined with generated network-based fuzzy logic structure. The numerical values of the parameters belonging to the generated structure are determined with genetic algorithm according to an objective function. The obtained results are graphically represented and examined.

2 Equations of motion of the system

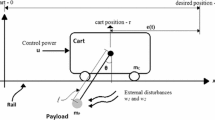
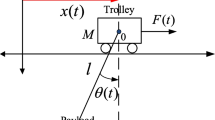
The system model which represents the plenary movement of overhead crane is shown in Fig. 1. While being defined with the position of the car that changes according to time, the oscillation angle of the load was shown with θ. Departing from Newton’s second law, the expression that ensures the condition of the total of forces that affect horizontal movement of the car being null can be written as follows:

$$ (M + m)\frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }} + B\frac{{{\text{d}}x}}{{{\text{d}}t}} + mL\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}t^{2} }}\cos \theta - mL\left( {\frac{{{\text{d}}\theta }}{{{\text{d}}t}}} \right)^{2} \sin \theta - u = 0 $$
(1)
Fig. 1
figure 1

System model that represents the plenary movement of overhead crane

Full size image

In addition, the expression that meets the requirement that the sum of moments according to the point P, which is the rotation center of the pendulum, can be obtained as follows:

$$ mL\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}t^{2} }} + b\frac{{{\text{d}}\theta }}{{{\text{d}}t}} + mg\sin\theta + m\frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }}\cos \theta = 0 $$
(2)

where the rope that holds the load is accepted as stiff and its length was shown with L. In addition, the damping coefficient B which affects the linear movement of the car, the damping coefficient b which affects the circular movement of the load, the mass of the car M, the mass of the load that was transported m, gravity acceleration g and control force u are included in the equation. From Eqs. (1)–(2), the acceleration equations of the car and the pendulum can be found as follows:

$$ \frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }} = \frac{{u + mL\left( {\frac{{{\text{d}}\theta }}{{{\text{d}}t}}} \right)^{2} \sin \theta - mL\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}t^{2} }}\cos \theta - B\frac{{{\text{d}}x}}{{{\text{d}}t}}}}{M + m} $$
(3)
$$ \frac{{{\text{d}}^{2} \theta }}{{{\text{d}}t^{2} }} = \frac{{ - b\frac{{{\text{d}}\theta }}{{{\text{d}}t}} - mg\sin \theta - m\frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }}\cos \theta }}{mL} $$
(4)

In Eq. (3), when the expression d2 θ/dt 2 is replaced by Eq. (4) and necessary abbreviations are made, the acceleration expression belonging to the car is obtained as follows:

$$ \frac{{{\text{d}}x^{2} }}{{{\text{d}}t^{2} }} = \frac{{u + mL\left( {\frac{{{\text{d}}\theta }}{{{\text{d}}t}}} \right)^{2} \sin \theta + b\frac{{{\text{d}}\theta }}{{{\text{d}}t}}\cos \theta + mg\sin\theta g\sin - B\frac{{{\text{d}}x}}{{{\text{d}}t}}}}{{M + m - m\cos^{2} \theta }} $$
(5)

Similarly, when the expression d2 x/dt 2 in Eq. (4) is replaced by Eq. (3) and necessary abbreviations are made, the angular acceleration expression belonging to the pendulum is found as

$$ \frac{{{\text{d}}^{2} \theta }}{{{\text{d}}t^{2} }} = \frac{{ - \left( {M + m} \right)\left( {b\frac{{{\text{d}}\theta }}{{{\text{d}}t}} + mg\sin \theta } \right) - um\cos \theta - \left( {m\frac{{{\text{d}}\theta }}{{{\text{d}}t}}} \right)^{2} L\sin \theta \sin \theta + mB\frac{{{\text{d}}\theta }}{{{\text{d}}t}}\cos \theta }}{{MmL + m^{2} L\sin^{2} \theta }} $$
(6)

Necessary variable transformations are made as x 1  = x, x 2  = dx/dt, dx 2 /dt = d2 x/dt 2, x 3  = θ, x 4  = dθ/dt, dx 4 /dt = d2 θ/dt 2, and the mathematical movement equations of the system can be obtained as

$$ \left. \begin{gathered} \frac{{{\text{d}}x_{1} }}{{{\text{d}}t}} = x_{2} \hfill \\ \frac{{{\text{d}}x_{2} }}{{{\text{d}}t}} = \frac{{u + mLx_{4}^{2} \sin x_{3} + bx_{4} \cos x_{3} + mg\sin x_{3} \cos x_{3} - Bx_{2} }}{{M + m - m\cos^{2} x_{3} }} \hfill \\ \frac{{{\text{d}}x_{3} }}{{{\text{d}}t}} = x_{4} \hfill \\ \frac{{{\text{dx}}_{4} }}{{{\text{d}}t}} = \frac{{ - \left( {M + m} \right)\left( {bbx_{4} + mg\sin x_{3} } \right) - um\cos x_{3} - \left( {mx_{4} } \right)^{2} L\sin x_{3} \cos x_{3} + mBx_{2} \cos x_{3} }}{{MmL + m^{2} L\sin^{2} x_{3} }} \hfill \\ \end{gathered} \right\} $$
(7)

3 Design of sliding mode controller

Sliding mode control is a special type of variable structured control. It is chosen by the user in a switching state space which is called sliding surface. Before the trajectory of the system reaches switching surface, system trajectory is directed toward the sliding surface with a control rule. As can be seen from Fig. 2, sliding mode control occurs when the system forces all of its states to appear in the switching surface, sliding. Once the trajectory reaches sliding surface system dynamics begin to make switching along the surface.

Fig. 2
figure 2

Sliding surface

Full size image

When a second degree system is considered, the equations of the system in state space can be written as

$$ \frac{{{\text{d}}z_{1} }}{{{\text{d}}t}} = z_{2} \,\,\frac{{{\text{d}}z_{2} }}{{{\text{d}}t}} = f(z) + g(z)u $$
(8)

Where f(z) and g(z) functions are thought as nonlinear functions. The function which defines sliding surface in stable area can be written as follows:

$$ S = z2 + Cz1 $$
(9)

and where the function is zero, it becomes

$$ z_{2} = - Cz_{1} $$
(10)

The time derivative of sliding surface function is obtained as follows:

$$ \frac{{{\text{d}}S}}{{{\text{d}}t}} = \frac{{{\text{d}}z_{2} }}{{{\text{d}}t}} + C\frac{{{\text{d}}z_{1} }}{{{\text{d}}t}} = f(z) + g(z)u + Cz_{2} $$
(11)

According to Lyapunov expressions [17];

$$ V = \frac{{S^{2} }}{2} $$
(12)
$$ \frac{{{\text{d}}V}}{{{\text{d}}t}} = S\frac{{{\text{d}}S}}{{{\text{d}}t}} = S\left[ {f\left( z \right) + g\left( z \right)u + Cz_{2} } \right] $$
(13)

Here, the following can be written so that dV/dt < 0 condition is met.

$$ f(z) + g(z)u + Cz_{2} \left\{ {\begin{array}{*{20}c} { < 0} & {\quad {\text{for}}\,{\kern 1pt} S > 0} \\ { = 0} & {\quad {\text{for}}\,{\kern 1pt} S = 0} \\ { > 0} & {\quad {\text{for}}\,{\kern 1pt} S < 0} \\ \end{array} } \right. $$
(14)

The values that control variable are set so that the system can be stable will be as follows:

$$ u\left\{ \begin{gathered} < \beta \left( z \right) \quad {\text{for }}\,S > 0 \hfill \\ = \beta \left( z \right)\,\quad {\text{for}}\,S = 0 \hfill \\ > \beta \left( z \right) \quad {\text{for}}\,S < 0 \hfill \\ \end{gathered} \right. $$
(15)

Where the value of β(z) is calculated by the expression:

$$ \beta (z) = - \left[ {\frac{{f(z) + Cz_{2} }}{g(z)}} \right] $$
(16)

In this case, control expression can be found by Eq. (17) where K is a positive coefficient and taken 100.

$$ u = \beta (z) - K{\text{sign}}(S) $$
(17)

when the fact that u control force is affected to the car in crane system is taken into account, Eq. (16) is rewritten for crane and Eq. (18) is obtained.

$$ \beta (z) = - \frac{f(x) + Cx}{g(x)} $$
(18)

where f(x) and g ( x) functions can be written as follows:

$$ f(x) = \frac{{mLx_{4}^{2} \sin (x_{3} ) + bx_{4} \cos (x_{3} ) + mg\sin (x_{3} )\cos (x_{3} ) - Bx_{2} }}{{M + m - m\cos^{2} (x_{3} )}} $$
(19)
$$ g(x) = \frac{1}{{M + m - m\cos^{2} (x_{3} )}} $$
(20)

4 Design of neural-based fuzzy logic sliding mode control with moving sliding surface

In the concerned sliding mode control design, explained in the sections up to here, a constant sliding is considered and a control is applied by determining sliding surface constant of the defined function. However, performed studies show that when sliding surface is assumed to be active performance of the controller increases incredibly [18]. In this section, using neural-based fuzzy sliding mode control algorithm is designed.

Moving sliding surface concept is shown in Fig. 3. Here, C is taken as sliding surface constant coefficient and designates the slope of sliding surface at the same time. The slope of the sliding surface keeps moving during control. When Fig. 3 is examined, line defining sliding surface rotates as its direction is about to change always in stable region of phase plane. Thus, performance of the system will change relative to the slope of sliding surface. Slope of the line can be determined any at that moment with any of the methods.

Fig. 3
figure 3

Rotating sliding surface

Full size image

In this study, neural-based fuzzy logic technique is used to determine the slope. If a big value is taken for slope of sliding surface, C the system will be more stable but the time passing during state variables are moving toward sliding surface will be longer, capturing a successful system answer will be delayed. On the other hand, if slope of sliding surface, C is taken small approaching speed of state variables through origin after reaching sliding surface will be slower and this will inversely affect the stability of the system.

Formerly determined C, constant coefficient, is removed, and a neural-based fuzzy logic is formed which will produce appropriate C values every time when it is necessary, during control to keep sliding surface moving. In Fig. 4, neural-based fuzzy logic structure which consists of 5 separate layers can be seen. These are, respectively, fuzzification layer, two hidden layers, function layer and defuzzification layer. In such a structure, each operation unit which constitutes the foundations of fuzzy logic connect each other with the help of network and each connection conveys the datum by multiplying it with a fixed coefficient called “weight.” During training, these weights are optimized in a purposive manner and the most appropriate association is ensured between units.

Fig. 4
figure 4

Neural-based fuzzy logic structure

Full size image

Membership functions are used so as to clarify the membership of any member to a fuzzy set. The membership of an x entry member to a fuzzy set can be shown as μ A (x). In fuzzy logic, the selection of membership function is left to the experience of the user, and in this study, gauss membership function has been performed. At fuzzification layer, x and dx/dt variables are used as entries so as to complete fuzzy working areas and 3 membership functions have been chosen for each entry. Parameters belonging to membership functions are c and a; these functions are shown as follows:

$$ \mu_{Ai} (x) = e^{{ - \left( {\frac{{x - c_{i} }}{{a_{i} }}} \right)^{2} }} \,\,\,\mu_{Bi} (\dot{x}) = e^{{ - \left( {\frac{{\dot{x} - c_{i} }}{{a_{i} }}} \right)^{2} }} \quad {\text{for} i } = \, 1,2,3,n $$
(21)

The crisp degrees of rules are found by using algorithmic multiplication with Eq. (22) at the second layer.

$$ w_{i} = \mu_{Ai} (x)\mu_{BAi} \frac{{{\text{d}}x}}{{{\text{d}}t}} $$
(22)

Normalization operation can be defined as the ratio of the crisp value of each rule to the crisp values of other rules. Thus, the impact of a rule to the exit in terms of sum of all rules can be displayed. These operations are performed at the third layer of the network.

$$ \bar{w}_{i} = \frac{{w_{i} }}{{w_{1} + w_{2} }}\quad {\text{for}i} = \, 1,2,3, \ldots n $$
(23)

Each normalized rule is multiplied with Eq. (24) and its own exit function at fourth layer.

$$ \bar{w}_{i} f_{i} = w_{i} (p_{i} x^{T} + q_{i} (\dot{x})^{T} ) $$
(24)

where p and q are fixed coefficient vectors at (nx1) dimension and linear parameters belonging to the functions used at function level. Defuzzification layer is fifth layer where defuzzification is performed with weight center method just as in Eq. (25) and a network exit is formed.

$$ {\text{O}}_{{ 5,{\text{i}}}} = \sum\limits_{i} {\bar{w}_{i} f_{i} = \frac{{\sum\nolimits_{i} {w_{i} f_{i} } }}{{\sum\nolimits_{i} {w_{i} } }}} $$
(25)

The control which will be applied in a crane system has two objectives. First of these objectives is the carriage of the load to the desired coordinate in a stable manner and as soon as possible; the second objective is minimization of load oscillation during the carriage of the load. In this study, the purpose is to develop and design a fast and high-performance control algorithm for the control of overhead cranes.

Widely used mamdani-type fuzzy logic is replaced with sugeno-type fuzzy logic in this network structure. The network structure reaches the conclusion with functions of entry variables at the fourth layer after it produces and creates the internal rules that perform association at second layer. With this feature, while it behaves like fuzzy logic, and determines through learning the most appropriate association between weight coefficients and layers on network roads that connect these layers to each other, it acts like neural networks.

In Fig. 5, the block diagram that is used for training of neural-based fuzzy logic sliding mode control with moving sliding surface is shown. The network structure that is shown in Fig. 4 can be found in the content of the operation box titled “neural-based fuzzy” and designation of appropriate sliding surface is provided.

Fig. 5
figure 5

Block diagram belonging to the method used for training of the controller

Full size image

5 Application of the designed controllers to the crane system

The car mass of the crane model handled in this study is accepted as 22 kg, and its rope length is accepted as 100 cm. The damping coefficient B is taken 0.2 Ns/m, and the damping coefficient b is taken 0.1 Nms. The mass of the load is taken as 3 kg, and according to these parameters, controllers were designed. The mass of a crane can change according to the type of the load that it will carry. In addition, the carriage height of the load also affects the length of the rope. For this reason, controls were repeated by changing some parameters in the system so as to display the success of the designed controllers.

Best values for the parameters belonging to the controller have to be chosen so that designed controllers can yield successful results. Trial and error method or various developed optimization techniques can be used so as to find the best. Parameters belonging to the controllers designed in this study were determined with genetic algorithm technique. For this purpose, genetic algorithm toolbox of the MATLAB package program was utilized. In genetic algorithm technique, an objective function is determined and the solutions that make this objective function minimum are investigated. For this problem, our purpose is to make sure that the car reaches the target without error, while load is being carried by the crane and, at the same time, to minimize the oscillation of the load. Accordingly throughout the control, the sum of the position error of the car e x and the oscillation angle made by the load eθ must be minimum. In this case, we can write our objective function as follows:

$$ J = Ae_{x} + Be_{\theta } $$
(26)

where parameters A and B are fixed-value significance coefficients. In the application, if less oscillation is more essential coefficient B will have bigger value; if the minimum time for carriage is more essential coefficient A will have bigger value. The controller has to be trained first so that the controller can be prepared for control. During training, the parameters of the controller are updated so that while it ensures the target for the system, it minimizes the objective function.

In this study, training activities were performed by means of carrying the load to the target 1 meter ahead. In Fig. 6, system responses of the sliding mode control graph that was obtained after the training was completed are provided. When these results are examined, it can be seen that especially the control force has switching values with very high frequency. This feature of the controller which causes problems in the application stands out as a disadvantage. System responses graph that was obtained as a result of the training of neural-based fuzzy logic sliding mode control with moving sliding surface, which is the feature of the controller that is the reason of this problem, can be seen in Fig. 7. Necessary improvements were made to the obtained responses.

Fig. 6
figure 6

System responses obtained as a result of the training of sliding mode control

Full size image
Fig. 7
figure 7

System responses obtained as a result of the training of neural-based fuzzy logic sliding mode control with moving sliding surface

Full size image

Controls have been repeated with the purpose of displaying the success of the designed controllers. Accordingly, system responses graph of the sliding mode control applied by taking the target as 3 m is shown in Fig. 8. System responses graph obtained by application of neural-based fuzzy logic sliding mode control with moving sliding surface is given in Fig. 9.

Fig. 8
figure 8

System responses of sliding mode control obtained for target = 3 m

Full size image
Fig. 9
figure 9

System responses of neural-based fuzzy logic sliding mode control with moving sliding surface obtained for target = 3 m

Full size image

For another application, system responses graph of the sliding mode control applied by taking the target as 5 m is shown in Fig. 10. System responses graph obtained by application of neural-based fuzzy logic sliding mode control with moving sliding surface is given in Fig. 11.

Fig. 10
figure 10

System responses of sliding mode control obtained for target = 5 m

Full size image
Fig. 11
figure 11

System responses of neural-based fuzzy logic sliding mode control with moving sliding surface obtained for target = 5 m

Full size image

Controls were repeated with different load and different rope length values so as to display the effect of parametric uncertainty, which is one of the advantages of sliding mode control. First, the mass of the load was increased and taken as 8 kg, and the target was chosen as 2 m. System responses graph of the sliding mode control applied by taking the target as 2 m is shown in Fig. 12. System responses graph obtained by application of neural-based fuzzy logic sliding mode control with moving sliding surface is given in Fig. 13.

Fig. 12
figure 12

System responses of sliding mode control obtained for m = 8 kg and target = 2 m

Full size image
Fig. 13
figure 13

System responses of neural-based fuzzy logic sliding mode control with moving sliding surface obtained for m = 8 kg and target = 2 m

Full size image

In order to be able to observe the effect of rope length, which is one of the essential parameters of the system, load mass was taken as 3 kg, target was taken as 2 m and rope length was taken as 50 cm. The responses of the system obtained by application of sliding mode control to the system graph are shown in Fig. 14. System responses graph obtained by application of neural-based fuzzy logic sliding mode control with moving sliding surface is given in Fig. 15.

Fig. 14
figure 14

System responses of sliding mode control obtained for L = 50 cm, m = 3 kg and target = 2 m

Full size image
Fig. 15
figure 15

System responses of neural-based fuzzy logic sliding mode control with moving sliding surface obtained for L = 50 cm, m = 3 kg and target = 2 m

Full size image

Although successful results are obtained with sliding mode control (SMC), the chattering of the control signals causes problems in terms of applicability as shown in Figs. 8, 9, 10 and 11. When the results obtained neural-based fuzzy logic sliding mode control with moving sliding surface (NF-MSMC) are investigated, the improvements in the control signals are observed clearly. Moreover, nice results are also obtained in terms of system performance. The success of the designed control is introduced by designation of different objective positions. According to the Figs. 12, 13, 14 and 15, the success of the control is not affected with the changes in the system parameters. The obtained results are compared in Table 1.

Table 1 Comparison of the conclusions
Full size table

Obtained results display the success of designed neural-based fuzzy logic sliding mode control with moving sliding surface. The graphs show that control force is applicable in practice.

6 Conclusion

Rope length takes different values depending on the carriage height and the mass of the load transported by cranes. Various developed control algorithms have been used against some problems faced in crane systems used in industry. The susceptibility toward external impacts and parametric changes of sliding mode controller, which is one of its advantages, made this controller attractive. In this study, sliding mode control algorithm is designed as control algorithm. But due to very frequent direction changes of sliding mode control force lines limits practical usage of controller. For this reason, fuzzy logic and artificial neural networks techniques are combined and neural-based fuzzy sliding mode control with moving sliding surface algorithm has been designed. Parameters of the completed controller have been determined by updating with genetic algorithm technique. Once its training was completed, the controller was applied to the crane and system responses were obtained graphically and the results were analyzed. According to obtained results, it is observed that performance of the controller is quite high and control force can be used practically. Controls were repeated with different load and different rope lengths so as to display the effect of parametric uncertainty, which is one of the advantages of sliding mode control. Obtained results show that the controller provides quite successful control. It has preserved all of the advantageous features of sliding mode controller with high performance. For numerical analysis, program developed on MATLAB software and genetic algorithm tools of MATLAB are used.