Super-twisting disturbance-observer-based nonlinear control of the overhead crane system

Abstract

In this paper, we consider the application of the disturbance observer technique and interconnection and damping assignment passivity-based control to the disturbance estimation and regulation control of underactuated overhead crane systems. In particular, based on the super-twisting sliding mode control technology, a finite time disturbance estimator is presented, which can identify uncertain disturbances exactly in finite time. Next, we obtain an equivalent system and an auxiliary control input in terms of the partial feedback linearization methodology, and a desired storage function with assigned characteristics is established. On the basis of the matching conditions, we derive the desired storage function by solving two ordinary differential equations, without necessity of solving partial differential equations. Subsequently, a novel disturbance-observer-based nonlinear controller is derived, and rigorous theoretical analysis is given to prove that all of the states of the closed-loop system asymptotically converge to the origin. Experimental tests are carried out to illustrate the disturbance estimation and regulation performance of the presented control law. In addition, to demonstrate the excellent robustness of the presented controller, a comparison study is included as well.

1 Introduction

Underactuated electromechanical systems are systems with fewer control variables than variables to be controlled. In the recent few decades, the control of underactuated systems has attracted considerable attention from the industrial electronics and control community [1,2,3,4,5,6,7,8]. Different from fully-actuated systems, the underactuated feature makes the control of such systems extremely challenging. As a typical underactuated system and a popular transportation tool, the automation control problem of overhead crane systems is also difficult.

To this today, to enhance the work efficiency of the overhead crane system, a lot of efficient control methods for crane control have been published in the literature. Open-loop control approaches, such as input shaping [9, 10], motion planning [11,12,13,14,15], etc., have been proposed for cranes. In order to possess strong robustness of the crane system, abundant closed-loop control methods are also proposed and reported in the literature, including passivity-based control (PBC) [16,17,18], partial feedback linearization [19, 20], fuzzy control [21,22,23], and so on [24,25,26,27]. In particular, in terms of the passivity characteristic of the overhead crane system, a series of nonlinear control methods have been proposed in [16,17,18]. However, uncertain disturbances are not taken into consideration for these methods. To tackle this drawback, some sliding-mode-based control methods are presented for the overhead crane control [28,29,30,31]. Nevertheless, the chattering phenomenon is another issue that needs to be addressed in the conventional sliding-mode-based control systems. In recent years, to deal with uncertain factors, based on the disturbance compensation technology [32], some works have been done for the disturbance elimination and regulation/tracking tasks of the overhead crane control. In [33], a finite-time tracking controller is investigated on the basis of the disturbance estimation technique. However, only the tracking control objective is achieved, the swing elimination objective is not accomplished. In [34,35,36,37,38], although some disturbance-observer-based nonlinear controllers have been proposed for the crane control, there exist disturbance estimation errors for these disturbance observers.

Although considerable attention has been attracted from different communities for the control of overhead cranes, it is still a fairly open topic. To deal with the above-mentioned problems for existing disturbance-observer-based controllers [33,34,35,36,37,38], we concentrate our attention on the application of the disturbance observer technique and the interconnection and damping assignment passivity-based control (IDA-PBC) [39] to the disturbance estimation and regulation control of overhead cranes. Finite-time disturbance observer can be used to estimate uncertain disturbances exactly. In addition, IDA-PBC methodology has been successfully implemented on many systems described by port-controlled Hamiltonian (PCH) models or Euler–Lagrange (EL) models [39]. Different from the “classical” PBC methodology, the closed-loop storage function is derived by solving a series of partial differential equations (PDEs). It is generally known that, in general, solving PDEs is not easy. The main difficulty is to solve matching conditions (e.g. PDEs) when using the IDA-PBC technique. To overcome this drawback, we present a methodology to reduce PDEs into ODEs, based on which a desired storage function can be obtained. In particular, first, a super-twisting-based disturbance observer is devised based on the dynamic equations of the overhead crane. Then, in order to make control design, a storage function with a desired structure is constructed based on IDA-PBC, and a solution of the storage function is obtained by solving two ODEs, which obviates solving PDEs. Subsequently, a novel disturbance-observer-based nonlinear control method is established and the stability of the whole closed-loop system is demonstrated by rigorous mathematical analysis. Finally, to illustrate the validity and efficiency of the presented method, some experimental tests are included, and a comparison test between the proposed method and an existing method is implemented as well.

The contributions of this paper include the following aspects. Firstly, unknown disturbances can be estimated exactly in finite time by the proposed super-twisting-based disturbance observer. Secondly, based on IDA-PBC, the assigned storage function has certain characteristics. Thirdly, we solve the matching equations by reducing PDEs into ODEs, which overcomes the main stumbling block in IDA-PBC’s applications.

The remaining part of this work is organized as follows. In Sect. 2, the dynamic equations are given and some model transformation manipulations are performed. The super-twisting-based disturbance observer is presented, and the detailed control development and stability analysis are given in Sect. 3. Experimental tests are implemented in Sect. 4. The last section wraps up this work with some concluding remarks.

2 Dynamic equations of the overhead crane system

Fig. 1

Overhead crane structure

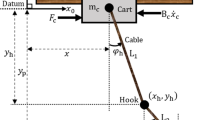
In this paper, we consider the control of the overhead crane system (as shown in Fig. 1) with two degrees of freedom and underactuation degree one, whose dynamics can be described as follows [33, 36, 37]:

$$\begin{aligned}&(M+m){\ddot{x}}+ml{\ddot{\theta }}\cos {\theta }-ml{{\dot{\theta }}}^2\sin {\theta }=F_x, \end{aligned}$$

(1)

$$\begin{aligned}&ml^2{{\ddot{\theta }}}+ml{{\ddot{x}}}\cos {\theta }+mgl\sin {\theta }=0, \end{aligned}$$

(2)

where M represents the cart mass; m is the load mass; x(t) and $\theta (t)$ represent the cart displacement and the load swing angle, respectively; l is the length of the cable; g stands for the gravitational acceleration coefficient; and $F_x(t)$ is the resultant force applied to the cart consisting of the following two parts:

$$\begin{aligned} F_x(t)=F_a(t)-d(t), \end{aligned}$$

(3)

where $F_a(t)$ represents the actuating force supplied by the motor; d(t) represents the lumped disturbance term, including uncertain disturbances, unmodeled dynamics, frictions, etc. Assume that the time derivative of d(t) satisfies the following condition:

$$\begin{aligned} |\dot{d} (t) | \le \alpha _d \end{aligned}$$

(4)

where $\alpha _d \in {{\mathbb {R}}}^+$ is a known upper bound.

Based on the Eq. (2), one can derive that

$$\begin{aligned} l{{\ddot{\theta }}}+{\ddot{x}} \cos \theta +g\sin \theta =0. \end{aligned}$$

(5)

Then, we can rearrange (1) as follows:

$$\begin{aligned} F_x=m(\theta ){\ddot{x}} +\varsigma (\theta ,{{\dot{\theta }}}), \end{aligned}$$

(6)

wherein the expressions of the auxiliary variables $m(\theta )$, $\varsigma (\theta ,{{\dot{\theta }}})$ are

$$\begin{aligned} m(\theta )&=M+m\sin ^2\theta , \end{aligned}$$

(7)

$$\begin{aligned} \varsigma (\theta ,{{\dot{\theta }}})&=-m\sin \theta (g\cos \theta + l {{\dot{\theta }}}^2 ). \end{aligned}$$

(8)

Taking practical implementations into consideration, the following assumption is reasonable [17].

Assumption 1

Due to the physical constraints, the load swing meets that

$$\begin{aligned} \theta (t) \in \left( -{\pi }, {\pi }\right) ,~ t \ge 0. \end{aligned}$$

(9)

3 Main results

In this section, first, a super-twisting-based disturbance observer will be designed to estimate the lumped disturbance. Then, to introduce a disturbance-observer-based nonlinear control method, a desired storage function—that can be considered as a Lyapunov function candidate for the desired equilibria—will be constructed via IDA-PBC technique. Finally, rigorous stability analysis will be provided.

3.1 Disturbance observer design

Based on the Eq. (1) of the system model of the overhead crane, the following auxiliary signals are introduced:

$$\begin{aligned} \chi _1&= (M+m)x+ml\sin \theta \end{aligned}$$

(10)

$$\begin{aligned} \chi _2&= (M+m)\dot{x} +ml{{\dot{\theta }}} \cos \theta \end{aligned}$$

(11)

Differentiating $\chi _1(t)$ and $\chi _2(t)$ with respect to time once, and using the Eq. (1), one can obtain the following equations:

$$\begin{aligned} {{\dot{\chi }}}_1&= \chi _2 \end{aligned}$$

(12a)

$$\begin{aligned} {{\dot{\chi }}}_2&= F_a(t)-d(t) \end{aligned}$$

(12b)

Define that the estimated value of d(t) is ${{\hat{d}}} (t)$, then, the following sliding surface is introduced:

$$\begin{aligned} s = \chi _2 + \chi _3 \end{aligned}$$

(13)

wherein the derivative of $\chi _3(t)$ is

$$\begin{aligned} {{\dot{\chi }}}_3 = -F_a + {{\hat{d}}} \end{aligned}$$

(14)

and the estimator is designed as

$$\begin{aligned} {{\hat{d}}} = -k_1\text{sgn}(s) \sqrt{|s|} - k_2 \int _0^t \text{sgn}(s) \text{d}\tau \end{aligned}$$

(15)

where $k_1,k_2 \in {{\mathbb {R}}}^+$ are observer gains and selected in terms of the selection rules in Theorem 2 of [40], that is

$$\begin{aligned} k_1 = \omega \sqrt{\frac{4\nu \alpha _d}{(1-\vartheta )\kappa }},~k_2 =\frac{2 \alpha _d(1+\vartheta )}{1-\vartheta } \end{aligned}$$

(16)

wherein $\omega ,\nu ,\vartheta ,\kappa$ should satisfy the inequalities as follows:

$$\begin{aligned}&\omega - \frac{2}{\nu }\kappa> \kappa ^2 - \vartheta (1+ \omega )\kappa +\frac{1}{4}(1+\omega )^2 \\&0<\vartheta <1,~\nu>1,~\vartheta \nu >1 \end{aligned}$$

Theorem 1

The disturbance d(t) can be exactly estimated by the proposed disturbance observer (15) in finite time, that is

$$\begin{aligned} {{\hat{d}}} = d \end{aligned}$$

(17)

in finite time.

Proof

Differentiating both sides of (13) with respect to time, and substituting ${{\dot{\chi }}}_2(t)$ and ${{\dot{\chi }}}_3(t)$ in (12b) and (14) into the resulting expression, one can obtain

$$\begin{aligned} \dot{s} = -k_1\text{sgn}(s) \sqrt{|s|} - k_2 \int _0^t \text{sgn}(s) \text{d}\tau -d \end{aligned}$$

(18)

which is equivalent to that

$$\begin{aligned} \dot{s}&= -k_1\text{sgn}(s) \sqrt{|s|} + \sigma \nonumber \\ {{\dot{\sigma }}}&= -k_2 \text{sgn}(s) - \dot{d} \end{aligned}$$

(19)

Then, by using the conclusion of Theorem 2 in [40], one can derive that s(t) and $\dot{s}(t)$ will equal to 0 in finite time. When $\dot{s} (t) =0$, based on (12b), (13) and (14), we can obtain the following equality:

$$\begin{aligned} \dot{s} = {{\dot{\chi }}}_2 + {{\dot{\chi }}}_3 = {{\hat{d}}} - d =0 \end{aligned}$$

(20)

Hence, the conclusion that the disturbance d(t) is exactly estimated by the proposed super-twisting-based disturbance observer (15) in finite time is proven. $\square$

3.2 Storage function construction and control design

On the basis of (6), a convenient partial feedback linearization input is introduced

$$\begin{aligned} F_x=m(\theta )\upsilon +\varsigma (\theta ,{{\dot{\theta }}}), \end{aligned}$$

(21)

wherein $\upsilon (t)$ is an auxiliary control variable yet to be designed. Based on Eqs. (5) and (21), the following equivalent equations can be obtained:

$$\begin{aligned} \dot{q}_1&= p_1, \end{aligned}$$

(22a)

$$\begin{aligned} \dot{q}_2&= p_2, \end{aligned}$$

(22b)

$$\begin{aligned} \dot{p}_1&= \upsilon , \end{aligned}$$

(22c)

$$\begin{aligned} \dot{p}_2&= ({-g\sin q_2-\upsilon \cos q_2})/{l}, \end{aligned}$$

(22d)

where ${\varvec{q}}=[~q_1~~q_2~]^{\mathrm T}=[~x-p_d~~\theta ~]^{\mathrm T}$ and ${\varvec{p}}=[~{p_1}~~{p_2}~]^{\mathrm T}=[~{\dot{x}}~~{{{\dot{\theta }}}}~]^{\mathrm T}$, and $p_d$ is the desired position. Accordingly, the control objective of this work is to regulate the system state to the equilibrium point under the control of $\upsilon (t)$, that is

$$\begin{aligned} \lim _{t \rightarrow \infty } [ \begin{array}{cccc} q_1&q_2&p_1&p_2 \end{array} ]^{\mathrm T} = [ \begin{array}{cccc} 0&0&0&0 \end{array} ]^{\mathrm T}. \end{aligned}$$

(23)

To synthesize the auxiliary control variable $\upsilon (t)$, on the basis of IDA-PBC technology, the auxiliary control variable $\upsilon (t)$ is decomposed into two terms

$$\begin{aligned} \upsilon =\upsilon _{es}+\upsilon _{di}, \end{aligned}$$

(24)

where the auxiliary terms $\upsilon _{es}(t)$ and $\upsilon _{di}(t)$ will be determined later. It is worth pointing out that $\upsilon _{es}(t)$ is introduced to achieve the energy shaping, $\upsilon _{di}(t)$ is devoted to realize the damping injection, and the sum of both terms is the to-be-designed auxiliary control variable $\upsilon (t)$.

By substituting (24) into (22), the Eq. (22) can be rewritten as

$$\begin{aligned} \dot{\varvec{q}}&= {\varvec{p}}, \end{aligned}$$

(25a)

$$\begin{aligned} \dot{\varvec{p}}&= {\varvec{f}}({\varvec{q}}, \upsilon _{es}) + {\varvec{h}}({\varvec{q}})\upsilon _{di}, \end{aligned}$$

(25b)

where

$$\begin{aligned} {\varvec{f}} = \left[ \begin{array}{c} \upsilon _{es} \\ ({-g\sin q_2-\upsilon _{es} \cos q_2})/{l} \end{array} \right] , \quad {\varvec{h}}= \left[ \begin{array}{c} 1 \\ -\cos q_2/l \end{array} \right] . \end{aligned}$$

(26)

Based on (25), we are motivated to seek for a suitable storage function with a desired structure, so that the auxiliary functions $\upsilon _{es}(t)$ and $\upsilon _{di}(t)$ are determined. Hence, the following function is introduced:

$$\begin{aligned} H_d(t)=V_d(\varvec{q}) + \frac{1}{2}{\varvec{p}}^{\mathrm T} M_d {\varvec{p}}, \end{aligned}$$

(27)

where $M_d \in {{\mathbb {R}}}^{2\times 2}$ is a positive definite, constant matrix; $V_d(\varvec{q})$ is a positive function to be determined. After taking the time derivative of $H_d(t)$ in (27), and applying (25), the following equality can be obtained:¹

$$\begin{aligned} {\dot{H}}_d(t)={\varvec{p}}^{\mathrm T} \left( \frac{\partial V_d}{\partial {\varvec{q}}}+ M_d {\varvec{f}} \right) + {\varvec{p}}^{\mathrm T} M_d {\varvec{h}} \upsilon _{di} . \end{aligned}$$

(28)

It is easy to see from the expression of ${\dot{H}}_d(t)$ that if we can seek for suitable variables ($\upsilon _{es}$, $\upsilon _{di}$, $V_d$, $M_d$) such that ${\dot{H}}_d(t) \le 0$ holds, then it is evident that the closed-loop system of (22) is Lyapunov stable. Based on the structure of ${\dot{H}}_d(t)$ in (28), ${\dot{H}}_d(t) \le 0$ holds provided that the following conditions are satisfied.

Condition 1

The unknown variables $\upsilon _{es}$, $V_d$, and $M_d$ are selected that

$$\begin{aligned} \frac{\partial V_d}{\partial {\varvec{q}}}+ M_d {\varvec{f}}= \varvec{0}. \end{aligned}$$

(29)

Condition 2

The auxiliary function $\upsilon _{di} = - k_d {\varvec{h}}^{\mathrm T} M_d{\varvec{p}}$ with $k_d \in {{\mathbb {R}}}^+$.

Based on the previous analysis and the matching condition (29), in order to construct a desired storage function $H_d(t)$, for convenience, we fix the positive matrix $M_d$ as the following special expression:

$$\begin{aligned} M_d={\text{diag}}\left\{ \alpha _1, \alpha _2\right\} , \end{aligned}$$

(30)

where $\alpha _1, \alpha _2 \in {{\mathbb {R}}}^+$ are positive constants. Substituting (26) and (30) into (29) for ${\varvec{f}}$ and $M_d$, respectively, yields

$$\begin{aligned}&\frac{\partial V_d}{\partial {q_1}} + \alpha _1 \upsilon _{es} =0, \end{aligned}$$

(31a)

$$\begin{aligned}&\frac{\partial V_d}{\partial {q_2}} - \alpha _2 \frac{g\sin q_2+\upsilon _{es} \cos q_2}{l}= 0, \end{aligned}$$

(31b)

then, substituting the Eq. (31a) into (31b) for $\upsilon _{es}(t)$, one can obtain the following result:

$$\begin{aligned} \frac{\partial V_d}{\partial {q_2}} + \frac{\partial V_d}{\partial {q_1}}\frac{\alpha _2 \cos q_2}{\alpha _1 l}= \frac{\alpha _2 g \sin q_2}{l} . \end{aligned}$$

(32)

In order to derive a solution of the above PDE, the following Lemma² is utilized.

Lemma 1

Consider the PDE described by

$$\begin{aligned} \frac{\partial V_d}{\partial {q_2}} + {\varLambda }(q_2) \frac{\partial V_d}{\partial {q_1}}= {\varUpsilon }(q_2) , \end{aligned}$$

(33)

where ${\varLambda }: {{\mathbb {R}}} \rightarrow {{\mathbb {R}}}$ and ${\varUpsilon }: {{\mathbb {R}}} \rightarrow {{\mathbb {R}}}$. Then, for all differential functions ${{\mathcal {S}}}: {{\mathbb {R}}}^2 \rightarrow {{\mathbb {R}}}$, a solution of (33) for $V_d(\varvec{q})$ can be given by

$$\begin{aligned} V_d(\varvec{q})= {{\mathcal {Q}}}(q_2) + {{\mathcal {S}}}(q_1+{{\mathcal {T}}}(q_2)) , \end{aligned}$$

(34)

where ${{\mathcal {Q}}}: {{\mathbb {R}}} \rightarrow {{\mathbb {R}}}$ and ${{\mathcal {T}}}: {{\mathbb {R}}} \rightarrow {{\mathbb {R}}}$ are solutions of the following ODEs:

$$\begin{aligned} \frac{{\mathrm d}{{\mathcal {Q}}} }{{\mathrm d} {q_2}} ={{\varUpsilon }}, ~\frac{{\mathrm d}{{\mathcal {T}}} }{{\mathrm d} {q_2}}=-{{\varLambda }} . \end{aligned}$$

(35)

Proof

Substituting the solution $V_d$ in (34) into (33), and applying the conclusions of (35), one can obtain that

$$\begin{aligned} \frac{\partial V_d}{\partial {q_2}} + {\varLambda } \frac{\partial V_d}{\partial {q_1}}&= \frac{{\mathrm d}{{\mathcal {Q}}} }{{\mathrm d} {q_2}} + \frac{{\mathrm d}{{\mathcal {S}}} }{{\mathrm d} (q_1+{{\mathcal {T}}})}\cdot \frac{{\mathrm d}{{\mathcal {T}}} }{{\mathrm d} {q_2}}+ {\varLambda }\frac{{\mathrm d}{{\mathcal {S}}} }{{\mathrm d} (q_1+{{\mathcal {T}}})} \nonumber \\&={{\varUpsilon }} -{{\varLambda }} \frac{{\mathrm d}{{\mathcal {S}}} }{{\mathrm d} (q_1+{{\mathcal {T}}})}+ {\varLambda }\frac{{\mathrm d}{{\mathcal {S}}} }{{\mathrm d} (q_1+{{\mathcal {T}}})}={{\varUpsilon }}. \end{aligned}$$

(36)

Obviously, the expression $V_d(\varvec{q})$ given in (34) is a solution of the PDE given in (33). $\square$

Hence, by applying the above Lemma to (32), one feasible solution for $V_d(\varvec{q})$ is

$$\begin{aligned} V_d(\varvec{q})=- \frac{\alpha _2 g}{l} \cos q_2 + {{\mathcal {S}}}(q_1 -\frac{\alpha _2}{\alpha _1 l}\sin q_2), \end{aligned}$$

(37)

Since $V_d(\varvec{q})$ is a positive function, the function ${{\mathcal {S}}}: {{\mathbb {R}}}^2 \rightarrow {{\mathbb {R}}}$ is selected as

$$\begin{aligned} {{\mathcal {S}}} = \frac{\alpha _2 g}{l} + \frac{1}{2}k_p \left( q_1 -\frac{\alpha _2}{\alpha _1 l}\sin q_2 \right) ^2 . \end{aligned}$$

(38)

Then, the expression of $V_d (\varvec{q})$ is derived as

$$\begin{aligned} V_d(\varvec{q})=\frac{\alpha _2 g}{l} \left( 1- \cos q_2 \right) + \frac{1}{2}k_p \left( q_1 -\frac{\alpha _2}{\alpha _1 l}\sin q_2 \right) ^2 . \end{aligned}$$

(39)

Hence, by applying the Eq. (31a) and the solution of $V_d(\varvec{q})$ in (39), we can derive

$$\begin{aligned} \upsilon _{es} = -\frac{k_p}{\alpha _1} \left( q_1 -\frac{\alpha _2}{\alpha _1 l}\sin q_2 \right) . \end{aligned}$$

(40)

On the basis of previous analysis, the auxiliary control variable $\upsilon (t)$ is obtained

$$\begin{aligned} \upsilon&= \upsilon _{es}+\upsilon _{di} \nonumber \\&= -\frac{k_p}{\alpha _1} \left( q_1 -\frac{\alpha _2}{\alpha _1 l}\sin q_2 \right) - k_d {\varvec{h}}^{\mathrm T} M_d{\varvec{p}} \nonumber \\&= -\frac{k_p}{\alpha _1} \left( q_1 -\frac{\alpha _2}{\alpha _1 l}\sin q_2 \right) - k_d\left( \alpha _1 p_1 - \frac{\alpha _2}{l} {p_2\cos q_2} \right) \end{aligned}$$

(41)

with $k_p, k_d, \alpha _1, \alpha _2 \in {{\mathbb {R}}}^+$ are positive control gains. Then, together with (3), (21) and the proposed super-twisting-based disturbance observer (15), the actual control force supplied by the motor is designed as

$$\begin{aligned} F_a (t) =&~m(q_2) \left[ -\frac{k_p}{\alpha _1} \left( q_1 -\frac{\alpha _2}{\alpha _1 l}\sin q_2 \right) \right. \nonumber \\&\left. - k_d\left( \alpha _1 p_1 - \frac{\alpha _2}{l} {p_2\cos q_2} \right) \right] +\varsigma (q_2,p_2) + {{\hat{d}}} \end{aligned}$$

(42)

where ${{\hat{d}}} (t)$ is derived by (15).

3.3 Stability analysis

Theorem 2

Under the control method (42), the cart is driven to the target location as well as the load swing is eliminated, that is

$$\begin{aligned} \lim _{t \rightarrow \infty } [ \begin{array}{cccc} q_1&q_2&p_1&p_2 \end{array} ]^{\mathrm T} = [ \begin{array}{cccc} 0&0&0&0 \end{array} ]^{\mathrm T}. \end{aligned}$$

(43)

Proof

To prove Theorem 2, the following storage function is chosen:

$$\begin{aligned} V(t)=&~\frac{\alpha _2 g}{l} (1- \cos q_2)+ \frac{1}{2}k_p \left( q_1 -\frac{\alpha _2}{\alpha _1 l}\sin q_2 \right) ^2 \nonumber \\&+ \frac{1}{2}{\varvec{p}}^{\mathrm T} M_d {\varvec{p}} + \frac{1}{2}{{\tilde{d}}}^2 \end{aligned}$$

(44)

Differentiating (44), substituting the proposed control method (42) into the resulting expression, one can obtain that

$$\begin{aligned} {\dot{V}}(t)=&~{\varvec{p}}^{\mathrm T} \left( \frac{\partial V_d}{\partial {\varvec{q}}}+ M_d {\varvec{f}} \right) + {\varvec{p}}^{\mathrm T} M_d {\varvec{h}} \upsilon _{di} \nonumber \\&+{\varvec{p}}^{\mathrm T} M_d {\varvec{h}}\frac{{{\tilde{d}}}}{m(q_2) } + {{\tilde{d}}} {\dot{{{\tilde{d}}}}} \nonumber \\ =&- k_d {\varvec{p}}^{\mathrm T} M_d {\varvec{h}} {\varvec{h}}^{\mathrm T} M_d{\varvec{p}} +{\varvec{p}}^{\mathrm T} M_d {\varvec{h}}\frac{{{\tilde{d}}}}{m(q_2) } + {{\tilde{d}}} {\dot{{{\tilde{d}}}}} \end{aligned}$$

(45)

where the Eqs. (28), (29) and the expression of $\upsilon _{di} (t)$ are utilized. From the conclusions of Theorem 1, we know that ${{\tilde{d}}}(t)$ and $\dot{{{\tilde{d}}}} (t)$ are bounded. Hence, it is easy to derive that V(t) will not escape to infinite in a finite time. Assume that the estimation deviation ${{\tilde{d}}}(t)$ converges to 0 at $t = T_f$. Then, for $t \ge T_f$, ${{\tilde{d}}} (t) =0$, the Eq. (45) becomes

$$\begin{aligned} \dot{V}(t)=- k_d \left( \alpha _1 p_1 - \frac{\alpha _2}{l}{ p_2\cos q_2}\right) ^2 \end{aligned}$$

(46)

which indicates that ${\dot{V}}(t) \le 0$ and the closed-loop system of (22) is Lyapunov stable. Then,the following results hold

$$\begin{aligned} q_1, q_2, p_1, p_2, \upsilon , F_a \in {{\mathcal {L}}}_\infty \end{aligned}$$

(47)

To finish the proof, it is required to employ invariant-based analysis to examine the convergence of the states, let ${\mathcal {M}}$ be the largest set in ${\varGamma }$

$$\begin{aligned} {\varGamma }= \left\{ (q_1, q_2 , p_1, p_2) \mid {\dot{V}} (t) = 0\right\} . \end{aligned}$$

(48)

Hence, based on (46) and (48), the following results hold in ${\mathcal {M}}$:

$$\begin{aligned} \alpha _1 p_1 - \frac{\alpha _2}{l}{ p_2\cos q_2} =0 , \end{aligned}$$

(49)

which further implies that

$$\begin{aligned}&\alpha _1 q_1 - \frac{\alpha _2}{l}{\sin q_2} = c_1, \end{aligned}$$

(50)

$$\begin{aligned}&\alpha _1 \dot{p}_1 -\frac{\alpha _2 }{l}{\dot{p}_2\cos q_2} + \frac{ \alpha _2}{l} {p_2^2\sin q_2}=0 , \end{aligned}$$

(51)

where $c_1 \in {{\mathbb {R}}}$ is an unknown constant. From (41), (49) and (50), we can derive the following equality:

$$\begin{aligned} \upsilon = -\frac{k_p}{\alpha _1} \left( q_1 -\frac{\alpha _2}{\alpha _1 l}\sin q_2 \right) =-\frac{k_p c_1}{\alpha _1^2} . \end{aligned}$$

(52)

To determine the value of $c_1$, we suppose that $c_1 \ne 0$, then, from (22c), one can derive that

$$\begin{aligned} \lim _{t \rightarrow \infty } \mid p_1 \mid \rightarrow \infty \text { if } \upsilon > 0 \text { or } \upsilon < 0 , \end{aligned}$$

(53)

which contradicts the conclusion of (47). Hence, the following conclusions can be obtained:

$$\begin{aligned} c_1 =0, ~ \upsilon = 0, ~ q_1 -\frac{\alpha _2}{\alpha _1 l}\sin q_2 = 0,~p_1 = c_2 , \end{aligned}$$

(54)

where $c_2 \in {{\mathbb {R}}}$ is a constant. By performing similar analysis, we can conclude that

$$\begin{aligned} p_1 = c_2 =0, ~ q_1 = \frac{\alpha _2}{\alpha _1 l}\sin q_2 = c_3 , \end{aligned}$$

(55)

which indicates

$$\begin{aligned} p_2 = 0,~\dot{p}_2 =0 , \end{aligned}$$

(56)

where $c_3 \in {{\mathbb {R}}}$ is a constant. From the conclusions of (54) and (56), applying the Eqs. (22d) and (9) of Assumption 1, one can obtain

$$\begin{aligned} \sin q_2 = 0 \Longrightarrow q_2 =0 \Longrightarrow c_3= q_1 =0 . \end{aligned}$$

(57)

It is obvious from the results of (55)−(57) that the closed-loop system includes the only desired equilibrium point of $\lim _{t \rightarrow \infty } \left[ ~q_1 ~~ q_2 ~~ p_1 ~~ p_2~ \right] ^{\mathrm T} = \left[ ~0 ~~ 0 ~~ 0 ~~ 0~ \right] ^{\mathrm T}$. By invoking LaSalle’s invariance principle [41], one can conclude that the closed-loop system state is asymptotically convergent to the equilibrium point. This completes the proof. $\square$

4 Experimental tests and analysis

In order to test the disturbance estimation and regulation performance of the proposed controller, some experimental results are presented in this section. The experimental tests are carried out on a laboratory testbed (as shown in Fig. 2), and the physical system parameters of the testbed are

$$\begin{aligned} M=9.473\,{\text{kg}},~m=1\,{\text{kg}},~l=0.55\,{\text{m}},~g=9.8\,{\mathrm {m/s^2}}. \end{aligned}$$

(58)

The tests are divided into three parts. In the first part, the regulation control performance will be verified. In the second part, system parameters will be changed to testify the flexibility of the proposed approach. In the third part, uncertain disturbances will be added to the load to demonstrate the robustness of the proposed approach, and an existing control method is chosen for comparison.

For the following tests, the initial condition is set as $[x(0) ~~\theta (0)]^{\text{T}}=[0 ~~0]^{\text{T}}$.The target position is set to be $p_d=0.4\,{\mathrm m}$ for the former two groups. The control gains of the super-twisting-based disturbance observer (15) are determined as

$$\begin{aligned} k_1=0.8,~k_2=1.8. \end{aligned}$$

(59)

The control parameters for the proposed control approach (42) are chosen as

$$\begin{aligned} k_p=0.146,~k_d=0.3,\alpha _1=1,\alpha _2=1.8. \end{aligned}$$

(60)

Fig. 2

The portable overhead crane platform

4.1 Group 1

The experimental results of this group are shown by the solid line in Fig. 3. From the obtained first subfigure of Fig. 3, we can find that the cart is driven to the target position $p_d = 0.4\,\text{m}$ quickly and precisely. From the obtained second subfigure of Fig. 3, we find that the load swing is small during the whole control process and there is no residual payload vibration when the cart arrives at the target location. The obtained results of this group show that the method here possesses excellent regulation performance.

Fig. 3

Experimental results for the group 1

4.2 Group 2

In this group, the load mass and the rope length are set to be $2\,\text{kg}$ and $0.6\,\text{m}$, respectively. The control parameters of the proposed approach are the same as those in group 1. The experimental results of this group are depicted in Fig. 4. One can see from the obtained experimental results that the control performance of the proposed approach is almost unaffected even the system parameters are changed. The cart is driven to the preset position finally. When the cart stops at the desired location, there is no residual vibration for the load.

Fig. 4

Experimental results for the group 2

4.3 Group 3

In this group, the robustness of the proposed approach is tested. In order to show the superior performance of the proposed method, the existing method in [19] is chosen for comparison. For brevity, the expression of the existing method is not provided here. The desired position of the cart is changed to $0.3\,\text{m}$ due to the scale limitation of the portable overhead crane platform. The system parameters and the control gains are selected the same as those in group 1. During the control process, twice uncertain disturbances are imposed on the load.

The derived results of this group are shown in Figs. 5 and 6, respectively. From the obtained results (about $7\,\text{s}$ in Fig. 5) of the existing control methods, one can find that the cart can be driven to the target position quickly and precisely, and there is no residual payload vibration before uncertain disturbances are added. However, when the payload suffers from uncertain external disturbances, the residual payload swing cannot be eliminated by the existing control method. On the contrary, for the proposed approach here, one can find from Fig. 6 that the trolley is driven to the target location, the load vibration is eliminated rapidly as well when the disturbances vanish, and there is no residual vibration at the end. These results clearly demonstrate that the robustness of the proposed approach is superior than that of the existing approach.

Fig. 5

Experimental results for the group 3: the existing method

Fig. 6

Experimental results for the group 3: the proposed method

5 Conclusions

In this work, a super-twisting-based disturbance observer and a constructive IDA-PBC method have been introduced for the disturbance estimation and regulation control of the underactuated overhead crane system. In particular, finite time estimation is guaranteed for uncertain disturbances. In addition, an ingenious way to solve the matching conditions has been presented, which allows us to obtain a desired storage function that qualifies as a Lyapunov function candidate, and corresponding IDA-PBC method is designed. Experimental results have been given to demonstrate the superior performance of the proposed control approach.