1 Introduction

In practice, cranes have been applied to far-ranging fields, such as harbors, factories, construction sites, manufacturing plants, for handling goods [1–3]. Based on the difference of cranes’ mechanical structures, cranes can be roughly classified into three categories as overhead cranes, tower cranes, and boom cranes [4, 5]. Regardless of the type of cranes, the underactuated characteristic is the fundamental nature of cranes. In modern industries, there have been a surge of applications of underactuated mechatronic systems because of such merits as high flexibility, simple mechanical structure, low manufacturing cost, reduced energy consumption, and so on [6]. Yet, compared with fully actuated mechatronic system, control of underactuated systems is much challenging. Therefore, a considerable amount of studies have been done to address the control problem of underactuated systems [7–15].

Overhead cranes are the most widely used ones in all types of cranes. As with the other cranes, the control objective of overhead cranes is to transport the payload to the desired position accurately as well as to suppress and eliminate the payload swing rapidly. In order to increase transportation efficiency and decrease payload swing, various control methods have been proposed recently. These methods can be classified into several categories: input shaping methods [16–18], optimal control methods [19–21], stabilization/regulation control methods [22–30], and motion planning methods [31–36]. Input shaping control method is a feed-forward control method, which is implemented by convolving the human-generated signal with a chosen impulsive sequence. Optimal control method aims to find an optimal solution to minimize (or maximize) the defined performance indicators. However, input shaping and optimal control methods are open-loop control methods, which are sensitive to the external disturbances. For most stabilization/regulation methods, the initial control force becomes much larger as the transferring distance gets longer; therefore, large-amplitude payload swing is excited by the corresponding large acceleration. The potential issue of stabilization/regulation methods can be addressed by motion planning methods. The importance of motion planning method has been illustrated in [37, 38]. In [31–33], the smooth trolley positioning trajectory is combined with anti-sway tracking control laws without taking the payload motion into account and the tracking control laws have a big influence on the control performance. Therefore, these control methods are not motion planning in the sense of simultaneous trolley positioning and swing elimination. In this paper, motion planning means the trajectory design of trolley displacement, velocity, and acceleration, which are supposed to be control inputs of the overhead crane systems. Based on this, Sun et al. [34, 35] propose phase plane analysis-based methods by analyzing the natural frequency of the overhead crane systems, and the obtained trajectories have analytical expressions. Yet, the phase plane analysis-based methods cannot eliminate external disturbances. In [6, 36], an online trajectory generating method and a kinematic coupling-based motion planning method are proposed by incorporating swing-damping components in a smooth trolley positioning trajectory.

In the aforementioned control methods, the payload swing is treated as that of a simple pendulum. However, specific types of payloads and hoisting mechanisms lead to double-pendulum dynamics [39]. The double-pendulum effects make most existing crane control methods fail to work normally, and hence, it is of important significance to design effective control methods for double-pendulum overhead crane systems. Numerous researchers have devoted themselves to the challenging control problems for two-pendulum overhead crane system. In [39], the input shaping techniques are successfully employed to reduce the oscillatory dynamics of double-pendulum overhead cranes. To reduce oscillations, Masoud and Nayfeh [40] design a delayed control law; Al-Sweiti and Söffker [41] design a variable gain observer and a variable gain controller; Guo et al. [42] propose a passivity-based control method; Tuan and Lee [43] design CSMC and HSMC controllers; Liu et al. [44] design a GA-based composite sliding mode fuzzy control method. By using parallel distributed fuzzy LQR controller, Adeli et al. [45] propose an anti-swing control method for double-pendulum overhead cranes. However, due to the nonlinear and strong-coupling behavior, the motion planning problem for double-pendulum overhead cranes is very challenging for which no results have ever been reported.

An online motion planning method for double-pendulum overhead cranes is proposed in this paper. With the proposed control method, the trolley can be driven to the desired location accurately and the payload swing can be suppressed and eliminated rapidly. Inspired by [6, 36], we introduce an anti-sway component into a smooth trolley trajectory generated online in real time.Footnote 1 The proposed trajectory achieves the payload swing elimination objective without any tracking controllers. Moreover, the anti-sway component has no effect on the performance of trolley positioning. The planned trajectory is composed of anti-swing component and trolley positioning component. It should be pointed out that the trolley positioning trajectory satisfies physical constraints of overhead cranes, such as maximum trolley velocity, acceleration, and even jerk constraints, and the anti-swing component does not affect the trolley positioning performance. Lyapunov techniques, LaSalle’s invariance theorem, and Barbalat’s lemma are used to prove the performance of the planned trajectory, including trolley positioning precision and swing elimination. Some simulation results are provided to demonstrate the superior performance and strong robustness of the constructed trajectory.

Briefly speaking, the main contribution lies in the following.

  1. (1)

    The planned trajectory is robust over different cable lengths, payload masses, and external disturbances.

  2. (2)

    The planned trajectory can be implemented online without the need of advance or offline planning.

  3. (3)

    To the best of our knowledge, the method proposed in this paper is the first motion planning method for double-pendulum overhead crane systems.

The rest of this paper is structured as follows. In Sect. 2, we introduce the double-pendulum overhead crane system model. Main results are provided in Sect. 3. In Sect. 4, some simulation results are presented. Section 5 summarizes this paper.

2 System modeling

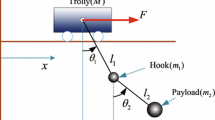
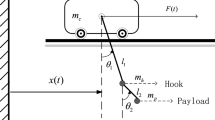
Figure 1 shows the physical model of a double-pendulum overhead crane system. As can be seen from Fig. 1, the payload is suspended on the cable by a hook. According to the Lagrangian mechanics, the dynamic equations of a double-pendulum overhead crane system are described as:

$$\begin{aligned}&\left( {M+m_1 +m_2 } \right) \ddot{x}+\left( {m_1 +m_2 } \right) l_1 \left( {\cos \theta _1 \ddot{\theta }_1 -\dot{\theta }_1^2 \sin \theta _1 } \right) \nonumber \\&\quad +\,m_2 l_2 \ddot{\theta }_2 \cos \theta _2 -m_2 l_2 \dot{\theta }_2^2 \sin \theta _2 =F \end{aligned}$$
(1)
$$\begin{aligned}&\left( {m_1 +m_2 } \right) l_1 \cos \theta _1 \ddot{x}+\left( {m_1 +m_2 } \right) l_1^2 \ddot{\theta }_1\nonumber \\&\quad +\,m_2 l_1 l_2 \cos \left( {\theta _1 -\theta _2 } \right) \ddot{\theta }_2 \nonumber \\&\quad +\,m_2 l_1 l_2 \sin \left( {\theta _1 -\theta _2 } \right) \dot{\theta }_1 \dot{\theta }_2\nonumber \\&\quad +\,\left( {m_1 +m_2 } \right) gl_1 \sin \theta _1 =0\end{aligned}$$
(2)
$$\begin{aligned}&m_2 l_2 \cos \theta _2 \ddot{x}+m_2 l_1 l_2 \cos \left( {\theta _1 -\theta _2 } \right) \ddot{\theta }_1 +m_2 l_2^2 \ddot{\theta }_2 \nonumber \\&\quad -\,m_2 l_1 l_2 \sin \left( {\theta _1 -\theta _2 } \right) \dot{\theta }_1^2 +m_2 gl_2 \sin \theta _2 =0 \end{aligned}$$
(3)

where M, \(m_{1}\) and \( m_{2}\) denote the trolley mass, the hook mass, and the payload mass, respectively, \(l_{1}\) and \(l_{2}\) represent the cable length and the distance of the payload cg from the hook cg, respectively, \(\vartheta _{1}\) and \(\vartheta _{2}\) are the swings of hook and payload, respectively, F represents the resultant force imposed on the trolley.

Fig. 1
figure 1

Physical model of a double-pendulum overhead crane system

Full size image

Equations (2)–(3) indicate the kinematic coupling relationship among the trolley translation, the hook swing, and the payload swing, which is the analytical basis of the online motion planning method proposed in this paper. It can be obtained from (2) and (3) that:

$$\begin{aligned}&\left[ {l_1^2 \dot{\theta }_1 +\frac{m_2 }{m_1 +m_2 }l_1 l_2 \cos \left( {\theta _1 -\theta _2 } \right) \dot{\theta }_2 } \right] \ddot{\theta }_1 \nonumber \\&\quad +\,\left[ {\frac{m_2 l_2 l_1 }{m_1 +m_2 }\cos \left( {\theta _1 -\theta _2 } \right) \dot{\theta }_1 +\frac{m_2 }{m_1 +m_2 }l_2^2 \dot{\theta }_2 } \right] \ddot{\theta }_2 \nonumber \\&\quad +\,\frac{m_2 }{m_1 +m_2 }l_2 g\dot{\theta }_2 \sin \theta _2 +l_1 g\dot{\theta }_1 \sin \theta _1 \nonumber \\&\qquad =-\,\left[ {l_1 \cos \theta _1 \dot{\theta }_1 +\frac{m_2 }{m_1 +m_2 }l_2 \cos \theta _2 \dot{\theta }_2 } \right] \ddot{x} \end{aligned}$$
(4)

In order to facilitate the subsequent motion planning method development and analysis, the following approximations are made based on the fact that the swings of hook and payload are small enough during the whole motion process:

$$\begin{aligned} \cos \left( {\theta _1 -\theta _2 } \right) \approx 1,\quad \cos \theta _1 \approx 1,\quad \cos \theta _2 \approx 1 \end{aligned}$$
(5)

Substituting (5) into (4), (4) is rewritten as:

$$\begin{aligned}&\left[ {l_1^2 \dot{\theta }_1 +\frac{m_2 }{m_1 +m_2 }l_1 l_2 \dot{\theta }_2 } \right] \ddot{\theta }_1 +\left[ {\frac{m_2 l_2 l_1 }{m_1 +m_2 }\dot{\theta }_1 +\frac{m_2 }{m_1 +m_2 }l_2^2 \dot{\theta }_2 } \right] \ddot{\theta }_2 \nonumber \\&\quad +\,\frac{m_2 }{m_1 +m_2 }l_2 g\dot{\theta }_2 \sin \theta _2 +l_1 g\dot{\theta }_1 \sin \theta _1 \nonumber \\&\qquad =-\left[ {l_1 \dot{\theta }_1 +\frac{m_2 }{m_1 +m_2 }l_2 \dot{\theta }_2 } \right] \ddot{x} \end{aligned}$$
(6)

3 Main results

In order to drive the trolley to the desired position accurately and eliminate the swings of hook and payload rapidly, swing-eliminating component is combined with the trolley positioning reference acceleration trajectory to construct the ultimate acceleration trajectory through the following linear combination:

$$\begin{aligned} \ddot{x}_\mathrm{f} \left( t \right) =\ddot{x}_\mathrm{d} \left( t \right) +\ddot{x}_\mathrm{e} \left( t \right) \end{aligned}$$
(7)

where \(\ddot{x}_\mathrm{e} (t)\) represents the swing-eliminating component, \(\ddot{x}_\mathrm{d} (t)\) denotes the trolley positioning reference acceleration trajectory, \(\ddot{x}_\mathrm{f}(t)\) is the final acceleration trajectory designed in this paper.

3.1 The swing elimination component

The purpose of the swing elimination component is to damp out the payload swing efficiently. Considering the coupling relationship (4) between the trolley motion and the swings of hook and payload, the swing-eliminating component is designed as follows:

$$\begin{aligned} \ddot{x}_\mathrm{e} \left( t \right) =k_1 \left[ {\dot{\theta }_1 +\frac{m_2 }{\left( {m_1 +m_2 } \right) l_1 }l_2 \dot{\theta }_2 } \right] \end{aligned}$$
(8)

where \(k_1 \in \mathbf{R}^{+}\) represents a positive control gain. The swing-eliminating component \(\ddot{x}_e(t)\) has the following properties:

Theorem 1

The swing-eliminating component \(\ddot{x}_e(t)\) guarantees the swing angles \((\theta _1 and \theta _2)\), angular velocity \((\dot{\theta }_1 and \dot{\theta }_2)\), and angular acceleration \((\ddot{\theta }_1 and \ddot{\theta }_2)\) asymptotically converge to zero.

Proof

A function V(t) is defined as:

$$\begin{aligned} V\left( t \right)= & {} \frac{1}{2}l_1^2 \dot{\theta }_1^2 +\frac{1}{2}\frac{m_2 }{m_1 +m_2 }l_2^2 \dot{\theta }_2^2 +\frac{m_2 }{m_1 +m_2 }l_1 l_2 \dot{\theta }_1 \dot{\theta }_2 \nonumber \\&+\,l_1 g\left( {1-\cos \theta _1 } \right) +\frac{m_2 }{m_1 +m_2 }l_2 g\left( {1-\cos \theta _2 } \right) \nonumber \\ \end{aligned}$$
(9)

By utilizing the arithmetic and geometric means inequality, (9) is calculated as:

$$\begin{aligned} V\left( t \right)\ge & {} \sqrt{\frac{m_2 }{m_1 +m_2 }}l_1 l_2 \left| {\dot{\theta }_1 } \right| \left| {\dot{\theta }_2 } \right| +\frac{m_2 }{m_1 +m_2 }l_1 l_2 \dot{\theta }_1 \dot{\theta }_2 \nonumber \\&+\,l_1 g\left( {1-\cos \theta _1 } \right) +\frac{m_2 }{m_1 +m_2 }l_2 g\left( {1-\cos \theta _2 } \right) \ge 0\nonumber \\ \end{aligned}$$
(10)

which indicates that the function V(t) is nonnegative. Taking the time derivative of (9) and substituting (4) into the resulting formula yields:

$$\begin{aligned} \dot{V}\left( t \right)= & {} -\left[ {l_1 \dot{\theta }_1 +\frac{m_2 }{m_1 +m_2 }l_2 \dot{\theta }_2 } \right] \ddot{x}_e \nonumber \\= & {} -k_1 l_1 \left[ {\dot{\theta }_1 +\frac{m_2 }{\left( {m_1 +m_2 } \right) l_1 }l_2 \dot{\theta }_2 } \right] ^{2}\le 0 \end{aligned}$$
(11)

Without loss of generality, the initial payload swing angles \(\theta _1(t)\), \(\theta _2(t)\) and angular velocity \(\dot{\theta }_1(t)\), \(\dot{\theta }_2(t)\) are considered as zero. To further prove Theorem 1, let M as the largest invariant set contained in S, and S is defined as follows:

$$\begin{aligned} S=\left\{ {\left( \theta _1 ,\theta _2 ,\dot{\theta }_1 ,\dot{\theta }_2 ,\ddot{\theta }_1 ,\ddot{\theta }_2 \right) :\dot{V}\left( t \right) =0} \right\} \end{aligned}$$
(12)

Then, in M, the following expression is obtained:

$$\begin{aligned} l_1 \dot{\theta }_1 +\frac{m_2 }{m_1 +m_2 }l_2 \dot{\theta }_2 =0\Rightarrow \dot{\theta }_1 =-\frac{m_2 l_2 }{l_1 \left( {m_1 +m_2 } \right) }\dot{\theta }_2 \end{aligned}$$
(13)

Substituting (13) into (8), it can be obtained that:

$$\begin{aligned} \ddot{x}_\mathrm{e} \left( t \right) =0 \end{aligned}$$
(14)

It follows from (13) and the initial swing angles \(\theta _1 (0)=\theta _2 (0)=0\) that:

$$\begin{aligned} \ddot{\theta }_1= & {} -\frac{m_2 l_2 }{l_1 \left( {m_1 +m_2 } \right) }\ddot{\theta }_2 \end{aligned}$$
(15)
$$\begin{aligned} \theta _1= & {} -\frac{m_2 l_2 }{l_1 \left( {m_1 +m_2 } \right) }\theta _2 \end{aligned}$$
(16)

Substituting (13)–(16) into (4), one has:

$$\begin{aligned} \frac{m_2 l_2 }{m_1 +m_2 }g\dot{\theta }_2 \left( {\sin \theta _2 -\sin \theta _1 } \right) =0 \end{aligned}$$
(17)

It follows from (17) that:

$$\begin{aligned} \dot{\theta }_2 =0, \text {or } \theta _2 =\theta _1 \end{aligned}$$
(18)

To complete the proof, the cases when \(\dot{\theta }_2 =0\) and \(\theta _2 =\theta _1 \) are examined.

Case 1 In this case:

$$\begin{aligned} \dot{\theta }_2 =0 \end{aligned}$$
(19)

is considered. It can be obtained from (13), (15), and (19) that:

$$\begin{aligned} \ddot{\theta }_2 =0,\dot{\theta }_1 =0,\ddot{\theta }_1 =0 \end{aligned}$$
(20)

Substituting (14), (19), and (20) into (2), and (3), it is derived that:

$$\begin{aligned}&\left( {m_1 +m_2 } \right) gl_1 \sin \theta _1 = 0 \end{aligned}$$
(21)
$$\begin{aligned}&m_2 gl_2 \sin \theta _2 = 0 \end{aligned}$$
(22)

Based on the fact that the swings of hook and payload are small enough during the whole motion process, the following results are obtained:

$$\begin{aligned} \theta _1 =0,\quad \theta _2 =0 \end{aligned}$$
(23)

Case 2 In this case

$$\begin{aligned} \theta _2 =\theta _1 \end{aligned}$$
(24)

is examined. It is straightforward to obtain from (16) and (24) that:

$$\begin{aligned} \theta _2 =\theta _1 =0 \end{aligned}$$
(25)

Thus, it can be obtained from (25) that:

$$\begin{aligned} \dot{\theta }_2 =\dot{\theta }_1 =0,\quad \ddot{\theta }_2 =\ddot{\theta }_1 =0 \end{aligned}$$
(26)

Based on the previous analysis, it can be concluded that, only the equilibrium point of

$$\begin{aligned} S=\left\{ {\left( {\theta _1 ,\theta _2 ,\dot{\theta }_1 ,\dot{\theta }_2 ,\ddot{\theta }_1 ,\ddot{\theta }_2 } \right) :\theta _1 ,\theta _2 ,\dot{\theta }_1 ,\dot{\theta }_2 ,\ddot{\theta }_1 ,\ddot{\theta }_2 \equiv 0} \right\} \end{aligned}$$
(27)

is included in the largest invariant set M. By invoking the LaSalle’s invariance theorem [46], Theorem 1 is proved. \(\square \)

3.2 The positioning reference trajectory

For the trolley, an S-shape smooth function is chosen as the positioning reference trajectory [31]:

$$\begin{aligned} x_\mathrm{d} \left( t \right) =\frac{p_\mathrm{d} }{2}+\frac{k_\mathrm{v}^2 }{4k_\mathrm{a} }\ln \left( {\frac{\cosh \left( {{2k_\mathrm{a} t}/{k_\mathrm{v} -\varepsilon }} \right) }{\cosh \left( {{2k_\mathrm{a} t}/{k_\mathrm{v} -\varepsilon -{2p_\mathrm{d} k_\mathrm{a} }/{k_\mathrm{v}^2 }}} \right) }} \right) \end{aligned}$$
(28)

where \(p_\mathrm{d}\) is the desired position, \(k_\mathrm{v}\) and \(k_\mathrm{a}\) denote the maximum permitted velocity and maximum permitted acceleration of the trolley. Define \(k_\mathrm{j}\) as the maximum permitted jerk of the trolley. The purpose of introducing \(\varepsilon \in \mathbf{R}^{+}\) is to regulate the initial acceleration of the trolley. Taking the first, second, and third derivatives of (28) with respect to time, the reference velocity, acceleration, and jerk trajectory of the trolley can be obtained as:

$$\begin{aligned}&\dot{x}_\mathrm{d} \left( t \right) =k_\mathrm{v} \frac{\tanh \left( {{2k_\mathrm{a} t}/{k_\mathrm{v} -\varepsilon }} \right) -\tanh \left( {{2k_\mathrm{a} t}/{k_\mathrm{v} -\varepsilon }-2p_\mathrm{d} {k_\mathrm{a} }/{k_\mathrm{v}^2 }} \right) }{2}\nonumber \\ \end{aligned}$$
(29)
$$\begin{aligned}&\ddot{x}_\mathrm{d} \left( t \right) =k_\mathrm{a} \left( \frac{1}{\cosh ^{2}\left( {{2k_\mathrm{a} t}/{k_\mathrm{v} -\varepsilon }} \right) }\right. \nonumber \\&\quad \left. -\,\frac{1}{\cosh ^{2}\left( {{2k_\mathrm{a} t}/{k_\mathrm{v} -\varepsilon }-2p_\mathrm{d} {k_\mathrm{a} }/{k_\mathrm{v}^2 }} \right) }\right) \end{aligned}$$
(30)
$$\begin{aligned}&x_\mathrm{d}^{\left( 3 \right) } \left( t \right) =\frac{4k_\mathrm{a}^2 }{k_\mathrm{v} }\left( \frac{-\sinh \left( {{2k_\mathrm{a} t}/{k_\mathrm{v} -\varepsilon }} \right) }{\cosh ^{3}\left( {{2k_\mathrm{a} t}/{k_\mathrm{v} -\varepsilon }} \right) }\right. \nonumber \\&\quad \left. +\,\frac{\sinh \left( {{2k_\mathrm{a} t}/{k_\mathrm{v} -\varepsilon }-2p_\mathrm{d} {k_\mathrm{a} }/{k_\mathrm{v}^2 }} \right) }{\cosh ^{3}\left( {{2k_\mathrm{a} t}/{k_\mathrm{v} -\varepsilon }-2p_\mathrm{d} {k_\mathrm{a} }/{k_\mathrm{v}^2 }} \right) } \right) \end{aligned}$$
(31)

wherein \(\dot{x}_\mathrm{d}(t)\), \(\ddot{x}_\mathrm{d}(t)\), and \(x_\mathrm{d}^{(3)} (t)\) denote the reference velocity, acceleration, and jerk of the trolley, respectively.

The positioning reference trajectory (29) has the following properties

  1. (1)

    Positioning reference trajectory (29) takes the limit of \(p_\mathrm{d}\), namely:

    $$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } x_\mathrm{d} \left( t \right) =p_\mathrm{d} \end{aligned}$$
    (32)
  2. (2)

    Reference velocity (30) is positive, and it is bounded by\(k_\mathrm{v} \), in the sense that:

    $$\begin{aligned} 0<\dot{x}_\mathrm{d} \left( t \right) \le k_\mathrm{v} \end{aligned}$$
    (33)
  3. (3)

    Reference acceleration (31) and jerk (32) are bounded by \(k_\mathrm{a}\) and \(k_\mathrm{j}\), respectively, that is:

    $$\begin{aligned} -k_\mathrm{a} \le \ddot{x}_\mathrm{d} \left( t \right) \le k_\mathrm{a} ,\quad -k_\mathrm{j} \le \dot{x}_\mathrm{d}^{\left( 3 \right) } \left( t \right) \le k_\mathrm{j} \end{aligned}$$
    (34)

    where \(k_\mathrm{j} ={4k_\mathrm{a}^2 }/{k_\mathrm{v} }\).

  4. (4)

    The initial trolley displacement and velocity are zero, in the sense that:

    $$\begin{aligned} x_\mathrm{d} \left( 0 \right) =0,\quad \dot{x}_\mathrm{d} \left( 0 \right) =0 \end{aligned}$$
    (35)

3.3 The ultimate trajectory generating and analysis

By combining the positioning reference acceleration trajectory (30) with the swing elimination component (8), the ultimate acceleration trajectory of the trolley is constructed as:

$$\begin{aligned} \ddot{x}_\mathrm{f} \left( t \right) =\ddot{x}_\mathrm{d} \left( t \right) +k_1 \left[ {\dot{\theta }_1 +\frac{m_2 }{\left( {m_1 +m_2 } \right) l_1 }l_2 \dot{\theta }_2 } \right] \end{aligned}$$
(36)

Hereon, \(k_1 \) is selected as:

$$\begin{aligned} k_1 >{l_1 }/2 \end{aligned}$$
(37)

The ultimate velocity trajectory and displacement trajectory of the trolley can be obtained as:

$$\begin{aligned} \dot{x}_\mathrm{f} \left( t \right)= & {} \dot{x}_\mathrm{d} \left( t \right) +k_1 \left[ {\theta _1 +\frac{m_2 }{\left( {m_1 +m_2 } \right) l_1 }l_2 \theta _2 } \right] \end{aligned}$$
(38)
$$\begin{aligned} x_\mathrm{f} \left( t \right)= & {} x_\mathrm{d} \left( t \right) +k_1 \int _0^t {\left( {\theta _1 +\frac{m_2 l_2 }{\left( {m_1 +m_2 } \right) l_1 }\theta _2 } \right) {\hbox {d}}t}\nonumber \\ \end{aligned}$$
(39)

The main results of the paper are given in the following theorems.

Theorem 2

The trolley ultimate trajectory \(\ddot{x}_\mathrm{f} (t)\) ensures asymptotically convergence of the swing angles \(\theta _1\) and \(\theta _2\), in the sense that:

$$\begin{aligned}&\mathop {\lim }\limits _{{t \rightarrow \infty }} \left[ {\theta _{1} \left( t \right) \theta _{2} \left( t \right) \dot{\theta }_{1} \left( t \right) \dot{\theta }_{2} \left( t \right) \ddot{\theta }_{1} \left( t \right) \ddot{\theta }_{2} \left( t \right) } \right] = \left[ {0\; 0\; 0\; 0\; 0\; 0} \right] \nonumber \\ \end{aligned}$$
(40)

Proof

Define the nonnegative function V(t) in (10) as the Lyapunov candidate function. Substituting (36) into (11), the following result is obtained:

$$\begin{aligned} \dot{V}\left( t \right)= & {} -\left[ {l_1 \dot{\theta }_1 +\frac{m_2 }{m_1 +m_2 }l_2 \dot{\theta }_2 } \right] \ddot{x}_f \nonumber \\= & {} -\,\left[ {l_1 \dot{\theta }_1 +\frac{m_2 }{m_1 +m_2 }l_2 \dot{\theta }_2 } \right] \ddot{x}_d \left( t \right) \nonumber \\&-\,k_1 l_1 \left[ {\dot{\theta }_1 +\frac{m_2 }{\left( {m_1 +m_2 } \right) l_1 }l_2 \dot{\theta }_2 } \right] ^{2} \end{aligned}$$
(41)

Based on the arithmetic and geometric means inequality, (41) can be rewritten as:

$$\begin{aligned} \dot{V}\left( t \right)\le & {} \frac{1}{2}\ddot{x}_\mathrm{d}^2 \left( t \right) +\frac{1}{2}l_1^2 \left[ {\dot{\theta }_1 +\frac{m_2 }{\left( {m_1 +m_2 } \right) l_1 }l_2 \dot{\theta }_2 } \right] ^{2}\nonumber \\&-\,k_1 l_1 \left[ {\dot{\theta }_1 +\frac{m_2 }{\left( {m_1 +m_2 } \right) l_1 }l_2 \dot{\theta }_2 } \right] ^{2} \nonumber \\\le & {} \frac{1}{2}\ddot{x}_\mathrm{d}^2 \left( t \right) +l_1 \left( {\frac{1}{2}l_1 -k_1 } \right) \nonumber \\&\times \,\left[ {\dot{\theta }_1 +\frac{m_2 }{\left( {m_1 +m_2 } \right) l_1 }l_2 \dot{\theta }_2 } \right] ^{2} \end{aligned}$$
(42)

By integrating both sides of (42) with respect to time, one derives:

$$\begin{aligned} V\left( t \right)\le & {} \frac{1}{2}\int _0^t {\ddot{x}_\mathrm{d}^2 \left( t \right) } {\hbox {d}}t+l_1 \left( {\frac{1}{2}l_1 -k_1 } \right) \nonumber \\&\int _0^t {\left[ {\dot{\theta }_1 +\frac{m_2 }{\left( {m_1 +m_2 } \right) l_1 }l_2 \dot{\theta }_2 } \right] ^{2}} {\hbox {d}}t+V\left( 0 \right) \nonumber \\ \end{aligned}$$
(43)

By some integration-by-parts operations, the first term of (43) is calculated as:

$$\begin{aligned} \frac{1}{2}\int _0^t {\ddot{x}_\mathrm{d}^2 \left( t \right) } {\hbox {d}}t=\frac{1}{2}\ddot{x}_\mathrm{d} \left( t \right) \dot{x}_\mathrm{d} \left( t \right) +\frac{1}{2}x_\mathrm{d}^{\left( 3 \right) } \left( t \right) x_\mathrm{d} \left( t \right) \in L_\infty \end{aligned}$$
(44)

It can be concluded from (37) that:

$$\begin{aligned} l_1 \left( {\frac{1}{2}l_1 -k_1 } \right) \int _0^t {\left[ {\dot{\theta }_1 +\frac{m_2 }{\left( {m_1 +m_2 } \right) l_1 }l_2 \dot{\theta }_2 } \right] ^{2}} {\hbox {d}}t\le 0 \end{aligned}$$
(45)

Thus, from (43), (44), and (45), it can be obtained that:

$$\begin{aligned} V\left( t \right) \in L_\infty \end{aligned}$$
(46)

From (9), it is obtained as:

$$\begin{aligned} \dot{\theta }_1 \left( t \right) ,\quad \dot{\theta }_2 \left( t \right) \in L_\infty \end{aligned}$$
(47)

It is clear from (34), (36), and (47) that:

$$\begin{aligned} \ddot{x}_f \in L_\infty \end{aligned}$$
(48)

Substituting (36) into (2) and (3), one has:

$$\begin{aligned} m_1 l_1 \ddot{\theta }_1= & {} \underbrace{-m_1 \ddot{x}_\mathrm{f} }_{g_1 \left( t \right) }\underbrace{-m_2 l_2 \sin \left( {\theta _1 -\theta _2 } \right) \dot{\theta }_1 \dot{\theta }_2 -m_2 l_1 \sin \left( {\theta _1 -\theta _2 } \right) \dot{\theta }_1^2 -\left( {m_1 +m_2 } \right) g\sin \theta _1 +m_2 g\sin \theta _2 }_{g_2 \left( t \right) } \end{aligned}$$
(49)
$$\begin{aligned} m_1 l_2 \ddot{\theta }_2= & {} \underbrace{\left( {m_1 +m_2 } \right) l_1 \sin \left( {\theta _1 -\theta _2 } \right) \dot{\theta }_1^2 +m_2 l_2 \sin \left( {\theta _1 -\theta _2 } \right) \dot{\theta }_1 \dot{\theta }_2 +\left( {m_1 +m_2 } \right) g\left( {\sin \theta _2 -\sin \theta _1 } \right) }_{f\left( t \right) } \end{aligned}$$
(50)

where the approximations of (5) have been utilized.

It can concluded from (47) and (48) that:

$$\begin{aligned} \ddot{\theta }_1 \left( t \right) \in L_\infty ,\quad \ddot{\theta }_2 \left( t \right) \in L_\infty , \end{aligned}$$
(51)

After some arrangements, (43) is rewritten as:

$$\begin{aligned}&l_1 \left( {k_1 -\frac{1}{2}l_1 } \right) \int _0^t {\left[ {\dot{\theta }_1 +\frac{m_2 }{\left( {m_1 +m_2 } \right) l_1 }l_2 \dot{\theta }_2 } \right] ^{2}} {\hbox {d}}t\nonumber \\&\qquad \le \,\frac{1}{2}\int _0^t {\ddot{x}_\mathrm{d}^2 \left( t \right) } {\hbox {d}}t+V\left( 0 \right) -V\left( t \right) \in L_\infty \end{aligned}$$
(52)

which indicates that:

$$\begin{aligned} \dot{\theta }_1 +\frac{m_2 }{\left( {m_1 +m_2 } \right) l_1 }l_2 \dot{\theta }_2 \in L_2 \end{aligned}$$
(53)

It can concluded from (47), (51), and (53) that:

$$\begin{aligned} \dot{\theta }_1 +\frac{m_2 }{\left( {m_1 +m_2 } \right) l_1 }l_2 \dot{\theta }_2 \in L_2 \cap L_\infty ,\quad \ddot{\theta }_1 ,\quad \ddot{\theta }_2 \in L_\infty \end{aligned}$$
(54)

By invoking Barbalat’s lemma [45], the following result is obtained:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } \left[ {\dot{\theta }_1 +\frac{m_2 }{\left( {m_1 +m_2 } \right) l_1 }l_2 \dot{\theta }_2 } \right] =0 \end{aligned}$$
(55)

It follows from (8) and (55) that:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } \ddot{x}_\mathrm{e} \left( t \right) =0 \end{aligned}$$
(56)

It is easy to conclude from (30) that:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } \ddot{x}_\mathrm{d} \left( t \right) =0 \end{aligned}$$
(57)

which, together with (56), indicates that:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } \ddot{x}_\mathrm{f} \left( t \right) =0 \end{aligned}$$
(58)

It can concluded from (49), (50), and the results of (47), (51), (58) that:

$$\begin{aligned}&\dot{g}_2 \left( t \right) \in L_\infty ,\mathop {\lim }\limits _{t\rightarrow \infty } g_1 \left( t \right) =0 \end{aligned}$$
(59)
$$\begin{aligned}&\dot{f}\left( t \right) \in L_\infty \end{aligned}$$
(60)

Therefore, by invoking the extended Barbalat lemma [45] yields:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } \ddot{\theta }_1 =0,\quad \mathop {\lim }\limits _{t\rightarrow \infty } \ddot{\theta }_2 =0 \end{aligned}$$
(61)

After rearranging (2) and (3), the following equations can be obtained as:

$$\begin{aligned}&\left( {m_1 +m_2 } \right) g\sin \theta _1 =\underbrace{-\left( {m_1 +m_2 } \right) \ddot{x}_f -\left( {m_1 +m_2 } \right) l_1 \ddot{\theta }_1 -m_2 l_2 \ddot{\theta }_2 }_{p_1 \left( t \right) }\underbrace{-m_2 l_2 \sin \left( {\theta _1 -\theta _2 } \right) \dot{\theta }_1 \dot{\theta }_2 }_{p_2 \left( t \right) } \end{aligned}$$
(62)
$$\begin{aligned}&g\sin \theta _2 =\underbrace{-\cos \theta _2 \ddot{x}_f -l_1 \cos \left( {\theta _1 -\theta _2 } \right) \ddot{\theta }_1 -l_2 \ddot{\theta }_2 }_{q_1 \left( t \right) }\underbrace{+l_1 \sin \left( {\theta _1 -\theta _2 } \right) \dot{\theta }_1^2 }_{q_2 \left( t \right) } \end{aligned}$$
(63)

Similarly, it can be obtained from (47), (51), (58), and (61) that:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } p_1 \left( t \right)= & {} 0,\quad \dot{p}_2 \left( t \right) \in L_\infty \end{aligned}$$
(64)
$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } q_1 \left( t \right)= & {} 0,\quad \dot{q}_2 \left( t \right) \in L_\infty \end{aligned}$$
(65)

Extended Barbalat’s lemma and the fact that the swings of hook and payload are small enough during the whole motion process are utilized to show that:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } \sin \theta _1= & {} 0,\mathop {\lim }\limits _{t\rightarrow \infty } \sin \theta _2 =0\Rightarrow \mathop {\lim }\limits _{t\rightarrow \infty } \theta _1 \left( t \right) \nonumber \\= & {} 0,\mathop {\lim }\limits _{t\rightarrow \infty } \theta _2 \left( t \right) =0 \end{aligned}$$
(66)

Based on the swings and angular velocities of hook and payload is small during the transportation process, (3) can be simplified as

$$\begin{aligned} \ddot{x}_f +l_1 \ddot{\theta }_1 +l_2 \ddot{\theta }_2 +g\theta _2 =0 \end{aligned}$$
(67)

By integrating both sides of (67), it is derived that:

$$\begin{aligned} \int _0^t {g\theta _2 {\hbox {d}}t} =\underbrace{-\dot{x}_\mathrm{f} }_{m_1 }\underbrace{-l_1 \dot{\theta }_1 -l_2 \dot{\theta }_2 }_{m_2 } \end{aligned}$$
(68)

where the initial conditions \(\dot{\theta }_1(0)=\dot{\theta }_2(0)=0\) and \(\dot{x}_\mathrm{d}(0)=0\) are used.

It follows from (33), (38), and (66) that:

$$\begin{aligned} \mathop {\lim }\limits _{x\rightarrow \infty } m_1 \left( t \right) =0 \end{aligned}$$
(69)

It is easy to conclude from (51) that:

$$\begin{aligned} \mathop {\lim }\limits _{x\rightarrow \infty } \dot{m}_2 \left( t \right) \in L_\infty \end{aligned}$$
(70)

which, together with (69), indicates that:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } \left( {-l_1 \dot{\theta }_1 -l_2 \dot{\theta }_2 } \right) =0 \end{aligned}$$
(71)

by utilizing the extended Barbalat’s lemma [45].

Then the following results are obtained from (55) and (71) as:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } \dot{\theta }_1 =0,\quad \mathop {\lim }\limits _{t\rightarrow \infty } \dot{\theta }_2 =0 \end{aligned}$$
(72)

Hereto, it can be concluded from (61), (66) and (72) that:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } \left[ {\theta _1 \left( t \right) \theta _2 \left( t \right) \dot{\theta }_1 \left( t \right) \dot{\theta }_2 \left( t \right) \ddot{\theta }_1 \left( t \right) \ddot{\theta }_2 \left( t \right) } \right] =\left[ {0\; 0\;0\; 0\;0} \right] \end{aligned}$$

\(\square \)

Theorem 3

The trolley ultimate trajectory \(\ddot{x}_\mathrm{f}(t)\) can drive the trolley to the desired position and ensure the asymptotically convergence of the trolley velocity, acceleration, in the sense that:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } \left[ {x_\mathrm{f} \left( t \right) \dot{x}_\mathrm{f} \left( t \right) \ddot{x}_\mathrm{f} \left( t \right) } \right] =\left[ {p_\mathrm{d} \; 0\; 0} \right] \end{aligned}$$
(73)

From (29), (38), and (66), one has:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } \dot{x}_\mathrm{f} \left( t \right) =0 \end{aligned}$$
(74)

Based on the swings and angular velocities of hook and payload is small during the transportation process, (2) is rearranged as:

$$\begin{aligned}&\left( {m_1 +m_2 } \right) \ddot{x}_\mathrm{f} +\left( {m_1 +m_2 } \right) l_1 \ddot{\theta }_1+m_2 l_2 \ddot{\theta }_2 \nonumber \\&\qquad \qquad +\,\left( {m_1 +m_2 } \right) g\theta _1 =0 \end{aligned}$$
(75)

Integrating both sides of (67) and (75) with respect to time, and then taking the time limit, one has:

$$\begin{aligned}&\left( {m_1 +m_2 } \right) g\int _0^\infty {\theta _1 } {\hbox {d}}t=-\left( {m_1 +m_2 } \right) \dot{x}_\mathrm{f} \left( \infty \right) \nonumber \\&\qquad \qquad -\,\left( {m_1 +m_2 } \right) l_1 \dot{\theta }_1 \left( \infty \right) -m_2 l_2 \dot{\theta }_2 \left( \infty \right) \nonumber \\\end{aligned}$$
(76)
$$\begin{aligned}&g\int _0^\infty {\theta _2 {\hbox {d}}t} =-\dot{x}_f \left( \infty \right) -l_1 \dot{\theta }_1 \left( \infty \right) -l_2 \dot{\theta }_2 \left( \infty \right) \nonumber \\ \end{aligned}$$
(77)

where the initial conditions \(\theta _1(0)=\theta _2(0)=0,\dot{\theta }_1(0)=\dot{\theta }_2(0)=0,x_d(0)=0,\dot{x}_d(0)=0\) are utilized.

It follows from (72), (74) that:

$$\begin{aligned} g\int _0^\infty {\theta _1 } {\hbox {d}}t=0,\quad g\int _0^\infty {\theta _2 {\hbox {d}}t} \end{aligned}$$
(78)

It can be concluded from (32), (39), and (78) that:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } x_\mathrm{f} \left( t \right) =\mathop {\lim }\limits _{t\rightarrow \infty } x_\mathrm{d} \left( t \right) =p_\mathrm{d} \end{aligned}$$
(79)

The following results are concluded from (58), (74), and (79) that:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } \left[ {x_\mathrm{f} \left( t \right) \dot{x}_\mathrm{f} \left( t \right) \ddot{x}_\mathrm{f} \left( t \right) } \right] =\left[ {p_\mathrm{d} \;0\;0} \right] \end{aligned}$$
Table 1 Design parameters
Full size table

4 Simulation results

In this section, to verify the superior performance of the online motion planning method proposed in this paper, we implement some numerical simulations. More specifically, the whole simulation process is divided into three groups. In the first group, we compare our method with the passivity-based control method in [41], and the CSMC method in [42]. Subsequently, the tolerance of the system to parameter variations (internal disturbance) is tested in the second group. Finally, the robustness of the two-pendulum overhead crane system against various external disturbances is further verified.

For literature completeness, the expression of the passivity-based control method in [41] is provided as follows:

$$\begin{aligned} F= & {} -\left( {k_\mathrm{E}{{\mathbf {I}}}+k_\mathrm{D} ZM^{-1}({{\mathbf {q}}})Z^{T}} \right) ^{-1}\left( {k_\mathrm{p} \left( {x-p_\mathrm{d} } \right) } \right) \nonumber \\&+\,k_\mathrm{D} ZM^{-1}({{\mathbf {q}}})({C({{\mathbf {{q}}},\dot{{{\mathbf {q}}}}})\dot{{{\mathbf {q}}}}+G({{\mathbf {q}}})}+k\dot{x} \end{aligned}$$
(80)

wherein \(k_\mathrm{E} ,k_\mathrm{D} ,k_\mathrm{p} ,k\in \mathbf{R}^{+}\) are the control gains, I represents the appropriate unit matrix, \(Z=[ {1\;0\;0} ],{{\mathbf {q}}}=[x \vartheta _{1 }\vartheta _{2}]^{T}\in \mathbf{R}^{3}\) is the system state vector, \(M({{\mathbf {q}}})\in \mathbf{R}^{3*3}\) represents the inertia matrix, \(C({{{\mathbf {q}}},\dot{{{\mathbf {q}}}}})\in \mathbf{R}^{3*3}\) denotes the centripetal-Coriolis matrix, \(G({{\mathbf {q}}})\in \mathbf{R}^{3}\) is the gravity vector, which are defined in detail as follows:

$$\begin{aligned} M({{\mathbf {q}}})= & {} \left[ {\begin{array}{lll} M+m_1 +m_2 &{}\quad \left( {m_1 +m_2 } \right) l_1 \cos \theta _1 &{} \quad m_2 l_2 \cos \theta _2 \\ \left( {m_1 +m_2 } \right) l_1 \cos \theta _1 &{}\quad \left( {m_1 +m_2 } \right) l_1^2 &{}\quad m_2 l_1 l_2 \cos \left( {\theta _1 -\theta _2 } \right) \\ m_2 l_2 \cos \theta _2&{}\quad m_2 l_1 l_2 \cos \left( {\theta _1 -\theta _2 } \right) &{}\quad m_2 l_2^2 \\ \end{array}} \right] \\ \end{aligned}$$
$$\begin{aligned}&C({{{\mathbf {q}}},\dot{{{\mathbf {q}}}}})=\left[ {\begin{array}{ccc} 0 &{}\quad - \left( {m_1 +m_2 } \right) l_1 \dot{\theta }_1 \sin \theta _1 &{}\quad -m_2 l_2 \dot{\theta }_2 \sin \theta _2 \\ 0 &{}\quad 0 &{}\quad m_2 l_1 l_2 \dot{\theta }_1 \sin \left( {\theta _1 -\theta _2 } \right) \\ 0 &{}\quad -m_2 l_1 l_2 \dot{\theta }_1 \sin \left( {\theta _1 -\theta _2 } \right) &{}\quad 0 \\ \end{array}} \right] \\&G({{\mathbf {q}}})=\left[ {0 \;\left( {m_1 +m_2 } \right) gl_1 \sin \theta _1 \; m_2 gl_2 \sin \theta _2 } \right] ^{T}\\&{{\mathbf {q}}}=\left[ {x \;\theta _1\;\theta _2 } \right] ^{T}\\&{{\mathbf {I}}}=\left[ {\begin{array}{lll} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \\ \end{array}} \right] ,\quad {{\mathbf {Z}}}=\left[ {1\;0\; 0} \right] \end{aligned}$$

and the expression of the CSMC method in [42] is given below:

$$\begin{aligned} F= & {} -\left( {m_1 +m_2 } \right) l_1 \left( {\cos \theta _1 \ddot{\theta }_1 -\dot{\theta }_1^2 \sin \theta _1 } \right) \nonumber \\&-\,m_2 l_2 \ddot{\theta }_2 \cos \theta _2 +m_2 l_2 \dot{\theta }_2^2 \sin \theta _2 \nonumber \\&-\,\left( {M+m_1 +m_2 } \right) \left( {\lambda \dot{x}+\alpha \dot{\theta }_1 +\beta \dot{\theta }_2 } \right) -K\hbox {sgn}\left( s \right) \nonumber \\ \end{aligned}$$
(81)

where \(\lambda ,\alpha ,K\in \hbox {R}^{\hbox {+}}\), and \(\beta \in \hbox {R}^{-}\) represent the control gains, s is the sliding surface, which is defined as:

$$\begin{aligned} s=\dot{x}+\lambda \left( {x-p_\mathrm{d} } \right) +\alpha \theta _1 +\beta \theta _2 \end{aligned}$$
(82)

The physical parameters of the system and the parameters of the three control methods are described in Table 1.

Fig. 2
figure 2

Simulation group 1: results for passivity-based control method

Full size image

Simulation group 1 In this group, we intend to validate the superior performance of the proposed motion planning method in comparison with the passivity-based controller and the CSMC controller.

The simulation results are shown in Figs. 2, 3 and 4. It can be concluded from Figs. 2, 3 and 4 that swings of hook and payload are better eliminated by the proposed motion planning method and there is almost no residual swing as the trolley stops, although the transferring time is a bit longer than the passivity-based controller and the CSMC controller.

Simulation group 2 In this group, the robustness against parameter variations of the planned trajectory is verified. To this end, the following two extreme cases (it is noted that parameter sudden changes are much harsher than parameter time variation) are considered.

Case 1 The payload mass is increased from 2 to 3 kg abruptly at \(t=2\) s.

Case 2 The cable length is changed from 0.7 to 1.5 m abruptly at \(t= 2\) s.

The derived results are recorded in Figs. 5, 6. As can be seen from Figs. 5, 6, under different cases, the trolley arrives the desired position accurately, and during the whole transportation process, the hook swing and the payload swing are \({<}1.2^{\circ }\) and converge to zero soon after the trolley stops. It can be concluded from Figs. 5, 6 that the performance of the constructed trajectory is not influenced by parameter variations, indicating the strong robustness of the closed-loop system.

Fig. 3
figure 3

Simulation group 1: results for CSMC method

Full size image
Fig. 4
figure 4

Simulation group 1: results for the proposed motion planning method

Full size image
Fig. 5
figure 5

Results for simulation group 2. (Red solid line) No parameter variations. (Green solid line) Case 1. (Color figure online)

Full size image
Fig. 6
figure 6

Results for simulation group 2. (Red solid line) No parameter variations. (Green solid line) Case 2. (Color figure online)

Full size image

Simulation group 3 In this group, the control performance of the planned trajectory is validated in the presence of external disturbances. Toward this end, we add an impulsive disturbance between 7 and 8 s, a sinusoid disturbance between 11 and 12 s, and a random disturbance between 15 and 16 s, respectively, all with a maximum amplitude of \(2^{\circ }\), to the hook swing and the payload swing.

The simulation results are given in Fig. 7. It is noticed that the external disturbances are suppressed and eliminated rapidly, indicating the strong robustness of the proposed method.

Fig. 7
figure 7

Simulation group 3: results for the proposed motion planning method with respect to different external disturbances

Full size image

5 Conclusions

Most of current researches on double-pendulum overhead crane systems are input shaping methods and regulation/stabilization methods, and no motion planning methods have ever been proposed for double-pendulum overhead cranes. This paper proposes an online motion planning method for double-pendulum overhead cranes systems. The advantages of the proposed method are that it is robust over different cable lengths, payload masses, desired trolley positions, and external disturbances, and can be implemented online without advance or offline planning. The convergence and swing-eliminating performance of the constructed trajectory are proven by Lyapunov techniques, LaSalle’s invariance theorem, and Barbalat’s lemma. Simulation results illustrate the superior performance of the planned trajectory and its robustness with respect to parameter variations and external disturbances. In our future work, we will extend the proposed method to the control of 3D overhead crane systems.