Introduction

In the twenty-first century, the increasing population and rapid industrialization have led to the exploitation of finite resources and disrupted the natural ecosystem. The COP-21 Paris Climate Agreement 2015 set a goal of reducing Greenhouse Emissions to keep temperature rise below + 2ºC. In a consumer company, the supply chain is one of the significant contributors to societal and environmental costs compared to its own operations, accounting for more than 80 percent of greenhouse-gas emissions. Hence, it is very likely that the supply chains are the primary driver force to achieve sustainability in their performance. The emerging trends in the supply chain, such as moving towards the circular economy model i.e. leveraging the used product recovery and material recycling to support the increasing level of consumption is a promising option.

In a traditional supply chain, there arises wastage due to the lack of coordination between the players. The product after its utility cycle always has some value remaining to it, which is wasted when disposed of by the end-user. Changing business landscapes, growing environmental consciousness, and increasing government regulations have compelled organizations to adapt to a 'cleaner', 'leaner', and a 'greener' supply chain. Legislations such as the Extended Product Responsibility (EPR), stress environmental performance and product lifecycle span [43] while holding the manufacturers responsible, both financially and physically for the ecological impact of their end-of-lifecycle (EOL) products [1]. Consequently, organizations have revamped their business strategies and adopted the triple bottom line concept, which has also led to a reduction in their carbon footprint. Also, the myopic view of managing only the company's environmental impact is discarded and emphasis is laid on adapting an integrated and multiplex approach by addressing the environmental impact of the supplier also [44, 50]. The rising importance of a holistic supply chain certification offered by the Forest Stewardship Council (FSC), known as the 'Chain of Custody (COC)' environmental certification, is evidence of the emerging trend & importance of sustainable management of the input materials in the supply chain domain.

A CLSC is a path to reach zero waste by forcing manufacturers to handle their products after their lifecycle. A CLSC integrates forward supply chain with recovery activities, which can be classified in 5R's: Recycle, Remanufacture, Reuse, Repair, and Refurbish. To gain a competitive advantage and achieve environmental sustainability, industries have adopted the remanufacturing strategy for recovering the scrap value of the returned product. According to a report remanufacturing in the light-duty automotive sector is a $32 billion industry that is forecasted to prosper at an average annual growth rate of 6.6% to $50 billion in 2022. Also, in other sectors, companies such as Dell, Xerox, Kodak, and HP have adopted remanufacturing as a strategy.

As evident from the above examples, the importance of remanufacturing a product used by the customers has gained widespread acceptance and recognition amongst current industrial players to drive sustainability in their respective businesses. The remanufactured product's cost is substantially low (around 40%-60%) of the newly manufactured product cost [7]. Decision-making is at the centre of supply chain management. Various studies have been carried out and models have been formulated to obtain a deeper insight regarding the optimal inventory policies necessary for making decisions in a centralized or decentralized manner. However, the majority of them are focused on single or two-echelon problems. But, in real-life scenarios, multiple players are a part of the supply chain and therefore necessitate joint decision-making to optimize the inventory policy of its integrated system. Considering this need for a more robust and inclusive model, we have developed a cohesive production inventory deterministic model for multi-echelon CLSC of four players viz. retailer, manufacturer, remanufacturer, and supplier. In this model, constant demand occurs at the downstream side (i.e. at the retailer). The manufacturer and remanufacturer satisfy this demand by producing the product in batches at a finite production rate. The supplier supplies raw material to the manufacturer, whereas the remanufacturer procures used products from the customer.

The rest of the paper is structured chronologically in the following manner: Section 2 outlines the Literature Review, Section 3 outlines the Notations & Assumptions, Section 4 deals with Mathematical modeling and Solution Technique, Section 5 with Sensitivity Analysis, and Section 6 concludes the present work and outlines the future scope of research in this field of work.

Literature study

Multiple research studies have been carried out in the CLSC domain, especially for the lot sizing problems considering both deterministic and stochastic inventory models. The field of reverse logistics is classified into 3 categories [8]: Inventory control, distribution planning and production planning. Inventory management models are generally framed to manage and control the specific product orders, level of inventory and recovery processes whilst maintaining specific service levels and minimizing total landed costs. Various studies [39, 46] also reviewed the literature about CLSC and identified that analysis of demand and return yield uncertainties in the remanufacturing cycle are the most preferred studies. The majority of the inventory models in the CLSC domain have been confined to single & two-echelon [4, 12, 16,17,18,19, 21, 33, 42, 51] and limited studies are carried out in the multi-echelon CLSC domain. The major incentive of this research work is propelled via the void present in the literature body in the domain of multi-echelon CLSC. It is also an endeavor to frame a production-inventory deterministic model for a multi-echelon CLSC environment. As a background study and an attempt to build upon the precedent in the CLSC domain, we have reviewed, analyzed, and summarized the previous literature work of various researchers in the domain of CLSC inventory models with product recovery options.

The pioneering work of Schrady [41] is considered a cornerstone for the EOQ based inventory modeling to determine joint economic lot size (JELS) in a reverse-logistics setting. Schrady [41] modeled a deterministic repairable inventory setting comprising two disparate inventories waiting for repair and determined the EOQ expressions for procurement and repair.

Schrady's repairable inventory model was furthered by Nahmias and Rivera [32], who incorporated a fixed rate of repair and assumed a bounded storage capacity. Similarly, Mabini et al. [24] also permitted backorders and considered a joint facility for repair. On the other hand, Richter [35] proposed an EOQ based repairable production inventory model assuming recovery of a fixed fraction of returned product instead of a continuous flow. Consequently, Richter [36], Richter [37], and Richter and Dobos [38] assumed the finite return and disposal rates as decision variables which were incorporated by Dobos and Richter [6] for finite production and repair cycles. Teunter [48] furthered Schrady's [41] model by considering separate inventory holding cost per unit for newly manufactured and remanufactured products for multiple production and repair cycles. This work was extended by Koh et al. [20] by presuming that rate of remanufacturing operation can be greater or less than the demand rate of the serviceable product. This model was generalized by Teunter [49], who obtained closed-form mathematical expressions for ascertaining optimal lot size in a (P, R) policy production environment assuming finite/infinite production and recovery rates. Various research studies on lot-sizing problems (EOQ/EPQ) with product returns have been conducted under various assumptions such as lost revenue [15], different quality of returned product and newly manufactured product [12, 15, 22], pronounced learning effect in remanufacturing & manufacturing processes [16, 51], unequal sizes of batch in the remanufacturing process [42]. A substantial literature in quantitative inventory models with product returns highlights the growing interest in this area.

The studies mentioned above consider only a single player in the production inventory environment. In contrast, in practice, multiple players are involved in a supply chain at various echelons exchanging physical information and financial flows. The studies carried out by Lee [23] in the field of the Forwarding supply chain as well as in CLSC domain by Chung et al. [3], have demonstrated that a centralized inventory-production policy for a two-echelon as well as for a multi-echelon system yields larger cost savings than adopting decentralized decision making policy for individual entities of the similar system.

Certain noteworthy studies for a two-echelon inventory system are elucidated below. Mitra [30] developed a cost minimization two-echelon model (for both deterministic & stochastic demand) to derive an optimal lot policy and shipment policy with a single recovery facility on the upstream side and the distributor on the downstream side. In this case, the variation in demand and return rates were assumed to be independent which was then relaxed by Mitra [31] by establishing a correlation between the two rates. An extension of Mitra [31] deterministic model by allowing partial backordering considering product returns and excess stocks was proposed by Teng et al. [47]. Tai and Ching [45] developed a two-echelon production inventory model consisting of a central warehouse to store newly manufactured & remanufactured items and multiple regional warehousing sites handling the remanufacturing operation. Various physical and financial constraints such as floor area, funds and variable lead time for the two-echelon CLSC consisting of a distributor and a warehouse facility for multiple players were proposed by Priyan and Uthayakumar [34]. Maiti and Giri [25] employed a dual approach for the collection of used products: (i) fraction of newly manufactured product sold as a part of Forward Supply Chain and (ii) Exchanging used product with a new one under an offer, while developing a two-echelon model. Jauhari et al. [17] developed a two-echelon mathematical inventory model for a CLSC system containing a manufacturer and a retailer under a stochastic environment with the intend of carbon emission reductions.

Further, Jauhari and Wangsa [18] developed a similar mathematical inventory model. They implemented a carbon tax policy to cut down the emissions from transportation, production, and storage for a two-echelon CLSC system. Keshavarz-Ghorbani and Pasandideh [19] incorporate the learning effect on vendor-managed inventory control problems in a two-echelon CLSC system to cope with the bullwhip effect associated shortages. Giri and Masanta [10] has developed a two-echelon CLSC system model by incorporating the effect of learning in production in stochastic environment, whereas Giri and Masanta [11] incorporated the learning-forgetting effect in production under consignment stock policy to investigate the effects of various parameters on optimal decisions. Further, Masanta and Giri [26] incorporated learning in the production and inspection process of newly manufactured product and returned products respectively in the two-echelon CLSC system. Zhou and Gupta [55] developed a pricing strategy model in system with a manufacturer, a remanufacturer, and a retailer to understand the customer's acceptance of remanufactured products and the technology obsolescence of new products the pricing decisions. In contrast, Huang et al. [14] studies the remanufacturing cost disruption in a two-echelon CLSC of a supplier, a manufacturer and a retailer.

The two-echelon production inventory model of Lee [23] was extended by [27,28,29] in a reverse logistics setting by incorporating a remanufacturer at the upper echelon for fulfilling the customer's demand through the remanufactured product along with the newly manufactured product. This work is the source of motivation for the current research study. Therefore, we attempt to further the work of Mawandiya et al. [28] to extrapolate the centrally controlled production inventory policy from a two-echelon CLSC system to a multi-echelon CLSC system. A limited number of studies have been carried out in the multi-echelon CLSC domain. The noteworthy contributions in the field of multi-echelon CLSC are discussed below. Hoadley and Hayman [13] modeled a single period multi-echelon framework incorporating lead time between successive stocking points in the same echelon. Chung and Huang [2] considered a multi-echelon CLSC model with a discounted price policy for the repairable inventory and focused on remanufacturing of deteriorating items. They thought demand as a dependent variable linked with the product's price. Giri and Sharma [9] considered an infinite time horizon multi-echelon CLSC model having an imperfect manufacturing process with the defects being reworked in the same cycle. It is an extension of the work of Chung et al. [3] in the following fronts: (i) imperfect production process with defects which are reworked, (ii) Acceptance quality of used/retuned items dictates the return rate and (iii) hybrid production system with multiple manufacturing and remanufacturing cycles.

Multiple studies were carried out for a multi-echelon CLSC system considering different objective functions, such as minimizing the total landed cost, maximizing the profit or reducing the carbon emissions. Diabat et al. [5] formulated a quantitative mathematical model for a multi-echelon logistics network with product returns. They employed MINLP technique to obtain the closed-form expression of optimal reverse logistic cost corresponding to the optimal number of collection points and location of the centralized return center. Chung et al. [3] considered a multi-echelon CLSC framework involving the manufacturer, the retailer, the supplier and the third party dealer handling recycling operations, designed under a binding contract in a centrally controlled and decentralized decision-making environment to maximize the total joint profits of the system. Giri et al. [9] furthered the work of Chung et al. [3] by including the following modifications: (i) imperfect production process with defects which are reworked, (ii) acceptance quality of used/returned items dictating the return rate and (iii) a mixed production system involving multiple manufacturing and remanufacturing operations. Sasikumar et al. [40] adopted a case study-based approach, who formulated a MILP multi-echelon reverse logistics model to maximize profits for a truck tyre company employing remanufacturing in its operational strategy. They demonstrated the impact of value creation in product recovery process (for used tyre segments), which motivated researchers to explore the recovery options in a RL setting. Xiao et al. [53] formulated a sustainable multi-echelon supply chain model with demands governed by the market prices, governmental carbon taxation, and acceptable emission standards to reduce the emission amount. They employed a contractual tax sharing agreement between the supplier and retailer. Ullah et al. [52] investigated an optimal remanufacturing strategy under the environment of stochastic demand and returned rate for single and multi-retailer CLSC models and showed that the hybrid policy is an optimal option for both single and multi-retailer cases.

The previous studies in the multi-echelon CSLC area are associated with maximizing/minimizing objective function with finite manufacturing rates and instantaneous remanufacturing operation of the returned product collected at the remanufacturer. Whereas in practice, remanufacturing process is not immediate and occurs at a limited rate. The primary motive of the present work is to formulate a centralized multi-echelon CLSC deterministic inventory model in a batch production environment with finite manufacturing and remanufacturing rates over an infinite time horizon. The previous works by Chung et al. [3] and Yuan and Gao [54] in the multi-echelon CLSC considered a single production line for the hybrid production system, whereas the present model classifies the manufacturer and the remanufacturer as a separate entity in the production environment.

Assumptions and notations

Assumptions

The formulated model is based on the following assumptions:

  1. 1)

    There is no difference in the quality and durability of remanufactured and manufactured products, and the retailer uses all of the remanufactured products to satisfy customer demand.

  2. 2)

    The customer's demand at the retailer and the rate of return from the customers is assumed to be constant and uniform (i.e. deterministic) over an infinite time horizon.

  3. 3)

    The production rate for the manufacturing and remanufacturing operation is assumed to be constant and greater than the demand rate.

  4. 4)

    The scrap generated during the remanufacturing process is immediately discarded.

  5. 5)

    The finished products are not subjected to deterioration and they are always available to the customers i.e. there is no shortage in the system.

  6. 6)

    It is a general consideration that the holding costs for inventory would increase in the subsequent processes owing to value addition.

    Hence, \(C_{1} > C_{2} ,C_{1} > C_{5} ,C_{1} > C_{6} ,C_{2} > C_{4} /f,C_{2} > C_{5} ,C_{5} > C_{3} /\alpha\).

  7. 7)

    The lead time between various stocking points is neglected in the proposed model.

  8. 8)

    The production cost for manufacturing a brand new product is more than remanufacturing from a recovered product.

The following notations are used in the proposed model (Table 1).

Table 1 List of notations
Full size table

Problem description & model formulation

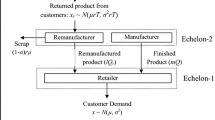
The proposed model deals with a centrally controlled multi-echelon deterministic CLSC framework in a production batch environment consisting of four players, viz. the supplier, the retailer, the manufacturer, and the remanufacturer. The supplier is at the top most echelon (Echelon-III). In contrast, manufacturer and remanufacturer are placed downstream of the supplier (Echelon-II), and the retailer facing the customer demand is being placed at the lower echelon (Echelon-I).

The model is formulated considering an alternate replenishment policy at the retailer with at least one manufacturing and one remanufacturing lot for one product, which is similar to the work of Teunter [48]. The retailer experiences a constant customer demand \((D)\), which is satisfied via alternate batches of the newly manufactured products and remanufactured products received from the manufacturer and remanufacturer respectively during each production cycle. The manufacturer procures \(Q_{fi}\) quantity of raw material from the supplier and transforms it at a finite production rate \(P\) with a transformation efficiency \(f\) to produce the finished product with \(m_{i} Q_{i}\) as the batch size. Similarly, the remanufacturer collects \(rD\) the amount of product returned from the customers. When the returned product's accumulated inventory reaches the maximum level, i.e. \(Q_{Ri}\), remanufacturing production cycle starts to produce \(l_{i} Q_{ri}\) batch size of the remanufactured product at a finite rate of production \(P_{r}\) and with a transformation efficiency of \(\alpha\).

The supplier on the upstream side of the CLSC procures the manufacturer's raw material in a batch of size \(z_{i} Q_{fi}\), thus acting as the repository of the raw material inventory for the manufacturer. The scrap generated at the remanufacturer i.e. \(\left(1-\alpha \right)rD\) is discarded immediately. The inventory setup of the proposed CLSC model is shown in the Fig. 1.

Fig. 1
figure 1

Inventory system setup

Full size image

During each cycle of production, \(m_{i}\) lots, each lot of equal size \(Q_{i}\) are shipped by the manufacturer to the retailer in a time interval of \(Q_{i} /D\). After the depletion of inventory of newly manufactured product at the retailer, the remanufacturer ships \(l_{i}\) lots, each lot of equal size \(Q_{ri}\) to the retailer after each interval of time \(Q_{ri} /D\). The demand at the retailer drives the coordinated production operations at the manufacturer and remanufacturer. The induction of manufacturing and remanufacturing process is in synchronization with the production completion time of the first delivered lot of newly manufactured product \(Q_{i}\) and the remanufactured product \(Q_{ri}\) to the retailer i.e. there is zero lead time for delivery of newly manufactured and remanufactured product.

Therefore, the first lot of size \(Q_{i}\) is produced by the manufacturer in time interval \(Q_{i} /P\) just after start of production process and shipped to the retailer. However, the remaining (\(m_{i} - 1\)) lots each of size \(Q_{i}\) are delivered to the retailer at a time interval of \(Q_{i} /D\) which is same as the time period in which the previously shipped lots are consumed at the retailer. Similarly, for the remanufacturer, delivery of the first remanufactured lot takes period of \(Q_{ri} /P_{r}\) whereas the remaining \((l_{i} - 1)\) lots of each size \(Q_{ri}\) are delivered to the retailer at a time interval of \(Q_{ri} /D\).

For each player in the multi-echelon CLSC production inventory model, the inventory variation pattern is depicted in the Figs. 2 & 3. It is observed that there are two different cases for raw material procurement by the manufacturer. Correspondingly, the supplier's inventory of the raw material procured will also be different for both cases (Table 2).

Fig. 2
figure 2figure 2

The pattern of variation in inventory levels for various players in the proposed model (Case-I)

Full size image
Fig. 3
figure 3figure 3

The pattern of variation in inventory levels for various players in the proposed model (Case-II)

Full size image
Table 2 Inventory variation pattern of Manufacturer and Supplier's raw material
Full size table

Joint total cost of the system

For the proposed model, the objective is to minimize the JTC production inventory system. As there are four players in the CLSC model, the JTC will be the summation of various costs such as cost per production setup, cost per order and holding cost of inventory associated with all of the four players at their respective levels of inventory.

Minimize JTC per unit time = 

{retailer's (Cost per order of newly manufactured & remanufactured product + Holding cost of inventory of finished and remanufactured product) + manufacturer's ( Cost per order of raw material from supplier + Holding cost of inventory of procured raw material + Cost per production setup for manufacturing process + Holding cost of inventory of newly manufactured product) + remanufacturer's (Holding cost of inventory of returned product + Cost per production setup for the remanufacturing process) + supplier's ( Cost per order of raw material + Holding cost of inventory of procured raw material)}/ Length of the Production cycle.

As there are two different cases for the procurement lot size of raw material for the manufacturer, the expression of JTC per unit time for both Case-I and Case-II will be different. Therefore, a suffix i is associated with both the cases (where i = 1 for Case-I and i = 2 for Case-II) to denote the costs associated as well as the dependent ( \(T_{i} ,Q_{ri} ,Q_{Ri} ,Q_{fi}\)) and the independent (\(m_{i} ,Q_{i} ,l_{i} ,n_{i} ,z_{i}\)) decision variables. In the subsequent sections, the individual costs for each player is derived and discussed.

Retailer

From the sub graph D of Figs. 2 & 3, it is evident that the retailer's inventory is replenished \(m_{i}\) times by the newly manufactured product and \(l_{i}\) times by the remanufactured product in one production cycle. It places orders from both manufacturer and remanufacturer according to the customer's demand and maintains an inventory of both manufactured and remanufactured products. Therefore, four different costs are related to the retailer- Cost per order of manufactured and remanufactured products and holding cost of inventory of manufactured and remanufactured products.

Cost per order for the retailer

The retailer places \(m_{i}\) orders and \(l_{i}\) orders to the manufacturer and remanufacturer respectively during each production cycle. Also, the number of production cycles per unit time is \(1/T_{i}\). The cost per order of the retailer per unit time is \((m_{i} S_{1} + l_{i} S_{5} )/T_{i}\) and on substituting the value of \(T_{i}\), we obtain the simplified expression as \((1 - \alpha r)(S_{1} + l_{i} S_{5} /m_{i} )D/Q_{i}\).

Holding cost of inventory for the retailer

The inventory variation graph for the retailer is shown in subgraph D of Figs. 2 & 3. The retailer's average inventory level is calculated by finding the total area of the triangles corresponding to the lots delivered by the manufacturer and remanufacturer.

\(\mathrm{Average\ level\ of\ inventory\ per\ unit\ time\ for\ the\ retailer:} \ \left( {m_{i} Q_{i}^{2} + l_{i} Q_{ri}^{2} } \right)/(2T_{i} D)\). On simplification we obtain, average level of inventory per unit time of the retailer as \((1 - \alpha r)\left\{ {1 + \frac{{m_{i} }}{{l_{i} }}\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)^{2} } \right\}\frac{{Q_{1} }}{2}\). Therefore, the holding cost of inventory for the retailer per unit time is expressed as \((1 - \alpha r)\left\{ {1 + \frac{{m_{i} }}{{l_{i} }}\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)^{2} } \right\}\frac{{Q_{1} C_{1} }}{2}\).

Manufacturer

During each production cycle, the manufacturer replenishes its inventory of raw material \(k_{i}\) times, installs a setup for the production of finished product and stacks raw material inventory (subgraph B of Figs. 2 & 3) and newly manufactured product inventory (subgraph E of Figs. 2 & 3). Hence, the related costs for the manufacturer are holding cost of inventory of raw material and newly manufactured product as well as the cost per order of the raw material and cost per production setup.

Cost per order of raw material for the manufacturer

It is evident from the subgraph B of Fig. 2 and Fig. 3 that the manufacturer places \(1/n_{1} T_{1}\) (Case-I) and \(n_{2} /T_{2}\) (Case-II) number of orders of raw material per unit time. This can be further simplified and written as \((1 - \alpha r)D/(n_{1} m_{1} Q_{1} )\) and \(n_{2} (1 - \alpha r)D/(m_{2} Q_{2} )\) respectively. Hence, Cost per order of raw material per unit time for the manufacturer is \((1 - \alpha r)DS_{4} /(n_{1} m_{1} Q_{1} )\) and \(n_{2} (1 - \alpha r)DS_{4} /(m_{2} Q_{2} )\) for Case-I and Case-II respectively.

Holding cost of inventory of raw material for the manufacturer

The manufacturer's average inventory level of raw material per unit time is derived using principles of geometry from the subgraph B of Figs. 2 and 3 for Case-I & II, respectively. For Case-I, the area of inventory diagram is calculated for '\(n_{1}\)' number of production cycles corresponding to a lot of procured raw material to obtain the average level of inventory. Similarly, for Case-II, the area of inventory diagram is calculated for \(^{\prime}n_{2} ^{\prime}\) lots of procured raw material by the manufacturer for one cycle of production to obtain the average level of inventory. Average level of inventory for Case-I is derived as \(\frac{1}{{n_{1} T_{1} }}\left\{ {\frac{{m_{1} n_{1} (n_{1} - 1)Q_{1} T_{1} }}{2f} + \frac{{m_{1}^{2} n_{1} Q_{1}^{2} }}{2Pf}} \right\}\) and for Case –II as \(\frac{1}{{T_{2} }}\left\{ {\frac{{m_{2}^{2} Q_{2}^{2} }}{{2n_{2} P}}} \right\}\).

On further simplification, the expressions for inventory holding cost of raw material for the manufacturer are written as Case-I: \(m_{1} \left\{ {(n_{1} - 1) + (1 - \alpha r)\frac{D}{P}} \right\}\frac{{Q_{1} C_{4} }}{2f}\) and Case-II: \(\frac{{m_{2} (1 - \alpha r)DQ_{2} C_{4} }}{{(2n_{2} Pf)}}\).

Cost per production setup for the manufacturer

The manufacturer installs one production setup at the beginning of the production cycle. The production cycle length is \(T_{i}\) and cost of production setup is \(S_{2}\). Hence, cost per production setup per unit time is expressed as \(S_{2} /T_{i}\) which is further simplified as \(\frac{{(1 - \alpha r)DS_{2} }}{{(m_{i} Q_{i} )}}\).

Holding cost of inventory of finished goods for the manufacturer

The finished goods are produced by the manufacturer at a production rate of \(P/f\), which are then supplied in the form of \(m_{i}\) lots of each size \(Q_{i}\) to the retailer during each production cycle. However, the rate of production of finished goods by the manufacturer is greater than the rate of delivery to the retailer. This leads to accumulation of inventory at the manufacturer which is obtained from the subgraph E of Figs. 2 & 3 by using principles of geometry.

$$\begin{array}{*{20}l} \begin{gathered} Average\ inventory\ per\ unit\ time = \ \ \ \ \ Accumulated\ inventory - \ \ \ \ \ Retailer^{\prime}s\ accumulated\ inventory\ \hfill \\ of\ manufaturer^{\prime}s\ finished\ product\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ of\ manufacturer\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ per\ unit\ time\ due\ to\ manufacturer^{\prime}s\ supply \hfill \\ \end{gathered} \hfill \\ {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\; = \frac{1}{{T_{i} }}\left[ {m_{i} Q_{i} \left\{ {\frac{{Q_{i} }}{P} + \frac{{(m_{i} - 1)Q_{{_{i} }} }}{D}} \right\} - \frac{{m_{i}^{2} Q_{i}^{2} }}{2P}} \right] - \frac{1}{{T_{i} }}\left[ {\frac{{m_{i} (m_{i} - 1)Q_{i}^{{^{2} }} }}{2D}} \right]} \hfill \\ \end{array}$$

This can be further simplified as \((1 - \alpha r)\left\{ {\left( {m_{i} - 1} \right) - (m_{i} - 2)\frac{D}{P}} \right\}\frac{{Q_{i} }}{2}\). Hence, the holding cost of inventory of finished product per unit time for the manufacturer is expressed as \((1 - \alpha r)\left\{ {\left( {m_{i} - 1} \right) - (m_{i} - 2)\frac{D}{P}} \right\}\frac{{Q_{i} C_{2} }}{2}\).

Remanufacturer

The remanufacturer collects the used product returned by the end user and recovers the value from the product by remanufacturing process. The rate of remanufacturing is \(P_{r}\) and the remanufacturer stacks and maintain level of returned and remanufactured product inventory and installs one production setup during each cycle of production for remanufacturing operation. Therefore, the costs associated with the remanufacturer are holding cost of inventory of the remanufactured and returned product and cost per production setup of remanufactured product.

Cost per production setup for the remanufacturer

The remanufacturer installs one production setup for the entire cycle production which is of length \(T_{i}\) and so, the cost per production setup for the remanufacturer will be \(S_{3} /T_{i}\). On simplifying, while substituting value of \(T_{i}\), the cost per production setup can be expressed as \((1 - \alpha r)S_{3} D/(m_{i} Q_{i} )\).

Holding cost of inventory of returned product for the remanufacturer

The remanufacturer collects the returned product \(rD\) continuously from the end user during the entire production cycle. When the retuned product reaches maximum inventory level \(Q_{Ri}\), the remanufacturer starts production process. Hence, in order to find the accumulated level of inventory of retuned product for the remanufacturer, the area of triangle (Subgraph C of Figs. 2 & 3) is calculated as \(T_{i} Q_{Ri} /2\) for one production cycle. Substituting value of \(T_{i}\), we obtain the holding cost of inventory of returned product per unit time for the remanufacturer as \(\frac{{m_{i} }}{\alpha }\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{\alpha rD}{{P_{r} }}} \right)\frac{{Q_{i} C_{3} }}{2}\).

Holding cost of inventory of remanufactured product for the remanufacturer

The remanufacturer supplies \(l_{i}\) lots of size \(Q_{ri}\) to the retailer during each cycle of production. The rate of remanufacturing operation is greater than the rate of delivery of remanufactured product to the retailer. Hence, inventory gets accumulated at the remanufacturer which can be obtained from the subgraph C of Figs. 2 & 3 using principles of geometry.

$$\begin{array}{*{20}l} \begin{gathered} Remanufacturer^{\prime}s\ accumulated\ inventory = \ \ \ \ \ \ \ \ \ \ Remanufacturer^{\prime}s \ \ \ \ \ \ \ \ \ \ - Retailer^{\prime}s\ accumulated\ inventory\ due\ to\ \hfill \\ of\ remanufactured\ product\ per\ unit\ time\ \ \ \ \ \ \ \ \ \ accumulated\ inventory \ \ \ \ \ remanufacturer^{\prime}s\ supply \hfill \\ \end{gathered} \hfill \\ {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\; = \frac{1}{{T_{i} }}\left[ {l_{i} Q_{ri} \left\{ {\frac{{Q_{ri} }}{{P_{r} }} + \frac{{(l_{i} - 1)Q_{ri} }}{D}} \right\} - \frac{{l_{i}^{2} Q_{ri}^{2} }}{{2P_{r} }}} \right] - \frac{1}{{T_{i} }}\left( {\frac{{l_{i} (l_{i} - 1)Q_{ri}^{2} }}{2D}} \right)} \hfill \\ \end{array}$$

This can be further simplified as \(\frac{{m_{i} \alpha r}}{{l_{i} }}(\frac{\alpha r}{{1 - \alpha r}})\left\{ {\left( {l_{i} - 1} \right) - (l_{i} - 2)\frac{D}{{P_{r} }}} \right\}\frac{{Q_{i} }}{2}\). Hence, the holding cost of inventory of remanufactured product for the remanufacturer is derived as \(\frac{{m_{i} \alpha r}}{{l_{i} }}(\frac{\alpha r}{{1 - \alpha r}})\left\{ {\left( {l_{i} - 1} \right) - (l_{i} - 2)\frac{D}{{P_{r} }}} \right\}\frac{{Q_{i} C_{5} }}{2}\).

Supplier

The supplier replenishes its inventory \(z_{i}\) times during each production cycle and supplies the raw material to the manufacturer. The costs associated with the supplier are the holding cost of inventory of raw material and cost per order of raw material.

Cost per order for the supplier

The supplier procures raw material during each production cycle in order to supply it to the manufacturer. The procurement lot size of the supplier is \(\frac{{z_{1} m_{1} n_{1} Q_{1} }}{f}\) for Case-I and \(\frac{{z_{2} m_{2} Q_{2} }}{{n_{2} f}}\) for Case-II.

The supplier places \(1/(z_{1} n_{1} T_{1} )\) and \(n_{2} /(z_{2} T_{2} )\) number of orders of raw material per unit time. By substituting value of \(T_{i}\), this can be written as \((1 - \alpha r)D/(z_{1} m_{1} n_{1} Q_{1} )\) for Case-I and \((1 - \alpha r)Dn_{2} /(z_{1} m_{1} Q_{1} )\) for Case-II. Hence, the Cost per order for the supplier is derived as \((1 - \alpha r)DS_{6} /(z_{1} m_{1} n_{1} Q_{1} )\) for Case-I and \((1 - \alpha r)Dn_{2} S_{6} /(z_{1} m_{1} Q_{1} )\) for Case-II.

Holding cost of inventory for the supplier

The inventory variation pattern of the supplier is depicted in the subgraph A of Figs. 2 & 3. The area of the inventory diagram gives the average inventory of the supplier for Case- I and Case-II.

Case-I: Total area of the inventory diagram of the supplier

$$= \sum\limits_{1}^{{z_{1} }} {cycles = } \frac{{m_{1} n_{1} Q_{1} (1 - \alpha r)}}{f}*\frac{{m_{1} Q_{1} }}{D}*\left\{ {z_{1}^{2} - \frac{{z_{1} (z_{1} + 1)}}{2}} \right\}$$

Average holding cost of inventory for the supplier per unit time = \(\frac{{(z_{1} - 1)m_{1} n_{1} (1 - \alpha r)C_{6} Q_{1} }}{2f}\).

Case-II: Total area of inventory diagram of the supplier

$$= \sum\limits_{1}^{{z_{1} }} {lots} = \frac{{z_{2} (z_{2} - n_{2} )(1 - \alpha r)m_{2} Q_{2} }}{{2X_{2}^{2} f}}*\left\{ {\frac{{m_{2} Q_{2} }}{{n_{2} D}} - \frac{{(n_{2} - 1)m_{2} Q_{2} (1 - \alpha r)}}{{n_{2} P}}} \right\}$$

Average holding cost of inventory for the supplier per unit time

$$= \frac{{(z_{2} - n_{2} )m_{2} (1 - \alpha r)C_{6} Q_{2} }}{{2n_{2} f}} + \frac{{D(n_{2} - 1)m_{2} (1 - \alpha r)^{2} C_{6} }}{{2n_{2} fP}}.$$

Objective function

The individual cost expressions for each of the players is derived above. The summation of all the cost components of all the players involved in the CLSC yields the JTC of the system which is the objective function of the proposed model.

For Case-I, JTC is expressed as

$$\begin{gathered} JTC_{1} (m_{1,} n_{1} ,l_{1} ,z_{1} ,Q_{1} ) = (1 - \alpha r)\left[ {S_{1} + \frac{{S_{2} }}{{m_{1} }} + \frac{{S_{3} }}{{m_{1} }} + \frac{{S_{4} }}{{m_{1} n_{1} }} + \frac{{l_{1} S_{5} }}{{m_{1} }} + \frac{{S_{6} }}{{m_{1} n_{1} z_{1} }}} \right]\frac{D}{{Q_{1} }} \hfill \\ + \left[ \begin{gathered} (1 - \alpha r)\left\{ {1 + \frac{{m_{1} }}{{l_{1} }}\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)^{2} } \right\}C_{1} + (1 - \alpha r)\left\{ {(m_{1} - 1) - (m_{1} - 2)\frac{D}{P}} \right\}C_{2} + \hfill \\ \frac{{m_{1} }}{\alpha }\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{\alpha rD}{{P_{r} }}} \right)C_{3} + m_{1} \left\{ {(n_{1} - 1) + (1 - \alpha r)\frac{D}{P}} \right\}C_{4} /f + \hfill \\ \frac{{m_{1} \alpha r}}{{l_{1} }}\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left\{ {(l_{1} - 1) - (l_{1} - 2)\frac{D}{{P_{r} }}} \right\}C_{5} + \frac{{(z_{1} - 1)m_{1} n_{1} (1 - \alpha r)C_{6} }}{f} \hfill \\ \end{gathered} \right]\frac{{Q_{1} }}{2} \hfill \\ \end{gathered}$$
(1)

Let \(\lambda_{1}\) = \((1 - \alpha r)\left[ {S_{1} + \frac{{S_{2} }}{{m_{1} }} + \frac{{S_{3} }}{{m_{1} }} + \frac{{S_{4} }}{{m_{1} n_{1} }} + \frac{{l_{1} S_{5} }}{{m_{1} }} + \frac{{S_{6} }}{{m_{1} n_{1} z_{1} }}} \right]\) and

$$\psi_{1} = \left[ \begin{gathered} (1 - \alpha r)\left\{ {1 + \frac{{m_{1} }}{{l_{1} }}\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)^{2} } \right\}C_{1} + (1 - \alpha r)\left\{ {(m_{1} - 1) - (m_{1} - 2)\frac{D}{P}} \right\}C_{2} + \hfill \\ \frac{{m_{1} }}{\alpha }\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{\alpha rD}{{P_{r} }}} \right)C_{3} + m_{1} \left\{ {(n_{1} - 1) + (1 - \alpha r)\frac{D}{P}} \right\}C_{4} /f + \hfill \\ \frac{{m_{1} \alpha r}}{{l_{1} }}\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left\{ {(l_{1} - 1) - (l_{1} - 2)\frac{D}{{P_{r} }}} \right\}C_{5} + \frac{{(z_{1} - 1)m_{1} n_{1} (1 - \alpha r)C_{6} }}{f} \hfill \\ \end{gathered} \right]$$

Hence,

$$JTC_{1} (Q_{1} ,m_{1} ,n_{1} ,l_{1} z_{1} ) = \frac{{D\lambda_{1} }}{{Q_{1} }} + \frac{{Q_{1} \psi_{1} }}{2}$$
(2)

Similarly, for Case-II, the JTC for the proposed model is expressed as

$$\begin{gathered} JTC_{2} (m_{2} ,n_{2} ,l_{2} ,z_{2} ,Q_{2} ) = (1 - \alpha r)\left[ {S_{1} + \frac{{S_{2} }}{{m_{2} }} + \frac{{S_{3} }}{{m_{2} }} + \frac{{n_{2} S_{4} }}{{m_{2} }} + \frac{{l_{2} S_{5} }}{{m_{2} }} + \frac{{n_{2} S_{6} }}{{m_{2} z_{2} }}} \right]\frac{D}{{Q_{2} }} \hfill \\ + \left[ \begin{gathered} (1 - \alpha r)\left\{ {1 + \frac{{m_{2} }}{{l_{2} }}\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)^{2} } \right\}C_{1} + (1 - \alpha r)\left\{ {(m_{2} - 1) - (m_{2} - 2)\frac{D}{P}} \right\}C_{2} + \hfill \\ \frac{{m_{2} }}{\alpha }\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{\alpha rD}{{P_{r} }}} \right)C_{3} + \frac{{m_{2} }}{{n_{2} }}\frac{(1 - \alpha r)D}{P}C_{4} /f \hfill \\ + \frac{{m_{2} \alpha r}}{{l_{2} }}\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left\{ {\left( {l_{2} - 1} \right) - (l_{2} - 2)\frac{D}{{P_{r} }}} \right\}C_{5} \hfill \\ + \left\{ {\frac{{(z_{2} - n_{2} )m_{2} (1 - \alpha r)}}{{n_{2} f}} + \frac{{D(n_{2} - 1)m_{2} (1 - \alpha r)^{2} }}{{n_{2} fP}}} \right\}C_{6} \hfill \\ \end{gathered} \right]\frac{{Q_{2} }}{2} \hfill \\ \end{gathered}$$
(3)

Solution technique

The above formulated objective function (i.e. JTC) is an unconstrained MINLP problem and the optimal solution can be found out by using classical optimisation technique. Hence, we use differentiation technique to find out first and second derivatives of the objective function with respect to each decision variable one by one while keeping other decision variables fixed and these derivatives are presented in Appendix 1. Also, the integer requirements on \(m_{1} ,n_{1} ,l_{1} ,\mathrm{and} {z_{1}}\) are relaxed temporarily while finding the optimal solution.

As the second derivatives for all the cases is greater than zero, we conclude that \(JTC_{1} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\) is convex in \(m_{1} ,n_{1} ,l_{1} \mathrm{and}\ z_{1}\) for fixed \(Q_{1} ,n_{1} ,l_{1} ,z_{1}\); for fixed \(Q_{1} ,m_{1} ,l_{1} ,z_{1}\); for fixed \(Q_{1} ,m_{1} ,n_{1} ,z_{1}\) and for fixed \(Q_{1} ,m_{1} ,n_{1} ,l_{1}\) respectively.

In order to obtain optimal solution for all the decision variables \(Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1}\), consider them as continuous variables and equating first derivatives to zero. We get,

$$Q_{1}^{*} (m_{1} ,n_{1} ,l_{1} ,z_{1} ) = \sqrt {2D\lambda_{1} /\psi_{1} }$$
(4)
$$m_{1}^{*} (Q_{1} ,n_{1} ,l_{1} ,z_{1} ) = \frac{1}{{Q_{1} }}\sqrt {\frac{{2D(1 - \alpha r)\left( {S_{2} + S_{3} + \frac{{S_{4} }}{{n_{1} }} + l_{1} S_{5} + \frac{{S_{6} }}{{z_{1} n_{1} }}} \right)}}{\begin{gathered} \frac{\alpha r}{{l_{1} }}\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left\{ {C_{1} - \left( {1 - \frac{2D}{{P_{r} }}} \right)C_{5} } \right\} + \hfill \\ \left[ \begin{gathered} (1 - \alpha r)\left( {1 - \frac{D}{P}} \right)C_{2} + \frac{1}{\alpha }\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{\alpha rD}{{P_{r} }}} \right)C_{3} \hfill \\ - \left\{ {1 - (1 - \alpha r)\frac{D}{P}} \right\}\frac{{C_{4} }}{f} + \alpha r\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{D}{{P_{r} }}} \right)C_{5} \hfill \\ \end{gathered} \right] \hfill \\ + \frac{{n_{1} C_{4} }}{f} + \frac{{(z_{1} - 1)C_{6} (1 - \alpha r)n_{1} }}{f} \hfill \\ \end{gathered} }}$$
(5)
$$n_{1}^{*} (Q_{1} ,m_{1} ,z_{1} ) = \frac{1}{{Q_{1} m_{1} }}\sqrt {\frac{{2Df(1 - \alpha r)\left( {S_{4} + \frac{{S_{6} }}{{z_{1} }}} \right)}}{{C_{4} + (z_{1} - 1)C_{6} (1 - \alpha r)}}}$$
(6)
$$l_{1}^{*} (Q_{1} ,m_{1} ) = Q_{1} m_{1} \sqrt {\frac{{\alpha r\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left\{ {C_{1} - \left( {1 - \frac{D}{{P_{r} }}} \right)C_{5} } \right\}}}{{2D\left( {1 - \alpha r} \right)S_{5} }}}$$
(7)
$$z_{1}^{*} (Q_{1} ,m_{1} ,n_{1} ) = \frac{1}{{Q_{1} m_{1} n_{1} }}\sqrt {\frac{{2DS_{6} f}}{{C_{6} }}}$$
(8)

The optimal value of decision variables is to be obtained solely in terms of constants. Hence, the Eqs. (4)-(5) are solved simultaneously to obtain the optimal solutions for the decision variables as

$$Q_{1}^{*} = \sqrt {\frac{{2DS_{1} }}{{C_{1} - \left( {1 - \frac{2D}{P}} \right)C_{2} }}}$$
(9)
$$m_{1}^{*} = \sqrt {\frac{{(S_{2} + S_{3} )(1 - \alpha r)\left\{ {C_{1} - \left( {1 - \frac{2D}{P}} \right)C_{2} } \right\}}}{{S_{1} \left[ \begin{gathered} (1 - \alpha r)\left( {1 - \frac{D}{P}} \right)C_{2} + \frac{1}{\alpha }\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{\alpha rD}{{P_{r} }}} \right)C_{3} \hfill \\ - \left\{ {1 - \left( {1 - \alpha r} \right)\frac{D}{P}} \right\}\frac{{C_{4} }}{f} + \alpha r\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{D}{{P_{r} }}} \right)C_{5} \hfill \\ \end{gathered} \right]}}}$$
(10)
$$n_{1}^{*} = \sqrt {\frac{{S_{4} f\left[ \begin{gathered} \left( {1 - \alpha r} \right)\left( {1 - \frac{D}{P}} \right)C_{2} + \frac{1}{\alpha }\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{\alpha rD}{{P_{r} }}} \right)C_{3} \hfill \\ - \left\{ {1 - \left( {1 - \alpha r} \right)\frac{D}{P}} \right\}\frac{{C_{4} }}{f} + \alpha r\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{D}{{P_{r} }}} \right)C_{5} \hfill \\ \end{gathered} \right]}}{{\left( {S_{2} + S_{3} } \right)\left[ {C_{4} - C_{6} (1 - \alpha r)} \right]}}}$$
(11)
$$l_{1}^{*} = \sqrt {\frac{{\left( {S_{2} + S_{3} } \right)\alpha r\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left\{ {C_{1} - \left( {1 - \frac{2D}{{P_{r} }}} \right)C_{5} } \right\}}}{{S_{5} \left[ \begin{gathered} (1 - \alpha r)\left( {1 - \frac{D}{P}} \right)C_{2} + \frac{1}{\alpha }\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{\alpha rD}{{P_{r} }}} \right)C_{3} \hfill \\ - \left\{ {1 - \left( {1 - \alpha r} \right)\frac{D}{P}} \right\}\frac{{C_{4} }}{f} + \alpha r\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{D}{{P_{r} }}} \right)C_{5} \hfill \\ \end{gathered} \right]}}}$$
(12)

And

$$z_{1}^{*} = \sqrt {\frac{{S_{6} \left[ {C_{4} - C_{6} (1 - \alpha r)} \right]}}{{C_{6} (1 - \alpha r)S_{4} }}}$$
(13)

For the sake of simplifying above equations,

Let

$$\begin{gathered} \phi_{1} = \left( {1 - \alpha r} \right)\left( {1 - \frac{D}{P}} \right)C_{2} + \frac{1}{\alpha }\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{\alpha rD}{{P_{r} }}} \right)C_{3} \hfill \\ - \left\{ {1 - \left( {1 - \alpha r} \right)\frac{D}{P}} \right\}\frac{{C_{4} }}{f} + \alpha r\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{D}{{P_{r} }}} \right)C_{5} \hfill \\ \end{gathered}$$
(14)
$$\varepsilon = \alpha r\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left\{ {C_{1} - \left( {1 - \frac{2D}{{P_{r} }}} \right)C_{5} } \right\}$$
(15)

And

$$\tau = C_{1} - \left( {1 - \frac{2D}{P}} \right)C_{2}$$
(16)

The Eqs. (9)-(10) can be written in simplified form as follow

$$Q_{1}^{*} = \sqrt {\frac{{2DS_{1} }}{\tau }}$$
(17)
$$m_{1}^{*} = \sqrt {\frac{{(S_{2} + S_{3} )(1 - \alpha r)\tau }}{{S_{1} \phi_{1} }}}$$
(18)
$$n_{1}^{*} = \sqrt {\frac{{S_{4} \phi_{1} f}}{{(S_{2} + S_{3} )\left[ {C_{4} - C_{6} (1 - \alpha r)} \right]}}}$$
(19)
$$l_{1}^{*} = \sqrt {\frac{{(S_{2} + S_{3} )\varepsilon }}{{A_{5} \phi_{1} }}}$$
(20)

And

$$z_{1}^{*} = \sqrt {\frac{{\left[ {C_{4} - (1 - \alpha r)C_{6} } \right]S_{6} }}{{C_{6} (1 - \alpha r)S_{4} }}}$$
(21)

Similarly, for Case-II the derived expressions of optimal value of decision variables considering them as continuous are expressed as follows

$$Q_{2}^{*} = \sqrt {\frac{{2DS_{1} }}{\tau }}$$
(22)
$$m_{2}^{*} = \sqrt {\frac{{(S_{2} + S_{3} )(1 - \alpha r)\tau }}{{S_{1} \phi_{2} }}}$$
(23)
$$n_{2}^{*} = \sqrt {\frac{{\left( {S_{2} + S_{3} } \right)\left( {1 - \alpha r} \right)D\left[ {C_{4} - C_{6} \left( {1 - \alpha r} \right)} \right]}}{{PfS_{4} \phi_{2} }}}$$
(24)
$$l_{2}^{*} = \sqrt {\frac{{(S_{2} + S_{3} )\varepsilon }}{{S_{5} \phi_{2} }}}$$
(25)
$$z_{2}^{*} = \sqrt {\frac{{S_{6} D\left[ {C_{4} - (1 - \alpha r)C_{6} } \right]}}{{C_{6} S_{4} P}}}$$
(26)

Where

$$\begin{gathered} \phi_{2} = (1 - \alpha r)\left( {1 - \frac{D}{P}} \right)C_{2} + \frac{1}{\alpha }\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{\alpha rD}{{P_{r} }}} \right)C_{3} + \alpha r\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{D}{{P_{r} }}} \right)C_{5} \hfill \\ - (1 - \alpha r)\frac{{C_{6} }}{f} + \frac{{DC_{6} (1 - \alpha r)^{2} }}{fP} \hfill \\ \end{gathered}$$
(27)

Formulation of algorithm

Case-I

For a fixed value of \(m_{1} ,n_{1} ,l_{1} \mathrm{and}\ z_{1}\), substituting the value of \(Q_{1}^{*}\) from Eq. (4) in Eq. (2), we get the minimum JTC of the system (\(JTC_{1}\))

$$JTC_{1} (m_{1} ,n_{1} ,l_{1} ,z_{1} ) = \sqrt {2D\lambda_{1} \psi_{1} }$$
(28)

As the values of \(m_{1} ,n_{1} ,l_{1} ,z_{1}\) are assumed as integers, the JTC for the proposed inventory model is calculated using the following procedure.

The minimisation of \([JTC_{1} (m_{1} ,n_{1} ,l_{1} ,z_{1} )]^{2}\) is equivalent to minimisation of \(JTC_{1} (m_{1} ,n_{1} ,l_{1} ,z_{1} )\) (from (28). This implies that \(MinJTC_{1} (m_{1} ,n_{1} ,l_{1} ,z_{1} ) \equiv Min[JTC_{1} (m_{1} ,n_{1} ,l_{1} ,z_{1} )]^{2} = Min2D\lambda_{1} \psi_{1}\)

$$\begin{gathered} = Min2D(1 - \alpha r)\left[ {S_{1} + \frac{{S_{2} }}{{m_{1} }} + \frac{{S_{3} }}{{m_{1} }} + \frac{{S_{4} }}{{m_{1} n_{1} }} + \frac{{l_{1} S_{5} }}{{m_{1} }} + \frac{{S_{6} }}{{m_{1} n_{1} z_{1} }}} \right] \hfill \\ \times \left[ \begin{gathered} (1 - \alpha r)\left\{ {1 + \frac{{m_{1} }}{{l_{1} }}\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)^{2} } \right\}C_{1} + (1 - \alpha r)\left\{ {(m_{1} - 1) - (m_{1} - 2)\frac{D}{P}} \right\}C_{2} + \hfill \\ \frac{{m_{1} }}{\alpha }\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left( {1 - \frac{\alpha rD}{{P_{r} }}} \right)C_{3} + m_{1} \left\{ {(n_{1} - 1) + (1 - \alpha r)\frac{D}{P}} \right\}C_{4} /f + \hfill \\ \frac{{m_{1} \alpha r}}{{l_{1} }}\left( {\frac{\alpha r}{{1 - \alpha r}}} \right)\left\{ {(l_{1} - 1) - (l_{1} - 2)\frac{D}{{P_{r} }}} \right\}C_{5} + \frac{{(z_{1} - 1)m_{1} n_{1} (1 - \alpha r)C_{6} }}{f} \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered}$$
(29)

The terms independent of \(m_{1} ,n_{1} ,l_{1} ,z_{1}\) are eliminated from the above expression (Eq. (29)). Let this new minimisation function of \(JTC_{1} (m_{1} ,n_{1} ,l_{1} ,z_{1} )\) be denoted by \(\omega_{1} (m_{1} ,n_{1} ,l_{1} ,z_{1} )\).Thus,

$$\omega_{1} (m_{1} ,n_{1} ,l_{1} ,z_{1} ) = \left[ \begin{gathered} \left( {m_{1} S_{1} + \frac{{S_{4} }}{{n_{1} }} + l_{1} S_{5} + \frac{{S_{6} }}{{n_{1} z_{1} }}} \right)\phi_{1} \hfill \\ + \left\{ {m_{1} n_{1} S_{1} + n_{1} (S_{2} + S_{3} ) + n_{1} l_{1} S_{5} + \frac{{S_{6} }}{{z_{1} }}} \right\}\frac{{C_{4} }}{f} \hfill \\ + \left( {\frac{{S_{2} + S_{3} }}{{m_{1} }} + \frac{{S_{4} }}{{m_{1} n_{1} }} + \frac{{l_{1} S_{5} }}{{m_{1} }} + \frac{{S_{6} }}{{m_{1} n_{1} z_{1} }}} \right)(1 - \alpha r)\tau \hfill \\ + \left\{ {\frac{{m_{1} S_{1} }}{{l_{1} }} + \frac{{S_{2} + S_{3} }}{{l_{1} }} + \frac{{S_{4} }}{{n_{1} l_{1} }} + \frac{{S_{6} }}{{n_{1} l_{1} z_{1} }}} \right\}\varepsilon \hfill \\ + \frac{{(1 - \alpha r)C_{6} }}{f}\left[ \begin{gathered} m_{1} n_{1} z_{1} S_{1} + S_{2} n_{1} z_{1} + S_{3} n_{1} z_{1} + S_{4} z_{1} + l_{1} n_{1} z_{1} S_{5} \hfill \\ - m_{1} n_{1} S_{1} - n_{1} S_{2} - n_{1} S_{3} - l_{1} n_{1} S_{5} - \frac{{S_{6} }}{{z_{1} }} \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} \right]$$
(30)

As the Eq. (28) is convex for a fixed value of \(m_{1} ,n_{1} ,l_{1} ,z_{1}\), hence the Eq. (30) is also convex for fixed value of \(m_{1} ,n_{1} ,l_{1} ,z_{1}\).

For minimising the function \(\omega_{1} (m_{1}^{*} ,n_{1}^{*} ,l_{1}^{*} ,z_{1}^{*} )\) in Eq. (30) for fixed \(n_{1}^{*} ,l_{1}^{*} ,z_{1}^{*}\), the corresponding optimal value of \(m_{1}^{*}\) will satisfy the inequalities (31) and (32) stated below.

$$\omega_{1} (m_{1}^{*} ,n_{1}^{*} ,l_{1}^{{^{*} }} ,z_{1}^{*} ) \le \omega_{1} (m_{1}^{*} + 1,n_{1}^{*} ,l_{1}^{{^{*} }} ,z_{1}^{*} )$$
(31)
$$\omega_{1} (m_{1}^{*} ,n_{1}^{*} ,l_{1}^{{^{*} }} ,z_{1}^{*} ) \le \omega_{1} (m_{1}^{*} - 1,n_{1}^{*} ,l_{1}^{{^{*} }} ,z_{1}^{*} )$$
(32)

Now, eliminating terms independent of \(m_{1}^{*}\) in Eq. (31), we get the simplified expression as below,

$$\begin{gathered} \left[ {m_{1}^{*} S_{1} \left( {\phi_{1} + \frac{{n_{1}^{*} C_{4} }}{f} + \frac{\varepsilon }{{l_{1}^{*} }} + \frac{{n_{1}^{*} C_{6} (1 - \alpha r)(z_{1}^{*} - 1)}}{f}} \right) + \frac{{(1 - \alpha r)\tau \left( {S_{2} + S_{3} + \frac{{S_{4} }}{{n_{1}^{*} }} + l_{1}^{*} S_{5} + \frac{{S_{6} }}{{n_{1}^{*} z_{1}^{*} }}} \right)}}{{m_{1}^{*} }}} \right] \hfill \\ \le \left[ {\left( {m_{1}^{*} + 1} \right)S_{1} \left( {\phi_{1} + \frac{{n_{1}^{*} C_{4} }}{f} + \frac{\varepsilon }{{l_{1}^{*} }} + \frac{{n_{1}^{*} C_{6} (1 - \alpha r)(z_{1}^{*} - 1)}}{f}} \right) + \frac{{(1 - \alpha r)\tau \left( {S_{2} + S_{3} + \frac{{S_{4} }}{{n_{1}^{*} }} + l_{1}^{*} S_{5} + \frac{{S_{6} }}{{n_{1}^{*} z_{1}^{*} }}} \right)}}{{(m_{1}^{*} + 1)}}} \right] \hfill \\ \end{gathered}$$

This is further simplified as

$$m_{1}^{*} (m_{1}^{*} + 1) \ge \frac{{\left( {S_{2} + S_{3} + \frac{{S_{4} }}{{n_{1}^{*} }} + l_{1}^{*} S_{5} + \frac{{S_{6} }}{{n_{1}^{*} z_{1}^{*} }}} \right)\left( {1 - \alpha r} \right)\tau }}{{S_{1} \left( {\phi_{1} + \frac{{n_{1}^{*} C_{4} }}{f} + \frac{\varepsilon }{{l_{1}^{*} }} + \frac{{n_{1}^{*} (1 - \alpha r)\left( {z_{1}^{*} - 1} \right)C_{6} }}{f}} \right)}}$$

In a similar way, from Eq. (2), we get

$$m_{1}^{*} (m_{1}^{*} - 1) \le \frac{{\left( {S_{2} + S_{3} + \frac{{S_{4} }}{{n_{1}^{*} }} + l_{1}^{*} S_{5} + \frac{{S_{6} }}{{n_{1}^{*} z_{1}^{*} }}} \right)\left( {1 - \alpha r} \right)\tau }}{{S_{1} \left( {\phi_{1} + \frac{{n_{1}^{*} C_{4} }}{f} + \frac{\varepsilon }{{l_{1}^{*} }} + \frac{{n_{1}^{*} (1 - \alpha r)\left( {z_{1}^{*} - 1} \right)C_{6} }}{f}} \right)}}$$

Combining both the expressions, we get

$$m_{1}^{*} (m_{1}^{*} - 1) \le \frac{{\left( {S_{2} + S_{3} + \frac{{S_{4} }}{{n_{1}^{*} }} + l_{1}^{*} S_{5} + \frac{{S_{6} }}{{n_{1}^{*} z_{1}^{*} }}} \right)\left( {1 - \alpha r} \right)\tau }}{{S_{1} \left( {\phi_{1} + \frac{{n_{1}^{*} C_{4} }}{f} + \frac{\varepsilon }{{l_{1}^{*} }} + \frac{{n_{1}^{*} (1 - \alpha r)\left( {z_{1}^{*} - 1} \right)C_{6} }}{f}} \right)}} \le m_{1}^{*} (m_{1}^{*} + 1)$$
(33)

Similarly, the expressions for other decision variables for Case-1 and Case-2 are as follows:

$$l_{1}^{*} (l_{1}^{*} - 1) \le \frac{{\left( {m_{1}^{*} S_{1} + S_{2} + S_{3} + \frac{{S_{4} }}{{n_{1}^{*} }} + \frac{{S_{6} }}{{n_{1}^{*} z_{1}^{*} }}} \right)\varepsilon }}{{S_{5} \left( {\phi_{1} + \frac{{n_{1}^{*} C_{4} }}{f} + \frac{(1 - \alpha r)\tau }{{m_{1}^{*} }} + \frac{{(z_{1}^{*} - 1)(1 - \alpha r)C_{6} n_{1}^{*} }}{f}} \right)}} \le l_{1}^{*} (l_{1}^{*} + 1)$$
(34)
$$z_{1}^{*} \left( {z_{1}^{*} - 1} \right) \le \frac{{\left( {\frac{{\phi_{1} }}{{n_{1}^{*} }} + \frac{{C_{4} }}{f} + \frac{{\left( {1 - \alpha r} \right)\tau }}{{n_{1}^{*} m_{1}^{*} }} + \frac{\varepsilon }{{n_{1}^{*} l_{1}^{*} }} - \frac{{\left( {1 - \alpha r} \right)C_{6} }}{f}} \right)S_{6} }}{{\frac{{\left( {1 - \alpha r} \right)C_{6} }}{f}\left( {m_{1}^{*} n_{1}^{*} S_{1} + n_{1}^{*} S_{2} + n_{1}^{*} S_{3} + S_{4} + l_{1}^{*} n_{1}^{*} S_{5} } \right)}} \le z_{1}^{*} \left( {z_{1}^{*} + 1} \right)$$
(35)

For Case-2 the expressions of inequalities of decision variables are

$$m_{2}^{*} (m_{2}^{*} - 1) \le \frac{{\left( {S_{2} + S_{3} + n_{2}^{*} S_{4} + l_{2}^{*} S_{5} + \frac{{n_{2}^{*} S_{6} }}{{z_{2}^{*} }}} \right)\tau }}{{S_{1} \left[ \begin{gathered} \phi_{2} + \frac{{(1 - \alpha r)DC_{4} }}{{n_{2}^{*} Pf}} + \frac{\varepsilon }{{l_{2}^{{^{*} }} }} + \hfill \\ \frac{{(1 - \alpha r)C_{6} }}{f}\left( {\frac{{z_{2}^{*} }}{{n_{2}^{*} }} - 1 + \frac{D(1 - \alpha r)}{P} - \frac{D(1 - \alpha r)}{{n_{2}^{*} P}}} \right) \hfill \\ \end{gathered} \right]}} \le m_{2}^{*} (m_{2}^{*} + 1)$$
(36)
$$l_{2}^{*} (l_{2}^{*} - 1) \le \frac{{\varepsilon \left( {m_{2}^{*} S_{1} + S_{2} + S_{3} + n_{2}^{*} S_{4} + \frac{{n_{2}^{*} S_{6} }}{{z_{2}^{*} }}} \right)}}{{S_{5} \left[ \begin{gathered} \phi_{2} + \frac{\tau }{{m_{2}^{*} }} + \frac{{(1 - \alpha r)DC_{4} }}{{Pfn_{2}^{*} }} + \hfill \\ \frac{{(z_{2}^{*} - n_{2}^{*} )(1 - \alpha r)}}{{n_{2}^{*} f}} + \frac{{\left( {n_{2}^{*} - 1} \right)D\left( {1 - \alpha r} \right)^{2} }}{{n_{2}^{*} Pf}} \hfill \\ \end{gathered} \right]}} \le l_{2}^{*} (l_{2}^{*} + 1)$$
(37)
$$z_{2}^{*} (z_{2}^{*} - 1) \le \frac{{S_{6} \left( \begin{gathered} n_{2}^{*} \phi_{2} + \frac{{(1 - \alpha r)DC_{4} }}{Pf} + \frac{{n_{2}^{*} \tau }}{{m_{2}^{*} }} + \frac{{n_{2}^{*} \varepsilon }}{{l_{2}^{*} }} - \frac{{(1 - \alpha r)n_{2}^{*} C_{6} }}{f} \hfill \\ + \frac{{n_{2}^{*} D(1 - \alpha r)^{2} C_{6} }}{fP} - \frac{{D(1 - \alpha r)^{2} C_{6} }}{fP} \hfill \\ \end{gathered} \right)}}{{\frac{{C_{6} (1 - \alpha r)}}{{n_{2}^{*} f}}\left( {m_{2}^{*} S_{1} + S_{2} + S_{3} + S_{4} n_{2}^{*} + S_{5} l_{2}^{*} } \right)}} \le z_{2}^{*} (z_{2}^{*} + 1)$$
(38)

The above mentioned solution technique gives the optimal integer values of \(m_{i}^{*}\) for fixed \(n_{i}^{*} ,l_{i}^{*} ,z_{i}^{*}\), of \(n_{i}^{*}\) for fixed \(m_{i}^{*} ,l_{i}^{*} ,z_{i}^{*}\) and of \(z_{i}^{*}\) for fixed \(m_{i}^{*} ,n_{i}^{*} ,l_{i}^{*}\) in terms of inequalities. Therefore, in order to find the exact optimal integer value of the decision variables (i.e. number of lots \(m_{i}^{*} ,n_{i}^{*} ,l_{i}^{*} ,z_{i}^{*}\)) corresponding to the minimum JTC, the method of iteration is used.

An algorithm for Case-I & Case-II is formulated to find the optimal value of independent decision variables.

Algorithm

Case-I

Main Routine-1

  • Step-1: Obtain the optimal value of \(n_{1}^{*}\) from Eq. (11).

  • Step-2: If \(n_{1}^{*} < 1\), find the value of \(n_{2}^{*}\) from Eq. (24), else go to Step 5;

  • Step-3: If \(n_{2}^{*} < 1\) then \(n_{1}^{*} = n_{2}^{*} = 1\);

  • Step-4: If \(n_{2}^{*} > 1\) then go to Main routine 2;

  • Step-5: To obtain the lower bound \(n_{1}^{*L}\), find \(\left[ {n_{1}^{*} } \right]\), \(n_{1}^{*L} = \left[ {n_{1}^{*} } \right]\);

  • Step-6: Let \(n_{1} = n_{1}^{*L}\) and Go to Subroutine-1a;

  • Step-7: Let \(JTC_{1}^{*} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) = JTC_{1}^{***} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\);

  • Step-8: Let \(n_{1} = n_{1} + 1\) and then go to Subroutine-1a;

  • Step-9: Let \(JTC_{1}^{*a} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) = JTC_{1}^{***} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\);

  • Step-10: Let \(n_{1} = n_{1} - 1\) and then go to Subroutine-1a;

  • Step-11: If \(n_{1} > 0\) then let \(JTC_{1}^{*b} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) = JTC_{1}^{***} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\) else go to Step-13;

  • Step-12: If \(JTC_{1}^{*b} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) > JTC_{1}^{*a} (Q_{1} ,m_{1} ,n_{1} .l_{1} ,z_{1} )\), else go to Step-16;

  • Step-13: If \(JTC_{1}^{*a} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) < JTC_{1}^{*} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\), then \(JTC_{1}^{*} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) = JTC_{1}^{*a} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\) else Stop;

  • Step-14: For \(n_{1} = n_{1} + 1\), go to Subroutine-1a;

  • Step-15: If \(JTC_{1}^{***} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) < JTC_{1}^{*} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\), then \(JTC_{1}^{*} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) = JTC_{1}^{***} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\) and go to Step14, else Stop;

  • Step-16: If \(JTC_{1}^{*b} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) < JTC_{1}^{*} (Q_{1} ,m_{1} ,l_{1} ,n_{1} ,z_{1} )\), then \(JTC_{1}^{*} (Q_{1} ,m_{1} ,n_{l} ,l_{1} ,z_{1} ) = JTC_{1}^{*b} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\) else Stop;

  • Step-17: For \(n_{1}^{*} = n_{1}^{*} - 1\), Go to Subroutine-1a;

  • Step-18: If \(JTC_{1}^{***} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) < JTC_{1}^{*} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\), the \(JTC_{1}^{*} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) = JTC_{1}^{***} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\) and go to Step17, else Stop;

    //*\(JTC_{1}^{*} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\) is the Optimal value//

Subroutine-1a

  • Step-1: Obtain the integral value of \(z_{1}^{U}\) by substituting value of \(n_{1}^{*}\) and considering \(m_{1}^{*} = 1\) and \(l_{1}^{*} = 1\) from Eq. (35);

  • Step-2: Let \(z_{1} = z_{1}^{U}\).

  • Step-3: Go to Subroutine-2a.

  • Step-4: Let \(JTC_{1}^{***} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) = JTC_{1}^{**} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\);

  • Step-5: Let \(z_{1} = z_{1} + 1\) and go to Subroutine-2a;

  • Step-6: If \(JTC_{1}^{**} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) < JTC_{1}^{***} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\) then \(JTC_{1}^{***} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) = JTC_{1}^{**} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\) and go to Step 5, else return;

Subroutine-2a:-

  • Step-1: Obtain the integral value of \(m_{1}^{L}\) by considering \(l_{1}^{*} = 1\) from Eq. (33)

  • Step-2: Let \(m_{1} = m_{1}^{L}\);

  • Step-3: Go to Subroutine-3a;

  • Step-4: Let \(JTC_{1}^{**} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) = JTC_{1} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\);

  • Step-5: Let \(m_{1} = m_{1} + 1\), Go to Subroutine-3a;

  • Step-6: If \(JTC_{1} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) < JTC_{1}^{**} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\) then \(JTC_{1} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} ) = JTC_{1}^{**} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\), go to Step5, else return;

Subroutine-3a:-

  • Step-1: By substituting the associated values of \(n_{1} ,m_{1} ,z_{1}\) into the Eq. (34) find the value of \(l_{1}\);

  • Step-2: Similarly, substitute all the associated values of \(n_{1} ,m_{1} ,l_{1} ,z_{1}\) in Eq. (4) to obtain the value of \(Q_{1}\);

  • Step-3: Using all of the values of decision variables find the JTC for given parameters \(JTC_{1} (Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1} )\) by substituting value of \(Q_{1} ,m_{1} ,n_{1} ,l_{1} ,z_{1}\) in Eq. (1) return;

Similarly, for Case-II,

Main Routine-2

  • Step 1: To obtain the lower bound \(n_{2}^{*L}\), find \(\left[ {n_{2}^{*} } \right]\), \(n_{2}^{*L} = \left[ {n_{2}^{*} } \right]\);

  • Step-2: Let \(n_{2} = n_{2}^{*L}\) and Go to Subroutine-1b;

  • Step-3: Let \(JTC_{2}^{*} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) = JTC_{2}^{***} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\);

  • Step-4: Let \(n_{2} = n_{2} + 1\) and then go to Subroutine-1b;

  • Step-5: Let \(JTC_{2}^{*a} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) = JTC_{2}^{***} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\);

  • Step-6: Let \(n_{2} = n_{2} - 1\) and then go to Subroutine-1b;

  • Step-7: If \(n_{2} > 0\) then let \(JTC_{2}^{*b} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) = JTC_{2}^{***} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\) else go to Step-9;

  • Step-8: If \(JTC_{2}^{*b} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) > JTC_{2}^{*a} (Q_{2} ,m_{2} ,n_{2} .l_{2} ,z_{2} )\), else go to Step-12;

  • Step-9: If \(JTC_{2}^{*a} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) < JTC_{2}^{*} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\), then \(JTC_{2}^{*} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) = JTC_{2}^{*a} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\) else Stop;

  • Step-10: For \(n_{2} = n_{2} + 1\), go to Subroutine-1b;

  • Step-11: If \(JTC_{2}^{***} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) < JTC_{2}^{*} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\), then \(JTC_{2}^{*} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) = JTC_{2}^{***} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\) and go to Step10, else Stop;

  • Step-12: If \(JTC_{2}^{*b} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) < JTC_{2}^{*} (Q_{2} ,m_{2} ,l_{2} ,n_{2} ,z_{2} )\), then \(JTC_{2}^{*} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) = JTC_{2}^{*b} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\) else Stop;

  • Step-13: For \(n_{2}^{*} = n_{2}^{*} - 1\), Go to Subroutine-1a;

  • Step-14: If \(JTC_{2}^{***} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) < JTC_{2}^{*} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\), then \(JTC_{2}^{*} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) = JTC_{2}^{***} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\) and go to Step13, else Stop;

    //\(JTC_{2}^{*} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\) is the Optimal value//

Subroutine-1b

  • Step-1: Obtain the integral value of \(z_{2}^{U}\) by substituting value of \(n_{2}^{*}\) and considering \(m_{2}^{*} = 1\) and \(l_{2}^{*} = 1\) from Eq. (38);

  • Step-2: Let \(z_{2} = z_{2}^{U}\).

  • Step-3: Go to Subroutine-2b.

  • Step-4: Let \(JTC_{2}^{***} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) = JTC_{2}^{**} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\);

  • Step-5: Let \(z_{2} = z_{2} + 1\) and go to Subroutine-2b;

  • Step-6: If \(JTC_{2}^{**} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) < JTC_{2}^{***} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\) then \(JTC_{2}^{***} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) = JTC_{2}^{**} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\) and go to Step 5, else return;

Subroutine-2b:-

  • Step-1: Obtain the integral value of \(m_{2}^{L}\) by considering \(l_{2}^{*} = 1\) from Eq. (36)

  • Step-2: Let \(m_{2} = m_{2}^{L}\);

  • Step-3: Go to Subroutine-3b;

  • Step-4: Let \(JTC_{2}^{**} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) = JTC_{2} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\);

  • Step-5: Let \(m_{2} = m_{2} + 1\), Go to Subroutine-3b;

  • Step-6: If \(JTC_{2} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) < JTC_{2}^{**} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\) then \(JTC_{2} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} ) = JTC_{2}^{**} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\), go to Step 5, else return;

Subroutine-3b:-

  • Step-1: By substituting the associated values of \(n_{2} ,m_{2} ,z_{2}\) into the Eq. (37) find the value of \(l_{2}\);

  • Step-2: Similarly, substitute all the associated values of \(n_{2} ,m_{2} ,l_{2} ,z_{2}\) in Eq. (22) to obtain the value of \(Q_{2}\);

  • Step-3: Using all of the values of decision variables find the JTC for given parameters \(JTC_{2} (Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2} )\) by substituting value of \(Q_{2} ,m_{2} ,n_{2} ,l_{2} ,z_{2}\) in Eq. (3) return;

Numerical illustration

For the above proposed model, sample data is assumed and the algorithm is executed sequentially to obtain the optimal solution (i.e. minimum JTC)

$$\begin{gathered} D = 29000,P = 55000,P_{r} = 55000,S_{1} = 100,S_{2} = 400,S_{3} = 200,S_{4} = 500,S_{5} = 75,S_{6} = 400, \hfill \\ C_{1} = 40,C_{2} = 20,C_{3} = 10,C_{4} = 12,C_{5} = 15,C_{6} = 8,r = 0.9,\alpha = 0.9,f = 0.9 \hfill \\ \end{gathered}$$

The solution for the above set of parameters belong to Case-I as value of \(n_{1}^{*}\) calculated from (16) is 1.72 (\(n_{1}^{*}\) > 1) and the optimal value of decision variables \(Q_{1} ,m_{1} ,l_{1} ,z_{1}\) are obtained from (19), (20), (22) and (23) respectively. The iterative method is initiated is by taking value of \(n_{1}^{*}\) = 1 (as \(n_{1}^{*}\) = 1.72). Subsequently, the iterations are carried out for all possible integer values of \(n_{1}^{*}\) which is depicted in the Table 3. It shows the JTC and corresponding value of all decision variables for the proposed model. The optimal solution is obtained when the value of decision variables \(Q_{1} ,m_{1} ,l_{1} ,n_{1} ,z_{1}\) for the given parameters is 382.26, 1, 5, 2, and 2, respectively, and the corresponding minimum JTC is 41080.05.

Table 3 JTC and corresponding value of decision variables at each stage of iterative method
Full size table

Sensitivity analysis

In order to ascertain the impact of key control parameters such as \(P,P_{r} ,r\) on the obective function i.e. JTC of the system, sensitivity analysis is carried out. This helps in understanding the cost variation pattern of individual players in the proposed model for a given set of parameters. However, the impact of other parameters such as \(D,\alpha ,f,S_{1} ,S_{2} ,S_{3} ,S_{4} ,S_{5} ,S_{6} ,C_{1} ,C_{2} ,C_{4} ,C_{5} ,C_{6}\) is predictable i.e. the JTC of the system increases as value of any of these parameters increases and therefore sensitivity analysis is not carried out for these parameters.

For the analysis, the following values are taken.

$$\begin{gathered} D = 15000,\alpha = 0.8,r = 0.625,f = 0.95,P = 25000,P_{r} = 25000,S_{1} = 200,S_{2} = 800,S_{3} = 400, \hfill \\ S_{4} = 1000,S_{5} = 150,S_{6} = 800,C_{1} = 800,C_{2} = 40,C_{3} = 20,C_{4} = 24,C_{5} = 30,C_{6} = 16 \hfill \\ \end{gathered}$$

The sensitivity analysis for each of the parameters \(P,P_{r} ,r\) is carried out by varying a single parameter one at a time and maintaining the other two parameter's value constant. The variation pattern in the JTC for the above proposed model corresponding to the key parameters is graphically represented as shown in the Figs. 4, 5 & 6.

Fig. 4
figure 4

Variation of JTC of the proposed model with respect to \(P\)

Full size image
Fig. 5
figure 5

Variation of JTC of the proposed model with respect to \(P_{r}\)

Full size image
Fig. 6
figure 6

Variation pattern of the JTC with \(r\)

Full size image

Also, certain results of the sensitivity analysis are highlighted in Tables 4 & 5, which includes breakup of cost components of individual players and optimal integral value of decision variables (\(m_{i} ,n_{i} ,l_{i} ,z_{i}\)) and replenisment lot size (\(Q_{i} ,Q_{ri}\)) for the minimum joint cost of the system (MJTC) corresponding to each parameter \(P,P_{r} ,r\).

Table 4 Results of sensitivity analysis along with cost break-up of each player corresponding to different values of r and P
Full size table
Table 5 Selected detailed results of sensitivity analysis along with cost break up for each players corresponding to different values of r and Pr
Full size table

The detailed analysis is elucidated in the subsequent subsections.

Impact of manufacturer's Production rate (P)

The variation in JTC of the system corresponding to manufacturer's production rate (\(P\)) for different rates of fraction of demand returned (\(r\)) [\(r\) = 0.325, 0.625, 0.925] is graphically represented in the Fig. 4.

From Fig. 4 & Table 4, it is evident that for a constant value of \(r\), MJTC of the production inventory system first increases with increase in manufacturer's production rate (\(P\)) upto a certain point and then it decreases with the increase in value of \(P\). The inflection point from where the variation pattern of JTC changes, shifts towards the lower end values of \(P\) with the increase in value of \(r\). The possible explanation for this trend is the increase in manufacturer's holding cost of inventory of finished product and cost per production setup with increase in \(P\) due to increase in lot size \(Q_{i}\), which initially accounts majorly for the JTC of the system. However, gradually beyond a certain value of \(P\), the holding cost of inventory of the finished product & raw material for the manufacturer as well as the cost per order of the raw material for the manufacturer decreases due to reduced length of production cycle of the system. The total cost per unit time related to the retailer and supplier remains almost constant with increase in \(P\). Also, with increase in \(P\), the remanufacturer handles a certain fraction of customer's demand with a corresponding lower cost per unit time than the manufacturer which leads to a net decrease in the MJTC of the system.

Also, it is observed from Fig. 4 & Table 4 that corresponding to a fixed production rate (P) as the value of fraction of demand returned (\(r\)) increases, the MJTC of the system decreases. This is largely due to the trend observed that with the increase in \(r\), the lot size \(Q_{i}\) decreases and the total cost per unit time related to the manufacturer decreases. However, the total cost per unit time related to the remanufacturer, retailer and supplier decreases significantly thus leading to a net decrease in MJTC of the system.

Impact of remanufacturer's Production rate (\(P_{r}\))

The variation in \(JTC\) with respect to remanufacturer's production rate (\(P_{r}\)) for different rates of fraction of demand returned [\(r = 0.325,r = 0.625,r = 0.925\)] is depicted in the Fig. 5. The MJTC of the production inventory system increases with increase in remnuafacturer's production rate \(P_{r}\), as the due to a higher production rate, the induction point of the remanufacturing process shifts towards the first point of delivery of the remanufactured product to the retailer which leads to accumulation of returned product for the remanufacturer for a relatively long period in each production cycle. This leads to increased holding cost of the inventory of returned products for the remanufacturer. Also, when the number of shipments is more than 1, the remanufactured product inventory has to be kept for a relatively longer time until the point of delivery to the retailer,which leads to increased holding cost of inventory of the remanufactured product for the remanufacturer. The total cost per unit time associated with the manufacturer and supplier also increases with increase in \(P_{r}\). In contrast, the change in total cost per unit time for the retailer remains almost constant. Hence, the net effect is increase in MJTC with increase in \(P_{r}\).

From Fig. 5 & Table 5, it is also observed that the JTC of the system (JTC) decreases with the increase in value of (\(r\)) for a fixed production rate \(P_{r}\) of the remanufacturer. Due to the increase in fraction of demand returned \(r\), the total cost per unit time associated with the remanufacturer increases. However, there is a significant decrease in the value of total cost per unit time related to retailer, supplier and manufacturer corresponding to decrease in (\(r\)) leading to a net decrease in MJTC of the system.

Impact of fraction of demand returns (\(r\))

The variation pattern of JTC of the system with fraction of demand returned (\(r\)) is depicted in the Fig. 6. The obsrved trend is that MJTC of the system decreases with increase in '\(r\)'.The value of MJTC is lowest when the value of '\(r\)' is equal to 1 and it is highest when the value of '\(r\)' is closer to zero. The significance of '\(r\)' value is related to the prevalence of remanufacturing operation in a production cycle. As a remanufactured product from returned product is cheaper than a manufactured product from raw material, it is always preferable to have a higher fraction of demand return (\(r\)).

Conclusion and future scope

In this paper, the production- inventory problem for a multi-echelon CLSC model consisting of players such as manufacturer, remanufacturer, retailer and supplier is formulated in terms of JTC of the system, which is to be minimized. The average inventory of the players is calculated using principles of geometry from the graph that depict their inventory variation pattern. The cost components of each player are calculated by inculcating costs related to ordering, production setup and holding of inventory. The summation of cost components for respective players per unit time comprises the objective function i.e. JTC. The objective function optimization is carried out analytically using method of differentiation and simultaneous equations are solved to give the optimal value of the independent decision variables. For deriving the minimum JTC of the system, an algorithm is devised using inequalities about integral decision variables. A sample calculation is carried out as per the devised algorithm to illustrate the iterative method used to calculate the minimum JTC of the system (MJTC).

Also, Sensitivity analysis is carried out in order to ascertain the impact of key control parameters on the JTC of the system. The graphs of \(JTC\) vs \(P,P_{r} \& r\) give an insight into the variation pattern of JTC with change in values of those parameters. Also, the individual cost components of the players involved are calculated for these key parameters keeping all other parameters constant to evaluate the variation pattern in JTC.

Results of sensitivity analysis illustrate that the JTC of the system is lowest when the value of demand return fraction is higher and the production rates are lower. Also, for higher values of transformation factor of raw material to finished product (f) and transformation factor of the returned product to remanufactured product (\(\alpha )\), the value of JTC is lowest. In the case of graph of \(JTC\) vs \(P\), the inflection point from where JTC starts decreasing shifts towards the left (i.e. lower production rate \(P\)) with increase in \(r\). It is inferred that the holding cost of inventory of raw material and finished product for the manufacturer decreases with increase in value of \(r\) for a constant value of \(P\). Similarly, in case of graph of \(JTC\) vs \(P_{r}\), the remanufacturer's holding cost of inventory of returned product and remanufactured product increases with increase in \(r\) leading to rise in value of JTC with increment in value of \(P_{r}\).This model can help the industries engaged in a centralised decision making roles regarding optimal inventory policy to simulate and adjudge the optimal parameters at which they should carry out their production or manage their supply chain to ensure minimum cost.

In this research work, a mathematical model is formulated considering constant demand and return rates in multi-echelon CLSC batch environment. However, in practice the demand may be dynamic and random due to the role of invisible forces of demand and supply in a market economy. Hence, a future research direction can be the formulation of a stochastic model that assumes a random demand with Standard or Poisson distribution.

Also, the delivery of finished products and remanufactured products is considered to be instantaneous in this model. In contrast, one can incorporate lead time and study the effect on the JTC of the system. The deterioration of inventory stacked at the various echelons can occur in practical scenarios. Hence, the effect of deteriorating inventory on the JTC of the system also needs to be examined.

The assumption of equal-sized shipments proposed by the manufacturer and remanufacturer to the retailer is impractical in certain scenarios. The unequal-sized shipments may lead to lower total cost for a particular set of parameters. Therefore, relaxing the equal lot-sized shipments may be another future direction for research. The incorporation of multiple retailers at the lower most echelon would help make the model a realistic one as in practice, the supply chain involves multiple players at various echelons coordinating with each other to ensure smooth flow of product and information.