Optimal production-inventory policy for closed-loop supply chain with remanufacturing under random demand and return

Abstract

This paper presents a centralized production-inventory model for an infinite planning horizon of a two-echelon closed-loop supply chain (CLSC) consisting a retailer, manufacturer, and remanufacturer. The demand at the retailer is satisfied through the new and remanufactured products received from the manufacturer and remanufacturer, respectively. The proposed model considers demand at the retailer and return at the remanufacturer as random. The manufacturer and remanufacturer produce the products at a finite rate, and they deliver to the retailer alternatively in multiple batches. An algorithm is developed to find the optimal-lot sizing and shipment policies of each entity of the CLSC by minimizing the expected joint total cost of the system. The results show that the CLSC is more profitable than the forward supply chain when the remanufacturing cost of the returned product is significantly low compared to the manufacturing cost of the new product, the demand variation at the retailer is low, and the fraction of demand returned is close to 1.

1 Introduction

In order to protect the environment and meet the regulatory requirements, remanufacturing is receiving attention among manufacturers. This helps to recover the residual value of used products and realize cost benefits. Contemporary researchers have investigated single or two-stage production-inventory problems in forward supply chain (FSC). However, the recent contributions by Teng et al. (2011), Jaber et al. (2014) and Mawandiya et al. (2017) have also incorporated remanufacturing under deterministic environment. In this paper, we relax this assumption and develop a production-inventory model under random demand and return rate for a closed-loop supply chain (CLSC).

Remanufacturing establishes the foundation for CLSC. According to Guide and Van Wassenhove (2009), CLSC is defined as “the design, control, and operation of a system to maximize value creation over the entire life cycle of a product with dynamic recovery of value from different types and volumes of returns over time”. The concept of CLSC is widely practiced by leading organizations such as Kodak (Savaskan and Van Wassenhove 2006), Hewlett Packard (Jorjani et al. 2004; Shi et al. 2011), Caterpillar, Xerox (Atasu et al. 2008), automotive industries (Guide et al. 2003). In the US more than 73,000 firms participate in CLSC and are engaged in some form of remanufacturing (Lund 1996).

The primary motivation of this research is set through the gaps in the present body of literature in the domain of two-echelon CLSC, specifically the growing concerns of industry and government for recycling of various products such as battery, photocopier, television, and others at the end of their useful lives. The issue of remanufacturing has gained prominence in the developing countries like India only in the recent past. The shrinking life cycle of products, because of change in customer preferences, technological advancements, promotional schemes for product exchange, etc., has created a huge opportunities for reuse, remanufacturing, cannibalization, and refurbishing of returned products. Remanufacturing not only helps to address environmental concerns but also reduces the cost of final product. As a remanufactured or refurbished component is invisible to customers, it exhibits the same value to them as the new component. This helps manufacturers to capture a bigger market share through price competitiveness.

Schrady (1967) was the first to work on CLSC, where he developed a deterministic model to find the EOQ for a repairable inventory system considering one procurement batch and at least one repairable batch in each production cycle assuming instant recovery. This work has been extended by Nahmias and Rivera (1979) for the case of finite repair rate and limited storage capacity. Mabini et al. (1992) also extended the work of Schrady (1967) for multiple products considering common repairing facility. Teunter (2001) considered different holding costs for manufactured and recovered products and allowed the partial disposal of returned product to generalize the work of Schrady (1967). Koh et al. (2002) permitted recovery rate to be both higher and lower than the demand rate of serviceable product for generalizing the work of Teunter (2001). Teunter (2004) extended the work of Koh et al. (2002) and derived a square root formula for optimal lot-sizing of production and recovery batches, and proposed an approximation method to obtain an integer value of the number of setups for production and recovery batches. Richter (1996a) developed an EOQ-based production, repairing and waste disposal model, and considered a fixed fraction of the returned material to be used for recovery purpose, but later Richter (1996b, 1997) and Richter and Dobos (1999) considered fraction of the returned material also as a decision variable. The extension of these models has been reported by Dobos and Richter (2004, 2006). Subsequently, attempts have been made to develop variants of EOQ/EPQ models considering product returns under different assumptions such as complete backorder (Konstantaras and Skouri 2010), partial backorder (Hasanov et al. 2012), lost sales (Jaber and El Saadany 2009), switching cost (El Saadany and Jaber 2008), different product quality of recovered and new products (Jaber and El Saadany 2009; Konstantaras et al. 2010; Hasanov et al. 2012), variable return rate of used product (El Saadany and Jaber 2010), effect of learning in manufacturing and remanufacturing processes (Jaber and El Saadany 2011; Tsai 2012), different batch sizes for remanufacturing (Schulz and Voigt 2014). A growing literature on modelling of production-inventory problems with product return justifies the importance of this area.

Lee (2005) highlighted that a centralized controlled production-inventory model provides better results for a forward supply chain, but such studies are limited for two-echelon CLSC in literature. The select contributions in the domain of two-echelon CLSC are noteworthy. Mitra (2009) developed the continuous review inventory models (deterministic and stochastic) for a depot with recovery facility at the upper echelon and a distributor at the lower echelon. In the stochastic model, the author considered demand and return rate normally distributed with full backordering at the distributor. Later, Mitra (2012) developed a periodic review inventory model for correlated demand and return rate. Teng et al. (2011) extended the deterministic model of Mitra (2009) to optimize the partial backordering along with product returns and excess stocks. Lin (2015) extended Teng et al.’s (2011) deterministic model to consider stochastic demand and return rates with partial backorder. Tai and Ching (2014) proposed a two-echelon system consisting a supply plant of infinite capacity, a central warehouse for storing the new and returned products and multiple local warehouses capable of remanufacturing the new product. Priyan and Uthayakumar (2015) proposed a two-echelon CLSC in a warehouse and a distributer for multiple products with additional constraints related to floor space, budget, permissible delay in payment, and variable lead time. Jaber et al. (2014) studied a vendor–buyer system with remanufacturing and consignment stock policy. Hariga et al. (2017) also addressed the consignment stock strategy for a single vendor–buyer system and developed a model for minimizing the total cost to determine the production cycle length, number and the sequence of manufacturing and remanufacturing batches. Mawandiya et al. (2016, 2017) extended the work of Lee (2005) and developed production-inventory models in a two-echelon CLSC by incorporating remanufacturer for satisfying customer demand by remanufactured product in addition to the new manufactured product. Maiti and Giri (2017) proposed a two-echelon CLSC model considering two ways collection of used product through the retailer such as (1) a fraction of the new product sold through the forward supply chain and (2) the exchange of used product with new one under exchange offers.

The summary of the contemporary literature in the field of CLSC production-inventory models for an infinite planning horizon is presented in Table 1. From Table 1, it can be observed that under random demand and return rate, none of the researchers has considered a finite rate for both production and remanufacturing of new and remanufactured products, respectively. Jaber et al. (2014) and Mawandiya et al. (2017) have considered finite production rate at the manufacturer as well as the remanufacturer, but they developed models under constant demand and return rate. On the other hand, Mitra (2009, 2012), Priyan and Uthayakumar (2015), and Lin (2015) developed models with random demand and return rate considering instantaneous replenishments of products from outside suppliers. The proposed model extends the work of Mawandiya et al. (2017) for the random demand and return rates considering collection of returned product during a current remanufacturing cycle, and recovery of the accumulated returned product in the next remanufacturing cycle. Due to consideration of uncertainty in demand and return, shortages are inevitable at the retailer and remanufacturer both. In this study, the model is developed assuming full backordering at the retailer and remanufacturer. The full backordering is justified when the unit cost is high, lead times from suppliers are reasonably short, there is limited competition, and customers are prepared to wait (Waters 2003).

Table 1 Summary of the literature on multi-echelon CLSC production-inventory models for an infinite planning horizon

The major contribution of this research can be summarized as follows. This research analyses a production-inventory problem in a two-echelon CLSC under random demand and return. According to Mitra (2009), return of used product is more uncertain than the demand of new (serviceable) product in terms of quantity, quality and timing, which makes the modelling of CLSC problems more complex. The model is developed considering finite production and remanufacturing rates with full backordering at the manufacturer and remanufacturer, which pose significant challenge to synchronize the ordering of the retailer with the production cycle of the manufacturer and remanufacturing cycle of the remanufacturer. Due to uncertainty associated with the quantity of returned product, it becomes interesting to conceptualize the derivation of the expected shortage of the returned product at the remanufacturer. In addition, a detailed comparison between the FSC and CLSC is provided with numerical illustrations to delineate the behaviour of the expected joint total cost (EJTC). The findings of this research demonstrate that the proposed integrated centralized decision making for the two-echelon CLSC can be substantially beneficial under low demand variability when the fraction of product return is close to 1.

The rest of this paper is organised as follows. Section 2 describes the problem and lists the notation and assumptions used for developing the mathematical model. Sections 3 and 4 present the model formulation and solution procedure, respectively. The numerical illustration and sensitivity analysis for the key parameters are provided in Sects. 5 and 6, respectively. A comparison between the CLSC and the corresponding forward supply chain is provided in Sect. 7. Finally, Sect. 8 concludes the paper and highlights the direction for future research.

2 Problem description

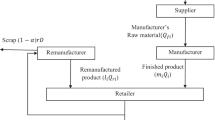
We consider a two-echelon CLSC consisting three entities: a retailer, a manufacturer and a remanufacturer. The manufacturer and remanufacturer are considered at echelon-2 and the retailer at echelon-1 as shown in Fig. 1.

Fig. 1

The CLSC system

The retailer faces a random demand from customers, which is satisfied using the new and remanufactured products received in multiple batches alternatively from the manufacturer and remanufacturer. The remanufacturer receives a fraction of the demand as a returned product continuously from customers, and the return rate to be random and independent of the demand. The remanufacturer accumulates the returned product during the current remanufacturing cycle (T), and then the remanufacturing process is inducted for recovery of the accumulated returned product in the next remanufacturing cycle. The production and remanufacturing lot sizes of the manufacturer and remanufacturer are integer multiples of the retailer’s order quantity for the new and remanufactured products, respectively. The aforementioned setup is presented in Fig. 2 which has been described in more detail in Sect. 3.

Fig. 2

Inventory variation pattern at the manufacturer, remanufacturer and retailer

The cost of remanufacturing of the returned product is assumed lower than the cost of producing the new product. Therefore, the demand at the retailer is satisfied first using the remanufactured product and the remaining demand using the new product. The other assumptions made to develop the mathematical model is listed in Table 2, and Table 3 presents the list of notation to describe the related parameters and decision variables of the problem.

Table 2 List of assumptions

Table 3 List of notation

3 The model

The demand and return rates are considered random, uniform, stationary and independent of each other over an infinite planning horizon. It is assumed that the product is a fast moving item. Therefore, it is reasonable to consider the demand per unit time at the retailer normally distributed with mean μ and variance σ². Likewise, the fraction of demand returned per unit time also follows the normal distribution with mean rμ and variance rσ² (Mitra 2009).

Figure 2 shows the inventory variation pattern at the manufacturer, remanufacturer and retailer. It can be observed from Fig. 2 that the manufacturer and remanufacturer have the same average cycle length (T). During each cycle time T, the retailer receives the new product in m consecutive lots each of size Q from the manufacturer, and then receives the remanufactured product in l consecutive lots each of size Q_r from the remanufacturer (sub-graph B of Fig. 2). The retailer has two different reorder points R_m and R_l for placing the orders to the manufacturer and remanufacturer, respectively. The retailer places an order of quantity Q to the manufacturer when the inventory level reaches the reorder point R_m for the replenishment of the new product in m consecutive lots. Similarly, the retailer places an order of quantity Q_r to the remanufacturer when the inventory level reaches the reorder point R_l for the replenishment of the remanufactured product in l consecutive lots. The procurement lead time of the new and remanufactured products from the manufacturer and remanufacturer are L_m and L_l, respectively. Therefore, the policy variables for the retailer are the reorder points (R_m, R_l) and the order quantities (Q, Q_r). The dotted lines in sub-graph B of Fig. 2 represent the accumulated inventory of the new and remanufactured products if the retailer has not satisfied the demand of customers, and the bold continuous lines represent the actual inventory status of the new and remanufactured products at the retailer after satisfying the demand of customers.

In each production cycle of the manufacturer (sub-graph A of Fig. 2), the new product is produced in a batch of size mQ with production rate P and is supplied to the retailer in m shipments each of size Q. Just after the start of production, the first lot of size Q is produced in time Q/P and immediately shipped to the retailer, and the remaining (m − 1) lots are shipped to the retailer at the interval of time Q/μ in which the previously shipped lot is expected to be consumed at the retailer. Thus, the policy variable for the manufacturer is production batch size mQ. Here, the dotted line represents the accumulated inventory of the new product at the manufacturer if the new product is not supplied to the retailer.

In each remanufacturing cycle, the remanufacturer collects, on average, μrT units of the returned product, which are used for remanufacturing in the next cycle. Also, in each remanufacturing cycle (sub-graph C of Fig. 2), the product is remanufactured in a batch of size lQ_r with remanufacturing rate P_r using R_r (= lQ_r/α) quantity of the returned product, and the remanufactured product is supplied to the retailer in l shipments each of size Q_r. Just after the start of remanufacturing process, the first lot of size Q_r is remanufactured in time Q_r/P_r and immediately shipped to the retailer, and the remaining (l − 1) lots are shipped to the retailer at the interval of time Q_r/μ in which the previously shipped lot is expected to be consumed at the retailer. Therefore, the policy variables for the remanufacturer are the induction point for remanufacturing (S_r+ R_r) and the remanufacturing batch quantity (lQ_r).

The cost components of the system are ordering/setup cost and inventory holding cost for the manufacturer, retailer and remanufacturer along with the backorder cost for the retailer and remanufacturer. The objective is to minimize the expected joint total cost per unit time of the CLSC system and find the policy variables of all entities of the CLSC. Therefore, the cost components of each entity of the system are discussed and derived subsequently.

3.1 The expected total cost of the retailer

The expected total cost per unit time of the retailer consists of ordering, inventory holding and backordering costs. The retailer receives m consecutive shipments during each production cycle of the manufacturer, and then l consecutive shipments during each remanufacturing cycle of the remanufacturer. The replenishment cycle length of the retailer is different for ordering from the manufacturer and the remanufacturer, therefore all cost components per unit time of the retailer are derived based on the cycle time T. Since the ordering cost per replenishment cycle of the retailer from the manufacturer and remanufacturer are A₁ and A₄, respectively, the expected ordering cost per unit time of the retailer is (mA₁ + lA₄)/T.

The average inventory (refer sub-graph B of Fig. 2) per replenishment cycle at the retailer is ${Q \mathord{\left/ {\vphantom {Q 2}} \right. \kern-0pt} 2} + S_{m}$ during the replenishment from the manufacturer and is ${{Q_{r} } \mathord{\left/ {\vphantom {{Q_{r} } 2}} \right. \kern-0pt} 2} + S_{l}$ when the replenishment takes place from the remanufacturer. Therefore, assuming a linear decrease in inventory of the new (remanufactured) product, the expression for the average inventory at the retailer based on cycle time T can be derived as ${{[ {m( {{Q \mathord{/ {\vphantom {Q 2}} \kern-0pt} 2} + S_{m} } ){Q \mathord{/ {\vphantom {Q \mu }} \kern-0pt} \mu } + l( {{{Q_{r} } \mathord{/ {\vphantom {{Q_{r} } 2}} \kern-0pt} 2} + S_{l} } ){{Q_{r} } \mathord{/ {\vphantom {{Q_{r} } \mu }} \kern-0pt} \mu }} ]} \mathord{/ {\vphantom {{[ {m( {{Q \mathord{/ {\vphantom {Q 2}} \kern-0pt} 2} + S_{m} } ){Q \mathord{/ {\vphantom {Q \mu }} \kern-0pt} \mu } + l( {{{Q_{r} } \mathord{/ {\vphantom {{Q_{r} } 2}} \kern-0pt} 2} + S_{l} } ){{Q_{r} } \mathord{/ {\vphantom {{Q_{r} } \mu }} \kern-0pt} \mu }} ]} T}} \kern-0pt} T}$. After substituting $S_{m} = k_{m} \sigma \sqrt {L_{m} }$ and $S_{l} = k_{l} \sigma \sqrt {L_{l} }$, the expected inventory holding cost per unit time of the retailer can be written as ${{ [ {m ( {{Q \mathord{ / {\vphantom {Q 2}} \kern-0pt} 2} + k_{m} \sigma \sqrt {L_{m} } } ){Q \mathord{ / {\vphantom {Q \mu }} \kern-0pt} \mu } + l ( {{{Q_{r} } \mathord{ / {\vphantom {{Q_{r} } 2}} \kern-0pt} 2} + k_{l} \sigma \sqrt {L_{l} } } ){{Q_{r} } \mathord{ / {\vphantom {{Q_{r} } \mu }} \kern-0pt} \mu }} ]h_{1} } \mathord{ / {\vphantom {{ [ {m ( {{Q \mathord{ / {\vphantom {Q 2}} \kern-0pt} 2} + k_{m} \sigma \sqrt {L_{m} } } ){Q \mathord{ / {\vphantom {Q \mu }} \kern-0pt} \mu } + l ( {{{Q_{r} } \mathord{ / {\vphantom {{Q_{r} } 2}} \kern-0pt} 2} + k_{l} \sigma \sqrt {L_{l} } } ){{Q_{r} } \mathord{ / {\vphantom {{Q_{r} } \mu }} \kern-0pt} \mu }} ]h_{1} } T}} \kern-0pt} T}$.

The expected shortage per replenishment cycle at the retailer during the replenishment from the manufacturer can be expressed as $B\left( {R_{m} } \right) = \int\limits_{{R_{m} }}^{\infty } {\left( {x_{m} - R_{m} } \right)f\left( {x_{m} } \right)dx_{m} }$. Since the demand x_m during the lead time L_m follows the normal distribution, i.e. $x_{m} \,\sim\,N(\mu L_{m} ,\sigma^{2} L_{m} ),$B(R_m) can be derived (Ravindran et al. 2010, p. 363) as

$$B\left( {R_{m} } \right) = \sigma \sqrt {L_{m} } \left[ {\phi \left( {k_{m} } \right) - k_{m} + k_{m} \Phi \left( {k_{m} } \right)} \right],$$

(1)

where $\phi ( \cdot )$ and $\Phi ( \cdot )$ are the pdf and cdf of the standard normal distribution, respectively. Similarly, the expected shortage per replenishment cycle at the retailer during the replenishments from the remanufacturer can be derived as

$$B\left( {R_{l} } \right) = \sigma \sqrt {L_{l} } \left[ {\phi \left( {k_{l} } \right) - k_{l} + k_{l} \Phi \left( {k_{l} } \right)} \right].$$

(2)

Therefore, the backorder cost per unit time of the retailer can be obtained as

$$\frac{{\left[ {m\sigma \sqrt {L_{m} } \left( {\phi \left( {k_{m} } \right) - k_{m} + k_{m} \Phi \left( {k_{m} } \right)} \right) + l\sigma \sqrt {L_{l} } \left( {\phi \left( {k_{l} } \right) - k_{l} + k_{l} \Phi \left( {k_{l} } \right)} \right)} \right]\pi }}{T}.$$

(3)

3.2 The expected total cost of the manufacturer

The expected total cost of the manufacturer consists of production setup and inventory holding costs of the new product. As the production cycle length of the manufacturer is T, the production setup cost per unit time of the manufacturer is given by A₂/T.

From sub-graph A of Fig. 2, it can be seen that the manufacturer’s average inventory is obtained by taking the difference of accumulated inventory at the manufacturer and accumulated inventory at the retailer due to the supply from the manufacturer per unit time. Hence, the expression for the manufacturer’s average inventory can be derived as

$$\frac{1}{T}\left\{ {mQ\left[ {\frac{Q}{P} + \frac{{\left( {m - 1} \right)Q}}{\mu }} \right] - \frac{{m^{2} Q^{2} }}{2P} - \frac{{m\left( {m - 1} \right)Q^{2} }}{2\mu }} \right\}.$$

On simplification, the average inventory holding cost per unit time of the manufacturer can be obtained as ${{\{ {\frac{mQ}{\mu } [ { ( {m - 1} ) - ( {m - 2} )\frac{\mu }{P}} ]\frac{Q}{2}h_{2} } \}} \mathord{ / {\vphantom {{ \{ {\frac{mQ}{\mu } [ { ( {m - 1} ) - ( {m - 2} )\frac{\mu }{P}} ]\frac{Q}{2}h_{2} } \}} T}} \kern-0pt} T}$.

3.3 The expected total cost of the remanufacturer

The total expected cost of the remanufacturer includes the costs of remanufacturing setup, inventory holding of the remanufactured and returned products and the backorder. Since the length of remanufacturing cycle is T, the setup cost per unit time of the remanufacturer is obtained as A₃/T.

The expression for the average inventory holding cost per unit time of the remanufactured product can be derived similar to the derivation of the manufacturer’s inventory holding cost, and is obtained as ${{\{ {\frac{{lQ_{r} }}{\mu } [ { ( {l - 1} ) - ( {l - 2} )\frac{\mu }{{P_{r} }}} ]\frac{{Q_{r} }}{2}h_{4} } \}} \mathord{ / {\vphantom {{ \{ {\frac{{lQ_{r} }}{\mu } [ { ( {l - 1} ) - ( {l - 2} )\frac{\mu }{{P_{r} }}} ]\frac{{Q_{r} }}{2}h_{4} } \}} T}} \kern-0pt} T}$ (sub-graph C of Fig. 2).

During each remanufacturing cycle, the remanufacturer collects the returned product for time T, which is used for remanufacturing in the next remanufacturing cycle. The remanufacturer requires lQ_r/α (= R_r) quantity of the returned product to remanufacture lQ_r quantity of the product in each remanufacturing cycle. The quantity x_r of the returned product during remanufacturing cycle time T is random and assumed to be normal distribution, i.e. x_r ~ N(μrT, σ²rT). Therefore, the remanufacturer may not have lQ_r/α quantity of the accumulated returned product to induct the remanufacturing process. This leads to the requirement of the safety stock S_r of the returned product for providing a cushion against uncertainty in return. The expected level of inventory of the returned product at the start (induction point) of the remanufacturing process will be S_r + R_r, and this will decline at the rate P_r and drops to the level S_r after producing lQ_r quantity of the remanufactured product in time lQ_r/P_r. At the same time, the remanufacturer continues to collect the returned product which is to be used in the next remanufacturing cycle. Therefore, assuming a linear increase in inventory of the returned product during a remanufacturing cycle, the average inventory of the returned product during each remanufacturing cycle time T can be derived as ${{[ {S_{r} T + {{R_{r} T} \mathord{ / {\vphantom {{R_{r} T} 2}} \kern-0pt} 2} + R_{r} {{lQ_{r} } \mathord{ / {\vphantom {{lQ_{r} } { ( {2P_{r} } )}}} \kern-0pt} { ( {2P_{r} } )}}} ]} \mathord{ / {\vphantom {{ [ {S_{r} T + {{R_{r} T} \mathord{ / {\vphantom {{R_{r} T} 2}} \kern-0pt} 2} + R_{r} {{lQ_{r} } \mathord{ / {\vphantom {{lQ_{r} } { ( {2P_{r} } )}}} \kern-0pt} { ( {2P_{r} } )}}} ]} T}} \kern-0pt} T}$ (refer sub-graph C of Fig. 2), which is equivalent to ${{ [ {S_{r} T + {{R_{r} T} \mathord{ / {\vphantom {{R_{r} T} 2}} \kern-0pt} 2} + {{\alpha R_{r}^{2} } \mathord{ / {\vphantom {{\alpha R_{r}^{2} } { ( {2P_{r} } )}}} \kern-0pt} { ( {2P_{r} } )}}} ]} \mathord{ / {\vphantom {{ [ {S_{r} T + {{R_{r} T} \mathord{ / {\vphantom {{R_{r} T} 2}} \kern-0pt} 2} + {{\alpha R_{r}^{2} } \mathord{ / {\vphantom {{\alpha R_{r}^{2} } { ( {2P_{r} } )}}} \kern-0pt} { ( {2P_{r} } )}}} ]} T}} \kern-0pt} T}$ as $R_{r} = {{lQ_{r} } \mathord{\left/ {\vphantom {{lQ_{r} } \alpha }} \right. \kern-0pt} \alpha }$.

Now, the expression for the safety stock S_r can be given by

$$\begin{aligned} & S_{r} = \int\limits_{0}^{\infty } {\left( {x_{r} - R_{r} } \right)f\left( {x_{r} } \right)dx_{r} } = \int\limits_{0}^{\infty } {x_{r} f\left( {x_{r} } \right)dx_{r} } - R_{r} \int\limits_{0}^{\infty } {f\left( {x_{r} } \right)dx_{r} } ,\quad {\text{that}}\;{\text{is}} \\ & S_{r} = \mu rT - R_{r} . \\ \end{aligned}$$

As $S_{r} = k_{r} \sigma \sqrt {rT}$, therefore

$$R_{r} = \mu rT - k_{r} \sigma \sqrt {rT} .$$

(4)

The above equation can also be written as

$$k_{r} = {{\left( {\mu rT - R_{r} } \right)} \mathord{\left/ {\vphantom {{\left( {\mu rT - R_{r} } \right)} {\sigma \sqrt {rT} }}} \right. \kern-0pt} {\sigma \sqrt {rT} }}.$$

(5)

Using the above relationships $S_{r} = k_{r} \sigma \sqrt {rT}$ and $R_{r} = \mu rT - k_{r} \sigma \sqrt {rT}$, the average inventory of the returned product can be expressed as $\frac{1}{2T} [ { ( {\mu rT + k_{r} \sigma \sqrt {rT} } )T + {{\alpha ( {\mu rT - k_{r} \sigma \sqrt {rT} } )^{2} } \mathord{ / {\vphantom {{\alpha ( {\mu rT - k_{r} \sigma \sqrt {rT} } )^{2} } {P_{r} }}} \kern-0pt} {P_{r} }}} ]$ and the corresponding inventory holding cost per unit time of the returned product can be obtained as $\frac{1}{2T}[ { ( {\mu rT + k_{r} \sigma \sqrt {rT} } )T + {{\alpha ( {\mu rT - k_{r} \sigma \sqrt {rT} } )^{2} } \mathord{ / {\vphantom {{\alpha ( {\mu rT - k_{r} \sigma \sqrt {rT} } )^{2} } {P_{r} }}} \kern-0pt} {P_{r} }}} ]h_{3} .$

When the quantity of the returned product received at the remanufacturer during the previous remanufacturing cycle is less than R_r − S_r, then lQ_r quantity of the remanufactured product cannot be remanufactured in the current cycle even utilizing the entire safety stock S_r. This results in a short supply of the remanufactured product to the retailer. The expected shortage of the returned product per remanufacturing cycle at the remanufacturer can be expressed as

$$B\left( {R_{r} } \right) = \int\limits_{0}^{{R_{r} - S_{r} }} {\left( {R_{r} - S_{r} - x_{r} } \right)f\left( {x_{r} } \right)dx_{r} } .$$

(6)

On solving Eq. (6), we get (see Appendix 1)

$$B\left( {R_{r} } \right) = \sigma \sqrt {rT} \left[ {\phi \left( {z_{r} } \right) - z_{r} + z_{r} \Phi \left( {z_{r} } \right)} \right],\quad {\text{where}}\;z_{r} = 2k_{r}$$

(7)

Thus, the expected shortage of the remanufactured product per remanufacturing cycle at the remanufacturer is αB(R_r). Then, the remanufacturer’s expected backorder cost per unit time is obtained as ${{( {\alpha \sigma \sqrt {rT} [ {\phi ( {z_{r} } ) - z_{r} + z_{r} \Phi ( {z_{r} } )} ]\pi_{r} } )} \mathord{ / {\vphantom {{ ( {\alpha \sigma \sqrt {rT} [ {\phi ( {z_{r} } ) - z_{r} + z_{r} \Phi ( {z_{r} } )} ]\pi_{r} } )} T}} \kern-0pt} T}$.

3.4 The expected joint total cost of the CLSC system

The expected joint total cost per unit time of the system under consideration is the sum of the total expected costs of the retailer, manufacturer and remanufacturer. Accordingly, the expected joint total cost per unit time of the system can be obtained as follows.

$${\text{The}}\;{\text{expected}}\;{\text{joint}}\;{\text{total}}\;{\text{cost}}\;{\text{per}}\;{\text{unit}}\;{\text{time}} = \frac{1}{T}\left\{ \begin{array}{l} \left( {mA_{1} + A_{2} + A_{3} + lA_{4} } \right) + \left[ {m\left( {{Q \mathord{\left/ {\vphantom {Q 2}} \right. \kern-0pt} 2} + k_{m} \sigma \sqrt {L_{m} } } \right){Q \mathord{\left/ {\vphantom {Q \mu }} \right. \kern-0pt} \mu } + l\left( {{{Q_{r} } \mathord{\left/ {\vphantom {{Q_{r} } 2}} \right. \kern-0pt} 2} + k_{l} \sigma \sqrt {L_{l} } } \right){{Q_{r} } \mathord{\left/ {\vphantom {{Q_{r} } \mu }} \right. \kern-0pt} \mu }} \right]h_{1} \hfill \\ \quad + \frac{mQ}{\mu }\left( {\left( {m - 1} \right) - \left( {m - 2} \right)\frac{\mu }{P}} \right)\frac{Q}{2}h_{2} \hfill \\ \quad + \frac{{h_{3} }}{2}\left[ {\left( {\mu rT + k_{r} \sigma \sqrt {rT} } \right)T + {{\alpha \left( {\mu rT - k_{r} \sigma \sqrt {rT} } \right)^{2} } \mathord{\left/ {\vphantom {{\alpha \left( {\mu rT - k_{r} \sigma \sqrt {rT} } \right)^{2} } {P_{r} }}} \right. \kern-0pt} {P_{r} }}} \right] \hfill \\ \quad + \frac{{lQ_{r} }}{\mu }\left( {\left( {l - 1} \right) - \left( {l - 2} \right)\frac{\mu }{{P_{r} }}} \right)\frac{{Q_{r} }}{2}h_{4} \hfill \\ \quad + \left[ {m\sigma \sqrt {L_{m} } \left( {\phi \left( {k_{m} } \right) - k_{m} + k_{m} \Phi \left( {k_{m} } \right)} \right) + l\sigma \sqrt {L_{l} } \left( {\phi \left( {k_{l} } \right) - k_{l} + k_{l} \Phi \left( {k_{l} } \right)} \right)} \right]\pi \hfill \\ \quad + \alpha \sigma \sqrt {rT} \left[ {\phi \left( {z_{r} } \right) - z_{r} + z_{r} \Phi \left( {z_{r} } \right)} \right]\pi_{r} \hfill \\ \end{array} \right\}$$

(8)

As discussed in Sect. 3.3, $R_{r} = {{lQ_{r} } \mathord{\left/ {\vphantom {{lQ_{r} } \alpha }} \right. \kern-0pt} \alpha }$, therefore $Q_{r} = {{\alpha R_{r} } \mathord{\left/ {\vphantom {{\alpha R_{r} } l}} \right. \kern-0pt} l}$. Using $R_{r} = \mu rT - k_{r} \sigma \sqrt {rT}$ from Eq. (4), we get

$$Q_{r} = \frac{{\alpha r\mu T - {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}}}{l}.$$

(9)

The production cycle length of the manufacturer and the remanufacturing cycle length of the remanufacturer are same and is given by $T = {{\left( {mQ + lQ_{r} } \right)} \mathord{\left/ {\vphantom {{\left( {mQ + lQ_{r} } \right)} \mu }} \right. \kern-0pt} \mu }$ which implies that $Q = {{\left( {\mu T - lQ_{r} } \right)} \mathord{\left/ {\vphantom {{\left( {\mu T - lQ_{r} } \right)} m}} \right. \kern-0pt} m}$. Using Eq. (9), the expression for Q can be expressed as

$$Q = \frac{{\left( {1 - \alpha r} \right)\mu T + {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}}}{m}.$$

(10)

On putting the expressions for Q_r and Q from Eqs. (9) and (10), respectively, and using k_r = z_r/2 in Eq. (8), the expected joint total cost per unit time can be expressed as

$$EJTC\left( \begin{array}{l} k_{m} ,k_{l} , \hfill \\ z_{r} ,m, \hfill \\ l,T \hfill \\ \end{array} \right) = \frac{1}{T}\left\{ \begin{array}{l} \left( {mA_{1} + A_{2} + A_{3} + lA_{4} } \right) \hfill \\ \quad + \frac{{h_{1} }}{\mu }\left( {\frac{{\left( {1 - \alpha r} \right)\mu T + {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}}}{2m} + k_{m} \sigma \sqrt {L_{m} } } \right)\left( {\left( {1 - \alpha r} \right)\mu T + {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right) \hfill \\ \quad + \frac{{h_{1} }}{\mu }\left( {\frac{{\alpha r\mu T - {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}}}{2l} + k_{l} \sigma \sqrt {L_{l} } } \right)\left( {\alpha r\mu T - {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right) \hfill \\ \quad + \frac{{h_{2} }}{2m\mu }\left( {\left( {m - 1} \right) - \left( {m - 2} \right)\frac{\mu }{P}} \right)\left( {\left( {1 - \alpha r} \right)\mu T + {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right)^{2} \hfill \\ \quad + \frac{{h_{3} }}{2}\left[ {\left( {\mu rT + {{z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right)T + {{\alpha \left( {\mu rT - {{z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right)^{2} } \mathord{\left/ {\vphantom {{\alpha \left( {\mu rT - {{z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right)^{2} } {P_{r} }}} \right. \kern-0pt} {P_{r} }}} \right] \hfill \\ \quad + \frac{{h_{4} }}{2l\mu }\left( {\left( {l - 1} \right) - \left( {l - 2} \right)\frac{\mu }{{P_{r} }}} \right)\left( {\alpha r\mu T - {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right)^{2} \hfill \\ \quad + \left[ {m\sigma \sqrt {L_{m} } \left( {\phi \left( {k_{m} } \right) - k_{m} + k_{m} \Phi \left( {k_{m} } \right)} \right) + l\sigma \sqrt {L_{l} } \left( {\phi \left( {k_{l} } \right) - k_{l} + k_{l} \Phi \left( {k_{l} } \right)} \right)} \right]\pi \hfill \\ \quad + \alpha \sigma \sqrt {rT} \left[ {\phi \left( {z_{r} } \right) - z_{r} + z_{r} \Phi \left( {z_{r} } \right)} \right]\pi_{r} \hfill \\ \end{array} \right\}$$

(11)

It can be noted that if σ is set to zero in Eq. (11), then the resulting expressions for all cost components, except the holding cost of the returned product, are exactly the same as those respective cost components in Eq. (1) with $Q_{1} = {{\left( {1 - \alpha r} \right)\mu T} \mathord{\left/ {\vphantom {{\left( {1 - \alpha r} \right)\mu T} m}} \right. \kern-0pt} m}$ (in Eq. (3) with $Q_{2} = {{\left( {1 - \alpha r} \right)\mu T} \mathord{\left/ {\vphantom {{\left( {1 - \alpha r} \right)\mu T} m}} \right. \kern-0pt} m}$) of Mawandiya et al. (2017). The holding cost of the returned product is different because Mawandiya et al. (2017) considered the remanufacturing of the returned product during the same remanufacturing cycle.

4 Solution technique

The model is developed to minimize the EJTC in Eq. (11), which appears as a mixed integer non-linear programming problem with six decision variables k_m, k_l, z_r, m, l and T, in which m and l are positive integer. To solve the problem of this nature, we use calculus based partial derivative approach by temporarily relaxing the integer requirements on m and l. Therefore, we take the first and second partial derivatives of the EJTC in Eq. (11) with respect to each decision variable one by one while keeping other decision variables fixed, and these derivatives are presented in Appendix 2.

Since the second derivatives of EJTC(·) with respect to k_m, k_l, z_r, m and l are positive, EJTC(·) is convex in k_m for fixed k_l, z_r, m, l and T, convex in k_l for fixed k_m, z_r, m, l and T, convex in z_r for fixed k_m, k_l, m, l and T, convex in m for fixed k_m, k_l, z_r, l and T, and convex in l for fixed k_m, k_l, z_r, m, and T. However, EJTC (·) will be convex in T for fixed k_m, k_l, z_rm and l if the following condition derived from Eq. (39) holds true.

$$\left\{ \begin{array}{l} 3\alpha \sigma \sqrt {rT} \left[ {\frac{{h_{1} z_{r} \sigma }}{2\mu }\left( {k_{m} \sqrt {L_{m} } - k_{l} \sqrt {L_{l} } } \right) + \left( {\phi \left( {z_{r} } \right) - z_{r} + z_{r} \Phi \left( {z_{r} } \right)} \right)\pi_{r} } \right] \hfill \\ \quad - \frac{{Tz_{r} \alpha \sigma \sqrt {rT} }}{2}\left\{ \begin{array}{l} h_{1} \left( {\frac{{\left( {1 - \alpha r} \right)}}{m} - \frac{\alpha r}{l}} \right) + \left( {1 - \alpha r} \right)h_{2} \left[ {\left( {1 - \frac{\mu }{P}} \right) - \frac{1}{m}\left( {1 - \frac{2\mu }{P}} \right)} \right] + h_{3} \left( {\frac{1}{2\alpha } - \frac{r\mu }{{P_{r} }}} \right) \hfill \\ - \alpha rh_{4} \left[ {\left( {1 - \frac{\mu }{{P_{r} }}} \right) - \frac{1}{l}\left( {1 - \frac{2\mu }{{P_{r} }}} \right)} \right] \hfill \\ \end{array} \right\} \hfill \\ \quad + 8\left\{ {\left( {mA_{1} + A_{2} + A_{3} + lA_{4} } \right) + \left[ {m\sigma \sqrt {L_{m} } \left( {\phi \left( {k_{m} } \right) - k_{m} + k_{m} \Phi \left( {k_{m} } \right)} \right) + l\sigma \sqrt {L_{l} } \left( {\phi \left( {k_{l} } \right) - k_{l} + k_{l} \Phi \left( {k_{l} } \right)} \right)} \right]\pi } \right\} \hfill \\ \end{array} \right\} > 0.$$

(12)

As the number of decision variables is large, therefore it is difficult and complex to establish the convexity of the cost function in (11) with respect to all decision variables simultaneously. However, for all decision variables as continuous, the convexity of the cost function can be shown with respect to all decision variables simultaneously for a numerical value of parameters. Then, it can be inferred that the cost function in (11) will also be convex for integer values of m and l (please see Appendix 3). Now, assuming m and l as continuous, the optimal solution for the decision variables k_m, k_l, z_r, m, l and T are obtained as follows by setting Eqs. (28), (30), (32), (34), (36) and (38) to zero.

$$1 - \Phi \left( {k_{m} } \right) = \frac{{h_{1} }}{m\mu \pi }\left[ {\left( {1 - \alpha r} \right)\mu T + \frac{{\alpha z_{r} \sigma \sqrt {rT} }}{2}} \right],$$

(13)

$$1 - \Phi \left( {k_{l} } \right) = \frac{{h_{1} }}{l\mu \pi }\left[ {\alpha r\mu T - \frac{{\alpha z_{r} \sigma \sqrt {rT} }}{2}} \right],$$

(14)

$$1 - \Phi \left( {z_{r} } \right) = \left\{ \begin{array}{l} \frac{{z_{r} \alpha \sigma \sqrt {rT} }}{{4\mu \pi_{r} }}\left\{ {h_{1} \left( {\frac{1}{m} + \frac{1}{l}} \right) + \frac{{h_{2} }}{m}\left[ {m\left( {1 - \frac{\mu }{P}} \right) - \left( {1 - \frac{2\mu }{P}} \right)} \right] + \frac{{h_{3} \mu }}{{\alpha P_{r} }} + \frac{{h_{4} }}{l}\left[ {l\left( {1 - \frac{\mu }{{P_{r} }}} \right) - \left( {1 - \frac{2\mu }{{P_{r} }}} \right)} \right]} \right\} \hfill \\ \quad + \frac{T}{{2\pi_{r} }}\left\{ \begin{array}{l} h_{1} \left[ {\frac{{\left( {1 - \alpha r} \right)}}{m} + \frac{\alpha r}{l}} \right] + \frac{{h_{2} \left( {1 - \alpha r} \right)}}{m}\left[ {m\left( {1 - \frac{\mu }{P}} \right) - \left( {1 - \frac{2\mu }{P}} \right)} \right] + h_{3} \left( {\frac{1}{2\alpha } - \frac{r\mu }{{P_{r} }}} \right) \hfill \\ - \frac{{h_{4} \alpha r}}{l}\left[ {l\left( {1 - \frac{\mu }{{P_{r} }}} \right) - \left( {1 - \frac{2\mu }{{P_{r} }}} \right)} \right] \hfill \\ \end{array} \right\} \hfill \\ \quad + \frac{{h_{1} \sigma }}{{2\mu \pi_{r} }}\left( {k_{m} \sqrt {L_{m} } - k_{l} \sqrt {L_{l} } } \right) \hfill \\ \end{array} \right\},$$

(15)

$$m = \sqrt {\frac{{\left[ {\left( {1 - \alpha r} \right)\mu T + {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right]^{2} \left[ {h_{1} - h_{2} \left( {1 - {{2\mu } \mathord{\left/ {\vphantom {{2\mu } P}} \right. \kern-0pt} P}} \right)} \right]}}{{2\mu \left[ {\sigma \sqrt {L_{m} } \left[ {\phi \left( {k_{m} } \right) - k_{m} + k_{m} \Phi \left( {k_{m} } \right)} \right]\pi + A_{1} } \right]}}} ,$$

(16)

$$l = \sqrt {\frac{{\left[ {\alpha r\mu T - {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right]^{2} \left[ {h_{1} - h_{4} \left( {1 - {{2\mu } \mathord{\left/ {\vphantom {{2\mu } {P_{r} }}} \right. \kern-0pt} {P_{r} }}} \right)} \right]}}{{2\mu \left[ {\sigma \sqrt {L_{l} } \left[ {\phi \left( {k_{l} } \right) - k_{l} + k_{l} \Phi \left( {k_{l} } \right)} \right]\pi + A_{4} } \right]}}}$$

(17)

and

$$\left\{ \begin{array}{l} \frac{{T^{2} \mu }}{2}\left\{ \begin{array}{l} h_{1} \left( {\frac{{\left( {1 - \alpha r} \right)^{2} }}{m} + \frac{{\alpha^{2} r^{2} }}{l}} \right) + \left( {1 - \alpha r} \right)^{2} h_{2} \left[ {\left( {1 - \frac{\mu }{P}} \right) - \frac{1}{m}\left( {1 - \frac{2\mu }{P}} \right)} \right] + rh_{3} \left( {1 + \frac{\alpha r\mu }{{P_{r} }}} \right) \hfill \\ \quad + \alpha^{2} r^{2} h_{4} \left[ {\left( {1 - \frac{\mu }{{P_{r} }}} \right) - \frac{1}{l}\left( {1 - \frac{2\mu }{{P_{r} }}} \right)} \right] \hfill \\ \end{array} \right\} \hfill \\ \quad + \frac{{Tz_{r} \alpha \sigma \sqrt {rT} }}{4}\left\{ \begin{array}{l} h_{1} \left( {\frac{{\left( {1 - \alpha r} \right)}}{m} - \frac{\alpha r}{l}} \right) + \left( {1 - \alpha r} \right)h_{2} \left[ {\left( {1 - \frac{\mu }{P}} \right) - \frac{1}{m}\left( {1 - \frac{2\mu }{P}} \right)} \right] + h_{3} \left( {\frac{1}{2\alpha } - \frac{r\mu }{{P_{r} }}} \right) \hfill \\ \quad - \alpha rh_{4} \left[ {\left( {1 - \frac{\mu }{{P_{r} }}} \right) - \frac{1}{l}\left( {1 - \frac{2\mu }{{P_{r} }}} \right)} \right] \hfill \\ \end{array} \right\} \hfill \\ \quad - \frac{{\alpha \sigma \sqrt {rT} }}{2}\left[ \begin{array}{l} \frac{{h_{1} z_{r} \sigma }}{2\mu }\left( {k_{m} \sqrt {L_{m} } - k_{l} \sqrt {L_{l} } } \right) \hfill \\ \quad + \left( {\phi \left( {z_{r} } \right) - z_{r} + z_{r} \Phi \left( {z_{r} } \right)} \right)\pi_{r} \hfill \\ \end{array} \right] - \left\{ {\left( {mA_{1} + A_{2} + A_{3} + lA_{4} } \right) + \left[ \begin{array}{l} m\sigma \sqrt {L_{m} } \left( {\phi \left( {k_{m} } \right) - k_{m} + k_{m} \Phi \left( {k_{m} } \right)} \right) \hfill \\ \quad + l\sigma \sqrt {L_{l} } \left( {\phi \left( {k_{l} } \right) - k_{l} + k_{l} \Phi \left( {k_{l} } \right)} \right) \hfill \\ \end{array} \right]\pi } \right\} \hfill \\ \end{array} \right\} = 0.$$

(18)

Next, the reorder points R_m and R_l of the retailer for procuring from the manufacturer and remanufacturer, respectively, are given by

$$R_{m} = \mu L_{m} + k_{m} \sigma \sqrt {L_{m} }$$

(19)

$$R_{l} = \mu L_{l} + k_{l} \sigma \sqrt {L_{l} }$$

(20)

It can be observed that Eqs. (13–18) derived above for finding the value of k_m, k_l, z_r, m, l and T are interdependent. Therefore, an iterative method is proposed to obtain the optimal value of decision variables. For the purpose, σ (variability in demand and return rate) is set to zero, and on solving Eqs. (16–18), we get

$$m = \sqrt {\frac{{\left( {A_{2} + A_{3} } \right)\left( {1 - \alpha r} \right)\left[ {h_{1} - \left( {1 - \frac{2\mu }{P}} \right)h_{2} } \right]}}{{A_{1} \left[ {\left( {1 - \alpha r} \right)(1 - \frac{\mu }{P})h_{2} + \frac{1}{\alpha }\left( {\frac{\alpha r}{1 - \alpha r}} \right)\left( {1 + \frac{\alpha r\mu }{{P_{r} }}} \right)h_{3} + \alpha r\left( {\frac{\alpha r}{1 - \alpha r}} \right)\left( {1 - \frac{\mu }{{P_{r} }}} \right)h_{4} } \right]}}} ,$$

(21)

$$l = \sqrt {\frac{{\left( {A_{2} + A_{3} } \right)\alpha r\left( {\frac{\alpha r}{1 - \alpha r}} \right)\left[ {h_{1} - \left( {1 - \frac{2\mu }{{P_{r} }}} \right)h_{4} } \right]}}{{A_{4} \left[ {\left( {1 - \alpha r} \right)(1 - \frac{\mu }{P})h_{2} + \frac{1}{\alpha }\left( {\frac{\alpha r}{1 - \alpha r}} \right)\left( {1 + \frac{\alpha r\mu }{{P_{r} }}} \right)h_{3} + \alpha r\left( {\frac{\alpha r}{1 - \alpha r}} \right)\left( {1 - \frac{\mu }{{P_{r} }}} \right)h_{4} } \right]}}}$$

(22)

and

$$T = \sqrt {\frac{{2\left( {A_{2} + A_{3} } \right)}}{{\mu \left( {1 - \alpha r} \right)\left[ {\left( {1 - \alpha r} \right)(1 - \frac{\mu }{P})h_{2} + \frac{1}{\alpha }\left( {\frac{\alpha r}{1 - \alpha r}} \right)\left( {1 + \frac{\alpha r\mu }{{P_{r} }}} \right)h_{3} + \alpha r\left( {\frac{\alpha r}{1 - \alpha r}} \right)\left( {1 - \frac{\mu }{{P_{r} }}} \right)h_{4} } \right]}}} .$$

(23)

Then, initial values of the decision variables m, l and T are obtained using Eqs. (21–23), respectively. Utilizing the initial value of m, l and T, and taking σ = 0, initial values of the remaining decision variables k_m, k_l and z_r are obtained using Eqs. (13–15), respectively. The complete step by step iterative procedure is presented in the following algorithm to obtain the global optimal solution of the proposed model.

Step 1::

Obtain an initial value of the decision variables m, l and T using Eqs. (21–23), respectively.

Step 2::

Obtain an initial value of k_m, k_l and z_r using Eqs. (13–15), respectively, taking σ = 0 and the value of m, l and T obtained in Step 1.

Step 3::

Use the initial value of k_m, k_l, z_r, m, l and T obtained in Steps 1 and 2 to find their revised value by solving Eqs. (13–18), respectively.

Step 4::

Calculate EJTC(k_m, k_l, z_r, m, l, T) using Eq. (11).

Step 5::

Use the revised value of k_m, k_l, z_r, m, l and T again to revise their value by solving Eqs. (13–18), respectively, and calculate the revised EJTC(k_m, k_l, z_r, m, l, T) using Eq. (11).

Step 6::

If the revised value of EJTC(k_m, k_l, z_r, m, l, T) is same up to the desired level of accuracy, then go to Step 7; otherwise go to Step 5.

Step 7::

If the decision variables m and l are temporarily considered continuous, then EJTC(k_m, k_l, z_r, m, l, T) is minimum and the corresponding value of k_m, k_l, z_r, m, l and T is the optimal solution.

Step 8::

For an integer value of m and l, consider all four possible combinations of the integer value of m and l, i.e. $\left( {\left\lfloor m \right\rfloor ,\left\lfloor l \right\rfloor } \right)$, $\left( {\left\lfloor m \right\rfloor ,\left\lceil l \right\rceil } \right)$, $\left( {\left\lceil m \right\rceil ,\left\lfloor l \right\rfloor } \right)$ and $\left( {\left\lceil m \right\rceil ,\left\lceil l \right\rceil } \right)$ corresponding to the value of m and l obtained in Step 7.

Step 9::

For each $m,l \in \left\{ {\left( {\left\lfloor m \right\rfloor ,\left\lfloor l \right\rfloor } \right),\left( {\left\lfloor m \right\rfloor ,\left\lceil l \right\rceil } \right),\left( {\left\lceil m \right\rceil ,\left\lfloor l \right\rfloor } \right),\left( {\left\lceil m \right\rceil ,\left\lceil l \right\rceil } \right)} \right\}$, perform Steps (9.1–9.3).

• (9.1) Use the value of k_m, k_l, z_r and T obtained in Step 7 to calculate EJTC(k_m, k_l, z_r, m, l, T) using Eq. (11).

• (9.2) Use the value of k_m, k_l, z_r and T to revise their value by solving Eqs. (13–15) and (18), respectively, and calculate the revised EJTC(k_m, k_l, z_r, m, l, T) using Eq. (11).

• (9.3) If the revised value of EJTC(k_m, k_l, z_r, m, l, T) is same up to the desired level of accuracy, then (k_m, k_l, z_r, T) is the optimal solution and the corresponding value of EJTC(k_m, k_l, z_r, m, l, T) is minimum for the fixed integer value of (m, l), else go to Step (9.2).

Step 10::

Select the minimum of all four EJTC(k_m, k_l, z_r, m, l, T) and the corresponding value of (k_m, k_l, z_r, m, l, T) found in Step 9 as the global optimal solution of the problem.

Step 11::

If the inequality (12) is satisfied, then the solution found in Step 10 is the global optimal solution and go to Step 12. Otherwise, the EJTC(·) is not convex with respect to T for the given value of the parameters and the problem has no feasible solution, and stop.

Step 12::

Compute the value of the policy variables Q, Q_r, R_m and R_l using Eqs. (10), (9), (19) and (20), respectively.

5 Numerical illustration

We illustrate the proposed solution approach using the following data: μ  = 10,000 units per year, P  = 20,000 units per year, P_r = 12,000 units per year, A₁ = $100 per order, A₂ = $400 per production setup, A₃ = $200 per remanufacturing setup, A₄ = $75 per order, h₁ = $40 per unit per year, h₂ = $20 per unit per year, h₃ = $8 per unit per year, h₄ = $15 per unit per year, r = 0.25, α  = 0.9, σ  = 100 units per year, L_m= 0.012 year, L_l = 0.01 year, π = $100 per unit and π_r = $75 per unit.

First, the optimal solution is found considering m and l as continuous variables and σ  = 0. The initial value of the decision variables m, l and T are calculated as 4.12, 1.54 and T  = 0.1188 years using Eqs. (21–23), respectively. The value of these decision variables are considered as input to obtain the initial value of other decision variables as k_m = 2.3679, k_l = 2.4610, z_r = 2.4053 using Eqs. (13–15), respectively. Next, Steps 3–7 are followed to find the optimal solution of the problem, which is obtained in the eighth iteration as EJTC (k_m, k_l, z_r, m, l, T) = $20,372.29 per year with the value of decision variables as k_m = 2.3625, k_l= 2.4562, z_r= 2.3947, m  = 4.10, l  = 1.40 and T  = 0.1180 year.

Next, the considered value of parameters and the corresponding optimal value of decision variables are used to calculate the Hessian determinant (please see Appendix 3) as

$$\left| {\begin{array}{*{20}c} {932.52} & {\quad 0.00} & {\quad 2.87} & {\quad - 84.24} & {\quad 0.00} & {\quad 2899.60} \\ {0.00} & {\quad 232.44} & {\quad - 2.62} & {\quad 0.00} & {\quad - 59.48} & {\quad 681.14} \\ {2.87} & {\quad - 2.62} & {\quad 26.69} & {\quad - 1.71} & {\quad - 1.71} & {\quad 185.25} \\ { - 84.24} & {\quad 0.00} & {\quad - 1.71} & {\quad 427.25} & {\quad 0.00} & {\quad - 14698.40 \, } \\ {0.00} & {\quad 59.48} & {\quad - 5.57} & {\quad 0.00} & {\quad 933.82} & {\quad - 11520.66 \, } \\ {2899.60} & {\quad 681.14} & {\quad 185.25} & {\quad - 14698.40} & {\quad 11520.66} & {\quad 1248528.96} \\ \end{array} } \right|.$$

Subsequently, the value of all principle minors of the corresponding Hessian matrix is calculated as 932.5229, 216,756.4, 5,776,829.75, 2,423,716,421, 2.22288 × 10¹² and 1.33506 × 10¹⁸. Since all principle minors of the Hessian determinant are positive, the obtained solution is global minimum (see Table 4).

Table 4 Results of the solution procedure

The optimal values of m and l are 4.10 and 1.40, respectively, if they are considered as continuous variable. Therefore, the possible four sets of integer values of m and l are given by (4, 1), (4, 2), (5, 1) and (5, 2). Now, the optimal solution of the problem is obtained as EJTC(k_m, k_l, z_r, m, l, T) = $ 20,460.21 per year, k_m= 2.3682, k_l= 2.3496, z_r= 2.5155 and T = 0.1129 year for m = 4, l = 1 using Steps 8–10 of the algorithm. Further, Q, Q_r, R_m and R_l are computed using Eqs. (10), (9), (19) and (20) as 223.42, 234.92, 145.94 and 123.50 units, respectively.

The replenishment policy of the CLSC system for the given data is as follows. The production (remanufacturing) cycle length of the manufacturer (remanufacturer) is 0.1129 years. In each production cycle of the manufacturer, the retailer places four consecutive orders, each of size 223.42 units, to the manufacturer whenever the inventory level of the retailer drops to 145.94 units. Then, the retailer places a single order of size 234.92 units during each remanufacturing cycle of the remanufacturer when the inventory level reaches 123.50 units. The manufacturer produces 893.68 (4 × 223.42) units of the new product during each production cycle, and the remanufacturer remanufacturers 234.92 (1 × 234.92) units during each remanufacturing cycle. The remanufacturer maintains the safety stock ($k_{r} \sigma \sqrt {rT}$) of 21.13 units of the returned product.

6 Sensitivity analysis

We conduct the sensitivity analysis to examine the impact of key parameters P, P_r, r, σ, L_m and L_l on the EJTC. For the purpose of sensitivity analysis, the base parameters are kept fixed to the values as considered for the numerical illustration.

The effects of the parameters P, P_r, r, σ, L_m and L_l on EJTC are shown in Figs. 3, 4, 5, 6 and 7, respectively. For selected values of these parameters, the optimal value of decision variables, EJTC and the corresponding cost components of each entity are presented in Table 5. The insights drawn are discussed in the subsequent subsections.

Fig. 3

Variation of the expected joint total cost with production rate of the manufacturer

Fig. 4

Variation of the expected joint total cost with remanufacturing rate

Fig. 5

Variation of the expected joint total cost with fraction of demand return

Fig. 6

Variation of the expected joint total cost with standard deviation of demand

Fig. 7

Variation of the expected joint total cost with procurement lead times of the retailer

Table 5 Select value of parameters and the corresponding optimal value of decision variables, and EJTC along with cost components of each entity

6.1 Impact of production rate (P) of the manufacturer

From Fig. 3, it is evident that EJTC increases with increase in P and is lowest when P is close to the lowest feasible value. It can also be seen that there is a rapid increase in EJTC when P is close to its lowest feasible value, and the rate of increase in EJTC is small for the higher values of P. From Table 5, it can be observed that the decrease in the expected total cost of the retailer and the change (initially decreases then increases) in the expected total cost of the remanufacturer are negligible with P, whereas the increase is significant for the manufacturer. This happens because the length of production cycle of the manufacturer decreases with increase in P, which increases the production setup cost per unit time of the manufacturer. Further, due to high production rate, the manufacturer gets the new product from the production process quickly. Therefore, the manufacturer has to hold the inventory of the finished product for a relatively longer time, which in turn increases the manufacturer’s inventory holding cost per unit time.

Further, the behaviour of the cost function EJTC with production rate can also be shown analytically by taking the first order partial derivative of the EJTC in Eq. (11) with respect to P. Thus, we have ${{\partial EJTC ( \cdot )} \mathord{ / {\vphantom {{\partial EJTC ( \cdot )} {\partial P}}} \kern-0pt} {\partial P}} = {{h_{2} \mu ( { ( {1 - \alpha r} )\mu T + {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{ / {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \kern-0pt} 2}} )^{2} ( {m - 2} )} \mathord{ / {\vphantom {{h_{2} \mu ( { ( {1 - \alpha r} )\mu T + {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{ / {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \kern-0pt} 2}} )^{2} ( {m - 2} )} { ( {2m\mu P^{2} T} )}}} \kern-0pt} { ( {2m\mu P^{2} T} )}}$, which will be positive, zero, and negative for m > 2, m = 2, and m < 2, respectively. Hence, the EJTC increases, remains constant, and decreases if m > 2, m = 2, and m < 2, respectively, with increase in P. This is also evident from Table 5 for m > 2.

6.2 Impact of production rate of the remanufacturer (P_r)

From Fig. 4 and Table 5, it can be observed that EJTC decreases with increase in P_r. This happens primarily because of decrease in the inventory holding cost of the returned and remanufactured products at the remanufacturer. However, the decrease in expected total cost of the manufacturer and the change (initially decreases and then increases) in the expected total cost of the retailer are almost negligible with P_r.

Similar to the production rate of the manufacturer, the behaviour of the cost function EJTC can also be shown analytically by taking the first order partial derivative of the EJTC in Eq. (11) with respect to P_r, and we obtain ${{\partial EJTC ( \cdot )} \mathord{ / {\vphantom {{\partial EJTC ( \cdot )} {\partial P_{r} }}} \kern-0pt} {\partial P_{r} }} = {{ ( {\alpha \mu rT - \alpha {{z_{r} \sigma \sqrt {rT} } \mathord{ / {\vphantom {{z_{r} \sigma \sqrt {rT} } 2}} \kern-0pt} 2}} )^{2} [ {{{h_{4} ( {l - 2} )} \mathord{ / {\vphantom {{h_{4} ( {l - 2} )} l}} \kern-0pt} l} - {{h_{3} } \mathord{ / {\vphantom {{h_{3} } \alpha }} \kern-0pt} \alpha }} ]} \mathord{ / {\vphantom {{ ( {\alpha \mu rT - \alpha {{z_{r} \sigma \sqrt {rT} } \mathord{ / {\vphantom {{z_{r} \sigma \sqrt {rT} } 2}} \kern-0pt} 2}} )^{2} [ {{{h_{4} ( {l - 2} )} \mathord{ / {\vphantom {{h_{4} ( {l - 2} )} l}} \kern-0pt} l} - {{h_{3} } \mathord{ / {\vphantom {{h_{3} } \alpha }} \kern-0pt} \alpha }} ]} { ( {2TP_{r}^{2} } )}}} \kern-0pt} { ( {2TP_{r}^{2} } )}}$. If l ≤ 2, ${{\partial EJTC\left( \cdot \right)} \mathord{\left/ {\vphantom {{\partial EJTC\left( \cdot \right)} {\partial P_{r} }}} \right. \kern-0pt} {\partial P_{r} }}$ is negative, therefore the EJTC decreases with increase in P_r, which can also be seen from Table 5. For l > 2, ${{\partial EJTC\left( \cdot \right)} \mathord{\left/ {\vphantom {{\partial EJTC\left( \cdot \right)} {\partial P_{r} }}} \right. \kern-0pt} {\partial P_{r} }}$ will be positive if ${{h_{4} \left( {l - 2} \right)} \mathord{\left/ {\vphantom {{h_{4} \left( {l - 2} \right)} l}} \right. \kern-0pt} l} - {{h_{3} } \mathord{\left/ {\vphantom {{h_{3} } \alpha }} \right. \kern-0pt} \alpha } > 0$, i.e. $\left( {1 - {2 \mathord{\left/ {\vphantom {2 l}} \right. \kern-0pt} l}} \right) > {{h_{3} } \mathord{\left/ {\vphantom {{h_{3} } {\left( {\alpha h_{4} } \right)}}} \right. \kern-0pt} {\left( {\alpha h_{4} } \right)}}$. Since ${{h_{3} } \mathord{\left/ {\vphantom {{h_{3} } {\left( {\alpha h_{4} } \right)}}} \right. \kern-0pt} {\left( {\alpha h_{4} } \right)}} > 0,$ which implies that $l > 2$. Therefore, for l > 2, ${{\partial EJTC\left( \cdot \right)} \mathord{\left/ {\vphantom {{\partial EJTC\left( \cdot \right)} {\partial P_{r} }}} \right. \kern-0pt} {\partial P_{r} }}$ is positive, and so the EJTC increases with increase in P_r.

6.3 Impact of fraction of average demand returns (r)

Figure 5 depicts that the EJTC first decreases and then increases with increase in r. For the assumed value of the parameters, the value of EJTC is lowest when r is close to 0.35. However, the value of r for the minimum value of EJTC will lie between 0 and 1 (0 < r < 1) depending on the value of different parameters of the model.

6.4 Impact of standard deviation of demand (σ)

From Fig. 6 and Table 5, it can be observed that the EJTC increases with increase in σ. This happens because of increase in the costs associated with the retailer’s safety stock of the new/remanufactured product, the remanufacturer’s safety stock of the returned product and the backorder at the retailer and remanufacturer with σ.

6.5 Impact of replenishment lead times of manufacturer (L_m) and remanufacturer (L_l)

It is evident from the Fig. 7 that the EJTC increases with increase in L_m and L_l. This is because of increase in the costs associated with the safety stock of the new/remanufactured product and the backorder at the retailer with increase in the procurement lead times L_m and L_l.

7 Comparison between CLSC and corresponding forward supply chain (FSC)

The expected joint total cost of the CLSC model is compared with the corresponding FSC (The derivation of cost function and solution approach of the FSC is given in Appendix 4) for different sets of values of the parameters A₃, h₃, A₄, h₄, r, σ, while keeping other parameters at the same value as used for numerical illustration. The results are summarized in Table 6. The value of r can be anywhere between 0 and 1 for the minimum value of EJTC of the CLSC. However, from Table 6, it can be observed that, if the remanufacturing cost of the returned product is significantly lower than the cost of manufacturing of the new product and the variation in demand (σ) is also low, then the EJTC of the CLSC will be lowest when r is close to 1. If the remanufacturing cost and σ both are high, EJTC of the CLSC is lowest when r is close to 0. From Table 6, it can also be observed that the CLSC is more profitable than the FSC when the remanufacturing cost is very low compared to the manufacturing of the new product, σ is low, and r is close to 1. On the other hand, the CLSC is more expensive than the FSC when the remanufacturing cost is relatively high (even though it is less than the cost of manufacturing of the new product), σ is high, and r is also close to 1.

Table 6 Comparison of EJTC of the CLSC and the corresponding FSC by varying r, A₃, A₄, h₃, h₄ and σ

8 Conclusions, limitations, and future scope

This paper made a contribution by addressing the inherent complexity involved in the real life production-inventory decisions for a two-echelon CLSC under uncertain demand and return with finite production rate of the manufacturer and remanufacturer in an infinite planning horizon. The study derives an optimal strategy for minimizing the expected joint total cost of the manufacturer, retailer and remanufacturer. The results show that the EJTC of the system is lowest when the production rate of the manufacturer is close to the lowest feasible value and it decreases with the remanufacturing rate of the remanufacturer. Whereas, the EJTC of the system increases with increase in demand variability at the retailer and lead time of the retailer for the procurement of the new and remanufactured products. The finding revealed a substantial reduction in the EJTC for the lower value of the fraction of demand returned (less than 0.35 for the present case) and increases thereafter. It has also been revealed that the CLSC is more profitable than the FSC when the remanufacturing cost of the returned product is significantly low compared to the manufacturing cost of the new product, σ is low and r is close to 1. On the other hand, it is most expensive than the FSC if the remanufacturing cost is relatively high (even though it is less than the cost of manufacturing of the new product), σ is high and r is close to 1.

The model developed in this paper has some limitations. First, the proposed model and results are applied to a two-echelon CLSC; however a multi-echelon closed-loop supply chain may be a future direction of research. Second, the development of periodic review policy for the slow moving items can add value to the present body of knowledge. Third, the proposed model considers the conversion rate at the remanufacturer but assumes that manufacturing of the new product has no rework or rejection. This may be considered to enhance the value of the proposed model. Fourth, carbon foot print consideration can add value to this research.

Appendices

Appendix 1: Derivation of the expected shortage of the returned product at the remanufacturer during each remanufacturing cycle

From Eq. (6), we have

$$B\left( {R_{r} } \right) = \int\limits_{0}^{{R_{r} - S_{r} }} {\left( {R_{r} - S_{r} - x_{r} } \right)f\left( {x_{r} } \right)dx_{r} }$$

(24)

The expression (24) can be rewritten as

$$\begin{aligned} B\left( {R_{r} } \right) & = \int\limits_{0}^{\infty } {\left( {R_{r} - S_{r} - x_{r} } \right)f\left( {x_{r} } \right)dx_{r} - } \int\limits_{{R_{r} - S_{r} }}^{\infty } {\left( {R_{r} - S_{r} - x_{r} } \right)f\left( {x_{r} } \right)dx_{r} } \\ & = \left( {R_{r} - S_{r} } \right)\int\limits_{0}^{\infty } {f\left( {x_{r} } \right)dx_{r} - \int\limits_{0}^{\infty } {x_{r} f\left( {x_{r} } \right)dx_{r} + } } \int\limits_{{R_{r} - S_{r} }}^{\infty } {\left( {x_{r} - \left( {R_{r} - S_{r} } \right)} \right)f\left( {x_{r} } \right)dx_{r} } \\ \end{aligned}$$

Since x_r ~ N(μrT, σ²rT), the above equation can be written as

$$B\left( {R_{r} } \right) = \left( {R_{r} - S_{r} - \mu rT} \right) + \int\limits_{{R_{r} - S_{r} }}^{\infty } {\left( {x_{r} - \left( {R_{r} - S_{r} } \right)} \right)f\left( {x_{r} } \right)dx_{r} } .$$

(25)

Let $I = \int\limits_{{R_{r} - S_{r} }}^{\infty } {\left( {x_{r} - \left( {R_{r} - S_{r} } \right)} \right)f\left( {x_{r} } \right)dx_{r} }$, which can be written as

$$\begin{aligned} & I = \int\limits_{{R_{r} - S_{r} }}^{\infty } {\left( {x_{r} - \mu rT + \mu rT - \left( {R_{r} - S_{r} } \right)} \right)f\left( {x_{r} } \right)dx_{r} } ,\;{\text{therefore}} \\ & I = \int\limits_{{R_{r} - S_{r} }}^{\infty } {\left( {x_{r} - \mu rT} \right)f\left( {x_{r} } \right)dx_{r} } + \int\limits_{{R_{r} - S_{r} }}^{\infty } {\left( {\mu rT - \left( {R_{r} - S_{r} } \right)} \right)f\left( {x_{r} } \right)dx_{r} } \\ \end{aligned}$$

On substituting $f\left( {x_{r} } \right) = \frac{1}{{\sigma \sqrt {rT} \sqrt {2\pi } }}e^{{ - \frac{1}{2}\left( {\frac{{x_{r} - \mu rT}}{{\sigma \sqrt {rT} }}} \right)^{2} }}$, we get

$$I = \int\limits_{{R_{r} - S_{r} }}^{\infty } {\left( {x_{r} - \mu rT} \right)\frac{1}{{\sigma \sqrt {rT} \sqrt {2\pi } }}e^{{ - \frac{1}{2}\left( {\frac{{x_{r} - \mu rT}}{{\sigma \sqrt {rT} }}} \right)^{2} }} dx_{r} } + \left[ {\mu rT - \left( {R_{r} - S_{r} } \right)} \right]\int\limits_{{R_{r} - S_{r} }}^{\infty } {\frac{1}{{\sigma \sqrt {rT} \sqrt {2\pi } }}e^{{ - \frac{1}{2}\left( {\frac{{x_{r} - \mu rT}}{{\sigma \sqrt {rT} }}} \right)^{2} }} dx_{r} }$$

Let $\frac{{x_{r} - \mu rT}}{{\sigma \sqrt {rT} }} = y$, therefore $dx_{r} = \sigma \sqrt {rT} dy$

Hence, $I = \sigma \sqrt {rT} \int\limits_{{\frac{{R_{r} - S_{r} - \mu rT}}{{\sigma \sqrt {rT} }}}}^{\infty } {y\frac{1}{{\sqrt {2\pi } }}e^{{ - \frac{1}{2}y^{2} }} dy} + \left[ {\mu rT - \left( {R_{r} - S_{r} } \right)} \right]\int\limits_{{\frac{{R_{r} - S_{r} - \mu rT}}{{\sigma \sqrt {rT} }}}}^{\infty } {\frac{1}{{\sqrt {2\pi } }}e^{{ - \frac{1}{2}y^{2} }} dy}$.

Let $I_{\text{I}} = \sigma \sqrt {rT} \int\limits_{{\frac{{R_{r} - S_{r} - \mu rT}}{{\sigma \sqrt {rT} }}}}^{\infty } {y\frac{1}{{\sqrt {2\pi } }}e^{{ - \frac{1}{2}y^{2} }} dy}$ and $I_{\text{II}} = \left[ {\mu rT - \left( {R_{r} - S_{r} } \right)} \right]\int\limits_{{\frac{{R_{r} - S_{r} - \mu rT}}{{\sigma \sqrt {rT} }}}}^{\infty } {\frac{1}{{\sqrt {2\pi } }}e^{{ - \frac{1}{2}y^{2} }} dy}$.

Consider the expression $I_{\text{I}} = \sigma \sqrt {rT} \int\limits_{{\frac{{R_{r} - S_{r} - \mu rT}}{{\sigma \sqrt {rT} }}}}^{\infty } {y\frac{1}{{\sqrt {2\pi } }}e^{{ - \frac{1}{2}y^{2} }} dy}$ and let ${{y^{2} } \mathord{\left/ {\vphantom {{y^{2} } 2}} \right. \kern-0pt} 2} = t$, therefore $ydy = dt$.

Hence, $I_{\text{I}} = \sigma \sqrt {rT} \int\limits_{{\frac{1}{2}\left( {\frac{{R_{r} - S_{r} - \mu rT}}{{\sigma \sqrt {rT} }}} \right)^{2} }}^{\infty } {\frac{1}{{\sqrt {2\pi } }}e^{ - t} dt} ,$ that is

$$I_{\text{I}} = \sigma \sqrt {rT} \frac{1}{{\sqrt {2\pi } }}e^{{ - \frac{1}{2}\left( {\frac{{R_{r} - S_{r} - \mu rT}}{{\sigma \sqrt {rT} }}} \right)^{2} }} .$$

Using $S_{r} = k_{r} \sigma \sqrt {rT}$, and $R_{r} = \mu rT - k_{r} \sigma \sqrt {rT}$ from Eq. (4), we have

$$\frac{{R_{r} - S_{r} - \mu rT}}{{\sigma \sqrt {rT} }} = - 2k_{r} .$$

Let z_r = 2k_r, and so

$$\frac{{R_{r} - S_{r} - \mu rT}}{{\sigma \sqrt {rT} }} = - z_{r}$$

(26)

Hence, $I_{\text{I}} = \sigma \sqrt {rT} \frac{1}{{\sqrt {2\pi } }}e^{{ - \frac{1}{2}\left( { - z_{r} } \right)^{2} }}$ that is

$$I_{\text{I}} = \sigma \sqrt {rT} \phi ( - z_{r} ) = \sigma \sqrt {rT} \phi (z_{r} ),\quad {\text{as}}\;\phi ( - z_{r} ) = \phi (z_{r} ),$$

where $\phi ( \cdot )$ is pdf of the standard normal distribution.

Next,

$$I_{\text{II}} = \left[ {\mu rT - \left( {R_{r} - S_{r} } \right)} \right]\int\limits_{{\frac{{R_{r} - S_{r} - \mu rT}}{{\sigma \sqrt {rT} }}}}^{\infty } {\frac{1}{{\sqrt {2\pi } }}e^{{ - \frac{1}{2}y^{2} }} dy} = \left[ {\mu rT - \left( {R_{r} - S_{r} } \right)} \right]\int\limits_{{ - z_{r} }}^{\infty } {\frac{1}{{\sqrt {2\pi } }}e^{{ - \frac{1}{2}y^{2} }} dy} .$$

Therefore,

$$I_{\text{II}} = \left[ {\mu rT - \left( {R_{r} - S_{r} } \right)} \right]\left[ {1 - \Phi ( - z_{r} )} \right] = \left[ {\mu rT - \left( {R_{r} - S_{r} } \right)} \right]\Phi (z_{r} ),$$

where $\Phi ( \cdot )$ is cdf of the standard normal distribution.

Now, from Eq. (30), $\left[ {\mu rT - \left( {R_{r} - S_{r} } \right)} \right] = z_{r} \sigma \sqrt {rT}$, and so

$$I_{\text{II}} = z_{r} \sigma \sqrt {rT} \Phi (z_{r} ).$$

Therefore, from Eq. (29), $B(R_{r} ) = \left( {R_{r} - S_{r} - \mu rT} \right) + \sigma \sqrt {rT} \left[ {\phi (z_{r} ) + z_{r} \Phi (z_{r} )} \right]$ and on substituting $\left( {R_{r} - S_{r} - \mu rT} \right) = - z_{r} \sigma \sqrt {rT}$ from Eq. (30), we get

$$B(R_{r} ) = \sigma \sqrt {rT} \left[ {\phi (z_{r} ) - z_{r} + z_{r} \Phi (z_{r} )} \right].$$

(27)

Appendix 2: The first and second partial derivatives of EJTC(·)

$$\frac{\partial EJTC\left( \cdot \right)}{{\partial k_{m} }} = \frac{{\sigma \sqrt {L_{m} } }}{T}\left[ {\frac{{h_{1} }}{\mu }\left( {\left( {1 - \alpha r} \right)\mu T + \frac{{\alpha z_{r} \sigma \sqrt {rT} }}{2}} \right) - m\pi \left( {1 - \Phi \left( {k_{m} } \right)} \right)} \right],$$

(28)

$$\frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial k_{m}^{2} }} = \frac{{m\pi \sigma \sqrt {L_{m} } \phi \left( {k_{m} } \right)}}{T} > 0,$$

(29)

$$\frac{\partial EJTC\left( \cdot \right)}{{\partial k_{l} }} = \frac{{\sigma \sqrt {L_{l} } }}{T}\left[ {\frac{{h_{1} }}{\mu }\left( {\alpha r\mu T - \frac{{\alpha z_{r} \sigma \sqrt {rT} }}{2}} \right) - l\pi \left( {1 - \Phi \left( {k_{l} } \right)} \right)} \right],$$

(30)

$$\frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial k_{l}^{2} }} = \frac{{l\pi \sigma \sqrt {L_{l} } \phi \left( {k_{l} } \right)}}{T} > 0,$$

(31)

$$\frac{\partial EJTC\left( \cdot \right)}{{\partial z_{r} }} = \left\{ \begin{array}{l} \frac{{z_{r} \alpha^{2} \sigma^{2} rT}}{4\mu }\left\{ {h_{1} \left( {\frac{1}{m} + \frac{1}{l}} \right) + \frac{{h_{2} }}{m}\left[ {m\left( {1 - \frac{\mu }{P}} \right) - \left( {1 - \frac{2\mu }{P}} \right)} \right] + \frac{{h_{3} \mu }}{{\alpha P_{r} }} + \frac{{h_{4} }}{l}\left[ {l\left( {1 - \frac{\mu }{{P_{r} }}} \right) - \left( {1 - \frac{2\mu }{{P_{r} }}} \right)} \right]} \right\} \hfill \\ + \frac{{T\alpha \sigma \sqrt {rT} }}{2}\left\{ \begin{array}{l} h_{1} \left[ {\frac{{\left( {1 - \alpha r} \right)}}{m} + \frac{\alpha r}{l}} \right] + \frac{{h_{2} \left( {1 - \alpha r} \right)}}{m}\left[ {m\left( {1 - \frac{\mu }{P}} \right) - \left( {1 - \frac{2\mu }{P}} \right)} \right] \hfill \\ + h_{3} \left( {\frac{1}{2\alpha } - \frac{r\mu }{{P_{r} }}} \right) - \frac{{h_{4} \alpha r}}{l}\left[ {l\left( {1 - \frac{\mu }{{P_{r} }}} \right) - \left( {1 - \frac{2\mu }{{P_{r} }}} \right)} \right] \hfill \\ \end{array} \right\} \hfill \\ + \frac{{h_{1} \sigma \alpha \sigma \sqrt {rT} \left( {k_{m} \sqrt {L_{m} } - k_{l} \sqrt {L_{l} } } \right)}}{2\mu } - \alpha \sigma \sqrt {rT} \left[ {1 - \Phi \left( {z_{r} } \right)} \right]\pi_{r} \hfill \\ \end{array} \right\},$$

(32)

$$\frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial z_{r}^{2} }} = \frac{{\alpha^{2} \sigma^{2} rT}}{4\mu }\left\{ \begin{array}{l} h_{1} \left( {\frac{1}{m} + \frac{1}{l}} \right) + h_{2} \left[ {\left( {1 - \frac{\mu }{P}} \right) - \frac{1}{m}\left( {1 - \frac{2\mu }{P}} \right)} \right] \hfill \\ + \frac{{h_{3} \mu }}{{\alpha P_{r} }} + h_{4} \left[ {\left( {1 - \frac{\mu }{{P_{r} }}} \right) - \frac{1}{l}\left( {1 - \frac{2\mu }{{P_{r} }}} \right)} \right] \hfill \\ \end{array} \right\} + \alpha \sigma \sqrt {rT} \phi \left( {z_{r} } \right)\pi_{r} > 0,$$

(33)

$$\frac{\partial EJTC\left( \cdot \right)}{\partial m} = \frac{1}{T}\left[ \begin{array}{l} A_{1} - \frac{{h_{1} }}{{2\mu m^{2} }}\left( {\left( {1 - \alpha r} \right)\mu T + {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right)^{2} \hfill \\ + \frac{{h_{2} }}{{2\mu m^{2} }}\left( {1 - \frac{2\mu }{P}} \right)\left( {\left( {1 - \alpha r} \right)\mu T + {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right)^{2} \hfill \\ + \sigma \sqrt {L_{m} } \left[ {\phi \left( {k_{m} } \right) - k_{m} + k_{m} \Phi \left( {k_{m} } \right)} \right]\pi \hfill \\ \end{array} \right],$$

(34)

$$\frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial m^{2} }} = \frac{1}{T}\left[ {\frac{1}{{\mu m^{3} }}\left( {\left( {1 - \alpha r} \right)\mu T + {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right)^{2} \left( {h_{1} - h_{2} + h_{2} \frac{2\mu }{P}} \right)} \right] > 0,\quad \left( {{\text{as}}\;h_{1} > h_{2} } \right),$$

(35)

$$\frac{\partial EJTC\left( \cdot \right)}{\partial l} = \frac{1}{T}\left[ \begin{array}{l} A_{4} - \frac{{h_{1} }}{{2\mu l^{2} }}\left( {\alpha r\mu T - {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right)^{2} \hfill \\ + \frac{{h_{4} }}{{2\mu l^{2} }}\left( {1 - \frac{2\mu }{{P_{r} }}} \right)\left( {\alpha r\mu T - {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right)^{2} \hfill \\ + \pi \sigma \sqrt {L_{l} } \left[ {\phi \left( {k_{l} } \right) - k_{l} + k_{l} \Phi \left( {k_{l} } \right)} \right] \hfill \\ \end{array} \right],$$

(36)

$$\frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial l^{2} }} = \frac{1}{T}\left[ {\frac{1}{{\mu l^{3} }}\left( {\alpha r\mu T - {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right)^{2} \left( {h_{1} - h_{4} + h_{4} \frac{2\mu }{{P_{r} }}} \right)} \right] > 0,\quad \left( {{\text{as}}\;h_{1} > h_{4} } \right),$$

(37)

$$\frac{\partial EJTC\left( \cdot \right)}{\partial T} = \left\{ \begin{array}{l} \frac{\mu }{2}\left\{ \begin{array}{l} h_{1} \left( {\frac{{\left( {1 - \alpha r} \right)^{2} }}{m} + \frac{{\alpha^{2} r^{2} }}{l}} \right) + \left( {1 - \alpha r} \right)^{2} h_{2} \left[ {\left( {1 - \frac{\mu }{P}} \right) - \frac{1}{m}\left( {1 - \frac{2\mu }{P}} \right)} \right] + \hfill \\ rh_{3} \left( {1 + \frac{\alpha r\mu }{{P_{r} }}} \right) + \alpha^{2} r^{2} h_{4} \left[ {\left( {1 - \frac{\mu }{{P_{r} }}} \right) - \frac{1}{l}\left( {1 - \frac{2\mu }{{P_{r} }}} \right)} \right] \hfill \\ \end{array} \right\} \hfill \\ + \frac{{z_{r} \alpha \sigma \sqrt {rT} }}{4T}\left\{ \begin{array}{l} h_{1} \left( {\frac{{\left( {1 - \alpha r} \right)}}{m} - \frac{\alpha r}{l}} \right) + \left( {1 - \alpha r} \right)h_{2} \left[ {\left( {1 - \frac{\mu }{P}} \right) - \frac{1}{m}\left( {1 - \frac{2\mu }{P}} \right)} \right] \hfill \\ + h_{3} \left( {\frac{1}{2\alpha } - \frac{r\mu }{{P_{r} }}} \right) - \alpha rh_{4} \left[ {\left( {1 - \frac{\mu }{{P_{r} }}} \right) - \frac{1}{l}\left( {1 - \frac{2\mu }{{P_{r} }}} \right)} \right] \hfill \\ \end{array} \right\} \hfill \\ - \frac{{\alpha \sigma \sqrt {rT} }}{{2T^{2} }}\left[ {\frac{{h_{1} z_{r} \sigma }}{2\mu }\left( {k_{m} \sqrt {L_{m} } - k_{l} \sqrt {L_{l} } } \right) + \left( {\phi \left( {z_{r} } \right) - z_{r} + z_{r} \Phi \left( {z_{r} } \right)} \right)\pi_{r} } \right] \hfill \\ - \frac{1}{{T^{2} }}\left[ {\left( {mA_{1} + A_{2} + A_{3} + lA_{4} } \right) + \left[ \begin{array}{l} m\sigma \sqrt {L_{m} } \left( {\phi \left( {k_{m} } \right) - k_{m} + k_{m} \Phi \left( {k_{m} } \right)} \right) \hfill \\ + l\sigma \sqrt {L_{l} } \left( {\phi \left( {k_{l} } \right) - k_{l} + k_{l} \Phi \left( {k_{l} } \right)} \right) \hfill \\ \end{array} \right]\pi } \right] \hfill \\ \end{array} \right\}$$

(38)

and

$$\frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial T^{2} }} = \left\{ \begin{array}{l} - \frac{{z_{r} \alpha \sigma \sqrt {rT} }}{{8T^{2} }}\left[ \begin{array}{l} h_{1} \left( {\frac{{\left( {1 - \alpha r} \right)}}{m} - \frac{\alpha r}{l}} \right) + \left( {1 - \alpha r} \right)h_{2} \left[ {\left( {1 - \frac{\mu }{P}} \right) - \frac{1}{m}\left( {1 - \frac{2\mu }{P}} \right)} \right] \hfill \\ + h_{3} \left( {\frac{1}{2\alpha } - \frac{r\mu }{{P_{r} }}} \right) - \alpha rh_{4} \left[ {\left( {1 - \frac{\mu }{{P_{r} }}} \right) - \frac{1}{l}\left( {1 - \frac{2\mu }{{P_{r} }}} \right)} \right] \hfill \\ \end{array} \right] \hfill \\ + \frac{{3\alpha \sigma \sqrt {rT} }}{{4T^{3} }}\left[ {\frac{{h_{1} z_{r} \sigma }}{2\mu }\left( {k_{m} \sqrt {L_{m} } - k_{l} \sqrt {L_{l} } } \right) + \left( {\phi \left( {z_{r} } \right) - z_{r} + z_{r} \Phi \left( {z_{r} } \right)} \right)\pi_{r} } \right] \hfill \\ + \frac{2}{{T^{3} }}\left[ {\left( {mA_{1} + A_{2} + A_{3} + lA_{4} } \right) + \left[ \begin{array}{l} m\sigma \sqrt {L_{m} } \left( {\phi \left( {k_{m} } \right) - k_{m} + k_{m} \Phi \left( {k_{m} } \right)} \right) \hfill \\ + l\sigma \sqrt {L_{l} } \left( {\phi \left( {k_{l} } \right) - k_{l} + k_{l} \Phi \left( {k_{l} } \right)} \right) \hfill \\ \end{array} \right]\pi } \right] \hfill \\ \end{array} \right\}.$$

(39)

Appendix 3: Test of convexity of the proposed model

To show the convexity of cost function in Eq. (11), all principal minors of the Hessian matrix of the cost function must be positive, i.e. $H_{1} > 0$,$H_{2} > 0$, $H_{3} > 0$, $H_{4} > 0$, $H_{5} > 0$, $H_{6} > 0$.

Here,

$$\begin{aligned} & H_{1} = \left| {\lambda_{11} } \right|,\quad H_{2} = \left| {\begin{array}{*{20}l} {\lambda_{11} } \hfill & {\quad \lambda_{12} } \hfill \\ {\lambda_{21} } \hfill & {\quad \lambda_{22} } \hfill \\ \end{array} } \right|,\quad H_{3} = \left| {\begin{array}{*{20}l} {\lambda_{11} } \hfill & {\quad \lambda_{12} } \hfill & {\quad \lambda_{13} } \hfill \\ {\lambda_{21} } \hfill & {\quad \lambda_{22} } \hfill & {\quad \lambda_{23} } \hfill \\ {\lambda_{31} } \hfill & {\quad \lambda_{32} } \hfill & {\quad \lambda_{33} } \hfill \\ \end{array} } \right|,\quad H_{4} = \left| {\begin{array}{*{20}l} {\lambda_{11} } \hfill & {\quad \lambda_{12} } \hfill & {\quad \lambda_{13} } \hfill & {\quad \lambda_{14} } \hfill \\ {\lambda_{21} } \hfill & {\quad \lambda_{22} } \hfill & {\quad \lambda_{23} } \hfill & {\quad \lambda_{24} } \hfill \\ {\lambda_{31} } \hfill & {\quad \lambda_{32} } \hfill & {\quad \lambda_{33} } \hfill & {\quad \lambda_{34} } \hfill \\ {\lambda_{41} } \hfill & {\quad \lambda_{42} } \hfill & {\quad \lambda_{43} } \hfill & {\quad \lambda_{44} } \hfill \\ \end{array} } \right| \\ & H_{5} = \left| {\begin{array}{*{20}l} {\lambda_{11} } \hfill & {\quad \lambda_{12} } \hfill & {\quad \lambda_{13} } \hfill & {\quad \lambda_{14} } \hfill & {\quad \lambda_{15} } \hfill \\ {\lambda_{21} } \hfill & {\quad \lambda_{22} } \hfill & {\quad \lambda_{23} } \hfill & {\quad \lambda_{24} } \hfill & {\quad \lambda_{25} } \hfill \\ {\lambda_{31} } \hfill & {\quad \lambda_{32} } \hfill & {\quad \lambda_{33} } \hfill & {\quad \lambda_{34} } \hfill & {\quad \lambda_{35} } \hfill \\ {\lambda_{41} } \hfill & {\quad \lambda_{42} } \hfill & {\quad \lambda_{43} } \hfill & {\quad \lambda_{44} } \hfill & {\quad \lambda_{45} } \hfill \\ {\lambda_{51} } \hfill & {\quad \lambda_{52} } \hfill & {\quad \lambda_{53} } \hfill & {\quad \lambda_{54} } \hfill & {\quad \lambda_{55} } \hfill \\ \end{array} } \right|\quad {\text{and}}\quad H_{6} = \left| {\begin{array}{*{20}l} {\lambda_{11} } \hfill & {\quad \lambda_{12} } \hfill & {\quad \lambda_{13} } \hfill & {\quad \lambda_{14} } \hfill & {\quad \lambda_{15} } \hfill & {\quad \lambda_{16} } \hfill \\ {\lambda_{21} } \hfill & {\quad \lambda_{22} } \hfill & {\quad \lambda_{23} } \hfill & {\quad \lambda_{24} } \hfill & {\quad \lambda_{25} } \hfill & {\quad \lambda_{26} } \hfill \\ {\lambda_{31} } \hfill & {\quad \lambda_{32} } \hfill & {\quad \lambda_{33} } \hfill & {\quad \lambda_{34} } \hfill & {\quad \lambda_{35} } \hfill & {\quad \lambda_{36} } \hfill \\ {\lambda_{41} } \hfill & {\quad \lambda_{42} } \hfill & {\quad \lambda_{43} } \hfill & {\quad \lambda_{44} } \hfill & {\quad \lambda_{45} } \hfill & {\quad \lambda_{46} } \hfill \\ {\lambda_{51} } \hfill & {\quad \lambda_{52} } \hfill & {\quad \lambda_{53} } \hfill & {\quad \lambda_{54} } \hfill & {\quad \lambda_{55} } \hfill & {\quad \lambda_{56} } \hfill \\ {\lambda_{61} } \hfill & {\quad \lambda_{62} } \hfill & {\quad \lambda_{63} } \hfill & {\quad \lambda_{64} } \hfill & {\quad \lambda_{65} } \hfill & {\quad \lambda_{66} } \hfill \\ \end{array} } \right|, \\ \end{aligned}$$

where $H_{6} = \left| H \right|$; $\left| \bullet \right|$ is the Hessian determinant and λ_ij (i, j = 1, 2, 3, 4, 5, 6) are the second order partial derivatives of the cost function given by Eq. (11).

The second order partial derivatives of the cost function (11) are given below:

$$\lambda_{12} = \lambda_{21} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial k_{m} \partial k_{l} }} = 0,\quad \lambda_{13} = \lambda_{31} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial k_{m} \partial z_{r} }} = \frac{{\sigma \sqrt {L_{m} } }}{2T}\frac{{h_{1} }}{\mu }\frac{{\alpha \sigma \sqrt {rT} }}{2},$$

$$\lambda_{14} = \lambda_{41} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial k_{m} \partial m}} = - \frac{{\sigma \sqrt {L_{m} } \pi \left( {1 - \Phi \left( {k_{m} } \right)} \right)}}{T},\quad \lambda_{15} = \lambda_{51} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial k_{m} \partial l}} = 0,$$

$$\lambda_{16} = \lambda_{61} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial k_{m} \partial T}} = \frac{{\sigma \sqrt {L_{m} } }}{{T^{2} }}\left[ { - \frac{{h_{1} }}{\mu }\frac{{\alpha z_{r} \sigma \sqrt {rT} }}{4} + m\pi \left( {1 - \Phi \left( {k_{m} } \right)} \right)} \right],$$

$$\lambda_{23} = \lambda_{32} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial k_{l} \partial z_{r} }} = - \frac{{\sigma \sqrt {L_{l} } }}{T}\frac{{h_{1} }}{\mu }\frac{{\alpha \sigma \sqrt {rT} }}{2},\quad \lambda_{24} = \lambda_{42} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial k_{l} \partial m}} = 0,$$

$$\lambda_{25} = \lambda_{52} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial k_{l} \partial l}} = - \frac{{\sigma \sqrt {L_{l} } \pi \left( {1 - \Phi \left( {k_{l} } \right)} \right)}}{T},$$

$$\lambda_{26} = \lambda_{62} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial k_{l} \partial T}} = \frac{{\sigma \sqrt {L_{l} } }}{{T^{2} }}\left[ { - \frac{{h_{1} }}{\mu }\frac{{\alpha z_{r} \sigma \sqrt {rT} }}{4} + l\pi \left( {1 - \Phi \left( {k_{l} } \right)} \right)} \right],$$

$$\lambda_{34} = \lambda_{43} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial z_{r} \partial m}} = - \frac{{\left[ {h_{1} - \left( {1 - \frac{2\mu }{P}} \right)h_{2} } \right]\left[ {\frac{{z_{r} \alpha^{2} \sigma^{2} rT}}{2\mu } + \left( {1 - \alpha r} \right)T\alpha \sigma \sqrt {rT} } \right]}}{{2m^{2} }},$$

$$\lambda_{35} = \lambda_{53} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial z_{r} \partial l}} = - \frac{{\left[ {h_{1} - \left( {1 - \frac{2\mu }{{P_{r} }}} \right)h_{4} } \right]\left( {\frac{{z_{r} \alpha^{2} \sigma^{2} rT}}{2\mu } + \alpha rT\alpha \sigma \sqrt {rT} } \right)}}{{2l^{2} }},$$

$$\lambda_{36} = \lambda_{63} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial z_{r} \partial T}} = \left\{ \begin{array}{l} \frac{{z_{r} \alpha^{2} \sigma^{2} r}}{4\mu }\left\{ \begin{array}{l} h_{1} \left( {\frac{1}{m} + \frac{1}{l}} \right) + \frac{{h_{2} }}{m}\left[ {m\left( {1 - \frac{\mu }{P}} \right) - \left( {1 - \frac{2\mu }{P}} \right)} \right] \hfill \\ + \frac{{h_{3} \mu }}{{\alpha P_{r} }} + \frac{{h_{4} }}{l}\left[ {l\left( {1 - \frac{\mu }{{P_{r} }}} \right) - \left( {1 - \frac{2\mu }{{P_{r} }}} \right)} \right] \hfill \\ \end{array} \right\} \hfill \\ \quad + \frac{{3\alpha \sigma \sqrt {rT} }}{4}\left\{ \begin{array}{l} h_{1} \left[ {\frac{{\left( {1 - \alpha r} \right)}}{m} + \frac{\alpha r}{l}} \right] + \frac{{h_{2} \left( {1 - \alpha r} \right)}}{m}\left[ {m\left( {1 - \frac{\mu }{P}} \right) - \left( {1 - \frac{2\mu }{P}} \right)} \right] \hfill \\ + h_{3} \left( {\frac{1}{2\alpha } - \frac{r\mu }{{P_{r} }}} \right) - \frac{{h_{4} \alpha r}}{l}\left[ {l\left( {1 - \frac{\mu }{{P_{r} }}} \right) - \left( {1 - \frac{2\mu }{{P_{r} }}} \right)} \right] \hfill \\ \end{array} \right\} \hfill \\ \quad + \frac{1}{2T}\left[ {\frac{{h_{1} \sigma \alpha \sigma \sqrt {rT} \left( {k_{m} \sqrt {L_{m} } - k_{l} \sqrt {L_{l} } } \right)}}{2\mu } - \alpha \sigma \sqrt {rT} \left[ {1 - \Phi \left( {z_{r} } \right)} \right]\pi_{r} } \right] \hfill \\ \end{array} \right\},$$

$$\lambda_{45} = \lambda_{54} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{\partial m\partial l} = 0,$$

$$\begin{aligned} & \lambda_{46} = \lambda_{64} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{\partial m\partial T} = - \left\{ \begin{array}{l} \frac{1}{{T^{2} }}\left( {A_{1} + \pi \sigma \sqrt {L_{m} } \left[ {\phi \left( {k_{m} } \right) - k_{m} + k_{m} \Phi \left( {k_{m} } \right)} \right]} \right) \hfill \\ \quad + \frac{{\left( {1 - \alpha r} \right)\left[ {\left( {1 - \alpha r} \right)\mu T - {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right]\left[ {h_{1} - \left( {1 - \frac{2\mu }{P}} \right)h_{2} } \right]}}{{2m^{2} T}} \hfill \\ \end{array} \right\} \\ \quad {\text{and}}\;\lambda_{56} = \lambda_{65} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{\partial l\partial T} = - \left\{ \begin{array}{l} \frac{1}{{T^{2} }}\left( {A_{4} + \pi \sigma \sqrt {L_{l} } \left[ {\phi \left( {k_{l} } \right) - k_{l} + k_{l} \Phi \left( {k_{l} } \right)} \right]} \right) \hfill \\ \quad + \frac{\alpha r}{{2l^{2} T}}\left( {\alpha r\mu T - {{\alpha z_{r} \sigma \sqrt {rT} } \mathord{\left/ {\vphantom {{\alpha z_{r} \sigma \sqrt {rT} } 2}} \right. \kern-0pt} 2}} \right)\left[ {h_{1} - \left( {1 - \frac{2\mu }{{P_{r} }}} \right)h_{4} } \right] \hfill \\ \end{array} \right\}. \\ \end{aligned}$$

The remaining expressions of the second order partial derivatives, i.e. $\lambda_{11} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial k_{m}^{2} }}$, $\lambda_{22} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial k_{l}^{2} }}$,$\lambda_{33} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial z_{r}^{2} }}$, $\lambda_{44} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial m^{2} }}$, $\lambda_{55} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial l^{2} }}$, and $\lambda_{66} = \frac{{\partial^{2} EJTC\left( \cdot \right)}}{{\partial T^{2} }}$ are mentioned in Appendix 2.

Appendix 4: Derivation of the FSC model

The expression of the EJTC per unit time of the FSC corresponding to the CLSC under study is obtained from Eq. (11) by setting the parameters associated with the returned and remanufactured products as zero (i.e. A₃, h₃, A₄, h₄, r, L_l, π_r= 0). Thus, the expression for the EJTC per unit time of the FSC is given by

$$EJTC\left( {k_{m} ,m,T} \right) = \left\{ \begin{array}{l} \frac{{mA_{1} + A_{2} }}{T} + \left( {\frac{\mu T}{2m} + k_{m} \sigma \sqrt {L_{m} } } \right)h_{1} + \frac{\mu T}{2m}\left[ {\left( {m - 1} \right) - \left( {m - 2} \right)\frac{\mu }{P}} \right]h_{2} \hfill \\ \quad + \frac{m}{T}\sigma \sqrt {L_{m} } \left[ {\phi \left( {k_{m} } \right) - k_{m} + k_{m} \Phi \left( {k_{m} } \right)} \right]\pi \hfill \\ \end{array} \right\}.$$

(40)

To minimize the EJTC in Eq. (40), we take the first partial derivatives of the EJTC in Eq. (40) with respect to each decision variable while keeping other decision variables fixed, and setting them to zero, we obtain

$$\frac{{\partial EJTC\left( {k_{m} ,m,T} \right)}}{{\partial k_{m} }} = h_{1} \sigma \sqrt {L_{m} } - \frac{m}{T}\sigma \sqrt {L_{m} } \left[ {1 - \Phi \left( {k_{m} } \right)} \right]\pi ,$$

(41)

$$\frac{{\partial EJTC\left( {k_{m} ,m,T} \right)}}{\partial m} = \frac{{A_{1} }}{T} - \frac{{\mu Th_{1} }}{{2m^{2} }} + \frac{\mu T}{{2m^{2} }}\left( {1 - \frac{2\mu }{P}} \right)h_{2} + \frac{1}{T}\sigma \sqrt {L_{m} } \left[ {\phi \left( {k_{m} } \right) - k_{m} + k_{m} \Phi \left( {k_{m} } \right)} \right]\pi ,$$

(42)

and

$$\frac{{\partial EJTC\left( {k_{m} ,m,T} \right)}}{\partial T} = \left\{ \begin{array}{l} - \frac{{\left( {mA_{1} + A_{2} } \right)}}{{T^{2} }} + \frac{{\mu h_{1} }}{2m} + \frac{\mu }{2m}\left[ {\left( {m - 1} \right) - \left( {m - 2} \right)\frac{\mu }{P}} \right]h_{2} \hfill \\ \quad - \frac{m}{{T^{2} }}\sigma \sqrt {L_{m} } \left[ {\phi \left( {k_{m} } \right) - k_{m} + k_{m} \Phi \left( {k_{m} } \right)} \right]\pi \hfill \\ \end{array} \right\}.$$

(43)

The optimal value of the decision variables k_m, m (integer) and T, and the corresponding EJTC of the FSC are obtained from Eqs. (41), (42), (43), and (40) by using the iterative method similar to the CLSC model as explained in Sect. 4.