1 Introduction

In the business world today, the manufacturing firms heavily rely on fast-forward technologies to achieve their efficiency and get an advantageous platform to control the other competing firms. It is, therefore, a crucial job for managers to deal with the machineries which are managed by none other than ‘human beings’. So the fact is, how much we improve our technology, at the end of the day it comes to manpower only because mankind does not limit its creativity. As a consequence, the ‘human factor’ has drawn the attention of researchers, practitioners, and especially manufacturing sectors where human involvement has surpassed the machinery use, e.g. garment factories, business firms of leather-goods, sports-items, etc. [30]. The human factor ‘learning’ was first introduced by Wright [44] for an aircraft company. Thereafter, several researchers followed his paved path to explore learning in different directions under diverse circumstances [20, 45]. Unlike the conventional production process, they addressed learning achievement in practice where the workers gain skill from repetitive works and implement that in subsequent operations.

Although supply chain management prevails the mainstream system, remanufacturing has an explicit contribution towards ecology as well as economy. Moving one step ahead of decreasing waste, manufacturing firms can actually bag some more profit through recycling. Schrady [40] was among the pioneer researchers to address remanufacturing in an EOQ model. After that, a new pathway of manufacturing was opened to satisfy the demand of different quality items produced through raw material as well as used material. Owing to the fact that used items are returned at different conditions, it is worth running a screening process to classify the inappropriate products. This manual inspection process may incur error which is again categorized in two types—type I error (qualified items are detected as non-qualified) and type II error (non-qualified items are identified as qualified). Manual inspection can find a maximum of \(80\%\) defect in product [25], and an error can generate a wide difference in competing business firms which deal with aircraft materials, multi-characteristic components, etc. [37]. To reduce error and to have access to some incredible achievements, it is very convincing to assume ‘learning effect’ in the screening process [28, 30]. In the literature, learning effect in inspection has been used to optimize the inspection time as well as inspection rate and get benefitted from that. However, its use to minimize inspection error is infrequent [8], specifically when remanufacturing is involved.

Remanufacturing has been practiced in different industries from the very beginning where the products are very expensive to manufacture and the used products can replace the over-priced components like aircraft [44]. A case study for household appliances in the Gulf Cooperation Council (GCC) region showed the efficiency of reverse logistic process on the economy [2]. Zhang et al. [47] made a real case study on waste electrical and electronics equipments (WEEE) using four dynamic game models. Inspection process is an integral part of remanufacturing where the quality and durability are checked. Inspection has been practically studied in various industries. Shen and Chen [41] performed a case study in a Japanese fashion industry where a quality-based inspection has been carried out for outsourcing production. Their findings suggest some important strategies to maintain the product quality and improve the supply chain performance.

It is evident from the above discussion that some questions are yet to be answered while dealing with learning and inspection in manufacturing/remanufacturing firms: How the manufacturing model will respond if we incorporate the learning effect in inspection? Specifically, what are the consequences of learning effect if we include it in a remanufacturing model? Our aim in this study is to figure out the answers and accomplish the practical scenarios with some favorable strategies.

2 Literature review

In the last few decades, a growing number of literatures have been observed on our presumed topics: remanufacturing, price and quality dependent demand, learning in production, and inspection. In the following, we discuss those research works which fall in the domain of our concerned areas.

Schrady [40] was one of the early researchers who carried out elementary works on remanufacturing. Inderfurth et al. [19] differentiated between product recovery environments where products can be recycled in various ways. They [18] further considered a manufacturing-remanufacturing model where newly manufactured items were used to satisfy the demand of remanufactured items if needed. They approved the loss in profit to maintain the goodwill. Savaskan et al. [39] discussed about three channels to collect the used items—either through manufacturer or retailer, or third party. Later, Hong et al. [16] considered three partnerships for collection of used materials: manufacturer and retailer, retailer and third party, and manufacturer and third party. They showed that the manufacturer–retailer partnership was the most profitable one. Das and Dutta [5] studied a multi-period CLSC model with a strategic recovery process depending on the promotional offer and buying pattern of the consumers. Further, they [6] extended their model with an expanded recovery system along with a probabilistic relation between the offered incentive for returning used items and its probability. Govindan et al. [15] made a literature survey on 382 papers on closed-loop supply chain and reverse logistics, to recognize the research gap and guide the practitioners to a new direction. Giri and Sharma [13] analyzed a model for both single and multi-manufacturing and remanufacturing cycles. Jena et al. [24] considered an investment for advertisement, to collect the returned products. This advertising was done in five different ways incorporating the cost sharing matter. Among them, the centralized advertising policy was found to be the most appropriate strategy. Giri and Dey [11] analyzed a dual channel recycling model with uncertainty in used product collection in which any shortfall amount of used products was met by fresh raw materials supplied by a backup supplier. Sun et al. [42] dealt with 3D printing waste materials to recycle and issue high-quality materials from it. They used real-life data which results in a significant implication of their model towards ecological balance along with business. Recently, Dutta et al. [10] studied about the challenges and barriers faced by different industries while adopting the concept of reverse logistics, the ongoing trend in Indian context. They used fuzzy method to analyze the model and found that, classification of the barriers into different zones is the most effective strategy to handle them.

Price and/or quality dependent demand has drawn attention of many researchers during the last couple of decades. Whitin [43] was among the seminal researchers to address price-dependent demand in an EOQ model. Reyniers and Tapiero [38] assumed the quality factor in a contractual issue and examined both the cooperative and non-cooperative settings. Baiman et al. [3] also discussed about product quality and price along with risk neutral supplier and buyer under a contractible situation. Later, assuming price and quality dependent market demand, a comparison was made by De Giovanni [7] to identify the effective strategy between quality improvement and advertising strategy. This type of demand was also adopted by Maiti and Giri [32, 33] in a game theoretic model where different game structures were analyzed to find the best solution. Nagare and Dutta [35] addressed price, inventory stock, and time dependent demand for short life-cycle products under a single-period ordering and realistic pricing policies. Recently, price dependent demand along with greening and sales effort was studied under coordination mechanism and cost sharing contract [34].

Learning can be defined as a power function between time and quantity [44]. Further explanation can be given as, when the product quantity doubles, a fixed percentage of cost decrease takes place [21]. Jaber and Bonney [20] analyzed learning effect in production along with forgetting effect which is a similar type of effect occurs in the course of non-production time. Glock and Jaber [14] developed a multi-stage production-inventory model with imperfect production, where defective items are recycled. Their production and recycling processes both are subject to learning and forgetting effects. Kar et al. [26] optimized some EPQ models using genetic algorithm with stock-dependent demand and permissible delay in payment. They developed these models for deteriorating products where the set up and production costs are subject to learning effect. Lolli et al. [31] presented an imperfect production system under the influence of learning and forgetting. Afshari et al. [1] also developed a model with learning-forgetting effect. Recently, Huang and wang [17] proposed three recycling modes: no remanufacturing, manufacturer remanufacturing, and third party remanufacturing. They investigated the influence of profit sharing as well as learning effect in production and pricing decisions. They observed that, for increasing learning effect, the production cost decreases, and from shared information, the pricing decision can also be optimized.

Another important human factor in this context is ‘inspection error’ which was introduced by Jacobson [22] and categorized into two types—Type I error (eligible products are rejected as non-eligible) and Type II error (non-eligible products are accepted as eligible). These errors have major impacts on industries [37]. Yoo et al. [46] considered a profit maximization model with imperfect production and imperfect inspection which result in defective products as well as inspection error. Khan et al. [30] assumed the same environment with learning in production process for a cost effective model. Duffuaa and El-Ga’aly [9] examined a multi-objective optimization model where inspection measurement error was introduced and screened items are marketed/recycled according to their quality. Jauhari et al. [23] considered a three-layer supply chain performed by a single supplier, a single manufacturer, and a single retailer under an imperfect production and inspection process. Pal and Mahapatra [36] considered a three-stage supply chain for deteriorating products where shortage and backorder were allowed. They assumed price and stock-dependent stochastic demand along with imperfect production and inspection. Khan et al. [28] developed an inventory model where inspection is subject to learning. This assumption was adopted by Giri and Glock [12] in their inventory model with remanufacturing. Recently, Dey and Giri [8] investigated an inventory model where batch-wise inspection process was introduced in retailer’s inventory and learning effect was implemented in inspection error. They observed that learning effect in inspection error basically minimizes the error percentage and eventually optimizes the cost function.

From the above literature review, it is noticed that learning effect has been exploited to either increase the rate or decrease the time. But its impact on inspection error has not been investigated in reverse logistics process. In this paper, we consider a closed-loop supply chain which is run by a manufacturer and a retailer. The market demand we presume as deterministic and dependent on price and quality of the product. The manufacturing-remanufacturing process and the inspection process are both inspired by the learning effect. The rest of the paper is organized as follows: In Sect. 3, assumptions and notations are provided. Formulation and analysis of the proposed model are presented in Sect. 4. Section 5 discusses the numerical results and sensitivity analysis of some model-parameters. Section 6 addresses some important managerial insights. Finally, Sect. 7 draws some concluding remarks with future research directions.

3 Assumptions and notations

The proposed model is structured through the specified assumptions as given below:

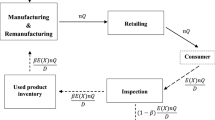
  • A closed-loop supply chain is formed by a single manufacturer and a single retailer for trading a single product.

  • The manufacturer produces the items in a lot and delivers in equal shipments to the retailer.

  • The used items are collected from the end-customers and undergo an inspection process.

  • Manufacturing and remanufacturing processes are operated jointly and are supported by both raw materials and qualified returned items. Produced items are of the same quality.

  • Production process is influenced by learning effect, which results in an increase in production rate as well as decrease in production time. Additionally, learning effect has an impact on the manufacturer’s setup cost.

  • The demand rate(D) of finished items is dependent on price and quality. We take \(D=d-\gamma p_{r}+\delta q\), where \(\gamma\), \(\delta >0\), d is the basic market demand, and \(p_{r}\) and q denote retail price and product quality, respectively.

  • The return rate is random and return of used items is managed by the retailer’s own channel.

  • Return items are inspected thoroughly and categorized into two groups—accepted and rejected. A fraction \(\beta\) (\(0 < \beta \le 1\)) of returned items is remanufacturable.

  • Inspection process is imperfect and it makes two types of error: Type I error (remanufacturable items are rejected as non-remanufacturable) and Type II error (non-remanufacturable items are accepted as remanufacturable).

  • Inspection process is subject to learning which has a positive impact on inspection error.

We use the following notations to develop the proposed model (m, r, and mu represent manufacturer, retailer and returned product, respectively):

Manufacturer:

  

\(A_{mj}\)

:

Setup cost per setup in the jth cycle

\(A_{m0}\)

:

Fixed setup cost per setup

\(A_{m1}\)

:

Variable setup cost per setup

\(h_{m}\)

:

Holding cost for finished products per unit per unit time

\(h_{mu}\)

:

Holding cost for returned items per unit per unit time

\(c_{mw}\)

:

Unit wholesale price of raw material

\(c_{m}\)

:

Production cost per unit time

\(c_{mu}\)

:

Unit purchase cost of used item

\(c_{mr}\)

:

Unit cost to purify and restore used item

\(c_{mi}\)

:

Unit inspection cost

\(c_{mI}\)

:

Unit penalty cost for Type I error

\(c_{mII}\)

:

Unit penalty cost for Type II error

\(c_{md}\)

:

Unit cost for disposing rejected item after inspection

P

:

Production rate

D

:

Demand rate

d

:

Basic market demand rate

\(\gamma >0\)

:

Price sensitivity coefficient

\(\delta >0\)

:

Quality sensitivity coefficient

\(\lambda >0\)

:

Quality improvement cost coefficient

\(T_{pj}(T_{dj})\)

:

Manufacturer’s production (non-production) period in cycle j

\(\beta\)

:

Effective/serviciable remanufacturable fraction of inspected items \((0 < \beta \le 1)\)

\(T_{1}\) \((=1/P)\)

:

Manufacturer’s production time to produce the first unit

\(e_{1j}\)

:

Probability of Type I error in the jth production cycle

\(e_{2j}\)

:

Probability of Type II error in the jth production cycle

X

:

Random variable \((0<X<1)\)

\(f_{X}(\cdot )\)

:

Probability density function of X

\(g_{e_{11}}(\cdot )\)

:

Probability density function of \(e_{11}\)

\(h_{e_{21}}(\cdot )\)

:

Probability density function of \(e_{21}\)

\(b\) \((0\le b<1)\)

:

Learning exponent for production

\(b_{1}\) \((0\le b_{1}<1)\)

:

Learning exponent for setup

\(b_{2}\) \((0\le b_{2} <1)\)

:

Learning exponent for Type I error

\(b_{3}\) \((0\le b_{3}<1)\)

:

Learning exponent for Type II error

Retailer:

  

\(A_{r}\)

:

Setup cost per setup

\(h_{r}\)

:

Holding cost for finished items per unit per unit time

\(p_{r}\)

:

Retail price (decision variable)

q

:

Product quality (decision variable)

n

:

Number of shipments from the manufacturer to the retailer (decision variable)

\(T_{r}\)

:

Length of an ordering cycle

Q

:

Batch size (decision variable)

4 Model formulation

We assume that the manufacturer produces the items in a lot and delivers to the retailer in n equal-sized batches of size Q. The production process is subject to learning, where learning induces growth in production rate, which regulates the production time as well as holding time. Setup cost also follows a decreasing pattern due to learning effect. The demand rate is dependent on retail price \(p_{r}\) and product quality q. The retailer conducts an inspection process to sort out the working items. We assume that the inspection process is imperfect and erroneous. A portion of the inspected items qualifies for recycling while the remaining portion is disposed off with a disposal cost. This inspection process is also subject to learning.

4.1 Manufacturer’s total cost

4.1.1 Manufacturing cost: learning in production

As per our assumption, the manufacturer produces a total of nQ items, in which one portion comes from raw materials and the rest portion from collected used items. The manufacturing process is subject to learning which follows the Wright’s learning curve. Wright’s learning curve represents a power function relating to production time and produced units, which basically explains the fact of lowering the unit production time by a constant percentage if the produced quantity is doubled. The learning curve is defined by the relation \(T_{i}=T_{1}i^{-b}\), where \(T_{i}\) is the time to produce the ith unit. Figure 1a, b shows the inventory pattern during a production period [30]. Using the wright’s learning curve function, the production time can be formulated as

$$\begin{aligned} Tp_{j}= \int _{(j-1)Q_{p}}^{jQ_{p}}T_{1}x^{-b}dx = \frac{T_{1}}{1-b}{Q_{p}^{1-b}[j^{1-b}-(j-1)^{1-b}]} \end{aligned}$$
(1)

The above can be rewritten as

$$\begin{aligned} Q_{p}=\left[ \frac{(1-b)Tp_{j}}{T_{1}}\frac{1}{j^{1-b}-(j-1)^{1-b}}\right] ^{\frac{1}{1-b}} \end{aligned}$$
(2)

Using (2), the production quantity Q(t) at any time t can be expressed as

$$\begin{aligned} Q(t)=\left[ \frac{(1-b)t}{T_{1}}\frac{1}{j^{1-b}-(j-1)^{1-b}}\right] ^{\frac{1}{1-b}} \end{aligned}$$
(3)

Therefore, the inventory incurred at the time of production for the jth production cycle can be written as

$$\begin{aligned} Ip_{j} =\int _{0}^{Tp_{j}}Q(t)dt = \frac{T_{1}}{2-b} [j^{1-b}-(j-1)^{1-b}](nQ)^{(2-b)} \end{aligned}$$
(4)

Hence, the first shipment in the jth cycle will take place after time \(T_{1j}\) where

$$\begin{aligned} T_{1j}=\int _{Q_{p}}^{Q+Q_{p}}T_{1}x^{-b}dx = \frac{T_{1}}{1-b} Q^{1-b}[(1+(j-1)n)^{1-b}-((j-1)n)^{1-b}] \end{aligned}$$
(5)

In the non-production period of the ith cycle, the inventory can be calculated from Fig. 1 as

$$\begin{aligned} Id_{j}= & {} \frac{nT_{1}}{1-b} Q^{2-b}\left[ (1+(j-1)n)^{1-b}-((j-1)n)^{1-b}\right] \nonumber \\&+\frac{n(n-1)Q^{2}}{D}-\frac{T_{1}(j^{1-b}-(j-1)^{1-b})}{2-b}(nQ)^{2-b} \end{aligned}$$
(6)
Fig. 1
figure 1

(a) Manufacturer’s inventory under learning. (b) Manufacturer’s total inventory under learning

Full size image

The total inventory moved from the manufacturer to the retailer in a cycle is \(\frac{n(n-1)Q^{2}}{2D}\). So, in the jth cycle, the manufacturer’s average inventory is

$$\begin{aligned}&Ip_{j}+Id_{j}-\frac{n(n-1)Q^{2}}{2D} \nonumber \\&\quad =\frac{nT_{1}}{1-b} Q^{2-b}\left[ (1+(j-1)n)^{1-b}-((j-1)n)^{1-b}\right] \nonumber \\&\qquad +\frac{n(n-1)Q^{2}}{2D}-\frac{T_{1}(j^{1-b}-(j-1)^{1-b})}{(2-b)(1-b)}(nQ)^{2-b} \end{aligned}$$

Therefore, the manufacturer’s holding cost for the jth cycle is obtained as

$$\begin{aligned}&h_{m}\left[ \frac{nT_1Q^{2-b}((1+(j-1)n)^{1-b}-((j-1)n)^{1-b})}{1-b}\right. \nonumber \\&\quad \left. -\frac{T_{1}(j^{1-b}-(j-1)^{1-b})}{(2-b)(1-b)}(nQ)^{2-b} +\frac{n(n-1)Q^{2}}{2D} \right] \end{aligned}$$

Hence, for the jth cycle, the manufacturing cost in case of learning is the sum of setup cost, production cost, and holding cost. Here the setup cost is also impacted by learning effect. The setup cost is composed of a fixed cost (\(A_{m0}\)) and a decreasing cost component (\(A_{m1}\)). The cost component \(A_{m1}\) decreases due to repeated number of setups made for production in each cycle. Therefore, the setup cost \(A_{m}\) for the jth cycle can be expressed as in [26]: \(A_{mj}=A_{m0}+A_{m1}j^{-b_{1}}\), where \(b_{1}\) is the learning exponent assumed for setup cost.

Thus, the manufacturer’s cost in case of learning is obtained as [30]:

$$\begin{aligned}&A_{mj}+ c_{m}\frac{T_{1}}{1-b}{(nQ)^{1-b}[j^{1-b}-(j-1)^{1-b}]} \nonumber \\&\quad +h_{m}\left[ \frac{nT_1Q^{2-b}}{1-b}((1+(j-1)n)^{1-b}-((j-1)n)^{1-b})+\frac{n(n-1)Q^{2}}{2D}\right. \nonumber \\&\quad \left. -\frac{T_{1}(j^{1-b}-(j-1)^{1-b})}{(2-b)(1-b)}(nQ)^{2-b}\right] \end{aligned}$$
(7)

4.1.2 Remanufacturing item cost: learning in inspection

Used items are supposed to collect from the end-customers through the retailer and stored at the manufacturer. We assume that the return rate is XD where the random variable X follows a uniform distribution. Here the return rate is basically a fraction of demand rate. Therefore, the expected quantity of returned items in each cycle is E[X]nQ.

As per our assumption, inspection is erroneous and it can generate Type I and Type II errors. Let \(e_{1j}\) and \(e_{2j}\) be the probabilities of Type I and Type II errors respectively, in the jth production run, where \(e_{1j}=e_{11}j^{-b_{2}}\) and \(e_{2j}=e_{21}j^{-b_{3}}\). \(e_{11}\) and \(e_{21}\) represent the respective probabilities of Type I and Type II errors during the first cycle. We assume that a fraction \(\beta\) of the total expected returned items is remanufacturable. Therefore, the expected number of rejected items for Type I error is \(\beta nQ E[X]E[e_{1j}]\). The expected number of rejected items for Type II error is \((1-\beta )nQ E[X](1-E[e_{2j}])\). So, at the end of inspection, the expected number of rejected items is \(\beta nQ E[X]E[e_{1j}]+(1-\beta )nQ E[X](1-E[e_{2j}])\). The rest portion of inspected items goes to the remanufacturing process. Now, the expected number of non-recyclable items identified for recycling as qualified item is \((1-\beta )nQ E[X]E[e_{2j}]\). This amount of items along with the rejected items is finally disposed off with some disposal cost. The expected number of recyclable items after inspection is \(E[X]nQ- \beta nQ E[X]E[e_{1j}]-(1-\beta )nQ E[X](1-E[e_{2j}])\).

Fig. 2
figure 2

Used item inventory

Full size image

If the inspection rate of returned items is I (\(I>P>D\)), then the accumulated used items is depleted at the current rate of production until time E[X]nQ/I. Now, the inventory level of returned items at any time t is \(E[X]nQ-Q(t)\) upto the time of inspection \(T_{j}=E[X]nQ/I\) (Fig. 2), where Q(t) can be obtained from Eq. (3). At the end of the inspection process, the inventory reaches to the level \(E[X]nQ- \beta nQ E[X]E[e_{1j}]-(1-\beta )nQ E[X](1-E[e_{2j}])\). So, the inventory level at any time t is \(E[X]nQ- \beta nQ E[X]E[e_{1j}]-(1-\beta )nQ E[X](1-E[e_{2j}])-Q(t)\). Let \(T_{dj}\) be the time of total depletion of remanufacturable items, which can be obtained as

$$\begin{aligned}&E[X]nQ- \beta nQ E[X]E[e_{1j}]-(1-\beta )nQ E[X](1-E[e_{2j}])\nonumber \\&\quad -\left[ \frac{(1-b)T_{dj}}{T_{1}(j^{1-b}-(j-1)^{1-b}) }\right] ^{\frac{1}{1-b}}=0\nonumber \\&\quad \Rightarrow T_{dj}=\frac{T_{1}(j^{1-b}-(j-1)^{1-b})}{1-b}\Big [E[X]nQ\big (\beta +E[e_{2j}]-\beta E[e_{1j}]-\beta E[e_{2j}]\big )\Big ]^{1-b} \end{aligned}$$
(8)

Therefore, the expected holding cost of returned items from the time of inspection 

$$\begin{aligned}&= h_{mu}\Bigg [\int _{0}^{T_{j}}\Big [E[X]nQ-\left( \frac{1-b}{T_{1}(j^{1-b}-(j-1)^{1-b})}t\right) ^{\frac{1}{1-b}}\Big ]dt\nonumber \\&\quad + \int _{T_{j}}^{T_{dj}}\Big [E[X]nQ-\beta nQ E[X]E[e_{1j}]\nonumber \\&\quad -(1-\beta )nQ E[X]E[e_{2j}]-\left( \frac{1-b}{T_{1}(j^{1-b}-(j-1)^{1-b})}t\right) ^{\frac{1}{1-b}}\Big ]dt\Bigg ]\nonumber \\&= h_{mu}\Bigg [\frac{(E[X]nQ)^{2}}{I}(1-\beta -E[e_{2j}]+\beta E[e_{1j}]+\beta E[e_{2j}])\nonumber \\&\quad +\frac{T_{1}(j^{1-b}-(j-1)^{1-b})}{(1-b)(2-b)}\Big [E[X]nQ\big (\beta +E[e_{2j}]-\beta E[e_{1j}]-\beta E[e_{2j}]\big )\Big ]^{2-b}\Bigg ] \end{aligned}$$
(9)

The used item cost includes purchasing cost, inspection cost, penalty cost, recovery cost, and disposal cost. Now, the manufacturer’s total cost is the sum of remanufacturing and manufacturing costs. Remanufacturing cost includes all the costs associated with returning of used items. So this cost can be written as

$$\begin{aligned}&A_{mj}+ c_{m}\frac{T_{1}}{1-b}{(nQ)^{1-b}[j^{1-b}-(j-1)^{1-b}]} \nonumber \\&\quad +c_{mi}E[X]nQ+c_{mr}[E[X]nQ-\beta nQ E[X]E[e_{1j}]-(1-\beta )nQ E[X](1-E[e_{2j}])]\nonumber \\&\quad +c_{mI}E[X]nQ \beta E[e_{1j}]+c_{mII}E[X]nQ (1-\beta ) E[e_{2j}]+c_{md}E[X]nQ(1-\beta +\beta E[e_{1j}])\nonumber \\&\quad +c_{mw}nQ(1-E[X]\beta +E[X]\beta E[e_{1j}])\nonumber \\&\quad +h_{m}\left[ \frac{nT_1Q^{2-b}}{1-b}((1+(j-1)n)^{1-b}-((j-1)n)^{1-b})\right. \nonumber \\&\quad \left. +\frac{n(n-1)Q^{2}}{2D}-\frac{T_{1}(j^{1-b}-(j-1)^{1-b})}{(2-b)(1-b)}(nQ)^{2-b}\right] \nonumber \\&\quad +h_{mu}\Bigg [\frac{(E[X]nQ)^{2}}{I}(1-\beta -E[e_{2j}]+\beta E[e_{1j}]+\beta E[e_{2j}])\nonumber \\&\quad +\frac{T_{1}(j^{1-b}-(j-1)^{1-b})}{(1-b)(2-b)}\Big [E[X]nQ\big (\beta +E[e_{2j}]-\beta E[e_{1j}]-\beta E[e_{2j}]\big )\Big ]^{2-b}\Bigg ] \end{aligned}$$
(10)

4.2 Retailer’s total cost

The retailer receives the ordered quantity in n shipments from the manufacturer (Fig. 3). The retailer’s total cost which includes ordering cost, purchasing cost, and holding cost can be written as

$$\begin{aligned} TC_{r}=nA_{r}+wnQ+h_{r}\frac{nQ^{2}}{2D} \end{aligned}$$
(11)
Fig. 3
figure 3

Retailer’s inventory

Full size image

4.3 Average expected total profit

The total expected cost of the supply chain system can be obtained by summing up the manufacturer’s expected cost and the retailer’s expected cost. Therefore, the average expected total profit can be obtained as

$$\begin{aligned} AETP_{j}= & {} \frac{D}{nQ}\Bigg [p_{r}nQ-A_{mj}-nA_{r}-\lambda q^{2}\frac{nQ}{D}-c_{m}\frac{T_{1}}{1-b}{(nQ)^{1-b}[j^{1-b}-(j-1)^{1-b}]}\nonumber \\&-c_{mi}E[X]nQ-c_{mr}[E[X]nQ-(1-\beta )nQ E[X](1-E[e_{2j}])]\nonumber \\&-\beta nQ E[X]E[e_{1j}]-c_{mI}E[X]nQ \beta E[e_{1j}]-c_{mII}E[X]nQ (1-\beta ) E[e_{2j}]\nonumber \\&-c_{md}E[X]nQ(1-\beta +\beta E[e_{1j}])-c_{mw}nQ(1-E[X]\beta +E[X]\beta E[e_{1j}])\nonumber \\&-h_{m}\left[ \frac{nT_1Q^{2-b}}{1-b}((1+(j-1)n)^{1-b}-((j-1)n)^{1-b})+\frac{n(n-1)Q^{2}}{2D}\right. \nonumber \\&\left. -\frac{T_{1}(j^{1-b}-(j-1)^{1-b})}{(2-b)(1-b)}(nQ)^{2-b}\right] -h_{r}\frac{nQ^{2}}{2D}-h_{mu}\Bigg [\frac{(E[X]nQ)^{2}}{I}\left( 1-\beta \right. \nonumber \\&\left. -E[e_{2j}]+\beta E[e_{1j}]+\beta E[e_{2j}]\right) +\frac{T_{1}(j^{1-b}-(j-1)^{1-b})}{(1-b)(2-b)}\Big [E[X]nQ\big (\beta +E[e_{2j}]\nonumber \\&-\beta E[e_{1j}]-\beta E[e_{2j}]\big )\Big ]^{2-b}\Bigg ]\Bigg ] \end{aligned}$$
(12)

Our main concern is to find the optimal values of n, Q, \(p_{r}\) and q that maximize the average expected total profit \(AETP_{j}(n, Q, p_{r}, q)\), \(j=~1,2,\ldots\).

Now, we check the concavity of profit function \(AETP_{j}\) w.r.t. the decision variables.

Differentiating (12) partially with respect to \(p_{r}\), we get

$$\begin{aligned} \frac{\partial AETP_{j}}{\partial p_{r}}= & {} D-\gamma p_{r}+ \frac{A_{mj}}{nQ}\gamma + \frac{A_{r}}{Q}\gamma +c_{m}\frac{\gamma T_{1}}{1-b}{(nQ)^{-b}[j^{1-b}-(j-1)^{1-b}]}\nonumber \\&+c_{mi}E[X]\gamma +c_{mr}\gamma \big (E[X]+\beta E[X]E[e_{1j}]-(1-\beta )nQ E[X](1-E[e_{2j}])\big )\nonumber \\&+c_{mI}E[X] \beta \gamma E[e_{1j}]+c_{mII}E[X]\gamma (1-\beta )E[e_{2j}]+c_{md}E[X]\gamma (1-\beta \nonumber \\&+\beta E[e_{1j}])+c_{mw}\gamma (1-E[X]\beta +E[X]\beta E[e_{1j}])+h_{m}\gamma \left[ \frac{T_1Q^{1-b}}{1-b}((1\right. \nonumber \\&\left. +(j-1)n)^{1-b}-((j-1)n)^{1-b})\right] -h_{m}\gamma \left[ \frac{T_{1}(j^{1-b}-(j-1)^{1-b})}{(1-b)(2-b)}(nQ)^{1-b}\right] \nonumber \\&+h_{mu}\Big [\frac{\gamma (E[X]nQ)}{I}(1-\beta -E[e_{2j}]+\beta E[e_{1j}]+\beta E[e_{2j}])\Big ]\nonumber \\&+h_{mu}\Big [\frac{\gamma T_{1}(nQ)^{1-b}(j^{1-b}-(j-1)^{1-b})}{(1-b)(2-b)}\Big [E[X]\big (\beta +E[e_{2j}]-\beta E[e_{1j}]\nonumber \\&-\beta E[e_{2j}]\big )\Big ]^{2-b}\Big ] \end{aligned}$$
(13)

Differentiating (13) partially with respect to \(p_{r}\), we can easily get

$$\begin{aligned} \frac{\partial ^{2}AETP_{j}}{\partial p_{r}^{2}} = -2\gamma < 0 \end{aligned}$$
(14)

Similarly, it can be shown that

$$\begin{aligned} \frac{\partial ^{2}AETP_{j}}{\partial q^{2}} = -2\lambda < 0 \end{aligned}$$
(15)

The above results indicate the concavity nature of the average expected total profit function \(AETP_{j}(n, Q, p_{r}, q)\) with respect to \(p_{r}\) and q for fixed n and Q.

Note: In case of no learning, we can check the concavity of the profit function with respect to the number of shipments n (for fixed Q, \(p_{r}\) and q) under some specific conditions.

Let us consider n as not discrete but a continuous variable. Then differentiating (12) twice partially with respect to n, we get

$$\begin{aligned} \frac{\partial ^{2}AETP_{j}}{\partial n^{2}}= & {} -\frac{2A_{m1}D}{n^{3}Q}-b(b+1)\frac{c_{m}DT_{1}n^{-b-2}Q^{-b}}{1-b}-bh_{m}\frac{DT_{1}n^{-b-1}Q^{1-b}}{1-b}\nonumber \\&\quad +bh_{mu}\frac{DT_{1}n^{-b-1}Q^{1-b}}{1-b}\Big [E[X]\big (\beta +E[e_{2j}]-\beta E[e_{1j}]-\beta E[e_{2j}]\big )\Big ]^{2-b} \end{aligned}$$
(16)

From (16), we see that the first three terms are negative. So, \(\frac{\partial ^{2}AETP_{j}}{\partial n^{2}} < 0\) provided that

$$\begin{aligned} \beta +E[e_{2j}]-\beta E[e_{1j}]-\beta E[e_{2j}]< 0 ~~ \Rightarrow ~~~ \beta +E[e_{2j}] < \beta E[e_{1j}]+\beta E[e_{2j}] \end{aligned}$$
(17)

Therefore, in case of no learning, the average expected total profit function \(AETP_{j}(n, Q, p_{r}, q)\) is concave with respect to real n provided that the condition \(~~\beta +E[e_{2j}] < \beta E[e_{1j}]+\beta E[e_{2j}]\) is satisfied.

We can also check the concavity of profit function (12) with respect to Q and \(p_{r}\) graphically (see Fig. 4) for fixed n and q. Assuming that the average expected profit function (12) is concave in Q, \(p_{r}\) and q, we can find the optimal solution following the algorithm as given below:

Algorithm:

  1. Step 1.

    Set \(j=1\) .

  2. Step 2.

    Set \(n=1\). Use line search technique on n to find the optimal values of Q, \(p_{r}\) and q for which \(AETP_{j}\) is maximized.

  3. Step 3.

    Determine the optimal value of \(AETP_{j}\).

  4. Step 4.

    Set \(j=j+1\).

  5. Step 5.

    Repeat steps 2, 3 and 4 until the desired number of cycles.

  6. Step 6.

    Stop.

5 Numerical example

In this section, we demonstrate the proposed model with a numerical example. The data for the numerical example are taken as follows:

$$\begin{aligned}\begin{array}{llll} c_{mw}= \$\hbox {120 per unit};&{}c_{mII}=\$\hbox {50 per unit}&{}A_{m0}= \$\hbox {300 per setup};&{} b = \hbox {0.32} ;\\ c_{mu}= \$\hbox {10 per unit}; &{} c_{mr}= \$\hbox {20 per unit}&{}A_{m1}= \$\hbox {100 per setup};&{}b_1 = \hbox {0.32};\\ c_{m}= \$\hbox {100000 per year};&{} h_{m}= \$\hbox {4 per unit per year};&{}\beta = \hbox {0.75};&{} b_2 = \hbox {0.4} ;\\ c_{mi}= \$\hbox {0.5 per unit};&{} h_{r}= \$\hbox {5 per unit per year};&{}P=\hbox {1500 units per year};&{} b_3 = \hbox {0.3} ; \\ c_{md}= \$\hbox {0.5 per unit};&{} h_{mu}= \$\hbox {2 per unit per year};&{} d=\hbox {2000 units per year};&{} \delta = \hbox {1};\\ c_{mI}=\$\hbox {200 per unit} &{} A_{r}= \$\hbox {50 per order}; ; &{} \lambda =\$ \hbox {200 per year}; &{} \gamma = \hbox {3.5};\\ I= \hbox {175200 units per year}. &{} &{} &{} \\ \end{array}\end{aligned}$$

Here we assume that X follows the uniform distribution:

$$\begin{aligned} f(X)=\left\{ \begin{array}{ll} \frac{1}{0.9-0.5},&{} 0.5 \le X \le 0.9 \\ 0, &{}\text{ otherwise } \end{array} \right. \end{aligned}$$

and \(e_{11}\) and \(e_{21}\) follow uniform distributions:

$$\begin{aligned} g(e_{11})=\left\{ \begin{array}{ll} \frac{1}{0.04},&{} 0 \le e_{11} \le 0.04 \\ 0,&{}\text{ otherwise } \end{array} \right. \end{aligned}$$
$$\begin{aligned} h(e_{21})=\left\{ \begin{array}{ll} \frac{1}{0.04},&{} 0 \le e_{21} \le 0.04 \\ 0,&{}\text{ otherwise } \end{array} \right. \end{aligned}$$

The concavity of average expected total profit with respect to Q and \(p_{r}\) (for fixed n and q) can be seen from Fig. 4.

Fig. 4
figure 4

Concavity of AETP w.r.t. Q and \(p_{r}\)

Full size image
Table 1 Optimal results for consecutive ten cycles
Full size table

Table 1 shows the optimal results for consecutive ten cycles. Note that the expected total profit of the supply chain increases as the number of cycles increases. This indicates the significance of learning in the proposed model. In the first few cycles, the percentage increase in profit is noteworthy. After that the percentage increase in profit becomes negligible i.e., the expected total profit becomes constant (approximately). In other words, the profit curve becomes plateau. This behaviour of the profit curve is due to the fact that the workers approach to their verge of potential after a few production cycles from the beginning.

Table 2 shows a comparison of the optimal results of the model under different circumstances. The first row shows the optimal results of the basic model without inspection error, where no learning is considered in the production process. The second row shows the optimal results of the model without learning in production, although inspection is considered with learning effect. Though learning effect influences inspection error, it can not reduce the error to zero level. This causes the diminution in profit compared to the base case.

Table 2 Comparison of different models
Full size table

The third row in Table 2 shows the results of the model when production is influenced by learning but there is erroneous inspection. Also learning is absent in inspection. As a result, the error occurs in a fixed percentage and cannot be minimized. However, the impact of learning in production induces greater optimal ordered quantity, which results in an enhanced expected profit. Finally, the last row shows the optimal results of our proposed model. Here the profit growth can be explained as in the case of previous model. Moreover, learning in inspection reduces the error, which leads to an extra profit added to the expected total profit of the proposed model.

We now compare our proposed model with Giri and Glock’s [12] model with some modifications. We assume price dependent demand by taking \(\delta =0\) and ignore the learning effect in production and inspection. So, in the profit function of our proposed model, we take \(\delta =0\), \(b=0\), \(b_1=0\), \(b_2=0\) and \(b_3=0\), and equate the other parameters with Giri and Glock’s model-parameters. We then obtain the optimal results as \(n^*=3\), \(Q^*=138.09\), \(p_{r}^*=353.27\) and the total profit as 165375 which is an improved profit compared to that of the basic closed-loop supply chain model of Giri and Glock [12] without learning and forgetting in production and inspection. Again, if we ignore the remanufacturing part and include the inspection process at the retailer’s end with inspection error then our model will be converted to Khan et al.’s [30] model. However, Khan et al. [30] considered a cost minimization model while we dealt with a profit maximization model. So quantitative comparison is not possible in this case.

Fig. 5
figure 5

Average expected total profit versus \(\beta\)

Full size image
Fig. 6
figure 6

Average expected total profit versus P

Full size image

In order to facilitate our model with more functional approach, we examine the impact of \(\beta\) (fraction of remanufacturable items) on the optimal decisions. It can be seen from Fig. 5 that, when the fraction increases, the average expected total profit increases. From the practical point of view, it is pretty obvious that, if we decrease the ineligible proportion from returned items, we can bag more profit. The impact of production rate on the optimal results is reflected in Fig. 6. As the manufacturer’s production rate increases, more items can be marketed over the same time span, which causes an increase in the expected total profit.

Now, we discuss the sensitivity of the human factor ‘learning’ in production as well as in inspection. In our numerical example, we take the value of the learning exponent b as 0.32, which means that the learning rate is about \(80\%\) for production. It is interesting to note from Table 3 that the expected profit varies on a larger scale when the learning exponent is comparatively low, but for higher value of b, the change in expected profit drastically reduces. If we look into the optimal quantity, it can be observed that, for increasing learning exponent, the number of shipments also goes down sharply, which reduces the ordering cost and upholds the principle of rising profit.

Table 3 Average values of optimal results for varying b
Full size table

A similar trend in profit is noticed in Fig. 7 which displays the influence of learning effect on setup cost, and Type I and Type II inspection errors. As the learning exponents increase, the average expected total profit increases. Learning in setup cost does not have an impressive effect on the expected total profit. It is observed that \(b_{2}\) has a major effect on profit compared to that of \(b_{3}\). One of the underlying reasons for this is the Type I error in which a remanufacturable item is categorized as non-remanufacturable. For large-scale industries where crucial parts are nurtured and where remanufacturing is more effectual than manufacturing, false rejection of good items affects more than the false acceptance of bad items.

Fig. 7
figure 7

Average expected total profit versus learning exponent

Full size image

We now consider the parameters \(\gamma\) and \(\delta\) which are sensitive parameters of price and quality. As the price sensitive coefficient increases, the retail price decreases. Price sensitivity coefficient and price are inversely related to one another. If one goes up then the other one must have to decrease.

Table 4 Average values of the optimal results for varying \(\gamma\) and \(\delta\)
Full size table

One more exciting observation can be made from Table 4 that, along with the retail price, the quality also decreases for increasing \(\gamma\). But it acts quite sensibly when variation in \(\delta\) comes into consideration. The more sensible the consumers, the greater quality they achieve. This causes a rise in profit, but it is very low in comparison.

We now consider the impact of \(\lambda\), the investment cost coefficient of quality. When \(\lambda\) increases, the product quality decreases (see Fig. 8). Therefore, more investment to maintain the product quality implies a lower quality of product.

Fig. 8
figure 8

Variation of product quality w.r.t. \(\lambda\)

Full size image

6 Managerial insights

From the numerical results and the sensitivity analysis, some important managerial implications can be established throughout the study.

First, the proposed model results in better profit compared to the other cases like no learning in production, no learning in inspection, and in the absence of learning in both production and inspection. In this situation, the manufacturer should recommend learning in both production and inspection to earn additional profit.

Second, though the positive impacts of learning effect make a higher profit line during the entire investigation, the increasing rate of profit decreases simultaneously and reaches a certain fixed level. In this regard, the managers have to take some effective steps like adopting new work methods, investing money, new mechanism, etc. to break the plateau form of the learning curve. This will have a beneficial influence on the workers which accordingly reinforces the profit.

Third, the price and quality sensitive factors influence the market demand and consequently control the profit function. The higher the price sensitivity, the lower the retail price, which eventually causes a profit drop. Similarly, the higher the quality sensitive factor, the higher the quality as well as the whole system profit. A strategic decision should be taken to fix the sensitive factors, so that the management can achieve a desirable profit margin.

Fourth, a lower used item proportion in remanufacturing leads to acquiring a lower profit. The manufacturer therefore should apply his/her best strategy to get hold of economic growth as well as eco-friendly behaviour.

7 Conclusion

In this paper, we have studied a closed-loop supply chain with one manufacturer and one retailer considering price and quality dependent demand, and random return under the influence of the human factor ‘learning’ in production and inspection. Both manufacturing and remanufacturing are performed by the manufacturer himself and the products from both processes are treated equally. A numerical example is provided to support the findings of the proposed model.

As higher price provokes customers to back off and greater quality draws customers’ attention, our model can help managers to choose the right decision to fix the desirable retail price as well as maintain the quality with minimal investment. It is observed from the numerical study that learning effect had a great impact on production for a few initial cycles. After that, the impact becomes negligible due to reaching workers’ maturity level of efficiency. At this juncture, managers should invest to break the plateau form of the learning curve by improving the workers’ performance through advanced training, adopting new technology, etc. It is also observed that learning in inspection has bagged some additional profit. Type I error is more functional compared to Type II error. So, when it comes to cost-effectiveness, the management should explore the efficient value of \(b_{2}\) to minimize the error. It is also observed that increasing the proportion of used items leads to raising an additional profit as well as diminishing waste resources. At this stage, manufacturers would like to get return items as much as possible but practically that can never happen. In this regard, what managers can do is to make some investment to collect used items. The industries handling aircrafts, ships, cars, etc. where production cost is very high, should take care of this type of investment.

This paper assumes that price and quality dependent demand can fulfil the customers' demand but now-a-days consumers prefer greenness of the product over price and quality. So, there can be a preferable extension considering greening level and carbon emission matter. In our study, we have assumed that the remanufactured products are as good as the manufactured products. But in reality, consumers may not accept the manufactured and the remanufactured products as the same. So, a price differentiation along with separate markets would be a practical approach to extend this work. One can immediately extend our model by assuming another human factor ‘forgetting’ which is an inseparable part of learning. Another extension can be done by incorporating multi-item instead of a single item in the production process. Further, the inclusion of multiple manufacturers/retailers can give us a major extension on a more general note.