Coordinating a three level supply chain under generalized parametric interval-valued distribution of uncertain demand

Abstract

In uncertain supply chain management problem, the optimal order quantity often depends heavily on the distribution of uncertain demand. When the exact possibility distribution is unavailable, it is required to develop a novel method to characterize the uncertain demand and deal with the corresponding supply chain coordination problem. This paper addresses the coordination problem for a three level supply chain in a single period model, where the uncertain demand is characterized by generalized parametric interval-valued possibility distribution. We define the lambda selection of uncertain demand, and discuss its parametric possibility distribution and mean value. In addition, we construct L–S measure by parametric possibility distribution of the lambda selection, and use it to define the L–S integral of uncertain profits under different scenarios. Under the risk-neutral criterion, we demonstrate that the mean supply chain profit in centralized decision is greater than the total mean supply chain profit in decentralized decision. Then a three level supply chain with revenue-sharing contract and return policy is studied and the analytical expressions of the optimal order quantity for different members are derived. Under the variable parametric possibility distribution of demand, we provide the sufficient conditions to ensure the three level supply chain can be fully coordinated and show the total mean profit of the channel can be allocated with any specified ratios among the members. Finally, we provide some managerial implications in a practical supply chain coordination problem. The computational results demonstrate the efficiency of the proposed parametric credibilistic optimization method.

1 Introduction

Supply chain is a complex system consisting of independent and economically rational members. In general, supply chain is composed of suppliers, manufacturers, distributors, retailers and customers. If there is no clear command and control structure, the supply chain is a decentralized control system. In this case, channel members make their own decisions independently to maximize their own profits. This self-serving action often leads to poor performance of the supply chain from the global supply chain point of view, such as inaccurate demand forecast, inadequate service level and excessive inventory. That is, the supply chain is lack of competitiveness in comparison with other supply chains. Supply chain coordination has been recognized as one of the key drivers of improvement in supply chain performance during the last 10–15 years (Hou et al. 2016). Therefore, it is essential to coordinate the actions and decisions among these members in supply chain. Because contracts can motivate all the members to be a part of the entire supply chain, the contracts are effective instruments to achieve the supply chain coordination. In the real business market, to encourage the retailer to order more products, one of effective methods for the manufacturer is to negotiate a contract with his retailer. For the same reason, the supplier also wants to negotiate a contract with the manufacturer. Obviously, if we can make the contracts work cooperatively, we may develop the potential competition of a three supply chain as much as possible. Thus, researchers have paid more and more attention to the supply chain coordination by considering different types of contract mechanisms. During the past two decades, some contract mechanisms have been explored in order to coordinate the supply chain, including return policies (Bose and Anand 1997; Hu et al. 2014), backup agreements (Eppen and Iyer 1997), quantity discounts (Ogier et al. 2013; Schotanus et al. 2009), revenue-sharing contracts (Cachon and Lariviere 2005; Henry and Wernz 2015), quantity flexibility contracts (Tsay 1999), sales rebate contracts (Taylor 2002) and options (Barnes-Schuster et al. 2002; Zhao et al. 2013).

Although supply chains often contain three or even more levels of members, most of the existing literature studied supply chain management problem in two level or three level supply chain environment. For example, Sarkar (2013) developed a production-inventory model for a deteriorating item in a two-echelon supply chain management. Munson and Rosenblatt (2001) considered a three level supply chain and explored the benefits of using quantity discounts on both end of the supply chain. Giannoccaro and Pontrandolfo (2004) showed a three level supply chain could be coordinated by revenue-sharing contracts, and they adopted simulation techniques to evaluate the performance of the three level supply chain. Ding and Chen (2008) considered the coordination of a three level supply chain with flexible return policies. They showed that the three level supply chain could be fully coordinated with appropriate contracts and the total profit of the channel could be allocated with any specified ratios among the members. Zhu et al. (2012) considered the coordination issue of a three level supply chain under random demand, where the manufacturer negotiated an option contract with the retailer and the manufacturer negotiated a buyback contract with the supplier. In order to incentivize the supplier to improve product quality, Lan et al. (2015) studied the supply chain contract design problem under incomplete information, where named inspection, price rebate and effort were simultaneously employed in the contract. The conventional studies focused on the case that uncertain parameter was modeled as a random variable. Under incomplete information about probability distribution of demand, some scholars considered the distribution free approach for the uncertain demand (Kamburowski 2014). However, in a practical supply chain management problem, historical data are always unavailable or unreliable because of market turbulence. In this case, it is required to study uncertain supply chain management problem from a new perspective.

As is well known, randomness is not the unique uncertainty in practical decision-making problems, and the fuzzy supply chain management problem is also an active research area (Lan et al. 2014; Yang et al. 2015). Based on the concept of echelon stock, Giannoccaro et al. (2003) presented a fuzzy echelon method for supply chain inventory management policy. Wang and Shu (2005) presented a fuzzy supply chain model and used genetic algorithm to find the optimal stock order-up-to levels for a supply chain. However, the solution process might be computationally intensive and the property of the solution could not be obtained. Xu and Zhai (2010) considered a two level supply chain coordination problem where the demand was characterized by a L–R type fuzzy number, and they proved that the maximum expected supply chain profit in centralized decision situation was greater than that in decentralized decision situation. A sharing scheme was given which implied both players could get more profit in the coordination situation than in the non-coordination situation. Under fuzzy demand assumption, Yu and Jin (2011) developed the optimal return policy in a two level supply chain with symmetric channel information and asymmetric channel information. Sang (2014) considered fuzzy supply chain models with a manufacturer and two competitive retailers, where the manufacturing cost and the parameters of demand function were treated as triangular fuzzy variables. Zhao and Wei (2014) discussed the coordination of a two level supply chain with fuzzy demand which was dependent on sales effort and retail price. In contrast with the decentralized and centralized decision models, two coordinating models based on symmetric information and asymmetric information about retailer’s scale parameter were developed by game theory, and the corresponding analytical solutions were obtained. Based on credibility measure and Lebesgue–Stieltjes (L–S) integral, Guo (2016) proposed two single-period inventory models with discrete and continuous demand variables, which provided a new perspective of the coordination of the supply chain. Besides treating fuzziness and randomness separately, some researchers considered the case that randomness and fuzziness coexisted in a practical decision-making problem. In this respect, the interested readers may refer to Li and Liu (2009) and Zhai et al. (2016).

The work mentioned above studied supply chain management problem under the assumption that the exact possibility distribution or membership function of fuzzy variable was available. The motivation of our work is based on the fact that growing innovation rates and shorter product life cycles make the market demand extremely variable. In this case, the exact possibility distribution of demand is usually unavailable due to the lack of related historical data, which motivates us to study supply chain management problem in a more advanced setting. The present paper studies the supply chain coordination problem under the assumption that the distribution of uncertain demand is partially known and characterized by the generalized parametric interval-valued possibility distribution. The advantage of this approach is that the distribution can be tailored to the information at hand for uncertain demand.

Our method differs from the existing supply chain coordination literature in several aspects. First, we propose a novel method to model the distribution of the uncertain demand which is substantially different from the existing literature in fuzzy possibility theory. Furthermore, we define the lambda selection of a generalized parametric interval-valued fuzzy variable which includes two different parameters. Second, we construct L–S measure by the parametric possibility distribution of lambda selection, and use it to define the L–S integral of uncertain profits in the centralized and decentralized three level supply chains. Third, different types of contracts on both end of the supply chain are considered in the proposed credibilistic optimization problem. Under the variable parametric possibility distribution of demand, we provide the sufficient conditions to ensure a three level supply chain can be fully coordinated. In addition, we show the total profit of the channel can be allocated with any specified ratios among members. Finally, based on theoretical analysis and numerical experiments, we provide some managerial implications in a practical supply chain coordination problem.

The remainder of this paper is organized as follows. Section 2 describes a three level supply chain management problem and characterizes the uncertain demand by generalized parametric interval-valued distribution. Section 3 defines the mean profit, and establishes the analytical expression of the optimal order quantity in the centralized three level supply chain. Section 4 analyzes the decentralized three level supply chain. Section 5 studies how to coordinate the three level supply chain with a revenue-sharing contract between the supplier and the manufacturer and a return policy between the manufacturer and the retailer. Section 6 performs some numerical experiments to demonstrate the validity of the proposed parametric credibilistic optimization method. Section 7 summarizes the main results of the paper.

2 Problem description, assumption conditions and notations

2.1 Problem description

Consider a three level supply chain management problem consisting of one supplier, one manufacturer and one retailer. The retailer sells short life cycle products, such as fashion items or consumer electronics, whose historical sales data are unavailable or unreliable because of market turbulence. That is, the exact possibility distribution of uncertain market demand is unavailable in our supply chain management problem. To encourage the retailer to order more products, the manufacturer is willing to offer a contract to his retailer. For the same reason, the supplier also wants to negotiate a contract to the manufacturer. Obviously, if we can make these contracts work cooperatively, then we can improve the competitive potential of the supply chain as much as possible. In the following sections, we will study how to fully coordinate the three level supply chain with different types of contracts, where a revenue-sharing contract between the supplier and the manufacturer and a return policy between the manufacturer and the retailer are considered.

2.2 Assumption conditions

We assume that the products are sold only in one period and the members have no chance to place a second order. Furthermore, it is assume that the information is symmetry, and every member of the supply chain is risk-neutral. The sequence of events satisfies the following assumption conditions:

• (A1) Retailer forecasts the uncertain market demand. The exact possibility distribution of uncertain demand is unavailable because of market turbulence and product innovation rate. Under incomplete information about possibility distribution of demand, we will give a new method to characterize the distribution of the uncertain demand;

• (A2) Supplier, manufacturer and retailer want to negotiate different policies in order to coordinate the whole system. Note that the three level supply chain involves three independent economic entities and two trading processes. To obtain more profits, one of members may negotiate different policies with his partners. Different combinations of contracts will lead to different mathematical models and solving methods. In our optimization model, a revenue-sharing contract between the supplier and the manufacturer and a return policy between the manufacturer and the retailer are considered;

• (A3) Supplier first produces basic parts and delivers them to manufacturer, then manufacturer embeds some key components into the basic parts and delivers the products to retailer. Suppose that one product contains one basic part and one key component. If this is not the case, one can solve this problem with an appropriate proportional coefficient;

• (A4) Retailer sells the products at a fixed price to customer under uncertain market demand. Suppose that any unmet demand incurs goodwill cost to retailer, manufacturer and supplier;

• (A5) Retailer returns all residual products to manufacturer after the selling season. Suppose that all the residual products are salvaged.

Figure 1plots the diagram of our three level supply chain, in which we consider the revenue-sharing contract negotiated by supplier and manufacturer and the return policy negotiated by retailer and manufacturer. In order to build our credibilistic optimization model, the following necessary notations and model parameters are required.

Fig. 1

Diagram of a three level supply chain

2.3 Notations

Fixed parameters

• $c_{s}$  supplier’s processing cost of unit basic part;

• $c_{m}$  manufacturer’s value-added cost of unit product;

• $c_{r}$  retailer’s treatment cost of unit product;

• c  total cost of unit product with $c=c_r+c_m+c_s$;

• $g_{s}$  supplier’s goodwill cost for unit unmet demand;

• $g_{m}$  manufacturer’s goodwill cost for unit unmet demand;

• $g_{r}$  retailer’s goodwill cost for unit unmet demand;

• g  total goodwill cost for unit unmet demand with $g=g_{r}+g_{m}+g_{s}$;

• p   retailer’s sales price of unit product;

• s   salvage value of unit residual product;

• $(r_1, r_2, r_3, r_4)$   trapezoidal fuzzy variable with possibility distribution function

  $$\begin{aligned} \mu (r)=\left\{ \begin{array}{ll} \frac{r-r_1}{r_2-r_1}, &{} \quad r\in [r_1, r_2]\\ 1, &{} \quad r\in [r_2, r_3]\\ \frac{r_4-r}{r_4-r_3}, &{} \quad r\in [r_3, r_4]; \end{array} \right. \end{aligned}$$

• $\theta _{l}$   downward perturbation degree of nominal possibility distribution;

• $\theta _{r}$   upward perturbation degree of nominal possibility distribution;

• $\lambda$   lambda selection parameter of demand;

• $\mu _\lambda$   mean value of the lambda selection variable;

• h   maximum value of parametric possibility distribution.

Decision variables

• Q  retailer’s order quantity;

• ${b_{{mr}}}$  return price of unit residual product charged by manufacturer;

• ${W_{{mr}}}$  wholesale price of unit product charged by manufacturer;

• ${W_{{sm}}}$  wholesale price of unit basic part charged by supplier;

• $\phi$  revenue-sharing rate.

Uncertain parameters

• $\xi$   uncertain market demand with variable possibility distribution function;

• $\pi _i$   subscript i takes r, m, s, denoting uncertain profits of retailer, manufacturer and supplier, respectively. Because the profits of retailer, manufacturer and supplier depend on uncertain market demand, $\pi _i$ is also uncertain.

In order to avoid trivial problems, model parameters are required to satisfy the following conditions: $p>c>s$, ${W_{{sm}}}>c_s$, ${W_{{mr}}}>{W_{{sm}}}+c_m$ , $p>{W_{{mr}}}+c_r$ and $s<{b_{{mr}}}<{W_{{mr}}}$. These inequalities can ensure that each member makes positive profit and the chain will not produce infinite products. In our supply chain management problem, one difficulty faced by the members is to forecast the exact demand due to the lack of historical sales data. In the next subsection, we will characterize uncertain demand via parametric interval-valued possibility distribution.

2.4 Parametric interval-valued distribution of uncertain demand

In practical supply chain management problem, the exact possibility distribution of uncertain demand is usually unavailable. In the following, we will give a new representation method for the interval-valued distribution of the uncertain demand to characterize the asymmetric perturbation of nominal possibility distribution, which is different from the existing literature in fuzzy possibility theory (Bai and Liu 2014, 2015; Liu and Liu 2010, 2016a) and its applications (Li et al. 2012; Bai and Liu 2016; Liu and Liu 2016b).

Based on the knowledge of the retailer, the value of uncertain demand $\xi$ during the sales cycle is between $r_1$ and $r_4$. Furthermore, the retailer assumes that the uncertain demand follows approximately trapezoidal possibility distribution $(r_1,r_2,r_3,r_4)$. However, the exact possibility distribution function on the interval $[r_1, r_4]$ is unavailable due to the lack of historical data about the sales. To describe this situation, we model the uncertain demand $\xi$ by parametric interval-valued possibility distribution, which is formally defined as follows:

Definition 1

Let $r_1<r_2\le r_3<r_4$ be real numbers. Uncertain demand variable $\xi$ is called a generalized parametric interval-valued trapezoidal fuzzy variable if its secondary possibility distribution is the following subinterval

$$\begin{aligned} \left[ \frac{r-r_1}{r_2-r_1}-\theta _{l}\frac{r-r_1}{r_2-r_1},\frac{r-r_1}{r_2-r_1}+\theta _{r}\frac{r_2-r}{r_2-r_1}\right] \end{aligned}$$

of [0, 1] for $r\in [r_1, r_2]$, the subinterval $[1-\theta _{l}, 1]$ of [0, 1] for $r\in [r_2, r_3]$, and the following subinterval

$$\begin{aligned} \left[ \frac{r_4-r}{r_4-r_3}-\theta _{l}\frac{r_4-r}{r_4-r_3},\frac{r_4-r}{r_4-r_3}+\theta _{r}\frac{r- r_3}{r_4-r_3}\right] \end{aligned}$$

of [0, 1] for $r\in [r_3, r_4]$, where $\theta _{l}, \theta _{r} \in [0,1]$ are two parameters characterizing the degree of uncertainty that $\xi$ takes on the value r.

For the sake of presentation, we use $\xi \sim \mathrm{Tra}(r_1,r_2,r_3,r_4;\theta )$ to denote $\xi$ is a generalized parametric interval-valued trapezoidal fuzzy variable, where the parameter $\theta =(\theta _{l},\theta _{r})$. It is evident that the possibility of event $\{\xi =r\}$ is an interval with variable boundaries characterized by parameters $\theta _l$ and $\theta _{r}$. In practical modeling process, the values of parameters $\theta _{l}$ and $\theta _{r}$ can be determined by decision makers or generated randomly in [0, 1]. When $\theta _{l}=\theta _{r}=0$, the corresponding secondary possibility distribution is called the nominal possibility distribution of demand $\xi$. The uncertain demand characterized by the nominal possibility distribution is denoted by $\xi ^n$.

In order to address uncertain demand with parametric interval-valued possibility distribution, we next define a new concept called selection variable.

Definition 2

Let uncertain demand variable $\xi \sim \mathrm{Tra}(r_1,r_2,r_3,r_4;\theta )$. A demand variable $\xi ^L$ is called the lower selection of demand variable $\xi$ if $\xi ^L$ has the following generalized parametric possibility distribution

$$\begin{aligned} \mu _{\xi ^L}(r;\theta _{l})=\left\{ \begin{array}{ll} \frac{r-r_1}{r_2-r_1}-\theta _{l}\frac{r-r_1}{r_2-r_1},&{} \quad r\in [r_1, r_2]\\ 1-\theta _{l}, &{} \quad r\in [r_2, r_3]\\ \frac{r_4-r}{r_4-r_3}-\theta _{l}\frac{r_4-r}{r_4-r_3},&{} \quad r\in [r_3, r_4]. \end{array} \right. \end{aligned}$$

A demand variable $\xi ^U$ is called the upper selection of demand variable $\xi$ if $\xi ^U$ has the following parametric possibility distribution

$$\begin{aligned} \mu _{\xi ^U}(r;\theta _{r})=\left\{ \begin{array}{ll} \frac{r-r_1}{r_2-r_1}+\theta _{r}\frac{r_2-r}{r_2-r_1}, &{} \quad r\in [r_1, r_2]\\ 1, &{} \quad r\in [r_2, r_3]\\ \frac{r_4-r}{r_4-r_3}+\theta _{r}\frac{r- r_3}{r_4-r_3},&{} \quad r\in [r_3, r_4]. \end{array} \right. \end{aligned}$$

For any given $\lambda _1,\lambda _2 \in [0,1]$, a variable $\xi ^\lambda$ with $\lambda =(\lambda _1,\lambda _2)$ is called a lambda selection of demand variable $\xi$ if it has the following generalized parametric possibility distribution

$$\begin{aligned} \mu _{\xi ^\lambda }(r;\theta )=\left\{ \begin{array}{ll} (1-\lambda _1)\mu _{\xi ^L}(r;\theta _{l})+\lambda _1\mu _{\xi ^U}(r;\theta _{r}),&{} \quad r\in [r_1, r_2]\\ 1-(1-\lambda _1)\theta _{l}+\frac{(r-r_2)(\lambda _2-\lambda _1)\theta _{l}}{r_3-r_2}, &{} \quad r\in [r_2, r_3]\\ (1-\lambda _2)\mu _{\xi ^L}(r;\theta _{l})+\lambda _2\mu _{\xi ^U}(r;\theta _{r}),&{} \quad r\in [r_3, r_4], \end{array} \right. \end{aligned}$$

i.e.,

$$\begin{aligned} \mu _{\xi ^\lambda }(r;\theta )=\left\{ \begin{array}{ll} \lambda _1\theta _{r}+\frac{(r-r_1)[1-(1-\lambda _1)\theta _{l}-\lambda _1\theta _{r}]}{r_2-r_1},&{} \quad r\in [r_1, r_2]\\ 1-(1-\lambda _1)\theta _{l}+\frac{(r-r_2)(\lambda _2-\lambda _1)\theta _{l}}{r_3-r_2}, &{} \quad r\in [r_2, r_3]\\ \lambda _2\theta _{r}+\frac{(r_4-r)[1-(1-\lambda _2)\theta _{l}-\lambda _2\theta _{r}]}{r_4-r_3},&{} \quad r\in [r_3, r_4].\\ \end{array} \right. \end{aligned}$$

By Definition 2, we find that the location of the generalized possibility distribution $\mu _{\xi ^\lambda }(r;\theta )$ depends on the values of lambda parameters $\lambda _1$ and $\lambda _2$. That is, parameters $\lambda _1$ and $\lambda _2$ represent two different selection methods in the left span and right span of the trapezoidal fuzzy variable, respectively. It is worth noting that the parametric possibility distributions of lambda selections of our generalized parametric interval-valued distribution are not necessarily normalized, i.e., the maximum values of parametric possibility distributions are not 1. Thus, we describe the interval-valued distribution as generalized parametric interval-valued distribution in Definition 1. For a uncertain demand $\xi \sim \mathrm{Tra}(r_1,r_2,r_3,r_4;\theta )$, the generalized possibility distributions of selection variables $\xi ^L$, $\xi ^U$ and $\xi ^\lambda$ with $\lambda _1<\lambda _2$ are plotted in Fig. 2.

Fig. 2

The generalized possibility distributions of uncertain demand variables $\xi ^L$, $\xi ^U$ and $\xi ^\lambda$

On the basis of parametric possibility distribution $\mu _{\xi ^\lambda }(r;\theta )$, we next derive the analytical expressions about the credibility $\mathrm{Cr}\{\xi ^\lambda \le r\}$, and the mean value $\mathrm {E}[\xi ^\lambda ]$ of lambda selection $\xi ^\lambda$ in the sense of L–S integral (Carter and Brunt 2000):

$$\begin{aligned} \mathrm {E}[\xi ^\lambda ]=\int _{[r_1, r_4]}r\mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}, \end{aligned}$$

where the measure is induced by the nondecreasing function $\mathrm {Cr}\{\xi ^\lambda \le r\}$ (see, (Feng and Liu 2016)).

First, the computational results about the credibility $\mathrm{Cr}\{\xi ^\lambda \le r\}$ are given in the following proposition:

Proposition 1

Let uncertain demand $\xi \sim \mathrm{Tra}(r_1,r_2,r_3,r_4;\theta )$ with parameter $\theta =(\theta _l,\theta _r)$.

• (i) If two lambda parameters satisfy $\lambda _1\le \lambda _2$ , then the credibility of event $\{\xi ^\lambda \le r\}$ is

  $$\begin{aligned} \mathrm {Cr}\{\xi ^\lambda \le r\}=\left\{ \begin{array}{ll} 0,&{} \quad r\in (-\infty , r_1)\\ \frac{1}{2}\lambda _1\theta _{{r}}+\frac{(r-r_1)[1-(1-\lambda _1)\theta _{{l}}-\lambda _1\theta _{{r}}]}{2(r_2-r_1)},&{} \quad r\in [r_1, r_2]\\ \frac{1}{2}[1-(1-\lambda _1)\theta _{{l}}]+\frac{(r-r_2)(\lambda _2-\lambda _1)\theta _{{l}}}{2(r_3-r_2)}, &{} \quad r\in [r_2, r_3]\\ 1-(1-\lambda _2)\theta _{{l}}-\frac{1}{2}\left\{ \lambda _2\theta _{{r}}+\frac{(r_4-r)[1-(1-\lambda _2)\theta _{{l}}-\lambda _2\theta _{{r}}]}{r_4-r_3}\right\} ,&{} \quad r\in [r_3, r_4)\\ 1-(1-\lambda _2)\theta _{{l}}, &{} \quad r\in [r_4, +\infty ). \end{array} \right. \end{aligned}$$

• (ii) If two lambda parameters satisfy $\lambda _1>\lambda _2$, then the credibility of event $\{\xi ^\lambda \le r\}$ is

  $$\begin{aligned} \mathrm {Cr}\{\xi ^\lambda \le r\}=\left\{ \begin{array}{ll} 0,&{} \quad r\in (-\infty , r_1)\\ \frac{1}{2}\lambda _1\theta _{{r}}+\frac{(r-r_1)[1-(1-\lambda _1)\theta _{{l}}-\lambda _1\theta _{{r}}]}{2(r_2-r_1)},&{} \quad r\in [r_1, r_2]\\ \frac{1}{2}[1-(1-\lambda _1)\theta _{{l}}]-\frac{(r-r_2)(\lambda _2-\lambda _1)\theta _{{l}}}{2(r_3-r_2)}, &{} \quad r\in [r_2, r_3]\\ 1-(1-\lambda _1)\theta _{{l}}-\frac{1}{2}\left\{ \lambda _2\theta _{{r}}+\frac{(r_4-r)[1-(1-\lambda _2)\theta _{{l}}-\lambda _2\theta _{{r}}]}{r_4-r_3}\right\} ,&{} \quad r\in [r_3, r_4)\\ 1-(1-\lambda _1)\theta _{{l}}, &{} \quad r\in [r_4, +\infty ). \end{array} \right. \end{aligned}$$

Proof

We only prove the first assertion, and the second can be proved similarly. According to Definition 2, if uncertain demand $\xi \sim { Tra}(r_1,r_2,r_3,r_4;\theta )$, then the parametric possibility distribution $\mu _{\xi ^\lambda }(r;\theta )$ is

$$\begin{aligned} \mu _{\xi ^\lambda }(r,\theta )=\left\{ \begin{array}{ll} \lambda _1\theta _{{r}}+\frac{(r-r_1)[1-(1-\lambda _1)\theta _{{l}}-\lambda _1\theta _{{r}}]}{r_2-r_1},&{} \quad r\in [r_1, r_2]\\ 1-(1-\lambda _1)\theta _{{l}}+\frac{(r-r_2)(\lambda _2-\lambda _1)\theta _{{l}}}{r_3-r_2}, &{} \quad r\in [r_2, r_3]\\ \lambda _2\theta _{{r}}+\frac{(r_4-r)[1-(1-\lambda _2)\theta _{{l}}-\lambda _2\theta _{{r}}]}{r_4-r_3},&{} \quad r\in [r_3, r_4].\\ \end{array} \right. \end{aligned}$$

According to the credibility measure and credibility theory (Gao and Yu 2013; Liu and Liu 2002), the credibility $\mathrm{Cr}\{\xi ^\lambda \le r\}$ is computed by

$$\begin{aligned} \mathrm{Cr}\{\xi ^\lambda \le r\}=\frac{1}{2}\left\{ \sup \limits _{x\in \mathfrak {R}}\mu _{\xi ^\lambda }(x,\theta )+\sup \limits _{x\le r}\mu _{\xi ^\lambda }(x,\theta )-\sup \limits _{x>r}\mu _{\xi ^\lambda }(x,\theta )\right\} . \end{aligned}$$

If two lambda parameters satisfy $\lambda _1\le \lambda _2$, then we have $\sup \nolimits _{x\in [r_1, r_4]}\mu _{\xi ^\lambda }(x,\theta )=1-(1-\lambda _2)\theta _l$. As a result, we can calculate the credibility of event $\{\xi ^\lambda \le r\}$ by

$$\begin{aligned} \mathrm {Cr}\{\xi ^\lambda \le r\}=\left\{ \begin{array}{ll} 0,&{} \quad r\in (-\infty , r_1)\\ \frac{1}{2}\lambda _1\theta _{{r}}+\frac{(r-r_1)[1-(1-\lambda _1)\theta _{{l}}-\lambda _1\theta _{{r}}]}{2(r_2-r_1)},&{} \quad r\in [r_1, r_2]\\ \frac{1}{2}[1-(1-\lambda _1)\theta _{{l}}]+\frac{(r-r_2)(\lambda _2-\lambda _1)\theta _{{l}}}{2(r_3-r_2)}, &{} \quad r\in [r_2, r_3]\\ 1-(1-\lambda _2)\theta _{{l}}-\frac{1}{2}\left\{ \lambda _2\theta _{{r}}+\frac{(r_4-r)[1-(1-\lambda _2)\theta _{{l}}-\lambda _2\theta _{{r}}]}{r_4-r_3}\right\} ,&{} \quad r\in [r_3, r_4)\\ 1-(1-\lambda _2)\theta _{{l}}, &{} \quad r\in [r_4, +\infty ), \end{array} \right. \end{aligned}$$

which completes the proof of assertion (i). $\square$

Based on Proposition 1, the computational results about the mean value $\mathrm {E}[\xi ^\lambda ]$ are given in the following proposition:

Proposition 2

Let uncertain demand $\xi \sim \mathrm{Tra}(r_1,r_2,r_3,r_4;\theta )$ with parameter $\theta =(\theta _l,\theta _r)$.

• (i) If two lambda parameters satisfy $\lambda _1\le \lambda _2$, then the mean value of lambda selection variable $\xi ^\lambda$ is

  $$\begin{aligned} \begin{array}{ll} \mathrm {E}[\xi ^\lambda ]&{}=\frac{(\theta _{{l}}+\theta _{{r}})(\lambda _1r_1+\lambda _2 r_4)+r_2(\lambda _2\theta _{{l}}-\lambda _1\theta _{{r}}) +r_3(2\lambda _2\theta _{{l}}-\lambda _1\theta _l-\lambda _2\theta _{{r}})}{4}\\ &{} \quad +\frac{r_1+r_2+r_3+r_4}{4}(1-\theta _{{l}}). \end{array} \end{aligned}$$

• (ii) If two lambda parameters satisfy $\lambda _1>\lambda _2$, then the mean value of lambda selection variable $\xi ^\lambda$ is

  $$\begin{aligned} \begin{array}{ll} \mathrm {E}[\xi ^\lambda ]&{}=\frac{(\theta _{{l}}+\theta _{{r}})(\lambda _1r_1+\lambda _2 r_4)+r_2(2\lambda _1\theta _{{l}}-\lambda _1\theta _r-\lambda _2\theta _{{l}}) +r_3(\lambda _1\theta _{{l}}-\lambda _2\theta _{{r}})}{4}\\ &{} \quad +\frac{r_1+r_2+r_3+r_4}{4}(1-\theta _{{l}}). \end{array} \end{aligned}$$

Proof

We only prove the first assertion, and the second can be proved similarly. Since the credibility of event $\{\xi ^\lambda \le r\}$ is a nondecreasing function with respect to r, the mean value of lambda selection variable $\xi ^\lambda$ is computed by

$$\begin{aligned} \mathrm {E}[\xi ^\lambda ]=\int _{[r_1, r_4]}r\mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}, \end{aligned}$$

where the L–S measure is generated by the nondecreasing function $\mathrm {Cr}\{\xi ^\lambda \le r\}$.

According to the analytical expression of $\mathrm{Cr}\{\xi ^\lambda \le r\}$ in Proposition 1(i), we have the following calculation result:

$$\begin{aligned} \begin{array}{ll} \mathrm {E}[\xi ^\lambda ]&{}=\int _{[r_1, r_1]}r\mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}+\int _{(r_1, r_2)}r\mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}+\int _{[r_2, r_3]}r\mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}\\ &{} \quad +\int _{(r_3, r_4)}r\mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}+\int _{[r_4, r_4]}r\mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}\\ &{} =\frac{(\theta _{{l}}+\theta _{{r}})(\lambda _1r_1+\lambda _2 r_4)+r_2(\lambda _2\theta _{{l}}-\lambda _1\theta _{{r}}) +r_3(2\lambda _2\theta _{{l}}-\lambda _1\theta _{{l}}-\lambda _2\theta _{{r}})}{4}\\ &{} \quad +\frac{r_1+r_2+r_3+r_4}{4}(1-\theta _{{l}}), \end{array} \end{aligned}$$

which completes the proof of assertion (i). $\square$

In the next sections, we will discuss the coordination problem of a three level supply chain, where the uncertain market demand $\xi$ is characterized by the generalized parametric interval-valued trapezoidal possibility distribution discussed in this section.

3 Centralized decision under interval-valued demand distribution

In our supply chain problem, the uncertain market demand $\xi$ is modeled as a generalized parametric interval-valued trapezoidal fuzzy variable $\mathrm{Tra}(r_1,r_2,r_3,r_4;\theta )$ and $\xi ^\lambda$ is the lambda selection of demand $\xi$. If a retailer wants to order Q units of products for sale, then the sales volume, shortage and holding quantity for the retailer are denoted as $\min (\xi ^\lambda , Q)$, $\max (\xi ^\lambda -Q,0)$ and $\max (Q-\xi ^\lambda , 0)$, respectively. In this section, we discuss the centralized decision problem of a three level supply chain, where three members are trying to integrate the channel and increase the total profit of the supply chain. Thus the objective is to maximize the profit of the supply chain. In this case, the profit expression for our supply chain is represented as

$$\begin{aligned} \begin{array}{ll} \pi _{c}^T(Q,\xi ^\lambda )&{}=p\min (\xi ^\lambda , Q)+s\max (Q-\xi ^\lambda , 0)-g\max (\xi ^\lambda -Q, 0)-(c_{{s}}+c_{{m}}+c_{{r}})Q.\\ \end{array} \end{aligned}$$

(1)

It is evident that the profit $\pi _{c}^T(Q,\xi ^\lambda )$ is a function of selection variable $\xi ^\lambda$, its mean profit is measured by the following L–S integral:

$$\begin{aligned} \begin{array}{ll} \int _{[r_1, r_4]}\pi _{c}^T(Q,r) \mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}, \end{array} \end{aligned}$$

where the analytic expressions of $\mathrm {Cr}\{\xi ^\lambda \le r\}$ are given by Proposition 1.

Based on the notations above, our centralized supply chain credibilistic optimization model is built as follows:

$$\begin{aligned} \begin{array}{ll} \max \qquad &{}\int _{[r_1, r_4]}\pi _{c}^T(Q,r) \mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}\\ \mathrm{s.\, t.}\qquad &{}r_1\le Q\le r_4. \end{array} \end{aligned}$$

(2)

In order to solve model (2), it is required to compute the mean profit $\int _{[r_1, r_4]}\pi _{c}^T(Q,r)\mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}$. For this purpose, we need the following lemma.

Lemma 1

If $\xi$ is a nonnegative uncertain demand with finite expected value, then the mean profit is computed by

$$\begin{aligned} \int _{[0, +\infty )}\pi (Q,r) \mathrm {d}\mathrm {Cr}\{\xi \le r\}=(p+g-c_s-c_m-c_r)hQ-(p+g-s)\int _0^Q\mathrm {Cr}\{\xi \le r\}{\mathrm {d}r}-g\mu , \end{aligned}$$

where $h=\lim \nolimits _{r\rightarrow +\infty }\mathrm {Cr}\{\xi \le r\}$ and $\mu =\int _{[0,+\infty )} r\mathrm {d}\mathrm {Cr}\{\xi \le r\}$

Proof

According to Eq. (1), the mean profit is computed by the following L–S integral:

$$\begin{aligned} \begin{array}{ll} \int _{[0,+\infty )}\pi (Q,r) \mathrm {d}\mathrm {Cr}\{\xi \le r\} &{}=p\int _{[0,+\infty )}\min (r, Q) \mathrm {d}\mathrm {Cr}\{\xi \le r\}+s\int _{[0,+\infty )}\max (Q-r, 0) \mathrm {d}\mathrm {Cr}\{\xi \le r\}\\ &{} \quad -g\int _{[0,+\infty )}\max (r-Q,0) \mathrm {d}\mathrm {Cr}\{\xi \le r\}-\int _{[0,+\infty )}(c_r+c_m+c_s)Q \mathrm {d}\mathrm {Cr}\{\xi \le r\}. \end{array} \end{aligned}$$

By calculation, one has

$$\begin{aligned} \begin{array}{ll} S(Q)&=\int _{[0,+\infty )}\min (r, Q) \mathrm {d}\mathrm {Cr}\{\xi \le r\}=hQ-\int _0^Q \mathrm {Cr}\{\xi \le r\}{\mathrm {d}r}, \end{array} \end{aligned}$$

where $\lim \nolimits _{r\rightarrow 0^-}\mathrm {Cr}\{\xi \le r\}=0$ due to $\xi \ge 0$ and $\lim \nolimits _{r\rightarrow +\infty }\mathrm {Cr}\{\xi \le r\}=h$,

$$\begin{aligned} \begin{array}{ll} I(Q)&=\int _{[0,+\infty )}\max (Q-r, 0) \mathrm {d}\mathrm {Cr}\{\xi \le r\}=\int _0^Q \mathrm {Cr}\{\xi \le r\}{\mathrm {d}r}, \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{ll} L(Q)&{}=\int _{[0,+\infty )}\max (r-Q,0) \mathrm {d}\mathrm {Cr}\{\xi \le r\} \\ &{}=\int _{(Q,+\infty )} r\mathrm {d}\mathrm {Cr}\{\xi \le r\}-Q \int _{(Q,+\infty )}\mathrm {d}\mathrm {Cr}\{\xi \le r\}. \end{array} \end{aligned}$$

Since $\int _0^{+\infty }\mathrm {Cr}\{\xi \ge r\}\mathrm {d}r$ is finite, the integral $\int _{[0,+\infty )} r\mathrm {d}\mathrm {Cr}\{\xi \le r\}$ is also finite. If we denote $\mu =\int _{[0,+\infty )} r\mathrm {d}\mathrm {Cr}\{\xi \le r\}$, then one has

$$\begin{aligned} L(Q)=\mu -\int _{[0,Q]} r\mathrm {d}\mathrm {Cr}\{\xi \le r\}-Q[h-\mathrm {Cr}\{\xi \le Q\}]=\mu -S(Q). \end{aligned}$$

As a consequence, the mean profit can be represented as

$$\begin{aligned} \begin{array}{ll} \int _{[0,+\infty )}\pi (Q,r) \mathrm {d}\mathrm {Cr}\{\xi \le r\}&{}=pS(Q)+sI(Q)-gL(Q)-(c_r+c_m+c_s)Qh\\ &{}=(p+g-c_s-c_m-c_r)hQ-(p+g-s)\int _0^Q\mathrm {Cr}\{\xi \le r\}{\mathrm {d}r}-g\mu . \end{array} \end{aligned}$$

The proof of lemma is complete. $\square$

As a consequence of Lemma 1, we can derive the optimal order quantity of model (2), which is stated as follows:

Theorem 1

Consider centralized supply chain credibilistic optimization model (2), its optimal order quantity $Q_c^*$ is represented as follows:

$$\begin{aligned} Q_c^*=\left\{ \begin{array}{ll} r_1, &{} \frac{p+g-c}{p+g-s}<\frac{\lambda _1\theta _r}{2h}\\ \inf \left\{ Q\mid \mathrm {Cr}\{\xi ^\lambda \le Q\}=\frac{h(p+g-c)}{p+g-s}\right\} ,&{} \frac{\lambda _1\theta _r}{2h}\le \frac{p+g-c}{p+g-s}<1-\frac{\lambda _2\theta _r}{2h}\\ r_4, &{}\frac{p+g-c}{p+g-s}\ge 1-\frac{\lambda _2\theta _r}{2h}, \end{array} \right. \end{aligned}$$

(3)

where the parameter $h=\mathrm {Cr}\{\xi ^\lambda \le r_4\}$.

Proof

According to Lemma 1, the mean profit in the centralized supply chain credibilistic optimization model (2) is computed by the following L–S integral:

$$\begin{aligned} \int _{[r_1, r_4]}\pi _{c}^T(Q,r) \mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\} =&p\int _{[r_1, r_4]}\min (r, Q) \mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}+s\int _{[r_1, r_4]}\max (Q-r, 0) \mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}\nonumber \\&\quad -g\int _{[r_1, r_4]}\max (r-Q,0) \mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}-\int _{[r_1, r_4]}(c_r+c_m+c_s)Q \mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}\nonumber \\ =&(p+g-c_s-c_m-c_r)hQ-(p+g-s)\int _{r_1}^Q{\mathrm {Cr}\{\xi ^\lambda \le r\}}{\mathrm {d}r}-g\mu _\lambda . \end{aligned}$$

(4)

where $\mu _\lambda =\mathrm {E}[\xi ^\lambda ]=\int _{[r_1,r_4]} r\mathrm {d}{\mathrm {Cr}\{\xi ^\lambda \le r\}}$ is the mean value of demand $\xi ^\lambda$, and its analytical expressions are given by Proposition 2.

Let $\frac{\mathrm {d}\int _{[r_1,r_4]}\pi _{c}^T(Q,r) \mathrm {d}{\mathrm {Cr}\{\xi ^\lambda \le r\}}}{\mathrm {d}Q}=0$, we can get $\mathrm {Cr}\{\xi ^\lambda \le Q\}=\frac{h(p+g-c)}{p+g-s}$, where $c=c_r+c_m+c_s$. Let $Q^*=\inf \left\{ Q\mid \mathrm {Cr}\{\xi ^\lambda \le Q\}=\frac{h(p+g-c)}{p+g-s}\right\}$. According to the condition $p>c>s$, we can get

$$\begin{aligned} \frac{\mathrm {d}\int _{[r_1,r_4]}\pi _{c}^T(Q,r) \mathrm {d}{\mathrm {Cr}\{\xi ^\lambda \le r\}}}{\mathrm {d}Q}\le 0 \end{aligned}$$

provided $Q>Q^*$; otherwise $\frac{\mathrm {d}\int _{[r_1,r_4]}\pi _{c}^T(Q,r) \mathrm {d}{\mathrm {Cr}\{\xi ^\lambda \le r\}}}{\mathrm {d}Q}\ge 0$. So the mean profit in model (2) is a concave function with respect to Q. If there is a unique point Q that satisfies $\frac{\mathrm {d}\int _{[r_1,r_4]}\pi _{c}^T(Q,r) \mathrm {d}{\mathrm {Cr}\{\xi ^\lambda \le r\}}}{\mathrm {d}Q}=0$, then the first order condition is sufficient and necessary to determine the optimal order quantity $Q_c^*$ that maximizes the mean profit. As for the actual economic significance, we should select the smallest order quantity if there are multiple values of Q that satisfy the equation $\frac{\mathrm {d}\int _{[r_1,r_4]}\pi _{c}^T(Q,r) \mathrm {d}{\mathrm {Cr}\{\xi ^\lambda \le r\}}}{\mathrm {d}Q}=0$.

According to Proposition 1, if $\frac{h(p+g-c)}{p+g-s}<\frac{\lambda _1\theta _r}{2}$, then we set $Q_c^*=r_1$. If $\frac{h(p+g-c)}{p+g-s}\ge h-\frac{\lambda _2\theta _r}{2}$, then we set $Q_c^*=r_4$. As a result, the optimal order quantity $Q_c^*$ of our centralized supply chain can be determined by the following formula

$$\begin{aligned} Q_c^*=\left\{ \begin{array}{ll} r_1, &{} \frac{p+g-c}{p+g-s}<\frac{\lambda _1\theta _r}{2h}\\ \inf \left\{ Q\mid \mathrm {Cr}\{\xi ^\lambda \le Q\}=\frac{h(p+g-c)}{p+g-s}\right\} ,&{} \frac{\lambda _1\theta _r}{2h}\le \frac{p+g-c}{p+g-s}<1-\frac{\lambda _2\theta _r}{2h}\\ r_4, &{}\frac{p+g-c}{p+g-s}\ge 1-\frac{\lambda _2\theta _r}{2h}. \end{array} \right. \end{aligned}$$

The proof of theorem is complete. $\square$

It is shown from the Eq. (3) that the optimal solution $Q_c^*$ in the centralized supply chain depends on the credibility $\mathrm {Cr}\{\xi ^\lambda \le Q\}$. Even a small perturbation in the nominal possibility distribution can affect the quality of nominal solution. Therefore, when the exact possibility distribution of uncertain demand is usually unavailable, the decision makers should employ the proposed parametric optimization method to model supply chain coordination problem. According to Proposition 1, we know the credibility $\mathrm {Cr}\{\xi ^\lambda \le Q\}$ is a piecewise function with respect to Q. Since we do not know in advance which subregion the global optimal solution locates in, we have to solve three sub-models by LINGO software to find three local optimal solutions of the problem. By comparing the objective values of the obtained local optimal solutions, we can find the global optimal solution $Q_c^*$. Given the values of distribution parameters $\theta _l, \theta _r, \lambda _1, \lambda _2$, the domain decomposition method’s process is summarized as follows.

• Step 1. Solve parametric programming sub-models of credibilistic optimization model (2) by LINGO software, where the constraints are $r_1\le Q\le r_2$, $r_2\le Q\le r_3$ and $r_3\le Q\le r_4$, respectively. We denote the obtained local optimal solutions as $Q_i, i=1,2,3$.

• Step 2. Compare the local objective values $v_i=\mathrm {E}[\pi _{c}^T(Q_i,\xi ^\lambda )]$ at local optimal solution $Q_i,$ for $i=1,2,3$, and find the global maximum profit by the following formula

  $$\begin{aligned} v_k=\max _{1\le i\le 3}v_i, \end{aligned}$$

  where $\mathrm {E}[\pi _{c}^T(Q,\xi ^\lambda )]$ is the mean profit of $\pi _{c}^T(Q,\xi ^\lambda )$.

• Step 3. Return $Q_k$ as the global optimal solution to model (2) with the optimal value $\mathrm {E}[\pi _{c}^T(Q_k,\xi ^\lambda )]$.

4 Decentralized decision under interval-valued demand distribution

In this section, we discuss the decentralized decision problem of a three level supply chain, where the supplier, the manufacturer and the retailer decide separately to maximize their profits. In addition, we assume that the members determine the wholesale prices based on their bargaining powers. Firstly, the supplier determines his wholesale price for the manufacturer. After that, the manufacturer determines his wholesale price for the retailer. Subsequently, the retailer determines the order quantity based on the manufacturer’s wholesale price and his own forecast of demand. Consequently, the mean profits of members are calculated as follows.

The mean profit of the retailer is

$$\begin{aligned} \begin{array}{ll} \mathrm {E}[\pi _{r}(Q_d,\xi ^\lambda )]&=pS(Q_d)+sI(Q_d)-g_rL(Q_d)-(c_r+{W_{{mr}}})Q_dh. \end{array} \end{aligned}$$

The mean profit of the manufacturer is

$$\begin{aligned} \begin{array}{ll} \mathrm {E}[\pi _{m}(Q_d,\xi ^\lambda )]&=({W_{{mr}}}-c_m-{W_{{sm}}})Q_dh-g_mL(Q_d). \end{array} \end{aligned}$$

The mean profit of the supplier is

$$\begin{aligned} \begin{array}{ll} \mathrm {E}[\pi _{s}(Q_d,\xi ^\lambda )]&=({W_{{sm}}}-c_s)Q_dh-g_sL(Q_d). \end{array} \end{aligned}$$

Based on the notations above, the retailer makes a decision to maximize his own profit. That is, the credibilistic optimization model is built as follows:

$$\begin{aligned} \begin{array}{ll} \max \qquad &{}\int _{[r_1, r_4]}\pi _{r}(Q_d,r) \mathrm {d}\mathrm {Cr}\{\xi ^\lambda \le r\}\\ \mathrm{s.\, t.}\qquad &{}r_1\le Q_d\le r_4. \end{array} \end{aligned}$$

According to Theorem 1, the optimal order quantity $Q_d^*$ of the decentralized supply chain can be determined by the following formula

$$\begin{aligned} Q_d^*=\left\{ \begin{array}{ll} r_1, &{} \frac{p+g_r-c_r-{W_{{mr}}}}{p+g_r-s}<\frac{\lambda _1\theta _r}{2h}\\ \inf \left\{ Q_d \mid \mathrm {Cr}\{\xi ^\lambda \le Q_d \}=\frac{h(p+g_r-c_r-{W_{{mr}}})}{p+g_r-s}\right\} ,&{} \frac{\lambda _1\theta _r}{2h}\le \frac{p+g_r-c_r-{W_{{mr}}}}{p+g_r-s}<1-\frac{\lambda _2\theta _r}{2h}\\ r_4, &{}\frac{p+g_r-c_r-{W_{{mr}}}}{p+g_r-s}\ge 1-\frac{\lambda _2\theta _r}{2h}. \end{array} \right. \end{aligned}$$

(5)

Because ${W_{{mr}}}>{W_{{sm}}}+c_m$, ${W_{{sm}}}>c_s$, $g_r<g$ and $\mathrm {Cr}\{\xi ^\lambda \le r\}$ is a nondecreasing function, we can easily verify that $Q^*_d<Q_c^*$ and $\mathrm {E}[\pi _{d}^T(Q^*_d,\xi ^\lambda )]\le \mathrm {E}[\pi _{c}^T(Q_c^*,\xi ^\lambda )]$, where $\mathrm {E}[\pi _{c}^T(Q_c^*,\xi ^\lambda )]$ denotes the mean profit in centralized decision, and $\mathrm {E}[\pi _{d}^T(Q_d^*,\xi ^\lambda )]$ denotes the total channel mean profit in decentralized decision:

$$\begin{aligned} \begin{array}{ll} \mathrm {E}[\pi _{d}^T(Q_d^*,\xi ^\lambda )]\!\!\!&{}=\mathrm {E}[\pi _{r}(Q_d^*,\xi ^\lambda )]+\mathrm {E}[\pi _{m}(Q_d^*,\xi ^\lambda )]+\mathrm {E}[\pi _{s}(Q_d^*,\xi ^\lambda )]\\ &{}=pS(Q_d^*)+sI(Q_d^*)-gL(Q_d^*)-cQ_d^*h. \end{array} \end{aligned}$$

In this case, the system is inefficient, that is, the total channel profit will be increased if the supplier, the manufacturer and the retailer take a coordination policy. Therefore, in order to improve the performance of the whole supply chain, the upstream member is willing to provide some incentive mechanisms to encourage the downstream member to order more products. The coordination problem of our three level supply chain will be discussed in the next section.

5 Coordination under revenue-sharing contract and return policy

5.1 The sufficient conditions of coordination

To the best of our knowledge, most of the existing literature consider a three level supply chain channel coordination by using the same type of contract on both end of the supply chain, such as return policies, quantity discounts and revenue-sharing contracts. However, a three level supply chain involves three independent economic entities and two trading processes. In order to obtain more profits, an enterprise may negotiate different policies with its cooperative enterprises. In this paper, a revenue-sharing contract between the supplier and the manufacturer and a return policy between the manufacturer and the retailer are introduced. The parameters $W_{mr}$ and $b_{mr}$ represent return policy and they depend on each other. Thus it is necessary to define one of them and the other would be calculated from some relations. The parameters $W_{sm}$ and $\phi$ represent revenue-sharing contract. According to the coordination contracts, we can gain the mean profits for each member as below. In order to simplify the problem, we do not consider the small possibility where the optimal order quantity takes on value $r_1$ or $r_4$.

When the manufacturer and the retailer take their actions independently, the profit of retailer is represented as

$$\begin{aligned} \begin{array}{ll} \pi _{r}(Q,\xi ^\lambda )&=p\min (\xi ^\lambda , Q)+{b_{{mr}}}\max (Q-\xi ^\lambda , 0)-g_r\max (\xi ^\lambda -Q, 0)-(c_r+{W_{{mr}}})Q. \end{array} \end{aligned}$$

According to Theorem 1, the optimal order quantity $Q_r^*$ of the retailer is computed by

$$\begin{aligned} \begin{array}{ll} Q_r^*=\inf \left\{ Q\mid \mathrm {Cr}\{\xi ^\lambda \le Q\}=\frac{h(p+g_r-c_r-{W_{{mr}}})}{p+g_r-{b_{{mr}}}}\right\} . \end{array} \end{aligned}$$

(6)

In this case, the manufacturer obtains the following profit

$$\begin{aligned} \begin{array}{ll} \pi _{m}(Q,\xi ^\lambda )&=\phi [{W_{{mr}}}Q-({b_{{mr}}}-s) \max (Q-\xi ^\lambda , 0)]-c_mQ-{W_{{sm}}}Q-g_m\max (\xi ^\lambda -Q, 0). \end{array} \end{aligned}$$

The optimal order quantity $Q_m^*$ of the manufacturer is computed by

$$\begin{aligned} \begin{array}{ll} Q_m^*=\inf \left\{ Q\mid \mathrm {Cr}\{\xi ^\lambda \le Q\}=\frac{h(\phi {W_{{mr}}}-c_m-{W_{{sm}}}+g_m)}{\phi ({b_{{mr}}}-s)+g_m}\right\} . \end{array} \end{aligned}$$

(7)

The profit of the supplier is represented as

$$\begin{aligned} \begin{array}{ll} \pi _{s}(Q,\xi ^\lambda )&=(1-\phi )[{W_{{mr}}}Q-({b_{{mr}}}-s) \max (Q-\xi ^\lambda , 0)]+{W_{{sm}}}Q-c_sQ-g_s \max (\xi ^\lambda -Q, 0). \end{array} \end{aligned}$$

The optimal order quantity $Q_s^*$ of the supplier is computed by

$$\begin{aligned} \begin{array}{ll} Q_s^*=\inf \left\{ Q\mid \mathrm {Cr}\{\xi ^\lambda \le Q\}=\frac{h[(1-\phi ) {W_{{mr}}}+{W_{{sm}}}-c_s +g_s]}{(1-\phi ) ({b_{{mr}}}-s)+g_s}\right\} . \end{array} \end{aligned}$$

(8)

Based on the above analysis, we arrive the following sufficient conditions:

Theorem 2

Let $\xi ^\lambda$ be a lambda selection of uncertain demand variable $\xi \sim \mathrm{Tra}(r_1,r_2,r_3,r_4;\theta )$. If there are a return policy between the manufacturer and the retailer and a revenue-sharing contract between the supplier and the manufacturer, then the sufficient conditions that the supply chain can be fully coordinated are

$$\begin{aligned} \begin{array}{ll} {W_{{mr}}}=p+g_r-c_r-\kappa (p+g_r-{b_{{mr}}}) \end{array} \end{aligned}$$

(9)

and

$$\begin{aligned} \begin{array}{ll} {W_{{sm}}}=\phi {W_{{mr}}}-c_m+g_m-\kappa [\phi ({b_{{mr}}}-s)+g_m], \end{array} \end{aligned}$$

(10)

where the parameter $\kappa =\frac{p+g-c}{p+g-s}$.

Proof

When the members take their actions independently, the optimal order quantities for the retailer, the manufacturer and the supplier are denoted by $Q_r^*$, $Q_m^*$ and $Q_s^*$, respectively. In order to obtain full coordination of the three level supply chain, the following equation should be satisfied,

$$\begin{aligned} Q_r^*=Q_m^*=Q_s^*=Q_c^*. \end{aligned}$$

According to Eqs. (3), (6) and $\mathrm {Cr}\{\xi ^\lambda \le Q_r^*\}=\mathrm {Cr}\{\xi ^\lambda \le Q_c^*\}$, we have the following equation

$$\begin{aligned} \frac{p+g_r-c_r-{W_{{mr}}}}{p+g_r-{b_{{mr}}}}=\frac{p+g-c_s-c_m-c_r}{p+g-s}, \end{aligned}$$

from which we obtain ${W_{{mr}}}=p+g_r-c_r-\kappa (p+g_r-{b_{{mr}}})$, where $\kappa =\frac{p+g-c}{p+g-s}$.

According to Eqs. (3), (7) and $\mathrm {Cr}\{\xi ^\lambda \le Q_m^*\}=\mathrm {Cr}\{\xi ^\lambda \le Q_c^*\}$, we can derive

$$\begin{aligned} \frac{\phi {W_{{mr}}}-c_m-{W_{{sm}}}+g_m}{\phi ({b_{{mr}}}-s)+g_m}=\frac{p+g-c_s-c_m-c_r}{p+g-s}, \end{aligned}$$

which implies ${W_{{sm}}}=\phi {W_{{mr}}}-c_m+g_m-\kappa [\phi ({b_{{mr}}}-s)+g_m].$

Substituting ${W_{{mr}}}$ and ${W_{{sm}}}$ into the right hand side of Eq. (8), we can get

$$\begin{aligned} \begin{array}{ll} &{}\frac{h[(1-\phi ) {W_{{mr}}}+{W_{{sm}}}-c_s +g_s]}{(1-\phi ) ({b_{{mr}}}-s)+g_s}\\ &{} \quad =\frac{h\{(1-\phi ) {W_{{mr}}}+\phi {W_{{mr}}}-c_m+g_m-\kappa [\phi ({b_{{mr}}}-s)+g_m]-c_s +\quad g_s\}}{(1-\phi ) ({b_{{mr}}}-s)+g_s} \\ &{} \quad =\frac{h\{ p+g_r-c_r-\kappa (p+g_r-{b_{{mr}}})-c_m+g_m-\kappa [\phi ({b_{{mr}}}-s)+g_m]-c_s +g_s\}}{(1-\phi ) ({b_{{mr}}}-s)+g_s}\\ &{} \quad =\frac{h\{\kappa [{b_{{mr}}}-s-\phi ({b_{{mr}}}-s)-p-g+s]+g_s\kappa +p+g-c\}}{(1-\phi ) ({b_{{mr}}}-s)+g_s}\\ &{} \quad =\frac{h\{\kappa [(1-\phi )({b_{{mr}}}-s)+g_s]-\kappa (p+g-s)+p+g-c\}}{(1-\phi ) ({b_{{mr}}}-s)+g_s}.\\ \end{array} \end{aligned}$$

(11)

According to Eq. (11), one has $\mathrm {Cr}\{\xi ^\lambda \le Q_s^*\}=\mathrm {Cr}\{\xi ^\lambda \le Q^*_c\}.$ Therefore, the supply chain is fully coordinated provided ${W_{{mr}}}=p+g_r-c_r-\kappa (p+g_r-{b_{{mr}}})$ and ${W_{{sm}}}=\phi {W_{{mr}}}-c_m+g_m-\kappa [\phi ({b_{{mr}}}-s)+g_m]$. The proof of theorem is complete. $\square$

5.2 The share of the supply chain profit

According to Theorem 2, our three level supply chain can be fully coordinated when conditions (9) and (10) hold true. However, if the profit of a member is smaller than his profit in the decentralized supply chain, then he will withdraw the supply chain coordination. We will discuss the share of the supply chain profit in the coordinated supply chain.

The mean profit of the retailer is represented as

$$\begin{aligned} \begin{array}{ll} \mathrm {E}[\pi _{r}(Q_c^*,\xi ^\lambda )]&{}=(p+g_r-c_r-{W_{{mr}}})hQ_c^*-(p+g_r-{b_{{mr}}})\int _{r_1}^{Q_c^*}\mathrm {Cr}\{\xi ^\lambda \le r\}-g_r\mu _\lambda \\ &{}=(p+g_r-{b_{{mr}}})[Q_c^* \mathrm {Cr}\{\xi ^\lambda \le Q_r^*\} -\int _{r_1}^{Q_c^*}\mathrm {Cr}\{\xi ^\lambda \le r\} {\mathrm {d}r}]-g_r\mu _\lambda . \end{array} \end{aligned}$$

It is easy to verify that

$$\begin{aligned} \frac{\mathrm {d}\mathrm {E}[\pi _{r}(Q_c^*,\xi ^\lambda )]}{\mathrm {d}{b_{{mr}}}}=-[Q_c^*\mathrm {Cr}\{\xi ^\lambda \le Q_r^*\}-\int _{r_1}^{Q_c^*}\mathrm {Cr}\{\xi ^\lambda \le r\} {\mathrm {d}r}]<0. \end{aligned}$$

So the function $\mathrm {E}[\pi _{r}(Q_c^*,\xi ^\lambda )]$ is decreasing with respect to ${b_{{mr}}}$.

The mean profit of the manufacturer is represented as

$$\begin{aligned} \begin{array}{ll} \mathrm {E}[\pi _{m}(Q_c^*,\xi ^\lambda )]&{}=[\phi {W_{{mr}}}-c_m-{W_{{sm}}}+g_m]hQ_c^*-[\phi ({b_{{mr}}}-s)+g_m]\int _{r_1}^{Q_c^*}{\mathrm {Cr}\{\xi ^\lambda \le r\}}{\mathrm {d}r}-g_m\mu _\lambda \\ &{}=[\phi ({b_{{mr}}}-s)+g_m][Q_c^*\mathrm {Cr}\{\xi ^\lambda \le Q_m^*\}-\int _{r_1}^{Q_c^*}{\mathrm {Cr}\{\xi ^\lambda \le r\}}{\mathrm {d}r}]-g_m\mu _\lambda . \end{array} \end{aligned}$$

If ${b_{{mr}}}$ is given, then the function $\mathrm {E}[\pi _{m}(Q_c^*,\xi ^\lambda )]$ is increasing with respect to $\phi$.

The mean profit of the supplier is represented as

$$\begin{aligned} \begin{array}{ll} \mathrm {E}[\pi _{s}(Q_c^*,\xi ^\lambda )]&{}=[(1-\phi ) {W_{{mr}}}-c_s+{W_{{sm}}}+g_s]hQ_c^*\\ &{} \quad -[(1-\phi )({b_{{mr}}}-s)+g_s]\int _{r_1}^{Q_c^*}{\mathrm {Cr}\{\xi ^\lambda \le r\}}{\mathrm {d}r}-g_s\mu _\lambda \\ &{}=[(1-\phi )({b_{{mr}}}-s)+g_s][Q_c^*\mathrm {Cr}\{\xi ^\lambda \le Q_s^*\}-\int _{r_1}^{Q_c^*}{\mathrm {Cr}\{\xi ^\lambda \le r\}}{\mathrm {d}r}]-g_s\mu _\lambda . \end{array} \end{aligned}$$

The function $\mathrm {E}[\pi _{s}(Q_c^*,\xi ^\lambda )]$ is increasing with respect to ${b_{{mr}}},$ but it is decreasing with respect to $\phi$.

The summation of the manufacturer’s mean profit and the supplier’s mean profit is

$$\begin{aligned} \begin{array}{ll} \mathrm {E}[\pi _{sm}(Q_c^*,\xi ^\lambda )]&{}=\mathrm {E}[\pi _{s}(Q_c^*,\xi ^\lambda )]+\mathrm {E}[\pi _{m}(Q_c^*,\xi ^\lambda )]\\ &{}=({W_{{mr}}}-c_m-c_s+g_m+g_s)Q_c^*h-({b_{{mr}}}-s+g_m+g_s)\int _{r_1}^{Q_c^*}{\mathrm {Cr}\{\xi ^\lambda \le r\}}{\mathrm {d}r}\\ &{} \quad -(g_m+g_s)\mu _\lambda . \end{array} \end{aligned}$$

Finally, the total channel mean profit of the supply chain is computed by

$$\begin{aligned} \begin{array}{ll} \mathrm {E}[\pi ^T(Q_c^*,\xi ^\lambda )]&{}=pS(Q_c^*)+sI(Q_c^*)-gL(Q_c^*)-cQ_c^*h\\ &{}=(p+g-c)hQ_c^*-(p+g-s)\int _{r_1}^{Q_c^*}{\mathrm {Cr}\{\xi ^\lambda \le r\}}{\mathrm {d}r}-g\mu _\lambda \\ &{}=(p+g-s)[Q_c^*\mathrm {Cr}\{\xi ^\lambda \le Q_c^*\}-\int _{r_1}^{Q_c^*}{\mathrm {Cr}\{\xi ^\lambda \le r\}}{\mathrm {d}r}]-g\mu _\lambda .\\ \end{array} \end{aligned}$$

Let $\alpha$ be the proportion of retailer’s mean profit in the total mean profit, i.e.,

$$\begin{aligned} \begin{array}{ll} \alpha =\frac{\mathrm {E}[\pi _{r}(Q_c^*,\xi ^\lambda )]}{\mathrm {E}[\pi ^T(Q_c^*,\xi ^\lambda )]}. \end{array} \end{aligned}$$

(12)

Then we have $\frac{\mathrm {E}[\pi _{sm}(Q_c^*,\xi ^\lambda )]}{\mathrm {E}[\pi ^T(Q_c^*,\xi ^\lambda )]}=1-\alpha .$ Let $\beta$ be the proportion of manufacturer’s mean profit in the summation of the manufacturer’s mean profit and the supplier’s mean profit, i.e.,

$$\begin{aligned} \begin{array}{ll} \beta &{}=\frac{\mathrm {E}[\pi _{m}(Q_c^*,\xi ^\lambda )]}{\mathrm {E}[\pi _{sm}(Q_c^*,\xi ^\lambda )]}.\\ \end{array} \end{aligned}$$

(13)

Hence the mean profits of manufacturer and supplier are $\mathrm {E}[\pi _{m}(Q_c^*,\xi ^\lambda )]=\beta (1-\alpha )\mathrm {E}[\pi ^T(Q_c^*,\xi ^\lambda )]$ and $\mathrm {E}[\pi _{s}(Q_c^*,\xi ^\lambda )]=(1-\beta )(1-\alpha )\mathrm {E}[\pi ^T(Q_c^*,\xi ^\lambda )]$, respectively.

As suggested above, the arbitrary allocation of supply chain profit among members can be realized by adjusting the corresponding contract parameters ${b_{{mr}}}$ and $\phi$. However, the share of the profit among members depends on the members’s bargaining powers. In this case, ${b_{{mr}}}$ and $\phi$ are decision variables, while ${W_{{mr}}}$ and ${W_{{sm}}}$ are the functions of ${b_{{mr}}}$ and $\phi$. The decision makers negotiating the contract parameters can refer to the following relations.

• (R1) Retailer’s mean profit is decreasing with respect to ${b_{{mr}}}$, and it is irrelevant to $\phi$;

• (R2) Manufacturer’s mean profit is increasing with respect to ${b_{{mr}}}$ or $\phi$;

• (R3) Supplier’s mean profit is increasing with respect to ${b_{{mr}}}$, but it is decreasing with respect to $\phi$.

6 Numerical experiments

6.1 Problem statement

In this section, we consider a practical supply chain management problem of smartphones during the sales cycle. The retailer needs to order the smartphones before a selling season. To begin with, according to the forecast of the market demand, the retailer negotiates the return policy with the manufacturer of smartphone and places his order. Next, the manufacturer negotiates the revenue-sharing contract with the supplier and places the order of basic parts. After that, the supplier delivers basic parts to the manufacturer, and the manufacturer assembles basic parts into smartphones and delivers them to the retailer. Finally, the retailer sells the smartphones to customer under uncertain demand.

The values of model parameters are specified as follows. The supplier’s processing cost of unit basic part $c_s$ is $40 and the manufacturer’s value-added cost of unit product $c_m$ is $15. The retailer’s treatment cost of unit product $c_r$ is $5 and the sales price of unit product p is $130. Based on the knowledge of the retailer, the value of demand $\xi$ during the sales cycle is between 800 and 1200, but the exact possibility distribution on the interval [800, 1200] is unavailable. In this situation, we model the uncertain demand $\xi$ of the smartphone as a generalized parametric interval-valued trapezoidal fuzzy variable $\mathrm{Tra}(800,1000,1100,1200;\theta _l,\theta _r),$ where the parameters $\theta _l$ and $\theta _r$ represent the uncertainty degrees about market demand $\xi$ in the interval [800, 1200]. Based on the experts’ experiences or subjective judgments, the values of parameters $\theta _l$ and $\theta _r$ are specified as 0.1 and 0.3, respectively. In addition, any unmet demand will incur goodwill cost. The values of goodwill costs to the retailer, the manufacturer and the supplier are $g_r=\$8$, $g_m=\$4$ and $g_s=\$3$, respectively. It is expected that any residual smartphones could be sold at the price $s=\$20$.

6.2 The centralized decision and decentralized decision

Consider the case that all three members are trying to integrate the channel and increase the total profit of the supply chain. The values of model parameters are set as follows: $\lambda _1=0.15$, $\lambda _2=0.25$, $\theta _l=0.1$ and $\theta _r=0.3$. In this case, according to our domain decomposition method’s process, we employ LINGO 11 to solve model (2) to obtain the optimal order quantity. The numerical experiments are executed on a personal computer (Lenovo with Intel Pentium(R) Dual-Core E5700 3.00 GHz CPU and RAM 4.00 GB) by using the Microsoft Windows 10 operating system. The optimal order quantity is 1139 with the mean profit 60917.67.

Table 1 The optimal order quantities and the mean profits with $\lambda _1=0.15$ and $\lambda _2=0.25$

Consider the case that the members of the supply chain decide separately to increase their profits. To identify the influence of wholesale price ${W_{{mr}}}$ on solution results, in our numerical experiment, we set the values of parameter ${W_{{mr}}}$ as 40, 45, 50, 52.8, 55, 60, 65 and 75, respectively, and observe the relations of the optimal order quantity and the total channel mean profit with the parameter ${W_{{mr}}}$. The computational results are reported in Table 1, from which we find that the optimal order quantity $Q^*$ is decreasing with respect to parameter ${W_{{mr}}}$, while the total channel mean profit is increasing firstly and then decreasing. The maximum of the total channel mean profit is obtained at ${W_{{mr}}}=52.8.$ and the corresponding results are highlighted in bold. That is, the whole supply chain profit can reach the maximum when the wholesale price ${W_{{mr}}}$ is less than the value of $c_s+c_m=55.$ However, the manufacturer will withdraw the supply chain in such a situation.

Table 2 The optimal order quantities and the mean profits with different selection parameters

When parameters $\lambda _1$ and $\lambda _2$ change, Table 2 provides the corresponding optimal order quantities and mean profits. From the computational results in Tables 1 and 2, we obtain the following observations. The maximal channel mean profit can be obtained in decentralized decision when the wholesale price charged by manufacturer ${W_{{mr}}}=52.8$. However, the manufacturer will withdraw the supply chain in such a situation. Therefore, it is impossible to coordinate the whole supply chain in the decentralized decision. More importantly, the optimal order quantity and the maximal channel mean profit in our supply chain coordination problem depend heavily on the parameters $\lambda _1$ and $\lambda _2$. That is, the coordination problem of our supply chain depends heavily on the distribution of uncertain demand.

6.3 Sensitivity analysis for cost parameters

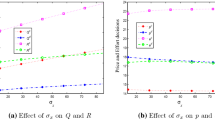
Under centralized decision, we carry out the sensitivity analysis of cost parameters $c_r, c_m, c_s$ and goodwill cost parameters $g_r, g_m, g_s$ in this subsection. In order to investigate the influence of all cost parameters on the solution quality, in our numerical experiment, we first compute the optimal solution by adjusting slightly the retailer’s treatment cost $c_r$, and observe the relation between the optimal order quantity and $c_r$ and the relation between the total mean profit and $c_r$. The computational results are plotted in Figs. 3 and 4, respectively. From the computational results, we find that the optimal order quantity and total mean profit are all monotone decreasing functions with respect to parameter $c_r$.

Fig. 3

The relation between optimal order quantity and parameter $c_r$

Fig. 4

The relation between total mean profit and parameter $c_r$

We next compute the optimal solution by adjusting slightly the retailer’s goodwill cost $g_r$, and observe the relation between the optimal order quantity and $g_r$ and the relation between the total mean profit and $g_r$. The computational results are plotted in Figs. 5 and 6, respectively. From the computational results, we find that the optimal order quantity is a monotone increasing function with respect to parameter $g_r$, while the total mean profit is a monotone decreasing function with respect to parameter $g_r$.

Fig. 5

The relation between optimal order quantity and parameter $g_r$

Fig. 6

The relation between mean profit and parameter $g_r$

So far, under centralized decision, we have discussed the relations between the optimal solution and parameters $c_r$ and $g_r$, respectively. According to the expression of the optimal order quantity in Theorem 1, we can obtain similar conclusions when other cost parameters are adjusted. As for how to coordinate the three level supply chain, the next subsection will provide a detailed discussion.

6.4 The optimal decision with coordination

In order to establish the three level supply chain coordination, a revenue-sharing contract between the supplier and the manufacturer and a return policy between the manufacturer and the retailer are considered. According to Proposition 1, the maximum value of generalized possibility distribution of selection variable has different analytical expressions based on two cases, i.e., $\lambda _1 \le \lambda _2$ and $\lambda _1> \lambda _2$. To identify the influence of lambda parameters $\lambda _1$ and $\lambda _2$ on solution results, we consider the following two cases in our numerical experiments.

Case I: Lambda parameters satisfy $\lambda _1\le \lambda _2$.

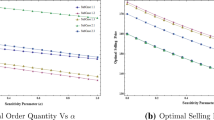
In this case, we set $\lambda _1=0.15$, while the values of parameter $\lambda _2$ are set as 0.15, 0.25 and 0.75, respectively. According to the result in Theorem 1, the corresponding optimal order quantities are $Q^*=1138$, $Q^*=1139$, $Q^*=1147$, respectively. The other computational results are reported in Tables 3, 4 and 5, from which we obtain the following observations: (i) the retailer’s mean profit is decreasing with respect to ${b_{{mr}}}$, and it is irrelevant to $\phi$; (ii) the manufacturer’s mean profit is increasing with respect to ${b_{{mr}}}$ or $\phi;$ (iii) the supplier’s mean profit is increasing with respect to ${b_{{mr}}}$, but it is decreasing with respect to $\phi$, and (iv) the optimal order quantity and the total channel mean profit are increasing with respect to $\lambda _2$.

Table 3 The mean profits of the members with $\lambda _1=0.15$ and $\lambda _2=0.15$

Table 4 The mean profits of the members with $\lambda _1=0.15$ and $\lambda _2=0.25$

Table 5 The mean profits of the members with $\lambda _1=0.15$ and $\lambda _2=0.75$

Case II: Lambda parameters satisfy $\lambda _1>\lambda _2$.

In this case, the values of parameter $\lambda _1$ are set as 0.25 and 0.75, respectively, while $\lambda _2=0.15$. From the result in Theorem 1, the corresponding optimal order quantities are $Q^*=1140$, $Q^*=1148$, respectively. The other computational results are provided in Tables 6 and 7, from which we obtain the similar observations as in Case I.

Table 6 The mean profits of the members with $\lambda _1=0.25$ and $\lambda _2=0.15$

Table 7 The mean profits of the members with $\lambda _1=0.75$ and $\lambda _2=0.15$

For the sake of comparison, we take the nominal possibility distribution as the exact possibility distribution of the uncertain demand $\xi$. In this case, $\theta _l=\theta _r=0$. By the result obtained in Theorem 1, we can obtain the nominal optimal order quantity 1136 with the nominal maximum mean profit 66030. The other computational results are reported in Table 8.

Table 8 The mean profits of the members under nominal possibility distribution

Obviously, the nominal maximum mean profit is larger than the optimal mean profits obtained in Tables 3-7. The influence of parameter lambda on the nominal optimal solution (the optimal solution corresponding to nominal possibility distribution) is reported in Table 9. To further analyze the influences of distribution parameters on the nominal optimal solution, we do additional experiments with different values of theta and lambda. The results are reported in Tables 10, 11 and 12. For convenience, we define the robust value which is the reduction from the nominal optimal profit to the optimal profits with different values of distribution parameters. From the computational results, we observe that the robust value is increasing with respect to $\theta _l$ or $\theta _r$, i.e., the larger the perturbation parameter, the larger the uncertainty degree embedded in the interval-valued possibility distribution of uncertain demand. The decision makers can adjust their values according to their preferences. Furthermore, the robust value is decreasing with respect to $\lambda _1$ or $\lambda _2$, i.e., the larger the parameter $\lambda$, the larger the credibility of event $\{\xi =r\}$. Of course, if the decision makers cannot identify the values of parameters theta and lambda, they may generate randomly their values from some prescribed subintervals of [0, 1]. The computational results demonstrate the advantages of variable possibility distributions over fixed possibility distribution (nominal possibility distribution).

Table 9 The influences of $\lambda _1$ and $\lambda _2$ on nominal optimal solution with $\theta _l=0.1$ and $\theta _r=0.3$

Table 10 The influences of $\lambda _1$ and $\lambda _2$ on nominal optimal solution with $\theta _l=0.3$ and $\theta _r=0.3$

Table 11 The influences of $\lambda _1$ and $\lambda _2$ on nominal optimal solution with $\theta _l=0.1$ and $\theta _r=0.1$

Table 12 The influences of $\lambda _1$ and $\lambda _2$ on nominal optimal solution with $\theta _l=0.3$ and $\theta _r=0.1$

6.5 Managerial implications

The outlined numerical studies in the above subsections lead to several observations:

• (i) The data of practical supply chain management problem are often uncertain, i.e., not known exactly at the time the problem is being solved. In the case that the nominal possibility distribution of the uncertain demand is available, we can build our supply chain management problem as a fuzzy optimization model. In this case, the computational results reported in Table 8 may help a decision maker to obtain his maximal profits. However, if the nominal possibility distribution of uncertain demand is unavailable, then the decision maker is advised not to adopt the obtained solution to make his order.

• (ii) When the nominal possibility distribution is unavailable, the decision maker cannot ignore the possibility that even a small perturbation in the nominal possibility distribution can affect the quality of nominal solution. From the computational results reported in Tables 3, 4, 5, 6 and 7, we observe that they are different from the total mean profit reported in Table 8. As a consequence, the total profit in our supply chain problem depends heavily on the distribution of uncertain demand. When the exact possibility distribution of uncertain demand is unavailable, a decision maker should employ the proposed parametric optimization method to model supply chain coordination problem. The computational results supported our arguments and demonstrated the advantages of parametric interval-valued possibility distributions over nominal possibility distribution.

• (iii) In our generalized parametric interval-valued possibility distribution, the variable lower and upper possibility distributions are characterized by perturbation parameters $\theta _l$ and $\theta _r$, respectively. Their values reflect the perturbation degrees of nominal possibility distribution. The parameter $\lambda$ characterizes the location of possibility distribution of selection variable in the interval-valued possibility distribution. If a decision maker cannot identify the values of parameters $\theta _l$, $\theta _r$ and $\lambda$, he may generate randomly their values from some prescribed subintervals of [0, 1]. From this viewpoint, the proposed parametric optimization method for supply chain management problem is flexible and can help the decision makers to make his informed decision.

7 Conclusions

In practical supply chain management problem, it is usually difficult to forecast the exact distribution of uncertain market demand. To model this situation, this paper studied a three level supply chain coordination problem from a new perspective. The major results of the paper include the following several aspects.

First, different from the existing literature, we employed generalized parametric interval-valued distribution to characterize the asymmetric perturbation of nominal possibility distribution. As a result, the parametric possibility distributions of lambda selections of our generalized parametric interval-valued distribution are not necessarily normalized, i.e., the maximum values of parametric possibility distributions are not 1. Thus, our generalized parametric interval-valued distribution can be tailored to information at hand for uncertain demand.

Second, for practical centralized and decentralized three level supply chain problems, when distribution uncertainty can heavily affect the quality of the nominal optimal solution, there exists a real need of a methodology which is capable of detecting the cases. In these cases, generating a new optimal solution corresponding to the variable parametric possibility distribution is very necessary. For this purpose, we constructed L–S measure by parametric possibility distribution of lambda selection demand, and used it to define the L–S integral of uncertain profits. The closed forms of optimal decentralized decision and centralized decision were obtained, from which we found that both optimal decisions depended on the distribution parameters $\lambda$ and $\theta$.

Third, given a revenue-sharing contract between the supplier and the manufacturer and a return policy between the manufacturer and the retailer, we focused on coordination problem under variable parametric possibility distribution. The sufficient conditions were established to ensure a three level supply chain could be fully coordinated. In this case, the allocated profits to the members also depended heavily on the distribution parameters $\lambda$ and $\theta$.

Finally, we considered a supply chain management problem of smartphones during the sales cycle and performed a number of numerical experiments. The computational results demonstrated that a decision maker couldn’t ignore the possibility that even a small perturbation in the possibility distribution could make the nominal optimal solution to our problem meaningless; instead the decision maker should employ the proposed parametric optimization method to find the optimal decision.

This study limits the consideration to the generalized parametric trapezoidal fuzzy variables with bounded supports. The future demands may have possibility distributions with unbounded supports. Hence extending the developed three level supply chain to the unbounded-support case will be a significant issue, which will be treated in our future reserch. Extension to considering other types of uncertain demand with a three level supply chain coordination is another interesting research direction.