1 Introduction

The universe’s accelerating expansion has been an interesting research topic for the past 20 years, which has been a contentious issue. Many scientific investigations have been conducted to understand the mysterious behavior of the universe during the last few decades. The early evolution of the cosmos continues to present difficulties for mankind, even with the successful explanation of accelerated cosmology. The supernova cosmology project and the High-Z supernova search team published Type Ia supernova observations in 1998, concluding that the universe is accelerating [1, 2]. This has been further supported by recent observations of SNe Ia [3,4,5], cosmic microwave background [6], and large-scale structure [7]. The idea of dark energy was put forth in the late 1990 s by examining the brightness of many supernovae that were exploding stars. A hypothesized dark energy opposes gravity by exerting a repulsive, negative pressure. One of the most effective initial theories was dark energy, which sought to explain late-time acceleration but failed to explain fine-tuning and coincidence problems [8, 9]. Two techniques have been proposed to solve the dark energy problems: one involves studying the dynamics of various dark energy models, and the other involves modifying general relativity’s Hilbert action to produce new theories of gravity(alternative theories of gravity). Although Einstein’s general theory of relativity has always been extremely helpful in revealing several of nature’s hidden mysteries, the evidence for the universe’s possible dark matter existence and late-time acceleration of the universe posses a serious theoretical challenge to this theory. Scalar fields like K-essence [10], Phantom [11,12,13,14], quintom [15, 16], quintessence [17,18,19,20], Chaplygin gas [21,22,23], and Holographic dark energy [24,25,26,27,28] can be found in significant and viable dynamical dark energy models. Among the various dynamic models of dark energy, the HDE model has recently become a successful approach for studying the dark energy puzzle. It was developed using the quantum properties of black holes, which have been extensively researched in the literature to examine quantum gravity. A new alternative to the dark energy issue can be found in the holographic principle. The most outstanding achievement of the holographic principle is the AdS/CFT correspondence, as seen from the reference [29]. Currently, the holographic principle ought to be a fundamental principle of quantum gravity because it has significance in other branches of physics, such as nuclear physics [30] and cosmology [31]. As a result, the two physical parameters of the universe’s boundary on which a dark energy model depends are the reduced Planck mass and a cosmological length scale, considered the universe’s future event horizon. Based on the dimensional analysis, we have

$$\begin{aligned} \rho _{de}=a_1m_p^4+a_2m_p^4L^{-2}+a_3L^{4-} \end{aligned}$$
(1)

where \(a_1, a_2\) and \(a_3\) are constants. According to the author [32], the \(a_1\) expression is not feasible using the Holographic principle. According to the holographic principle, the local quantum field (LQF) theory should not be used to describe a black hole. Specifically, the usual estimate \(\rho _{de} \approxeq a_1m_p^4\) the (LQF) this explanation should not involve any theory. The LQF hypothesis achieves a significant ’UV cutoff’ \(\Lambda\). As a result of the QF theory, the determined vacuum fluctuation is \(\rho _{de} \approxeq a_2m_p^4L^{-2}\). The HDE idea was based on the notion of (QF) theory, which states that a short-distance cutoff is coupled with a long-distance cutoff owing to the limit established by forming a black hole [33,34,35,36,37,38,39]. We compared only the second term and ignored the other terms, yielding HDE. The holographic dark energy density [32] is defined as \(\rho _{de}=3c^2m_p^2L^{-2}\), where \(m_p^2\), c and L are the reduced Planck mass, numerical constant and IR cutoff, taken as \(H^{-1}\) respectively. In Eq. (2) the \(a_1\) term is not present in the \(\rho _{de}\) expression. It is worth noting that this formulation of \(\rho _{de}\) is determined by dimensional analysis and holographic principle rather than simply adding a dark energy component to the Lagrangian. This distinguishing characteristic differentiates HDE theory from other dark energy theories. Due to the constraint of forming a black hole, a short-distance (UV) cutoff in quantum field theory is coupled to a long-distance(IR) cutoff. The holographic principle, which declares that the entropy of a particular system depends on its surrounding surface area rather than its volume, has drawn much focus in the present years because of its significance in quantum gravity. The HDE model is the first theoretical dark energy model influenced by the holographic principle and is consistent with current cosmological findings. As a result, HDE is an attractive alternative to dark energy. Furthermore, the HDE concept has attracted much attention and has been thoroughly researched recently. These are the following: 1. The characteristics of HDE are addressed in numerous modified gravity theories, including scalar-tensor theories such as Brans-Dicke theory, Saez-Ballester theory, and DGP brane-world theories, which may be found in the literature [40,41,42,43] 2. The HDE reconstructs different scalar-field dark energy and modified gravity models. The Saez-Ballester theory gives a dynamical framework that is more appropriate for studying HDE models since HDE belongs to the family of dynamical dark energy candidates. Many researchers have studied various cosmological models with different aspects of holographic dark energy. Vinutha et al. [44], studied “The study of hypersurface-homogeneous space-time in Renyi holographic dark energy". Sharma and Dubey [45] have worked on “Exploring the Sharma-Mittal HDE models with different diagnostic tools". Manoharan et al. [46], investigated “Holographic dark energy from the laws of thermodynamics with Renyi entropy". Iqbal and Jawad [47] have explored “Tsallis, Renyi and Sharma-Mittal holographic dark energy models in DGP braneworld". Jawad et al. [48], worked on “Tsallis, Renyi, and Sharma-Mittal Holographic Dark Energy Models in Loop Quantum Cosmology". Maity and Debnath [49] have studied “Tsallis, Renyi, and Sharma-Mittal holographic and new agegraphic dark energy models in D-dimensional fractal universe". Dubey et al. [50], have explored the “Sharma-Mittal holographic dark energy model in conharmonically flat space-time". Shekh et al. [51] investigated the “Physical Acceptability of the Renyi, Tsallis, and Sharma-Mittal Holographic Dark Energy Models in the f(T, B) Gravity under Hubble’s Cutoff". Gao [52] investigated the “Explaining Holographic Dark Energy". Ali et al. [53] have worked on “The Sharma-Mittal Model’s Implications on FRW Universe in Chern-Simons Gravity". Korunur [54] studied “Kaniadakis holographic dark energy with scalar field in Bianchi type-V universe". Korunur [55] worked on “Sharma-Mittal holographic dark energy and scalar field in Bianchi type-I cosmology". Several theories of gravity have been produced in recent years as alternatives to Einstein’s theory. The most significant of these theories of gravity are the scalar-tensor theories given by Brans and Dicke [56], Nordvedt [57], Wagoner [58], Ross [59], Dun [60], Sáez and Ballester [61], Barber [62], La and Steinhardt [63]. In the inflationary period, the scalar-tensor theories of gravitation are crucial for removing the graceful exit problem [64]. In the last few decades, much research has been done on cosmological models within the context of scalar-tensor theories. There are two ways gravitational theories are based on the scalar field; one is the Brans-Dicke theory of gravity, which includes a scalar field with a dimension equal to the inverse of the gravitational constant G, and the other is the Saez-Ballester theory, where the metric is associated with a dimensionless scalar field which provides an excellent summary of the weak fields. Despite the scalar field’s lack of dimensions, the theory predicts the existence of an antigravity regime. In 1986, Saez and Ballester proposed a Saez-Ballester theory of gravitation, and by using this theory, the missing matter problem in non-flat FRW cosmologies may be resolved. In this theory, the metric potentials connect with a scalar field. In this scenario, the intensity of the relationship between gravity and field was determined by the parameter w. Scalar fields \((\phi )\) have significance in gravity and cosmology because they may describe phenomena like dark energy, dark matter, and others. These may be factors in the universe’s future time acceleration.

The Saez and Ballester (1986) theory’s Lagrangian is given by

$$\begin{aligned} L=R-w {\phi }^n {\phi }_{,\alpha } {\phi }^{,\alpha }, \end{aligned}$$
(2)

where \(\phi\) and R are dimensionless scalar field and scalar curvature. n and w are arbitrary dimensionless constants, \({\phi }^{,i}=g^{ij} {\phi }_{,j}\). The two terms on the right hand of equation (2) have different dimensions for a scalar field with the dimension \(G^{-1}\), hence the Lagrangian is not physically possible. In the case of a dimensionless scalar field, it is much more appropriate to use a Lagrangian.

The general Saez-Ballester theory action is given by

$$\begin{aligned} I=\int _{\sum }(L+\zeta L_{m}) \sqrt{-}g dx^{1} dx^{2} dx^{3} dx^{4}, \end{aligned}$$
(3)

where \(\sum\), \(L_{m}\) and g are the arbitrary region of integration, matter Lagrangian and determinant of the matrix \(g_{ij}\) respectively, \(\zeta =-8\pi\). As a result, the action principle leads to the following equation

$$\begin{aligned} R_{ij}-\frac{1}{2}Rg_{ij}-w \phi ^{n} ({\phi }_{,i} {\phi }_{,j}-\frac{1}{2}g_{ij}{\phi }_{,k}{\phi }^{,k})=-8\pi T_{ij}, \end{aligned}$$
(4)

and

$$\begin{aligned} 2\phi ^{n}{\phi }_{;i}^{,i}+n\phi ^{n-1}{\phi }_{,k}{\phi }^{,k}=0, \end{aligned}$$
(5)

where \(T_{ij}\) is the matter Lagrangian’s stress energy-tensor and here \(8\pi\) is taken to be one.

The energy-conservation equation is defined as

$$\begin{aligned} T^{ij}_{;j}=0. \end{aligned}$$
(6)

The authors who explored Saez-Ballester’s scalar-tensor theory on anisotropic spacetime are given in the references [65,66,67,68,69,70,71,72,73,74,75,76]. However, SMHDE in this theory with Bianchi-\(VI_{0}\) space-time is a quite new study. Moreover, Vinutha et al. [77,78,79,80], have investigated Saez-Ballester theory very clearly and explained it in detail in their works. Considering these studies, this article aims to formulate an SMHDE model in Bianchi-\(VI_{0}\) using Saez-Ballester’s theory.

2 Bianchi-\(VI_0\) cosmology in Saez-Ballester theory

Furthermore, in the early epochs of the cosmos, the isotropic FRW model may not comprehensively and accurately describe matter. As a result, for a precise investigation of cosmological models to examine whether they may evolve to the observed amount of homogeneity and isotropy, one needs to assume spatially homogenous and anisotropic spacetimes. Among the numerous anisotropic spacetimes, many researchers have been drawn to Bianchi-type cosmological models, which are homogenous but not necessarily isotropic. In recent years, several researchers have developed intriguing cosmological models in the presence of dark energy against the background of anisotropic Bianchi spacetimes. In the early universe, spatially homogeneous and anisotropic Bianchi-type cosmological models play an important role. The study of anisotropic geometries is becoming increasingly important due to recent Planck probe results. The existence of an anisotropic phase that transforms into an isotropic one is provided by the theoretical argument and the most recent experimental results. In the framework of Bianchi-type space times, it is found that the anisotropy of the dark energy can be used to generate arbitrary ellipsoidal of the universe and fine-tune the observed CMBR anisotropies. Due to their less symmetrical structure, Bianchi-type models were investigated to expand more universal cosmological models than the FRW model. Bianchi-\(VI_0\) metric takes the form

$$\begin{aligned} ds^{2}=dt^{2}-L^{2}dx^{2}-M^{2}e^{2x}dy^{2}-N^{2}e^{-2x}dz^{2}, \end{aligned}$$
(7)

where L, M and N are metric potentials and functions of cosmic time t. Here the co-moving co-ordinates are (t, x, y, z). Sahoo et al. [81] have explored Bianchi-III and \(VI_0\) cosmological models with string fluid source in f(R, T) gravity in the context of late time accelerating universe expansion. Prasanthi and Aditya [82, 83] have studied an anisotropic universe with Renyi holographic dark energy in general relativity. Vinutha et al. [84,85,86], have worked on an anisotropic universe in f(R, T) gravity. Mishra and Sahoo [87] have worked on Bianchi-type \(VI_h\) perfect fluid cosmological model in f(R, T) theory. Hegazy and Rahaman [88] studied Bianchi-type \(VI_0\) cosmological model in self-creation theory in general relativity and Lyra geometry. Rodrigues et al. [89], investigated anisotropic universe models in f(T) gravity. The Saez-Ballester field equations are stated as

$$\begin{aligned} R_{ij}-\frac{1}{2}Rg_{ij}-w \phi ^{n} ({\phi }_{,i} {\phi }_{,j}-\frac{1}{2}g_{ij}{\phi }_{,k}{\phi }^{,k})=-(T_{ij}+\bar{T_{ij}}), \end{aligned}$$
(8)

and the conservation equation is

$$\begin{aligned} (T_{ij}+\bar{T_{ij}})_{;j}=0, \end{aligned}$$
(9)

where \(T_{ij}\) and \(\bar{T_{ij}}\) are pressureless matter and HDE, respectively, which are given as

$$\begin{aligned} T_{ij}=\rho _m u_{i} u_{j}, \end{aligned}$$
(10)

where \(\rho _m\) and \(u_i\) are the energy density of matter and fluid’s four-velocity vector components, i.e., \(u_i=(0,0,0,1)\), respectively.

$$\begin{aligned} {{\bar{T}}}_{ij}=u_{i} u_{j}(\rho _{de}+p_{de})-p_{de}g_{ij}, \end{aligned}$$
(11)

here, \(\rho _{de}\) and \(p_{de}\) are energy density and pressure of HDE respectively. By using EoS parameter (\(\omega _{de}=\frac{p_{de}}{\rho _{de}}\)) the above equations of pressureless matter are written as

$$\begin{aligned} T_{ij}=diag[0,0,0,\rho _{m}], \end{aligned}$$
(12)

and HDE is written as \(\bar{T}_{ij}=[-\omega _{de}\rho _{de},-\omega _{de}\rho _{de}, -\omega _{de}\rho _{de}, \rho _{de}]\),

$$\begin{aligned} \bar{T}_{ij}=[-\omega _{de}\rho _{de},-(\omega _{de}+\alpha )\rho _{de}, -(\omega _{de}+\beta )\rho _{de}, \rho _{de}], \end{aligned}$$
(13)

using pressureless matter (12), HDE (13), Bianchi-\(VI_0\) spacetime (7), and Saez-Ballester field Eq. (8) gives the following equations.

$$\begin{aligned} \frac{{\ddot{M}}}{M}+\frac{\ddot{N}}{N}+\frac{{\dot{M}}{\dot{N}}}{{M}{N}}+\frac{1}{L^2}-\frac{w \phi ^n \dot{\phi ^2}}{2}=-\rho _{de}\omega _{de}, \end{aligned}$$
(14)
$$\begin{aligned} \frac{{\ddot{L}}}{L}+\frac{\ddot{N}}{N}+\frac{{\dot{L}}{\dot{N}}}{{L}{N}}-\frac{1}{L^2}-\frac{w \phi ^n \dot{\phi ^2}}{2}=-(\omega _{de}+\alpha )\rho _{de}, \end{aligned}$$
(15)
$$\begin{aligned} \frac{{\ddot{L}}}{L}+\frac{\ddot{M}}{M}+\frac{{\dot{L}}{\dot{M}}}{{L}{M}}-\frac{1}{L^2}-\frac{w \phi ^n \dot{\phi ^2}}{2}=-(\omega _{de}+\beta )\rho _{de}, \end{aligned}$$
(16)
$$\begin{aligned} \frac{{\dot{L}}{\dot{M}}}{{L}{M}}+\frac{{\dot{M}}{\dot{N}}}{{M}{N}}+\frac{{\dot{L}}{\dot{N}}}{{L}{N}}-\frac{1}{L^2}+\frac{w \phi ^n \dot{\phi ^2}}{2}=\rho _{de}+\rho _m, \end{aligned}$$
(17)
$$\begin{aligned} \frac{\dot{M}}{M}-\frac{\dot{N}}{N}=0, \end{aligned}$$
(18)
$$\begin{aligned} \ddot{\phi }+{\dot{\phi }}\left(\frac{\dot{L}}{L}+\frac{\dot{M}}{M}+\frac{\dot{N}}{N}\right)+\frac{n{\dot{\phi }}^2}{2 \phi }=0. \end{aligned}$$
(19)

From Eq. (18), we get

$$\begin{aligned} M=N, \end{aligned}$$
(20)

with the aid of above Eq. (20), Eqs. (14)–(19) reduces to

$$\begin{aligned} \frac{2\ddot{M}}{M}+\frac{{\dot{M}}^2}{{M}^2}+\frac{1}{L^2}-\frac{w \phi ^n \dot{\phi ^2}}{2}=-\rho _{de}\omega _{de}, \end{aligned}$$
(21)
$$\begin{aligned} \frac{{\ddot{L}}}{L}+\frac{\ddot{M}}{M}+\frac{{\dot{L}}{\dot{M}}}{{L}{M}}-\frac{1}{L^2}-\frac{w \phi ^n \dot{\phi ^2}}{2}=-(\omega _{de}+\alpha )\rho _{de}, \end{aligned}$$
(22)
$$\begin{aligned} \frac{{\ddot{L}}}{L}+\frac{\ddot{M}}{M}+\frac{{\dot{L}}{\dot{M}}}{{L}{M}}-\frac{1}{L^2}-\frac{w \phi ^n \dot{\phi ^2}}{2}=-(\omega _{de}+\beta )\rho _{de}, \end{aligned}$$
(23)
$$\begin{aligned} \frac{2{\dot{L}}{\dot{M}}}{{L}{M}}+\frac{\dot{M}^2}{M^2}-\frac{1}{L^2}+\frac{w \phi ^n \dot{\phi ^2}}{2}=\rho _{de}+\rho _m, \end{aligned}$$
(24)
$$\begin{aligned} \ddot{\phi }+{\dot{\phi }}\left(\frac{\dot{L}}{L}+\frac{2\dot{M}}{M}\right)+\frac{n{\dot{\phi }}^2}{2 \phi }=0. \end{aligned}$$
(25)

The conservation equation for matter and HDE is

$$\begin{aligned} {{\dot{\rho }}}_m+{{\dot{\rho }}}_{de}+\Big (\frac{\dot{L}}{L}+\frac{2\dot{M}}{M}\Big )\Big (\rho _m+(1+\omega _{de})\rho _{de}\Big )+\Big ( \frac{(\alpha +\beta ) \dot{M}}{M}\Big )=0. \end{aligned}$$
(26)

From Eqs. (22) and (23), we get

$$\begin{aligned} \alpha =\beta . \end{aligned}$$
(27)

2.1 Solutions of the field equations

As per Eq. (27), the field Eqs. (21)–(25) form a system of four independent equations with seven unknowns. The following physical condition is considered to solve these equations. The relationship between two metric potentials L and M, i.e., expansion scalar \(\theta\) is proportional to shear scalar \(\sigma\) which is given as,

$$\begin{aligned} L=M^l \end{aligned}$$
(28)

\(l\not = 0, 1\) is constant. Throne’s [90] work can describe the physical reason for this supposition, i.e., the Hubble expansion of the universe is currently isotropic by approximately \(30\%\) according to the observations of the velocity redshift relation for extragalactic sources. In the vicinity of our galaxy, redshift places the limit as the ratio of shear scalar (\(\sigma\)) and Hubble constant (H) \(\frac{\sigma }{H}\le 0.30\) [91, 92].

From Eqs. (28), (21) and (22), we get

$$\begin{aligned} \dot{M} M^{1+l}=c_1exp\int \Bigg (\frac{M}{(l-1)\dot{M}}\Big (\frac{2}{M^{2l}}-\beta \rho _{de}\Big )\Bigg )dt. \end{aligned}$$
(29)

To solve the above Eq. (29), the following relationship between the skewness parameter \((\beta )\) and the energy density of dark energy \((\rho _{de})\) is taken into consideration.

$$\begin{aligned} \beta =\frac{1}{\rho _{de}}\Big [\frac{2}{M^{2l}}+\beta _1(1-l)\frac{\dot{M}}{M}\Big ], \end{aligned}$$
(30)

here \(\beta _1\) is an arbitrary constant.

Now solving Eqs. (29) and (30), the metric potentials are procured as

$$\begin{aligned} L=\Big [\frac{c_1(l+2)e^{\beta _1 t}}{\beta _1}+c_2(l+2)\Big ]^{\frac{l}{l+2}}, \end{aligned}$$
(31)
$$\begin{aligned} M=N=\Big [\frac{c_1(l+2)e^{\beta _1 t}}{\beta _1}+c_2(l+2)\Big ]^{\frac{1}{l+2}}, \end{aligned}$$
(32)

where \(c_1\), \(c_2\) are arbitrary constants. Using Eqs. (31) and (32), the metric is procured as

$$\begin{aligned} ds^2=dt^2-\Big (\frac{c_1(l+2)e^{\beta _1 t}}{\beta _1}+c_2(l+2)\Big )^{\frac{2l}{l+2}}dx^2-\Big (\frac{c_1(l+2)e^{\beta _1 t}}{\beta _1}+c_2(l+2)\Big )^{\frac{2}{l+2}}(e^{2x}dy^2+e^{-2x}dz^2). \end{aligned}$$
(33)

3 Sharma-Mittal HDE

A novel type of holographic dark energy model, known as Sharma-Mittal holographic dark energy, has recently been developed [93], using the generalized entropy measure proposed by Sharma-Mittal and inspired by the holographic principle. The Sharma-Mittal holographic dark energy model is significant because it can give a theoretical framework for understanding the essential characteristics of dark energy and its consequences for the universe’s fate. A two-parametric entropy generated by Sharma-Mittal, and is given as

$$\begin{aligned} S_{SM}=\frac{1}{R}\Big ((1+\delta \frac{A}{4})^\frac{R}{\delta }-1\Big ), \end{aligned}$$
(34)

here \(A=4\pi L^2\), and L is the IR cutoff. \(\delta\) and R are two free parameters. Tsallis and Renyi entropies can be retrieved at the appropriate limits of R. Sharma-Mittal entropy changes into Renyi entropy when the limit \(R \rightarrow 0\), and it changes into Tsallis entropy when \(R \rightarrow 1-\delta\). As stated by Cohen et al., the energy density is produced by the relationship between the IR and UV cutoffs.

$$\begin{aligned} \rho _{de}\propto \frac{S_{SM}}{L^4}\rightarrow \frac{3c^2S_{SM}}{8\pi L^4}. \end{aligned}$$
(35)

Here suppose the Hubble horizon cutoff as \(L=\frac{1}{H}\). Using above equation, the energy density of SMHDE is obtained as

$$\begin{aligned} \rho _{de}=\frac{3c^2H^4}{8\pi R}\Big ((1+\frac{\delta \pi }{H^2})^\frac{R}{\delta }-1\Big ), \end{aligned}$$
(36)

where \(c^2\) is numerical constant and assume \(8\pi\)=1. In the above equation, H denotes the Hubble parameter and its value is given by

$$\begin{aligned} H=\frac{c_1exp(\beta _1 t)\beta _1}{(3c_1exp(\beta _1 t)+3c_2\beta _1)}. \end{aligned}$$
(37)

By the use of Eq. (37) in (36), the energy density for Sharma-Mittal HDE (\(\rho _{de}\)) is attained as

$$\begin{aligned} \rho _{de}=\frac{c^2c_1^4exp(4\beta _1t)\beta _1^4\big (\iota _1-1\big )}{27(c_1exp(\beta _1t)+c_2\beta _1)^4R}. \end{aligned}$$
(38)

The energy density (\(\rho _{m}\)) of pressureless matter and skewness parameter (\(\beta\)) are obtained by using the Eq. (38) in Eqs. (24) and (30)

$$\begin{gathered} \rho _{m} = - 54R(l + 2)^{2} (\beta _{1}^{4} c_{2}^{4} + 4\beta _{1}^{3} exp(\beta _{1} t)c_{1} c_{2}^{3} + 6\beta _{1}^{2} exp(2\beta _{1} t)c_{1}^{2} c_{2}^{2} + 4\beta _{1} exp(3\beta _{1} t)c_{1}^{3} c_{2} + c_{1}^{4} exp(4\beta _{1} t)) \hfill \\ (\frac{{(l + 2)(c_{1} exp(\beta _{1} t) + c_{2} \beta _{1} )}}{{\beta _{1} }})^{{\frac{{ - 2l}}{{l + 2}}}} - 2( - 54c_{1}^{2} (c_{2}^{2} (l + 1/2)\beta _{1}^{2} + (1/4)wc_{3}^{2} )Rexp(2\beta _{1} t) + c_{1}^{4} n(\iota _{1}^{{\frac{R}{\delta }}} - 1))c^{2} (l + 2)^{2} \beta _{1}^{2} - 54Rl - 27R)exp(4\beta _{1} t) - \iota _{7} )\beta _{1}^{2} , \hfill \\ \end{gathered}$$
(39)
$$\beta = \frac{{\iota _{8} }}{{(l + 2)\left( {(\iota _{1} - 1)\beta _{1}^{4} c_{1}^{4} c^{2} } \right)}}$$
(40)

where

$$\iota _{1} = \left( {\frac{{(9\pi exp(2\beta _{1} t)c_{1}^{2} \delta + 18\pi exp(\beta _{1} t)\beta _{1} c_{1} c_{2} \delta + 9\pi \beta _{1}^{2} c_{2}^{2} \delta + c_{1}^{2} exp(2\beta _{1} t)\beta _{1}^{2} )exp( - 2\beta _{1} t)}}{{c_{1}^{2} \beta _{1}^{2} }}} \right)^{{\frac{R}{\delta }}} .{\text{ }}$$
(41)
$$\iota _{7} = \frac{{\left( {27\left( {8c_{1}^{3} \left( {l + \frac{1}{2}} \right)exp\left( {3\beta _{1} t} \right) + wc_{3}^{2} \left( {c_{2} \beta _{1} + 2c_{1} exp} \right)\left( {\beta _{1} t} \right)} \right)} \right)Rc_{2} \beta _{1} }}{2}.$$
(42)
$$\iota _{8} = 54R(c_{1} exp(\beta _{1} t) + c_{2} \beta _{1} )^{3} exp( - 4\beta _{1} t)((l + 2)(c_{1} exp(\beta _{1} t) + c_{2} \beta _{1} )\left( {\left( {\frac{{(l + 2)(c_{1} exp(\beta _{1} t) + c_{2} \beta _{1} )}}{{\beta _{1} }}} \right)^{{\frac{1}{{l + 2}}}} } \right)^{{ - 2l}} - \frac{{c_{1} \beta _{1}^{2} exp(\beta _{1} t)( - 1 + l)}}{2}).$$
(43)
Fig. 1
figure 1

Plot of energy density (\(\rho _{de}\)) versus redshift (z)

Full size image
Fig. 2
figure 2

Plot of energy density (\(\rho _{m}\)) versus redshift (z)

Full size image
Fig. 3
figure 3

Plot of skewness parameter (\(\beta\)) versus redshift (z)

Full size image

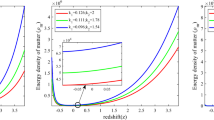
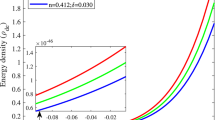
Figs. 1, 2, and 3 study the graphical behavior of energy density (\(\rho _{de}\)) of SMHDE, energy density (\(\rho _{m}\)) of pressureless matter, and skewness parameter (\(\beta\)), respectively, for two different values of \(\beta _1=0.135, 0.139\) with respect to redshift (z). Figures 1 and 2 show that \(\rho _{de}\) and \(\rho _{m}\) are positive throughout the universe’s evolution. \(\rho _{de}\) and \(\rho _m\) decreases with the decrease of redshift (z), i.e., decreases as time increases for both the values of \(\beta _1=0.135, 0.139\). Figure 3, shows that the skewness parameter \((\beta )\) is a positive value that increases at an early time and gradually decreases at a late time against redshift for both the values of \(\beta _1=0.135, 0.139\).

4 Properties of the model

Here in this part, the investigation of cosmological behavior such as volume (V), deceleration parameter (q), squared speed of sound (\(v_s^2\)), EoS parameter (\(\omega _{de}\)), and statefinder parameter (r, s) of the model is discussed.

The average scale factor of the model is given by

$$a(t) = (LMN)^{{\frac{1}{3}}} = \left( {\frac{{(l + 2)(c_{1} exp(\beta _{1} t) + c_{2} \beta _{1} )}}{{\beta _{1} }}} \right)^{{\frac{1}{3}}} .$$
(44)

The volume of the model is obtained as

$$V = (a(t))^{3} = \frac{{(l + 2)(c_{1} exp(\beta _{1} t) + c_{2} \beta _{1} )}}{{\beta _{1} }}.$$
(45)

From Fig. 4, it is noticed that the volume is positive throughout the universe’s evolution and increases with the decrease of redshift (z), i.e., increases as time increases for both the values of \(\beta _1=0.135, 0.139\), which represents the expansion of the cosmos.

Fig. 4
figure 4

Plot of volume (V) versus redshift (z)

Full size image

4.1 Decelaration parameter

The nature of the universe’s expansion rate is determined by the deceleration parameter q. The deceleration parameter explains both the universe’s accelerations and deceleration behavior. The cosmos exhibits five different types of expansion: accelerating power-law expansion for \(-1<q<0\), decelerating expansion for \(q > 0\), constant rate expansion for \(q = 0\), exponential growth for \(q = -1\), and super-exponential expansion for \(q<-1\). The deceleration parameter is stated as

$$\begin{aligned} q =\frac{d}{dt}\Big (\frac{1}{H}\Big )-1. \end{aligned}$$

The deceleration parameter of our model is attained as

$$q = \frac{{ - exp( - \beta _{1} t)(c_{1} exp(\beta _{1} t) + 3c_{2} \beta _{1} )}}{{c_{1} }}.$$
(46)

It is observed from Fig. 5 that, the deceleration parameter (q) changes its sign from positive to negative values. From this, it is clear that it exhibits a transition from decelerating (\(q>0\)) to the accelerating phase (\(q<0\)). The transition point (\(z_t\)) observed in the present model is 0.56 for both the values of \(\beta _1=0.135, 0.139\) which match with various theoretical observations such as Capozziello et al. [94], \(z_t=0.7679^{+0.1831}_{-0.1829}\), Yang and Gong [95] \(z_t=0.60^{+0.21}_{-0.12}\), Lu et al. [96] \(z_t=0.69^{+0.23}_{-0.12}\). In the current model, the decelerating phase is noticed if \(q>0\), accelerating phase is noticed if \(q<0\). At \(z=0\), the value of the deceleration parameter obtained in the present model is \(q=-0.6491, -0.6581\) for \(\beta _1=0.135, 0.139\) respectively and matches with the observations of [97].

Fig. 5
figure 5

Plot of deceleration parameter (q) versus redshift (z)

Full size image

4.2 EoS parameter

The equation of state parameter (EoS) plays a significant part in evaluating the expanding cosmos. Three different classes of scalar field dark energy models are available to examine the model’s dark energy characteristics: quintessence \(-1<\omega _{de}<\frac{-1}{3}\), phantom \(\omega _{de}<-1\), and quintom \(\omega _{de}=1\). The EoS parameter (\(\omega _{de}\)) is defined as

$$\begin{aligned} \omega _{de}=\frac{p_{de}}{\rho _{de}}. \end{aligned}$$

The EoS parameter of the present model is obtained as

$$d\omega _{{de}} = \frac{{\iota _{2} }}{{\iota _{3} }}.$$
(47)
Fig. 6
figure 6

Plot of EoS parameter (\(\omega _{de}\)) versus redshift (z)

Full size image

The behavior of the EoS (\(\omega _{de}\)) parameter against redshift (z) for both the values of \(\beta _1=0.135, 0.139\) is graphically shown in Fig. 6. For both values of \(\beta _1\), the model enters into quintessence from matter dominated phase at \(z=0.18\), and the model has transitioned from decelerating to accelerating phase. The model matches with present observational data, which is a good result.

4.3 Statefinder parameter

Sahni et al. [98], initially developed a cosmological diagnostic parameter set known as the statefinder pair. The statefinder parameter is directly derived from a space-time metric, making it more general compared to physical variables that are model-dependent and rely on the characteristics of physical fields characterizing dark energy. Dark energy models’ reliability is evaluated using the statefinder diagnostic pair (r, s), which indicates the model’s geometrical nature. The values of this pair give different ranges of the scenarios those are \(\Lambda CDM\) model for \((r, s)=(1, 0)\), (ii) the CDM limit for \((r, s)=(1, 1)\), (iii) the quintessence region if \(r<1\), \(s>0\) and (iv) Chaplygin gas model if \(r>1\), \(s<0\). The general form of this parameter set is stated as

$$\begin{aligned} r=\frac{\dddot{a}}{aH^3}, s=\frac{r-1}{3(q-\frac{1}{2})}, \end{aligned}$$

where a and q are the scale factor and deceleration parameter, respectively. The present values of this set for our model are obtained as

$$r = \frac{{(c_{1}^{2} exp(2\beta _{1} t) + 9\beta _{1}^{2} c_{2}^{2} )exp( - 2\beta _{1} t)}}{{c_{1}^{2} }},$$
(48)
$$s = - \frac{{2(\beta _{1}^{3} c_{2}^{3} exp( - \beta _{1} t) + exp(2\beta _{1} t)c_{1}^{3} + 3\beta _{1} exp(\beta _{1} t)c_{1}^{2} c_{2} + 3\beta _{1}^{2} c_{1} c_{2}^{2} ))\beta _{1}^{2} c_{2}^{2} }}{{(c_{1} exp(\beta _{1} t) + c_{2} \beta _{1} )^{3} (c_{1} exp(\beta _{1} t) + 2c_{2} \beta _{1} )c_{1} }}.$$
(49)
Fig. 7
figure 7

Plot of r versus s

Full size image

From Fig. 7, it is observed that, it shows Chaplygin gas behavior, i.e., \(r > 1\), \(s < 0\) for both the values of \(\beta _1\), and for all values of r, it is clear that the parameter s remains negative all over the region.

4.4 Scalar field

Scalar fields are essential because they illustrate matter fields with spin-less quanta and represent gravitational fields. Zero mass scalar fields and massive scalar fields are two different types of scalar fields that indicate long-range interactions and short-range interactions, respectively. This is the primary motivator for why so many researchers are interested in studying scalar fields. Besides this, scalar fields help solve the horizon problem in the cosmos, and it is also presumed that the scalar fields are responsible for cosmic expansion. The scalar field affects all the physical parameters in the model, giving better results.

$$\phi = \frac{{d(log(exp(\beta _{1} t)) - log(c_{1} exp(\beta _{1} t) + c_{2} \beta _{1} ))}}{{c_{2} (l + 2)\beta _{1} }}.$$
(50)
Fig. 8
figure 8

Plot of scalar field (\(\phi\)) versus redshift (z)

Full size image

The plot of the scalar field \((\phi )\) against redshift (z) is shown in Fig. 8. This figure shows that the scalar field is positive for both the values of \(\beta _1 = 0.135, 0.139\) throughout the evolution of the cosmos.

4.5 Squared speed of sound

The squared speed of sound is an essential parameter in cosmology that is crucial in verifying the stability analysis of any dark energy model and in the context of the theory of cosmic perturbations and the evolution of structure in the cosmos. It is also very significant in understanding the development of density fluctuations, such as those found in the cosmic microwave background (CMB), as well as the large-scale structure of the cosmos. Depending on the sign value of \(v_s^2\) represents whether the model is stable or unstable. If \(v^2_s\) is positive, the model has a stable behavior, whereas if \(v^2_s\) is negative, it shows unstable model behavior. It is described as

$$v_{s}^{2} = \frac{{\dot{p}_{{de}} }}{{\dot{\rho }_{{de}} }} = \dot{\omega }_{{de}} + \frac{{\omega _{{de}} \dot{\rho }_{{de}} }}{{\rho _{{de}} }}.$$
(51)

The stability of the model can be obtained by substituting the values of \(\rho _{de}\) and \(\omega _{de}\) and its derivatives, as

$$v_{s}^{2} = \frac{{\iota _{4} }}{{\iota _{5} }}.$$
(52)
Fig. 9
figure 9

Plot of squared speed of sound (\(v_s^2\)) versus redshift (z)

Full size image

The \(\iota _4\) and \(\iota _5\) values are given in the appendix section. Moreover, our model exhibits stable behavior as for all values of z, we have \(v_s^2>0\) for both the values \(\beta _1=0.135, 0.139\), whose behavior was represented graphically in Fig. 9.

5 Analysis of solution through perturbation techniques

The perturbation approach [99,100,101] is mostly used to determine approximations of the acquired exact solutions. In this part, the stability of the solution against metric perturbation will be examined.

$$a_{i} \to a_{{B_{i} }} + \delta a_{i} = a_{{B_{i} }} (1 + \delta b_{i} ).$$
(53)

The perturbation of volume scale factor, mean Hubble factors and directional Hubble factors are

\(V\rightarrow V_{B}\sum _i \delta b_{i}+V_{B}\),

\(\theta \rightarrow \frac{1}{3}\sum _i\delta b_{i}+\theta _{B}\),

\(\theta _{i}\rightarrow \sum _i\delta b_{i}+\theta _{Bi}\).

The metric perturbations \(\delta b _{i}\) are shown in the equations given below

$$\sum\limits_{i} \delta \ddot{b}_{i} + 2\sum\limits_{i} {\theta _{{Bi}} } \delta \dot{b}_{i} = 0,$$
(54)
$$\delta \ddot{b}_{i} + \frac{{\dot{V}_{B} }}{{V_{B} }}\delta \dot{b}_{i} + \sum\limits_{j} \delta \dot{b}_{j} \theta _{{Bi}} = 0,$$
(55)
$$\sum\limits_{i} \delta \dot{b}_{i} = 0.$$
(56)

Solving Eqs. (54)–(56) we obtain

$$\delta \mathop {b_{i} }\limits^{{..}} + \frac{{\dot{V}_{B} }}{{V_{B} }}\delta \mathop {b_{i} }\limits^{.} = 0,$$
(57)

in Eq. (54), \(V_B\) is background volume factor. The value of \(V_B\) for the present model is given as,

$$V_{B} = \frac{{(l + 2)(c_{1} exp(\beta _{1} t) + c_{2} \beta _{1} )}}{{\beta _{1} }},$$
(58)

Now on integrating Eq. (59) with the help \(V_B\), we obtain the value of \(\delta b_i\) as,

$$\delta b_{i} = \frac{{d_{1} (\beta _{1} t - log(c_{1} exp(\beta _{1} t) + c_{2} \beta _{1} ))}}{{(l + 2)c_{2} \beta _{1} }} + d_{2} .$$
(59)

here \(d_{1}\), \(d_{2}\) are integrating constants. The actual fluctuations \((\delta a_i)\) can be obtained by substituting \(\delta b_i\) in the equation \(\delta a_i=a_{Bi}\delta b_i\)

$$\delta a_{i} = \frac{{\beta _{1} }}{{(l + 2)(c_{1} exp(\beta _{1} t) + c_{2} \beta _{1} )}}\left( {\frac{{d_{1} (\beta _{1} t - log(c_{1} exp(\beta _{1} t) + c_{2} \beta _{1} ))}}{{(l + 2)c_{2} \beta _{1} }} + d_{2} } \right).$$
(60)
Fig. 10
figure 10

Plot of actual fluctuations (\(\delta a_i\)) versus redshift (z)

Full size image

The behavior of actual fluctuations is shown against redshift in Fig. 10, and it is clear that it decreases with the decrease of redshift, i.e., decreases as time increases.

6 Conclusions

Bianchi’s space-time plays a significant role in describing the accelerated expansion of the cosmos. The Sharma-Mittal HDE model was investigated in this work within the context of the Saez-Ballester theory while considering the Bianchi-\(VI_0\) space-time. The consistency of the Sharma-Mittal HDE model in our work is studied by applying the Infrared cutoff as \(L=H^{-1}\). The graphical behavior of the model is accomplished using specific cosmological parameters like the deceleration parameter, EoS parameter (\(\omega _{de}\)), statefinder parameter(r, s), squared speed of sound (\(v_s^2\)) for two different values of \(\beta _1=0.135, 0.139\). In the analysis of the present work, the following results were found.

Figures 1 and 2 depict the behavior of energy density (\(\rho _{de}\)) of Sharma-Mittal HDE and energy density (\(\rho _{m}\)) of pressureless matter respectively against redshift (z). Graphs 1 and 2 depict that \(\rho _{de}\) and \(\rho _{m}\) are positive for the entire cosmos evolution and decreases with the decrease of redshift (z) for both the values of \(\beta _1=0.135, 0.139\). The positive nature of energy density is accountable for the universe’s accelerating expansion.

Figure 3 exhibits the behavior of the skewness parameter (\(\beta\)) against redshift (z). This figure shows that the skewness parameter is positive for \(z>0\), and at present, \(z=0\), whereas it is negative for \(z<0\) for both the values of \(\beta _1=0.135, 0.139\).

Figure 4 illustrates that the volume increases with the decrease of redshift z, demonstrating that the universe is expanding. The exciting aspect of the deceleration parameter elucidates the transition from the decelerating to the accelerating phase for both the values of \(\beta _1\)=0.135, 0.139, and it is shown in Fig. 5. The transition point (\(z_t=0.56\)) obtained here matches with the recent observational data.

Figure 6 shows that the EoS parameter (\(\omega _{de}\)) displays a transition from the decelerating to the accelerating phase and enters into the quintessence phase (\(\omega _{de}>-1\)) from the matter-dominated phase representing the acceleration expansion of the cosmos. \(\omega _{de}=-1.13^{+0.24}_{-0.25}\) [102](Planck+nine years WMAP), SNe Ia data with galaxy clustering, CMBR anisotropy statistics \(-1.33<\omega _{de}<-0.79\) and \(-1.67<\omega _{de}<-0.62\) [103] respectively and present Planck collaboration data (2018) [104] gives the range of EoS as \(\omega _{de}=-1.028\pm 0.031\) (\(68\%\), Planck TT, TE, EE+lowE+ lensing+SNe+BAO), \(\omega _{de}=-0.76\pm 0.20\) (Planck+BAO/RSD+WL), \(\omega _{de}=-0.957\pm 0.080\) (Planck+SNe+BAO), \(\omega _{de}<-0.95\) (\(95\%\), Planck TT, TE, EE+low E+ lensing+SNe+BAO) with the help of these observations, it is clear that the current model’s EoS parameter (\(\omega _{de}\)) is in good agreement with the observational data.

From Fig. 7, it is noticed that, the statefinder parameter exhibits the Chaplygin gas phase \((s < 0, r > 1)\) for both the values of \(\beta _1= 0.135, 0.139\). Figure 8 shows that scalar field \(\phi\) is positive all through the universe’s evolution and increases with the decrease of redshift (z) for both the values of \(\beta _1= 0.135, 0.139\).

From Fig. 9, it is observed that \((v_s^2)\) is positive throughout the evolution of the model i. e. for all the values of (z). As \((v_s^2)\) is positive, it is observed that our model shows stable behavior for both the values of \(\beta _1= 0.135, 0.139\).

From Fig. 10, the actual fluctuations decreases with the decrease of redshift (z) which is obvious that \(\delta a_i \rightarrow 0\) at future epoch. Hence, the background solution remains stable even in a perturbated gravitational field. The current model’s cosmological parameters are discussed clearly in this article and the most favorable results that corroborate the present cosmology are obtained. This research can extend to other anisotropic models and examine their similarities and differences.

A comparative study of the obtained model with the recent works on this subject and a comparison of our results with current observational data related to the dynamical parameters are given below: Shekh et al. [51] investigated the Physical Acceptability of the Renyi, Tsallis, and Sharma Mittal Holographic Dark Energy Models in the f(T, B) Gravity under Hubble’s Cutoff. The obtained energy density for SMHDE is in good agreement with their work. But we noticed by the behavior of EoS parameter, that our model displays a transition from the decelerating to the accelerating phase and enters into the quintessence phase from the matter dominated phase representing the acceleration expansion of the cosmos, where as in their work it shows \(\Lambda\)CDM. Divya Prasanthi and Aditya [82] have investigated Anisotropic Renyi holographic dark energy models in general relativity. We observed that our findings are in good agreement with their work. Vinutha et al. [44, 79] have explored the study of anisotropic space-time in holographic dark energy. Our results of EoS parameter and deceleration parameter are in good agreement with their results. The deceleration parameter of our model are consistent with the observational data such as Capozziello et al. [94], \(z_t=0.7679^{+0.1831}_{-0.1829}\), Yang and Gong [95] \(z_t=0.60^{+0.21}_{-0.12}\), Lu et al. [96] \(z_t=0.69^{+0.23}_{-0.12}\). We have made a comparison of our results with present \(\omega _{de}=-1.13^{+0.24}_{-0.25}\) [102](Planck+nine years WMAP), SNe Ia data with galaxy clustering, CMBR anisotropy statistics \(-1.33<\omega _{de}<-0.79\) and \(-1.67<\omega _{de}<-0.62\) [103] respectively and present Planck collaboration data (2018) [104] gives the range of EoS as \(\omega _{de}=-1.028\pm 0.031\) (\(68\%\), Planck TT, TE, EE+lowE+ lensing+SNe+BAO), \(\omega _{de}=-0.76\pm 0.20\) (Planck+BAO/RSD+WL), \(\omega _{de}=-0.957\pm 0.080\) (Planck+SNe+BAO), \(\omega _{de}<-0.95\) (\(95\%\), Planck TT, TE, EE+low E+ lensing+SNe+BAO).