1 Introduction

At present, the universe is going through a phase of accelerated expansion, and this is suggested by numerous observational data such as type Ia supernovae [1,2,3,4], cosmic microwave background (CMB) anisotropies [5,6,7], large-scale structure (LSS) [8,9,10,11]. This expanding phase of cosmos is due to some mysterious force containing repulsive gravitational effects, referred as dark energy (DE). This exotic type of fluid consists of positive energy density and negative pressure. There are mainly two ways to study this mysterious force and cosmic acceleration. To understand this strange component, the first approach is a modification in the geometric part of the action principle in general relativity (GR), resulting in alternative theories of gravity. The modification in geometric parts involves some invariants depending on specific features like scalars, torsion, curvature, etc. The different alternative theories of gravity are scalar-tensor theories like Brans–Dicke theory [12], Saez–Ballester theory [13] and modified theories of gravity like f(R) [14,15,16], f(T) [17,18,19], f(R, T) [20] and so on. Another approach is by modifying the matter part of Einstein field equations, which leads to various dynamical DE models. Besides these various dynamical DE models, the cosmological constant(\(\Lambda\)) is the simplest fundamental candidate, but this cosmological constant experiences enormous incidents and fine-tuning problems [21, 22]. Due to this reason, various dynamical DE models have been proposed like ghost [23], K-essence [24, 25], quintessence [26], phantom [27, 28], Chaplygin gas [29,30,31], tachyon [84], polytropic gas [33, 34], holographic dark energy models (HDE) [35,36,37,38,39].

The holographic dark energy (HDE) has become an interesting concept in present period as it has some significant features regarding quantum gravity [35, 40, 41], so it has been proposed as candidate of dark energy (DE) to explain the recent phase transition of cosmos. The HDE is based on holographic principle (HP) [40], which is originated from the thermodynamics of the blackhole. The holographic principle is even applied to string theory by Susskind [41]. This principle proposes that the degrees of freedom of entropy of a system depends on its bounding area but not on its volume. The formation of blackholes gives a limit as it gives a relation between ultraviolet cutoff (short-distance cutoff \(\Lambda\)) and the infrared cutoff (long-distance cutoff L). The energy density related to HDE [42] is given as

$$\begin{aligned} \rho _{de}=3c^2m_p^2L^{-2}, \end{aligned}$$

in the above equation, the reduced Planck mass and infrared (IR) cut-off were denoted as \(m_p, L\), respectively, and the numerical parameter as c. The HDE is inversely proportional to the square of infrared cutoff, so due to this fact, the horizon is taken in the form of Hubble horizon (\(H^{-1}\)), event horizon, particle horizon, conformal universe age, Ricci scalar radius, Grand-Oliveros cutoff. Hence, horizon entropy is treated as the backbone of HDE.

Li [35] has shown that Hubble horizons and particle horizons are not in good agreement with the cosmos while the future event horizon is the best model for non-interacting holographic DE with suitable constant c. The Hubble horizon is a natural candidate for IR cut-off which is also free from causality, but Hsu [43] found that it gives wrong equation of state (EoS) of DE. Later on, it was shown [36] that if there is an interaction between two dark components of the cosmos the identification of L with Hubble horizon, \(L=H^{-1}\), may give suitable EoS of DE. It has also been shown that it necessarily implies a constant ratio of the energy densities of the two components regardless of the details of the interaction. Thus, the HDE models may also alleviate the cosmic coincidence problem which provides an advantage to HDE models over the other DE models. These HDE models with various infrared cutoffs prove that the value of transition redshift from early deceleration phase (\(q>0\)) to current acceleration phase (\(q<0\)) is in agreement with modern observational [44,45,46,47,48,49,50,51]. Shanthi and Sobhan babu [52, 53] have investigated the Tsallis holographic dark energy (considering IR cut-off as Hubble radius, i.e., \(L=H^{-1}\)) in homogeneous and anisotropic Kantowski–Sachs and Bianchi type-III cosmological models within the frame-work of Saez–Ballester scalar tensor theory of gravitation

As gravity is a long-range interaction, generalized statistical mechanics can be used to investigate gravitational systems. According to this, the Bekenstein entropy can be determined by applying Tsallis statistics to the system [54,55,56]. Based on this recently, three new HDE models have been proposed, titled Tsallis holographic dark energy (THDE) [57, 58], Renyi holographic dark energy (RHDE) [59] and Sharma–Mittal holographic dark energy (SMHDE) [60]. The late-time accelerated universe can be described by these three models with Bekenstein entropy. In non-interacting universe, Tsallis HDE is never stable [57, 58] at the classical level, Renyi HDE shows more stability by itself [59], Sharma HDE is stable at the classical level [60]. Aditya et al. [61] worked on Tsallis HDE in logarithmic Brans–Dicke theory using flat FRW universe. Aditya and Prasanthi [62, 63] worked on the Renyi HDE model in general relativity using Bianchi-\(VI_0\) and Kantowski–Sachs space-time.

Several authors worked on these three newly proposed HDE models using different theories in a flat FRW universe. A few of them are Younas et al. [64], who have studied Tsallis, Renyi, Sharma–Mittal entropies in flat FRW universe using Chern–Simons gravity. Maity and Debnath [65] worked on D-dimensional fractal universe discussing these three HDE models. Iqbal and Jawad [66] studied these three HDE models in a flat FRW universe within the frame of DGP braneworld. Jawad et al. [67] have investigated Tsallis, Renyi, Sharma–Mittal HDE models in loop quantum cosmology. All these works are carried on homogeneous and isotropic FRW universe. The observations from CMBR [68] have revealed the existence of transition from the anisotropic phase of the universe to the isotropic phase. So to represent the early phase of cosmos, only the isotropic model cannot express the early stage of cosmos; to overcome this, it is always suggestible to study anisotropic and spatially homogeneous space-time [69]. So due to this cause, the interest in anisotropic and spatially homogeneous space-times has been increased over the last few decades in theoretical cosmology. With these exciting aspects in the present-day universe, we consider spatially homogeneous and anisotropic axially symmetric space-time in the present paper.

As Einstein’s theory of general relativity does not seem to resolve some of the important problems in cosmology such as dark matter or the missing matter problem there has been considerable interest in alternative theories of gravitation. The most important among them are scalar-tensor theories proposed by Brans–Dicke, Saez–Ballester and so on. The Saez–Ballester scalar-tensor theory of gravitation was developed by Saez and Ballester [13] in 1986. In this scalar-tensor theory, the metric potentials are coupled with dimensionless scalar field \(\phi\). Here, the dimensionless coupling constant w governs the strength of coupling between gravity and field further the missing matter problem in non-flat FRW cosmologies can be solved using this theory.

The action principle for this scalar-tensor theory is expressed as

$$\begin{aligned} A=\int _R(L+\chi L_m)\sqrt{-g}dx^1dx^2dx^3dx^4, \end{aligned}$$

With a slight variation to this A (action principle) so that the metric and scalar field vanishes at the boundary region R. Hence, the action principle gives rise to field equations of this scalar-tensor theory as

$$\begin{aligned} R_{ij}-\frac{1}{2}Rg_{ij}-w\phi ^n\left( \phi _{,i}\phi _{,j}-\frac{1}{2}g_{ij}\phi _{,k}\phi ^{,k}\right) =-8\pi GT_{ij}, \end{aligned}$$
(1)

In the above equation (1), w is the dimensionless constant, \(T_{ij}\) is energy momentum tensor, n is the arbitrary dimensionless constant, G is gravitational constant (\(8\pi G=1\)) and \(\phi\) is the scalar field satisfying the following equation

$$\begin{aligned} 2\phi ^n\phi ^{,i}_{;i}+n\phi ^{n-1}\phi _{,k}\phi ^{,k}=0, \end{aligned}$$
(2)

here, in equation (2) the partial and covariant differentiation are denoted by comma (,) and semi-colon (;), respectively. The energy conservation equation is given by

$$\begin{aligned} T^{ij}_{;j}=0 \end{aligned}$$
(3)

Many researchers like Ramesh et al. [70], Rao et al. [71], Rasouli et al. [72], Sharma et al. [73], have worked with different cosmological models using this scalar-tensor theory. Mishra et al. [74,75,76] worked on this theory using time-varying deceleration parameter (DP), cosmological and gravitational constants (\(\Lambda , G\)) and bilinear varying deceleration parameter (DP). Rasouli et al. [77] have discussed the cosmic acceleration for the future time by considering two scalar fields, the first scalar representing the Saez–Ballester theory and the second one having an extra dimension. Also, few works can be found in [78,79,80,81,82,83].

The HDE model is the first theoretical model of DE inspired by the HP, and it agrees well with current cosmological evidence. As a result, HDE is a really attractive option for DE. Moreover, the HDE hypothesis has received a lot of interest and has been intensively investigated in the last few years. These are as follows

1. The features of HDE are addressed in several modified gravity theories, including the scalar-tensor theories like Brans–Dicke theory, Saez–Ballester theory, and DGP brane-world theories, which can be found in the works [71, 84,85,86,87].

2. The HDE is employed in the reconstruction of various scalar-field DE and modified gravity models.

The Saez–Ballester theory provides a dynamical framework that is more suitable to study HDE models as HDE belongs to the family of dynamical DE candidates. Setare [84] discussed the holographic dark energy model in the Brans–Dicke theory. The cosmological dynamics of the interacting holographic dark energy model are obtained by Setare and Vanegas [88]. Aditya and Reddy discussed FRW type kaluza–klein modified holographic Ricci dark energy models in Brans–Dicke theory of gravitation [89].

Hence, by the motivation of these works we have discussed Tsallis, Renyi, Sharma–Mittal HDE models in axially symmetric space-time using Saez–Ballester scalar-tensor theory of gravitation in the present work. The plan of this paper is as follows metric, and its field equations are discussed in Sect. 2, and the solutions of the field equations are obtained in Sect. 3. The behavior of cosmological parameters along with graphical representation is discussed in Sect. 4, and finally, the conclusions are discussed in Sect. 5.

2 Metric and field equations

The homogeneous and anisotropic axially symmetric space-time proposed by Bhattacharaya and Karade [90] is given by

$$\begin{aligned} ds^2=dt^2-A^2(t)\left[ d\chi ^2+f^2(\chi )d\phi ^2\right] -B^2(t)dz^2, \end{aligned}$$
(4)

where \(\chi , \phi , z\) are comoving coordinates, A, B are functions of cosmic time t and f is a function of coordinate \(\chi\) alone.

The Saez–Ballester field equations for combined matter and dark energy (DE) are given as

$$\begin{aligned} R_{ij}-\frac{1}{2}Rg_{ij}-w\phi ^n\left( \phi _{,i}\phi _{,j}-\frac{1}{2}g_{ij}\phi _{,k}\phi ^{,k}\right) =-(T_{ij}+\overline{T}_{ij}) \end{aligned}$$
(5)

The conservation equation for energy momentum tensor is given by

$$\begin{aligned} \left( T_{ij}+\overline{T}_{ij}\right) _{;j}=0 \end{aligned}$$
(6)

In equation (5), \(T_{ij}\) is energy momentum tensor for pressureless matter and \(\overline{T}_{ij}\) is HDE which are given as

$$\begin{aligned} T_{ij} & = \rho _m u_iu_j \end{aligned}$$
(7)
$$\begin{aligned} \overline{T}_{ij} & = (\rho _{de}+p_{de})u_iu_j-p_{de}g_{ij} \end{aligned}$$
(8)

where \(\rho _m\) is energy density of matter, \(p_{de}\) and \(\rho _{de}\) are the pressure and energy density of HDE, respectively, \(u_i\) is the four-velocity vector component of fluid satisfying \(u_i=(0,0,0,1)\). As the equation of state (EoS) parameter is defined as \(\omega _{de}=\frac{p_{de}}{\rho _{de}}\), equations (7) and (8) become

$$\begin{aligned} T_{ij} & = diag[0,0,0,\rho _{m}] \end{aligned}$$
(9)
$$\begin{aligned} \overline{T}_{ij} & = diag[-\omega _{de}\rho _{de}, -\omega _{de}\rho _{de}, -\omega _{de}\rho _{de}, \rho _{de}] \end{aligned}$$

and after parametrization it reduces to

$$\begin{aligned} \overline{T}_{ij}=diag \left[ -\omega _{de}\rho _{de}, -\omega _{de}\rho _{de}, -(\omega _{de}+\gamma )\rho _{de}, \rho _{de}\right] \end{aligned}$$
(10)

here, the skewness parameter \(\gamma\) is the deviation from EoS parameter (\(\omega _{de}\)) on z-direction.

The field equations (5), (2) for the metric (4) are as follows

$$\begin{aligned} \frac{\ddot{A}}{A}+\frac{\dot{A} \dot{B} }{A B}+\frac{\ddot{B}}{B}-\frac{w\phi ^n\dot{\phi }^2}{2}= & {} -\omega _{de}\rho _{de} \end{aligned}$$
(11)
$$\begin{aligned} \frac{\dot{A}^2}{A^2}+\frac{2\ddot{A}}{A}-\frac{f^{''}}{A^2 f}-\frac{w\phi ^n\dot{\phi }^2}{2}= & {} -\omega _{de}\rho _{de}-\gamma \rho _{de} \end{aligned}$$
(12)
$$\begin{aligned} \frac{\dot{A}^2}{A^2}+\frac{2\dot{A} \dot{B}}{A B}-\frac{f^{''}}{A^2 f}+\frac{w\phi ^n\dot{\phi }^2}{2} = & {} \rho _{de}+\rho _{m} \end{aligned}$$
(13)
$$\ddot{\phi } + \dot{\phi }\left( {\frac{{2\dot{A}}}{A} + \frac{{\dot{B}}}{B}} \right) + \frac{{n\mathop {\phi ^{2} }\limits^{.} }}{{2\phi }}\; = \;0$$
(14)

The functional dependence of the given line element with the help of (12) and (13) gives the relation

$$\begin{aligned} \frac{f^{''}}{f}=k_{1}^2, k_{1}^2=const \end{aligned}$$
(15)

If \(k_{1}=0\), then

$$f(\chi ) = ({\text{const}})\chi ,\;0 < lt;\chi {\text{ < }}lt;\infty$$

For suitable choice of units for \(\phi\), the constant can be equal to unity. This leads to \(f(\chi )=\chi\) resulting in a flat model of the universe [91].

3 Solutions of field equations

With the help of equation (15), equations (11)-(14) reduce to

$$\begin{aligned} \frac{\ddot{A}}{A}+\frac{\dot{A} \dot{B} }{A B}+\frac{\ddot{B}}{B}-\frac{w\phi ^n\dot{\phi }^2}{2}= & {} -\omega _{de}\rho _{de} \end{aligned}$$
(16)
$$\begin{aligned} \frac{\dot{A}^2}{A^2}+\frac{2\ddot{A}}{A}-\frac{w\phi ^n\dot{\phi }^2}{2}= & {} -\omega _{de}\rho _{de}-\gamma \rho _{de} \end{aligned}$$
(17)
$$\begin{aligned} \frac{\dot{A}^2}{A^2}+\frac{2\dot{A} \dot{B}}{A B}+\frac{w\phi ^n\dot{\phi }^2}{2} = & {} \rho _{de}+\rho _{m} \end{aligned}$$
(18)
$$ \ddot{\phi }+\dot{\phi }\bigg (\frac{2\dot{A}}{A}+\frac{\dot{B}}{B}\bigg )+\frac{n\dot{\phi ^2}}{2\phi } = 0 $$
(19)

The energy conservation equation (\(T_{ij}+\overline{T}_{ij})_{;j}=0\) is obtained as

$$\begin{aligned} \dot{\rho }_{m}+\dot{\rho }_{de}+\left( \rho _{m}+\rho _{de}+\rho _{de}\omega _{de}\right) \left( \frac{2\dot{A}}{A}+\frac{\dot{B}}{B}\right) +\gamma \rho _{de}\frac{\dot{B}}{B}=0 \end{aligned}$$
(20)

Here, we assume there is no energy transfer between dark matter and dark energy, so the above equation reduces into two separate conservation equations as

$$\begin{aligned} \dot{\rho }_{m}+\rho _{m}\left( \frac{2\dot{A}}{A}+\frac{\dot{B}}{B}\right) =0 \end{aligned}$$
(21)
$$\begin{aligned} \dot{\rho }_{de}+\left( \rho _{de}+\rho _{de}\omega _{de}\right) \left( \frac{2\dot{A}}{A}+ \frac{\dot{B}}{B}\right) +\gamma \rho _{de}\frac{\dot{B}}{B}=0 \end{aligned}$$
(22)

The obtained four field equations (16)-(19) contain six unknowns namely \(A, B, \phi , \omega _{de}, \rho _{m}, \gamma\), so in order to solve these unknowns we assume the following two physical valid conditions.

Here, we assume the power law relationship between metric potentials by using the condition \(\sigma \propto \theta\) (shear scalar (\(\sigma\)), expansion scalar (\(\theta\))), which is considered as,

$$\begin{aligned} A=B^l \end{aligned}$$
(23)

here, l is a positive constant that preserves the anisotropy of the model for \(l\not =1\) and for \(l=1\), the model leads to a isotropic model. The physical importance for considering this relation is given by Thorne [92], and from the velocity-redshift observations for extragalactic sources advice that Hubble expansion of cosmos is isotropic for present time with the range \(\approx 33 \%\) [93, 94]. These observations suggest that the cosmos attains isotropy for \(\frac{\sigma }{H}\le 0.3\). Further, the valid physical assumption was given by Collins [95] for the case of perfect fluids and barotropic EoS. Many authors have derived the solutions by using this condition few of them are Aditya et al. [62, 96], Mishra and Sahoo [97].

From equations (16), (17) and (23), we obtain

$$\begin{aligned} \frac{\ddot{B}}{\dot{B}}+2l\frac{\dot{B}}{B}=\frac{B}{\dot{B}}\frac{\gamma \rho _{de}}{(1-l)} \end{aligned}$$
(24)

As in recent times, it has been a quite interesting part in finding the general and explicit solutions of the derived equations, so the skewness parameter is assumed in terms of energy density of dark energy (DE). The relation among skewness parameter (\(\gamma\)) and energy density of DE (\(\rho _{de}\)) was considered by Akarsu et al. [98], in the process of solving anisotropic DE models with LRS Bianchi type-I universe. Now, in order to solve equation (24) we consider a relationship between skewness parameter (\(\gamma\)) and energy density (\(\rho _{de}\)) of DE as

$$\begin{aligned} \gamma =\frac{\dot B}{B}\frac{(1-l)\gamma _1}{\rho _{de}}, \end{aligned}$$
(25)

where \(\gamma _1\) is an arbitrary constant. Various authors have worked with this assumption [99, 100]; alternatively, in the literatures [96, 101] the authors have studied this assumption in the study of anisotropic DE models in various theories of gravitation. Now, on solving equation (24) with the help of (25), we obtain the metric coefficients

$$\begin{aligned} A = & {} \bigg ({c_1(2l+1)\frac{exp(\gamma _1 t)}{\gamma _1}+c_2(2l+1)}\bigg )^{\frac{l}{(2l+1)}} \end{aligned}$$
(26)
$$\begin{aligned} B = & {} {\left( c_1(2l+1)\frac{exp(\gamma _1 t)}{\gamma _1}+c_2(2l+1)\right) }^{\frac{1}{(2l+1)}} \end{aligned}$$
(27)

and using the values of A, B in (19) we obtain Saez–Ballester scalar field \(\phi\) as

$$\begin{aligned} \phi =\bigg (\frac{2+n}{2}\bigg )^{\frac{2}{2+n}}\bigg (\frac{\gamma _1c_3t-c_3log(c_1exp(\gamma _1t) +\gamma _1c_2)}{\gamma _1c_2+2\gamma _1c_2l}\bigg )^{\frac{2}{2+n}} \end{aligned}$$
(28)

In above equations (26), (27), (28), \(c_1, c_2, c_3\) are integrating constants and by substituting the values of A, B in (4) the line-element becomes

$$\begin{aligned} \begin{aligned}ds^2&=dt^2-\bigg ({c_1(2l+1)\frac{exp(\gamma _1 t)}{\gamma _1}+c_2(2l+1)}\bigg )^{\frac{2l}{(2l+1)}}\left[ d\chi ^2+f^2(\chi )d\phi ^2\right] \\&\quad -\bigg ({c_1(2l+1)\frac{exp(\gamma _1 t)}{\gamma _1}+c_2(2l+1)}\bigg )^{\frac{2}{(2l+1)}}dz^2 \end{aligned} \end{aligned}$$

4 Tsallis holographic dark energy

The energy density (\(\rho _{de}\)) for Tsallis HDE [57] is defined as

$$\begin{aligned} \rho _{de}=\alpha L^{2\delta -4} \end{aligned}$$
(29)

where \(\alpha\) is a unknown parameter, L is infrared (IR) cutoff. Here, we assume Hubble horizon as IR cutoff, so we have \(L=H^{-1}\). From this, energy density of THDE becomes

$$\begin{aligned} \rho _{de}=\alpha H^{4-2\delta } \end{aligned}$$
(30)

H is the Hubble parameter and its value for the present model is obtained as

$$\begin{aligned} H=\frac{1}{3}\left( \frac{2\dot{A}}{A}+\frac{\dot{B}}{B}\right) =\frac{c_1\gamma _1exp(\gamma _1t)}{(3c_1exp(\gamma _1t)+3c_2\gamma _1)} \end{aligned}$$
(31)

By substituting equation (31) in (30), we obtain the energy density (\(\rho _{de}\)) for Tsallis HDE as

$$\begin{aligned} \rho _{de}=\frac{\alpha 9^{\delta }c_1^{4}\gamma _1^4exp(4\gamma _1 t)(\frac{c_1\gamma _1exp(\gamma _1t)}{(c_1exp(\gamma _1t)+c_2\gamma _1)} )^{-2\delta }}{81(c_1exp(\gamma _1 t)+c_2\gamma _1)^4} \end{aligned}$$
(32)

Now, from equations (18), (25) with the help of equation (32) we obtain the values of \(\rho _{m}, \gamma\)

$$\begin{aligned}{} & {} \left. \begin{aligned}\rho _m&=\frac{-1}{81(l+\frac{1}{2})^2(c_1exp(\gamma _1t)+c_2\gamma _1)^4}\Big (\gamma _1^2\Big (c_1^4exp(4\gamma _1t)\Big (\alpha \gamma _1^2 9^\delta (l+\frac{1}{2})^2(\frac{c_1\gamma _1exp(\gamma _1t)}{(c_1exp(\gamma _1t)+c_2\gamma _1)} )^{(-2\delta )}-\frac{81l^2}{4}-\frac{81l}{2}\Big )\\&\quad -\frac{81c_1^2(c_2^2l(l+2)\gamma _1^2+\frac{wc_3^2}{2})exp(2\gamma _1t)}{4}-\frac{81c_2\gamma _1(c_1^3l(l+2)exp(3\gamma _1 t)+\frac{wc_3^2(c_1exp(\gamma _1 t)+\frac{c_2\gamma _1}{2})}{2})}{2}\Big )\Big ) \end{aligned}\right\} \end{aligned}$$
(33)
$$\begin{aligned}{} & {} \begin{aligned}&\gamma =-\frac{819^{-\delta }(-1+l)exp(-3\gamma _1t)(c_1exp(\gamma _1t)+c_2\gamma _1)^3(\frac{c_1\gamma _1exp(\gamma _1t)}{(c_1exp(\gamma _1t)+c_2\gamma _1)} )^{2\delta }}{\alpha \gamma _1^2c_1^3(2l+1)} \end{aligned} \end{aligned}$$
(34)
Fig. 1
figure 1

Plot of scalar field (\(\phi\)) versus redshift (z) for \(n=0.01, l=0.325, \gamma _1=0.12\)

Full size image
Fig. 2
figure 2

Plot of energy density (\(\rho _{de}\)) versus redshift (z) for THDE model

Full size image
Fig. 3
figure 3

Plot of energy density of matter (\(\rho {_m}\)) versus redshift (z)

Full size image
Fig. 4
figure 4

Plot of skewness parameter (\(\gamma\)) versus redshift (z)

Full size image

In order to study the behavior of energy densities \(\rho _m\), \(\rho _{de}\), skewness parameter (\(\gamma\)) of Tsallis, Renyi, Sharma–Mittal HDE models, we plot them (\(\rho _m\), \(\rho _{de}\), \(\gamma\)) with respect to redshift (z) (redshift is defined as \(1+z=\frac{a_0}{a(t)}\); we assume \(a_0=1\)).

From Fig. 1, it is observed that the scalar field (\(\phi\)) is positive throughout the evolution of cosmos and increases as redshift (z) decreases. The plots of energy density (\(\rho _{de}\)) of THDE and energy density for pressureless matter with respect to redshift (z) for two different values of \(\delta =0.89, 1.2\) are given in Figs. 2, 3. It is observed that for both the values of \(\delta\) the energy density (\(\rho _{de}\)) of THDE and pressureless matter (\(\rho _{m}\)) are positive throughout the evolution of cosmos and decreases as redshift (z) decreases.

The skewness parameter (\(\gamma\)) corresponding to redshift (z) for \(\delta =0.89, 1.2\) is shown in Fig. 4. For both the values of \(\delta\), the skewness parameter is positive throughout the evolution of cosmos and increases as redshift (z) decreases.

5 Renyi holographic dark energy

The energy density for Renyi HDE [59] is defined as

$$\begin{aligned} \rho _{de}=\frac{3c^2}{8\pi L^2(1+\delta \pi L^2)}, \end{aligned}$$
(35)

where \(c, \delta\) are constants, and IR cutoff is considered as Hubble radius (i. e. \(L=H^{-1}\)). Hence, the energy density for Renyi HDE is given as

$$\begin{aligned} \rho _{de}=\frac{3c^2H^2}{8\pi \left( 1+\frac{\delta \pi }{H^2}\right) } \end{aligned}$$
(36)

Now, using equation (31) in (36), we obtain the energy density (\(\rho _{de}\)) for Renyi HDE as

$$\begin{aligned} \rho _{de}=\frac{c^2c_1^4\gamma _1^4exp(4\gamma _1t)}{24\pi (c_1exp(\gamma _1t)+c_2\gamma _1)^2(18\pi c_2\gamma _1 \delta c_1exp(\gamma _1t)+9\pi c_2^2\gamma _1^2\delta +9c_1^2exp(2\gamma _1t)\pi \delta +c_1^2exp(2\gamma _1t)\gamma _1^2)} \end{aligned}$$
(37)

From equations (18) and (25) with the help of (37) we obtain the expressions for \(\rho _{m}, \gamma\) as

$$\begin{aligned}{} & {} \rho _m=\frac{\iota _1}{\iota _2} \end{aligned}$$
(38)
$$\begin{aligned}{} & {} \left. \begin{aligned}\gamma &=\frac{1}{{c_1^3(2l+1)c^2\gamma _1^2}}-216\pi (-1+l) exp(-3\gamma _1t)(c_1exp (\gamma _1t)+c_2\gamma _1)\bigg (c_1^2exp(2\gamma _1t)\left( \delta \pi +\frac{\gamma _1^2}{9}\right) \\&\qquad +2\gamma _1\delta \pi c_2(c_1exp(\gamma _1t)+\frac{c_2\gamma _1}{2})\bigg ) \end{aligned}\right\} \end{aligned}$$
(39)

where

$$\begin{aligned}{} & {} \iota _1=-\gamma _1^2\bigg (c_1^4exp(4\gamma _1t)\bigg (\gamma _1^2\big (\pi (-6l^2-12l) +\left( l+\frac{1}{2}\right) ^2c^2\big )-54\pi ^2\delta l(l+2)\bigg )-54\pi \bigg ( c_1^2exp(2\gamma _1t)\bigg (\gamma _1^2 \\ {}{} & {} \qquad \bigg (l c_2^2\delta (l+2)\pi +\frac{wc_3^2}{18}\bigg )+\frac{w\pi c_3^2\delta }{2}\bigg )+\frac{\pi \delta \gamma _1c_2\big (4c_1^3l(l+2)exp(3\gamma _1t)+wc_3^2(c_2\gamma _1+2c_1exp(\gamma _1t))\big )}{2}\bigg )\bigg ) \\{} & {} \iota _2= {24\pi \left( l+\frac{1}{2}\right) ^2\bigg (c_1^2exp(2\gamma _1t)(9\pi \delta +\gamma _1^2)+9\gamma _1\pi c_2\delta \big (c_2\gamma _1+2c_1exp(\gamma _1t)\big )\bigg )(c_1exp(\gamma _1t)+c_2)^2} \end{aligned}$$
Fig. 5
figure 5

Plot of energy density (\(\rho _{de}\)) versus redshift (z) for RHDE model

Full size image
Fig. 6
figure 6

Plot of energy density of matter (\(\rho _{m}\)) versus redshift (z)

Full size image
Fig. 7
figure 7

Plot of skewness parameter (\(\gamma\)) versus redshift (z)

Full size image

For RHDE model, the energy density (\(\rho _{de}\)), energy density of pressureless matter corresponding to redshift (z) is shown in Figs. 5, 6. It is observed that both \(\rho _{de}, \rho _{m}\) are positive throughout the evolution of cosmos and decreases as redshift (z) decreases for both the values of \(\delta =0.89, 1.2\). Similarly, the positive value of skewness parameter with respect to redshift (z) for \(\delta =0.89, 1.2\) is observed in Fig. 7.

6 Sharma–Mittal holographic dark energy

The energy density (\(\rho _{de}\)) for Sharma–Mittal HDE [102] is defined as

$$\begin{aligned} \rho _{de}= \frac{3c^2\bigg (\big (1+\delta \pi L^2\big )^{\frac{R}{\delta }}-1\bigg )}{8\pi RL^4} \end{aligned}$$
(40)

where \(R, \delta\) are two constants, L is the IR cutoff. By considering IR cutoff as Hubble horizon cutoff \(L=H^{-1}\), the energy density of Sharma–Mittal HDE becomes

$$\begin{aligned} \rho _{de}= \frac{3c^2H^4\bigg (\big (1+\frac{\delta \pi }{H^2}\big )^{\frac{R}{\delta }}-1\bigg )}{8\pi R} \end{aligned}$$
(41)

By substituting equation (31) in (41), we obtain the energy density of Sharma–Mittal HDE as

$$\begin{aligned} \begin{aligned} \rho _{de}=\frac{c^2c_1^4\gamma _1^4(\iota _7-1)exp(4\gamma _1t)}{216(c_1exp(\gamma _1t)+c_2\gamma _1)^4\pi R} \end{aligned} \end{aligned}$$
(42)

Now, from Eqs. (18) and (25) with the help of (42) we obtain the expressions for \(\rho _{m}, \gamma\) as

$$\begin{aligned}{} & {} \left. \begin{aligned}&\rho _{m}=\frac{-1}{216R\pi (l+\frac{1}{2})^2(c_1exp(\gamma _1t)+c_2\gamma _1)^4}\bigg (-54\bigg (c_2^2\gamma _ 1^2l(l+2)+\frac{wc_3^2}{2}\bigg )Rc_1^2\pi exp(2\gamma _1t) \\&\qquad\, +c_1^4exp(4\gamma _1t)\bigg((\iota _7-1) \bigg(l+\frac{1}{2}\bigg)^2c^2\gamma _1^2-54\pi Rl(l+2)\bigg )-27(4c_1^3l(l+2)exp(3\gamma _1t)\\&\qquad\, +wc_3^2(c2\gamma _1+2c_1exp(\gamma _1t)))c_2R\pi \gamma _1\bigg )\gamma _1^2 \end{aligned}\right\} \end{aligned}$$
(43)
$$\begin{aligned}{} & {} \left. \begin{aligned}&\gamma =\frac{-216\pi R(-1+l)exp(-3\gamma _1t)(c_1exp(\gamma _1t)+c_2\gamma _1)^3}{c^2\gamma _1^2c_1^3(2l+1)(\iota _7-1)} \end{aligned}\right\} \end{aligned}$$
(44)
Fig. 8
figure 8

Plot of energy density (\(\rho _{de}\)) versus redshift (z) for SHDE model

Full size image
Fig. 9
figure 9

Plot of energy density of matter (\(\rho _{m}\)) versus redshift (z)

Full size image
Fig. 10
figure 10

Plot of skewness parameter (\(\gamma\)) versus redshift (z)

Full size image

The energy density (\(\rho _{de}\)) of Sharma–Mittal HDE, energy density of pressureless matter for \(\delta =0.89, 1.2\) corresponding to redshift (z) are shown in Figs. 8, 9. From graphs, it can be observed that for both values of \(\delta =0.89, 1.2\) energy densities are positive throughout the evolution of cosmos and decreases as redshift (z) decreases. The skewness parameter with respect to redshift is shown in Fig. 10, and it is observed that it is positive throughout the evolution of cosmos and increases as redshift (z) decreases.

7 Cosmological parameters

Here, we discuss both physical and geometrical aspects such as volume (V), Hubble parameter (H), expansion scalar (\(\theta\)), EoS parameter (\(\omega _{de}\)), deceleration parameter (q), statefinder parameters \(\{r, s\}\), squared speed of sound (\(v_s^2\)).

The average scale factor of the present model is obtained as

$$a(t)=(A^2B)^{\frac{1}{3}}=\bigg (\frac{(2l+1)(c_1exp(\gamma _1t)+c_2\gamma _1)}{\gamma _1}\bigg )^{1/3}$$

The volume (V) of the present model is obtained as

$$V=\frac{(2l+1)(c_1exp(\gamma _1t)+c_2\gamma _1)}{\gamma _1}$$
Fig. 11
figure 11

Plot of volume (V) versus redshift (z)

Full size image

The volume (V) corresponding to redshift (z) is shown in Fig. 11. It is observed that volume is positive throughout the evolution of cosmos and increases as the redshift (z) decreases. These observations confirm the fact that the universe is expanding in an accelerating way, that is as the volume increases, the energy density decreases for the obtained model.

The Hubble parameter (H) of the present model is obtained as

$$H=\frac{c_1\gamma _1exp(\gamma _1t)}{(3c_1exp(\gamma _1t)+3c_2\gamma _1)}$$

The expansion scalar for the present model is obtained as

$$\theta =3H=\frac{c_1\gamma _1exp(\gamma _1t)}{(c_1exp(\gamma _1t)+c_2\gamma _1)}$$

8 EoS parameter

For \(\Lambda\) cold dark matter (CDM) model, the state of dark energy remains constant. For describing dark energy, an important model associated with it is equation of state (EoS) parameter, which is defined in terms of pressure (\(p_{de}\)) and energy density (\(\rho _{de}\)) and denoted as \(\omega _{de}\). Nowadays, to explain dark energy models, different equations of state (EoS) parameters came into existence, whose value needs not be a constant. Quintessence (\(-1<\omega _{de}<-\frac{-1}{3}\)) model of dark energy, phantom model of dark energy (\(\omega _{de}<-1\)), vacuum era (\(\omega _{de}=-1\)) and quintom like behavior (combination of quintessence and phantom regions).

The EoS parameter for Tsallis HDE model is obtained by solving equation (22), with the help of equations (26), (27), (32), (34).

$$\left. {\begin{array}{*{20}l} {\omega _{{de}} = \frac{{ - 1}}{{\alpha c_{1}^{3} \gamma _{1}^{2} (2l + 1)^{2} (c_{1} exp(\gamma _{1} t) + c_{2} \gamma _{1} )}}\left( {4exp( - \gamma _{1} t)} \right.} \hfill \\ {\quad \quad \left( {\frac{{ - 819^{{ - \delta }} ( - 1 + l)(3H)^{{2\delta }} exp( - 2\gamma _{1} t)(c_{1} exp(\gamma _{1} t) + c_{2} \gamma _{1} )^{4} }}{4}} \right.} \hfill \\ {\left. {\quad \quad + \alpha \left( {\left( {\left( {exp(2\gamma _{1} t)c_{1}^{2} - \quad 2(c_{1} \left( {\delta - \frac{5}{2}} \right)exp(\gamma _{1} t) + c_{2} \gamma _{1} ( - 2 + \delta )} \right)\gamma _{1} c_{2} } \right)\left( {l + \frac{1}{2}} \right)^{2} c_{1}^{2} \gamma _{1}^{2} } \right)} \right)} \hfill \\ \end{array} } \right\}$$
(45)

Similarly, the EoS parameter (\(\omega _{de}\)) for Renyi, Sharma–Mittal HDE models is obtained by solving equation (22), with the help of equations (26), (27), (37), (39), (42), (44).

$$\begin{aligned} \omega _{de}=-1-\iota _3-\iota _4 \end{aligned}$$
(46)
$$\begin{aligned} \omega _{de}=-1-\iota _5-\iota _6 \end{aligned}$$
(47)

The values \(\iota _3, \iota _4, \iota _5, \iota _6\) are given in the appendix section.

Fig. 12
figure 12

Plot of EoS parameter (\(\omega _{de}\)) of THDE versus redshift (z)

Full size image
Fig. 13
figure 13

Plot of EoS parameter (\(\omega _{de}\)) of RHDE versus redshift (z)

Full size image
Fig. 14
figure 14

Plot of EoS parameter (\(\omega _{de}\)) of SHDE versus redshift (z)

Full size image

The EoS parameter (\(\omega _{de}\)) for Tsallis, Renyi, Sharma–Mittal HDE models with respect to redshift (z) for two values of \(\delta =0.89, 1.2\) is shown in Figs. 12, 13, 14, respectively. From Fig. 12, it is observed that for \(\delta =0.89\) the \(\omega _{de}\) exhibits phantom phase and for \(\delta =1.2\) the \(\omega _{de}\) starts from quintessence phase and reaches to phantom phase crossing phantom divide line (\(\omega _{de}=-1\)) (that is it shows quintom like behavior). The EoS parameter for Renyi HDE shows transition from decelerating phase to accelerating phase for both the values of \(\delta =0.89, 1.2\) at \(z=0.67\), \(z=0.72\), respectively. And the model starts from matter dominated phase and exhibits quintom like behavior for both the values of \(\delta =0.89, 1.2\) is shown in Fig. 13. The EoS parameter for Sharma–Mittal HDE for both the values of \(\delta =0.89, 1.2\) shows transition from decelerating phase to accelerating phase at \(z=0.475\), and model enters into quintessence phase from matter dominated phase is shown in Fig. 14.

9 Deceleration parameter

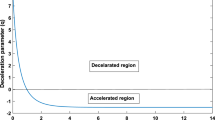
The evolution of the cosmos can be described by the deceleration parameter (q). Based on the deceleration parameter, we can test whether our model is accelerating or decelerating. It is defined as

$$\begin{aligned} q=\frac{-a\ddot{a}}{\dot{a}^2} \end{aligned}$$
(48)

here, a is the scale factor, if \(q>0\), the model decelerates; if \(-1<q<0\), the model accelerates, if \(q=0\) a stable rate in expansion will be observed. Further, if \(q=-1\), the universe shows de Sitter or exponential expansion; if \(q<-1\), the universe shows super exponential expansion. The value of q for our model is obtained as

$$\begin{aligned} q=-\frac{exp(-\gamma _1t)(c_1exp(\gamma _1t)+3c_2\gamma _1)}{c_1} \end{aligned}$$
(49)

According to observations from high redshift supernova, type Ia supernova combined with BAO and CMB observations investigated that present-day universe is undergoing a phase of transition from deceleration to acceleration.

The plot of deceleration parameter (q) with respect to redshift (z) for \(c_1=0.265, c_2=-1.25, \gamma _1=0.12\) is shown in Fig. 15. It is observed that in the present model, the transition of universe occurs at \(z_t=0.6\) for \(q=0\). This \(z_t=0.6\) matches with observations obtained by various theoretical values by Busca [103] \(z_t=0.82\pm 0.08\), Capozziello et al. [104], \(z_t=0.7679^{+0.1831}_{-0.1829}\), Yang and Gong [105] \(z_t=0.60^{+0.21}_{-0.12}\), Lu et al. [106] \(z_t=0.69^{+0.23}_{-0.12}\). In the present model, the decelerating phase is observed for \(q>0\), accelerating phase is observed for \(q<0\). The present value of the deceleration parameter is obtained as \(q=-0.6758\).

Fig. 15
figure 15

Plot of deceleration parameter (q) versus redshift (z)

Full size image

10 Stability analysis

In this section, the stability analysis of Tsallis, Renyi and Sharma–Mittal HDE models is verified through an important quantity namely squared speed of sound (\(v_s^2\)). The value of \(v_s^2\) is identified as

$$\begin{aligned} v_s^2=\frac{\dot{p}_{de}}{\dot{\rho }_{de}} ~ =\omega _{de}+\frac{\rho _{de}}{\dot{\rho }_{de}}\dot{\omega }_{de} \end{aligned}$$
(50)

The stability of the model is described depending on the signature of \(v_s^2\). The model is said to be stable if \(v_s^2\) is positive, whereas it is unstable if \(v_s^2\) is negative. The squared speed of sound \(v_s^2\) value for the three models is given in the appendix section.

The behavior of \(v_s^2\) for all the three models corresponding to redshift (z) is shown in Figs. 16, 17, 18, respectively. For both the values of \(\delta =0.89, 1.2\) in Tsallis HDE model the \(v_s^2<0\) which indicates unstable behavior of the model, whereas in Renyi HDE model for \(\delta =0.89\) it is observed that \(v_s^2>0\) in early-times and at present (\(z=0\)) which indicates stable behavior of the model, \(v_s^2<0\) for late-times which indicates unstability. For \(\delta =1.2\) in Renyi HDE \(v_s^2>0\) in early-times indicating stable behavior of model, \(v_s^2<0\) at present (\(z-0\)), late-times indicating unstable behavior model of the universe. Sharma–Mittal HDE model exhibits stable behavior throughout for both the values of \(\delta =0.89, 1.2\) as \(v_s^2>0\).

Fig. 16
figure 16

Plot of squared speed of sound (\(v^2_{s}\)) of THDE versus redshift (z)

Full size image
Fig. 17
figure 17

Plot of squared speed of sound (\(v^2_{s}\)) of RHDE versus redshift (z)

Full size image
Fig. 18
figure 18

Plot of squared speed of sound (\(v^2_{s}\)) of SHDE versus redshift (z)

Full size image

11 Statefinder parameters

The expansion of the present-day cosmos in an accelerating way is being illustrated by much dark energy (DE) models. Many dark energy models have been constructed to overcome the fine-tuning issue and analyze the cosmos accelerating phase. A cosmological diagnostic pair (r, s) known as statefinder parameter to discuss these various forms of dark energy models was proposed by Shani et al. [107], Alam et al. [108]which is defined as

$$\begin{aligned} r=\frac{\dddot{a}a^2}{\dot{a}^3} ~~,~~ s=\frac{r-1}{3\left( q-\frac{1}{2}\right) } \end{aligned}$$
(51)

here, q is the deceleration parameter, a is the scale factor, and H is the Hubble parameter. The study of dark energy in (r, s) parameter is being independent of the model, instead of depending on the theory of gravity. Hence, the statefinder is referred to as a ’geometric’ tool as it depends on the scale and the metric describing space-time. This geometric tool is analyzed for various dark energy candidates, including holographic dark energy, agegraphic dark energy, quintessence, Chaplygin gas, etc. The values of these parameters obtained for our model are as follows

$$\begin{aligned} r & = \frac{(exp(2\gamma _1t)c_1^2+9c_2^2\gamma _1^2)exp(-2\gamma _1t)}{c_1^2} \end{aligned}$$
(52)
$$\begin{aligned} s & = -\frac{2c_2^2\gamma _1^2(c_2^3\gamma _1^3exp(-\gamma _1t)+c_1^3exp(2\gamma _1t)+3\gamma _1c_1^2c_2exp (\gamma _1t)+3\gamma _1^2c_1c_2^2)}{c_1(c_1exp(\gamma _1t)+c_2\gamma _1)^3(c_1exp(\gamma _1t)+2c_2\gamma _1)} \end{aligned}$$
(53)
Fig. 19
figure 19

Plot of r versus s

Full size image

The graphical representation of statefider parameter (r, s) is shown in Fig. 19. For all values of r, we have \(s<0\) which indicates the present model is exhibiting Chaplygin gas and at late-times it reaches to \(\Lambda CDM\) model (\(r=1, s=0\)).

12 Analysis of solution through perturbation techniques

The solutions of the present model are verified through perturbation technique. This process is carried by many researchers like, Chen and Kao [109] who have studied the perturbations in anisotropic space-time in a detailed manner, in f(R, T) theory this analysis is done by Sharif and Zubair [110]. Sahoo et al. [111], Saha et al. [112], Sharma et al. [113], have studied perturbation techniques in both isotropic and anisotropic models for obtaining desired results. For the three expansion factors \(a_i\) the perturbations of metric are given as

$$\begin{aligned} a_{i}\rightarrow a_{B_{i}}+\delta a_{i}=a_{B_{i}}(1+\delta b_{i}) \end{aligned}$$
(54)

Corresponding to the above equation the perturbations expression in terms of volume (\(V_B=\Pi _{i=1}^3 a_i\)), directional Hubble parameter (\(\theta _{i}=\frac{\dot{a}_{i}}{a}\)), mean Hubble parameter (\(\theta =\sum\nolimits_ {i=1}^ {3}\frac{\theta _{i}}{3}\)) is given as

$$V\rightarrow V_{B}+V_{B}\sum\nolimits_{i}\delta b_{i}$$
$$\theta _{i}\rightarrow \theta _{B_{i}}+\sum\nolimits_{i}\delta b_{i}$$
$$\theta \rightarrow \theta _{B}+\frac{1}{3}\sum\nolimits_{i}\delta b_{i}$$

The linear order perturbations \(\delta b_i\) of the metric perturbations satisfy the following conditions

$$ \sum _{i} \delta \ddot{b}_{i}+2\sum \theta _{B_{i}} \delta \dot{b}_{i} = 0 $$
(55)
$$\delta \ddot{b_{i}}+\frac{\dot{V}_{B}}{V_{B}}\delta \dot{b_{i}}+\sum \delta \dot{b_{j}}\theta _{B_{i}} = 0 $$
(56)
$$ \sum \delta \dot{b}_{i}= 0 $$
(57)

By solving these three equations (55)-(57), we obtain

$$\begin{aligned} \delta \ddot{b_{i}}+\frac{\dot{V}_{B}}{V_{B}}\delta \dot{b_{i}} = 0 \end{aligned}$$
(58)

Here, in equation (58) \(V_B\) is volume, for present model \(V_B\) is given as

$$\begin{aligned} V_B=\frac{(2l+1)(c_1exp(\gamma _1t)+c_2\gamma 1)}{\gamma _1} \end{aligned}$$
(59)

with the help of equation (59) in (58) and on integrating, we obtain

$$\begin{aligned} \delta b_i=\frac{d_1(\gamma _1t-ln(c_1exp(\gamma _1t)+c_2\gamma _1))}{c_2\gamma _1(2l+1)}+d_2 \end{aligned}$$
(60)

where \(d_1, d_2\) are integrating constants. By substituting equation (60) in (54) we obtain the actual fluctuations \(\delta a_i=a_{B_i} \delta b_i\) as

$$\begin{aligned} \delta a_i=\frac{\gamma _1}{(2l+1)(c_1exp(\gamma _1t)+c_2\gamma _1)}\bigg (\frac{d_1(\gamma _1t-ln(c_1exp (\gamma _1t)+c_2\gamma _1))}{c_2\gamma _1(2l+1)}+d_2\bigg ) \end{aligned}$$
(61)
Fig. 20
figure 20

Plot of actual fluctuations (\(\delta a_i\)) versus redshift (z)

Full size image

Figure  20 shows that the actual fluctuations (\(\delta a_i\)) are plotted against redshift (z). The \(\delta a_i\) initially starts with small positive value and later approaches to zero value, which indicates the background solution is stable corresponding to perturbations of gravitational field.

13 Conclusions

The scalar fields in the universe produce long-range forces. Due to this reason, the scalar-tensor theories are fundamental in various disciplines in cosmology and gravitational physics. The dark matter or missing matter issue in cosmology is not discussed in Einstein’s general theory of relativity. But an alternative to Einstein’s theory, scalar-tensor theories can discuss these problems. These dimensionless scalar field models have been studied by several authors. Due to these interesting aspects in the present work, we have worked with the Saez–Ballester scalar-tensor theory of gravitation. Here, we studied the homogeneous and anisotropic axially symmetric metric. The field equations of this space-time are obtained using Saez–Ballester theory by considering the two fluids, one being pressureless matter and the second being HDE (Tsallis, Renyi, Sharma–Mittal models). Moreover, in the study of these three Tsallis, Renyi, Sharma–Mittal HDE models, we constructed different cosmological parameters along with their graphical representation such as deceleration parameter, EoS parameter, squared speed of sound (\(v_s^2\)), statefinder parameters (r, s) for two different values of \(\delta =0.89, 1.2\) and observed the following.

\(*\) The graphical behavior of scalar field (\(\phi\)) with respect to redshift (z) is shown in Fig. 1 and it is observed that scalar field (\(\phi\)) is positive throughout the evolution of cosmos and it increases as redshift (z) decreases. From the behavior of this plot along with the plots of matter energy density, energy density of Tsallis HDE, Renyi HDE, and Sharma–Mittal HDE, it is observed that there is a clear contribution from the scalar field and the HDE to the cosmic expansion. Because as the scalar field increases, the dominance of matter energy density \(\rho _m\), the energy density \(\rho _{de}\) of Tsallis, Renyi, Sharma–Mittal HDE is delayed considerably and both the energy densities were positive throughout the evolution of cosmos and decreases as redshift (z) decreases, which shows the expansion of cosmos.

\(*\) For the obtained three models, the energy density (\(\rho _m\)) of pressureless matter and energy density (\(\rho _{de}\)) of Tsallis, Renyi, Sharma–Mittal HDE models are positive throughout the evolution of cosmos and decreases as redshift (z) decreases for both values of \(\delta =0.89, 1.2\) which is shown in Figs. 2, 3, 5, 6 and 8, 9.

\(*\) The skewness parameters (\(\gamma\)) for all the three Tsallis, Renyi, Sharma–Mittal HDE models are positive throughout the evolution of cosmos and increases as redshift (z) decreases. In Figs. 4, 7 and 10, the behavior of the skewness parameter with respect to redshift (z) is plotted.

\(*\) From Fig. 11, it is observed that volume is positive throughout the evolution of cosmos and increases as redshift (z) decreases this indicates that the present universe is expanding in an accelerating way.

\(*\) The deceleration parameter (q) in the present work shows the transition from decelerating phase to the accelerating phase, which agrees with recent observational data. The transition (\(z_t\)) observed is \(z_t=0.6\), and the present value of the deceleration parameter is \(q=-0.6758\), and it is in the acceptable range.

\(*\) In modern cosmology, the EoS parameter plays an important role as it controls the gravitational properties of DE and its evolution. The EoS parameter (\(\omega _{de}\)) of Tsallis HDE model for \(\delta =0.89\) exhibits phantom behavior (\(\omega _{de}<-1\)), and for \(\delta =1.2\) it exhibits quintom like behavior (i.e., \(\omega _{de}\) starts from quintessence phase, passes through phantom divide line (\(\omega _{de}=-1\)) and reaches the phantom phase ) which represents the accelerating expansion of universe.

\(*\) In the case of the RHDE model, the EoS parameter (\(\omega _{de}\)) for the values of \(\delta =0.89, 1.2\) shows the transition from decelerating phase to accelerating phase at \(z=0.67, 0.72\), respectively, and the model starts from matter-dominated phase exhibiting quintom like behavior. In Sharma–Mittal HDE, the EoS parameter for the values of \(\delta =0.89, 1.2\) shows the transition from decelerating phase to accelerating phase at \(z=0.475\). It enters into the quintessence phase from the matter-dominated phase, representing the universe’s accelerating expansion. The EoS parameter \(\omega _{de}\) for the three HDE models in the present work meets the range \(\omega _{de}=-1.13^{+0.24}_{-0.25}\) [114](Planck+nine years WMAP), SNe Ia data with galaxy clustering, CMBR anisotropy statistics \(-1.33<\omega _{de}<-0.79\) and \(-1.67<\omega _{de}<-0.62\) [115], respectively, and present Planck collaboration data (2018) [116] gives the range of EoS as \(\omega _{de}=-1.028\pm 0.031\) (\(68\%\), Planck TT, TE, EE+lowE+ lensing+SNe+BAO), \(\omega _{de}=-0.76\pm 0.20\) (Planck+BAO/RSD+WL), \(\omega _{de}=-0.957\pm 0.080\) (Planck+SNe+BAO), \(\omega _{de}<-0.95\) (\(95\%\), Planck TT, TE, EE+low E+ lensing+SNe+BAO) with these observations the EoS parameter (\(\omega _{de}\)) in present model matches with recent observational data. The complete behavior of EoS parameters for three models is plotted in Figs. 12, 13 and 14.

\(*\) The stability analysis of these three HDE models is verified through squared speed of sound (\(v_s^2\)) and depicted in Figs. 16, 17, 18. The Tsallis HDE model shows unstable behavior for both the \(\delta =0.89, 1.2\). The Renyi HDE model shows stable behavior at present and early times for \(\delta =0.89\), and at late times it shows unstable behavior. Whereas for \(\delta =1.2\) it exhibits stability at early times, unstability at present, and late times. The \(v_s^2\) of Sharma–Mittal is always positive, so it shows stable behavior throughout the universe’s expansion for both the values of \(\delta =0.89, 1.2\).

\(*\) Statefinder parameters are plotted in Fig. 19 and observed that initially, it represents Chaplygin gas model (\(r>1, s<0\)) and later approaches to \(\Lambda CDM\) model. The background solutions for the obtained models are verified through perturbation techniques and observed that background solutions are stable against perturbation of the gravitational field represented in Fig. 20.

Finally, Tsallis, Renyi, Sharma–Mittal HDE models are obtained, and different cosmological parameters like deceleration parameter, EoS parameter, squared speed of sound, statefinder parameters, etc., are discussed thoroughly. The value of \(q=-0.6758\) obtained in this work matches with recent observational data. Interestingly, all the obtained values match the recent observational data, and this type of study can be extended to other anisotropic models.