1 Introduction

Peristalsis is a vital liquid physiological transportation mechanism in living organs. It is caused by the continuous contraction and relaxation of the vessel walls. The intestinal network, lymphatic vessels, glandular ducts, and blood vessels are all said to have peristaltic pumping as a built-in property in some cases. Peristalsis-based explorations in the industry include finger and roller pumps, the transportation of sanitary, and several corroding materials. It is used in MRIs, endoscopes, heart–lung devices, catheters, and various other bioscience applications. After Latham [1] introduced his work on peristaltic flow, scientists and researchers have used experimental, numerical, and analytical techniques to add to the literature under various assumptions and boundary conditions. In this regard, some appropriate studies have been reported in [2,3,4,5,6,7,8,9,10]. Peristaltic motion through a permeable medium has also gained attention due to its vast industrial and biomedical applications [11,12,13,14].

The failure of water and natural oil to fulfill the needs of thermal conductivity has created space for nanofluid research since the nanofluids enhance the thermal conductivity of conventional flow. They provide the various purposes of biomedical engineering such as drug delivery and tumor treatment and hence have become a topic of research interest [15,16,17,18,19,20,21,22,23,24,25,26].

Many industrial equipment’s (control generators, heat exchange structures, MHD blowers, etc.) are based on the principle of MHD. It is also effective in drug delivery, control of blood flow during surgery, cell separation magnetic gadgets, etc. These and many more applications have promoted the study of MHD analysis in peristaltic flow [27,28,29,30,31,32,33,34,35,36,37]. Several articles can be found regarding the study of radiation and the MHD effect on the flow through stretching sheets [38,39,40,41,42,43,44,45,46,47]. Instead of using convective derivatives, the Jeffrey model proposes a linear simple model that uses the time derivatives and can also be reduced to a Newtonian fluid model easily. This behavior of Jeffrey fluid exhibiting both Newtonian and non-Newtonian characteristics has attracted many researchers. The usual viscous fluid models fail to describe the stress relaxation property of non-Newtonian fluids but is well explained by the Jeffrey fluid model. The linear viscoelastic effect of Jeffrey fluid has many examples that include the dilute polymer solution thus finding numerous applications in the polymer industry. The numerous applications of Jeffry fluid have created interest in many researchers [48,49,50,51,52].

One of the biggest challenges in designing microfluidic transportation systems in many of the above appliances is to make sure that the flow of liquid can be limited to the maximum amount possible. Since it does not require the typical relocating constituents attributed to usual micro-pumps, it has significant advantages in microfluidic pumping. It consents an efficient policy of microchannel motion parts using electrical fields. Electro-osmotic pumping has been discovered by affecting an electrical field to an electrolyte in contact via the surface to generate a continuous pulse-free motion. The viscous drag causes the liquid to flow tangentially toward the area, resulting in a reliable net ion migration. The strict requirement for easy-to-handle, tiny, and economical analytic mechanisms has resulted from the demand for quickly, reliable, and reputable microfluidic systems. DNA analysis/sequencing systems, chemical/biological agent discovery sensors, and drug delivery on integrated circuits are examples of such applications. In few of the above applications, one of the major challenges in the design of microfluidic transport systems is to reduce the cost of liquid movement to the lowest possible level by arranging for perfect mixes of flow activating systems. However, electro-osmosis has proven to be a simple system for creating plug-shaped like speed profiles in microchannels by controlling the statement of a pertained electrical field with free density gradients near the solid–liquid user interface. Because it does not require the typical relocating parts found in usual micro-pumps, it has significant advantages in microfluidic pumping. It allows for very reliable microchannel flow areas through electric fields. Electro-osmotic pumping has been thought to generate a continuous flow with no pulses. At the microscale, these pumps are a lot more malleable. They are widely used in pharmaceutical division, electro-osmotically activated bio-microfluidic mechanisms plasma, and splitting. Flow control is accomplished via implementing an electric field to an electrolyte in contact through a surface. The electrolyte connects the area, resulting in a web indict thickness in the remedy. The viscous drag causes the liquid to flow tangentially to the surface, resulting in a continuous ions web. Driven through the request of electro-osmotic transfer toward the peristaltic mechanism, Chakraborty [53] proposed the peristaltic circulation with electric field. Nonetheless, a slim electrical double layer (EDL) estimation was carried. Bandopadhyay et al. [54] modified another model to review the stress circulation, channel size, and impacts of the electric field and EDL thickness. Guo and Qi [55] researched the fractional Jeffreys design of electro-osmotic peristaltic flow in a limitless microchannel to evaluate the results of electro-osmosis and fractional parameters on peristaltic circulation of fractional viscoelastic liquid. Waheed et al. [56] examined the mass and heat transport effect for EOF of a third-order drink through viscous dissipation in a microchannel. Waheed et al. [57] scrutinized the electro-osmotic modulated peristaltic flow of third-grade liquid through slip conditions. Nooren et al. [58] examined the heat qualities of an electro-osmotic phenomenon in biofluid via a peristaltic wavy microchannel. Many theoretical as well as computational researches on electro-osmotic flow with and also without heat transport have been presented [59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76].

Numerous studies conducted by considering animal physiology found that the biological liquids show variation in viscosity. The consideration is evident because the average animal or human of comparable dimensions consumes as much as two liters of water, causing a modification in the focus of physical fluids over time. Thus, considering the variation in viscosity is an essential factor while examining the peristaltic system. Ali et al. [77] inspected the effect of slip conditions over the peristaltic system and found that the pumping region diminishes for larger values of slip parameter. Nadeem et al. [78] emphasize the heat transport qualities for a third-order non-Newtonian liquid taking 2 designs of variable thickness right into account, particularly variation via temperature level and a variant through the channel's size. The nature of the walls under examination likewise plays an essential duty in the peristaltic system, and therefore, several research studies have been performed for various wall surface arrangements. In addition, the temperature variation has been revealed to transform the residential properties of the physical liquid under monitoring. Therefore, variable thermal conductivity is likewise a crucial factor to consider for the research of peristalsis for physical liquid circulations. To this end, numerous analyses have been carried out for various setups of channel wall surfaces. Temperature-dependent thermal conductivity was thought about by Hayat et al. [79] by taking Jeffrey liquid over a non-linear stretching area through variable heat change. Vaidya et al. [80] scrutinized the impact of both changeable viscosity and changeable thermal conductivity by taking Rabinowitsch liquid in a channel. Further, Manjunatha et al. [81] examined the impacts of slip conditions over the peristaltic flow of Jeffrey liquid under the consideration of different liquid properties. The studies accounting for these properties have assisted in a better understanding of non-Newtonian fluids. Some vital researches regarding the employ of the non-Newtonian fluids in modeling and evaluation of peristaltic circulation with variable fluid properties can be found in [82,83,84,85,86,87,88,89].

The current study is the first of its kind in modeling the electrokinetically modulated peristaltic circulation of Jeffrey liquid through variable fluid properties. In addition, the effects of heat and mass transport and wall properties are considered. The governing equations are simplified through utilizing trusted estimation, namely lubrication, as well as Debye–Hückel estimate. After that, the perturbation strategy solves the resulting equation, and outcomes are contrasted numerically utilizing the MATLAB software program. The impact of relevant terms on velocity, streamlines, concentrations, and temperature is discussed graphically.

2 Mathematical formulation

2.1 Flow analysis

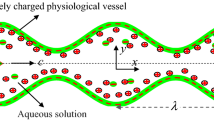
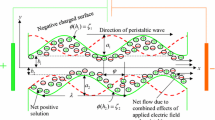
Consider a 2-D electrokinetic adjusted flow of Jeffrey fluid through a uniform microfluidic conduit of \(2\overline{a }\) width. The propagation of sinusoidal wave shapes this flow at a continuous velocity \(c\) beside the complaint conduit walls (See Fig. 1). Let \(\overline{Y }=\pm \overline{h }(\overline{X },\overline{t }\)) be the transverse displacements of the lower and upper walls, respectively. Here, propagation of wave is along the \(x-axis\). The mass and heat transport inspection is maintained with giving \({T}_{0}, {C}_{0}\) and \({T}_{1},{C}_{1}\) to the superior conduit wall and the inferior conduit wall, respectively. The electric field \(E\) is axially to the fluid movement.

Fig. 1
figure 1

Geometry of the electro-osmotic modulated peristaltic flow

Full size image

The microchannel wall equation: [55]

$$\overline{Y} = \pm \overline{h}\left( {\overline{X},\overline{t}} \right) = \pm \left( {\overline{a} + \overline{b}\sin \left[ {2\pi \frac{{\left( {\overline{X} - c\overline{t}} \right)}}{\lambda }} \right]} \right)$$
(1)

2.2 Mathematical formulations

The governing equation as given by [55] is.

Continuity equation:

$$\frac{{\partial \overline{U}}}{{\partial \overline{X}}} + \frac{{\partial \overline{V}}}{{\partial \overline{Y}}} = 0$$
(2)

Equation of momentum:

$$\rho \left( {\frac{{\partial \overline{U}}}{{\partial \overline{t}}} + \overline{U}\frac{{\partial \overline{U}}}{{\partial \overline{X}}} + \overline{V}\frac{{\partial \overline{U}}}{{\partial \overline{Y}}}} \right) = - \frac{{\partial \overline{P}}}{{\partial \overline{X}}} + \frac{\partial }{{\partial \overline{X}}}\overline{S}_{{\overline{X}\overline{X}}} + \frac{\partial }{{\partial \overline{Y}}}\overline{S}_{{\overline{X}\overline{Y}}} + \rho_{e} E_{x}$$
(3)
$$\rho \left( {\frac{{\partial \overline{U}}}{{\partial \overline{t}}} + \overline{U}\frac{{\partial \overline{V}}}{{\partial \overline{X}}} + \overline{V}\frac{{\partial \overline{V}}}{{\partial \overline{Y}}}} \right) = - \frac{{\partial \overline{P}}}{{\partial \overline{Y}}} + \frac{\partial }{{\partial \overline{X}}}\overline{S}_{{\overline{Y}\overline{X}}} + \frac{\partial }{{\partial \overline{Y}}}\overline{S}_{{\overline{Y}\overline{Y}}}$$
(4)

Energy equation with viscous dissipation [56]

$$\rho c_{p} \left( {\frac{{\partial \overline{T}}}{{\partial \overline{t}}} + \overline{U}\frac{{\partial \overline{T}}}{{\partial \overline{X}}} + \overline{V}\frac{{\partial \overline{T}}}{{\partial \overline{Y}}}} \right) = \frac{\partial }{{\partial \overline{Y}}}\left( {k\left( {\overline{T}} \right)\frac{{\partial \overline{T}}}{{\partial \overline{Y}}}} \right) + \frac{\partial }{{\partial \overline{X}}}\left( {k\left( {\overline{T}} \right)\frac{{\partial \overline{T}}}{{\partial \overline{X}}}} \right) + \overline{S}_{{\overline{X}\overline{X}}} \frac{{\partial \overline{U}}}{{\partial \overline{X}}} + \overline{S}_{{\overline{Y}\overline{Y}}} \frac{{\partial \overline{V}}}{{\partial \overline{Y}}} + \overline{S}_{{\overline{X}\overline{Y}}} \left( {\frac{{\partial \overline{V}}}{{\partial \overline{X}}} + \frac{{\partial \overline{U}}}{{\partial \overline{Y}}}} \right)$$
(5)

Concentration equation:

$$\left( {\frac{{\partial \overline{C}}}{{\partial \overline{t}}} + \overline{U}\frac{{\partial \overline{C}}}{{\partial \overline{X}}} + \overline{V}\frac{{\partial \overline{C}}}{{\partial \overline{Y}}}} \right) = D\left( {\frac{{\partial^{2} \overline{C}}}{{\partial \overline{X}^{2} }} + \frac{{\partial^{2} \overline{C}}}{{\partial \overline{Y}^{2} }}} \right) + \frac{{DK_{T} }}{{T_{m} }}\left( {\frac{{\partial^{2} \overline{T}}}{{\partial \overline{X}^{2} }} + \frac{{\partial^{2} \overline{T}}}{{\partial \overline{Y}^{2} }}} \right)$$
(6)

The constitutive equation for Jeffrey fluid is: [3]

$$\overline{\tau } = - \overline{p}\overline{I} + \overline{S},\;\overline{S} = \frac{\mu \left( y \right)}{{1 + \lambda_{1} }}\left( {\overline{{\mathop \gamma \limits^{ \bullet } }} + \lambda_{2} \overline{{\mathop \gamma \limits^{ \bullet \bullet } }} } \right)$$
(7)

where \(\overline{\tau }\) is the Cauchy stress tensor, \(\overline{p}\) is the pressure, \({\lambda }_{2}\) is the retardation time, \({\lambda }_{1}\) is the ratio of relaxation to retardation times,\(\overline{S}\) is the extra stress tensor, \(\overline{I}\) is the identity tensor,\(\dot{\gamma }\) is the shear rate, and dots over the quantities specify differentiation through revere to time.

2.3 Electrohydrodynamics

In a microchannel, the Poisson equation is written [52] as:

$$\nabla^{2} \overline{\phi } = - \frac{{\rho_{e} }}{\xi }$$
(8)

here \(\overline{\phi }\) denotes the electric potential, \(\xi \mathrm{ is the dielectric permittivity},\) and \({\rho }_{e}\) represents the total charge density.

The net charge density \({\rho }_{e}\) follows the Boltzmann variation [59], which is

$$\rho_{e} = - z_{v} e\left( {\overline{n}^{ - } - \overline{n}^{ + } } \right)$$
(9)

The anions \(\left({\overline{n}}^{-}\right)\) and captions \(\left({\overline{n}}^{+}\right)\) are distinct by \({\rho }_{e}\) of the Boltzmann equation:

$$\overline{n}^{ \pm } = \overline{{n_{0} }} e^{{\left( { \pm \frac{{ez_{v} }}{{T_{av} K_{B} }}\overline{\phi }} \right)}}$$
(10)

\({n}_{0}\) denotes bulk concentration, \({K}_{B}\) is the Boltzmann constant, \({z}_{v}\) is the charge balance, \(e\) is the electronic charge, and \({T}_{av}\) is the average temperature.

Employing Debye–Hückel linearization estimation [59] Eq. (8) revolves into

$$+ \frac{{d^{2} \phi }}{{dy^{2} }} = m_{e}^{2} \phi$$
(11)

where \({m}_{e}\) represents the electro-osmotic expression. The analytical solution of Eq. (11) with boundary conditions (BCs) \(\frac{{\partial \phi }}{{\partial y}} = 0,{\text{at}}\;y = 0\;{\text{and}}\;\phi = 1,{\text{at}}\;y = h\left( x \right)\) is reached as:

$$\phi \left( y \right) = \frac{{\cosh \left( {m_{e} y} \right)}}{{\cosh \left( {m_{e} h} \right)}}$$
(12)

2.4 Nondimensionalization

The switch from laboratory frame \(\left(\overline{X },\overline{Y }\right)\) to wave frame of references \(\left(\overline{x},\overline{y}\right)\) is:

$$\bar{y} = \overline{{Y,}} \;x = \bar{X} - c\bar{t},\bar{p}\left( {\bar{x},\bar{y}} \right) = \bar{U}\left( {\bar{X},\bar{Y},\bar{t}} \right) - c = \bar{V}\left( {\bar{X},\bar{Y},\bar{t}} \right),T\left( {\bar{x},\bar{y}} \right) = \bar{T}\left( {\bar{X},\bar{Y},\bar{t}} \right),\bar{v}\left( {\bar{x},\bar{y}} \right) = \bar{P}\left( {\bar{X},\bar{Y},\bar{t}} \right),\bar{u}\left( {\bar{x},\bar{y}} \right)$$
(13)

The above conversions are employed in Eqs. (2)–(6) and then introducing the non-dimensional variables:

$$\begin{gathered} x = \frac{{2\pi \overline{x}}}{\lambda },y = \frac{{\overline{y}}}{a},t = \frac{{2\pi \overline{t}c}}{\lambda },u = \frac{{\overline{u}}}{c},v = \frac{{\overline{v}}}{c},p = \frac{{2\pi a^{2} \overline{p}}}{{\lambda \mu_{0} c}},\alpha_{1} = \frac{2\pi a}{\lambda },h = \frac{{\overline{h}}}{a},m_{e} = \frac{a}{{\lambda_{D} }}, \hfill \\ n = \frac{{\overline{n}}}{{n_{0} }},\smallint = \frac{b}{a},\theta = \frac{{\overline{T} - T_{0} }}{{T_{0} }},\Omega = \frac{{\overline{C} - C_{0} }}{{C_{0} }},\lambda_{D} = \frac{1}{{eZ_{v} }}\sqrt {\frac{{T_{0} \xi K_{B} }}{{2n_{0} }}} ,\phi = \frac{{ez_{v} \overline{\phi }}}{{T_{av} K_{B} }},U_{hs} = - \frac{{E_{x} \xi }}{{c\mu_{0} }}, \hfill \\ S = \frac{{a\overline{S}}}{{c\mu_{0} }},\psi = \frac{{\overline{\psi }}}{ca},u = \frac{\partial \psi }{{\partial y}},v = - \alpha_{1} \frac{\partial \psi }{{\partial x}},R_{e} = \frac{\rho ca}{{\mu_{0} }},P_{r} = \frac{{\mu_{0} c_{p} }}{k\left( T \right)},Br = E_{c} \times P_{r} , \hfill \\ Sr = \frac{{\rho T_{0} K_{T} D_{m} }}{{\mu_{0} T_{m} C_{0} }},Sc = \frac{{\mu_{0} }}{{\rho D_{m} }},E_{c} = \frac{{c^{2} }}{{c_{p} T_{0} }},\mu_{0} = \frac{{\overline{{\mu_{0} }} }}{\mu },E_{1} = \frac{{\tau a^{3} }}{{\mu_{0} \lambda^{3} c}},E_{2} = \frac{{n_{1} a^{3} }}{{\mu_{0} \lambda^{3} c}},E_{3} = \frac{{n_{2} a^{3} }}{{\mu_{0} \lambda^{3} }}. \hfill \\ \end{gathered}$$
(14)

where \({U}_{hs}\) represents the Helmholtz–Smoluchowski speed, \(Sc\) is the Schmidt number, \({\uplambda }_{D}\) denotes the Debye length, \(\Omega\) is the concentration, \(y\) is the non-dimensional transverse coordinate, \({m}_{e}\) represents the electro-osmotic term, \(p\) is dimensionless pressure, \({\alpha }_{1}\) is peristaltic wave number, \({P}_{r}\) is the Prandtl number, \(\theta\) denotes the temperature, \(\psi\) is a non-dimensional stream function, \(S\) is the non-dimensional shear stress, \({R}_{e}\) is the Reynolds number, \(\upepsilon\) is the amplitude ratio, \(Br\) is the Brinkman number, \(Sr\) is the non-dimensional Soret number, \(x\) is the non-dimensional axial coordinate, and \({E}_{c}\) is the Eckert number.

2.5 Wall properties

The governing equation of the flexible wall movement is [5]:

$$R\left( h \right) = p - p_{0}$$
(15)

\(R\) denotes an operator, which is employed to symbolize the motion of stretched membrane via viscous damping forces such that:

$$R = - \tau \frac{{\partial^{2} }}{{\partial x^{2} }} + n_{1} \frac{{\partial^{2} }}{{\partial t^{2} }} + n_{2} \frac{\partial }{\partial t}$$
(16)

Continuity of stress at \(y=h\) and employing \(x\)-momentum equation yield

$$\frac{\partial R\left( h \right)}{{\partial x}} = \frac{\partial p}{{\partial x}} = \frac{\partial }{\partial y}S_{xy} + \rho_{e} E_{x}$$
(17)

\(\tau\) is the elastic tension in the membrane, \(h\) is the dimensional slip expression, \({n}_{1}\) denotes the mass per unit surface, \({n}_{2}\) is the coefficient of viscous damping forces, and \({p}_{0}\) is the pressure over the exterior surface of the wall due to the tension in the muscles. We assumed \({p}_{0}=0\).

The relation of the stream function \(\psi\) and the velocity is described as:

$$u = \frac{\partial \psi }{{\partial y}},v = - \alpha_{1} \frac{\partial \psi }{{\partial x}}$$
(18)

From Eqs. (3–6), subject to long-wavelength supposition and ignoring higher powers of \({\alpha }_{1}\), we arrive at:

$$\frac{\partial p}{{\partial x}} = \frac{\partial }{\partial y}\left[ {\left( {\frac{1 - \alpha y}{{1 + \lambda_{1} }}} \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right] + m_{e}^{2} U_{hs} \phi$$
(19)
$$\frac{\partial p}{{\partial y}} = 0$$
(20)
$$\frac{\partial }{\partial y}\left( {k\left( \theta \right)\frac{\partial \theta }{{\partial y}}} \right) + Br\left[ {\left( {\frac{1 - \alpha y}{{1 + \lambda_{1} }}} \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right]\frac{{\partial^{2} \psi }}{{\partial y^{2} }} = 0,$$
(21)
$$\frac{{\partial^{2} \Omega }}{{\partial y^{2} }} + Sc \times Sr\left( {\frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right) = 0.$$
(22)

The non-dimensional boundary conditions are:

$$\frac{{\partial ^{2} \psi }}{{\partial y^{2} }} = 0,\psi = 0,\frac{{\partial \theta }}{{\partial y}} = 0,\frac{{\partial \Omega }}{{\partial y}} = 0,\;at\;y = 0,$$
(23)
$$\frac{{\partial \psi }}{{\partial y}} = - 1,\Omega = 0,\theta = 0\;at\;y = h\left( x \right) = 1 + \in \sin x$$
(24)

The expression for variable viscosity is:

$$\mu (y) = 1 - \alpha y\;for\;\alpha < < 1$$
(25)

The thermal conductivity term:

$$k\left( \theta \right) = 1 + \beta \theta \;for\;\beta \ll 1$$
(26)

here \(\alpha\) denotes the viscosity coefficient, and \(\beta\) is the thermal conductivity coefficient.

3 Perturbation solution

Equations (19)–(22) stipulate a governing differential scheme through BCs (23) and (24) that are exceptionally non-linear. It is not possible to get an exact solution to this scheme of equations. Consequently, the scheme is solved analytically employing the perturbation technique, which utilizes \(\alpha\) and \(\beta\) terms.

Hence, \(\psi\) and \(\theta\) are developed as:

$$\psi = \psi_{0} + \alpha \psi_{1} + O\left( {\alpha^{2} } \right)$$
(27)
$$\theta = \theta_{0} + \beta \theta_{1} + O\left( {\beta^{2} } \right)$$
(28)

3.1 Zeroth order system

$$\frac{{\partial^{3} \psi_{0} }}{{\partial y^{3} }} - \left( {1 + \lambda_{1} } \right)\left( {P - m_{e}^{2} U_{hs} \phi } \right)$$
(29)
$$\frac{{\partial \theta_{0} }}{\partial y} = - Br\smallint \left( {\frac{1 - \alpha y}{{1 + \lambda_{1} }}\frac{{\partial \psi^{2} }}{{\partial y^{2} }}} \right)\frac{{\partial \psi^{2} }}{{\partial y^{2} }}$$
(30)

Subject to these BCs

$$\psi_{0} = 0,\;\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }} = 0,\;\frac{{\partial \theta_{0} }}{\partial y} = 0\;at\;y = 0$$
(31)
$$\frac{{\partial \psi_{0} }}{\partial y} = - 1,\;\theta_{0} = 0\;at\;y = h$$
(32)

3.2 First-order system

$$\frac{{\partial^{3} \psi_{1} }}{{\partial y^{3} }} = y\frac{{\partial^{3} \psi_{0} }}{{\partial y^{3} }} + \frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }}$$
(33)
$$\frac{{\partial \theta_{1} }}{\partial y} = - \theta_{0} \frac{{\partial \theta_{0} }}{\partial y}$$
(34)

Subject to these BCs

$$\psi_{1} = 0,\;\frac{{\partial^{2} \psi_{1} }}{{\partial y^{2} }} = 0,\;\frac{{\partial \theta_{1} }}{\partial y} = 0\;at\;y = 0$$
(35)
$$\frac{{\partial \psi_{1} }}{\partial y} = 0,\;\theta_{0} = 0\;at\;y = h$$
(36)

The resolution of zeroth and first-order schemes along via BCs is achieved employing the MATLAB 2019b programming. The segregate code has been written to achieve the solutions for temperature, streamline, and velocity. Then, the solution for Eq. (22) is achieved by double integrating the temperature expression via the BCs (23) and (24).

4 Results and discussion

This part emphasizes on the impact of Helmholtz–Smoluchowski/maximum electro-osmotic velocity \(\left({U}_{hs}\right)\), electro-osmotic parameter \(\left({m}_{e}\right)\), Jeffrey parameter \(\left({\lambda }_{1}\right)\), variable viscosity \(\left(\alpha \right)\), amplitude ratio \(\left(\epsilon \right)\), elasticity parameter \(\left({E}_{1}\right)\), mass parameter \(\left({E}_{2}\right)\), viscous damping force parameter \(\left({E}_{3}\right)\), variable thermal conductivity \(\left(\beta \right)\), Brinkmann number \(\left(Br\right)\), Schmidt number \(\left(Sc\right)\) and Soret number \(\left(Sr\right)\) over stream line \(\left(\psi \right),\) velocity \(\left(u\right)\), temperature \(\left(\theta \right)\) and concentration \(\left(\Omega \right)\). The outcomes are shown in Figs. 2–10.

Fig. 2
figure 2

\(u\left(y\right)\) for fluctuating (a) \({U}_{hs}\), (b) \({m}_{e}\), (c) \({\lambda }_{1}\), (d) \(\alpha\), (e) \(\epsilon\), (f) \({E}_{1}-{E}_{3}\)

Full size image
Fig. 3
figure 3

\(\theta \left(y\right)\) for fluctuating (a) \({U}_{hs}\), (b) \({m}_{e}\), (c) \({\lambda }_{1}\), (d) \(\beta\), (e) \(\alpha\), (f) \(Br\), (g) \(\epsilon\), and (h) \({E}_{1}-{E}_{3}\)

Full size image
Fig. 4
figure 4

\(\Omega \left(y\right)\) for fluctuating (a) \({U}_{hs}\), (b) \({m}_{e}\), (c) \({\lambda }_{1}\), (d) \(\beta\), (e) \(\alpha\), (f) \(Br\), (g) \(\epsilon\), and (h) \({E}_{1}-{E}_{3}\)

Full size image
Fig. 5
figure 5

\(\Omega \left(y\right)\) for varying (a) \(Sc\) and (b) \(Sr\)

Full size image
Fig. 6
figure 6

\(\psi \left(x,y\right)\) for varying (a) \({U}_{hs}=-1\), (b) \({U}_{hs}=0\), (c) \({U}_{hs}=1\), and (d) \({U}_{hs}=2\)

Full size image
Fig. 7
figure 7

\(\psi \left(x,y\right)\) for varying (a) \({m}_{e}=1\) and (b) \({m}_{e}=3\)

Full size image
Fig. 8
figure 8

\(\psi \left(x,y\right)\) for fluctuating (a) \({\lambda }_{1}=0\) and (b) \({\lambda }_{1}=2\)

Full size image
Fig. 9
figure 9

\(\psi \left(x,y\right)\) for varying (a) \(\alpha =0\) and (b) \(\alpha =0.02\)

Full size image
Fig. 10
figure 10

\(\psi \left(x,y\right)\) for varying (a) \({{E}_{2}=0.05,{E}_{3}=0.05,E}_{1}=0.03,\) (b) \({{E}_{3}=0.05, {E}_{2}=0.05, E}_{1}=0.05,\)(c) \({E}_{1}=0.05,{{E}_{2}=0.07,E}_{3}=0.05\), (d) \({E}_{2}=0.07,{{E}_{3}=0.07, E}_{1}=0.05\)

Full size image

Figure 2 illustrates the impact of relevant parameters over speed. The velocity profiles have a parabolic form because to an optimum speed in the channel's center. Figure 2a explains that as \({U}_{hs}\), or the optimal electro-osmotic velocity (or Helmholtz–Smoluchowski speed), rises from −1 to 4, the axial motion has considerable momentum. For higher \({U}_{hs}\), a succeeding improvement in an axial electric field involves a considerable deceleration. The motion is maintained and delayed with an important electrical field strength. Tripathi et al. [65] investigated a similar trend. Other critical values of \({m}_{e}\) in Fig. 2b initially reduce the velocity profiles. In addition, there is a minor difference in velocity profiles for larger values. The joint of λD is the Debye–Hückel design. Since raised ion migration occurs as we budge away from the accused surface, reducing λD, i.e., augmenting Debye–Hückel parameter, is thought to rise electrical capacity. Consequently, λD is a vital manner criterion in controlling potential electrical distinction, which influences the axial speed field. Figure 2c is drawn for several values of λ1. The velocity profile progresses as the λ1 augments, as exposed here. With taking \({\lambda }_{1}=0\), the finding reduces to Newtonian fluid. Figure 2d describes the impact of α on velocity distributions. The velocity profile improves for more considerable values of α. Since a boost in α terms reduces the liquid's viscosity and therefore enhances the liquid movement. Figure 2e exposes a rise in the velocity profiles for more considerable values of amplitude ratio. Amplitude ratio is the relation between wave amplitude to channel width. Hence, a boost in amplitude ratio significantly improves the velocity profiles. The impact of flexibility, mass parameter, and viscous damping force term is exposed in Fig. 2f. With an improvement in the flexibility parameter, the fluid viscosity weakens since the particle moves at higher speeds. As the mass per unit area, the liquid travel particles freely develop the speed uplift. Since damping operates to resist the circulation speed because of energy loss, a minimizing response is apprehended. Clinically, once blood walls are supple or the mass per unit area augments (as in blood capillaries), the switch of water, oxygen, and other nutrients turns into easy. The damping tends to react in contradictory ways.

Here, we scrutinize the influence of diverse stipulations on temperature evolutions. The temperature evolutions are parabolic, via a maximum temperature level in the center of the channel. The consequences of viscous dissipation, which increases the temperature in the middle of the conduit, may discuss these patterns. The viscosity of the fluid causes this event, which transforms kinetic energy in the fluid into heat energy in it. Figure 3a indicates that the temperature of the fluid augments via an enhance in the maximum electro-osmotic velocity. Thus, the temperature profile diminishes for rising Debye–Hückel term (See Fig. 3b). Figure 3c is plotted to observe the influence of the Jeffrey design over the temperature distribution. It indicates that temperature is an increasing function of the Jeffrey pattern. Figure 3d is plotted to observe the effect of β on the temperature distribution. β is the liquid's aptitude to release or protect heat to its locations. As an outcome, when β of the fluid in the canal is superior to the wall temperature, the liquid's thermal evaluation rises. The effect of α on temperature distribution is demonstrated in Fig. 3e. α increases the temperature profile, and when α amounts to absolutely zero, consistent viscosity may be derived. The liquid's α improves, the heat transports prospective eliminates and increases the temperature profile. Figure 3f shows that larger values of Br improve the temperature profile. It is through an argument that less heat conducts the viscous dissipation. Br illustrates dissipation intensity. Known that the wall temperature is convectively adjusted, heat transports are just considered due of the effects of heat dissipation. A similar pattern is seen for increasing values of amplitude ratio (See Fig. 3g). It has been observed that the temperature level increase is seen for the rising importance of flexible stress and mass per unit is parameter. The opposite behavior is spotted for an increasing value of the viscous damping force parameter (See Fig. 3h).

The repercussions of various criteria on concentration profiles are shown in Figs. 4 and 5. The concentration distribution behaves conflicting to that of temperature distribution in Fig. 4. This behavior is anticipated physically because heat and mass are known to be opposite to straight proportion. Also, the profiles expose particle matter in the fluid that is more at the periphery than in the central position of the channel. This behavior assists in spreading necessary nutrients to nearby tissues and cells in the blood and other fluxes. Figure 5 is drawn to observe the effect of Soret and Schmidt number on the velocity profiles. The figures reveal that the concentration profile substantially diminishes with an augment in the value of the Soret and Schmidt number.

It is usually known that the phenomenon of trapping is an integral element of peristaltic research studies. The liquid, therefore, caught within the bolus is pushed forward along through the peristaltic wave. Figure 6 shows a streamlined makeup for various \({U}_{hs}\). It shows that the build-up of streamlines reduces through a rise in \({U}_{hs}\). Hence, stronger \({U}_{hs}\) means a more powerful electrical field; the diversity of enclosed boluses considerably reduces for high values of \({U}_{hs}\). Figure 7 shows that the combination of enclosed boluses increases with arise in the electro-osmotic criterion. For greater \(m{}_{e}\), the enclosed bolus appears stronger in EDL. Figure 8 illustrates the streamlines for varying Jeffrey specifications. It reveals that the streamlines considerably increase with arise in the value of the Jeffrey parameter. Similar behavior is noticed for a boost in the importance of α, flexible tension, mass per unit area, and viscous damping force parameter (See Figs. 9 and 10).

5 Conclusions

The influences of electro-osmotic, variable liquid properties, and wall properties toward the peristaltic flow of Jeffrey liquid via a uniform conduit are analyzed. MATLAB 2020a programming is utilized to confer the effect of critical expressions toward concentration, velocity, temperature level, and streamlines. The findings seen in this article have potential implications in both medical research and industry. Moreover, considering slip and changeable liquid properties in peristaltic movement, physical conditions such as a tapered/asymmetric uneven artery via a porous medium can be implemented in future research. This work gives a fair theoretical estimation for further research in this way. The main findings of the scheme are summarized as:

  • The velocity profiles rise for larger values of optimum electro-osmotic velocity.

  • The electro-osmotic specification is observed to be a reducing function of velocity.

  • The Jeffrey criterion improves the temperature and velocity profiles.

  • An increase in the velocity and temperature profiles is observed for increasing value of α.

  • The temperature profile improves for more significant values of variable thermal conductivity.

  • The concentration profile significantly diminishes for more significant values of Soret and Sc.

  • The accumulation of streamlines reduces through a boost in maximum electro-osmotic velocity.

  • The number of enclosed boluses increases through a boost in the electro-osmotic criterion.