Heat Transfer on MHD Peristaltic Rotating Flow of a Jeffrey Fluid in an Asymmetric Channel

Abstract

This paper addresses heat transfer and rotation effects on MHD peristaltic flow of a Jeffrey fluid in an asymmetric channel with partial slip. Mathematical modeling is carried out by utilizing long wavelength and small Reynolds number assumptions. The analytical solution has been computed for the stream function, velocity and temperature distribution. The expression for pressure rise is carried out using numerical integration. The effects of various emerging parameters on the flow characteristics are shown and discussed with the help of graphs. The pumping characteristics, axial pressure gradient and trapping phenomenon have been studied. The axial velocity depresses with increasing of Hartmann number, Jeffrey fluid parameter and slip parameter. The size of trapping bolus enhances when an increase in Hartmann number, Jeffrey fluid parameter and rotation parameter. The temperature diminishes as the larger values of slip parameter. A comparison of a special case of our results with the one previously reported in the literature shows a very good agreement.

Introduction

Peristaltic transport in recent times has collected considerable attention due to its applications in physiological fluids such as vasomotion of small blood vessels, chyme motion in the gastrointestinal tracts, sperm transport in the ductus efferent us of the male reproductive tract, movement of ovum in the fallopian tube, swallowing of food through esophagus etc. The principle of peristaltic motion is also exploited in many industrial applications. Sanitary fluid transport, transport of incisive fluids and blood pumps in heart lung tools are few of these. Several theoretical and experimental attempts have been made to examine the peristaltic flows in view of their obvious importance since the seminal researches of Latham [1] and Shapiro et al. [2]. Such investigations have been presented under various assumptions of long wavelength, low Reynolds number, small wave number, small amplitude ratio, etc. The peristaltic flows of viscous and non-Newtonian fluids have been discussed by many authors recently in the studies [3,4,5,6].

The effects of magnetic field on the peristaltic mechanisms are important in connection with certain problems of the movement of the conductive physiological fluids, e.g., the blood and blood pump machines. The analytical and numerical analysis of peristaltic flows in viscous and non-Newtonian fluids has been analyzed by Nadeem and Akram [7]. Hayat et al. [8] discussed the effect of compliant wall properties and heat transfer on the peristaltic transport of an incompressible viscous fluid in an arched channel. Nadeem and Akbar [9] studied the peristaltic transport of an incompressible MHD Newtonian fluid in a vertical annulus. The peristaltic motion of a non-Newtonian fluid in a channel possessing compliant boundaries is presented by Ali et al. [10]. Vajravelu et al. [11] studied the impact of heat transfer on peristaltic transport of a Jeffrey fluid in a vertical porous lamina. Kothandapani and Srinivas [12] Peristaltic flow of a Jeffrey fluid under the influence of magnetic field in an asymmetric channel. The characteristics of the Jeffrey fluid model for the peristaltic flow of chime in the small intestine with magnetic field have been investigated by Akbar et al. [13]. Very recently, the peristaltic flow of Jeffrey nanofluid over an asymmetric channel under the influence of applied magnetic field was investigated by Gnaneswara Reddy and Makinde [14].

The phenomenon of rotation has its numerous applications in cosmic and geophysical flows. Moreover occurrence of rotation also helps in better understanding the behavior of ocean circulation and galaxies formation. Rotation also helps in the measurement of the energies of transitions between quantized rotational states of molecules in the gas phase (rotational spectroscopy). In particular the peristalsis of MHD fluid in presence of rotation is relevant with regard to certain flow cases involving the movement of physiological fluids for example the blood and saline water. Obviously the magnetic field and rotation are useful for biofluid transport in the intestines, ureters and arterioles. Abd-Alla et al. [15] studied the effects of rotation and magnetic field on nonlinear peristaltic motion of second-order fluid in an asymmetric channel through a porous medium. Mahmoud et al. [16] investigated the impact of the rotation on wave motion through cylindrical bore in a micro polar porous medium. The influence of the rotation, magnetic field and initial stress on peristaltic motion of micro polar fluid is studied by Abd-Alla et al. [17]. Hayat et al. [18] have studied the influences of rotation and thermophoresis on MHD peristaltic transport of Jeffrey fluid with convective conditions and wall properties. Hayat et al. [19] have investigated the homogeneous-heterogeneous reactions and heat source/sink effects in MHD peristaltic flow of micropolar fluid with Newtonian heating in a curved channel.

It is now known that the no-slip condition for velocity condition is not appropriate for momentum in micro devices. The velocity slip condition is adequate for the flow of liquids at the micro scale level especially in view of the lack of data on the thermal accommodation coefficient. Among the utilization of micro devices, several complex micro channels arise. Investigations of the effects of slip on the peristaltic motion have been recently reported in [20,21,22]. Abd-Alla et al. [23] reported the influence of magnetic field and rotation effects on peristaltic flow of a Jeffrey fluid in an asymmetric channel. Gnaneswara Reddy and Venugopal Reddy [24] have investigated the impact of velocity slip and joule heating on MHD peristaltic flow through a porous medium with chemical reaction. Gnaneswara Reddy et al. [25] have analyzed the hydromagnetic peristaltic motion of a reacting and radiating couple Stress fluid in an inclined asymmetric channel filled with a porous medium. Mishra and Rao [26] have investigated the peristaltic transport of a Newtonian fluid in an asymmetric channel. Kothandapani and Srinivas [27] have analyzed the peristaltic transport of a Jeffrey fluid under the effect of magnetic field in an asymmetric channel.

The studies of heat transfer have significant applications in industry and medicine. Especially heat transfer in human body is an important area of research. Bio heat transfer in tissues has attracted the attention of biomedical engineers in view of thermotherapy and the human thermoregulation system. The heat transfer in humans takes place as conduction in tissues, perfusion of the arterial–venous blood through the pores of the tissue, metabolic heat generation etc. The other applications are destruction of undesirable cancer tissues, dilution technique in examining blood flow and vasodilation. In addition mass transfer also occurs when nutrients diffusion out from the blood to neighboring tissues, membrane separation process, reverse osmosis, distillation process, combustion process and diffusion of chemical impurities. The combined heat and mass transfer effects can be seen in processes like drying, evaporation, thermodynamics at the surface of a water body and oxygenation etc. With this view point the recent researchers have made efforts for peristalsis with combined effect of heat and mass transfer [28,29,30,31,32,33].

The aim of the present paper is to analyze the effects of heat transfer and rotation on MHD peristaltic motion of a Jeffrey fluid in an asymmetric channel in the presence of velocity slip. The mathematical formulation taking into account of heat transfer analysis and partial slip. The governing equations of momentum and energy have been simplified using long wave length and low Reynolds number approximations. Numerical results for the velocity, temperature, pressure gradient, pressure rise and shear stress to the pertinent parameters are presented graphically and discussed in detail. Also, the trapping phenomenon discussed for the flow parameters.

Mathematical Formulation

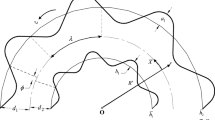
In this paper, we investigate the problem for two-dimensional peristaltic flow of a Jeffrey liquid in a asymmetric channel of width $d_1 +d_2$. The channel walls are convectively heated. A uniform magnetic field of strength $B_o$ is applied. Electric field effects are taken zero and induced magnetic field is neglected due to small magnetic Reynolds number. The whole system is in a rotating frame of reference with constant angular velocity $\Omega$. Flow configuration is presented in Fig. 1. Flow inside the channel is induced due to propagation of sinusoidal waves of wavelength $\lambda$ along the flexible walls of the channel with constant speed c.

Fig. 1

Physical model of the problem

The geometries of the wall surfaces are described by

$$\begin{aligned} \bar{{h}}_1 \left( {\bar{{X}},\bar{{t}}} \right)= & {} d_1 +a_1 \cos \left[ {\frac{2\pi }{\lambda }\left( {\bar{{X}}-c\bar{{t}}} \right) } \right] ,\hbox { at upper wall}\nonumber \\ \bar{{h}}_2 \left( {\bar{{X}},\bar{{t}}} \right)= & {} -d_2 -b_1 \cos \left[ {\frac{2\pi }{\lambda }\left( {\bar{{X}}-c\bar{{t}}} \right) +\phi } \right] ,\hbox { at lower wall} \end{aligned}$$

(1)

where $a_1$ and $b_1$ are the amplitudes of the waves, $\lambda$ is the wavelength, $d_1 +d_2$ is the channel width, c is the wave speed, $\phi$ is the phase difference, $\phi =0, \phi =\pi$ the waves are in phase, and further $a_1 ,b_{1,} d_1 ,d_2$ and $\phi$ should satisfy the following condition

$$\begin{aligned} a_1^2 +b_1^2 +2a_1 b_1 \cos \phi \le \left( {d_1 +d_2 } \right) ^{2}. \end{aligned}$$

(2)

Now utilizing the Mathematical analysis of the relevant published literature [18, 23, 28, 30, 31] with long wavelength and low Reynolds number approximations, the reduced dimensionless governing equation of flow and energy are given by

$$\begin{aligned}&\frac{\partial ^{2}}{\partial y^{2}}\left[ {\frac{1}{1+\lambda _1 }\frac{\partial ^{2}\psi }{\partial y^{2}}} \right] +\left( {\frac{2\rho a^{2}\Omega }{\mu }-M^{2}} \right) \frac{\partial ^{2}\psi }{\partial y^{2}}=0 \end{aligned}$$

(3)

$$\begin{aligned}&\frac{1}{\Pr }\frac{\partial ^{2}\theta }{\partial y^{2}}+\frac{Ec}{\left( {1+\lambda _1 } \right) }\frac{\partial ^{2}\psi }{\partial y^{2}}=0 \end{aligned}$$

(4)

The relevant boundary conditions for the stream function and temperature in the wave frame are given by

$$\begin{aligned} \psi= & {} \frac{q}{2} , \frac{\partial \psi }{\partial y}+\frac{L}{1+\lambda _1 }\frac{\partial ^{2}\psi }{\partial y^{2}}=-1, \theta =0\quad \hbox { at }y=h_1 \left( x \right) =1+a\cos \left[ x \right] , \end{aligned}$$

(5)

$$\begin{aligned} \psi= & {} -\frac{q}{2}, \frac{\partial \psi }{\partial y}-\frac{L}{1+\lambda _1 }\frac{\partial ^{2}\psi }{\partial y^{2}}=-1, \theta =1\quad \hbox { at }y= h_2 \left( x \right) =-d-b\cos \left[ {\frac{2\pi }{\lambda }\left( x \right) +\phi } \right] ,\nonumber \\ \end{aligned}$$

(6)

where M is the Hartmann number, $\Pr$ is the Prandtl number, Ec is the Eckert number, $\lambda _1$ is the Jeffrey fluid parameter, $\Omega$ is the rotation parameter, $\phi$ is phase difference, L is the slip parameter, q is the flux in the wave frame and $a,b,\phi$ and d satisfies the relation

$$\begin{aligned} a^{2}+b^{2}+2ab\cos \phi \le \left( {1+d} \right) ^{2}. \end{aligned}$$

(7)

Solution of the Problem

The solution of the Eq. (3) subject to the boundary conditions (5) and (6) are given by

$$\begin{aligned} \psi =F_0 +F_1 y+F_2 \cosh \left( {Ny} \right) +F_3 \sinh \left( {Ny} \right) \end{aligned}$$

(8)

where

$$\begin{aligned} F_0= & {} \frac{\left( {h_1 +h_2 } \right) \left[ {Nq+\frac{\left( {qLN^{2}+2\left( {1+\lambda _1 } \right) } \right) }{\left( {1+\lambda _1 } \right) }\tanh \left( {\frac{N\left( {h_1 -h_2 } \right) }{2}} \right) } \right] }{2N\left( {h_2 -h_1 } \right) +2\frac{\left( {N^{2}L\left( {h_2 -h_1 } \right) +2\left( {1+\lambda _1 } \right) } \right) }{1+\lambda _1 }\tanh \left( {\frac{N\left( {h_1 -h_2 } \right) }{2}} \right) },\\ F_1= & {} \frac{\left[ {Nq+\frac{\left( {qLN^{2}+2\left( {1+\lambda _1 } \right) } \right) }{\left( {1+\lambda _1 } \right) }\tanh \left( {\frac{N\left( {h_1 -h_2 } \right) }{2}} \right) } \right] }{N\left( {h_1 -h_2 } \right) -\frac{\left( {N^{2}L\left( {h_2 -h_1 } \right) +2\left( {1+\lambda _1 } \right) } \right) }{1+\lambda _1 }\tanh \left( {\frac{N\left( {h_1 -h_2 } \right) }{2}} \right) },\\ F_2= & {} \frac{\left( {q+h_1 -h_2 } \right) \hbox {sech}\left( {\frac{N\left( {h_1 -h_2 } \right) }{2}} \right) \sinh \left( {\frac{N\left( {h_1 +h_2 } \right) }{2}} \right) }{N\left( {h_1 -h_2 } \right) -\frac{\left( {N^{2}L\left( {h_2 -h_1 } \right) +2\left( {1+\lambda _1 } \right) } \right) }{1+\lambda _1 }\tanh \left( {\frac{N\left( {h_1 -h_2 } \right) }{2}} \right) },\\ F_3= & {} \frac{\left( {q+h_1 -h_2 } \right) \hbox {sech}\left( {\frac{N\left( {h_1 -h_2 } \right) }{2}} \right) \cosh \left( {\frac{N\left( {h_1 +h_2 } \right) }{2}} \right) }{N\left( {h_1 -h_2 } \right) +\frac{\left( {N^{2}L\left( {h_2 -h_1 } \right) +2\left( {1+\lambda _1 } \right) } \right) }{1+\lambda _1 }\tanh \left( {\frac{N\left( {h_1 -h_2 } \right) }{2}} \right) }, \end{aligned}$$

and $N^{2}=\left( {M^{2}-\frac{2\rho a^{2}\Omega }{\mu }} \right) \left( {1+\lambda _1 } \right)$.

The velocity distribution is given by

$$\begin{aligned} u=\frac{\partial \psi }{\partial y}=F_1 +NF_2 \cosh \left( {Ny} \right) +NF_3 \cosh \left( {Ny} \right) \end{aligned}$$

The solution of Eq. (4) using the Eq. (8) subject to the boundary conditions (5) and (6) is given by

$$\begin{aligned} \theta= & {} \frac{E_c \Pr }{\left( {1+\lambda _1 } \right) }\left[ \frac{F_3^2 }{2}N^{4}y^{2}-\frac{N^{4}}{8}\left( {F_2^2 +F_3^2 } \right) \cosh 2Ny-\frac{y^{2}}{4}N^{4}\left( {F_2^2 +F_3^2 } \right) \right. \nonumber \\&\quad \left. -\,\frac{F_2 F_3 }{4}N^{2}\sinh 2Ny \right] +c_2 y+c_1 \end{aligned}$$

(9)

where

$$\begin{aligned} c_2= & {} \frac{1}{h_1 -h_2 }\left[ {-1-\frac{\Pr Ec}{1+\lambda _1 }\left[ {\begin{array}{l} \frac{F_3^2 N^{4}}{2}\left( {h_1^2 -h_2^2 } \right) +\frac{F_2 F_3 N^{2}}{4}\left( {\sinh \left( {2Nh_2 } \right) -\sinh \left( {2Nh_1 } \right) } \right) +\frac{N^{4}}{4}\left( {F_2^2 +F_3^2 } \right) \left( {h_2^2 -h_1^2 } \right) + \\ \frac{N^{4}}{8}\left( {F_2^2 +F_3^2 } \right) \left( {\cosh \left( {2Nh_2 } \right) -\cosh (2Nh_1 } \right) \\ \end{array}} \right] } \right] \nonumber \\ c_1= & {} \frac{-E_c \Pr }{\left( {1+\lambda _1 } \right) }\left[ {\frac{F_3^2 }{2}N^{4}h_1^2 -\frac{N^{4}}{8}\left( {F_2^2 +F_3^2 } \right) \cosh \left( {2Nh_1 } \right) -\frac{h_1^2 }{4}N^{4}\left( {F_2^2 +F_3^2 } \right) -\frac{F_2 F_3 }{4}N^{2}\sinh \left( {2Nh_1 } \right) } \right] -c_2 h_1 \end{aligned}$$

It is noticed that in the absence of heat transfer and slip parameter L the results of Abd-Alla and Abo-Dahab [23] can be recovered as special case of our problem. Moreover, the results of Mishra and Rao [26] can be recovered if $\lambda _1 \rightarrow 0,L\rightarrow 0$ and in the absence of heat transfer.

The flux at any axial station in the fixed frame is

$$\begin{aligned} Q=\int _{h_2 }^{h_1 } {\left( {\frac{\partial \psi }{\partial y}+1} \right) } dy=h_1 -h_2 +q \end{aligned}$$

(10)

The time-mean flow over a period $T_2$ is defined as

$$\begin{aligned} \Theta =\frac{1}{T_2 }\int \limits _0^{T_2 } {Qdt=\frac{1}{T_2 }\int \limits _0^{T_2 } {\left( {q+h_1 -h_2 } \right) dt=q+1+d} } \end{aligned}$$

(11)

The pressure gradient is obtained from the dimensionless momentum equation for the axial velocity is given by

$$\begin{aligned} \frac{dp}{dx}= & {} \frac{1}{1+\lambda _1 }\left[ {\frac{\partial ^{3}\psi }{\partial y^{3}}-N^{2}\left( {\frac{\partial \psi }{\partial y}+1} \right) } \right] \end{aligned}$$

(12)

$$\begin{aligned} \frac{dp}{dx}= & {} \frac{-N^{2}}{1+\lambda _1 }\left[ {F_1 +1} \right] \end{aligned}$$

(13)

The dimensionless expression for the pressure rise per wavelength $\Delta p_\lambda$ on the lower is defined as follows:

$$\begin{aligned} \Delta p_\lambda =\int \limits _0^{2\pi } {\left( {\frac{dp}{dx} } \right) dx} \end{aligned}$$

(14)

The dimensionless shear stress at the upper wall of the channel is reduced to

$$\begin{aligned} s_{xy}= & {} \frac{1}{1+\lambda _1 }\frac{\partial ^{2}\psi }{\partial y^{2}}, \end{aligned}$$

(15)

$$\begin{aligned} s_{xy}= & {} \frac{N^{2}}{1+\lambda _1 }\left[ {F_2 \cosh Nh_1 +F_3 \sinh Nh_1 } \right] \end{aligned}$$

(16)

Fig. 2

Effect of M on velocity profile

Fig. 3

Effect of $\lambda _1$ on velocity profile

Fig. 4

Effect of Q on velocity profile

Results and Discussion

The variation of the stream lines, axial velocity $\left( u \right)$, temperature $\left( \theta \right)$, pressure gradient $\left( {\frac{dp}{dx}} \right)$, pressure rise $\left( {\Delta P_\lambda } \right)$ and shear stress $\left( {S_{xy} } \right)$ have been analyzed for the impact of sundry dynamical parameters. The following fixed constants are adopted for numerical computations unless specified in the graph.

$$\begin{aligned}&x=1, M=1.0, L= 0.1, \lambda _1 =0.5, Q= -2.0, \phi =\frac{\pi }{3}, \Omega =5.0, a=0.4, b=0.5, \\&d=2.0,\Pr =0.71, Ec=1 \\ \end{aligned}$$

Fig. 5

Effect of $\Omega$ on velocity profile

Fig. 6

Effect of $\phi$ on velocity profile

Flow Behavior Analysis

To investigate the effects of Hartmann number M, Jeffrey fluid parameter $\lambda _1$, mean flux Q, the non-dimensional amplitude of wave b, rotation parameter $\Omega$, phase difference $\phi$ and slip parameter L on the axial velocity through Figs. 2, 3, 4, 5, 6 and 7. Figures 2 and 3 observed that the axial velocity depresses in the central part of the channel by increasing of Hartmann number M and Jeffrey fluid parameter $\lambda _1$. Since larger M provides a resistance to flow and thus velocity depresses. Figure 4 depicts that axial velocity enhances when an increase in Q. Figure 5 illustrates that axial velocity depresses as increasing values of rotation parameter $\Omega$. Figure 6 shows that the magnitude of axial velocity diminishes by an increase in the phase angle $\phi$. Figure 7 depicts that the axial velocity diminishes with increasing L values.

Fig. 7

Effect of L on velocity profile

Fig. 8

Effect of M on temperature

Fig. 9

Effect of $\lambda _1$ on temperature

Fig. 10

Effect of Q on temperature

Fig. 11

Effect of $\Pr$ on temperature

Fig. 12

Effect of Ec on temperature

Fig. 13

Effect of L on temperature

Heat Transfer Analysis

The temperature field for different values of Hartmann number $\left( M \right)$, material parameter $\left( {\lambda _1 } \right)$, mean flux $\left( Q \right)$, Prandtl number $\left( {\Pr } \right)$, Eckert number $\left( {Ec} \right)$ and slip parameter $\left( L \right)$ are shown in Figs. 8, 9, 10, 11, 12 and 13. The temperature depresses with an increase in M and $\lambda _1$ from Figs. 8 and 9. The temperature rises as the magnitude of Q increases from Fig. 10. The temperature enhances by increasing of $\Pr$ in Fig. 11. This is due to the fact that heat generation due to friction caused by shear in the flow is more prominent when the fluid is largely viscous or flowing at a high speed. Similar behavior is noticed for Eckert number Ec that can be seen from Fig. 12. Such rise in temperature resulted from the heat generation due to friction caused by shear in the flow. The temperature depresses when an increase in L from Fig. 13.

Fig. 14

Effect of M on pressure gradient

Fig. 15

Effect of $\lambda _1$ on pressure gradient

Fig. 16

Effect of Q on pressure gradient

Fig. 17

Effect of b on pressure gradient

Fig. 18

Effect of $\Omega$ on pressure gradient

Fig. 19

Effect of $\phi$ on pressure gradient

Fig. 20

Effect of L on pressure gradient

Pumping Characteristics: Pressure Gradient

Figures 14, 15, 16, 17, 18, 19 and 20 represent the profiles of pressure gradient $\left( {\frac{dp}{dx}} \right)$ for the effects of Hartmann number $\left( M \right)$, Jeffrey fluid parameter $\left( {\lambda _1 } \right)$, the non-dimensional amplitude of wave $\left( b \right)$, mean flux $\left( Q \right)$, rotation parameter $\left( \Omega \right)$, phase difference $\left( \phi \right)$ and slip parameter $\left( L \right)$. The pressure gradient has oscillatory behavior in the whole range of the x-axis. From all figures, it is clear that the pressure gradient has a non-zero value only in a bounded region of space. It is depicted from these figures that for $x\in \left[ {0,1} \right]$ and $x\in \left[ {5,6} \right]$ the pressure gradient is small, i.e., the flow can easily pass, while in the region $x\in \left[ {1,5} \right]$, the pressure gradient observed from Figs. 14, 15, 16, 17, 18, 19 and 20. Figure 14 depicts that pressure gradient increases when an increase in M while pressure gradient has opposite behavior with the effect of $\lambda _1$ increases in Fig. 15. Figure 16 found that the pressure gradient enhances by decrease in Q. Figures 17, 18 and 19 shown that pressure gradient increase by increasing in b, $\Omega$ and $\phi$. Figure 20 illustrates that pressure gradient diminishes with an increase in L and much pressure is required to maintain the flux to pass. Moreover, it can be noticed that on the other hand, in the wider part of the channel, the pressure gradient is relatively small, i.e. the flow can easily pass without imposition of a large pressure gradient. On the other hand, in a narrow part of the channel a much pressure gradient is required to maintain the flux to pass it.

Fig. 21

Effect of M on pressure rise

Fig. 22

Effect of $\lambda _1$ on pressure rise

Fig. 23

Effect of $\Omega$ on pressure rise

Fig. 24

Effect of M on shear stress

Fig. 25

Effect of $\lambda _1$ on shear stress

Fig. 26

Effect of b on shear stress

Pressure Rise

To study the effects of Hartmann number $\left( M \right)$, Jeffrey fluid parameter $\left( {\lambda _1 } \right)$ and rotation parameter $\left( \Omega \right)$ on the Pressure rise $\left( {\Delta P_\lambda } \right)$ with respect to the time mean flow $\left( \Theta \right)$ are carried out from Figs. 21, 22 and 23. We have observed that the pressure rise has a non-zero value only in a bounded region of space. It is shown that the pressure rise increases with increasing of the Hartmann number and rotation parameter while it decreases with increasing the ratio of relaxation to retardation times (Jeffrey fluid parameter) through Figs. 21, 22 and 23. The graph is sectored so that the upper right-hand quadrant (I) denotes the region of the peristaltic pumping $\left( {\Theta>0,\Delta p_\lambda >0} \right)$. Quadrant (II) is designated as an augmented flow when $\left( {\Theta<0,\Delta p_\lambda <0} \right)$. Quadrant (III) is for co pumping $\left( {\Theta >0,\Delta P_\lambda <0} \right)$ and free pumping $\left( {\Theta =0,\Delta P_\lambda =0} \right)$. Quadrant (IV) is designated as $\left( {\Theta <0,\Delta p_\lambda >0} \right)$ is called retrograde or backward pumping.

Fig. 27

Effect of Q on shear stress

Fig. 28

Effect of $\Omega$ on shear stress

Fig. 29

Effect of $\phi$ on shear stress

Shear Stress

The axial shear stress distribution $\left( {S_{xy} } \right)$ on the upper wall of an asymmetric channel for different values of Hartmann number $\left( M \right)$, Jeffrey fluid parameter $\left( {\lambda _1 } \right)$, the non-dimensional amplitude of wave $\left( b \right)$, mean flux $\left( Q \right)$, rotation parameter $\left( \Omega \right)$ and phase difference $\left( \phi \right)$ are presented in Figs. 24, 25, 26, 27, 28 and 29. It depicts that stress is in oscillatory behavior, which may be due to peristalsis. The absolute value of shear stress enhances with increasing of M, $\lambda _1$, b, Q, $\Omega$ and $\phi$ from Figs. 24, 25, 26, 27, 28 and 29. Moreover, the absolute values of shear stress are larger in case of a Jeffrey fluid when compared with Newtonian fluid.

Fig. 30

Effect of $\lambda _1$ on Nusselt number

Fig. 31

Effect of $\Pr$ on Nusselt number

Fig. 32

Effect of Ec on Nusselt number

Fig. 33

Effect of L on Nusselt number

Nusselt Number (Heat Transfer Coefficient)

The behaviors of Jeffrey fluid parameter, Prandtl number, Eckert number and slip parameter on Nusselt number have been observed through Figs. 30, 31 and 33. Figure 30 depicts that Nusselt number depresses when an increase in $\lambda _1$ while opposite behavior observed by increasing of $\Pr$ and Ec from Figs. 31 and 32. Nusselt number diminishes when an increase in L from Fig. 33. It is noticed that the effects of all the parameters on the Nusselt number is almost similar to that of temperature. Moreover, the oscillatory behavior of Nusselt number occurs due to sinusoidal travelling along the walls of the channel.

Fig. 34

Effect of M on stream lines for $M = 0$

Fig. 35

Effect of M on stream lines for $M = 2$

Fig. 36

Effect of $\lambda _1$ on stream lines for $\lambda _1 = 0.5$

Fig. 37

Effect of $\lambda _1$ on stream lines for $\lambda _1 = 2$

Fig. 38

Effect of $\Omega$ on stream lines for $\Omega = 0$

Fig. 39

Effect of $\Omega$ on stream lines for $\Omega = 5$

Trapping Phenomenon

The phenomenon of trapping is another interesting topic in peristaltic transport. The formation of an internally circulating bolus of the fluid by closed streamlines is called trapping and this trapped bolus pushed ahead along the peristaltic wave. The effects of Hartmann number $\left( M \right)$, Jeffrey fluid parameter $\left( {\lambda _1 } \right)$ and rotation parameter $\left( \Omega \right)$ are analyzed on stream lines from Figs. 34, 35, 36, 37, 38 and 39. The size of trapped bolus depresses with increasing values of M from Figs. 34 and 35. The size of trapped bolus diminishes as the higher values of $\lambda _1$ in Figs. 36 and 37 while the same behavior observed when an increase in $\Omega$ from Figs. 38 and 39.

Tables 1 and 2 show the comparison of the present solution in limiting case of obtained results with the ones from the open literature for some particular values of the governing parameters and found to be good agreement with the existing literature.

Table 1 Comparison of pressure rise with volume flow rate for fixed $a= 0.7, b=1.2, d=2, M=0.1, \phi =\frac{\pi }{6}, \lambda _1 =0.4, \Omega =0.5$

Table 2 Comparision of axial velocity for fixed $a= 0.4,b=0.5,d=2,Q=2,M=1,\phi =\frac{\pi }{3},\lambda _1 =0.4,\Omega =0.5$

Concluding Remarks

A mathematical model under long wavelength and low Reynolds number approximations is presented to study the influence of heat transfer analysis on MHD peristaltic transport of a Jeffrey fluid in an asymmetric channel with velocity slip condition. Analytical solutions are obtained for the stream function, axial velocity, temperature, pressure gradient, pressure rise, and shear stress. The behaviors of the flow characteristics are analyzed through graphs. A comparative study is made for axial velocity and pressure rise through tables.

• 1. The axial velocity for the MHD fluid is less when compared with hydrodynamic fluid in the central part of the channel.

• 2. The temperature depresses with increasing of slip parameter.

• 3. The temperature enhances as the larger values of Prandtl number and Eckert number.

• 4. The magnitude of pressure gradient enhances with increasing of M, b and Q.

• 5. The magnitude of shear stress at the upper wall in a symmetric channel is greater than in an asymmetric channel.

• 6. If $L=0$ and in the absence of heat transfer, our results are in good agreement with Abd-Alla and Abo-Dahab [23].

• 7. The size of the trapped bolus enhances as the effect of Hartmann number and Jeffrey fluid parameter increases.