1 Introduction

The word peristalsis means clasping and compressing. It describes a progressive wave of contraction along a channel or tube whose cross-sectional area consequently varies along the axis. Peristalsis is a very efficient mechanism for transporting the fluid through a distensible tube or channel using the mechanism of contraction or expansion of the waves propagating along the walls of the conduit. Peristaltic transport is very significant in different biological systems, such as the gastrointestinal tract, lymphatic vessels, insect microscale internal flows etc. [1,2,3,4,5]. Peristaltic pumping is also deployed in a number of industrial applications such as roller and finger pumps and transfer of biological and chemical toxic liquids to avoid contamination via leakage [6, 7].

The fundamentals of peristaltic pumping at low Reynolds number have been explored by Jaffrin and Shapiro [8]. Pozrikidis [9] considered channel width, wave amplitude and phase shift effects in peristaltic flow under sinusoidal waves in a channel Stokes flow by applying a boundary integral method, noting that under varying mean pressure gradient, efficient molecular-convective transport is achieved. Subsequently a number of researchers have explored peristaltic flow for different wave forms and geometries, both experimentally and numerically. These peristaltic studies have also included both Newtonian and non-Newtonian models and representative works in this regard are Hayat et al. [10] who considered magnetic Maxwell fluids, Wang et al. [11] on Sisko fluids, Hina et al. [12] on Johnson–Segalman fluids in a curved channel, Abd elmaboud and Mekheimer [13] on second-order fluids, Sutradhar et al. [14] on Casson fluids, Tripathi and Bég [15] on generalized Burgers’ fluids, Abd-Alla and Abo-Dahab [16] on Jeffrey’s viscoelastic fluids, Tripathi and Bég [17] on a variety of viscoplastic fluids (including Herschel-Bulkley and Vocaldo models) and Mekheimer [18] on couple-stress fluids.

In recent time, microfluidcs is becoming a major area of research due to its numerous applications in separation techniques in medical systems. BioMEMS and lab-on-a-chip devices usually involve sample preparation, treatment, injection, delivery, separation and detection. Most substances acquire surface electric charges when in contact with an aqueous (polar) medium. With electric field applied tangentially along a charge surface, a body force is generated on the ions in the diffuse layer and this results in an electroosmotic force (EOF). This phenomenon is used in electroosmotic pumping such as valve-less switching, accurate control of transportation and manipulation of liquid samples by an electrical field. Since no solid moving parts are involved, this feature makes electroosmosis a preferred method for transporting liquids in microfluidics.

Mathematical simulations of peristaltic transport in microfluidic devices have recently attracted some attention. Chakraborty [19] studied the augmentation of peristaltic transport via electroosmotic means, considering Newtonian fluids. This model however constitutes a relatively simple formulation for analyzing electro-peristaltic transport. In this direction, some more recent investigations [20,21,22,23,24,25] have been reported to analyze the electro-peristaltic transport with channel flow [20], capillary flow [21], power law fluids [22], couple stress fluid [23], magnetohydrodynamics [24], Viscoelastic fluids [25]. They have concluded that peristaltic transport/physiological flow may be controlled by adding and opposing the external electric field. Some other investigations of electroosmotic induced flow of non-Newtonian fluids have been communicated. However these generally involve pumping through straight micro-channels or tubes [26,27,28,29,30,31]. It is of greater practical importance to analyze the more general case of peristaltic pumping in the presence of applied electric fields with a peristaltic pumping zone of fixed length. Advances in silicon micromachining and novel actuation mechanisms of the channel wall such as electrostatic actuation and thermo-pneumatic actuation have been implemented for the development of micro-peristaltic pumps [32]. It has been observed that electroosmosis plays a key role in controlling and stabilizing the interface between two-fluids driven by a pressure gradient [33]. Owing to applications in capillary electrophoresis [34] there has been a significant amount of effort towards understanding the process of combined pressure driven and electroosmosis in various configurations [35, 36]. More recently, from a molecular viewpoint, Gillespie and Pennathur [37] have investigated enhanced ionic separation by means of a combined pressure driven and electroosmotic flow where the direction of electroosmosis opposes the direction of the pressure driven flow.

The volume of work indicates that there is a need for more robust mathematical models for electro-osmotic pumping processes. A unification of the Nernst–Plank theory for the transport of the electrolytes in the lubrication framework of peristalsis is a possible methodology for further elucidating the mechanisms of electro-osmotic pumping in microscale devices. This is the motivation for the present work. Furthermore the Jeffrey’s non-Newtonian viscoelastic model is employed. This rheological model has been used previously by Kothandapani and Srinivas [38] for magnetohydrodynamic peristaltic pumping in an asymmetric channel. The rheology of the Jeffrey model is different from the Newtonian fluid as it encloses a linear model using time derivatives. It has further been utilized by Tripathi et al. [39] for thermal transport in intestinal peristalsis, Ellahi et al. [40] for MHD flow and Bhatti et al. [41] for peristaltic flow through non-uniform rectangular duct having compliant walls. In the present investigation, electro-kinetic peristaltic pumping of an aqueous ionic solution of Jeffrey’s fluid in an asymmetric channel is examined as a simulation of microscale electro-osmotic transport. There exist many different viscoelastic formulations in the literature, including the Oldroyd-B model, PTT model, FENE-P model, the Giesekus model, Williamson model etc. Each has its relative merits. The attraction with the Jeffery’s model is that is a modified form of the Maxwell model achieved by an additional linear relationship, i.e. the time derivative of shear strain to the Maxwell model. The convected Jeffrey model in due course gives the Oldroyd-B model. Since we are considering biological flows, not polymer flows, the Jeffrey model is adequate. It is known (as with the convected Maxwell model) to be able to predict the appearance of the first difference of normal stresses but does not predict non-Newtonian behavior of the shear viscosity nor the second difference of the normal stresses, these characteristics being more important in polymer flows.

2 Mathematical model

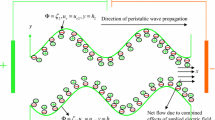
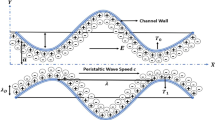
The two-dimensional peristaltic flow of a non-Newtonian aqueous ionic solution in an infinite asymmetric channel having width \(b_{1} + b_{2}\) is considered, as illustrated in Fig. 1. An asymmetric flow regime is produced by choosing the peristaltic wave train, travelling with wave velocity \(c\) along the walls to have different amplitudes (\(a_{1} ,\,a_{2}\)) and phase (\(\varphi\)).The upper and lower walls of the asymmetric microchannel (see Fig. 1) are geometrically modelled using the respective relations:

$$\bar{h}_{2} = b_{1} + a_{1} \sin \left( {\frac{2\pi }{\lambda }(\bar{x} - c\bar{t})} \right),\quad {\text{upper wall}}$$
(1a)
$$\bar{h}_{1} = - \,b_{2} - a_{2} \sin \left( {\frac{2\pi }{\lambda }(\bar{x} - c\bar{t}) + \varphi } \right),\quad {\text{lower wall}}$$
(1b)

where \(\lambda\), \(\bar{x}\), \(\bar{t}\) are the wavelength, axial coordinate, and time. The phase difference \(\varphi\) varies in the range \(0 \le \varphi \le \pi\). When \(\varphi = 0\), a symmetric channel with waves out of phase can be described and for \(\varphi = \pi\), the waves are in phase.

Fig. 1
figure 1

Physical model for peristaltic pumping in an asymmetric microchannel under an applied external electric field

Full size image

The aqueous ionic solution of Jeffrey viscoelastic fluid is sensitive to an externally applied electric field along the length of the asymmetric channel. The positive ions \(n_{ + }\) and negative ion \(n_{ - }\) are both assumed to have bulk concentration (number density) \(n_{0}\), and a valency of \(z_{ + }\) and \(z_{ - }\) respectively. For simplicity, we consider the electrolyte to be a \(z:z\) symmetric electrolyte, i.e. \(z_{ + } = - \,z_{ - } = z\). It may be noted that the channel material for typical peristaltic pumps comprise silicone elastomers, Teflon, polyvinyl chloride, polyurethane rubber or similar substances. These materials are typically employed in a wide variety of microfluidic devices owing to their flexibility and ease of fabrication. When an aqueous solution is brought into contact with such materials, it acquires a net surface potential (referred to as zeta potential, \(\zeta\)) relative to the bulk through a solution pH-dependent surface charging process. It may be observed that for majority cases, with pH near 7, the zeta potential is around − 25 mV or less. Regardless of the charging mechanism, the presence of a negative surface potential leads to an attraction of \(n_{ + }\) ions and repulsion of \(n_{ - }\) ions, leading to the establishment of the electrical double layer (EDL). It is assumed that the wavelength of the pulse is much larger than the channel height; i.e. we assume that the lubrication approximation is valid (\(\delta \ll 1\)). The governing equations for unsteady, two-dimensional, viscous, incompressible flow under an applied axial electrical field are given as:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(2)
$$\rho \left( {\frac{\partial }{\partial t} + u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)u = - \,\frac{\partial p}{\partial x} + \frac{{\partial S_{xx} }}{\partial x} + \frac{{\partial S_{xy} }}{\partial y} + \rho_{e} \,E_{x} ,$$
(3)
$$\rho \left( {\frac{\partial }{\partial t} + u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)v = - \frac{\partial p}{\partial y} + \frac{{\partial S_{yx} }}{\partial x} + \frac{{\partial S_{yy} }}{\partial y},$$
(4)

where \(S_{xx} ,S_{xy} ,S_{yx} ,S_{yy}\) are the extra stress components and \(\rho ,u,v,p,\mu ,\) and \(E_{x}\) denote the fluid density, axial velocity, transverse velocity, pressure, fluid viscosity, and axial electrical field. The constitutive equation of extra stress \(S\) for the Jeffrey viscoelastic model, following [38,39,40,41] may be defined as:

$$S = \frac{\mu }{{1 + \lambda_{1} }}(\dot{\gamma } + \lambda_{2} \ddot{\gamma }),$$
(5)

where \(\dot{\gamma },\lambda_{1} ,\lambda_{2}\) are the rate of strain, the ratio of relaxation and retardation times, the retardation time and dots denote differentiation with respect to time.

Also, \(\rho_{e} \equiv z_{ + } n_{ + } e + z_{ - } n_{ - } e\), denotes the charge number density of the aqueous solution present with \(e\) being the protonic charge. The charge number density is related to the electrical potential in the transverse direction (\(\phi\)) through the Poisson equation:

$$\nabla^{2} \phi = - \frac{{\rho_{e} }}{\varepsilon },$$
(6)

where \(\varepsilon\) is the electrical permittivity. Furthermore in order to determine the potential distribution, it is necessary to describe the charge number density. For this, the ionic number distributions of the individual species are given by the Nernst–Planck equation for each species as:

$$\frac{{\partial n_{ \pm } }}{\partial t} + u\frac{{\partial n_{ \pm } }}{\partial x} + v\frac{{\partial n_{ \pm } }}{\partial y} = D\left( {\frac{{\partial^{2} n_{ \pm } }}{{\partial x^{2} }} + \frac{{\partial^{2} n_{ \pm } }}{{\partial y^{2} }}} \right) \pm \frac{Dze}{{k_{B} T}}\left( {\frac{\partial }{\partial x}\left( {n_{ \pm } \frac{\partial \phi }{\partial x}} \right) + \frac{\partial }{\partial y}\left( {n_{ \pm } \frac{\partial \phi }{\partial y}} \right)} \right),$$
(7)

where, we have assumed equal ionic diffusion coefficients for both the species, and that the mobility of the species is given by the Einstein formula where \(D\) represents the diffusivity of the chemical species, \(T\) is the average temperature of the electrolytic solution and \(k_{B}\) is Boltzmann constant.

To facilitate analytical solutions of Eqs. (2–7) it is advantageous to introduce a group of non-dimensional parameters; \(\bar{x} = \frac{x}{\lambda },\bar{y} = \frac{y}{{b_{1} }},\bar{t} = \frac{tc}{\lambda },\bar{\lambda }_{1} = \frac{{\lambda_{1} c}}{\lambda },\bar{\lambda }_{2} = \frac{{\lambda_{2} c}}{\lambda },\bar{p} = \frac{{pb_{1}^{2} }}{\mu c\lambda },\bar{h}_{1} = \frac{{h_{1} }}{{b_{1} }},\bar{h}_{2} = \frac{{h_{2} }}{{b_{1} }},\phi_{1} = \frac{{a_{1} }}{{b_{1} }},\phi_{2} = \frac{{a_{2} }}{{b_{1} }},b = \frac{{b_{2} }}{{b_{1} }},\delta = \frac{{b_{1} }}{\lambda },\bar{\phi } = \frac{ze\phi }{{k_{B} T}},\bar{n} = \frac{n}{{n_{0} }}\), where \(\delta\) are the wave number. The nonlinear terms in the Nernst–Planck equations are \(O(Pe\,k^{2} )\), where \(Pe = Re\,Sc\) represents the ionic Peclét number, \(Sc = {\mu \mathord{\left/ {\vphantom {\mu {\rho D}}} \right. \kern-0pt} {\rho D}}\) denotes the Schmidt number and \(Re = \frac{c\lambda }{{{\mu \mathord{\left/ {\vphantom {\mu \rho }} \right. \kern-0pt} \rho }}}\) denotes the Reynolds number, where the nonlinear terms in the momentum equation are found to be \(O(Re\,\delta^{2} )\). Therefore, the nonlinear terms may be dropped in the limit that \(Re,\,Pe,\delta \ll 1\).

In the above approximations, dropping the bars, the emerging Poisson equation is:

$$\frac{{\partial^{2} \phi }}{{\partial y^{2} }} = - \kappa^{2} \left( {\frac{{n_{ + } - n_{ - } }}{2}} \right),$$
(8)

where \(\kappa = b_{1} ez\sqrt {\frac{{2n_{0} }}{{\varepsilon \,K_{B} T}}} = \frac{{b_{1} }}{{\lambda_{d} }}\), is known as the electro-osmotic parameter and \(\lambda_{d} \propto \frac{1}{\kappa }\) is Debye length or characteristic thickness of the electrical double layer (EDL).

And the ionic distribution may be determined by means of the simplified Nernst Planck equations:

$$0 = \frac{{\partial^{2} n_{ \pm } }}{{\partial y^{2} }} \pm \frac{\partial }{\partial y}\left( {n_{ \pm } \frac{\partial \phi }{\partial y}} \right),$$
(9)

subjected to \(n_{ \pm } = 1\) at \(\phi = 0\) and \({{\partial n_{ \pm } } \mathord{\left/ {\vphantom {{\partial n_{ \pm } } {\partial y}}} \right. \kern-0pt} {\partial y}} = 0\) where \({{\partial \phi } \mathord{\left/ {\vphantom {{\partial \phi } {\partial y}}} \right. \kern-0pt} {\partial y}} = 0\) (bulk conditions). These yield the much celebrated Boltzmann distribution for the ions

$$n_{ \pm } = e^{ \mp \phi } .$$
(10)

Combining Eqs. (8) and (10), we obtain the Poisson–Boltzmann paradigm for determining the electrical potential distribution:

$$\frac{{\partial^{2} \phi }}{{\partial y^{2} }} = \kappa^{2} \sinh \left( \phi \right).$$
(11)

In order to make further analytical progress, we must simplify Eq. (11). Equation (11) may be linearized under the low-zeta potential approximation. This assumption is not ad hoc since for a wide range of pH, the magnitude of zeta potential is less than 25 mV. Therefore, Eq. (11) may be simplified to yield:

$$\frac{{\partial^{2} \phi }}{{\partial y^{2} }} = \kappa^{2} \phi ,$$
(12)

which may be solved subject to \(\left. \phi \right|_{{y = h_{1} }} = \zeta_{1}\) and \(\left. \phi \right|_{{y = h_{2} }} = \zeta_{2}\). The electrical potential function thereafter emerges in terms of transcendental hyperbolic functions:

$$\phi = C_{1} e^{\kappa y} + C_{2} e^{ - \kappa y} ,$$
(13)

where \(C_{1} = \frac{{e^{{h_{2} \kappa }} \zeta_{2} - e^{{h_{1} \kappa }} \zeta_{1} }}{{e^{{2h_{2} \kappa }} - e^{{2h_{1} \kappa }} }}\) and \(C_{2} = \frac{{e^{{h_{1} \kappa + h_{2} \kappa }} \left( {e^{{h_{1} \kappa }} \zeta_{2} - e^{{h_{2} \kappa }} \zeta_{1} } \right)}}{{e^{{2h_{1} \kappa }} - e^{{2h_{2} \kappa }} }}.\)

In the above limit, dropping the bars, the continuity and momentum equations are reduced as:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(14)
$$\frac{\partial p}{\partial x} = \left( {\frac{1}{{1 + \lambda_{1} }}} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} + \kappa^{2} u_{hs} \phi ,$$
(15)
$$\frac{\partial p}{\partial y} = 0,$$
(16)

where \(u_{hs} = - \frac{{E_{x} \varepsilon \zeta }}{\mu \,c}\) is the Helmholtz–Smoluchowski velocity or maximum electro-osmotic velocity. The associated normalized boundary conditions are:

$$u = 0\quad \text{at}\quad y = h_{1} ,$$
(17a)
$$u = 0\quad \text{at}\quad y = h_{2} ,$$
(17b)

Integrating Eq. (15) and imposing the above boundary conditions, the axial velocity is found to be:

$$u = \left( {1 + \lambda_{1} } \right)\left( {\frac{{y^{2} }}{2}\frac{\partial p}{\partial x} - u_{hs} (C_{2} e^{ - y\kappa } + C_{1} e^{y\kappa } )} \right) + C_{3} + yC_{4} ,$$
(18)

where \(C_{3} = \frac{{1 + \lambda_{1} }}{{h_{1} - h_{2} }}\left\{ {h_{2} \left( {\frac{{h_{1}^{2} }}{2}\frac{\partial p}{\partial x} - u_{hs} (C_{2} e^{{ - h_{1} \kappa }} + C_{1} e^{{h_{1} \kappa }} )} \right) - h_{1} \left( {\frac{{h_{2}^{2} }}{2}\frac{\partial p}{\partial x} - u_{hs} (C_{2} e^{{ - h_{2} \kappa }} + C_{1} e^{{h_{2} \kappa }} )} \right)} \right\},\) \(C_{4} = \frac{{\left( {1 + \lambda_{1} } \right)e^{{ - h_{1} \kappa - h_{2} \kappa }} }}{{2\left( {h_{2} - h_{1} } \right)}}\left\{ {e^{{h_{1} \kappa + h_{2} \kappa }} \frac{\partial p}{\partial x}\left( {h_{2}^{2} - h_{1}^{2} } \right) + u_{hs} \left( {2C_{2} (e^{{h_{2} \kappa }} - e^{{h_{1} \kappa }} ) + 2C_{1} (e^{{2h_{1} \kappa + h_{2} \kappa }} - e^{{h_{1} \kappa + 2h_{2} \kappa }} )} \right)} \right\}.\)

The volumetric flow rate in laboratory frame of reference is defined as:

$$Q = \int\limits_{{h_{1} }}^{{h_{2} }} {u\,\,dy} ,$$
(19)

which, by virtue of Eq. (18), assumes the following form:

$$\begin{aligned} Q = \frac{{e^{{ - \left( {h_{1} + h_{2} } \right)\kappa }} }}{\kappa }\left\{ {C_{2} u_{hs} \left( {1 + \lambda_{1} } \right)\left( {e^{{h_{1} \kappa }} - e^{{h_{2} \kappa }} } \right) + e^{{\left( {h_{1} + h_{2} } \right)\kappa }} \left( {C_{1} \left( {e^{{h_{1} \kappa }} - e^{{h_{2} \kappa }} } \right)u_{hs} \left( {1 + \lambda_{1} } \right)} \right.\,\,\,} \right. \hfill \\ \,\,\,\,\,\,\,\,\left. {\left. { + \frac{\kappa }{6}\left( { - 6C_{3} \left( {h_{1} - h_{2} } \right) - 3C_{4} \left( {h_{1}^{2} - h_{2}^{2} } \right) - \frac{\partial p}{\partial x}\left( {1 + \lambda_{1} } \right)\left( {h_{1}^{3} - h_{2}^{3} } \right)} \right)} \right)} \right\}. \hfill \\ \end{aligned}$$
(20)

The transformations between a wave frame \((x_{w} ,y_{w} )\) moving with velocity \(c\) and the fixed frame (\(x,y\)) are given by:

$$x = x_{w} - ct,\,\,\,\,\,y = \,y_{w} ,\,\,\,\,\,\,\,u = \,u_{w} + c,\,\,\,\,\,\,\,v = \,\,\,v_{w} ,$$
(21)

where \((u_{w} ,\,v_{w} )\) and \((u,v)\) are the velocity components in the wave and fixed frame respectively.

The volumetric flow rate in the wave frame is given by:

$$q_{w} = \int\limits_{{h_{1} }}^{{h_{2} }} {u_{w} d} y_{w} = \int\limits_{{h_{1} }}^{{h_{2} }} {(u - 1)dy_{w} } ,$$
(22)

which, on integration, yields:

$$q_{w} = Q + h_{1} - h_{2} .$$
(23)

Averaging the volumetric flow rate along one time period, we get:

$$\bar{Q} = \int\limits_{0}^{1} {Qdt} = \int\limits_{0}^{1} {(q + h_{2} - h_{1} )dt} ,$$
(24)

which, on integration, yields

$$\bar{Q} = q_{w} + 1 + b = Q + 1 + b + h_{1} - h_{2} .$$
(25)

Rearranging the terms of Eq. (18) and using Eq. (23), the pressure gradient is obtained as:

$$\begin{aligned} \frac{\partial p}{\partial x} = \frac{{16e^{{ - 2\left( {h_{1} + h_{2} } \right)\kappa }} }}{{\left( {h_{1} - h_{2} } \right)^{3} \kappa \left( {1 + \lambda_{1} } \right)}}\left( {C_{2} e^{{\left( {h_{1} + h_{2} } \right)\kappa }} u_{hs} } \right.\left( {e^{{h_{1} \kappa }} \left( { - 2} \right.} \right. + h_{1} \kappa - h_{2} \left. \kappa \right) + e^{{h_{2} \kappa }} \left( 2 \right. + h_{1} \kappa - h_{2} \left. {\left. \kappa \right)} \right)\left( {1 + \lambda_{1} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, + e^{{2\left( {h_{1} + h_{2} } \right)\kappa }} \left( {2Q\kappa + C_{1} u_{hs} } \right.\left( {e^{{h_{1} \kappa }} \left( { - 2} \right.} \right. + h_{1} \kappa - h_{2} \left. \kappa \right)\, + e^{{h_{2} \kappa }} \left( 2 \right. + h_{1} \kappa - h_{2} \left. {\left. {\left. \kappa \right)} \right)\left( {1 + \left. {\lambda_{1} } \right)} \right)} \right). \hfill \\ \end{aligned}$$
(26)

The pressure difference across one wavelength (\(\Delta p\)) is defined as follows:

$$\Delta p = \int\limits_{0}^{1} {\frac{\partial p}{\partial x}dx} ,$$
(27)

Using Eq. (18), the stream function in the wave frame (obeying the Cauchy–Riemann equations, \(u_{w} = \frac{\partial \psi }{{\partial y_{w} }}\) and \(v_{w} = - \frac{\partial \psi }{{\partial x_{w} }}\)) takes the form:

$$\begin{aligned} \psi & = \frac{{e^{{ - \left( {2\left( {h_{1} + h_{2} } \right) + y} \right)\kappa }} }}{{\left( {h_{1} - h_{2} } \right)^{3} \kappa }}\left( {ye^{{\left( {2\left( {h_{1} + h_{2} } \right) + y} \right)\kappa }} (\bar{Q} - 1 - b + h_{2} - h_{1} )\left( {6h_{1} h_{2} - 3h_{1} y + 3h_{2} y + 2y^{2} } \right)\kappa } \right) \\ & \quad + \,C_{2} u_{hs} \left( {e^{{2\left( {h_{1} + h_{2} } \right)\kappa }} \left( {h_{1} - h_{2} } \right)^{3} } \right) + e^{{\left( {h_{1} + 2h_{2} + y} \right)\kappa }} y\left( {2y^{2} } \right. - h_{2}^{3} \kappa - h_{1}^{2} \left( {2h_{2} - y} \right)\kappa + 2h_{2}^{2} y\kappa \\ & \quad - \,h_{2} y\left( {3 + y\kappa } \right) - h_{1} \left( {h_{2}^{2} \kappa + y\left( {3 - y\kappa } \right) + h_{2} \left( { - 6 + \left. {y\kappa } \right)} \right)} \right) + e^{{\left( {2h_{1} + h_{2} + y} \right)\kappa }} y\left( {h_{1}^{3} } \right.\kappa + h_{1}^{2} \left( {h_{2} - 2y} \right)\kappa \\ & \quad + \,y\left( { - 2y + h_{2}^{2} \kappa + h_{2} \left( {3 - y\kappa } \right)} \right) + h_{1} \left( { - 2} \right.h_{2}^{2} \kappa + h_{2} \left( { - 6 + y\kappa } \right) + y\left( {3 + y\left. {\left. {\left. \kappa \right)} \right)} \right)} \right)\left( {1 - \lambda_{1} } \right) \\ & \quad + \,C_{1} u_{hs} \left( - \right.e^{{2\left( {h_{1} + h_{2} + y} \right)\kappa }} \left( {h_{1} - h_{2} } \right)^{3} + e^{{\left( {2h_{1} + 3h_{2} + y} \right)\kappa }} y\left( {h_{1}^{3} \kappa - h_{1}^{2} \left( {h_{2} - 2y} \right)\kappa } \right) + y\left( {2y + h_{2}^{2} \kappa - h_{2} \left( {3 + y\kappa } \right)} \right) \\ & \quad + \,h_{1} \left( { - 2} \right.h_{2}^{2} \kappa + y\left( { - 3 + y\kappa } \right) + h_{2} \left( {6 + y\left. {\left. \kappa \right)} \right)} \right) + e^{{\left( {3h_{1} + 2h_{2} + y} \right)\kappa }} y\left( { - 2y^{2} } \right. - h_{2}^{3} \kappa + h_{1}^{2} \left( {2h_{2} - y} \right)\kappa + 2h_{2}^{2} y\kappa \\ & \quad + \,h_{2} y\left( {3 - y\kappa } \right) - h_{1} \left( {h_{2}^{2} \kappa - y\left( {3 + y\kappa } \right) + h_{2} \left( {6 + \left. {y\left. \kappa \right)} \right)} \right)} \right)\left( {1 - \lambda_{1} } \right) \\ \end{aligned}$$
(28)

3 Computational results

The solutions of governing equations are analytically solved. However some integrations present in Eqs. (19) and (27) are solved numerically by using Simpson’s 1/3rd Rule. The plots are drawn by Mathematica symbolic software. Figures 2, 3, 4 and 5 present selected graphical solutions for velocity, volumetric flow rate, pressure difference and streamline distributions, with different values of κ (ratio of the one side width of the capillary b1 and the Debye length λ), \(u_{hs}\) (Helmholtz-Smoluchowski velocity or maximum electro-osmotic velocity) and \(\lambda_{1}\) (ratio of relaxation to retardation times).

Fig. 2
figure 2

Velocity profile (axial velocity vs. transverse coordinate) at \(\phi_{1} = 0.6,\,\phi_{2} = 0.5,\,b = 1,\,\zeta_{1} = 0.5,\,\zeta_{2} = 1,\) and a \(u_{hs} = 1,\,\lambda_{1} = 1,\,\varphi = \pi /2\), b \(\kappa = 1,\,\lambda_{1} = 1,\,\varphi = \pi /2\), c \(u_{hs} = 1,\,\kappa = 1,\,\varphi = \pi /2\) d \(u_{hs} = 1,\,\kappa = 1,\,\lambda_{1} = 1\)

Full size image
Fig. 3
figure 3

Volumetric flow rate versus channel length at constant pressure gradient and \(\phi_{1} = 0.6,\,\phi_{2} = 0.5,\,b = 1,\zeta_{1} = 0.5,\,\zeta_{2} = 1,\) and a \(u_{hs} = 1,\,\lambda_{1} = 1,\,\varphi = \pi /2\), b \(\kappa = 1,\,\lambda_{1} = 1,\,\varphi = \pi /2\), c \(u_{hs} = 1,\kappa = 1,\,\varphi = \pi /2\), d \(u_{hs} = 1,\kappa = 1,\lambda_{1} = 1\)

Full size image
Fig. 4
figure 4

Pressure difference across one wavelength versus time averaged volumetric flow rate at \(\phi_{1} = 0.6,\,\phi_{2} = 0.5,\,{\text{b}} = 1,\,\zeta_{1} = 0.5,\,\zeta_{2} = 1,\,\varphi = \pi /2\), a \(u_{hs} = 1,\,\lambda_{1} = 1\), b \(\kappa = 1,\,\lambda_{1} = 1\), c \(u_{hs} = 1,\,\kappa = 1\)

Full size image
Fig. 5
figure 5figure 5

Stream lines in wave form at \(\phi_{1} = 0.7,\,\phi_{2} = 1.5,\,b = 3,\,\bar{Q} = 1.5\), \(\zeta_{1} = 0.5,\,\zeta_{2} = 1,\) \(\varphi = \pi /2\) for a \(u_{hs} = 0,\,\kappa = 1,\,\lambda_{1} = 1\), b \(u_{hs} = - \,1,\,\kappa = 1,\,\lambda_{1} = 1\), c \(u_{hs} = 1,\kappa = 1,\lambda_{1} = 1\), d \(u_{hs} = - 1,\kappa = 2,\lambda_{1} = 1\), e \(u_{hs} = - 1,\kappa = 3,\lambda_{1} = 1\), f \(u_{hs} = - \,1,\,\kappa = 1,\,\lambda_{1} = 2\), g \(u_{hs} = - \,1,\kappa = 1,\,\lambda_{1} = 3\), h \(u_{hs} = - \,1,\,\kappa = 1,\,\lambda_{1} = 0\)

Full size image

4 Discussion

The velocity of the fluid with varying magnitude of the electro-osmotic parameter is shown in Fig. 2 for the fixed values of \(\phi_{1} = 0.6,\phi_{2} = 0.6,b = 1,\) \(\zeta_{1} = 0.5,\zeta_{2} = 1,\) \(\varphi = \pi /2\) and \(u_{hs} = 1,\lambda_{1} = 1\). Since κ denotes the ratio of one side width of the capillary b 1 and the Debye length λ, it follows that for κ → 1, the one side thickness of the capillary is reduced to the same order of magnitude as the Debye length. This situation is not completely compatible with the solution for which Debye–Hückel approximation is valid. However it still remains a reasonable approximation to follow. In the present analysis, therefore we consider three different values of electro-osmotic parameter i.e. \(\kappa = b_{1} ez\sqrt {\frac{{2n_{0} }}{{\varepsilon \,K_{B} T}}} = \frac{{b_{1} }}{{\lambda_{d} }}\) i.e. 2, 3 and 4. Flow reversal is computed for all the cases. It is emphasized that the velocity of the fluid attains its minimum value at the wall of the capillary i.e. strongest deceleration is induced at the wall. It is also evident that beyond a critical height of the capillary there is no significant change in the velocity with electro-osmotic parameter and near the wall, with increasing electro-osmotic parameter (i.e. for smaller Debye length) there is a substantial deceleration in the axial velocity. \(u_{hs} = - \frac{{E_{x} \varepsilon \zeta }}{\mu \,c}\) and it is clear that the maximum velocity is directly proportional to the external applied electric field. The axial velocity of the fluid is studied for three different values of \(u_{hs}\) each depicting the case of adding (\(u_{hs} > 0\)), opposing (\(u_{hs} < 0\)) and vanishing applied electric field (\(u_{hs} = 0\)). Increasing \(u_{hs}\) depletes the electrokinetic body force resistance and manifests in increasing axial velocity (Fig. 2b). Quite an opposite phenomenon observed when the rheology of the fluid changes from Newtonian (λ 1 = 0) to a Jeffrey fluid (λ 1 > 0) in the presence of aiding applied electric field. The velocity of the fluid is markedly decelerated with an increase in λ 1 i.e. ratio of relaxation to retardation times (which signifies stronger viscoelastic effect).

Figure 3 depicts the variation of the time-mean flow rate as a function of electroosmotic parameter (κ), characteristic electro-osmotic velocity (\(u_{hs}\)) and ratio of relaxation to retardation times (λ 1). It is observed that the volumetric flow rate increases with greater electro-osmotic parameter i.e., as the EDL becomes thinner, as seen in Fig. 3a. This is a result of the increased body force for thin EDL. Volumetric flow rate becomes positive for higher values of κ. Volumetric flow rate decreases (in the negative sense) when an opposing electric field changes to the case of an aiding electric field. Volumetric flow rate is increased with positive electro-osmotic velocity (\(u_{hs}\)) whereas it is reduced with negative electro-osmotic velocity, as plotted in Fig. 3b. Volumetric flow rate is decreased with greater ratio of relaxation to retardation parameter as observed in Fig. 3c. Lower values are obtained for the Jeffrey fluid (λ 1 > 0) rather than the Newtonian fluid (λ 1 = 0) in the presence of aiding electric field.

Figure 4 depicts the variation in pressure difference as a function of time averaged volumetric flow rate across a single wavelength for different values of κ, \(u_{hs}\) and λ 1 . Figure 4a–c demonstrate that the relation between pressure difference and the volumetric flow rate is inversely proportional i.e., the pressure rise gives larger values for small volumetric rate and vice versa. It is also noted that the pressure difference is larger for the absence time averaged flow rate. However, all the variations are linearly dependent. The electroosmotic parameter introduces an additional electro-osmotic force which enhances the pressure difference (Fig. 4a). The pressure difference and the time average flow rate are larger for the favorable electric field. Pressure difference is increased with positive electro-osmotic velocity (\(u_{hs}\)) whereas it is reduced with negative electro-osmotic velocity, as plotted in Fig. 4b. The pressure difference decreases with increase of λ 1. This implies that pressure difference is larger for the Newtonian fluid than the Jeffrey fluid but only up to a critical flow rate; thereafter the reverse trend is computed.

Another interesting phenomenon in peristaltic motion is trapping. It is basically the formation of an internally circulating bolus of fluid by closed stream lines. This trapped bolus is pushed along by peristaltic waves. The streamlines for the different governing parameters \(u_{hs}\), κ, λ1 are shown in Fig. 5a–h. Figure 5a–c depict the streamlines for different values of \(u_{hs}\) with κ = 1 and λ 1 = 1. It is evident that with increase of the electro-kinetic slip velocity, there is a decreasing resistance to the fluid motion. It is this reduction in resistance which ensures an augmented propensity of the fluid particles to propagate along the axial direction and contributes to the elimination of trapping. In the presence of opposing electric field, the effect of the electro-osmotic parameter on the streamlines is shown in Fig. 5b, d, e for κ = 1, 2 and 3. It is clear that smaller value of κ leads to parallel streamlines while for the case of higher value of κ, there is a small region where there is a fluid bolus which is trapped. It observed that the trapping of the bolus decreases in both upper and lower half of the channel with an increase in osmotic parameter. The characteristic of bolus with different value of λ 1 (= 0, 1 and 3) is visualized in Fig. 5f–h, with all other parameters invariant. It is evident that the shape of the bolus is larger for the case of Newtonian fluid than the non-Newtonian Jeffrey fluid. The trapping bolus for both upper and lower channel decreases with an increase in viscoelastic parameter, λ 1.

5 Conclusions

A mathematical study has been conducted for peristaltic motion of aqueous electrolyte solution of a non-Newtonian Jeffrey fluid through an asymmetric microchannel altered by concomitant applied electric field. The study is motivated by further expounding the electro-hydrodynamics of peristaltic electro-osmotic (EO) mechanisms in on-chip drug release and micro-scale biomimetic EO pumps. Assuming low Reynolds number and lubrication theory approximations, exact solutions for the transformed boundary value problem are derived for velocity, volumetric flow rate and pressure difference. Streamlines are also computed. The influence of electroosmotic parameter, Helmholtz–Smoluchowski velocity (varying magnitudes of the electric field for both aiding and opposing cases) and the ratio of relaxation and retardation time parameter on flow characteristics is investigated. Furthermore a comparison is made between the Newtonian and Jeffrey fluid results. The existence of the trapping is observed to be highly dependent on the electric field (aiding, opposing and neutral). Bolus magnitude is enhanced for a Newtonian fluids compared with non-Newtonian Jeffrey fluid. Increasing relaxation to retardation time ratio parameter therefore decreases bolus size. Pressure difference is enhanced with positive electro-osmotic velocity (u hs ) whereas it is decreased with negative electro-osmotic velocity. Stronger viscoelasticity as characterized by greater relaxation to retardation time ratio parameter suppresses the pressure difference. Increasing electro-osmotic parameter (i.e. smaller Debye length) induces a significant retardation in the axial. Furthermore the flow is decelerated with an increase in ratio of relaxation to retardation times indicating that stronger viscoelasticity of the aqueous solution is inhibiting. The present computations may provide deeper insight into electro-osmotic propulsion mechanisms for micro-scale applications including lab-on-a-chip devices for flow mixing, cell manipulation, etc. The one-dimensional solutions derived herein furthermore provide a more realistic insight into non-Newtonian electroosmotics since we evaluate simultaneously the combined effects of peristaltic waves, viscoelasticity and electro-osmotic body force. These solutions also provide a solid foundation for benchmarking more complex computational fluid dynamics models of flow characteristics of rheological fluids deployed in electro-osmotic pumps. The current work has been restricted to a one-fluid viscoelastic model and has ignored slip effects at the walls. It has also only considered a simple conduit. Important work in two-fluid electro-kinetic transport has been reported by Afonso et al. [42], in slip electro kinetic flows also by Afonso et al. [43] and in annular electro-osmotic pumping by Ferrás et al. [44]. These complexities constitute interesting pathways for extending the current work and will be addressed imminently.