1 Introduction

In modern applied mathematics, engineering and the physiological world, the subject of peristalsis is of great importance. This is attributable to its many uses in real life. Following the leading significances of peristalsis phenomenon in the human body and other physical systems, special attention has been deserted by investigators recently. The peristalsis process is associated with liquids pumping which is based on the propagation of sinusoidal waves. The urinary system has also followed the phenomenon of peristaltic, which deals with the expansion and contraction of inadvertently muscular to pump the urine from kidneys to the bladder. It process is associated with the pumping of fluid, mixing movements as well as propulsive against pressure rise. In biotechnology and biological systems, the peristaltic transport encountered fundamental and prestigious applications like the movement of blood in arteries and vessels, pumping of blood, food in the esophagus, etc. Besides this, this interesting phenomenon involves the applications in many industrial and biomedical sciences like sanitary liquid transfer, heart-pumping machines and instruments, open-heart surgery, ventilators, etc. The early investigations on the peristaltic motion dealt with taking linear and nonlinear fluid models in various geometrical configurations (Latham 1966; Raju and Devanatham 1972; Waldrop and Miller 2016; Butt et al. 2020).

It is a trivially justified fact that the cooling process is the most necessary need of all industries and technological systems. However, the ultrahigh-performance cooling process is inherently affected due to poor thermal efficiencies of base materials and subsequently results in the form of limited energy development. The modern scientific revolution in nanotechnology enables to suggest metallic and nonmetallic tiny-sized particles with excellent thermal consequences. With nanometer dimensions, these particles proved as most thermally enhanced performances and subsequently play fundamental applications in industries, manufacturing processes, cooling and heating applications, medical sciences, energy production, chemical reactive materials, fission processes, mechanical industries and many more. The utilization of these effective particles in traditional materials like ethylene glycol and water successfully enhances the thermal performance more stably. Due to prestigious nanoparticle appliances, foremost work has been utilized by scientists on this topic. The word nanofluid refers to a liquid suspension which contains ultrafine particles of less than 100 nm in diameter. Such particles can be present in metals such as oxides (Al2O2), nitrides (AlN, SiN), (Al, Cu), carbides (SiC) and non-metals (graphite, carbon nanotubes). The nanoscale metallic particles in the base fluid were first introduced by Choi (Choi 1960), and he named the resulting liquid as nanofluid. He narrated that heat transfer can be improved by an innovative technique that is by dissolving nanoscale particles in the base fluid. The purpose of this was further explained by Choi and co-workers (Choi et al. 2001). It was experimentally confirmed that a fundamental thermal efficiency to base materials is predicted while making the addition of nanoparticles in it. Another prominent investigation on nanofluid regarding slip mechanisms aspects were reported by Buongiorno (Buongiorno 2005). This novel theory reports the Brownian movement and thermophoresis slip prospective of nanoparticles. It was finally concluded that the phenomenon of variation in heat/mass transportation is significantly affected by two important thermophoretic and Brownian motion prospective. Some apparent contribution involves the interaction of nanoparticles to investigate the peristalsis in recent times by taking different physiological conditions (Umair Khan 2020; Mebarek-Oudina 2018; Fateh Mebarek-Oudina et al. 2020; Marzougui et al. 2020; Hassanan 2019; Turkyilmazaglu 2020; Rida Ahmad and Mustafa 2017). As well, nanofluids play a prominent role and has its wide range of applications in the peristaltic mechanism. Some of the novel pioneering investigations examined by the researchers on the peristaltic transport of nanofluids are listed in the references (Ali et al. 2020; Kayani et al. 2020; Srinivas et al. 2018; Prakash et al. 2020; Vaidya et al. 2020; Khan et al. 2020).

From a biological point of view, the magnetic force impact in peristaltic transport is significant, such as the existence of hemoglobin molecules that render the blood a biomagnetic fluid. In therapeutic skill, biomagnetic fluids are studied as a working fluid and are considered as a part of physiological fluids. The examination of magnetohydrodynamics in biomagnetic fluid flow has an extreme biological interest in numerous important medicinal implications. Examples consist of the magnetic drug targeting to transport the drugs to all over human body, the application of magnetic devices for cell separation, monitoring the blood flow rates in clinical procedures and assessing the effect of strong magnetic fields on the human cardiovascular system. Keeping all these applications in cognizance, some of the investigators have examined the MHD biomagnetic fluid flows in different suppositions under different considerations (Wakif et al. 2019, 2020; Wakif 2020; Raza et al. 2020a; Qasim et al. 2020, 2019; Rasool and Wakif 2020; Turkyilmazoglu 2011, 2012). Magnetic resonance imaging (MRI), electrical machines and magnetic particles used as a product carrier are a range of uses of the magnetic field in physiology. Besides, the nanofluid magnetic field is prominent in medical applications like contemporary medication distribution and cancer therapy (Tripathi and Beg 2014). Cancer patients have delivered radiation utilizing nanoparticles and nanofluids built on titanium, possessing magnetic properties that twig on tumor cells without killing healthy cells. In view of aforementioned usages of magnetic nanofluids, Sucharitha et al. (Sucharitha et al. 2019) examined the magnetohydrodynamic nanofluid flow in a non-uniform aligned channel with Joule heating. Explorations have rendered some essential contributions to the idea of nanofluids, taking Brownian motion and thermophoresis into account (Hayat et al. 2012; Kothandapani and Prakash 2015; Abbasi et al. 2015; Reddy and Makinde 2016; Raza et al. 2020b).

Most of the initial studies on peristaltic transport have dealt with no-slip conditions. It is a movement under which the velocity of particles associated near the surface is perturbed efficiently. However, the flow of fluids through porous surfaces, emulsion, hardened and rough surface, silicone solutions and gas flow in micro-devices is commonly predicted, and the interference of no-slip conditions becomes quite traditional. The premier concept of slip phenomenon was originated by the theory of Navier (Navier 1827), where it was explicitly rendered that there exists a fundamental relationship between shear stress and fluid velocity near the surface. Nowadays, the methodology involving both nanofluid and slip conditions finds tremendous interest from many researchers and strong demand from thermal systems dependent on the industry. Afterward, the partial slip boundary constraints concept was used by several researchers with varying fluids and complex geometries (Mandviwalla and Archer 2008; Akram and Nadeem 2014; Akbarzadeh 2017; Hayat et al. 2019; Manjunatha et al. 2019, 2020a, 2020b; Farooq et al. 2019; Akram et al. 2020; Rajashekhar et al. 2020).

Due to the high importance of peristaltic flow with slip boundary constraints, authors were inspired to investigate the influence of slip and aligned magnetic field on the peristaltic flow of Jeffery nanofluid subjected to multiple slip conditions which helps in examining the movement of chyme motion in the gastrointestinal tract and during the surgery to take control of the flow of blood by adjusting the magnetic field intensity. Such a dimension of research has not yet been debated. The fluid flows are formulated beneath the assumptions of long wavelength and low Reynolds number and non-dimensionalized using dimensionless parameters. The modeled governing equations are resolved using the perturbation technique. The physical quantities of relevant parameters are debated graphically, and the trapping phenomena against relevant parameters are discussed through graphs.

2 Problem formulation

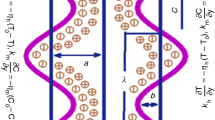
Consider the peristaltic motion of a non-uniform verticalchannel. The channel walls are compliant and are sustained at a relentless temperature \(T_{0}\). The sinusoidal wave trains are of a wavelength \(\lambda\) which moves along the walls of the channel with speed \(c\) (Fig. 1). The mathematical appearance of the geometry of sinusoidal wave trains is given by

$$h = 1 + mx + \varepsilon {\text{cos}}\left( {\frac{2\pi }{\lambda }\left( {x - ct} \right)} \right)$$
(1)

The physical quantities in above fundamental relations are axial velocity \(\left( x \right)\), sinusoidal wave speed \(\left( c \right)\), time \(\left( t \right),\) channel irregularity \(\left( m \right)\), amplitude ratio \(\left( \varepsilon \right)\) and wavelength \(\left( \lambda \right).\)

Fig. 1
figure 1

Illustration of flow

Full size image

The flow equations are constituted giventhe following assumptions.

  • The length of the channel has been taken as integral power of the wavelength \(\lambda .\)

  • In the stationary frame, the flow has been considered unsteady in contrast to the moving frame where assumed flow is steady.

  • Following relations are suggested between moving co-ordinates \((\overline{x} ,\overline{y} )\) and stationary co-ordinates \((\overline{X} ,\overline{Y} )\).

    $$\begin{gathered} \overline{x} = \overline{X} - c\overline{t} ,\,\,\overline{y} = \overline{Y} ,\,\,\overline{p} = \overline{P} (x,t), \hfill \\ \overline{u} = \overline{U} - c,\overline{\chi } = \,\overline{\psi } \, - \frac{{R^{2} }}{2} \hfill \\ \end{gathered}$$
    (2)

wherever \(\overline{p}\) and \(\overline{P}\) are pressures, \(\overline{\chi } \,\,{\text{and}}\,\,\overline{\psi }\) are stream functions, and \(\overline{u}\) and \(\overline{U}\) are velocities in the moving co-ordinates and stationary co-ordinates, respectively.

The equations for 2-D flow model (Srinivas et al. 2018) are:

$$\begin{aligned} & - \frac{{{\text{d}}\overline{p} }}{{{\text{d}}\overline{x} }} + \frac{{{\text{d}}\overline{{\tau _{{\bar{x}\bar{y}}} }} }}{{{\text{d}}\overline{{y^{2} }} }} - \sigma B_{0}^{2} \left( {\overline{u} + c} \right) + \left( {1 - C_{0} } \right)\rho _{{f_{0} }} g\beta \left( {T - T_{0} } \right) \\ & + (\rho _{f} - \rho _{{f_{0} }} )g\beta ^{*} (C - C_{0} ) = 0 \\ \end{aligned}$$
(3)
$$\begin{aligned} & k\frac{{{\text{d}}^{2} T}}{{{\text{d}}\overline{{y^{2} }} }} + \left( {\rho c} \right)_{p} \left[ {D_{B} \frac{{{\text{d}}C}}{{{\text{d}}\overline{y} }}\frac{{{\text{d}}T}}{{{\text{d}}\overline{y} }} + \frac{{D_{T} }}{{T_{0} }}\left( {\frac{{dT}}{{d\overline{y} }}} \right)^{2} } \right] \\ & + \mu \left( {\frac{{{\text{d}}\overline{u} }}{{{\text{d}}\overline{y} }}} \right)^{2} + \sigma B_{0}^{2} \left( {\bar{u} + c} \right)^{2} = 0 \\ \end{aligned}$$
(4)
$$D_{B} \frac{{{\text{d}}{}^{2}C}}{{{\text{d}}\overline{{y^{2} }} }} + \left( {\frac{{D_{T} }}{{T_{0} }}} \right)\frac{{{\text{d}}{}^{2}T}}{{{\text{d}}\overline{{y^{2} }} }} = 0$$
(5)

Following the flow structure, the following boundary conditions are assumed:

$$\frac{{{\text{d}}\overline{u} }}{{{\text{d}}\overline{y} }} = 0,\,\,\frac{{{\text{d}}T}}{{{\text{d}}\overline{y} }} = 0,\,\,\frac{{{\text{d}}C}}{{{\text{d}}\overline{y} }} = 0\,\,\,{\text{at}}\,\,y = 0$$
(6)
$$\overline{u} + \alpha_{1} \frac{{{\text{d}}\overline{u} }}{{{\text{d}}\overline{y} }} = - c,\,T + \alpha_{2} \frac{{{\text{d}}T}}{{{\text{d}}\overline{y} }} = T_{1} ,\,C + \alpha_{3} \frac{{{\text{d}}C}}{{{\text{d}}\overline{y} }} = C_{1} \,{\text{at}}\,y = h$$
(7)

The stress tensor for in-compressible Jeffery fluid model can be written as

$$\tau = \frac{\mu }{{1 + \lambda_{1} }}\left( {\dot{\gamma } + \lambda_{2} \ddot{\gamma }} \right)$$
(8)

The dimensionless involved quantities are defined as.

\(\begin{gathered} x = \frac{{\bar{x}}}{\lambda },\,y = \frac{{\overline{y} }}{a},\,u = \frac{{\overline{u} }}{c},\,t = \frac{{c\overline{t} }}{\lambda },\,p = \frac{{\bar{p}a^{2} }}{{\lambda \mu c}},\,\varepsilon = \frac{b}{a},\, \hfill \\ {\text{Re}} = \frac{{\rho ca}}{\mu },\,{\text{Pr}} = \frac{{\mu c_{p} }}{k},\,{\text{Ec}} = \frac{{c^{2} }}{{c_{p} \left( {T_{1} - T_{0} } \right)}},\, \hfill \\ \theta = \frac{{T - T_{0} }}{{T_{1} - T_{0} }},\,\phi = \frac{{C - C_{0} }}{{C_{1} - C_{0} }},\,h = \frac{H}{a},\,{\text{Mn}}\, = \,\sqrt {\frac{\sigma }{\mu }} B_{0} a,\, \hfill \\ {\text{Nb}} = D_{B} \frac{{\left( {\rho c} \right)_{p} \left( {C_{1} - C_{0} } \right)}}{k},\,N = {\text{Ec}}\,{\text{Pr}}, \hfill \\ {\text{Gr}} = \frac{{\left( {1 - C_{0} } \right)g\beta \left( {T_{1} - T_{0} } \right)a^{2} }}{{\vartheta ^{2} }},\,G = \frac{{{\text{Gr}}}}{{{\text{Re}}}},\, \hfill \\ {\text{Nt}} = \frac{{\left( {\rho c} \right)_{p} \left( {T_{1} - T_{0} } \right)}}{{T_{0} k}},\,{\text{Br}} = \frac{{\left( {\rho _{f} - \rho _{{f_{0} }} } \right)\left( {C_{1} - C_{0} } \right)g\beta ^{ * } a^{2} }}{{\mu c}} \hfill \\ \end{gathered}\).

Substituting the consecutive equation of Jeffery fluid (8) and applying the above dimensionless.

parameters, the basic Eqs. (3)–(5) and the boundary conditions (6) and (7) are simplified.

as follows:

$$\frac{1}{{1 + \lambda_{1} }}\frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }} + G\theta - {\text{Br}}\phi - {\text{Mn}}^{2} (u + 1) = \frac{{{\text{d}}p}}{{{\text{d}}x}}$$
(9)
$$\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}y^{2} }} + {\text{Nb}}\frac{{{\text{d}}\theta }}{{{\text{d}}y}}\frac{{{\text{d}}\phi }}{{{\text{d}}y}} + {\text{Nt}}\left( {\frac{{{\text{d}}\theta }}{{{\text{d}}y}}} \right)^{2} + N\left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} + N{\text{Mn}}^{2} \left( {u + 1} \right)^{2} = 0$$
(10)
$$\frac{{{\text{d}}{}^{2}\phi }}{{{\text{d}}y^{2} }} + \frac{{{\text{Nt}}}}{{{\text{Nb}}}}\frac{{{\text{d}}{}^{2}\theta }}{{{\text{d}}y^{2} }} = 0$$
(11)

Similarly, the constructed boundary assumptions are

$$\frac{{{\text{d}}u}}{{{\text{d}}y}} = 0,\,\frac{{{\text{d}}\theta }}{{{\text{d}}y}} = 0,\,\frac{{{\text{d}}\phi }}{{{\text{d}}y}} = 0\,{\text{at}}\,y = 0$$
(12)
$$u + \alpha_{1} \frac{{{\text{d}}u}}{{{\text{d}}y}} = - 1,\,\theta + \alpha_{2} \frac{{{\text{d}}\theta }}{{{\text{d}}y}} = 1,\,\phi + \alpha_{3} \frac{{{\text{d}}\phi }}{{{\text{d}}y}} = 1\;{\text{at}}\,y = h$$
(13)

3 Solution methodology

Equations (9)–(11) are coupled and nonlinear equations, and it is difficult to get the solution by analytical methods. The constituted equations are treated analytically with the appliance of perturbation method (Nayfeh 1973). Here, \(N = {\text{Ec}}\,{\text{Pr}}\) is preferred to be perturbation parameter since the value of \({\text{N}}\) is small in almost all applied obstacles. To employ the perturbation technique, we propose the following series assumptions by keeping the value of parameter \({\text{N}}\) very small.

$$\left( {u,\theta ,\phi ,\frac{{{\text{d}}p}}{{{\text{d}}x}}} \right) = \sum\limits_{n = 0}^{\infty } {N^{n} \left( {u_{n} ,\theta_{n} ,\phi_{n} ,\frac{{{\text{d}}p_{n} }}{{{\text{d}}x}}} \right)}$$
(14)

Here,\(\left( {u_{0} ,\theta_{0} ,\phi_{0} ,\frac{{{\text{d}}p_{0} }}{{{\text{d}}x}}} \right)\) be the known solution to the exactly solvable initial problem and \(\left( {u_{1} ,\theta_{1} ,\phi_{1} ,\frac{{{\text{d}}p_{1} }}{{{\text{d}}x}}} \right)\),\(\left( {u_{2} ,\theta_{2} ,\phi_{2} ,\frac{{{\text{d}}p_{2} }}{{{\text{d}}x}}} \right)\) are higher-order terms. For smaller N, these higher-order terms are successively smaller. Hence, a suitable perturbation solution is obtained by truncating the series, typically by keeping only the first two terms. i.e. upto first-order series solution is sufficient to capture the physical insight since the higher order terms in the perturbation series solution are successively smaller for smaller values of the chosen perturbation parameter N. With the aid of the above relation (14), Eqs. (9)–(11) and perturbed boundary assumptions are expressed in the system of expressions at zeroth and first order).

3.1 Zeroth-order system (N0)

$$\frac{1}{{1 + \lambda_{1} }}\frac{{{\text{d}}^{2} u_{0} }}{{{\text{d}}y^{2} }} + G\theta_{0} - {\text{Br}}\phi_{0} - {\text{Mn}}^{2} (u_{0} + 1) = \frac{{{\text{d}}p_{0} }}{{{\text{d}}x}}$$
(15a)
$$\frac{{{\text{d}}^{2} \theta_{0} }}{{{\text{d}}y^{2} }} + {\text{Nb}}\frac{{{\text{d}}\theta_{0} }}{{{\text{d}}y}}\frac{{{\text{d}}\phi_{0} }}{{{\text{d}}y}} + {\text{Nt}}\left( {\frac{{{\text{d}}\theta_{0} }}{{{\text{d}}y}}} \right)^{2} = 0$$
(15b)
$$\frac{{{\text{d}}{}^{2}\phi_{0} }}{{{\text{d}}y^{2} }} + \frac{{{\text{Nt}}}}{{{\text{Nb}}}}\frac{{{\text{d}}{}^{2}\theta_{0} }}{{{\text{d}}y^{2} }} = 0$$
(15c)

Similarly, conditions at the surface are constructed into following form

$$\frac{{{\text{d}}u_{0} }}{{{\text{d}}y}} = 0,\,\,\frac{{{\text{d}}\theta_{0} }}{{{\text{d}}y}} = 0,\,\,\frac{{{\text{d}}\phi_{0} }}{{{\text{d}}y}} = 0\,\;{\text{at}}\,\,y = 0$$
(16a)
$$u_{0} + \alpha_{1} \frac{{{\text{d}}u_{0} }}{{{\text{d}}y}} = - 1,\,\,\theta_{0} + \alpha_{2} \frac{{{\text{d}}\theta_{0} }}{{{\text{d}}y}} = 1,\,\,\phi_{0} + \alpha_{3} \frac{{{\text{d}}\phi_{0} }}{{{\text{d}}y}} = 1\;{\text{at}}\,\,y = h\,$$
(16b)

3.2 First-order approximation (N1)

$$\frac{1}{{1 + \lambda_{1} }}\frac{{{\text{d}}^{2} u_{1} }}{{{\text{d}}y^{2} }} - {\text{Mn}}^{2} (u_{1} + 1) + G\theta_{1} - {\text{Br}}\phi_{1} = \frac{{{\text{d}}p_{1} }}{{{\text{d}}x}}$$
(17a)
$$\frac{{{\text{d}}^{2} \theta_{1} }}{{{\text{d}}y^{2} }} + Nb\left( {\frac{{{\text{d}}\theta_{0} }}{{{\text{d}}y}}\frac{{{\text{d}}\phi_{1} }}{{{\text{d}}y}} + \frac{{{\text{d}}\theta_{1} }}{{{\text{d}}y}}\frac{{{\text{d}}\phi_{0} }}{{{\text{d}}y}}} \right) + 2{\text{Nt}}\frac{{{\text{d}}\theta_{0} }}{{{\text{d}}y}}\frac{{{\text{d}}\theta_{1} }}{{{\text{d}}y}} + \left( {\frac{{{\text{d}}u_{0} }}{{{\text{d}}y}}} \right)^{2} + {\text{Mn}}^{2} \left( {u_{0} + 1} \right)^{2} = 0$$
(17b)
$$\frac{{{\text{d}}{}^{2}\phi_{1} }}{{{\text{d}}y^{2} }} + \frac{{{\text{Nt}}}}{{{\text{Nb}}}}\frac{{{\text{d}}{}^{2}\theta_{1} }}{{{\text{d}}y^{2} }} = 0$$
(17c)

The corresponding boundary conditions are

$$\frac{{{\text{d}}u_{1} }}{{{\text{d}}y}} = 0,\,\,\frac{{{\text{d}}\theta_{1} }}{{{\text{d}}y}} = 0,\,\,\frac{{{\text{d}}\phi_{1} }}{{{\text{d}}y}} = 0\,\,\,{\text{at}}\,\,y = 0$$
(18a)
$$u_{1} + \alpha_{1} \frac{{{\text{d}}u_{1} }}{{{\text{d}}y}} = 0,\,\,\theta_{1} + \alpha_{2} \frac{{{\text{d}}\theta_{1} }}{{{\text{d}}y}} = 0,\,\,\phi_{1} + \alpha_{3} \frac{{{\text{d}}\phi_{1} }}{{{\text{d}}y}} = 0\,\;{\text{at}}\,\,y = h\,$$
(18b)

On solving Eq. (15a) to (15c) using the boundary conditions (16a) and (16b), we get

$$u_{0} \, = \,A_{3} {\text{cos}}h\left( {\sqrt {A_{1} } y} \right) + \frac{{\frac{{{\text{d}}p_{0} }}{{{\text{d}}x}} - G - {\text{Br}}}}{{{\text{Mn}}^{2} }} - 1$$
(19a)
$$\theta_{0} \, = \,1$$
(19b)
$$\phi_{0} \, = \,1$$
(19c)

On solving Eq. (17a) to (17c) using the boundary conditions (18a) and (18b), we get

$$u_{1} \, = \,\left( \begin{gathered} \left( {1 + \lambda_{1} } \right)A_{7} \left( {\frac{{A_{4} }}{{3A_{1}^{2} }}} \right.\left( {\left. {\frac{{A_{3} A_{1} }}{{A_{2} }}\cos h\left( {\sqrt {A_{1} } y} \right){\text{cos}}h\left( {2\sqrt {A_{1} } h} \right) - {\text{cos}}h\left( {2\sqrt {A_{1} } y} \right)} \right)} \right. + \hfill \\ \frac{{2A_{5} }}{{A_{1}^{2} }}\left( {\frac{{A_{3} A_{1} }}{{A_{2} }}\cos h\left( {\sqrt {A_{1} } y} \right)\,h{\text{sin}}h\left( {\sqrt {A_{1} } h} \right) - y\sin h\left( {\sqrt {A_{1} } y} \right)} \right) + A_{9} \left. {\left( {\frac{{A_{3} A_{1} }}{{A_{2} }}} \right.\cos h\left( {\sqrt {A_{1} } y} \right) - 1} \right) \hfill \\ - \,\frac{{A_{6} }}{{2A_{1} }}\left( {y^{2} - h^{2} } \right) + \alpha_{1} \left( {\frac{{A_{3} A_{1} }}{{A_{2} }}} \right.\cos h\sqrt {A_{1} } y\left( {\frac{{2A_{4} \sqrt {A_{1} } }}{{3A_{1}^{2} }}} \right.\sin h\left( {2\sqrt {A_{1} } h} \right) + \frac{{A_{6} h}}{{A_{1} }} + \hfill \\ \frac{{2A_{5} }}{{A_{1}^{2} }}\left. {\left. {\left. {\left. {\left( {\sqrt {A_{1} } } \right.h\cos h\left( {\sqrt {A_{1} } h} \right) + \sin h\left( {\sqrt {A_{1} } h} \right)} \right)} \right)} \right) - \frac{{{\text{d}}p_{1} }}{{{\text{d}}x}}} \right) \hfill \\ \end{gathered} \right)$$
(20a)
$$\theta_{1} \, = \,\left( \begin{gathered} \frac{{A_{4} }}{{4A_{1} }}\left( {{\text{cos}}h\left( {2\sqrt {A_{1} } h} \right) - {\text{cos}}h\left( {2\sqrt {A_{1} } y} \right)} \right) + \frac{{A_{5} }}{{A_{1} }}\left( {{\text{cos}}h\left( {\sqrt {A_{1} } h} \right) - {\text{cos}}h\left( {\sqrt {A_{1} } y} \right)} \right) + \hfill \\ \frac{{A_{6} }}{2}\left( {y^{2} - h^{2} } \right) + \alpha_{2} \left( {\frac{{A_{4} }}{{2\sqrt {A_{1} } }}{\text{sin}}h\left( {2\sqrt {A_{1} } h} \right) + \frac{{A_{5} }}{{\sqrt {A_{1} } }}{\text{sin}}h\left( {\sqrt {A_{1} } h} \right) - A_{6} h} \right) \hfill \\ \end{gathered} \right)$$
(20b)
$$\phi_{1} \, = - \frac{{{\text{Nt}}}}{{{\text{Nb}}}}\,\left( \begin{gathered} \frac{{A_{4} }}{{4A_{1} }}\left( {{\text{cos}}h\left( {2\sqrt {A_{1} } h} \right) - {\text{cos}}h\left( {2\sqrt {A_{1} } y} \right)} \right) + \frac{{A_{5} }}{{A_{1} }}\left( {{\text{cos}}h\left( {\sqrt {A_{1} } h} \right) - {\text{cos}}h\left( {\sqrt {A_{1} } y} \right)} \right) \hfill \\ + \frac{{A_{6} }}{2}\left( {y^{2} - h^{2} } \right) + \alpha_{3} \left( {\frac{{A_{4} }}{{2\sqrt {A_{1} } }}{\text{sin}}h\left( {2\sqrt {A_{1} } h} \right) + \frac{{A_{5} }}{{\sqrt {A_{1} } }}{\text{sin}}h\left( {\sqrt {A_{1} } h} \right) - A_{6} h} \right) \hfill \\ \end{gathered} \right)$$
(20c)

The expressions for wall shear stress, heat transfer rate (Nusselt number) and mass transfer rate (Sherwood number) are attributed in forms:

$$C_{f} = \left. { - h^{\prime}\frac{{{\text{d}}^{2} \psi }}{{{\text{d}}y^{2} }}} \right|_{y = h}$$
(21)
$${\text{Nu}} = - \left. {h^{\prime}\frac{{{\text{d}}\theta }}{{{\text{d}}y}}} \right|_{y = h}$$
(22)
$${\text{Sh}} = - \left. {h^{\prime}\frac{{{\text{d}}\phi }}{{{\text{d}}y}}} \right|_{y = h}$$
(23)

In above reported relations, \(h^{\prime} = m - \frac{{2{\uppi }\varepsilon }}{\lambda }{\text{sin}}\left[ {\frac{{2{\uppi }}}{\lambda }\left( {x - t} \right)} \right]\) while stream function \(\left( \psi \right)\) is justified as

$$u = \frac{{{\text{d}}\psi }}{{{\text{d}}y}}$$
(24)

The relation between mean flow \(\left( \Theta \right)\) associated in some fixed ordinates and \(F\) which is related to moving reference is denoted via \(\Theta = F + 1\) where

$$F = \int\limits_{0}^{h} {u\,{\text{d}}y}$$
(25)

i.e.

$$F_{0} = \frac{h}{{{\text{Mn}}{}^{2}}}\frac{{{\text{d}}p_{0} }}{{{\text{d}}x}} - \frac{{A_{3} }}{{\sqrt {A_{1} } }}\sinh \sqrt {A_{1} } y - \frac{{h\left( {{\text{G}} - {\text{Br}} + {\text{Mn}}{}^{2}} \right)}}{{{\text{Mn}}{}^{2}}}$$
(26a)
$$\begin{aligned} F_{1} = & - A_{7} h\left( {1 + \lambda _{1} } \right){\text{ }}\frac{{{\text{d}}p_{1} }}{{{\text{d}}x}} \\ & \quad + \frac{1}{{3A_{1} ^{3} A^{2} {\text{ }}}}A_{7} \left( {1 + \lambda _{1} } \right)\left( {A_{{10}} + \alpha _{1} A_{{11}} + A_{{12}} + A_{{13}} } \right) \\ \end{aligned}$$
(26b)

Solving Eqs. (26a) and (26b) for \(\frac{{{\text{d}}p_{0} }}{{{\text{d}}x}}\) and \(\frac{{{\text{d}}p_{1} }}{{{\text{d}}x}}\), respectively, yields

$$\frac{{{\text{d}}p_{0} }}{{{\text{d}}x}} = \left( {\Theta_{0} - 1 + \frac{{A_{3} }}{{\sqrt {A_{1} } }}\sinh \sqrt {A_{1} } y + \frac{{h\left( {{\text{G}} - {\text{Br}} + {\text{Mn}}{}^{2}} \right)}}{{{\text{Mn}}{}^{2}}}} \right)\frac{{{\text{Mn}}{}^{2}}}{h}$$
(27a)
$$\frac{{{\text{d}}p_{1} }}{{{\text{d}}x}} = \frac{1}{{A_{7} h\left( {1 + \lambda_{1} } \right)}}\left( {\frac{1}{{3A_{1}^{3} A^{2} \, }}A_{7} \left( {1 + \lambda_{1} } \right)\left( {A_{10} + \alpha_{1} A_{11} + A_{12} + A_{13} } \right) - \Theta_{1} } \right)$$
(27b)

The dimensionless pressure at both zeroth and first order is utilizing via following relations

$$\Delta p_{0} = \int\limits_{0}^{1} {\frac{{{\text{d}}p_{0} }}{{{\text{d}}x}}} dx,\;\Delta p_{1} = \int\limits_{0}^{1} {\frac{{{\text{d}}p_{1} }}{{{\text{d}}x}}} {\text{d}}x$$

4 Graphical results and deliberations

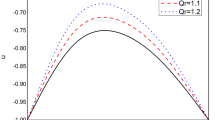
The purpose of the current section is to explicate the behavior of pertinent parameters on different physiological quantities for Newtonian and non-Newtonian Jeffery fluid with the aid of graphs. The value of λ1 is fixed for Newtonian fluid (λ1 = 0) and Jeffery fluid (λ1 = 0.1). It is remarked that each physical parameter assigns some numerical values while remaining parameters kept fixed like Mn = 0.1, Nb = 0.01, Nt = 0.01, λ1 = 0.1, λ = 0.01, t = 0.1, Gr = 0.1, c = 0.01, N = 0.1, Br = 0.1, α1 = 0.01, α2 = 0.01, α3 = 0.1, E1 = 0.1, E2 = 0.04, E3 = 0.4, E4 = 0.02, E5 = 0.01, є = 1. The trapping phenomena for the pertinent parameter also deliberated. It is motivated to grasp the noteworthy variations between linear and nonlinear fluid materials. The graphical observations reveal that variation in temperature and velocity distributions are lower for Jeffrey fluid when compared with viscous case; however, concentration displays the contradictory trend. Figure 2 parades the validation results for velocity, temperature and concentration of the fluid flow for the current study with Srinivas et al. (Srinivas et al. 2018). It is identified that the present results are agreed with the results of Srinivas et al. (Srinivas et al. 2018).

Fig. 2
figure 2

Validation graphs for a velocity, b temperature and c concentration profile

Full size image

4.1 Velocity Profile

This subsection aims to deliberate the effects of \({\text{Mn,}}\,\alpha_{1} {,}\,{\text{Nt,}}\,\,{\text{Nb,}}\,{\text{Gr,}}\,\,{\text{Br,}}\,{\text{N,}}\,m\) on the velocity distributions, which are perceived in Figs. 3a–h, respectively. It is witnessed from the graphs that parabolic nature for distribution of velocity is obtained. Further, a leading velocity variation at the channel center is also searched out efficiently. The outcomes of the magnetic field Mn on the velocity component are portrayed by preparing as shown in Fig. 3a. A peak variation in velocity is noticed due to declining numerical values of Mn. Physical aspects for current observations are attributed to the involvement of Lorentz force, which resists the magnetic field. The enhancement of the velocity profile, along with the enhancement of the slip parameter α1, is shown in Fig. 3b. The effect of the Brownian motion constant Nb on fluid velocity is portrayed in Fig. 3c from which it is clear that velocity shrinks with increment in the value of Nb. The influence of local nanoparticle Grashof number Br on the velocity is illustrated in Fig. 3d. The observations notified here that leading values of Br are associated with maximum velocity. A hiking distribution of velocity is attributed due to the thermophoresis parameter Nt which is rendered in Fig. 3e. Due to the non-uniform trend associated with nanoparticles, the concentration boosts up while considering the thermophoresis, which enhances the velocity. The characteristic of Gr on velocity is depicted in Fig. 3f. A reduction in particle velocity is seen due to Gr. The Grashof number is associated with buoyancy force and thermal impact which results in such declining distribution. The impact of the perturbation parameter on the velocity shape is demonstrated in Fig. 3g. At this instant, analysis reveals that the expansion of the perturbation parameter N hikes the velocity of a fluid. The plot of non-uniformity constant m on velocity is shown in Fig. 3h. A reverse trend is noticed at the narrow and deviating channel. Increasing velocity is noted deviating channel while the lower trend is seen at the narrow channel.

Fig. 3
figure 3

Distribution of velocity for a Mn b α1 c Nb d Br e Nt f Gr g N h m

Full size image

4.2 Temperature profile

Temperature variation with relevant parameters of fluid is portrayed in Fig. 4a–f. Like velocity profiles, temperature profiles also show the parabolic nature of the graph with maximum temperature occurring at the center. Figure 4a is plotted to demonstrate the variation of temperature slip α2 escalating value of α2 on the temperature distribution. The prepared results evident that it escalates the temperature profile. From Fig. 4b, it is illustrated that temperature falls off with raising variation of magnetic field parameter Mn. The results for perturbation constant N are confined in Fig. 4c, which reveals conflicting results. An intensifying trend in temperature is shown in Fig. 4d where the impact of Gr is considered. A progressive temperature gradient is confined to the assigned maximum values of Gr which improve the heat transfer rate. The graphical observations intended in Fig. 4e report the output of the local nanoparticle Grashof number Br. It is perceptibly noticed that temperature declines with increasing values of local nanoparticle Grashof number Br. The curve 4f is executed to examine the altered temperature distribution when m assigns leading numerical values. Interestingly, two major reverse observations result in deviating and narrow part of the channel. The temperature reached a maximum level in the deviating region in contrast to the narrow region where the heat transfer rate is relatively slower.

Fig. 4
figure 4

Distribution of temperature for a α2 b Mn c N d Gr e Br f m

Full size image

4.3 Concentration profile

Now we examine the impact of pertinent parameters on concentration distribution ϕ by exploiting Fig. 5a–h. Alike velocity and temperature profiles ϕ, concentration profile ϕ as well shows parabolic nature of the graph. Figure 5a evaluates the variation of concentration slip α3. An effective demising change in ϕ is obtained with the impact of concentration slip α3. From Fig. 4b, again, a declining trend in ϕ has been claimed due to maximum values of magnetic field constant Mn. Figure 5c and d epitomizes the significance of Nb and Br, respectively. A hiked distribution of ϕ is thrashed out due to both Nb and Br. The graphical observations for ϕ due to a higher variation of thermophoresis parameter Nt and Grashof number Gr are suggested in Fig. 5e and f. The results show that increment in thermophoresis parameter Nt and Grashof number Gr declines the profile of ϕ in vertical part of the channel. Further, observations search out from Fig. 5g reveal that enhancing the values of the perturbation parameter N declines the concentration of the fluid. The impact of the non-uniformity parameter m on ϕ is evaluated in Fig. 5h. The mass flow rate is minimum in deviating part of the channel as compared to the narrow channel region.

Fig. 5
figure 5

Distribution of concentration for a α3b Mn c Nb d Br e Nt f Gr g N h m

Full size image

4.4 Impact of physical quantities

A real fluid while flowing in the channel progresses shear stress, rate of heat transfer and rate of mass transfer on the walls of the channel. Hence, this subsection deals with the distribution of (shear stress) skin-friction coefficient, (heat transfer rate) Nusselt number and (mass transfer rate) Sherwood number for the diverse values of various physical constants. The appliances of Mn, m, N, Nt, Nb on wall shear stress, Nusselt and Sherwood numbers are structured via Figs. 6, 7, 8, 9, 10. The curves show that both wall shear stress and Nusselt number display a similar trend, but Sherwood number displays a conflicting trend. The observations find out here reveal that the skin-friction coefficient and Nusselt number of Newtonian fluids are sophisticated than the Jeffery fluid, but Sherwood number shows the contrary trend. The effect of the magnetic field parameter Mn is seen in Fig. 6. It is perceived that a decrease in Mn rises wall shear force and Nusselt number while the contrary trend has been noted in Sherwood number. Further, the effects of non-uniform parameter m and perturbation parameter N on skin-friction, Nusselt and Sherwood physical quantities are sketched by preparing Figs. 7,8. Both physical quantities get increasing behavior for growing values of m and N, whereas Sherwood number shows a converse trend. The effect of thermophoresis parameter Nt and Brownian motion parameter Nb on skin-friction coefficient and Sherwood number is depicted in Figs. 9–10. It manifests from the figures that the rise in the thermophoresis parameter Nt raises the skin-friction coefficient, but the decline in Brownian motion parameter Nb raises the skin-friction coefficient, whereas opposite behavior is observed for Sherwood number for both thermophoresis parameter Nt and Brownian parameter Nb.

Fig. 6
figure 6

Variation in a wall shear stress, b Nusselt number and c Sherwood number for Mn

Full size image
Fig. 7
figure 7

Variation in a wall shear stress, b Nusselt number and c Sherwood number for m

Full size image
Fig. 8
figure 8

Variation in a wall shear stress, b Nusselt number and c Sherwood number for N

Full size image
Fig. 9
figure 9

Variation in a Skin-friction coefficient and b Sherwood number with variation of Nt

Full size image
Fig. 10
figure 10

Variation in a wall shear stress and b Sherwood number with variation of Nb

Full size image

4.5 Pumping characteristics

Peristaltic pumping procedure is exercised to conveyance numerous biotic fluids in diagnostic problems to scrutinize the pumping characteristics. Pumping action is because of the dynamic pressure employed by the walls on the fluid surrounded between the contraction region. Pumping characteristics are defined by the variation in the pressure rise contrary to the time averaged flow rate. It is found that the relation between pressure rise in contrast to the time averaged flow rate is linear and inversely proportional to each other. The variations of pressure rise versus mean flow for different values of physical parameters are illustrated in Fig. 11a–f. The pressure rise shows a declining trend with mean flow, and it is also seen that Jeffery fluid has more pressure than Newtonian fluid. The increase in the values of the magnetic field parameter Mn, non-uniform parameter m, local nanoparticle Grashof number Br and velocity slip parameter α1 increases the pressure rise which is observed in Fig. 11a–d but the opposite trend is seen in Grashof number Gr and perturbation parameter N which is depicted in 11e–f.

Fig. 11
figure 11

Pressure rise verses mean flow with impact of a Mn b m c Br d α1 e Gr f N

Full size image

4.6 Trapping phenomena

An inimitable hydrodynamic property accompanying to peristaltic mechanism is trapping phenomena that occasionally occur when subjected to a large amplitude ratio. In the laboratory frame, the set of streamlines represents a fluid bolus moving with and within the wave, and while streamlines bypass the trapped bolus, they attain the shape like that of the wall’s shape. And also, the boluces are periodic in nature that are noticed in the Figs. 12, 13, 14, 15, 16, 17, 18. Figure 12 is to analyze the effect of the magnetic field parameter Mn on the trapped bolus. Through the figure, it manifests that the size of the trapped bolus diminishes, and the boluses decline on cumulative values of the magnetic field parameter Mn for weak streamlines circulations. Thus, the magnetic field force can be operated to control the bolus formations. The effect of the Jeffery parameter λ1 and Br is depicted in Figs. 13 and 14, respectively. The rise in the Jeffery parameter α1 and Br declines trapped bolus size. Conflicting behavior is observed in non-uniform parameter m, velocity slip parameter α1, perturbation parameter N, Grashof number Gr; i.e., increase in non-uniform parameter, velocity slip parameter, perturbation parameter, Grashof number increases the size of bolus which is portrayed in Figs. 15 and 18, respectively.

Fig. 12
figure 12

Streamlines with variation of Mn

Full size image
Fig. 13
figure 13

Streamlines with variation of λ1

Full size image
Fig. 14
figure 14

Streamlines with variation of Br

Full size image
Fig. 15
figure 15

Streamlines with variation of m

Full size image
Fig. 16
figure 16

Streamlines with variation of α1

Full size image
Fig. 17
figure 17

Streamlines with variation of N

Full size image
Fig. 18
figure 18

Streamlines for different values of Gr

Full size image

5 Conclusion

The present manuscript emphasizes on the peristalsis of Jeffrey nanofluid when subjected to multiple slip effects. The findings of the model help to examine the movement of chyme in the gastrointestinal tract. Further, it helps the doctors during the surgery to take control of the flow of blood by adjusting the magnetic field intensity. Also, the present study finds its application in designing the dialysis machine, roller-finger pumps, heart–lung machine, etc. The important finds of the model are as follows:

  • The velocity and thermal slip parameters enhance the velocity profiles, whereas the contrary behavior is noticed for the concentration slip parameter.

  • The magnetic parameter is a decreasing function of velocity and temperature.

  • The velocity and concentration profiles show the decreasing behavior for Grashof number.

  • The reducing values of magnetic constants improve the wall shear stress and Nusselt number while the impact of this parameter of Sherwood number is opposite.

  • The increase in the values of the magnetic field parameter, non-uniform parameter, local nanoparticle Grashof number and velocity slip parameter increases the pressure rise.

  • A reduced bolus size has been noticed when local nanoparticles Grashof constant and Jeffery parameter get leading values.