1 Introduction

Researchers have devoted their interest over the years, towards investigating the bound state solutions of nonrelativistic wave equations for different potentials [1, 2]. A few of these potentials have been solved exactly [3], while others can only be solved approximately [4,5,6,7,8,9,10], with the use of different approximation schemes [11,12,13]. Also, different methods have been employed to obtain the solutions of the nonrelativistic wave equations with a chosen potential model. These include the factorization method [14], functional analysis approach [15,16,17], supersymmetry quantum mechanics (SUSYQM) [18,19,20,21], asymptotic iteration method (AIM) [22, 23], algebraic approach [24], exact and proper quantization rules [25, 26], Laplace transformation [27], Nikiforov–Uvarov method (NU) [28,29,30,31,32,33,34], and others.

The Kratzer potential [35] is mostly applied in atomic physics, molecular physics, and quantum chemistry [36]. It is used to describe the interactions of molecular structure in quantum mechanics. The Kratzer potential is made up of a long-range attraction and a repulsive part. The integration of these parts makes this potential reliable in terms of its vibrational and rotational energy eigenvalues [37, 38]. The Kratzer potential is known to approach infinity when the internuclear distance approaches zero, due to the repulsion that exist between the molecules of the potential. As the internuclear molecular distance approaches infinity, the potential decomposes to zero [39, 40].

The screened Coulomb potential, which is also known as the Yukawa potential, is greatly important with applications cutting across nuclear physics and condensed matter physics [41]. The screened Coulomb potential is used mostly in short-range interactions [42,43,44]. The screened Coulomb potential is known to be the potential of a charged particle in a weakly non-ideal plasma. It also describes the charged particle effects in a sea of conduction electrons in solid-state physics [45].

Recently, Bayrak et al. [38] have presented an exact analytical solution of the radial Schrodinger equation for the Kratzer potential using the asymptotic iteration method (AIM). The exact bound state energy eigenvalues (Enl) and corresponding eigenfunctions (Rnl) were calculated for various values of n and l quantum numbers for selected diatomic molecules. In another development, a noncentral modified Kratzer potential was considered and the solutions of the Schrodinger equation obtained using the factorization method [36]. An approximate solution of the Schrodinger equation interacting with an inversely quadratic Yukawa potential was obtained using SUSYQM [46], where the screened Coulomb potential was obtained as a special case by varying the potential strength. Also, an approximate analytical solution of the radial Schrodinger equation for the screened Coulomb potential was obtained, with energy eigenvalues and its corresponding eigenfunctions computed in closed forms [47]. With the above-mentioned studies on these different potentials and their lofty importance, we seek to investigate the bound state solutions of the Schrodinger equation with the combined modified Kratzer and screened Coulomb potential of the form:

$$ V(r) = D_{\text{e}} \left( {\frac{{r - r_{\text{e}} }}{r}} \right)^{2} - \frac{{Ae^{ - \alpha \,r} }}{r} $$
(1)

where De is the dissociation energy, re is the equilibrium internuclear separation, A is the depth of the potential, and α is the range of the potential. It can be deduced that when De = 0, the above combined potential reduces to the screened Coulomb potential. When De = 0 and \( \alpha \to 0 \), the potential of Eq. 1 reduces to the Coulomb potential. Also, when A = 0, Eq. 1 reduces to the modified Kratzer potential. Using the conventional NU method, we derive the \( \ell - \) wave bound state solutions and their eigenfunctions of the Schrodinger equation for the modified Kratzer potential plus screened Coulomb potential, analytically and numerically. Special cases are also considered, and our results are compared with existing literatures for confirmation sake.

2 Bound state solution

The radial Schrodinger equation is given as [48]:

$$ \frac{{{\text{d}}^{2} R_{n\ell } (r)}}{{{\text{d}}r^{2} }} + \frac{2\mu }{{\hbar^{2} }}\left[ {E_{nl} - V(r) - \frac{{\ell (\ell + 1)\hbar^{2} }}{{2\mu r^{2} }}} \right]R_{n\ell } (r) = 0 $$
(2)

where \( \mu \) is the reduced mass, \( E_{nl} \) is the rotational–vibrational energy spectra of the diatomic molecules, \( \hbar \) is the reduced Planck’s constant, and n and ℓ are the radial and orbital angular momentum quantum numbers, respectively (or vibration–rotation quantum numbers in quantum chemistry) [49]. Substituting Eq. (1) into Eq. (2) gives:

$$ \frac{{{\text{d}}^{2} R_{n\ell } (r)}}{{{\text{d}}r^{2} }} + \left[ {\frac{{2\mu E_{nl} }}{{\hbar^{2} }} - \frac{{2\mu D_{\text{e}} }}{{\hbar^{2} }} + \left( {\frac{{4\mu D_{\text{e}} r_{\text{e}} }}{{\hbar^{2} }}} \right)\left( {\frac{1}{r}} \right) - \left( {\frac{{2\mu D_{\text{e}} r_{\text{e}}^{2} }}{{\hbar^{2} }}} \right)\left( {\frac{1}{{r^{2} }}} \right) + \frac{2\mu A}{{\hbar^{2} }}\left( {\frac{{e^{ - \alpha \,r} }}{r}} \right) - \frac{\ell (\ell + 1)}{{r^{2} }}} \right]R_{n\ell } (r) = 0. $$
(3)

We employ the approximation scheme to get rid of the centrifugal barrier as [50]

$$ \frac{1}{{r^{2} }} \approx \frac{{\alpha^{2} }}{{\left( {1 - e^{ - \alpha \,r} } \right)^{2} }} $$
(4)
$$ \frac{1}{r} \approx \frac{\alpha }{{\left( {1 - e^{ - \alpha \,r} } \right)}} $$
(5)

Sustituting Eqs. (4) and (5) into Eq. (3), we have

$$ \frac{{{\text{d}}^{2} R_{n\ell } (r)}}{{{\text{d}}r^{2} }} + \left[ \begin{aligned} \frac{2\mu }{{\hbar^{2} }}\left( {E_{nl} - D_{\text{e}} } \right) + \left( {\frac{{4\mu D_{\text{e}} r_{\text{e}} }}{{\hbar^{2} }}} \right)\left( {\frac{\alpha }{{1 - e^{ - \alpha \,r} }}} \right) - \left( {\frac{{2\mu D_{\text{e}} r_{\text{e}}^{2} }}{{\hbar^{2} }}} \right)\left( {\frac{{\alpha^{2} }}{{\left( {1 - e^{ - \alpha \,r} } \right)^{2} }}} \right) \hfill \\ + \frac{2\mu A}{{\hbar^{2} }}\left( {\frac{{\alpha e^{ - \alpha \,r} }}{{1 - e^{ - \alpha \,r} }}} \right) - \frac{{\alpha^{2} \ell (\ell + 1)}}{{\left( {1 - e^{ - \alpha \,r} } \right)^{2} }} \hfill \\ \end{aligned} \right]R_{n\ell } (r) = 0 $$
(6)

Equation (6) can be simplified into the form

$$ \frac{{{\text{d}}^{2} R_{n\ell } (r)}}{{{\text{d}}r^{2} }} + \frac{1}{{\left( {1 - e^{ - \alpha \,r} } \right)^{2} }}\left[ { - \varepsilon_{n} \left( {1 - e^{ - \alpha \,r} } \right)^{2} + \beta \left( {1 - e^{ - \alpha \,r} } \right) + \gamma e^{ - \alpha \,r} \left( {1 - e^{ - \alpha \,r} } \right) - \delta } \right]R_{n\ell } (r) = 0 $$
(7)

where

$$ \begin{aligned} \varepsilon_{n} & = - \frac{2\mu }{{\hbar^{2} \alpha^{2} }}\left( {E_{n\,\ell } - D_{\text{e}} } \right) \\ \beta & = \frac{{4\mu D_{\text{e}} r_{\text{e}} }}{{\hbar^{2} \alpha }} \\ \gamma & = \frac{2\mu A}{{\hbar^{2} \alpha }} \\ \delta & = \left( {\frac{{2\mu D_{\text{e}} r_{\text{e}}^{2} }}{{\hbar^{2} }} + \ell (\ell + 1)} \right) \\ \end{aligned} $$
(8)

By using the coordinate transformation

$$ s = e^{ - \alpha \,r} , $$
(9)

we obtain the differential equation of the form

$$ \frac{{{\text{d}}^{2} R_{n\,\ell } }}{{{\text{d}}s^{2} }} + \frac{(1 - s)}{s(1 - s)}\frac{{{\text{d}}R_{n\,\ell } }}{{{\text{d}}s}} + \frac{1}{{s^{2} (1 - s)^{2} }}\left[ { - \left( {\varepsilon_{n} + \gamma } \right)s^{2} + \left( {2\varepsilon_{n} + \gamma - \beta } \right)s - \left( {\varepsilon_{n} - \beta + \delta } \right)} \right]R_{n\,\ell } (s) = 0 $$
(10)

Comparing Eqs. (10) and (41) (see the appendix section), we have the following parameters

$$ \begin{aligned} \tilde{\tau }(s) & = 1 - s \\ \sigma (s) & = s(1 - s) \\ \tilde{\sigma }(s) & = - (\varepsilon_{n} + \gamma )s^{2} + (2\varepsilon_{n} + \gamma - \beta )s - (\varepsilon_{n} - \beta + \delta ) \\ \end{aligned} $$
(11)

Substituting these polynomials into Eq. (48), we obtain \( \pi (s) \) to be

$$ \pi (s) = - \frac{s}{2} \pm \sqrt {(a - k)s^{2} + (k + b)s + c} $$
(12)

where

$$ \begin{aligned} a & = \frac{1}{4} + \varepsilon_{n} + \gamma \\ b & = \beta - 2\varepsilon_{n} - \gamma \\ c & = \varepsilon_{n} - \beta + \delta \\ \end{aligned} $$
(13)

To find the constant k, the discriminant of the expression under the square root of Eq. (12) must be equal to zero. As such, we have that

$$ k \pm = - (2\delta - \beta - \gamma ) \pm 2\sqrt {\varepsilon_{n} - \beta + \delta } \sqrt {\left( {\frac{1}{4} + \delta } \right)} $$
(14)

Substituting Eq. (14) into Eq. (12) yields

$$ \pi (s) = - \frac{s}{2} \pm \left\{ {\begin{array}{*{20}l} {\left( {\sqrt {\varepsilon_{n} - \beta + \delta } - \sqrt {\frac{1}{4} + \delta } } \right)s - \sqrt {\varepsilon_{n} - \beta + \delta } ;} \hfill & {{\text{for}}\;\;k_{ + } = - (2\delta - \beta - \gamma ) + 2\sqrt {\varepsilon_{n} - \beta + \delta } \sqrt {\left( {\frac{1}{4} + \delta } \right)} } \hfill \\ {\left( {\sqrt {\varepsilon_{n} - \beta + \delta } - \sqrt {\frac{1}{4} + \delta } } \right)s + \sqrt {\varepsilon_{n} - \beta + \delta } ;} \hfill & {{\text{for}}\;\;k_{ - } = - (2\delta - \beta - \gamma ) - 2\sqrt {\varepsilon_{n} - \beta + \delta } \sqrt {\left( {\frac{1}{4} + \delta } \right)} } \hfill \\ \end{array} } \right. $$
(15)

From the knowledge of NU method, we choose the expression \( \pi (s)_{ - } \) in which the function \( \tau (s) \) has a negative derivative. This is given by

$$ \,\pi (s)_{ - } = - \left( {\frac{1}{2} + \sqrt {\varepsilon_{n} - \beta + \delta } - \sqrt {\left( {\frac{1}{4} + \delta } \right)} } \right)s - \sqrt {\varepsilon_{n} - \beta + \delta } $$
(16)

with \( \tau (s) \) being obtained as

$$ \tau (s) = 1 - 2s - 2\left( {\sqrt {\varepsilon_{n} - \beta + \delta } - \sqrt {\frac{1}{4} + \delta } } \right)s + 2\sqrt {\varepsilon_{n} - \beta + \delta } $$
(17)

Referring to Eq. (49), we define the constant \( \lambda \) as

$$ \lambda = - (2\delta - \beta - \gamma ) - 2\sqrt {\varepsilon_{n} - \beta + \delta } \sqrt {\left( {\frac{1}{4} + \delta } \right)} - \frac{1}{2} - \left( {\sqrt {\varepsilon_{n} - \beta + \delta } - \sqrt {\frac{1}{4} + \delta } } \right) $$
(18)

Substituting Eq. (18) into Eq. (50) and carrying out simple algebra, where

$$ \tau^{\prime}(s) = - 2 - 2\left( {\sqrt {\varepsilon_{n} - \beta + \delta } - \sqrt {\frac{1}{4} + \delta } } \right) $$
(19)

and

$$ \sigma^{\prime\prime}(s) = - 2 $$
(20)

We have

$$ \varepsilon_{n} = - \delta + \beta + \frac{1}{4}\left[ {\frac{{ - \gamma - \beta + \delta + \left( {n + \zeta } \right)^{2} }}{(n + \zeta )}} \right]^{2} $$
(21)

where

$$ \zeta = \frac{1}{2}\left( {1 + \sqrt {1 + 4\delta } } \right) $$
(22)

Substituting Eqs. (8) and  (22) into Eq. (21) yields the energy eigenvalue equation of the modified Kratzer potential plus screened Coulomb potential in the form

$$ E_{n\,\ell } = \frac{{\hbar^{2} \alpha^{2} }}{2\mu }\left[ {\frac{{2\mu D_{\text{e}} r_{\text{e}}^{2} }}{{\hbar^{2} }} + \ell (\ell + 1) - \frac{{4\mu D_{\text{e}} r_{\text{e}} }}{{\hbar^{2} \alpha }}} \right] + D_{\text{e}} - \frac{{\hbar^{2} \alpha^{2} }}{2\mu }\left[ {\frac{{\left( {n + \zeta } \right)}}{2} + \frac{{\frac{{2\mu D_{\text{e}} r_{\text{e}}^{2} }}{{\hbar^{2} }} + \ell (\ell + 1) - \left( {\frac{{4\mu D_{\text{e}} r_{\text{e}} + 2\mu A}}{{\hbar^{2} \alpha }}} \right)}}{{2\left( {n + \zeta } \right)}}} \right]^{2} $$
(23)

The corresponding wave functions can be evaluated by substituting \( \pi (s)_{ - } \,\,{\text{and}}\,\,\sigma (s) \) from Eqs. (15) and (11), respectively, into Eq. (44) and solving the first-order differential equation. This gives

$$ \varPhi (s) = s^{{\sqrt {\varepsilon_{n} + \delta } }} (1 - s)^{{\frac{1}{2} + \sqrt {\frac{1}{4} + \beta + \delta } }} $$
(24)

The weight function \( \rho (s) \) from Eq. (46) can be obtained as

$$ \rho (s) = s^{{2\sqrt {\varepsilon_{n} + \delta } }} (1 - s)^{{2\sqrt {\frac{1}{4} + \beta + \delta } }} $$
(25)

From the Rodrigues relation of Eq. (45), we obtain

$$ y_{n} (s) = B_{n} s^{{ - 2\sqrt {\varepsilon_{n} + \delta } }} (1 - s)^{{ - 2\sqrt {\frac{1}{4} + \beta + \delta } }} \frac{{{\text{d}}^{n} }}{{{\text{d}}s^{n} }}\left[ {s^{{n + 2\sqrt {\varepsilon_{n} + \delta } }} (1 - s)^{{n + 2\sqrt {\frac{1}{4} + \beta + \delta } }} } \right] $$
(26)
$$ y_{n} (s) \equiv B_{n} P_{n}^{{\left( {2\sqrt {\varepsilon_{n} + \delta } ,\,2\sqrt {\frac{1}{4} + \beta + \delta } } \right)}} (1 - 2s) $$
(27)

where \( P_{n}^{{\left( {\theta ,\vartheta } \right)}} \) is the Jacobi polynomial.

Substituting \( \varPhi (s)\,\,{\text{and}}\,\,y_{n} (s) \) from Eqs. (24) and (27), respectively, into Eq. (42), we obtain

$$ \psi (s) = B_{n} s^{{\sqrt {\varepsilon_{n} + \delta } }} (1 - s)^{G} P_{n}^{{\left( {2\sqrt {\varepsilon_{n} + \delta } ,\,2G - 1} \right)}} (1 - 2s) $$
(28)

where

$$ G = \frac{1}{2} + \sqrt {\frac{1}{4} + \beta + \delta } $$
(29)

From the definition of the Jacobi polynomials [51],

$$ P_{n}^{{\left( {\theta ,\vartheta } \right)}} (\omega ) = \frac{{\varGamma \left( {n + \theta + 1} \right)}}{{n!\varGamma \left( {\theta + 1} \right)}}\,{}_{2}F_{1} \left( { - n,\,\theta + \vartheta + n + 1,\,\theta + 1;\frac{1 - \omega }{2}} \right) $$
(30)

In terms of hypergeometric polynomials, Eq. (28) can be written as

$$ \psi (s) = B_{n} s^{{\sqrt {\varepsilon_{n} + \delta } }} (1 - s)^{G} \frac{{\varGamma \left( {n + 2\sqrt {\varepsilon_{n} + \delta } + 1} \right)}}{{n!\varGamma \left( {2\sqrt {\varepsilon_{n} + \delta } + 1} \right)}}\,{}_{2}F_{1} \left( { - n,\,\,2\sqrt {\varepsilon_{n} + \delta } + 2G + n,\,\,2\sqrt {\varepsilon_{n} + \delta } + 1;\,\,s} \right). $$
(31)

3 Special cases

In this section, we make some adjustments of constants in Eq. (1) to have the following cases:

3.1 Screened Coulomb potential

If De = 0 in Eq. (1), we can obtain the screened Coulomb potential of the form

$$ V(r) = - \frac{{Ae^{ - \alpha \,r} }}{r} $$
(32)

From Eq. (23), the energy eigenvalue equation for the screened Coulomb potential reduces to

$$ E_{n\,\ell } = \frac{{\hbar^{2} \alpha^{2} \ell (\ell + 1)}}{2\mu } - \frac{{\hbar^{2} \alpha^{2} }}{2\mu }\left[ {\frac{{ - \left( {{\raise0.7ex\hbox{${2\mu A}$} \!\mathord{\left/ {\vphantom {{2\mu A} {\hbar^{2} \alpha }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\hbar^{2} \alpha }$}}} \right) + \ell (\ell + 1) + (n + \ell + 1)^{2} }}{{2\left( {n + \ell + 1} \right)}}} \right]^{2} $$
(33)

Equation (33) is in full agreement with the results in Ref. [46, 47].

3.2 Standard Coulomb potential

We can rewrite Eq. (23) to have

$$ E_{n\,\ell } = \frac{{\hbar^{2} }}{2\mu }\left[ {\frac{{2\mu \alpha^{2} D_{\text{e}} r_{\text{e}}^{2} }}{{\hbar^{2} }} + \alpha^{2} \ell (\ell + 1) - \frac{{4\mu \alpha D_{\text{e}} r_{\text{e}} }}{{\hbar^{2} }}} \right] + D_{\text{e}} - \frac{{\hbar^{2} }}{2\mu }\left[ {\frac{{\alpha \left( {n + \zeta } \right)}}{2} + \frac{{\frac{{2\mu \alpha D_{\text{e}} r_{\text{e}}^{2} }}{{\hbar^{2} }} + \alpha \ell (\ell + 1) - \left( {\frac{{4\mu D_{\text{e}} r + 2\mu A}}{{\hbar^{2} }}} \right)}}{{2\left( {n + \zeta } \right)}}} \right]^{2} $$
(34)

As \( \alpha \to 0\,\,{\text{and}}\,\,D_{\text{e}} = 0, \) Eq. (1) reduces to the standard Coulomb potential of the form

$$ V(r) = - \frac{A}{r} $$
(35)

Its energy eigenvalue equation can be deduced from Eq. (34) as

$$ E_{n\,\ell } = - \frac{{\mu A^{2} }}{{2\hbar^{2} \left( {n + \ell + 1} \right)^{2} }} $$
(36)

The result of Eq. (36) is very consistent with the result obtained in Eq. (101) of Ref. [52]. Also, comparing our work with the result obtained in Eq. 33 of Ref. [46], it is worthy to note here that the authors in Ref. [46] failed to set the screening parameter (i.e. \( \delta \) in Eq. (1) of Ref. [46]) equal to zero. If that is done, then there would be a clear consistency in the energy eigenvalue equation obtained in Eq. (36) of our computation and Eq. (33) of Ref. [46].

3.3 Modified Kratzer potential

When the parameter A is set to zero, Eq. (1) reduces the potential to the modified Kratzer potential of the form

$$ V(r) = D_{\text{e}} \left( {\frac{{r - r_{\text{e}} }}{r}} \right)^{2} $$
(37)

And its energy eigenvalue equation can also be deduced from Eq. (23) as

$$ E_{n\,\ell } = \frac{{\hbar^{2} \alpha^{2} }}{2\mu }\left[ {\frac{{2\mu D_{\text{e}} r_{\text{e}}^{2} }}{{\hbar^{2} }} + \ell (\ell + 1) - \frac{{4\mu D_{\text{e}} r_{\text{e}} }}{{\hbar^{2} \alpha }}} \right] + D_{\text{e}} - \frac{{\hbar^{2} \alpha^{2} }}{2\mu }\left[ {\frac{{\left( {n + \zeta } \right)}}{2} + \frac{{\frac{{2\mu D_{\text{e}} r_{\text{e}}^{2} }}{{\hbar^{2} }} + \ell (\ell + 1) - \left( {\frac{{4\mu D_{\text{e}} r_{\text{e}} }}{{\hbar^{2} \alpha }}} \right)}}{{2\left( {n + \zeta } \right)}}} \right]^{2} $$
(38)

Rewriting Eq. (38), we have

$$ E_{n\,\ell } = \frac{{\hbar^{2} \alpha^{2} }}{2\mu }\left[ {\frac{{2\mu D_{\text{e}} r_{\text{e}}^{2} }}{{\hbar^{2} }} + \ell (\ell + 1) - \frac{{4\mu D_{\text{e}} r_{\text{e}} }}{{\hbar^{2} \alpha }}} \right] + D_{\text{e}} - \frac{{\hbar^{2} }}{2\mu }\left[ {\frac{{\alpha \left( {n + \zeta } \right)}}{2} + \frac{{\frac{{2\mu \alpha D_{\text{e}} r_{\text{e}}^{2} }}{{\hbar^{2} }} + \alpha \ell (\ell + 1) - \left( {\frac{{4\mu D_{\text{e}} r_{\text{e}} }}{{\hbar^{2} }}} \right)}}{{2\left( {n + \zeta } \right)}}} \right]^{2} $$
(39)

As \( \alpha \to 0, \) we obtain the energy eigenvalue for the modified Kratzer potential to be

$$ E_{n\,\ell } = D_{\text{e}} - \frac{{\hbar^{2} }}{2\mu }\left[ {\frac{{\left( {\frac{{4\mu D_{\text{e}} r_{\text{e}} }}{{\hbar^{2} }}} \right)}}{{\left( {1 + 2n + \sqrt {1 + 4\left( {\frac{{2\mu D_{\text{e}} r_{\text{e}}^{2} }}{{\hbar^{2} }} + \ell (\ell + 1)} \right)} } \right)}}} \right]^{2} $$
(40)

The result in Eq. (40) is very consistent with result of Eq. (14) in Ref. [53].

4 Results and discussion

In our study, the energy eigenvalues of the modified Kratzer potential plus the screened Coulomb potential are computed for N2, CO, NO, and CH diatomic molecules using Eq. (23), with the aid of the spectroscopic parameters given in Table 1. The explicit values of these energies for different vibrational and rotational quantum numbers are presented in Table 2. For validity purposes, we have also computed the energy eigenvalues of the modified Kratzer potential for the selected diatomic molecules, using the reduced energy equation given in Eq. (40) as a special case. Our results shown in Tables 3 and 4 are in good agreement with the results given in Ref. [53].

Table 1 Spectroscopic parameters of the molecules used in this work
Full size table
Table 2 Energy eigenvalues (in eV) of modified Kratzer potential plus screened Coulomb potential for different values of n and ℓ for different diatomic molecules
Full size table
Table 3 Energy eigenvalues (in eV) of modified Kratzer potential for different values of n and ℓ for N2 and CO diatomic molecules
Full size table
Table 4 Energy eigenvalues (in eV) of modified Kratzer potential for different values of n and ℓ for NO and CH diatomic molecules
Full size table

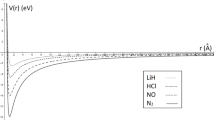
We have plotted the shape of the modified Kratzer potential plus screened Coulomb potential for the different diatomic molecules considered, as shown in Fig. 1. This figure gives an insight into the behaviour of the combined potential when r = re. Also, the variation in the energy eigenvalues with different parameters of the combined potential such as \( D_{\text{e}} ,\,\,r_{\text{e}} ,\,\,\alpha ,\,\,{\text{and}}\,\,A \) is shown in Figs. 2–5, respectively, for various values of n and l quantum numbers. In these figures, there is an increase in energy eigenvalues as the various parameters increase. In Figs. 2 and 3, there exists an asymptotic convergence at zero energy. In Fig. 4, the increase in energy tends to spread out from zero position for different vibrational quantum numbers. We also observe a uniform increase in energy as the parameter “A” increases for the different vibrational quantum numbers.

Fig. 1
figure 1

Shape of modified Kratzer potential plus screened Coulomb potential for different diatomic molecules

Full size image
Fig. 2
figure 2

Energy eigenvalues variation with dissociation energy for various vibrational quantum numbers

Full size image
Fig. 3
figure 3

Energy eigenvalues variation with equilibrium bond length for various vibrational quantum numbers

Full size image
Fig. 4
figure 4

Energy eigenvalues variation with screening parameter for various vibrational quantum numbers

Full size image
Fig. 5
figure 5

Energy eigenvalues variation with parameter “A” for various vibrational quantum numbers

Full size image

5 Conclusion

In this study, the approximate bound state solutions of the Schrodinger equation with the modified Kratzer molecular potential plus screened Coulomb potential model were obtained, via the Nikiforov–Uvarov method. The energy eigenvalues of the selected diatomic molecules (N2, CO, NO, and CH) were computed, and a special case was considered. Our results are consistent with the results in available literatures. The shape of the combined potential model for the diatomic molecules was plotted, and this gives a better understanding to the behaviour of the selected diatomic molecules when the equilibrium bond length equals the interatomic distance of the molecules. The variation in the combined energy eigenvalue with the potential parameters (De, re, α, and A) was also plotted. It was discovered that the energy eigenvalues increase as the various potential parameters increase. This study can be extended even to the relativistic regime using other methods [54,55,56]. Recently, there has been investigation into areas covering vibrational partition function [57,58,59] and thermochemical properties of diatomic molecules [60,61,62]. Worth mentioning is the current research done on the prediction of enthalpy and entropy of gaseous dimers [63, 64].