1 Introduction

In relativistic quantum mechanics the particle motions are commonly described using either Klein–Gordon equation or Dirac equation [1, 2] depending on spin character of the particle. Klein Gordon equation is one of the most frequently used wave equation that describes spin-zero particles such as mesons. On the other hand, however, electrons are described satisfactorily by Dirac equation.

The solution of Klein–Gordon equation under different potentials plays an important role because one can understand physics that can be brought by such solutions. Among the most successful methods that have been used to solve Schrödinger, Dirac and Klein–Gordon equation, Nikiforov–Uvarov (NU) and supersymmetric quantum mechanics (SUSYQM) methods have great importance [3–13].

Recently Klein–Gordon equation with different potentials have been solved and investigated by different researchers [14–24]. For instance, Egrifes and Sever [25] have obtained bound state solutions of Klein–Gordon equation for generalized PT-symmetric Hulthen potential, Soylu et al. [26] considered Klein–Gordon equation under Rosen–Morse type potentials.

Aim of this paper is to obtain approximate solutions of Klein–Gordon equation with equal scalar and vector Mobius square plus Yukawa potentials in D-dimensional space.

2 Nikiforov–Uvarov (NU) method

Nikiforov–Uvarov method [8–11] is based on the solution of a generalized second order linear differential equation with special orthogonal function. Schrödinger equation

$$ \Uppsi^{\prime\prime} \left( x \right) + \left( {E - V(x)} \right)\Uppsi \left( x \right) = 0 $$
(1)

can be solved by this method. This can be done by transforming this equation into equation of hypergeometric type with appropriate transformation, S = S(x)

$$ \Uppsi^{\prime\prime} \left( s \right) + \frac{{\overline{\tau } (s)}}{\sigma (s)}\Uppsi^{\prime} \left( s \right) + \frac{{\overline{\sigma } (s)}}{{\sigma^{2} (s)}}\Uppsi \left( s \right) = 0 $$
(2)

where σ(s) and \( \overline{\sigma } (s) \) must be polynomials of at most second-degree and \( \overline{\tau } (s) \) is a polynomial with at most first-degree. In order to find exact solution to Eq. (2) we set wave function as

$$ \Uppsi \left( s \right) = \Upphi (s)\chi (s) $$
(3)

On substituting Eq. (3) in Eq. (2), then Eq. (2) reduces to hypergeometric type,

$$ \sigma \left( s \right)\chi^{\prime\prime} (s) + \tau (s)\chi^{\prime} (s) + \lambda \chi (s) = 0 $$
(4)

where wave function Φ(s) is defined as logarithmic derivative [8]

$$ \frac{{\Upphi^{'} (s)}}{\Upphi (s)} = \frac{\pi (s)}{\sigma (s)} $$
(5)

where π(s) is at most first order polynomial. Likewise, hypergeometric type function χ(s) in Eq. (4) for a fixed n is given by Rodriques relation as

$$ \chi_{n} (s) = \frac{{B_{n} }}{\rho (s)}\frac{{d^{n} }}{{ds^{n} }}\left[ {\sigma^{n} (s)\rho (s)} \right] $$
(6)

where B n is normalization constant and weight functions ρ(s) must satisfy the condition

$$ \frac{d}{ds}\left[ {\sigma (s)\rho (s)} \right] = \tau (s)\rho (s) $$
(7)

with

$$ \tau (s) = \overline{\tau } (s) + 2\pi (s) $$
(8)

In order to accomplish the condition imposed on weight function ρ(s), it is necessary that classical orthogonal polynomials τ(s) be equal to zero at some point of an interval (a, b) and its derivatives within this interval at σ(s) > 0 is negative, i.e.,

$$ \frac{d}{ds}\tau (s) < 0 $$
(9)

Therefore, function π(s) required for NU method are defined as follows:

$$ \pi (s) = \frac{{\sigma^{\prime } - \overline{\tau } }}{2} \pm \sqrt {\left( {\frac{{\sigma^{\prime } - \overline{\tau } }}{2}} \right)^{2} - \overline{\sigma } + k\sigma } $$
(10)
$$ \lambda = k + \pi^{\prime } (s) $$
(11)

k-value in Eq. (10) is possible to evaluate if the expression under square root is square of polynomials. This is possible if and only if its discriminant is zero. With this, new eigenvalues equation becomes

$$ \lambda = \lambda_{n} = - n\frac{d\tau }{ds} - \frac{{n\left( {n - 1} \right)}}{2}\frac{{d^{2} \sigma }}{{ds^{2} }},\quad n = 0,1,2, \ldots $$
(12)

On comparing Eq. (11) with Eq. (12), we obtain energy eigenvalues.

Parametric generalization of NU method is given by generalized hypergeometric type equation as [27]

$$ \Uppsi^{''} (s) + \frac{{\left( {c_{1} - c_{2} s} \right)}}{{s\left( {1 - c_{3} s} \right)}}\Uppsi^{'} (s) + \frac{1}{{s^{2} \left( {1 - c_{3} s} \right)^{2} }}\left[ { - \xi_{1} s^{2} + \xi_{2} s - \xi_{3} } \right]\Uppsi (s) = 0 $$
(13)

Eq. (13) is solved by comparing it with Eq. (20) and following polynomials are obtained

$$ \overline{\tau } (s) = \left( {c_{1} - c_{2} s} \right),\quad \sigma (s) = s\left( {1 - c_{3} s} \right),\overline{\sigma } (s) = - \xi_{1} s^{2} + \xi_{2} s - \xi_{3} $$
(14)

where

$$ c_{4} = \frac{1}{2}\left( {1 - c_{1} } \right),\quad c_{5} = \frac{1}{2}\left( {c_{2} - 2c_{3} } \right),\quad c_{6} = c_{5}^{2} + \xi_{1} ,\quad c_{7} = 2c_{4} c_{5} - \xi_{2} ,\quad c_{8} = c_{4}^{2} + \xi_{3} $$
(15)

The resulting value of k in Eq. (15) is obtained from condition that function under square root must be square of a polynomials and it yields,

$$ k_{ \pm } = - \left( {c_{7} + 2c_{3} c_{8} } \right) \pm 2\sqrt {c_{8} c_{9} } , $$
(16)

where

$$ c_{9} = c_{3} c_{7} + c_{3}^{2} c_{8} + c_{6} . $$
(17)

The new π(s) for each k becomes

$$ \pi \left( s \right) = c_{4} + c_{5} s - \left[ {\left( {\sqrt {c_{9} } + c_{3} \sqrt {c_{8} } } \right)s - \sqrt {c_{8} } } \right], $$
(18)

For k − value as

$$ k_{ - } = - \left( {c_{7} + 2c_{3} c_{8} } \right) - 2\sqrt {c_{8} } c_{9} $$
(19)

Using Eq. (8), we obtain

$$ \tau \left( s \right) = c_{1} + 2c_{4} - \left( {c_{2} - 2c_{5} } \right)s - 2\left[ {\left( {\sqrt {c_{9} } + c_{3} \sqrt {c_{8} } } \right)s - \sqrt {c_{8} } } \right]. $$
(20)

The physical condition for bound state solution is τ′ < 0 and thus

$$ \tau^{\prime } = - 2c_{3} - 2\left( {\sqrt {c_{9} } + + c_{3} \sqrt {c_{8} } } \right) < 0 $$
(21)

With aid of Eqs. (11) and (12), we derive energy equation as

$$ \left( {c_{2} - c_{3} } \right)n + c_{3} n^{2} - \left( {2n + 1} \right)c_{5} + \left( {2n + 1} \right)\left( {\sqrt {c_{9} } + c_{3} \sqrt {c_{8} } } \right) + c_{7} + 2c_{3} c_{8} + 2\sqrt {c_{8} c_{9} } = 0 $$
(22)

The weight function ρ(s) is obtained from e.g. Eq. (7) as

$$ \rho \left( s \right) = s^{{c_{10} - 1}} \left( {1 - c_{3} s} \right)^{{\frac{{c_{11} }}{{c_{3} }} - c_{10} - 1}} $$
(23)

together with e.g. Eq. (6), we have

$$ \chi_{n} \left( s \right) = {\rm P}_{n}^{{^{{\left( {c_{10} - 1,\frac{{c_{11} }}{{c_{3} }} - c_{10} - 1} \right)}} }} \left( {1 - 2c_{3} s} \right) $$
(24)

where

$$ c_{10} = c_{1} + 2c_{4} + 2\sqrt {c_{8} } $$
(25)
$$ c_{11} = c_{2} - 2c_{5} + 2\left( {\sqrt {c_{9} } + c_{3} \sqrt {c_{8} } } \right) $$
(26)
$$ P_{n}^{{^{{\left( {\alpha ,\beta } \right)}} }} \left( x \right) = \frac{{\Upgamma \left( {\alpha + n + 1} \right)}}{{n!\Upgamma \left( {\alpha + \beta + n + 1} \right)}}\sum\limits_{m = 0}^{n} {\left( {\begin{array}{*{20}c} n \\ m \\ \end{array} } \right)} \frac{{\Upgamma \left( {\alpha + \beta + n + m + 1} \right)}}{{\Upgamma \left( {\alpha + m + 1} \right)}}\left( {\frac{x - 1}{2}} \right)^{m} $$

and \( P_{n}^{{\left( {\alpha ,\beta } \right)}} \) is Jacobi polynomial.

Second part of wave function is obtained from Eq. (5) as

$$ \Upphi (s) = s^{{c_{12} }} \left( {1 - c_{3} s} \right)^{{ - c_{12} - \frac{{c_{13} }}{{c_{3} }}}} $$
(27)

where

$$ c_{12} = c_{4} + \sqrt {c_{8} } ,c_{13} = c_{5} - \left( {\sqrt {c_{9} } + c_{3} \sqrt {c_{8} } } \right) $$
(28)

Thus, the wave function is

$$ \Uppsi \left( s \right) = s^{{c_{12} }} \left( {1 - c_{3} s} \right)^{{c_{12} - \frac{{c_{13} }}{{c_{3} }}}} P_{n}^{{( {c_{10} - 1,\frac{{c_{11} }}{{c_{3} }} - c_{10} - 1})}} \left( {1 - 2c_{3} s} \right) $$
(29)

3 Radial part of Klein–Gordon equation in D-dimensions

The radial part of Klein–Gordon equation in presence of vector and scalar potentials in D-dimensional space is written as [28–30]

$$ \left[ {\frac{{d^{2} }}{{dr^{2} }} + E_{nl}^{2} + V^{2} (r) - 2E_{nl} V(r) - m^{2} - S^{2} (r) - 2mS(r) - \frac{{\left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{{4r^{2} }}} \right]\mathop U\nolimits_{n,l} \left( r \right) = 0 $$
(30)

For equal scalar and vector potentials Eq. (30) reduces to

$$ \left[ {\frac{{d^{2} }}{{dr^{2} }} + E_{nl}^{2} - m^{2} - 2\left( {E_{nl} + m} \right)V\left( r \right) - \frac{{\left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{{4r^{2} }}} \right]U_{nl} (r) = 0 $$
(31)

Here, we consider Mobius square plus Yukawa potentials defined as [31, 32]

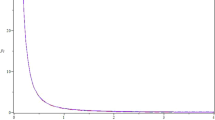
$$ V(r) = V_{0} \left( {\frac{{A + Be^{ - \alpha r} }}{{C + D^{\prime } e^{ - \alpha r} }}} \right)^{2} - \frac{{V_{1} e^{ - \alpha r} }}{r}, $$
(32)

where V 0, V 1, A, B, C, D′ and α are constant coefficients. A good approximation for centrifugal barrier is taken as [33] (see Fig. 1)

$$ \frac{1}{{\mathop r\nolimits^{2} }} \approx \mathop \alpha \nolimits^{2} \left( {\frac{C}{{C + D^{\prime } e^{ - \alpha r} }}} \right)^{2} = \mathop {\lim }\limits_{\alpha \to 0} \left( {\frac{1}{{r^{2} }} + \frac{\alpha }{r} + \frac{5}{12}\alpha^{2} + \frac{1}{12}\alpha^{3} r + \frac{1}{240}\alpha^{4} r^{2} - \frac{1}{720}\alpha^{5} r^{3} - \frac{1}{6045}\alpha^{6} r^{4} + O\left( {r^{5} } \right)} \right) $$
(33)

which is valid for αr ≤ 1 when C = 1 and D′ = −1 [33–36], similar to other related works [37, 38]. In addition, when performing a power series expansion and setting α → 0, Eq. (33) gives the desired r −2 suggested by Greene and Aldrich [39]. By substituting Eqs. (32) and (33) into Eq. (31) we obtain

$$ \left\{ {\frac{{d^{2} }}{{dr^{2} }} + E_{nl}^{2} - m^{2} - 2\left( {E_{nl} + m} \right)V_{0} \left( {\frac{{A + Be^{ - \alpha r} }}{{C + D^{\prime } e^{ - \alpha r} }}} \right)^{2} + \frac{{2\alpha C\left( {E_{nl} + m} \right)V_{1} e^{ - \alpha r} }}{{\left( {C + D^{\prime } e^{ - \alpha r} } \right)}} - \frac{{\alpha^{2} C^{2} \left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{{4\left( {C + D^{\prime } e^{ - \alpha r} } \right)^{2} }}} \right\}U_{nl} (r) = 0. $$
(34)

By a change of variable of the form

$$ s = e^{ - \alpha r} $$
(35)

Eq. (34) is written as

$$ \frac{{d^{2} U_{nl} }}{{ds^{s} }} + \frac{{\left( {1 + \frac{{D^{\prime } }}{C}s} \right)}}{{s\left( {1 + \frac{{D^{\prime } }}{C}s} \right)}}\frac{{dU_{nl} }}{ds} + \frac{1}{{s^{2} \left( {1 + \frac{{D^{\prime } }}{C}s} \right)^{2} }}\left[ { - Q_{1} s^{2} + Q_{2} s - Q_{3} } \right]U_{nl} (r) = 0. $$
(36)

where

$$ \begin{gathered} \varepsilon ^{2} = \frac{{E_{{nl}}^{2} - m^{2} }}{{\alpha ^{2} }}, \hfill \\ Q_{1} = \frac{{ - D^{{\prime 2}} }}{{C^{2} }}\varepsilon ^{2} + \frac{{2\left( {E_{{nl}} + m} \right)}}{{\alpha ^{2} C^{2} }}V_{0} B^{2} - \frac{{2D^{\prime } }}{C}\frac{{\left( {{\text{E}}_{{nl}} + m} \right)}}{\alpha }V_{1} , \hfill \\ Q_{2} = \frac{{2D^{\prime } }}{C}\varepsilon ^{2} - 4\frac{{\left( {{\text{E}}_{{nl}} + m} \right)}}{{\alpha ^{2} C^{2} }}V_{0} AB + 2\frac{{\left( {{\text{E}}_{{nl}} + m} \right)}}{\alpha }V_{1} , \hfill \\ Q_{3} = - \varepsilon ^{2} + \frac{{2\left( {E_{{nl}} + m} \right)}}{{\alpha ^{2} c^{2} }}V_{0} A^{2} + \frac{{\left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{4}. \hfill \\ \end{gathered} $$
(37)

By comparing Eq. (36) with Eq. (13), we obtain energy spectrum for Mobius square plus Yukawa potentials as

$$ \begin{gathered} - \frac{{D^{\prime } }}{c}n^{2} - \left( {2n + 1} \right)\frac{{D^{\prime } }}{2C} + \left( {2n + 1} \right)\left( \begin{gathered} \sqrt {\frac{{D^{\prime 2} }}{{4C^{2} }} - \frac{{4D^{\prime } }}{C}\frac{{\left( {E_{nl} + m} \right)V_{0} AB}}{{\alpha^{2} C^{2} }} + \frac{{2D^{\prime 2} }}{{C^{2} }}\frac{{\left( {E_{nl} + m} \right)V_{0} A^{2} }}{{\alpha^{2} C^{2} }} + \frac{{2\left( {E_{nl} + m} \right)V_{0} B^{2} }}{{\alpha^{2} C^{2} }} + \frac{{D^{\prime 2} }}{{C^{2} }}\frac{{\left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{4}} \hfill \\ - \frac{{D^{\prime } }}{c}\sqrt { - \left( {\frac{{E_{nl}^{2} - m^{2} }}{{\alpha^{2} }}} \right) + \frac{{2\left( {E_{nl} + m} \right)V_{0} A^{2} }}{{\alpha^{2} C^{2} }} + \frac{{\left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{4}} \hfill \\ \end{gathered} \right) \hfill \\ + \frac{{4\left( {E_{nl} + m} \right)V_{0} AB}}{{\alpha^{2} C^{2} }} - \frac{{2\left( {E_{nl} + m} \right)V_{1} }}{\alpha } - 2\frac{{D^{\prime } }}{C}\left[ {\frac{{2\left( {E_{nl} + m} \right)V_{0} A^{2} }}{{\alpha^{2} C^{2} }} + \frac{{\left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{4}} \right] \hfill \\ + 2\sqrt {\left[ { - \left( {\frac{{E_{nl}^{2} - m^{2} }}{{\alpha^{2} }}} \right) + \frac{{2\left( {E_{nl} + m} \right)V_{0} A^{2} }}{{\alpha^{2} C^{2} }} + \frac{{\left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{4}} \right]\left[ {\frac{{D^{\prime 2} }}{{4C^{2} }} - \frac{{4D^{\prime } }}{C}\frac{{\left( {E_{nl} + m} \right)V_{0} AB}}{{\alpha^{2} C^{2} }} + \frac{{2D^{\prime 2} }}{{C^{2} }}\frac{{\left( {E_{nl} + m} \right)V_{0} A^{2} }}{{\alpha^{2} C^{2} }} + \frac{{2\left( {E_{nl} + m} \right)V_{0} B^{2} }}{{\alpha^{2} C^{2} }} + \frac{{D^{\prime 2} }}{{C^{2} }}\frac{{\left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{4}} \right]} = 0 \hfill \\ \end{gathered} $$
(38)

or more explicitly, we have,

$$ {\rm E}_{m}^{2} - m^{2} = \frac{{ - \alpha^{2} }}{4}\left[ {\frac{{\gamma + \frac{{D^{\prime } }}{C}\left( {n + \frac{1}{2} - \beta } \right)^{2} }}{{\frac{{D^{\prime } }}{C}\left( {n + \frac{1}{2} - \beta } \right)}}} \right]^{2} + \frac{{2\left( {E_{nl} + m} \right)}}{{C^{2} }}V_{0} A^{2} + \alpha^{2} \frac{{\left( {D + 21 - 1} \right)\left( {D + 21 - 3} \right)}}{4} $$
(39)

where

$$ \begin{gathered} \gamma = \frac{{2D^{\prime } }}{C}\frac{{\left( {E_{nl} + m} \right)V_{o} A^{2} }}{{\alpha^{2} C^{2} }} + 2\frac{{\left( {E_{nl} + m} \right)V_{1} }}{\alpha } - \frac{2C}{{D^{\prime } }}\frac{{\left( {E_{nl} + m} \right)V_{0} B^{2} }}{{\alpha^{2} C^{2} }} + \frac{{D^{\prime } }}{C}\frac{{\left( {D + 21 - 1} \right)\left( {D + 21 - 3} \right)}}{4} \hfill \\ \beta = \frac{C}{{D^{\prime } }}\sqrt {\frac{{D^{\prime 2} }}{{4C^{2} }} - \frac{{4D^{\prime } }}{C}\frac{{\left( {E_{nl} + m} \right)}}{{\alpha^{2} C^{2} }}V_{o} AB + \frac{{2D^{\prime 2} }}{{C^{2} }}\left( {\frac{{E_{nl} + m}}{{\alpha^{2} C^{2} }}} \right)V_{0} A^{2} + 2\frac{{\left( {E_{nl} + m} \right)}}{{\alpha^{2} C^{2} }}V_{o} B^{2} + \frac{{D^{\prime 2} }}{{C^{2} }}\frac{{\left( {D + 21 - 1} \right)\left( {D + 21 - 3} \right)}}{4}} \hfill \\ \end{gathered} $$
(40)

wave function of the system is obtained as

Fig. 1
figure 1

\( \frac{1}{{r^{2} }} \) and its approximation for α = 0.01

Full size image
$$ U_{nl} \left( r \right) = N_{nl} \left( {e^{ - \alpha r} } \right)^{{c_{12} }} \left( {1 + \frac{{D^{\prime } }}{C}e^{ - \alpha r} } \right)^{{ - c_{12} + \frac{C}{{D^{\prime}}}c_{13} }} \quad P_{n}^{{\left( {c_{10} - 1, - \frac{C}{{D^{\prime}}}c_{11} - c_{10} - 1} \right)}} \left( {1 + 2\frac{{D^{\prime } }}{C}e^{ - \alpha r} } \right) $$
(41)

4 Results and discussion

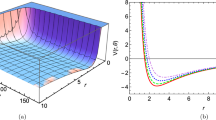
In order to test accuracy of our work, we compute numerical values for energy spectrum and graphical solutions. In Table 1, we have reported numerical values of energy for various states. Also, we have reported behaviour of energy in Fig. 2, We see that energy increases with increasing D. In Fig. 3, we show behaviour of energy versus alpha. It reveals that energy decreases as alpha decreases and tends to a constant value. Finally, energy has also been plotted versus the potential coefficients in Figs. 4 and 5. It shows well how energy increases for increasing V 0 and decreases for increasing V 1. Now a few special cases are discussed below. By adjusting some potential parameters, some well kwon potentials can be obtained. Setting V 0 = 0, C = 1, D′ = −1 into Eq. (32), Yukawa potential [32]

$$ V(r) = \frac{{ - V_{1} e^{ - \alpha r} }}{r}, $$
(42)

is obtained. Corresponding energy eigenvalues become

$$ \begin{aligned} E_{nl}^{2} - m^{2} = & - \frac{{ - \alpha^{2} }}{4}\left[ {\frac{{\frac{{\left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{4} - \frac{{2\left( {E_{nl} + m} \right)V_{1} }}{\alpha } + \left( {n + \frac{1}{2} - \sqrt {\frac{1}{4} + \frac{{\left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{4}} } \right)^{{^{2} }} }}{{\left( {n + \frac{1}{2} - \sqrt {\frac{1}{4} + \frac{{\left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{4}} } \right)}}} \right]^{2} \\ & \quad\quad + \frac{{\alpha^{2} }}{4}\left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right). \\ \end{aligned} $$
(43)

Similarly we set V o  = 0, C = 1, D′ = −1 and α → 0 into Eq. (32), the potential reduces to Coulomb potential [37]

$$ V(r) = \frac{{ - V_{1} }}{r}, $$
(44)

Corresponding energy eigenvalues become

$$ E_{nl}^{2} - m^{2} = - \frac{{\left( {E_{nl} + m} \right)^{2} V_{1}^{2} }}{{\left( {n + \frac{1}{2} - \sqrt {\frac{1}{4} + \frac{{\left( {D + 21 - 1} \right)\left( {D + 21 - 3} \right)}}{4}} } \right)^{2} }} $$
(45)

where V 1 = 0, potential reduces to Mobius square potential. The generalized form of Mobius square potential can be written as

$$ V(r) = \frac{{V_{0} }}{{C^{2} }}\left[ {\frac{{A^{2} + 2ABe^{ - \alpha r} + B^{2} e^{ - 2\alpha r} }}{{\left( {1 + \frac{{D^{\prime } }}{C}e^{ - \alpha r} } \right)^{2} }}} \right] $$
(46)

Comparing Eq. (46) with Deng–Fan potential [38]

$$ V(r) = D_{e} \left[ {\frac{{1 - 2\left( {1 + b} \right)e^{ - \alpha r} + \left( {1 + b} \right)^{2} e^{ - 2\alpha r} }}{{\left( {1 - e^{ - \alpha r} } \right)^{2} }}} \right] $$
(47)

for C = 1 and D′ = −1, we have V 0 A 2 = D e , V 0 AB = −D e (1 + b), V 0 B 2 = D e (1 + b)2, where \( b = e^{{\alpha r_{d} }} - 1 \) and r d is equilibrium inter-nuclear distance. Substitution of these parameters in Eq. (39) gives energy spectrum of Deng–Fan potential as

$$ E_{nl}^{2} - m^{2} = \frac{{ - \alpha^{2} }}{4}\left[ {\frac{{\gamma_{1} + \left( {n + \frac{1}{2} + \beta_{1} } \right)^{2} }}{{\left( {n + \frac{1}{2} + \beta_{1} } \right)}}} \right]^{2} + 2D_{e} \left( {E_{nl} + m} \right) + \frac{{\alpha^{2} \left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{4}, $$
(48)

where

$$ \begin{gathered} \gamma_{1} = \frac{{2D_{e} \left( {E_{nl} + m} \right)}}{{\alpha^{2} }} - 2D_{e} \left( {1 + b} \right)^{2} \frac{{\left( {E_{nl} + m} \right)}}{{\alpha^{2} }} + \frac{{\left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{4}, \hfill \\ \beta_{1} = \sqrt {\frac{1}{4} - 4D_{e} \left( {1 + b} \right)\frac{{\left( {E_{nl} + m} \right)}}{{\alpha^{2} }} + \frac{{2D_{e} \left( {E_{nl} + m} \right)}}{{\alpha^{2} }} + 2D_{e} \left( {1 + b} \right)^{2} \frac{{\left( {E_{nl} + m} \right)}}{{\alpha^{2} }} + \frac{{\left( {D + 2l - 1} \right)\left( {D + 2l - 3} \right)}}{4}} , \hfill \\ \end{gathered} $$
(49)

This result is consistent with that of Dong [38] when D = 3.

Table 1 Energy for \( D = 3,\alpha = 0.01 \, , \, A = 1,B = - 2,m = 1,C = 1,D^{\prime } = - 1,V_{0} = 0.2 \)
Full size table
Fig. 2
figure 2

Energy versus D for \( \alpha = 0.01, \, A = 1,B = - 2,m = 1,C = 1,D^{\prime } = - 1,V_{0} = 0.2,V_{1} = 0.1 \)

Full size image
Fig. 3
figure 3

Energy versus α for \( D = 3, \, A = 1,B = - 2,m = 1,C = 1,D^{\prime } = - 1,V_{0} = 0.2,V_{1} = 0.1 \)

Full size image
Fig. 4
figure 4

Energy versus V 0 for \( D = 3,\alpha = 0.01, \, A = 1,B = - 2,m = 1,C = 1,D^{\prime } = - 1,V_{1} = 0.1 \)

Full size image
Fig. 5
figure 5

Energy versus V 1 for \( D = 3,\alpha = 0.01, \, A = 1,B = - 2,m = 1,C = 1,D^{\prime } = - 1,V_{0} = 0.2 \)

Full size image

5 Conclusions

Approximate solutions of Klein–Gordon equation in case of equal scalar and vector Mobius square plus Yukawa potentials have been obtained using parametric form of NU method. By adjusting some parameters of potential in Eq. (3), three well known potentials are obtained. With a good approximation to centrifugal term, we have obtained energy eigenvalues and unnormalized wave function in terms of Jacobi polynomials. Numerical data for the energy spectrum are discussed indicating usefulness for other physical systems [40].