Introduction

Recently, much attention has been drawn towards the Eckart-type potential model as a molecular potential model due to its wide applications in physics and chemical physics [1]. It is expressed as

$$ -\eta \frac{e^{-\propto r}}{\left(1-{e}^{-\propto r}\right)}+\zeta \frac{e^{-\propto r}}{{\left(1-{e}^{-\propto r}\right)}^2} $$
(1)

where ζ and η are the potential depths of the Eckart potential and α is an adjustable positive screening parameter. Sari et al. in 2015 studied the analytical approximations to the bound state solutions of the Dirac equation with the Eckart potential by using the asymptotic method [2]. Also the l-wave scattering state solutions of the Schrödinger equation for the Eckart potential has been studied analytically by using this same approximation scheme proposed by Greene and Aldrich [3, 4]. Ikhdair and colleagues solved the D-dimensional radial Klein-Gordon equation for any orbital angular momentum quantum number and for the scalar and vector Eckart-type exponential potentials using a general mathematical model of the Nikiforov-Uvarov method [5]. Hassanabadi et al. in 2013 obtained the bound state solutions by studying the s-wave Klein–Gordon equation with equally mixed Eckart potentials [6]. Zhang in 2008 investigated the bound state solutions of the Klein–Gordon equation with equal vector and scalar Eckart potentials using the approximation for the centrifugal term proposed by Greene and Aldrich for any orbital angular momentum quantum number [7]. Taskin and Kocak investigated the solution of the Schrodinger equation for the Eckart potential by using the approximation for the centrifugal term given by Greene and Aldrich for any arbitrary l state [8]. Akpan et al. studied the Klein-Gordon equation subject to equal q-deformed scalar and vector Eckart potentials to obtain the bound state solutions using an improved approximation scheme proposed by Qiang and Dong [9, 10]. Surpami et al. investigated the bound state solutions to the three-dimensional Schrodinger equation for Eckart plus trigonometric Poschl-Teller non-central potential approximately using Romanovski polynomials with suitable coordinate transformation [11]. Unfortunately, analytical solutions for the s-wave Eckart potential is only possible for zero angular momentum state because of the presence of the centrifugal term.

Another potential that has attracted attention recently is the inversely quadratic Yukawa potential expressed as

$$ -\frac{V_0{e}^{-\propto r}}{r^2} $$
(2)

Where V0 represents the potential depth. This potential was first studied by Hamzavi and coworkers where they obtained the approximate analytic spin and pseudospin solutions of the Dirac equation for the inversely quadratic Yukawa potential with a Coulomb-like tensor interaction through the Nikiforov-Uvarov method [12]. The bound state analytical solutions of both the Schrodinger and the Klein-Gordon equations with Manning-Rosen potential plus a class of Yukawa potential of the Pekeris-type approximation of the Coulomb term via the Nikiforov-Uvarov method have been also studied in the literature [13, 14]. The solutions of the Schrodinger equation with inversely quadratic Yukawa plus Woods-Saxon potential (IQYWSP) have been also presented using the parametric Nikiforov-Uvarov (NU) method. The bound state energy eigenvalues and the corresponding un-normalized eigen functions were obtained in terms of Jacobi polynomials [15].

The sum of these potentials given as EIQYP is expressed as

$$ V(r)=-\eta \frac{e^{-\propto r}}{\left(1-{e}^{-\propto r}\right)}+\zeta \frac{e^{-\propto r}}{{\left(1-{e}^{-\propto r}\right)}^2}-\frac{V_0{e}^{-\propto r}}{r^2}. $$
(3)

In this present work, a mixed potential known as the Eckart plus Inversely Quadratic Yukawa potential (EIQYP) is investigated through the Nikiforov-Uvarov quantum formalism. The motivation for the superposition of Yukawa and Eckart potentials is to see how the eigenvalues vary with those of the pure Yukawa and Eckart potentials and what information could be obtained from the combination of potentials. We organize the work as follows; firstly, a brief introduction in “Introduction” (this section). In “Theoretical approach,” the parametric Nikiforov-Uvarov method was introduced and briefly discussed. The approximate solutions of the Schrodinger equation was explicitly obtained in “Solutions of Eckart plus inversely quadratic Yukawa potential.” “Results and discussion” is dedicated to the numerical analysis of the obtained bound state solutions. Finally, the conclusion was given in “Conclusions.”

Theoretical approach

The generalization of the parametric NU method is very similar to the more generalized expression in Eq. (4). The parametric form is simply using parameters to obtain explicitly energy eigenvalues and it is still based on the solutions of a generalized second-order linear differential equation with special orthogonal functions. The hypergeometric NU method has shown its power in calculating the exact energy levels of all bound states for some solvable quantum systems.

The equation below is a Schrodinger-like second-order differential equation of the form

$$ {\psi}^{\prime \prime }(s)+\frac{\overline{\tau}(s)}{\sigma (s)}{\psi}^{\prime }(s)+\frac{\overline{\sigma}(s)}{\sigma^2(s)}\psi (s)=0 $$
(4)

Where σ(s) and \( \overline{\sigma} \)(s) are both polynomials at most second degree and \( \overset{\sim }{\tau } \)(s) is a first-degree polynomial. The parametric generalization of the N-U method is given by the generalized hypergeometric-type Eq. (5)

$$ \varPsi^{\prime\prime }(s)+\frac{c_1-{c}_2s}{s\left(1-{c}_3s\right)}\varPsi^{\prime }(s)+\frac{1}{s^2{\left(1-{c}_3s\right)}^2}\left[-{\epsilon}_1{s}^2+{\epsilon}_2s-{\epsilon}_3\right]\varPsi (s)=0. $$
(5)

Thus, Eq. (4) can be solved by comparing it with Eq. (5) and the following polynomials are obtained

$$ \overline{\tau}(s)=\left({c}_1-{c}_2s\right),\sigma (s)=s\left(1-{c}_3s\right),\kern0.5em \overline{\sigma}(s)=-{\epsilon}_1{s}^2+{\epsilon}_2s-{\epsilon}_3 $$
(6)

The parameters obtainable from Eq. (5) serve as important tools to finding the energy eigenvalues and eigenfunctions.

The function π(s) and the parameters λ required for the NU method are given as follows:

$$ \pi (s)=\frac{\sigma^{\prime }-\overset{\sim }{\tau }}{2}\pm \sqrt{{\left(\frac{\sigma^{\prime }-\overset{\sim }{\tau }}{2}\right)}^2-\overline{\sigma}+ k\sigma} $$
(7)
$$ \lambda =k+\pi (s). $$
(8)

Now substituting Eq. (6) into Eq. (7), we find

$$ \overline{\sigma}(s)={c}_4+{c}_5s\pm {\left[\left({c}_6-{c}_3{k}_{\pm}\right){s}^2+\left({c}_7+{k}_{\pm}\right)s+{c}_8\right]}^{\frac{1}{2}} $$
(9)

where

$$ {\displaystyle \begin{array}{c}{c}_4=\frac{1}{2}\left(1-{c}_1\right),{c}_5=\frac{1}{2}\left({c}_2-2{c}_3\right),{c}_6={c_5}^2+{\epsilon}_1,{c}_7=2{c}_4{c}_5-{\epsilon}_2,{c}_8={c_4}^2+{\epsilon}_3,\\ {}{c}_9={c}_3{c}_7+{c_3}^2{c}_8+{c}_6\end{array}} $$
(10)

The resulting value of k in Eq. (9) is obtained from the condition that the function under the square root be square of a polynomial and it yields,

$$ {k}_{\pm }=-\left({c}_7+2{c}_3{c}_8\right)\pm 2\sqrt{c_8{c}_9.} $$
(11)

The new π(s) for k− becomes

$$ \uppi \left(\mathrm{s}\right)={c}_4+{c}_5s-\left[\left(\sqrt{c_9}+{c}_3\sqrt{c_8}\right)s-\sqrt{c_8}\right] $$
(12)

for the k− value,

$$ {k}_{-}=-\left({c}_7+2{c}_3{c}_8\right)-2\sqrt{c_8{c}_9} $$
(13)

Using Eq. (15), we obtain

$$ \tau (s)={c}_1+2{c}_4-\left({c}_2-2{c}_5\right)s-2\left[\left(\sqrt{c_9}+{c}_3\sqrt{c_8}\right)s-\sqrt{{\mathrm{c}}_8}\right] $$
(14)

The physical condition for the bound state solution is τ′ < 0 and thus

$$ {\tau}^{\prime }(s)=-2{c}_3-2\left(\sqrt{c_9}+{c}_3\sqrt{c_8}\right)<0 $$
(15)

with the aid of Eq. (9), we obtain the energy equation as

$$ \left({c}_2-{c}_3\right)n+{c}_3{n}^2-\left(2n+1\right){c}_5+\left(2n+1\right)\left(\sqrt{c_9}+{c}_3\sqrt{c_8}\right)+{c}_7+2{c}_3{c}_8+2\sqrt{c_8{c}_9}=0 $$
(16)
$$ \psi (s)={N}_n{s}^{c_{12}}{\left(1-{c}_3s\right)}^{-{c}_{12}-\frac{c_{13}}{c_3}}{P_n}^{\left({c}_{10}-1,\frac{c_{11}}{c_3}-{c}_{10}-1\right)}\left(1-2{c}_3s\right) $$
(17)

Solutions of Eckart plus inversely quadratic Yukawa potential

Solutions to the radial part of the Schrodinger equation (SE) with Eckart plus inversely quadratic Yukawa potential

To obtain the bound state solutions of Eq. (3), we consider Eq. (17) and obtain

(18a)

Where λ = l(l + 1) and V(r) is the potential energy function.

Eq. (18) can also be expressed as

(18b)

where

$$ {V}_{eff}(r)=V(r)+\frac{l\left(l+1\right){\mathrm{\hbar}}^2}{2{\mu r}^2}=-\eta \frac{e^{-\propto r}}{\left(1-{e}^{-\propto r}\right)}+\zeta \frac{e^{-\propto r}}{{\left(1-{e}^{-\propto r}\right)}^2}-\frac{V_0{e}^{-\propto r}}{r^2}+\frac{l\left(l+1\right){\mathrm{\hbar}}^2}{2{\mu r}^2} $$
(19a)

However, since the SE with the Eckart plus inversely quadratic Yukawa potential has no exact solution, we then use the Greene and Aldrich approximation [3] for the centrifugal term as Hamzavi et al. [16].

$$ \frac{1}{r^2}\approx \frac{\propto^2}{{\left(1-{e}^{-\propto r}\right)}^2} $$
(19b)

which is valid for αr ≪ 1 . Therefore the EIQYP becomes

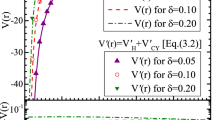
$$ {V}_{eff}(r)=V(r)+\frac{l\left(l+1\right){\mathrm{\hbar}}^2}{2{\mu r}^2}=-\eta \frac{e^{-\propto r}}{\left(1-{e}^{-\propto r}\right)}+\zeta \frac{e^{-\propto r}}{{\left(1-{e}^{-\propto r}\right)}^2}-\frac{V_0{e}^{-\propto r}{\propto}^2}{{\left(1-{e}^{-\propto r}\right)}^2}+\frac{l\left(l+1\right){\mathrm{\hbar}}^2{\propto}^2}{2\mu {\left(1-{e}^{-\propto r}\right)}^2}. $$
(19c)

To test the accuracy of our approximation, we plotted the Eckart plus inversely quadratic Yukawa potential (3) and its approximation (19a) with parameters η = 0.01 MeV, ζ = 0.5 MeV, and V0 = 1.0 MeV at different screening parameters α = 0.01, 0.05, and 0.5 in Fig. 3. In Fig. 1 and Fig. 2, a plot of the Eckart potential and inversely Yukawa potential against internuclear distance ‘r’ at different screening parameters was reported. Additionally, in Fig. 3, Fig. 4, and Fig. 5, the effective potential and its approximation (19c) for angular momentum numbers l = 5, at different screening parameters is demonstrated.

Fig. 1
figure 1

Eckart potentials versus r with η = 0.01 MeV and ζ = 0.5 MeV for parameter α = 0.01, 0.05, 0.5

Full size image
Fig. 2
figure 2

Inversely quadratic Yukawa potentials versus r with V0 = 1.0 MeV for parameter α = 0.01, 0.05, 0.5

Full size image
Fig. 3
figure 3

Effective potential and its approximation for Eckart potentials plus inversely quadratic Yukawa potentials with η = 0.01 MeV and ζ = 0.5 MeV, V0 = 1.0 MeV for parameter α = 0.01 at l = 5

Full size image
Fig. 4
figure 4

Effective potential and its approximation for Eckart potentials plus inversely quadratic Yukawa potentials with η = 0.01 MeV and ζ = 0.5 MeV, V0 = 1.0 MeV for parameter α = 0.5 at l = 5

Full size image
Fig. 5
figure 5

Plot of energy eigenvalues against principal quantum number ‘n’ for 1 ≤ l ≤ 5 at C =  − 0.05 MeV, D =  − 0.1875 MeV, a = 2 MeV, b =  − 1 MeV, and α = 0.01

Full size image

Making the transformation s = e−αreq. (19) becomes

$$ V(s)=-\eta \frac{s}{\left(1-s\right)}+\zeta \frac{s}{{\left(1-s\right)}^2}-\frac{V_0{\propto}^2s}{{\left(1-s\right)}^2}. $$
(20)

Again, applying the same transformation to get the form that NU method is applicable, Eq. (21) gives a generalized hypergeometric-type equation as

$$ \frac{d^2R(s)}{ds^2}+\frac{\left(1-s\right)}{\left(1-s\right)s}\frac{dR(s)}{ds}+\frac{1}{{\left(1-s\right)}^2{s}^2}\left[-\left({\beta}^2+A\right){s}^2+\left(2{\beta}^2+A+B-C\right)s-\left({\beta}^2+\lambda \right)\right]R(s)=0, $$
(21)

Where

$$ \lambda =l\left(l+1\right),-{\beta}^2=\frac{2\mu E}{\alpha^2{\mathrm{\hbar}}^2},A=\frac{2\mu \eta}{\alpha^2{\mathrm{\hbar}}^2},B=\frac{2\mu {V}_0}{{\mathrm{\hbar}}^2},C=\frac{2\mu \zeta}{\alpha^2{\mathrm{\hbar}}^2}. $$
(22)

Hence, comparing Eq. (21) with Eq. (5) yields the following parameters below:

$$ {c}_1={c}_2={c}_3=1,{c}_4=0,{c}_5=-\frac{1}{2},{c}_6=\frac{1}{4}+{\beta}^2+A,{c}_7=-2{\beta}^2-A-B+C,{c}_8={\beta}^2+\lambda, {c}_9=\frac{1}{4}+C-B+\lambda, {c}_{10}=1+2\sqrt{\beta^2+\lambda },{c}_{11}=2+2\left(\sqrt{\frac{1}{4}+C-B+\lambda }+\sqrt{\beta^2+\lambda}\right),{c}_{12}=\sqrt{\beta^2+\lambda },{c}_{13}=-\frac{1}{2}-\left(\sqrt{\frac{1}{4}+C-B+\lambda }+\sqrt{\beta^2+\lambda}\right),{\epsilon}_1=\left({\beta}^2+A\right),{\epsilon}_2=2{\beta}^2+A-B-C,{\epsilon}_3={\beta}^2+\lambda . $$
(23)

Now using Eqs. (5), (22), and (23), we obtain the energy eigen spectrum of the EIQYP as

$$ {\beta}^2={\left[\frac{A+B-C-2\lambda -\left({n}^2+n+\frac{1}{2}\right)-\left(2n+1\right)\sqrt{\frac{1}{4}+C-B+\lambda }}{\left(2n+1\right)+2\sqrt{\frac{1}{4}+C-B+\lambda }}\right]}^2-\lambda $$
(24)

Equation (24) can be solved explicitly and the energy eigen spectrum of EIQYP becomes, for l ≠ 0

$$ E=\frac{\alpha^2{\mathrm{\hbar}}^2}{2\mu}\left\{{\left[\frac{\frac{2\mu \eta}{\alpha^2{\mathrm{\hbar}}^2}+\frac{2\mu {V}_0}{{\mathrm{\hbar}}^2}-\frac{2\mu \zeta}{\alpha^2{\mathrm{\hbar}}^2}-2l\left(l+1\right)-\left({n}^2+n+\frac{1}{2}\right)-\left(2n+1\right)\sqrt{\frac{1}{4}+l\left(l+1\right)+\frac{2\mu \zeta}{\alpha^2{\mathrm{\hbar}}^2}-\frac{2\mu {V}_0}{{\mathrm{\hbar}}^2}}}{\left(2n+1\right)+2\sqrt{\frac{1}{4}+l\left(l+1\right)+\frac{2\mu \zeta}{\alpha^2{\mathrm{\hbar}}^2}-\frac{2\mu {V}_0}{{\mathrm{\hbar}}^2}}}\right]}^2-l\left(l+1\right)\right\} $$
(25a)

also for s-wave state where l = 0

$$ E=\frac{\alpha^2{\mathrm{\hbar}}^2}{2\mu }{\left[\frac{\frac{2\mu \eta}{\alpha^2{\mathrm{\hbar}}^2}+\frac{2\mu {V}_0}{{\mathrm{\hbar}}^2}-\frac{2\mu \zeta}{\alpha^2{\mathrm{\hbar}}^2}-\left({n}^2+n+\frac{1}{2}\right)-\left(2n+1\right)\sqrt{\frac{1}{4}+\frac{2\mu \zeta}{\alpha^2{\mathrm{\hbar}}^2}-\frac{2\mu {V}_0}{{\mathrm{\hbar}}^2}}}{\left(2n+1\right)+2\sqrt{\frac{1}{4}+\frac{2\mu \zeta}{\alpha^2{\mathrm{\hbar}}^2}-\frac{2\mu {V}_0}{{\mathrm{\hbar}}^2}}}\right]}^2 $$
(25b)

We now calculate the radial wave function of the EIQYP as follows.

The weight function ρ(s) is given as

$$ \rho (s)={s}^{c_{10}-1}{\left(1-{c}_3s\right)}^{\frac{c_{11}}{c_3}-{c}_{10}-1}. $$
(26)

Using Eq. (23), we get the weight function as

$$ \rho (s)={s}^U{\left(1-s\right)}^V, $$
(27)

Where \( U=2\sqrt{\beta^2-\lambda } \) and \( V=2\sqrt{\frac{1}{4}+C-B+\lambda .} \)

Also we obtain the wave function χ(s) as

$$ \chi (s)={P}_n^{c_{10}-1,\frac{c_{11}}{c_3}-{c}_{10}-1}\left(1-2{c}_3s\right). $$
(28)

Using Eq. (23), we get the function χ(s) as

$$ \chi (s)={P}_n^{\left(U,V\right)}\left(1-2s\right), $$
(29)

Where \( {P}_n^{\left(U,V\right)} \) are Jacobi polynomials.

Lastly,

$$ \varphi (s)={s}^{c_{12}}{\left(1-{c}_3s\right)}^{-{c}_{12}-\frac{c_{13}}{c_3}}, $$
(30)

and using Eq. (23), we get

$$ \varphi (s)={s}^{\raisebox{1ex}{$U$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\left(1-s\right)}^{\raisebox{1ex}{$V-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}. $$
(31)

We then obtain the radial wave function from the equation

$$ {R}_n(s)={N}_n\varphi (s){\chi}_n(s), $$
(32)
$$ {R}_n(s)={N}_n{s}^{\raisebox{1ex}{$U$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\left(1-s\right)}^{\raisebox{1ex}{$\left(V-1\right)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{P}_n^{\left(U,V\right)}\left(1-2s\right), $$
(33)

Where n is a positive integer and Nn is the normalization constant.

Results and discussion

Figures 6 and 7 show graphically the energy against principal quantum number ‘n’ for different choices of parameters C, D, a, and b at α = 0.01 for 1 ≤ l ≤ 5. As the principal quantum number increases, the energy at various l-states decreases. The explicit bound state energy expression obtained in this work (Eq. (25)) was used to calculate the numerical bound state energies of some selected diatomic molecules (H2, CO, ScH, N2, NO, and CH) using python programming language (version 3.7.7) in an Anaconda navigator environment. The spectroscopic parameters (mainly the dissociation energies and the molecular reduced mass) for the diatomic molecules selected for this work were obtained from previously reported works [17,18,19,20]. In comparison, our numerical results for some of the selected diatomic molecules CO, N2, NO, and CH are in good agreement with the results reported by Ramazan, Sever., and co [19]. The numerical computed bound state energies for the selected diatomic molecules at different n and l are shown in Table 1. From the calculated results, it can be observed that the bound state energies of the diatomic molecules increase as the values of n and l increase. The numerical values of the explicit bound state energies of some of these diatomic molecules for various values of n and l are obtained and compared with the Poisson summation approach [17] and the exact method [18] for H2, CO, ScH, and NO.

Fig. 6
figure 6

Plot of energy eigenvalues against principal quantum number ‘n’ for 1 ≤ l ≤ 5 at C = 0 MeV, D =  − 3.1875 MeV, a = 2 MeV, b =  − 4 MeV, and α = 0.01

Full size image
Fig. 7
figure 7

Plot of energy eigenvalues against principal quantum number ‘n’ for 1 ≤ l ≤ 5 at C =  − 0.05 MeV, D = 0 MeV, a =  − 3 MeV, b = 1 MeV, and α = 0.01

Full size image
Table 1 The energy eigenvalues En, l(ineV) corresponding to the Eckart plus Inversely Quadratic Yukawa Potential (EIQYP) for various principal (n) and angular momentum (l) quantum number
Full size table

Conclusions

In this study, we investigate the solutions of the Schrodinger equation for the mixed proposed potential consisting of the Eckart and Inversely Quadratic Yukawa Potential (EIQYP) by using the Greene and Aldrich type approximation for the centrifugal term. We obtained the energy eigenvalues and the corresponding wave function for several values of the screening parameter for an arbitrary state. To show the accuracy of the approximation used in this study, we plotted graphs of the potentials and its approximation with the PYTHON 3.6 program.