Thermodynamics properties of diatomic molecules with general molecular potential

Abstract

In this paper, the energy spectra of the general molecular potential are obtained using the asymptotic iteration method within the framework of non-relativistic quantum mechanics.With the energy spectrum obtained, the vibrational partition function is calculated in a closed form and is used to obtain an expression for other thermodynamic functions such as vibrational mean energy U, vibrational mean free energy F, vibrational entropy S and vibrational specific heat capacity C. These thermodynamic functions are studied for the electronic state $\mathrm{X}^{1}\Sigma _g^+$ of $K_2$ diatomic molecules.

1 Introduction

The central point of studying the thermodynamics properties of a given system is to calculate its partition function. The partition function, which is a function of temperature, is usually regarded as the distribution function and if it is known, other thermodynamics properties can be obtained from it. The vibrational partition function of diatomic molecules for certain potential models can easily be obtained by calculating the rotation–vibrational energy levels of the system whose applications are widely used in statistical mechanics and molecular physics [1, 2]. Strekalov [3] obtained a closed form expression for the partition function for Morse oscillators. The Morse oscillator has been identified as the simplest and the most realistic oscillator model that has many applications in the description of vibrational state of diatomic molecules [4]. A simple analytic formula for the partition function has been derived by Strekalov [5]. Maximum numbers of vibrational and rotational states are needed to evaluate the partition function for the vibrational and rotational states of diatomic molecules [6]. The resulting partition function had been reported to have been used to calculate the thermodynamic properties of partially ionised and dissociated gas of stellar atmosphere [7]. Recently, Song et al [8] studied the thermodynamic properties of sodium dimer with Rosen–Morse potential and Jia et al [9] investigated the thermodynamic properties of lithium dimer with improved Manning–Rosen potential model. In another development, Jia et al [10] obtained the partition function for improved Tietz oscillators. Different mathematical techniques have been employed by many researchers in evaluating partition function such as Poisson summation fornula [11], commulant expansion method [12], standard method [13] and Wigner–Kirkwood formulation [14]. Motivated by the recent achievement in the determination of the thermodynamic properties of some diatomic molecules, we shall attempt to obtain the rotation–vibrational energy spectrum for the general potential model using asymptotic iteration method (AIM) [15] and use the result to obtain a closed form expression for the partition function which we shall use in calculating other thermodynamic properties of the diatomic molecules.

The general molecular potential (GMP) model is given by [16]

$$\begin{aligned} V(r)=\frac{A-B\mathrm{e}^{-\alpha \left( {r-r_{e} } \right) }+\tilde{q}\left( {C-D\mathrm{e}^{-\alpha \left( {r-r_{e} } \right) }} \right) ^{2}}{\left( {1-q\mathrm{e}^{-\alpha \left( {r-r_{e} } \right) }} \right) ^{2}}, \end{aligned}$$

(1)

where $A,B,C,\alpha$ are adjustable potential parameters, $\tilde{q}$, q are dimensionless parameters and $r_e$ is the equilibrium bond length. To the best of our knowledge, no one has reported the thermodynamic properties of GMP.

2 Ro-vibrational energy spectrum

The radial Schrödinger equation is defined as [17]

$$\begin{aligned} \frac{\mathrm{d}^{2}\psi (r)}{\mathrm{d}r^{2}}+\frac{2\mu }{\hbar ^{2}}\left( {E-V(r)-\frac{J(J+1)\hbar ^{2}}{2\mu r^{2}}} \right) \psi (r)=0, \end{aligned}$$

(2)

where $\mu$ is the reduced mass, E is the ro-vibrational energy, $\hbar$ is the reduced Planck’s constant and J is the rotational quantum number. Substituting eq. (1) into eq. (2) yields,

$$\begin{aligned}&\frac{\mathrm{d}^{2}\psi (r)}{\mathrm{d}r^{2}}+\frac{2\mu }{\hbar ^{2}}\nonumber \\&\quad \times \left( E-\frac{A-B\mathrm{e}^{-\alpha \left( {r-r_e } \right) }+\tilde{q}\left( {C-D\mathrm{e}^{-\alpha \left( {r-r_e } \right) }} \right) ^{2}}{\left( {1-q\mathrm{e}^{-\alpha \left( {r-r_e } \right) }} \right) ^{2}}\right. \nonumber \\&\quad \left. -\frac{J(J+1)\hbar ^{2}}{2\mu r^{2}} \right) \psi (r)=0. \end{aligned}$$

(3)

In order to solve eq. (3), we invoke the following approximation for the centrifugal term $r^{-2}$ as [18]

$$\begin{aligned} \frac{1}{r^{2}}\approx D_0 +\frac{D_1 }{1-q\mathrm{e}^{-\alpha \left( {r-r_e } \right) }}+\frac{D_2 }{\left( {1-q\mathrm{e}^{-\alpha \left( {r-r_e } \right) }} \right) ^{2}}, \end{aligned}$$

(4)

where

$$\begin{aligned} D_0= & {} \frac{\left( {3-\alpha r_e } \right) -2\left( {3+\alpha r_e } \right) q+\left( {3+3\alpha r_e + \alpha ^{2}r_e^2 } \right) q^{2}}{\alpha ^{2}q^{2}r_e^4 }, \nonumber \\ D_1= & {} \frac{2\left( {q-1} \right) ^{2}\left( {-3+\alpha r_e +3q+2\alpha qr_e } \right) }{\alpha ^{2}q^{2}r_e^4 },\nonumber \\ D_2= & {} \frac{\left( {q-1} \right) ^{3}\left[ {3\left( {q-1} \right) +\left( {q+1} \right) \alpha r_e } \right] }{\alpha ^{2}q^{2}r_e^4 }. \end{aligned}$$

(5)

In order to solve eq. (3) with the AIM, then we must transform eq. (3) into the form [15]

$$\begin{aligned} {y}''(x)=\lambda _0 (x){y}'(x)+s_0 (x)y(x). \end{aligned}$$

(6)

To do this, we make a coordinate transformation $z=q\mathrm{e}^{-\alpha \left( {r-r_e } \right) }$ and this transform eq. (3) into the following equation:

$$\begin{aligned}&z\left( {1-z} \right) {\psi }''(z)+\left( {1-z} \right) {\psi }'(z)\nonumber \\&\quad +\frac{1}{z\left( {1-z} \right) }\left\{ {\gamma _1 z^{2}+\gamma _2 z+\gamma _3 } \right\} \psi (z)=0, \end{aligned}$$

(7)

where

$$\begin{aligned} \gamma _1= & {} \frac{2\mu E}{\hbar ^{2}\alpha ^{2}}-\frac{J\left( {J+1} \right) D_0 }{\alpha ^{2}}-\frac{2\mu D^{2}\tilde{q}}{\hbar ^{2}\alpha ^{2}q^{2}}, \nonumber \\ \gamma _2= & {} -\frac{4\mu E}{\hbar ^{2}\alpha ^{2}}+\frac{2J\left( {J+1} \right) D_0 }{\alpha ^{2}}+\frac{J\left( {J+1} \right) D_1 }{\alpha ^{2}}\nonumber \\&+\frac{2\mu B}{\hbar ^{2}q^{2}\alpha ^{2}}+\frac{4\mu CD\tilde{q}}{\hbar ^{2}\alpha ^{2}q^{2}},\nonumber \\ \gamma _3= & {} \frac{2\mu E}{\hbar ^{2}\alpha ^{2}}-\frac{J\left( {J+1} \right) D_0 }{\alpha ^{2}}-\frac{J\left( {J+1} \right) D_1 }{\alpha ^{2}}\nonumber \\&-\frac{J\left( {J+1} \right) D_2 }{\alpha ^{2}}-\frac{2\mu A}{\hbar ^{2}\alpha ^{2}}-\frac{2\mu \tilde{q}C^{2}}{\hbar ^{2}\alpha ^{2}}. \end{aligned}$$

(8)

A close inspection of eq. (7) shows that it has two singular points at $z=0$ and $z=1$. Thus, we can write the solution of eq. (7) as

$$\begin{aligned} \psi (z)=z^{\mu }\left( {1-z} \right) ^{\sigma }f(z). \end{aligned}$$

(9)

Substituting eq. (9) into eq. (7), we obtain

$$\begin{aligned} {f}''(z)= & {} \frac{\left( {2\mu +2\sigma +1} \right) z-\left( {1+2\mu } \right) }{z\left( {1-z} \right) }{f}'(z)\nonumber \\&+\frac{\left( {\sigma ^{2}+2\mu \sigma +\gamma _1 -\gamma _3 } \right) }{z\left( {1-z} \right) }f(z), \end{aligned}$$

(10)

where

$$\begin{aligned}&\mu =i\sqrt{\gamma _3 }, \nonumber \\&\sigma =\frac{1}{2}+\sqrt{\frac{1}{4}-\left( {\gamma _1 +\gamma _2 +\gamma _3 } \right) }. \end{aligned}$$

(11)

Now comparing eqs (10) and (6), we get the values of $\lambda _0 (z)$ and $s_0 (z)$ as follows:

$$\begin{aligned} \lambda _0 (z)= & {} \frac{\left( {1+2\mu +2\sigma } \right) z-\left( {1+2\mu } \right) }{z\left( {1-z} \right) } \nonumber \\ s_0 (z)= & {} \frac{\left( {\sigma ^{2}+2\mu \sigma +\gamma _1 -\gamma _3 } \right) }{z\left( {1-z} \right) }. \end{aligned}$$

(12)

The corresponding ro-vibrational energy spectrum is calculated by means of the quantisation condition [15]. With these, we obtain

$$\begin{aligned}&s_0 \lambda _1 -s_1 \lambda _0 =0\Rightarrow \mu _0 =-\frac{1}{2}\left( {\frac{\gamma _1 -\gamma _3 +\sigma ^{2}}{\sigma }} \right) , \nonumber \\&s_1 \lambda _2 -s_2 \lambda _1 =0\Rightarrow \mu _1 \nonumber \\&\qquad =-\frac{1}{2}\left( {\frac{\gamma _1 -\gamma _3 +\sigma ^{2}+2\sigma +1}{\sigma +1}} \right) , \nonumber \\&s_2 \lambda _3 -s_3 \lambda _2 =0\Rightarrow \mu _2 \nonumber \\&\qquad =-\frac{1}{2}\left( {\frac{\gamma _1 -\gamma _3 +\sigma ^{2}+4\sigma +4}{\sigma +2}} \right) \end{aligned}$$

(13)

and generally for arbitrary n, we have

$$\begin{aligned} \mu _n =\left( {\frac{\gamma _3 -\gamma _1 }{2\left( {\nu +\sigma } \right) }-\frac{\nu +\sigma }{2}} \right) , \end{aligned}$$

(14)

where $\nu$ is the vibrational quantum number.

Using eqs (8) and (11), we obtain the ro-vibrational energy spectrum for the GMP as

$$\begin{aligned} E_{nl} =-\frac{\hbar ^{2}\alpha ^{2}}{2\mu }\left( {\frac{Q_1 }{2\left( {\nu +\sigma } \right) }+\frac{\nu +\sigma }{2}} \right) ^{2}+Q_2 , \end{aligned}$$

(15)

where

$$\begin{aligned} Q_1= & {} \frac{J(J+1)\left( {D_1 +D_2 } \right) }{\alpha ^{2}}\nonumber \\&+\frac{2\mu }{\hbar ^{2}\alpha ^{2}}\left( {\frac{\tilde{q}D}{q^{2}}+A+\tilde{q}C^{2}} \right) , \nonumber \\ Q_2= & {} \frac{J\left( {J+1} \right) \hbar ^{2}}{2\mu }\left( {D_0 +D_1 +D_2 } \right) \nonumber \\&+\left( {A+\tilde{q}C^{2}} \right) . \end{aligned}$$

(16)

3 Partition function and thermodynamic properties

The total contribution of the bound state to the ro-vibrational partition function of a diatomic molecule at temperature T can be written as

$$\begin{aligned} Z\left( \beta \right) =\sum _{\nu =0}^{\nu _{\max } } {\mathrm{e}^{-\beta E_{n,J} }} , \end{aligned}$$

(17)

where $\beta =\left( {k_\mathrm{B} T} \right) ^{-1}$ with $k_\mathrm{B}$ being the Boltzmann constant and $E_{\nu ,J}$ is the rotation–vibrational energy of the $\nu$th bound state. Substituting eq. (16) into eq. (17) gives

$$\begin{aligned} Z\left( \beta \right) =\sum _{\nu =0}^{\nu _{\max } } {\mathrm{e}^{-\beta \left[ {Q_2 -\frac{\hbar ^{2}\alpha ^{2}}{2\mu }\left( {\frac{Q_1 }{2\left( {\nu +\sigma } \right) }+\frac{\nu +\sigma }{2}} \right) ^{2}} \right] }} , \end{aligned}$$

(18)

where

$$\begin{aligned} \nu _{\max } =\sqrt{Q_1 }-\frac{1}{2}\left( {1+\sqrt{1-4\left( {\gamma _1 +\gamma _2 +\gamma _3 } \right) }} \right) .\qquad \end{aligned}$$

(19)

In order to evaluate partition function, we write the Poisson summation formula as [3, 5, 11],

$$\begin{aligned} \sum _{\nu =0}^{\nu _{\max } } {f(n)}= & {} \frac{1}{2}\left[ {f\left( 0 \right) -f\left( {\nu _{\max } +1} \right) } \right] \nonumber \\&+\sum _{m=-\infty }^\infty {\int _0^{\nu _{\max } +1} {f(x)\mathrm{e}^{-i2\pi mx}\mathrm{d}x} }. \end{aligned}$$

(20)

However, for the lowest order approximation, the Poisson summation formula becomes [3, 5, 11]

$$\begin{aligned} \sum _{\nu =0}^{\nu _{\max } } {f(n)} =\frac{1}{2}\left[ {f\left( 0 \right) -f\left( {\nu _{\max } +1} \right) } \right] +\int _0^{\nu _{\max } +1} {f(x)\mathrm{d}x}. \end{aligned}$$

(21)

Applying eq. (21) for the partition function of eq. (18), we get

$$\begin{aligned} Z\left( \beta \right)= & {} \frac{1}{2}\left[ \mathrm{e}^{-\beta \left( {Q_2 -p_1 p_2^2 } \right) }-\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_3^2 } \right) }\right. \nonumber \\&\left. +\int _0^{\nu _{\max } } {\left( {\mathrm{e}^{-a\beta -\frac{b\beta }{\rho ^{2}}-c\beta \rho ^{2}}} \right) \mathrm{d}\rho } \right] \end{aligned}$$

(22)

where

$$\begin{aligned}&p_1 =\frac{\hbar ^{2}\alpha ^{2}}{2\mu },\quad p_2 =\left( {\frac{Q_1 }{2\nu _{\max } }+\frac{\nu _{\max } }{2}} \right) ,\nonumber \\&p_3 =\left( {\frac{Q_1 }{2(\nu _{\max } +1+\sigma )}+\frac{(\nu _{\max } +1+\sigma )}{2}} \right) , \nonumber \\&\rho =x+\sigma ,\quad a=\frac{\hbar ^{2}\alpha ^{2}Q_1^2 }{4\mu }-Q_2 ,\nonumber \\&b =\frac{\hbar ^{2}\alpha ^{2}Q_1^2 }{8\mu },\quad c=\frac{\hbar ^{2}\alpha ^{2}}{4\mu }. \end{aligned}$$

(23)

Evaluating the integral in eq. (22), we obtain the ro-vibrational partition function for the diatomic molecules with GMP model as

$$\begin{aligned} Z\left( \beta \right)= & {} \frac{1}{2}\left[ \mathrm{e}^{-\beta \left( {Q_2 -p_1 p_2^2 } \right) }-\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_3^2 } \right) }\right. \nonumber \\&\left. +\,\mathrm{e}^{-c\beta \rho ^{2}-a\beta }\sqrt{b\beta }\left( \frac{2\nu _{\max } \mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\sqrt{b\beta }}\right. \right. \nonumber \\&\left. \left. +\,\frac{2\sqrt{b\pi \beta }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) }{\sqrt{b\beta }}-2\sqrt{\pi } \right) \right] , \end{aligned}$$

(24)

where $\mathrm{erfi}(x)$ is the imaginary error function defined as [8, 9]

$$\begin{aligned} \mathrm{erfi}(x)=-i\mathrm{erf}(ix)=\frac{2}{\sqrt{\pi }}\int _0^x {\mathrm{e}^{t^{2}}\mathrm{d}t} \end{aligned}$$

(25)

and $\mathrm{erf}(x)$ denotes the error function which is a special function of the sigmoid shape [8, 9]. In Maple software the imaginary error function is given as $\mathrm{erfi}(x)$ and can be used in many numerical calculations.

Fig. 1

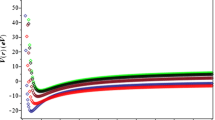
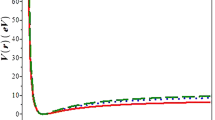
(a) Plot of the exact partition function (eq. (18)) and the semiclassical partition function (eq. (22)) as a function of $\beta$ at $\nu _{\max } =25$, (b) plot of the exact partition function (eq. (18)) and the semiclassical partition function (eq. (22)) as a function of $\beta$ at zero temperature and at $\nu _{\max } =25$ and (c) vibrational partition function Z as a function of $\beta$ for different $\nu _{\max }$.

We have plotted in figure 1a, the exact and semiclassical partition functions as a function of temperature. Also, we have plotted the exact, semiclassical partition including zero temperature in figure  1b. As shown in figure 1a, the semiclassical partition function is very close to the exact partition function. It deviates from exact partition function as the temperature increases. Similarly, as shown in figure 1b the semiclassical partition function deviates from the exact partition function and it is approximately the same at zero temperature.

With the help of the vibrational partition function of eq. (24), we can determine the thermodynamic properties for the potential model as follows:

(1) The vibrational mean energy U

$$\begin{aligned} U(\beta )= & {} -\frac{\partial \ell nZ\left( \beta \right) }{\partial \beta } \nonumber \\= & {} -\left( \frac{1}{2}\mathrm{e}^{-c\rho ^{2}\beta -a\beta }\sqrt{\beta b}\left( \frac{2\nu _{\max } \mathrm{e}^{-\frac{\beta b}{\nu _{\max }^2 }}}{\sqrt{\beta b}}\right. \right. \nonumber \\&\left. \left. +\frac{2\sqrt{\beta b}\mathrm{erf}\left( {\frac{\sqrt{\beta b}}{\nu _{\max } }} \right) }{\sqrt{\beta b}}-2\sqrt{\pi } \right) \right. \nonumber \\&\left. +\frac{1}{2}\left[ {\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_2^2 } \right) }-\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_3^2 } \right) }} \right] \right) ^{-1}\nonumber \\&\times \left[ {\Sigma _1 +\Sigma _2 } \right] , \end{aligned}$$

(26)

where

$$\begin{aligned} \Sigma _1= & {} -\frac{1}{2}\left( {c\rho ^{2}+a} \right) \mathrm{e}^{-c\rho ^{2}\beta -a\beta }\sqrt{\beta b}\left( \frac{2\nu _{\max } \mathrm{e}^{-\frac{\beta b}{\nu _{\max }^2 }}}{\sqrt{\beta b}}\right. \nonumber \\&\left. +\frac{2\sqrt{\pi \beta b}\mathrm{erf}\left( {\frac{\sqrt{\beta b}}{\nu _{\max } }} \right) }{\sqrt{\beta b}}-2\sqrt{\pi } \right) \nonumber \\&+\frac{1}{4}\mathrm{e}^{-c\rho ^{2}\beta -a\beta }\sqrt{\beta b}\left( \frac{2\nu _{\max } \mathrm{e}^{-\frac{\beta b}{\nu _{\max }^2 }}}{\sqrt{\beta b}}\right. \nonumber \\&\left. +\frac{2\sqrt{\pi \beta b}\mathrm{erf}\left( {\frac{\sqrt{\beta b}}{\nu _{\max } }} \right) }{\sqrt{\beta b}}-2\sqrt{\pi } \right) B, \end{aligned}$$

(27)

$$\begin{aligned} \Sigma _2= & {} \frac{1}{2}\mathrm{e}^{-c\rho ^{2}\beta -a\beta }\sqrt{\beta b}\left( \frac{-\nu _{\max } \mathrm{e}^{-\frac{\beta b}{\nu _{\max }^2 }}b}{\left( {b\beta } \right) ^{\frac{3}{2}}}\right. \nonumber \\&\left. -\frac{b^{\frac{3}{2}}\sqrt{\beta \pi }\mathrm{erf}\left( {\frac{\sqrt{\beta b}}{\nu _{\max } }} \right) }{\left( {b\beta } \right) ^{\frac{3}{2}}}+\frac{\sqrt{\beta b}\mathrm{erf}\left( {\frac{\sqrt{\beta b}}{\nu _{\max } }} \right) }{\sqrt{\beta b}}\right. \nonumber \\&\left. -2\sqrt{\pi } \right) +\frac{1}{2}\left( {\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_2^2 } \right) }-\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_3^2 } \right) }} \right) .\nonumber \\ \end{aligned}$$

(28)

(2) Vibrational mean free energy F

$$\begin{aligned} F= & {} -\frac{1}{\beta }\ell nZ\left( \beta \right) =-\frac{1}{\beta }\ell n \left( \frac{1}{2}\left[ \mathrm{e}^{-\beta \left( {Q_2 -p_1 p_2^2 } \right) }-\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_3^2 } \right) }\right. \right. \nonumber \\&\left. \left. +\,\mathrm{e}^{-c\beta \rho ^{2}-a\beta }\sqrt{b\beta }\left( \frac{2\nu _{\max } \mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\sqrt{b\beta }}+\frac{2\sqrt{b\pi \beta }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) }{\sqrt{b\beta }}-2\sqrt{\pi } \right) \right] \right) . \ \ \ \end{aligned}$$

(29)

(3) Vibrational specific heat capacity C

$$\begin{aligned} C= & {} \frac{\partial U}{\partial T}=-k\beta ^{2}\frac{\partial U(\beta )}{\partial \beta } =-k\beta ^{2}\frac{1}{\Gamma }\left( {\frac{\Upsilon }{\Pi }} \right) \ \ \end{aligned}$$

(30)

where

$$\begin{aligned} \Gamma= & {} \left( \frac{1}{2}\mathrm{e}^{-\beta c\rho ^{2}-a\beta }\sqrt{b\beta }\left( \frac{2\nu _{\max } \mathrm{e}^{-\frac{\beta b}{\nu _{\max }^2 }}}{\sqrt{\beta b}} +\frac{2\sqrt{\pi \beta b}\mathrm{erf}\left( {\frac{\sqrt{\beta b}}{\nu _{\max } }} \right) }{\sqrt{\beta b}}-2\sqrt{\pi } \right) +\frac{1}{2}\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_2^2 } \right) }-\frac{1}{2}\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_3^2 } \right) } \right) ^{2},\nonumber \\ \end{aligned}$$

(31)

$$\begin{aligned} \Pi= & {} \left( \frac{1}{2}\mathrm{e}^{-\beta c\rho ^{2}-a\beta }\sqrt{\beta b}\left( \frac{2\nu _{\max } \mathrm{e}^{-\frac{\beta b}{\nu _{\max }^2 }}}{\sqrt{\beta b}}+\frac{2\sqrt{\pi b\beta }\mathrm{erf}\left( {\frac{\sqrt{\beta b}}{\nu _{\max } }} \right) }{\sqrt{\beta b}}-2\sqrt{\pi } \right) +\frac{1}{2}\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_2^2 } \right) }-\frac{1}{2}\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_2^2 } \right) } \right) \nonumber \\&-\left( {\begin{array}{l} \frac{1}{2}\left( {-c\rho ^{2}-a} \right) \mathrm{e}^{-\beta c\rho ^{2}-a\beta }\sqrt{\beta b}\left( {\frac{2\nu _{\max } \mathrm{e}^{-\frac{\beta b}{\nu _{\max }^2 }}}{\sqrt{\beta b}}+\frac{2\sqrt{\pi b\beta }\mathrm{erf}\left( {\frac{\sqrt{\beta b}}{\nu _{\max } }} \right) }{\sqrt{\beta b}}-2\sqrt{\pi }} \right) \\ +\frac{1}{4}\frac{\mathrm{e}^{-\beta c\rho ^{2}-a\beta }}{\sqrt{\beta b}}\left( {\frac{2\nu _{\max } \mathrm{e}^{-\frac{\beta b}{\nu _{\max }^2 }}}{\sqrt{\beta b}}+\frac{2\sqrt{\pi b\beta }\mathrm{erf}\left( {\frac{\sqrt{\beta b}}{\nu _{\max } }} \right) }{\sqrt{\beta b}}-2\sqrt{\pi }} \right) b \\ +\frac{1}{2}\mathrm{e}^{-\beta c\rho ^{2}-a\beta }\sqrt{\beta b}\left( {\begin{array}{l} \frac{-2b\mathrm{e}^{-\frac{\beta b}{\nu _{\max }^2 }}}{\nu _{\max } \sqrt{\beta b}}-\frac{\nu _{\max } b\mathrm{e}^{-\frac{\beta b}{\nu _{\max }^2 }}}{\left( {b\beta } \right) ^{\frac{3}{2}}}+\frac{\sqrt{\pi b\beta }\mathrm{erf}\left( {\frac{\sqrt{\beta b}}{\nu _{\max } }} \right) }{\beta \sqrt{b}}-\frac{b\sqrt{\pi \beta b\beta }\mathrm{erf}\left( {\frac{\sqrt{\beta b}}{\nu _{\max } }} \right) }{\left( {\beta b} \right) ^{\frac{3}{2}}} \\ +\frac{2b\mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\nu _{\max } \sqrt{\beta b}} \\ \end{array}} \right) \\ \\ +\frac{1}{2}\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_2^2 } \right) }-\frac{1}{2}\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_2^2 } \right) } \\ \end{array}} \right) ^{2}, \end{aligned}$$

(32)

$$\begin{aligned} \Upsilon= & {} \left( \frac{1}{2}\left( {-c\rho ^{2}-a} \right) ^{2}\mathrm{e}^{-\beta c\rho ^{2}-a\beta }\sqrt{b\beta }\left( {\frac{2\nu _{\max } \mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\sqrt{b\beta }}+\frac{2\sqrt{\pi b\beta }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) }{\sqrt{b\beta }}-2\sqrt{\pi }} \right) \right) \nonumber \\&+\frac{1}{2}\frac{\left( {-c\rho ^{2}-a} \right) \mathrm{e}^{-\beta c\rho ^{2}-a\beta }}{\sqrt{b\beta }}\left( \frac{2\nu _{\max } \mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\sqrt{b\beta }}+\frac{2\sqrt{\pi b\beta }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) }{\sqrt{b\beta }}-2\sqrt{\pi } \right) b\nonumber \\&+\frac{\sqrt{b\beta }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) }{\beta \sqrt{b}} +\frac{2b\mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\nu _{\max } \sqrt{b\beta }} -\frac{\sqrt{\pi b\beta }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) b}{\left( {b\beta } \right) ^{\frac{3}{2}}} +\left( {-c\rho ^{2}-a} \right) \mathrm{e}^{-\beta c\rho ^{2}-a\beta }\sqrt{b\beta }\nonumber \\&\times \left( {\frac{-2b\mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\sqrt{b\beta }}-\frac{\nu _{\max } b\mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\left( {b\beta } \right) ^{\frac{3}{2}}}} \right) -\frac{1}{8}\frac{\mathrm{e}^{-\beta c\rho ^{2}-a\beta }}{\left( {b\beta } \right) ^{\frac{3}{2}}}\left( \frac{2\nu _{\max } \mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\sqrt{b\beta }}\right. \nonumber \\&\left. +\frac{2\sqrt{b\pi \beta }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) }{\sqrt{b\beta }}-2\sqrt{\pi } \right) b^{2}+\frac{1}{2}\frac{\mathrm{e}^{-\beta c\rho ^{2}-a\beta }}{\sqrt{b\beta }}\left( \frac{-2b\mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\nu _{\max } \sqrt{b\beta }}-\frac{2\nu _{\max } b\mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\left( {b\beta } \right) ^{\frac{3}{2}}}\right. \nonumber \\&\left. +\frac{\sqrt{b\pi \beta }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) }{\beta \sqrt{b}}+\frac{2b\mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\nu _{\max } \sqrt{b\beta }}-\frac{\sqrt{b\pi \beta }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) b}{\left( {b\beta } \right) ^{\frac{3}{2}}}-2\sqrt{\pi } \right) b \nonumber \\&+\frac{1}{2}\mathrm{e}^{-\beta c\rho ^{2}-a\beta }\sqrt{b\beta }\left( {\begin{array}{l} \frac{2b^{2}\mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\nu _{\max }^3 \sqrt{b\beta }}+\frac{2b^{2}\mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\nu _{\max } \left( {b\beta } \right) ^{\frac{3}{2}}}-\frac{1}{2}\frac{\sqrt{b\beta }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) }{\beta ^{\frac{3}{2}}\sqrt{b\beta }}+\frac{3}{2}\frac{\nu _{\max } b^{2}\mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\left( {b\beta } \right) ^{\frac{5}{2}}} \\ -\frac{\sqrt{b\pi }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) b}{\sqrt{\beta }\left( {b\beta } \right) ^{\frac{3}{2}}}+\frac{b\mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\beta \nu _{\max } \left( {b\beta } \right) ^{\frac{1}{2}}}-\frac{2b^{\frac{5}{2}}\mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\nu _{\max }^3 \sqrt{b\beta }}-\frac{2b^{\frac{5}{2}}\mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\nu _{\max } \left( {b\beta } \right) ^{\frac{3}{2}}}+\frac{3}{2}\frac{\sqrt{b\beta \pi }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) b^{2}}{\left( {b\beta } \right) ^{\frac{5}{2}}} \\ \end{array}} \right) \nonumber \\&+\frac{1}{2}\left( {p_1 p_2^2 -Q_2 } \right) ^{2}\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_2^2 } \right) }-\frac{1}{2}\left( {p_1 p_3^2 -Q_2 } \right) ^{2}\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_3^2 } \right) }. \end{aligned}$$

(33)

Fig. 2

Vibrational partition function Z as a function of $\nu _{\max }$ for different $\beta$.

Fig. 3

Vibrational mean energy U as a function of $\beta$ for different $\nu _{\max }$.

(4) Vibrational entropy S

$$\begin{aligned} S= & {} k\ell nZ\left( \beta \right) -k\beta \frac{\partial }{\partial \beta }\ell nZ\left( \beta \right) \nonumber \\= & {} k\ell nZ\left( \beta \right) -\frac{k\beta }{Z\left( \beta \right) }\left( {\Lambda _1 +\Lambda _2 } \right) , \end{aligned}$$

(34)

where

$$\begin{aligned} \Lambda _1= & {} \frac{1}{2}\left( {-c\rho ^{2}-a} \right) \mathrm{e}^{-\beta c\rho ^{2}-a\beta }\sqrt{b\beta }\nonumber \\&\times \left( {\frac{2\nu _{\max } \mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\sqrt{b\beta }}+\frac{2\sqrt{\pi b\beta }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) }{\sqrt{b\beta }}-2\sqrt{\pi }} \right) \nonumber \\&+\frac{1}{4}\frac{\mathrm{e}^{-\beta c\rho ^{2}-a\beta }}{\sqrt{b\beta }}\left( \frac{2\nu _{\max } \mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\sqrt{b\beta }}\right. \nonumber \\&\left. +\frac{2\sqrt{\pi b\beta }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) }{\sqrt{b\beta }}-2\sqrt{\pi } \right) b, \end{aligned}$$

(35)

$$\begin{aligned} \Lambda _2= & {} \frac{1}{2}\mathrm{e}^{-\beta c\rho ^{2}-a\beta }\sqrt{b\beta }\left( \frac{-\nu _{\max } b\mathrm{e}^{-\frac{b\beta }{\nu _{\max }^2 }}}{\left( {b\beta } \right) ^{\frac{3}{2}}}\right. \nonumber \\&\left. +\frac{\sqrt{\pi b}\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) }{\beta \sqrt{b}}-\frac{b^{\frac{3}{2}}\sqrt{\pi \beta }\mathrm{erf}\left( {\frac{\sqrt{b\beta }}{\nu _{\max } }} \right) }{\left( {b\beta } \right) ^{\frac{3}{2}}} \right) \nonumber \\&+\frac{1}{2}\left( {p_1 p_2^2 -Q_2 } \right) ^{2}\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_2^2 } \right) }\nonumber \\&-\frac{1}{2}\left( {p_1 p_3^2 -Q_2 } \right) ^{2}\mathrm{e}^{-\beta \left( {Q_2 -p_1 p_3^2 } \right) }. \end{aligned}$$

(36)

Fig. 4

Vibrational mean energy U as a function of $\nu _{\max }$ for different $\beta$.

Fig. 5

Ro-vibrational entropy S as a function of $\beta$ for different $\nu _{\max }$.

Fig. 6

Vibrational entropy as a function of $\nu _{\max }$ for different $\beta$.

Fig. 7

Vibrational specific heat capacity as a function of $\beta$ for different $\nu _{\max }$.

Fig. 8

Vibrational specific heat capacity as a function of $\nu _{\max }$ for different $\beta$.

Fig. 9

Vibrational free energy F as a function of $\beta$ for different $\nu _{\max }$.

Fig. 10

Vibrational free energy as a function of $\nu _{\max }$ for different $\beta$.

4 Discussions

In this paper, we consider electronic state of the potassium dimer $K_2 ( {\mathrm{X}^{1}\Sigma _g^+ } )$ molecules using the energy eigenvalues of eq. (15). We take into account the GMP with the following potential parameters as [16]

$$\begin{aligned}&A+\tilde{q}C^{2}=D_e , \nonumber \\&\left( {B+2\tilde{q}CD} \right) =2D_e , \nonumber \\&q=-\exp \left( {-\alpha r_e } \right) . \end{aligned}$$

(37)

The experimental values of $\mathrm{X}^{1}\Sigma _g^+$ states of potassium ($K_2 )$ dimer are taken from ref. [19]: $D_e =4400.00\, \mathrm{cm}^{-1},r_e =3.9244\, \mathrm{A}, \alpha =0.0562\times 10^{3}\, \mathrm{cm}^{-1}$ and $\mu =19.4800 \,\mathrm{U}$. Now using these experimental data as our input, we plot the vibrational partition function for the $\mathrm{X}^{1}\Sigma _g^+$ states of $K_2$ for various upper bound vibration quantum number $\nu _{\max } =25,50$ and 75 and temperature $\beta =0.005,0.008$ and 0.01 in figures 1 and 2 respectively. It is observed that the partition function Z monotonically increases as $\beta$ and $\nu _{\max }$ increase for the potassium dimer. We show in figures 3 and 4 the plot of the vibrational mean energy for various values of $\beta$ and $\nu _{\max }$. It shows that the mean energy U decreases monotonically with increasing values of $\beta$ and $\nu _{\max }$. We plotted the entropy S as a function of temperature $\beta$ and upper bound vibration quantum number $\nu _{\max }$ in figures 5 and 6 respectively. It is shown that the entropy S monotonically increases as $\beta$ and $\nu _{\max }$ increase for the potassium dimer. Figures 7 and 8 show the plot of the vibrational specific heat capacity C of potassium dimer. In figure 7 the specific heat capacity C decreases with increase in temperature. However, in figure 8, the specific heat capacity first increases to maximum values and converge as $\nu _{\max }$ is increased. The plot of the mean free energy F is shown in figures 9 and 10. As shown in figure 9 the mean free energy F decreases monotonically with increasing $\nu _{\max }$ while F increases with $\beta$ as shown in figure 10.

5 Conclusions

In this work, we solved the Schrödinger equation with GMP within the framework of asymptotic iteration method and obtained the energy spectra in a closed form. We calculated the vibrational partition function Z in a closed form and used it to study the thermodynamic properties of vibrational mean energy U, vibrational entropy S, vibrational mean free energy F and vibrational specific heat capacity C. We have plotted the behaviour of the thermodynamic functions as a function of temperature $\beta$ and the upper bound vibration quantum number $\nu _{\max }$ for the electronic state $\mathrm{X}^{1}\Sigma _g^+$ of potassium dimer. Finally, the improved Rosen–Morse [20] and Manning–Rosen potentials [21, 22] are all special cases of general molecular potential [16] and this study has many applications in entropy of a gaseous system [23] and in non-central potential model [24].