1 Introduction

The nonlinear Schrödinger (NLS) equation is one of the most important nonlinear models to explain nonlinear phenomena in various scientific fields, including plasma physics [1], Bose–Einstein condensates (BECs) [8, 9], optics [4,5,6,7], hydrodynamics [2], molecular biology [3] and so on.

Recently, a kind of nonautonomous Schrödinger equations with parity-time(PT)-symmetric potentials

$$\begin{aligned} \mathrm{i}\psi _t+\psi _{xx}+g{|\psi |}^2+V_{PT}(x)\psi =0 \end{aligned}$$

has attracted a lot of attention because of its special features and potential applications [18,19,20,21,22,23]. The external potential \( V_{PT} \) is assumed to be complex and satisfies the so-called parity-time(PT)-symmetric condition \(V^*(x)=V(-\,x)\), where \(*\) denotes complex conjugation, see references [15,16,17, 42, 43]. Many kinds of parity-time(PT)-symmetric potentials have been introduced to the NLS equations in fiber and waveguide optics, see [23,24,25, 33,34,35]. Two celebrated examples are the NLS equations with PT-symmetric Scarff-II potential [23, 26,27,28,29, 32] and periodic potential [30, 31], etc.

Recently, various types of vector nonlinear Schrödinger systems have been studied in [8,9,10,11,12,13,14]. It is well known that the scalar soliton is governed by a single nonlinear Schrödinger equation and the vector solitons can be governed by the vector nonlinear Schrödinger systems. The classical model of vector NLS systems is:

$$\begin{aligned} \begin{aligned} \mathrm{i} q_{1,t}+\frac{1}{2}q_{1,xx}+\sigma \left( {|{q_1}|}^2+\alpha {|{q_2}|}^2\right) q_{1}=0,\\ \mathrm{i} q_{2,t}+\frac{1}{2}q_{2,xx}+\sigma \left( \alpha {|{q_1}|}^2+{|{q_2}|}^2\right) q_{2}=0. \end{aligned} \end{aligned}$$
(1.1)

When \(\alpha =1\), (1.1) is the integrable Manakov equation, but (1.1) is not integrable when \( \alpha =2 \). In [12], the authors studied the following integrable vector NLS systems

$$\begin{aligned} \begin{aligned} \mathrm{i}q_{1,t}+\frac{1}{2}q_{1,xx}-{|{q_1}|}^2 q_{1}-2{|{q_2}|}^2 q_{1}+{q_1}^*{q_2}^2=0,\\ \mathrm{i}q_{2,t}+\frac{1}{2}q_{2,xx}-{|{q_2}|}^2 q_{2}-2{|{q_1}|}^2 q_{2}+{q_2}^*{q_1}^2=0. \end{aligned} \end{aligned}$$
(1.2)

Under a linear transformation, Eq. (1.2) was reduced into independent classical nonlinear Schrödinger equation and the stability of (1.2) were discussed in [12]. Other vector NLS systems with various external potentials were also studied, see [37, 40,41,42, 44, 46,47,48].

In [44], the authors studied vector nonlinear Schrödinger equations with PT symmetric potentials:

$$\begin{aligned} \begin{aligned} \mathrm{i} q_{1,t}+q_{1,xx}+g\left( {|{q_1}|}^2+\beta {|{q_2}|}^2\right) q_{1}+V(x)q_{1}=0,\\ \mathrm{i} q_{2,t}+q_{2,xx}+g\left( {|{q_2}|}^2+\beta {| {q_1}|}^2\right) q_{2}+V(x)q_{2}=0, \end{aligned} \end{aligned}$$
(1.3)

where \(q_{1}\) and \(q_{2}\) are complex functions of x, t,  t is the propagation direction, \(g=\pm \,1\), \(\beta \ge 0\) is the cross-phase modulation coefficient, and V(x) is the complex PT symmetric potential. Equation (1.3) could describe two interacting paraxial waves propagating in inhomogeneous nonlinear Kerr media. The authors of [44] obtained a class of exact vector constant-intensity solutions for (1.3) and studied the modulational instability for the solutions. In [44], the authors mentioned that instability for scalar or vector nonlinear Schrödinger equations with complex potentials in the presence of four-wave mixing remained open.

In [45], the authors studied vector nonlinear Schrödinger equations in the presence of four-wave mixing without PT symmetric potentials:

$$\begin{aligned} \begin{aligned} \mathrm{i} q_{1,t}-\beta q_1+\frac{1}{2}q_{1,xx}+\left( {| {q_1}|}^2+a{| {q_2}|}^2\right) q_{1}+\frac{a}{2}{q_1}^*{q_{2}}^2=0,\\ \mathrm{i} q_{2,t}+\beta q_2+\frac{1}{2}q_{2,xx}+\left( {| {q_2}|}^2+a{| {q_1}|}^2\right) q_{2}+\frac{a}{2}{q_2}^*{q_{1}}^2=0. \end{aligned} \end{aligned}$$
(1.4)

where \(q_1\) and \(q_2\) are the appropriately normalized, slowly-varying, complex field envelopes for the transverse electric (TE) and transverse magnetic (TM) polarized waves, respectively. \(\frac{a}{2}\) and a are the coefficients of the four wave mixing (FWM) term and the cross-phase modulation (CPM) term, respectively. It is well known that four-wave mixing (FWM) is an important nonlinear process in the context of silica fibers. Equation (1.4) have been extensively studied in a number of publications, see [45] and the references therein.

In this paper, we consider the following vector nonlinear Schrödinger equations with PT symmetric potentials in the presence of four-wave mixing:

$$\begin{aligned} \begin{aligned} \mathrm{i} q_{1,t}+q_{1,xx}+g\left( {| {q_1}|}^2 q_{1}+2{| {q_2}|}^2 q_{1}-{q_1}^*{q_2}^2\right) +V_1q_1- \mathrm{i}V_2q_2=0,\\ \mathrm{i} q_{2,t}+q_{2,xx}+g\left( {| {q_2}|}^2 q_{2}+2{| {q_1}|}^2 q_{2}-{q_2}^*{q_1}^2\right) +V_1q_2+ \mathrm{i}V_2q_1=0, \end{aligned} \end{aligned}$$
(1.5)

where \({q_1}^*{q_2}^2\), \({q_2}^*{q_1}^2\) are four-wave mixing terms, \(q_1(x,t)\), \(q_2(x,t)\) are complex functions of x, t. \(V_1(x)\), \(V_2(x)\) are complex PT-symmetric potentials, satisfying \(V_1^*(x)=V_1(-\,x)\), \(V_2^*(x)=V_2(-\,x)\), respectively. g characterizes the self-focusing or defocusing Kerr nonlinearity. When \(V_2=0 \), the modulational instability of (1.5) is an open problem proposed in [44] (\(\beta =2\) and \(g_2=-g\) in (53)). There are lots of methods to study soliton solutions for nonlinear evolution equations, such as the inverse scattering method [22], Darboux transformation [35], the Lie method [21] and similarity transformation method [29], see the papers [15, 27, 28, 34, 39, 49, 50] and the references therein. In this paper, by employing a linear transformation as [12], Eq. (1.5) is reduced into two independent classical nonlinear Schrödinger equations with PT potentials. Through the solutions of classical nonlinear Schrödinger equation with PT potentials, we finally obtain soliton solutions for Eq. (1.5). Then we show the stability for soliton waves, under PT-symmetric k-wave-number Scarff-II potential and PT-symmetric multiwell Scarff-II potential. We also find soliton solutions for Eq. (1.5) in high dimensional case.

The organization of this paper is as follows: In Sect. 2, we map the coupled Eq. (1.5) into the independent NLSEs by using the linear transformation, then through solutions of independent NLSEs with PT-symmetric potentials, we get solitary waves of Eq. (1.5). In Sect. 3, we design two interesting PT-symmetric potentials, and obtain the detailed solitary waves. In Sect. 4, we show some soliton solution of Eq. (1.5) in high dimensional case. In Sect. 5, we discuss the stability for the solitary waves obtained in Sect. 3.

2 The linear transformation

In this section, we map the vector nonlinear Schrödinger equation (1.5) into the independent NLSEs by using the linear transformation. Then through solutions of independent NLSE with PT-symmetric potentials, we get solitary waves of Eq. (1.5).

We rewrite the vector NLSE (1.5) into matrix form:

$$\begin{aligned} \mathrm{i}A_t+A_{xx}+gAA^\dag A+EA=0, \end{aligned}$$
(2.1)

where \(\dag \) stands for the Hermite conjugation and

$$\begin{aligned} {\begin{matrix} A=\left( \begin{array}{ll} q_1&{}\quad q_2\\ -\,q_2&{}\quad q_1 \end{array}\right) ,&{}\quad E=\left( \begin{array}{ll} V_1&{} \quad \mathrm{i}V_2\\ -\,\mathrm{i}V_2&{}\quad V_1 \end{array}\right) . \end{matrix}} \end{aligned}$$

Next, we diagonalize the matrix A and E. Choose invertible matrix J as

$$\begin{aligned} J=\begin{pmatrix} \frac{1}{2}&{}\quad \frac{1}{2}\\ -\frac{\mathrm{i}}{2}&{}\quad \frac{\mathrm{i}}{2} \end{pmatrix}, \end{aligned}$$

then

$$\begin{aligned} {\begin{matrix} B:=J^{-1}EJ=\begin{pmatrix} V_1+V_2&{}\quad 0\\ 0&{}\quad V_1-V_2 \end{pmatrix},&{}\quad D:=J^{-1}AJ=\begin{pmatrix} q_1-\mathrm{i}q_2&{}\quad 0\\ 0&{}\quad q_1+\mathrm{i}q_2 \end{pmatrix} \end{matrix}}. \end{aligned}$$

Through transformation,

$$\begin{aligned} A=JDJ^{-1},\quad A^\dag =JD^\dag J^{-1},\quad E=JBJ^{-1}, \end{aligned}$$

Equation (2.1) is reduced into:

$$\begin{aligned} \mathrm{i}D_t+D_{xx}+gDD^\dag D+BD=0. \end{aligned}$$
(2.2)

Let

$$\begin{aligned} q_1=\frac{u_1+u_2}{2},\quad q_2=\frac{u_2-u_1}{2\mathrm{i}}. \end{aligned}$$
(2.3)

We can finally rewrite Eqs. (2.1) or (2.3) into the independent NLS equations about \(u_1\) and \(u_2\):

$$\begin{aligned} \begin{aligned} \mathrm{i} u_{1,t}+u_{1,xx}+g{| u_1|}^2u_1+(V_1-V_2)u_1=0,\\ \mathrm{i} u_{2,t}+u_{2,xx}+g{| u_2|}^2u_2+(V_1+V_2)u_2=0, \end{aligned} \end{aligned}$$
(2.4)

where \( V_1-V_2 \), \( V_1+V_2 \) are still complex PT-symmetric potentials, as \(V_1(x)\), \( V_2(x)\) are complex PT-symmetric potentials.

If we obtain the solutions for (2.4), we will finally obtain the solutions for (1.5) from (2.3).

3 Solutions in the one-dimensional vector NLSEs

In this section, we design two interesting PT-symmetric Scarff-II potentials for Eq. (2.4), including PT-symmetric k-wave-number Scarff-II potential and PT-symmetric multiwell Scarff-II potential [23]. We obtain soliton solutions and plot some figures for the solitary waves.

3.1 PT-symmetric k-wave-number Scarff-II potential

In this subsection, we design the external potentials of Eq. (2.4) into an interesting PT-symmetric k-wave-number Scarff-II potential.

Let

$$\begin{aligned} V_1(x)-V_2(x)=N_1(x)+\mathrm{i}M_1(x),\quad V_1(x)+V_2(x)=N_2(x)+ \mathrm{i}M_2(x), \end{aligned}$$

where the PT-symmetric k-wave-number Scarff-II potential is given as

$$\begin{aligned} \begin{aligned} N_1(x)=N_{01}sech^2(k_1x), \quad \quad M_1(x)=M_{01}sech(k_1x)tanh(k_1x),\\ N_2(x)=N_{02}sech^2(k_2x), \quad \quad M_2(x)=M_{02}sech(k_2x)tanh(k_2x), \end{aligned} \end{aligned}$$
(3.1)

where \( k_1, k_2>0 \) denotes the wave number, \( N_{01}, N_{02}>0 \) and \( M_{01}, M_{02}\in R \). When \(k_1=k_2=1\), \(N_{j}+ \mathrm{i}M_{j} (j=1, 2)\) is the PT-symmetric potential considered in [36].

For the PT-symmetric k-wave-number Scarff-II potential given in (3.1), we could obtain the solutions for Eq. (2.4) as following (see [23]):

$$\begin{aligned} u_1=\sqrt{\frac{1}{g}\left( \frac{{M_{01}}^2}{9{k_1}^2}-N_{01}+2{k_1}^2\right) }sech(k_1x)e^{\mathrm{i}[\varphi _1(x)+{k_1}^2t]}, \end{aligned}$$
(3.2)

where \(g(\frac{{M_{01}}^2}{{9k_1}^2}-N_{01}+2{k_1}^2)>0 \) and \( \varphi _1(x)=\frac{M_{01}}{3{k_1}^2}arctan[sinh(k_1x)] \),

$$\begin{aligned} u_2=\sqrt{\frac{1}{g}\left( \frac{{M_{02}}^2}{9{k_2}^2}-N_{02}+2{k_2}^2\right) }sech(k_2x)e^{\mathrm{i}[\varphi _2(x)+{k_2}^2t]}, \end{aligned}$$
(3.3)

where \( g(\frac{{M_{02}}^2}{9{k_2}^2}-N_{02}+2{k_2}^2)>0 \) and \( \varphi _2(x)=\frac{M_{02}}{3{k_2}^2}arctan[sinh(k_2x)]\).

From (3.2), (3.3) and (2.3),

$$\begin{aligned} q_1=\frac{u_1+u_2}{2},\quad q_2=\frac{u_2-u_1}{2 \mathrm{i}}. \end{aligned}$$

We could obtain that the solutions for the vector NLSE (1.5) are:

$$\begin{aligned} q_1= &\, {} \frac{1}{2}\left( \sqrt{\frac{1}{g}\left( \frac{{M_{01}}^2}{9{k_1}^2}-N_{01} +2{k_1}^2\right) }sech(k_1x)e^{\mathrm{i}[\varphi _1(x)+{k_1}^2t]}\right. \nonumber \\&\left. +\,\sqrt{\frac{1}{g}\left( \frac{{M_{02}}^2}{9{k_2}^2}-N_{02}+2{k_2}^2\right) }sech(k_2x)e^{\mathrm{i}[\varphi _2(x)+{k_2}^2t]}\right) , \end{aligned}$$
(3.4)
$$\begin{aligned} q_2=&\, {} \frac{i}{2}\left( \sqrt{\frac{1}{g}\left( \frac{{M_{01}}^2}{9{k_1}^2}-N_{01}+2{k_1}^2\right) }sech(k_1x)e^{\mathrm{i}[\varphi _1(x)+{k_1}^2t]}\right. \nonumber \\&\left. -\,\sqrt{\frac{1}{g}\left( \frac{{M_{02}}^2}{9{k_2}^2}-N_{02}+2{k_2}^2\right) }sech(k_2x)e^{\mathrm{i}[\varphi _2(x)+{k_2}^2t]}\right) . \end{aligned}$$
(3.5)

Through some calculation, we get the spatial–temporal distribution of \( {| q_1|}^2 \) and \( {| q_2|}^2 \) as:

$$\begin{aligned} {| q_1|}^2= & {} \frac{1}{4g}\left[ \left( \frac{M_{01}^2}{9k_1^2}-N_{01}+2k_1^2\right) sech^2(k_1x)+2 \sqrt{\left( \frac{M_{01}^2}{9k_1^2}-N_{01}+2k_1^2\right) \left( \frac{M_{02}^2}{9k_2^2}-N_{02}+2k_2^2\right) }sech(k_1x)\right. \nonumber \\&\left. sech(k_2x)cos\left[ (\varphi _1-\varphi _2)+(k_1^2-k_2^2)t\right] +\left( \frac{M_{02}^2}{9k_2^2}-N_{02}+2k_2^2\right) sech^2(k_2x)\right] , \\ {| q_2|}^2= & {} \frac{1}{4g}\left[ \left( \frac{M_{01}^2}{9k_1^2}-N_{01} +2k_1^2\right) sech^2(k_1x)-2\sqrt{\left( \frac{M_{01}^2}{9k_1^2} -N_{01}+2k_1^2\right) \left( \frac{M_{02}^2}{9k_2^2}-N_{02}+2k_2^2\right) }sech(k_1x)\right. \nonumber \\&\left. sech(k_2x)cos\left[ (\varphi _1-\varphi _2) +(k_1^2-k_2^2)t\right] +\left( \frac{M_{02}^2}{9k_2^2} -N_{02}+2k_2^2\right) sech^2(k_2x)\right] . \end{aligned}$$

where \((\frac{M_{01}^2}{9k_1^2}-N_{01}+2k_1^2)(\frac{M_{02}^2}{9k_2^2}-N_{02}+2k_2^2)>0\).

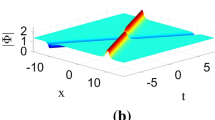
The spatial–temporal distribution of \({| q_1|}^2\) and \({| q_2|}^2\) are ploted in Fig. 1 with \( g=1\), \( N_{01}=5\), \( M_{01}=5.2 \), \( k_{1}=\sqrt{2} \), \( N_{02}=1\), \( M_{02}=0.5 \), \( k_{2}=\frac{1}{\sqrt{2}}\).

Fig. 1
figure 1

\((1-a)\) is the spatial–temporal distribution of \({| q_1|}^2\) with \( g=1\), \( N_{01}=5\), \( M_{01}=5.2 \), \( k_{1}=\sqrt{2} \), \( N_{02}=1\), \( M_{02}=0.5 \), \( k_{2}=\frac{1}{\sqrt{2}}\); \((1-b)\) is the spatial–temporal distribution of \({| q_2|}^2\) with \( g=1\), \( N_{01}=5\), \( M_{01}=5.2 \), \( k_{1}=\sqrt{2} \), \( N_{02}=1\), \( M_{02}=0.5 \), \( k_{2}=\frac{1}{\sqrt{2}}\)

Full size image

3.2 PT-symmetric multiwell Scarff-II potential

In this subsection, we design the external potentials of Eq. (2.4) into anthor meaningful PT-symmetric multiwell Scarff-II potential.

Let

$$\begin{aligned} V_1(x)-V_2(x)=N_1(x)+ \mathrm{i}M_1(x),\quad V_1(x)+V_2(x)=N_2(x)+ \mathrm{i}M_2(x), \end{aligned}$$

where the PT-symmetric multiwell Scarff-II potential is given as

$$\begin{aligned} \begin{aligned} N_1(x)=\left[ \frac{{M_{01}}^2}{9}+2-\sigma cos(\omega x)\right] sech^2(x),\quad \quad M_1(x)=M_{01}sech(x)tanh(x),\\ N_2(x)=\left[ \frac{{M_{02}}^2}{9}+2-\sigma cos(\omega x)\right] sech^2(x),\quad \quad M_2(x)=M_{02}sech(x)tanh(x), \end{aligned} \end{aligned}$$
(3.6)

where \(M_{01}, M_{02}, \sigma \in R\) and \( \omega \ge 0 \) denotes the wave number. When \( \omega =0 \) and \(\sigma =\frac{{M_{01}}^2}{9}+2-N_{01}\), then \(N_{j}+ { \mathrm i}M_{j} (j=1, 2)\) is PT-symmetric potentials considered in [36].

For the given PT-symmetric multiwell Scarff-II potential in (3.6) with \(\omega =0\), \( \sigma =\pm 1\), we could obtain the solutions for Eq. (2.4) as following (see [23]):

$$\begin{aligned} u_1\,= &\, {} sech(x)e^{\mathrm{i}[\varphi _1(x)+t]}, \end{aligned}$$
(3.7)
$$\begin{aligned} u_2\,= &\, {} sech(x)e^{\mathrm{i}[\varphi _2(x)+t]}, \end{aligned}$$
(3.8)

where \( \varphi _1(x)=\frac{M_{01}}{3}arctan[sinh(x)] \), \( \varphi _2(x)=\frac{M_{02}}{3}arctan[sinh(x)] \), and \( g=\pm 1 \).

From (3.7), (3.8) and (2.3), we could obtain that the solutions for the vector NLSE (1.5) are:

$$\begin{aligned} q_1\,= &\, {} \frac{1}{2}\left( e^{\mathrm{i}\varphi _1(x)}+e^{\mathrm{i}\varphi _2(x)}\right) sech(x)e^{\mathrm{i}t}, \end{aligned}$$
(3.9)
$$\begin{aligned} q_2\,= &\, {} \frac{\mathrm{i}}{2}\left( e^{\mathrm{i}\varphi _1(x)}-e^{\mathrm{i}\varphi _2(x)}\right) sech(x)e^{\mathrm{i}t}, \end{aligned}$$
(3.10)

where \( \varphi _1(x)=\frac{M_{01}}{3}arctan[sinh(x)] \), \(\varphi _2(x)=\frac{M_{02}}{3}arctan[sinh(x)]\).

Through some calculation, we get the spatial–temporal distribution of \({| q_1|}^2 \)and \( {| q_2|}^2 \) as:

$$\begin{aligned} {| q_1|}^2\,= &\, {} \frac{1}{4}sech^2(x)[2+2cos(\varphi _2-\varphi _1)],\\ {| q_2|}^2\,= &\, {} \frac{1}{4}sech^2(x)[2-2cos(\varphi _2-\varphi _1)]. \end{aligned}$$

The spatial–temporal distribution of \({| q_1|}^2\) and \( {| q_2|}^2 \) are ploted in Fig. 2 with \( g=1\), \(\omega =0\), \( \sigma =1\), \( M_{01}=0.3 \), \( M_{02}=15.3\).

Fig. 2
figure 2

\((2-a)\) is the spatial–temporal distribution of \({| q_1|}^2\) with \( g=1\), \(\omega =0\), \( \sigma =1\), \( M_{01}=0.3 \), \( M_{02}=15.3\); \((2-b)\) is the spatial–temporal distribution of \({| q_2|}^2\) with \( g=1\), \(\omega =0\), \( \sigma =1\), \( M_{01}=0.3 \), \( M_{02}=15.3\)

Full size image

4 Solutions for the high-dimensional vector NLSEs

Recently, soliton solutions of high dimensional nonlinear evolution equations have also attracted great attention of researchers, see [16, 20, 26, 48]. In this section, we generalize our method to the high-dimensional case. In high dimensional case, Eq. (1.5) takes the form

$$\begin{aligned} \begin{aligned} \mathrm{i}q_{1,t}+\triangle q_1+g\left( {| {q_1}|}^2 q_{1}+2{| {q_2}|}^2 q_{1}-{q_1}^*{q_2}^2\right) +V_1q_1-\mathrm{i}V_2q_2=0,\\ \mathrm{i}q_{2,t}+\triangle q_2+g\left( {| {q_2}|}^2 q_{2}+2{| {q_1}|}^2 q_{2}-{q_2}^*{q_1}^2\right) +V_1q_2+\mathrm{i}V_2q_1=0, \end{aligned} \end{aligned}$$
(4.1)

where \( V_1\) and \(V_2 \) are PT-symmetric potentials, g is a real constant with \(g=\pm 1\), and \(\triangle \) is the Laplace operator.

Through the linear transformation in Sect. 2 [see (2.1), (2.2), (2.3)], Eq. (4.1) is transformed into the independent NLS equations about \(u_1\) and \(u_2\):

$$\begin{aligned} \begin{aligned} \mathrm{i}u_{1,t}+\triangle u+g{| u_1|}^2u_1+(V_1-V_2)u_1=0,\\ \mathrm{i}u_{2,t}+\triangle u+g{| u_2|}^2u_2+(V_1+V_2)u_2=0, \end{aligned} \end{aligned}$$
(4.2)

where \( V_1-V_2 \), \( V_1+V_2 \) are still complex PT-symmetric potentials, since \(V_1\), \( V_2\) are complex PT-symmetric potentials.

4.1 Solutions under 2D PT-symmetric Scarff-II potential

First, we consider the formation of PT bright spatial solitons in two-dimensional symmetric geometries, where \( q_1=q_1(x,y,t)\), \(q_2=q_2(x,y,t) \) are complex functions with respect to \( x, y, t\in R \), \(\triangle =\partial _x^2+\partial _y^2\). The 2D PT-symmetric potential requires the sufficient condition \( V_1^*(x,y)=V_1(-x,-y)\), \( V_2^*(x,y)=V_2(-x,-y)\).

Let

$$\begin{aligned} V_1(x,y)-V_2(x,y)=N_1(x,y)+ \mathrm{i}M_1(x,y),\quad V_1(x,y)+V_2(x,y)=N_2(x,y)+ \mathrm{i}M_2(x,y), \end{aligned}$$

where the generalized 2D PT-symmetric Scarff-II potential is given as:

$$\begin{aligned} \begin{aligned}&N_1(x,y)=\sum _{\eta =x,y}\left( \frac{{M_{01}}^2}{9{k_\eta }^2} +2{k_\eta }^2\right) sech^2(k_\eta \eta )-ga^2\prod _{\eta =x,y}sech^2(k_\eta \eta ),\\&M_1(x,y)=M_{01}\sum _{\eta =x,y}sech(k_\eta \eta )tanh(k_\eta \eta ),\\&N_2(x,y)=\sum _{\eta =x,y}\left( \frac{{M_{02}}^2}{9{k_\eta }^2} +2{k_\eta }^2\right) sech^2(k_\eta \eta )-gb^2\prod _{\eta =x,y}sech^2(k_\eta \eta ),\\&M_2(x,y)=M_{02}\sum _{\eta =x,y}sech(k_\eta \eta )tanh(k_\eta \eta ), \end{aligned} \end{aligned}$$
(4.3)

where \( k_\eta >0 \) are the wave numbers in the x, y directions, and \( M_{01}, M_{02}, a, b \) are real constants. We could obtain the solutions for Eq. (4.2) as following (see [17]):

$$\begin{aligned} u_1(x,y,t)=asech(k_xx)sech(k_yy)e^{\mathrm{i}[\varphi _1+\mu t]}, \end{aligned}$$
(4.4)

where \( \mu ={k_x}^2+{k_y}^2 \) and \( \varphi _1(x,y)=\frac{M_{01}}{3}\sum _{\eta =x,y}{k_\eta }^{-2}arctan[sinh(k_\eta \eta )]\) is the phase.

$$\begin{aligned} u_2(x,y,t)=bsech(k_xx)sech(k_yy)e^{\mathrm{i}[\varphi _2+\mu t]}, \end{aligned}$$
(4.5)

where \( \mu ={k_x}^2+{k_y}^2 \) and \( \varphi _2(x,y)=\frac{M_{02}}{3}\sum _{\eta =x,y}{k_\eta }^{-2}arctan[sinh(k_\eta \eta )]\) is the phase,

From Eq. (2.3), we could obtain that the solutions for the vector NLSE (4.1) are:

$$\begin{aligned} q_1=\frac{u_1(x,y,t)+u_2(x,y,t)}{2},\quad q_2=\frac{u_2(x,y,t)-u_1(x,y,t)}{2 \mathrm{i}}. \end{aligned}$$
(4.6)

Through some computation, we get the spatial–temporal distribution of \( {| q_1|}^2 \) and \( {| q_2|}^2 \) as:

$$\begin{aligned} {| q_1|}^2\,= &\, {} \frac{1}{4}\left( a^2+b^2+2abcos(\varphi _2-\varphi _1)\right) sech^2(k_xx),\\ {| q_2|}^2\,= &\, {} \frac{1}{4}\left( a^2+b^2-2abcos(\varphi _2-\varphi _1)\right) sech^2(k_xx). \end{aligned}$$

The spatial–temporal distribution of \({| q_1|}^2\) and \( {| q_2|}^2 \) are ploted in Fig. 3 with \( k_x=k_y=1 \), \( M_{01}=0.3 \), \( \mu =2 \), \( M_{02}=3 \), \( a=3 \), \(b=0.3\).

Fig. 3
figure 3

\((3-a)\) is the spatial–temporal distribution of \({| q_1|}^2\) with \( k_x=k_y=1 \), \( M_{01}=0.3 \), \( \mu =2 \), \( M_{02}=3 \), \( a=3 \), \(b=0.3\); \((3-b)\) is the spatial–temporal distribution of \({| q_2|}^2\) with \( k_x=k_y=1 \), \( M_{01}=0.3 \), \( \mu =2 \), \( M_{02}=3 \), \( a=3 \), \(b=0.3\)

Full size image

4.2 Solutions under 3D PT-symmetric potential

Second, we consider the three dimensional NLSE with the PT-symmetric potential, where \( q_1=q_1(x,y,z,t) \), \( q_2=q_2(x,y,z,t) \) are complex functions with respect to \( x, y, z, t\in R \), \( \triangle =\partial _x^2+\partial _y^2+\partial _z^2 \). The 3D PT-symmetric potential requires the sufficient condition \( V_1^*(x,y,z)=V_1(-\,x,-\,y,-\,z) \), \( V_2^*(x,y,z)=V_2(-\,x,-\,y,-\,z) \).

Let

$$\begin{aligned} \begin{aligned} V_1(x,y,z)-V_2(x,y,z)=N_1(x,y,z)+ \mathrm{i}M_1(x,y,z),\\ V_1(x,y,z)+V_2(x,y,z)=N_2(x,y,z)+ \mathrm{i}M_2(x,y,z). \end{aligned} \end{aligned}$$

where the generalized 3D PT-symmetric Scarff-II potential is given as:

$$\begin{aligned} \begin{aligned}&N_1(x,y,z)=\sum _{\eta =x,y,z}\left( \frac{{M_{01}}^2}{9{k_\eta }^2} +2{k_\eta }^2\right) sech^2(k_\eta \eta )-ga^2\prod _{\eta =x,y,z}sech^2(k_\eta \eta ),\\&M_1(x,y,z)=M_{01}\sum _{\eta =x,y,z}sech(k_\eta \eta )tanh(k_\eta \eta ),\\&N_2(x,y,z)=\sum _{\eta =x,y,z}\left( \frac{{M_{02}}^2}{9{k_\eta }^2} +2{k_\eta }^2\right) sech^2(k_\eta \eta )-gb^2\prod _{\eta =x,y,z}sech^2(k_\eta \eta ),\\&M_2(x,y,z)=M_{02}\sum _{\eta =x,y,z}sech(k_\eta \eta )tanh(k_\eta \eta ), \end{aligned} \end{aligned}$$
(4.7)

where \( k_\eta >0 \) are the wave numbers in the x, y, z directions, and \( M_{01}, M_{02}, a, b \) are real constants. We could obtain the solutions of Eq. (4.2) as following (see [23]):

$$\begin{aligned} u_1(x,y,z,t)=asech(k_xx)sech(k_yy)sech(k_zz)e^{ \mathrm{i}[\varphi _1+\mu t]}, \end{aligned}$$
(4.8)

where \( \mu ={k_x}^2+{k_y}^2+{k_z}^2\) and the phase is \( \varphi _1(x,y,z)=\frac{M_{01}}{3}\sum _{\eta =x,y,z}{k_\eta }^{-2}arctan[sinh(k_\eta \eta )]\),

$$\begin{aligned} u_2(x,y,z,t)=bsech(k_xx)sech(k_yy)sech(k_zz)e^{ \mathrm{i}[\varphi _2+\mu t]}, \end{aligned}$$
(4.9)

where \( \mu ={k_x}^2+{k_y}^2+{k_z}^2 \) and the phase is \( \varphi _2(x,y,z)=\frac{M_{02}}{3}\sum _{\eta =x,y,z}{k_\eta }^{-2}arctan[sinh(k_\eta \eta )]\).

From Eq. (2.3), we could obtain that the solutions for the vector NLSE (4.1) are:

$$\begin{aligned} q_1=\frac{u_1(x,y,z,t)+u_2(x,y,z,t)}{2},\quad q_2=\frac{u_2(x,y,z,t)-u_1(x,y,z,t)}{2 \mathrm{i}}. \end{aligned}$$
(4.10)

5 Stability of nonlinear modes

In order to analyze the linear stability of the solution in one dimensional case, we compute the linear-stability spectrum for solitary waves by using the numerical methods [12, 38]. First we consider perturbations on the solutions of Eq. (1.5) of the form

$$\begin{aligned} \begin{aligned}&Q_1(x,t)=\left( r_1(x)+[v_1(x)+w_1(x)]e^{\lambda t}+[v_1^*(x)-w_1^*(x)]e^{\lambda ^* t}\right) e^{\mathrm{i}\mu t},\\&Q_2(x,t)=\left( r_2(x)+[v_2(x)+w_2(x)]e^{\lambda t}+[v_2^*(x)-w_2^*(x)]e^{\lambda ^* t}\right) e^{ \mathrm{i} \left( \mu t-\frac{\pi }{2}\right) }, \end{aligned} \end{aligned}$$
(5.1)

where \(r_1(x)e^{\mathrm{i} \mu t},\) \(r_2(x)e^{\mathrm{i} (\mu t-\frac{\pi }{2})} \) are stationary solutions of Eq. (1.5), \(*\) is complex conjugate operator, \(v_1,v_2,w_1,w_2\ll 1 \) are perturbations, and \(\lambda \) indicates the perturbation growth gate.

By inserting the perturbed solution (5.1) into the vector NLSE (1.5) and linearizing it, one could obtain the following linearized eigenvalue problem:

$$\begin{aligned} L\Psi =\lambda \Psi , \end{aligned}$$
(5.2)

where

$$\begin{aligned} L\,= &\, {} i\begin{pmatrix} 0&{}\quad G_1+\partial _{xx}&{}\quad 0&{}\quad G_3\\ G_2+\partial _{xx}&{}\quad 0&{}\quad G_4&{}\quad 0\\ 0&{}\quad G_3&{}\quad 0&{}\quad G_1+\partial _{xx}\\ G_4&{}\quad 0&{}\quad G_2+\partial _{xx}&{}\quad 0 \end{pmatrix}, \quad \Psi =\begin{pmatrix} v_1\\ w_1\\ v_2\\ w_2 \end{pmatrix},\\ G_1= & {} -\,\mu +\left( 2r_1r_1^*+2r_2r_2^*-{r_1}^2-{r_2}^2\right) g+V_1 ,\quad G_3=\left( 2r_1r_2^*+2r_2r_1^*-2r_1r_2\right) g-V_2, \\ G_2= & {} -\mu +\left( 2r_1r_1^*+2r_2r_2^*+{r_1}^2+{r_2}^2\right) g+V_1 ,\quad G_4=\left( 2r_1r_2^*+2r_2r_1^*+2r_1r_2\right) g-V_2, \end{aligned}$$

and \(\lambda \) is the associated eigenvalue of the linear stability operator L.

Since linear stability spectrum is the set of eigenvalues of the linear stability operator of a soliton, the stability of the perturbed soliton of (1.5) is related to the real parts \(Re(\lambda ) \) of all eigenvalues \(\lambda \). The criterion of the linear stability can be given as follows: the stability of the perturbed soliton of the solution is unstable if the eigenvalues satisfy \(Re(\lambda ) >0\), as in this case the eigenmode of the perturbation solution increase exponentially. The solution is stable if the eigenvalues satisfy \(Re(\lambda )<0 \). And \(Re(\lambda )=0\) corresponds to two cases of stability and instability. In order to compute the linear-stability spectrum for solitary waves, we reduce the linearized eigenvalue problem into a matrix eigenvalue problem by applying the Fourier collocation method [12], then we use the QR algorithm to solve the matrix eigenvalue problem.

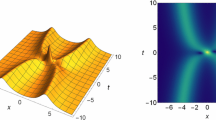
In the following we will present some numerical results to show the solutions of the eigenvalue problem (5.2). Let \(V_1\), \( V_2\) are given as PT-symmetric k-wave-number Scarff-II potential in (3.1), we compute the spectrum for the linear spectral problem (see Fig. 4). It is seen from the figure that the solutions (3.4) and (3.5) are unstable in the sense of linear stability analysis, since some of the eigenvalues contain some positive real parts.

Fig. 4
figure 4

Eigenvalues for linearized eigenvalue problem of Eqs. (3.4) and (3.5) with \( g=1\), \( N_{01}=0.1 \), \( M_{01}=0.6\), \( k_{1}=k_{2}=\sqrt{2}\), \( N_{02}=0.2\), \( M_{02}=9\)

Full size image

Let \(V_1\), \( V_2\) are given as PT-symmetric multiwell Scarff-II potential in (3.6), we compute the spectrum for the linear spectral problem (see Fig. 5). It is clear from the figure that the solutions (3.9) and (3.10) are unstable with the linear analyzing method. In particular, we notice that a series of eigenvalues with positive real parts exist in the linear spectrum.

Fig. 5
figure 5

Eigenvalues for linearized eigenvalue problem of Eqs. (3.9) and (3.10) with \( g=1\), \(\omega =0\), \( \sigma =1\), \( M_{01}=0.3\), \( M_{02}=15.3\)

Full size image

6 Conclusions

In this work, we mainly study the soliton solutions and instability for optical solitions governed by vector nonlinear Schrödinger equations with PT symmetric potential in the presence of four-wave mixing. It is well known that four-wave mixing is an important method for producing phase conjugation and is widely used in photorefractive materials. Firstly, soliton solutions are obtained by means of the linear transformation and two external potentials are considered. Second, the linear stability of solitons under PT-symmetric k-wave-number Scarff-II potential and PT-symmetric multiwell Scarff-II potential is investigated in detail by means of linear spectrum analysis. Finally, the solitons of high dimensional vector NLS equations with PT-symmetric potential in the presence of four-wave mixing are considered. More results about high dimensional case would be discussed in the future.