Nondegenerate soliton dynamics of nonlocal nonlinear Schrödinger equation

Abstract

We obtain the nondegenerate one- and two-soliton solutions of the nonlocal nonlinear Schrödinger equation by using the nonstandard Hirota method. This unconventional method is used to bilinearize the nonlocal nonlinear Schrödinger equation and its related auxiliary equations, and some novel interaction properties of parity-time-symmetric two-soliton solutions are derived. The detailed asymptotic analysis is used to reveal the characteristics of energy conservation and energy redistribution before and after the collision between nondegenerate solitons. Experimental scheme to observe nondegenerate solitons is also proposed. This provides potential applications for the soliton interaction in the nonlocal wave model.

1 Introduction

We all know that nonlinear Schrödinger (NLS) systems are an awfully significant class of nonlinear systems [1,2,3]. The formation of solitons governed by NLS systems [4, 5] benefits from a unique balance between dispersion and nonlinear effects which are the key effect to control the propagation in dispersive media through the cross-phase modulation and coherent energy exchange. So far, different aspects of vector solitons described by NLS systems have been extensively studied [6,7,8]. NLS system is not only used for all-optical switch [9], logical calculation [10] and optical fiber communication system [11]. It also widely appears in atomic condensation [12] and plasma physics [13].

In 2013, a nonclassical integrable nonlocal nonlinear Schrödinger (NNLS) equation was recommended by Mussliani and Ablowitz, and was turned out that it is parity-time(PT)-symmetric [14]. In recent years, the NNLS equation has been deeply studied in nonlinear optics [15,16,17]. Horikis et al. [15] found various elastic interactions between dark solitons or anti-dark solitons of NNLS equation in the continuous wave background. Yang [16] studied bright solitons and multiple solitons of NNLS equation under the framework of Riemann–Hilbert formula. Rao et al. [17] constructed interesting soliton collision dynamics in the zero background of the NNLS equation. To sum up, this nonclassical nonlocal equations have been concluded to dominate multiple types of solutions. From these studies, in all modes, the collisions between solitons with the equivalent wave number have been well discussed [18]. Nevertheless, to our knowledge, this nonlocal equation with specific physical background has not considered to study solitons which govern inconsistent wave numbers. Therefore, we intend to unveil the effect of this supplemental wave number which is applied to the soliton structure and collision scene.

In practical physics, the redistribution of energy between multipeaked solitons is an important topic. In the coupled model, the solution with the identical wave number of a single component is degenerate soliton [19,20,21], while the solution with distinct wave numbers is nondegenerate soliton [22]. Nondegenerate solitons allow multipeaked distribution and can realize the construction of optical logic gates [23]. Stalin et al. introduced unequal wave numbers into several distinct systems such as Manakov system [24] and 2-coupled NLS equations [25] to construct nondegenerate solitons. Later, nondegenerate solitons have also been studied in the multi-component Bose–Einstein condensation(BEC) [26] and so on. The multipeaked structure in nondegenerate solitons has been applied to various nonlinear models of coupled fields [27]. Whether multipeaked nondegenerate solitons are governed by the coupled NNLS(CNNLS), equation is the question that we intend to discuss.

In this paper, we construct the nondegenerate bright solitons of integrable CNNLS system which is derived from a reduction in the Manakov system with specific physical significance [16]. The nonstandard Hirota method [28, 29] of CNNLS equation is introduced in detail in Sect. 2. In Sect. 3, the specific one- and two-soliton solutions of the CNNLS equations are given, and their asymptotic analysis is made in detail to illustrate their soliton dynamics. Next, we also reveal the interesting phenomenon that nondegenerate solitons and degenerate solitons coexist. We summarize the results and discuss how nondegenerate solitons can be realized experimentally. Finally, we introduce the explicit form of some parameters that appear in the paper in the appendix.

2 Hirota method for CNNLS equation with PT symmetry

The traditional coupled NLS equation is

$$ iq_{j,t} + q_{j,xx} + 2\sigma \sum\limits_{p = 1}^{2} {\left| {q_{p} } \right|^{2} } q_{j} = 0,j = 1,2 $$

(1)

with $\sigma = \pm 1$. When $\sigma = 1$, the Manakov system allows various soliton solutions, which can be used to simulate the tunable transmission of optical dielectric solitons and the optimization of optical devices [30]. Optical logic gates which could be NOR gate and OR gate [31] can be constructed theoretically through the energy sharing collision of solitons. This collision also can be used to physical systems, such as non-ideal Bose gas [32], BEC [33], and so on. When $\sigma = - 1$, Eq. (1) becomes the defocusing coupled NLS equation which admits dark–dark and bright–dark soliton solutions[34, 35].

Considering the PT symmetry, CNNLS equation becomes

$$ iq_{j,t} (x,t) + q_{j,xx} (x,t) + 2\sigma \sum\limits_{p = 1}^{2} {[q_{p}^{*} ( - x,t)q_{p} (x,t)q_{p} (x,t)} ] = 0,\;j = 1,2. $$

(2)

In Eq. (2), “$*$” represents the complex conjugation,$x$ and $t$ denote normalized distance and delay time, respectively. The self-induced potential $V = q_{p}^{*} ( - x,t)q_{p} (x,t),p = 1,2$ satisfies the PT symmetry condition $V^{*} ( - x,t) = V(x,t)$, which is the parity-charge symmetry for a more precise statement in Ref. [36], and here, we still use the habitual statement as the PT symmetry. $q_{j} (x,t),j = 1,2$ are two complex functions of real variables $x$ and $t$. Equation (2) which possess the law of conservation of infinite quantity is integrable [14]. After the substitution $x \to - x,t \to - t$, Eq. (2) remains unchanged and has symmetry and complex conjugation. It is obvious that the PT symmetry is one of the properties of the new nonlocal equation, which is equivalent to the invariance of the so-called self-induced potential in classical optics.

The nondegenerate exact solutions of the CNNLS equation will be derived by Hirota method [37]. In this paper, the nonstandard bilinear process [38] is used to generate more general soliton solutions of the CNNLS equation. We first introduce rational transformation

$$ q_{j} (x,t) = \frac{{g^{(j)} }}{f},q_{j}^{*} ( - x,t) = \frac{{h^{(j)} }}{s}, $$

(3)

where $f,s,g^{(j)} ,h^{(j)} ,j = 1,2$ are complex functions. We obtain the bilinear form of Eq. (2) by introducing $S^{(j)} ( - x,t),j = 1,2$. We can match the number of unknown functions with the number of bilinear equations [39] by introducing $S^{(j)} ( - x,t),j = 1,2$. The bilinear form is as follows

$$ \begin{gathered} \left( {iD_{t} \pm D_{x}^{2} } \right)g^{(j)} (h^{(j)} ) \cdot f = \mp 2g^{(j)} (h^{(j)} ) \cdot S^{(j)} , \hfill \\ D_{x}^{2} f(s) \cdot f(s) = 4S^{(j)} \cdot s,j = 1,2. \hfill \\ \end{gathered} $$

(4)

In the above formula, $D_{x}$ and $D_{t}$ are defined by the following expression

$$ D_{x}^{m} D_{t}^{n} (f \cdot g) = (\frac{\partial }{\partial x} - \frac{\partial }{{\partial x^{\prime } }})^{m} (\frac{\partial }{\partial t} - \frac{\partial }{{\partial t^{\prime } }})^{n} f(x,t)g(x^{\prime } ,t^{\prime } )_{{|x = x^{\prime } ,t = t^{\prime } }} . $$

(5)

The auxiliary functions are

$$ S^{(j)} ( - x,t) \cdot M = \sum\limits_{n = 1}^{2} {g^{(n)} } (x,t)h^{(n)} ( - x,t),\;M = \left\{ {\begin{array}{*{20}c} {f^{*} ( - x,t),\;j = 1} \\ {f(x,t),\;j = 2}. \\ \end{array} } \right. $$

(6)

We truncate and expand functions $f,s,g^{(j)} ,h^{(j)} ,j = 1,2$ into

$$ \begin{gathered} g^{(j)} = g_{1}^{(j)} \chi + g_{3}^{(j)} \chi^{3} + ...,h^{(j)} = h_{1}^{(j)} \chi + h_{3}^{(j)} \chi^{3} + ..., \hfill \\ f(s) = 1 + f_{2} \chi^{2} + f_{4} \chi^{4} + ..., \hfill \\ S^{(j)} ( - x,t) = S_{2}^{(j)} \chi^{2} + S_{4}^{(j)} \chi^{4} + ..., \hfill \\ \end{gathered} $$

(7)

and $\chi$ as a parameter of series expansion is used to bring the truncated expansion into the bilinear equation. A set of equations that can be solved is obtained by collecting the coefficients of the same power of $\chi$. Then, these linear partial differential equations are solved recursively, and the relevant explicit form of $f,s,g^{(j)} ,h^{(j)} ,j = 1,2$ obtained constitutes the fundamental soliton solution.

3 Nondegenerate soliton

3.1 One-soliton

3.1.1 Solution expression

We expand the truncated expansion to the following form to get nondegenerate soliton solutions

$$ \begin{gathered} g^{(1)} = \sum\limits_{n = 1}^{2} {} g_{2n - 1}^{{}} \chi^{2n - 1} ,\,h^{(1)} = \sum\limits_{n = 1}^{2} {} h_{2n - 1}^{{}} \chi^{2n - 1} , \hfill \\ f = 1 + \sum\limits_{n = 1}^{2} {} f_{2n} \chi^{2n} ,\,s = 1 + \sum\limits_{n = 1}^{2} {} s_{2n}^{{}} \chi^{2n} ,\,S^{(j)} = \sum\limits_{n = 1}^{2} {} S_{2n}^{(j)} \chi^{2n} ,\;j = 1,2. \hfill \\ \end{gathered} $$

(8)

We consider unequal fundamental solutions of all modes as $g_{1}^{\left( 1 \right)} = \alpha_{1} e^{{\eta_{1} }} ,\;h_{1}^{\left( 1 \right)} = \beta_{1} e^{{\xi_{1} }}$ and set solution forms; thus, one-soliton solution reads

$$ \begin{gathered} q(x,t) = \frac{{g_{1}^{{}} + g_{3}^{{}} }}{{1 + f_{2} + f_{4} }} = \frac{{\alpha_{1} e^{{\eta_{1} }} + A_{1}^{1} e^{{\eta_{1} + \xi_{1} + \overline{\xi }_{1} }} }}{{1 + B_{{_{1} }}^{1} e^{{\eta_{1} + \overline{\eta }_{1} }} + B_{{_{2} }}^{1} e^{{\xi_{1} + \overline{\xi }_{1} }} + C_{1}^{1} e^{{\eta_{1} + \overline{\eta }_{1} + \xi_{1} + \overline{\xi }_{1} }} }}, \hfill \\ q^{*} ( - x,t) = \frac{{h_{1}^{{}} + h_{3}^{{}} }}{{1 + s_{2}^{{}} + s_{4}^{{}} }} = \frac{{\beta_{1} e^{{\xi_{1} }} + A_{{_{1} }}^{2} e^{{\xi_{1} + \eta_{1} + \overline{\eta }_{1} }} }}{{1 + B_{{_{1} }}^{2} e^{{\eta_{1} + \overline{\eta }_{1} }} + B_{{_{2} }}^{2} e^{{\xi_{1} + \overline{\xi }}} + C_{{_{1} }}^{2} e^{{\eta_{1} + \overline{\eta }_{1} + \xi_{1} + \overline{\xi }_{1} }} }}, \hfill \\ \end{gathered} $$

(9)

where $\eta_{1} ,\xi_{1}$ the wave number of soliton, which affects the velocity of soliton motion. $\overline{\eta }_{1} ,\overline{\xi }_{1}$ represent the complex conjugate of wave number $\eta_{1} ,\xi_{1}$. $A_{1}^{m} ,B_{m}^{n} ,C_{1}^{m}$ are parameters that cannot be missing in the one-soliton of the required solution. The detailed expressions of $\eta_{1} ,\overline{\eta }_{1} ,\xi_{1} ,\overline{\xi }_{1} ,A_{1}^{m} ,B_{m}^{n} ,C_{1}^{m}$ are listed in the appendix. When $\kappa_{1} = \iota_{1}$, the degenerate one-soliton solutions are the same as that obtained in [40].

3.1.2 Asymptotic analysis

We study the dynamics of nondegenerate solitons by making the following asymptotic analysis of solitons. We consider Eq. (8) with conditions $\kappa_{1R}^{1} > 0,\kappa_{2R}^{1} < 0,\kappa_{2I}^{1} > \kappa_{1I}^{1} > 0$ and apply the asymptotic form of wave number $\xi_{1R} ,\overline{\xi }_{1R}$ in (9). The following asymptotic expression for one-soliton is obtained by considering the dominant term alone:

Before(After) collision:$t \to \mp \infty ,\eta_{1R} ,\overline{\eta }_{1R} \sim 0,\xi_{1R} ,\overline{\xi }_{1R} \to \mp \infty ,$

$$ \begin{gathered} q(x,t) \sim \frac{{\alpha_{1} e^{{\eta_{1} }} }}{{1 + B_{{_{1} }}^{1} e^{{\eta_{1} + \overline{\eta }_{1} }} }} = \frac{{2a_{{_{j} }}^{1 - } \kappa_{1R}^{1} e^{{\frac{{\overline{\eta }_{1R} - \eta_{1R} }}{2} + \frac{{i(\overline{\eta }_{1I} - \eta_{1I} )}}{2}}} }}{{2i[\cosh (\phi_{{_{1} }}^{ \mp } )\cos (\phi_{{_{2} }}^{ \mp } ) + i\sinh (\phi_{{_{1} }}^{ \mp } )\sin (\phi_{{_{2} }}^{ \mp } )]}}, \hfill \\ q^{*} ( - x,t) \sim \frac{{\beta_{1} e^{{\xi_{1} }} }}{{1 + B_{{_{1} }}^{1} e^{{\xi_{1} + \overline{\xi }_{1} }} }} = \frac{{2a_{{_{j} }}^{2 - } \kappa_{2R}^{1} e^{{\frac{{\overline{\xi }_{1R} - \xi_{1R} }}{2} + \frac{{i(\overline{\xi }_{1I} - \xi_{1I} )}}{2}}} }}{{2i[\cosh (\varphi_{{_{1} }}^{ \mp } )\cos (\varphi_{{_{2} }}^{ \mp } ) + i\sinh (\varphi_{{_{1} }}^{ \mp } )\sin (\varphi_{{_{2} }}^{ \mp } )]}}, \hfill \\ \end{gathered} $$

(10)

where $\phi_{{_{1} }}^{ \pm } = \frac{{\overline{\eta }_{1R} + \eta_{1R} + \Delta_{{_{R} }}^{ \pm } }}{2},\phi_{{_{2} }}^{ \pm } = \frac{{\overline{\eta }_{1I} + \eta_{1I} + \Delta_{{_{I} }}^{ \pm } }}{2},\varphi_{{_{1} }}^{ \pm } = \frac{{\overline{\xi }_{1R} + \xi_{1R} + \Delta_{{_{R} }}^{ \pm } }}{2},\varphi_{{_{2} }}^{ \pm } = \frac{{\overline{\xi }_{1I} + \xi_{1I} + \Delta_{{_{I} }}^{ \pm } }}{2},$$a_{{_{j} }}^{1 \pm } = \frac{i}{{\kappa_{1}^{1} + \overline{\kappa }_{1}^{1} }}e^{{\ln \alpha - \frac{{\Delta^{ \pm } }}{2}}} ,a_{{_{j} }}^{2 \pm } = \frac{i}{{\kappa_{2}^{1} + \overline{\kappa }_{2}^{1} }}e^{{\ln \beta - \frac{{\hat{\Delta }^{ \pm } }}{2}}} ,\Delta^{j - } = \ln a_{1}^{j} ,\Delta^{j + } = \ln C_{{_{1} }}^{j} - \ln B_{{_{1} }}^{j} ,l,j = 1,2.$

From the above asymptotic analysis, we can conclude that $a_{j}^{l} (\kappa_{l}^{1} + \overline{\kappa }_{l}^{1} )/2i,a_{j}^{1} = \alpha_{1}$ $/\sqrt {\left| {\alpha_{1} \beta_{1} } \right|^{2} } ,$ $a_{j}^{2} = \beta_{1} /\sqrt {\left| {\alpha_{1} \beta_{1} } \right|^{2} } ,j,l = 1,2$ are the complex amplitudes of the solitons. The unit polarization vectors $a_{j}^{l} ,j,l = 1,2$ are given in Eq. (10). The central position is $\Delta_{R} /\kappa_{1}^{1} + \overline{\kappa }_{1}^{1}$.

3.1.3 Dynamics of nondegenerate one-solitons

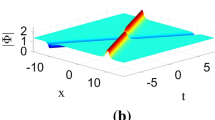
The real part of the wave number influences the velocity of the soliton and thus, affects the distance between the solitons in Ref.[41]. Nevertheless, we find that not only the real part of the wave number can affect the velocity of the solitons in the CNNLS equations, but also the imaginary part of the wave number can. The quasi-intensity of nondegenerate one-soliton is shown in Figs. 1 and 2, respectively.

Fig. 1

Nondegenerate one-soliton. a Value of the wave number of soliton, and quasi-intensity of nondegenerate one-soliton with, b$\left| {{\text{Im}} (\kappa_{1}^{1} )} \right| = \left| {{\text{Im}} (\kappa_{2}^{1} )} \right| = 0.1,$ c$\left| {{\text{Im}} (\kappa_{1}^{1} )} \right| = 0.4,\left| {{\text{Im}} (\kappa_{2}^{1} )} \right| = 0.2,$ d$\left| {{\text{Im}} (\kappa_{1}^{1} )} \right|{ = }\left| {{\text{Im}} (\kappa_{2}^{1} )} \right| = 0.45$. Other parameters are $\alpha_{1} = 0.45$$+ 0.5i,\;\alpha_{2} = 0.5 + 0.55i,\;{\text{Re}} \left( {\kappa_{j}^{1} } \right) = 0.4$

Fig. 2

Nondegenerate one-soliton. a Value of the wave number of soliton, and quasi-intensity of nondegenerate one-soliton with, b${\text{Re}} (\kappa_{1}^{1} ) = {\text{Re}} (\kappa_{2}^{1} ) = 0.4,$ c ${\text{Re}} (\kappa_{1}^{1} ) = 0.3,{\text{Re}} (\kappa_{2}^{1} ) = 0.35,$ d ${\text{Re}} (\kappa_{1}^{1} ) = {\text{Re}} (\kappa_{2}^{1} ) = 0.3$. Other parameters are $\alpha_{1} = 0.45 + 0.5i,$$\alpha_{2} = 0.5 + 0.55i,\left| {{\text{Im}} (\kappa_{j}^{1} )} \right| = 0.1.$

Figure 1a shows the wave number of soliton for two components [39] when we fix the real part of the wave number to 0.4 and adjust the value of the corresponding imaginary part. Here, ${\text{Re}}$ and ${\text{Im}}$ represent the real and imaginary part of the wave number $w$. Points C and D in Fig. 1a correspond to Fig. 1b, points B and E correspond to Fig. 1c, and points A and F correspond to Fig. 1d. From Fig. 1a, when the real part of the wave number affecting the soliton velocity is fixed, the farther the value of imaginary part is from 0, the closer two peaks are. Furthermore, with the increase in the absolute value of the imaginary part, the distance between two peaks will continue to shorten, and finally, change from a double-peaked structure to a single-peaked structure from Fig. 1b, c and d. We will get the symmetric structure when the absolute values of the imaginary parts are equal.

However, the effect of the real part of the wave number on the distance between the two peaks is just opposite to the imaginary part of the wave number. Figure 2a shows the wave number of soliton for two components when we fix the imaginary part of the wave number to 0.1 and adjust the value of the corresponding real part. Points B and E in Fig. 2a correspond to Fig. 2b, points A and D correspond to Fig. 2c, and points A and C correspond to Fig. 2d. When the value of real part decreases, the distance between two peaks will also be shortened, and the double-peaked structure will eventually become a single peak in Fig. 2b–d. Correspondingly, we will obtain the symmetric structure when the real parts are the same. We find the condition of the double-peaked soliton state for both components. That is, when the absolute value of the imaginary part of the wave number is small enough or the real part is large enough, the nondegenerate soliton will have a double-peaked structure. When the tunable double-peaked nondegenerate soliton is used as the signal carrier, a communication system with four stages (00, 01, 10, 11) can be realized [23].

3.2 Two-soliton

3.2.1 Solution expression

We truncate and expand equations to the following number of terms

$$ \begin{gathered} g^{(1)} = \sum\limits_{n = 1}^{4} {} g_{2n - 1}^{{}} \chi^{2n - 1} ,h^{(1)} = \sum\limits_{n = 1}^{4} {} h_{2n - 1}^{{}} \chi^{2n - 1} ,f = 1 + \sum\limits_{n = 1}^{4} {} f_{2n} \chi^{2n} , \hfill \\ s = 1 + \sum\limits_{n = 1}^{4} {} s_{2n}^{{}} \chi^{2n} ,S^{(j)} = \sum\limits_{n = 1}^{4} {} S_{2n}^{(j)} \chi^{2n} ,j = 1,2. \hfill \\ \end{gathered} $$

(11)

We give the seed solution

$$ g_{1}^{{}} = \alpha_{12} e^{{\xi_{1} }} + \alpha_{22} e^{{\xi_{2} }} ,h_{1}^{{}} = \alpha_{11} e^{{\eta_{1} }} + \alpha_{21} e^{{\eta_{2} }} . $$

(12)

and derive the nondegenerate two-soliton solution

$$ \begin{gathered} q(x,t) = \frac{{g_{1}^{{}} + g_{3}^{{}} + g_{5}^{{}} + g_{7}^{{}} }}{{1 + f_{2} + f_{4} + f_{6} + f_{8} }}, \hfill \\ q^{*} ( - x,t) = \frac{{h_{1}^{{}} + h_{3}^{{}} + h_{5}^{{}} + h_{7}^{{}} }}{{1 + s_{2}^{{}} + s_{4}^{{}} + s_{6}^{{}} + s_{8}^{{}} }}, \hfill \\ \end{gathered} $$

(13)

where $g_{1} = \alpha_{12} e^{{\xi_{1} }} + \alpha_{22} e^{{\xi_{2} }} ,h_{1} = \alpha_{11} e^{{\eta_{1} }} + \alpha_{21} e^{{\eta_{2} }} ,g_{3} = \sum\limits_{m,n,p = 1}^{2} {D_{m}^{n\left( p \right)} e^{{\eta_{n} + \xi_{m} + \overline{\xi }_{p} }} + E_{m}^{1} e^{{\eta_{1} + \eta_{2} + \overline{\eta }_{m} }} } ,$

$$ \begin{gathered} h_{3} = \sum\limits_{m,n,p = 1}^{2} {d_{m}^{n\left( p \right)} e^{{\eta_{n} + \xi_{m} + \overline{\xi }_{p} }} + E_{m}^{2} e^{{\eta_{1} + \eta_{2} + \overline{\eta }_{m} }} } ,\;g_{5} = \sum\limits_{m,n,M = 1}^{2} {J_{1M2m}^{{{\text{mn}}}} e^{{\overline{\eta }_{n} + \eta_{m} + \overline{\xi }_{n} + \xi_{m} + \eta_{M} }} } ,\;h_{5} = \sum\limits_{m,n,M = 1}^{2} {j_{1M2m}^{{{\text{mn}}}} e^{{\overline{\eta }_{n} + \eta_{m} + \overline{\xi }_{n} + \xi_{m} + \xi_{M} }} } , \hfill \\ g_{7} = \sum\limits_{m = 1}^{2} {K_{m} e^{{\eta_{1} + \overline{\eta }_{m} + \eta_{2} + \xi_{1} + \overline{\xi }_{1} + \xi_{2} + \overline{\xi }_{2} }} } ,\;h_{7} = \sum\limits_{m = 1}^{2} {L_{m} e^{{\eta_{1} + \overline{\eta }_{1} + \eta_{2} + \overline{\eta }_{2} + \xi_{1} + \overline{\xi }_{m} + \xi_{2} }} } ,\;f_{2} = s_{2} { = }\sum\limits_{m,n = 1}^{2} {N_{m}^{n} } e^{{\eta_{m} + \overline{\eta }_{n} }} + P_{m}^{n} e^{{\xi_{m} + \overline{\xi }_{n} }} , \hfill \\ f_{4} = s_{4} = \sum\limits_{m,n,M,N = 1}^{2} {F_{1M2N}^{{{\text{mn}}}} e^{{\eta_{M} + \overline{\eta }_{m} + \xi_{N} + \overline{\xi }_{n} }} } + F_{1} e^{{\eta_{1} + \overline{\eta }_{1} + \eta_{2} + \overline{\eta }_{2} }} + F_{2} e^{{\xi_{1} + \overline{\xi }_{1} + \xi_{2} + \overline{\xi }_{2} }} ,\;f_{6} = s_{6}^{{}} = H_{{{\text{mn}}}}^{1} e^{{\eta_{m} + \overline{\eta }_{m} + \eta_{n} + \overline{\eta }_{n} + \overline{\xi }_{m} + \xi_{n} }} + H_{mn}^{2} e^{{\overline{\xi }_{m} + \xi_{m} + \overline{\xi }_{n} + \xi_{n} + \eta_{m} + \overline{\eta }_{n} }} , \hfill \\ f_{8} = s_{8} = {\text{Me}}^{{\eta_{1} + \overline{\eta }_{1} + \eta_{2} + \overline{\eta }_{2} + \xi_{1} + \overline{\xi }_{1} + \xi_{2} + \overline{\xi }_{2} }} . \hfill \\ \end{gathered} $$

(14)

In the above formula, superscript “−” represents the conjugate. The detailed form of $N_{m}^{n} ,P_{m}^{n} ,D_{m}^{n\left( p \right)} ,d_{m}^{n\left( p \right)} ,E_{m}^{n} ,J_{1M2m}^{mn} ,j_{1M2m}^{mn} ,K_{m} ,L_{m} ,C_{1}^{n} ,F_{1M2N}^{mn} ,F_{n} ,H_{mn}^{1} ,H_{mn}^{2}$ with $m,n,p,M,N = 1,2$ is given in the appendix. In [39], the soliton dynamics of degenerate two-soliton solutions in [40] are introduced, including soliton collisions, bound state solitons. When we set $\kappa_{j} = \iota_{j} ,j = 1,2$, we can obtain degenerate two-soliton solution. We can obtain the soliton dynamics that are completely consistent with the degenerate two-soliton solution when we take the same parameters in [39].

3.2.2 Asymptotic analysis

We consider the interaction of nondegenerate two-solitons by making a detailed asymptotic analysis of nondegenerate two-soliton solutions (13). We derive the explicit form of two-soliton at limit $t \to \mp \infty$ with $\kappa_{lR}^{j} > 0,j,l = 1,2.\kappa_{1I}^{j} < \kappa_{2I}^{j}$. The wave numbers $\eta_{jR} = - \kappa_{jI} (x + 2\kappa_{jR} t),$ $\xi_{jR} = - \iota_{jI} (x + 2\iota_{jR} t)$ gradually behave as (i) soliton $S_{1}$: $t \to \mp \infty ,\eta_{1R} ,\xi_{1R} \simeq 0,\eta_{2R} ,\xi_{2R} \to \pm \infty ,$ and (ii) soliton $S_{2}$:$t \to \mp \infty ,\eta_{1R} ,\xi_{1R} \simeq 0,\eta_{2R} ,\xi_{2R} \to \pm \infty$.

Correspondingly, two solitons have the following asymptotic form.

Before collision: $t \to - \infty ,\eta_{1R} ,\xi_{1R} \simeq 0,\eta_{2R} ,\xi_{2R} \to - \infty$,

$$ \begin{gathered} S_{j} :q_{1} (x,t) \simeq \frac{{2a_{j}^{1 - } \kappa_{jR} e^{{i(\eta_{jI} + d\theta_{1}^{ - } )}} \cosh (\xi_{jR} + \Phi_{{_{1} }}^{j1} )}}{{\sqrt {b_{22}^{ - j} /b_{21}^{ + j} } \cosh (\eta_{jR} + \xi_{jR} + \phi_{1}^{j1} ) + \sqrt {b_{12}^{ + j} /b_{11}^{ - j} } \cosh (\eta_{jR} - \xi_{jR} + \phi_{2}^{j1} )}}, \hfill \\ q_{2} (x,t) \simeq \frac{{2a_{j}^{2 - } \iota_{jR} e^{{i(\xi_{jI} + d\theta_{2}^{ - } )}} \cosh (\eta_{jR} + \Phi_{2}^{j1} )}}{{\sqrt {b_{22}^{ - j} /b_{12}^{ + j} } \cosh (\eta_{jR} + \xi_{jR} + \phi_{1}^{j1} ) + \sqrt {b_{21}^{ + j} /b_{11}^{ - j} } \cosh (\eta_{jR} - \xi_{jR} + \phi_{2}^{j1} )}}, \hfill \\ \end{gathered} $$

(15)

$$ \begin{gathered} e^{{i\theta_{j}^{ - } }} = \frac{{(\kappa_{2}^{1} - \kappa_{2}^{2} )(\kappa_{j}^{1} + \overline{\kappa }_{j}^{2} )(\kappa_{2}^{2} + \overline{\kappa }_{2}^{1} )^{p} (\kappa_{1}^{1} - \kappa_{1}^{2} )^{p} \sqrt {(\kappa_{1}^{l} - \kappa_{2}^{j} )(\kappa_{l}^{1} + \overline{\kappa }_{j}^{2} )} }}{{(\overline{\kappa }_{2}^{1} - \overline{\kappa }_{2}^{2} )(\overline{\kappa }_{j}^{1} + \kappa_{j}^{2} )(\kappa_{2}^{1} + \overline{\kappa }_{2}^{2} )^{p} (\overline{\kappa }_{1}^{1} - \overline{\kappa }_{1}^{2} )^{p} \sqrt {(\overline{\kappa }_{1}^{l} - \overline{\kappa }_{2}^{j} )(\kappa_{j}^{2} + \overline{\kappa }_{l}^{1} )} }}, \hfill \\ e^{{i\theta_{j}^{ + } }} = \frac{{(\kappa_{j}^{1} - \kappa_{j}^{2} )(\kappa_{j}^{2} + \overline{\kappa }_{j}^{1} )\sqrt {(\kappa_{1}^{j} - \kappa_{2}^{l} )(\kappa_{l}^{2} + \overline{\kappa }_{j}^{1} )} }}{{(\overline{\kappa }_{j}^{1} - \overline{\kappa }_{j}^{2} )(\kappa_{j}^{1} + \overline{\kappa }_{j}^{2} )\sqrt {(\overline{\kappa }_{1}^{j} - \overline{\kappa }_{2}^{l} )(\kappa_{1}^{j} + \overline{\kappa }_{2}^{l} )} }},d = \left\{ {\begin{array}{*{20}c} {0,j = 1} \\ {1,j = 2} \\ \end{array} } \right.,p = \left\{ {\begin{array}{*{20}c} {1,j = 1} \\ {0,j = 2} \\ \end{array} } \right.,j,l = 1,2,j \ne l. \hfill \\ \end{gathered} $$

After collision: $t \to + \infty ,\eta_{1R} ,\xi_{1R} \simeq 0,\eta_{2R} ,\xi_{2R} \to + \infty$,

$$ \begin{gathered} S_{j} :q_{1} (x,t) \simeq \frac{{2a_{j}^{1 + } \kappa_{jR} e^{{i(\eta_{1I} + d\theta_{1}^{ + } )}} \cosh (\xi_{jR} + \Phi_{{_{1} }}^{j2} )}}{{\sqrt {b_{22}^{ - j} /b_{21}^{ + j} } \cosh (\eta_{jR} + \xi_{jR} + \phi_{1}^{j2} ) + \sqrt {b_{12}^{ + j} /b_{11}^{ - j} } \cosh (\eta_{jR} - \xi_{jR} + \phi_{2}^{j2} )}}, \hfill \\ q_{2} (x,t) \simeq \frac{{2a_{j}^{2 + } \iota_{jR} e^{{i(\xi_{1I} + d\theta_{2}^{ + } )}} \cosh (\eta_{jR} + \Phi_{2}^{j2} )}}{{\sqrt {b_{22}^{ - j} /b_{12}^{ + j} } \cosh (\eta_{jR} + \xi_{jR} + \phi_{1}^{j2} ) + \sqrt {b_{21}^{ + j} /b_{11}^{ - j} } \cosh (\eta_{jR} - \xi_{jR} + \phi_{2}^{j2} )}}, \hfill \\ \end{gathered} $$

(16)

$$ \begin{gathered} b_{mn}^{ \pm j} = N \pm M,M = \left\{ {\begin{array}{*{20}c} {\kappa_{2}^{j} ,n = 1} \\ {\overline{\kappa }_{2}^{j} ,n = 2} \\ \end{array} } \right.,N = \left\{ {\begin{array}{*{20}c} {\kappa_{1}^{j} ,m = 1} \\ {\overline{\kappa }_{1}^{j} ,m = 2} \\ \end{array} } \right. \hfill \\ a_{1}^{1\Delta } = \sqrt {\alpha_{11} /\alpha_{110} } ,a_{1}^{2\Delta } = \sqrt {\alpha_{12} /\alpha_{120} } ,a_{2}^{1\Delta } = i^{p} \sqrt {\alpha_{21} /\alpha_{210} } ,a_{2}^{2\Delta } = i^{p + 1} \sqrt {\alpha_{22} /\alpha_{220} } ,p = \left\{ {\begin{array}{*{20}c} {1,\Delta = - } \\ {0,\Delta = + } \\ \end{array} } \right. \hfill \\ \end{gathered} $$

$$ e^{{i\theta_{1}^{ + } }} = \frac{{(\kappa_{1}^{1} - \kappa_{1}^{2} )(\kappa_{1}^{2} + \overline{\kappa }_{1}^{1} )\sqrt {(\kappa_{1}^{1} - \kappa_{2}^{2} )(\kappa_{2}^{2} + \overline{\kappa }_{1}^{1} )} }}{{(\overline{\kappa }_{1}^{1} - \overline{\kappa }_{1}^{2} )(\kappa_{1}^{1} + \overline{\kappa }_{1}^{2} )\sqrt {(\overline{\kappa }_{1}^{1} - \overline{\iota }_{2} )(\kappa_{1}^{1} + \overline{\kappa }_{2}^{2} )} }},e^{{i\theta_{2}^{ + } }} = \frac{{(\kappa_{2}^{1} - \kappa_{2}^{2} )(\kappa_{2}^{2} + \overline{\kappa }_{2}^{1} )\sqrt {(\kappa_{1}^{2} - \kappa_{2}^{1} )(\kappa_{1}^{2} + \overline{\kappa }_{2}^{1} )} }}{{(\overline{\kappa }_{2}^{1} - \overline{\kappa }_{2}^{2} )(\overline{\kappa }_{2}^{2} + \kappa_{2}^{1} )\sqrt {(\overline{\kappa }_{1}^{2} - \overline{\kappa }_{2}^{1} )(\overline{\kappa }_{1}^{2} + \kappa_{2}^{1} )} }}, $$

$$ \begin{gathered} \Phi_{m}^{jj} = \frac{1}{2}\log \frac{{(\kappa_{m}^{j} - \kappa_{n}^{j} )\left| {\alpha_{nj} } \right|^{2} }}{{(\kappa_{m}^{j} + \overline{\kappa }_{n}^{j} )(\kappa_{n}^{j} + \overline{\kappa }_{n}^{j} )^{2} }},\Phi_{m}^{jl} = N^{m - 1} \Phi_{m}^{jj} + \frac{1}{2}\log \frac{{\left| {( - 1)^{n} (\kappa_{m}^{l} - \kappa_{n}^{j} )} \right|^{2} \left| {\kappa_{n}^{1} - \kappa_{n}^{2} } \right|^{4} }}{{\left| {\kappa_{m}^{l} + \overline{\kappa }_{n}^{j} } \right|^{2} \left| {\kappa_{n}^{1} + \overline{\kappa }_{n}^{2} } \right|^{4} }} \hfill \\ \phi_{1}^{jj} = \frac{1}{2}\log \frac{{\left| {\kappa_{1}^{j} - \kappa_{2}^{j} } \right|^{2} \left| {\alpha_{1j} } \right|^{2} \left| {\alpha_{2j} } \right|^{2} }}{{\left| {\kappa_{1}^{j} + \overline{\kappa }_{2}^{j} } \right|^{2} (\kappa_{1}^{j} + \overline{\kappa }_{1}^{j} )^{2} (\kappa_{2}^{j} + \overline{\kappa }_{2}^{j} )^{2} }},\phi_{2}^{jj} = \frac{1}{2}\log \frac{{\left| {\alpha_{1j} } \right|^{2} (\kappa_{2}^{j} + \overline{\kappa }_{2}^{j} )^{2} }}{{\left| {\alpha_{2j} } \right|^{2} (\kappa_{1}^{j} + \overline{\kappa }_{1}^{j} )^{2} }}, \hfill \\ \phi_{1}^{jl} = N\phi_{1}^{jj} + \frac{1}{2}\log \frac{{\phi_{1} \phi_{2} \left| {\kappa_{1}^{1} - \kappa_{2}^{2} } \right|^{2} \left| {\kappa_{1}^{2} - \kappa_{2}^{1} } \right|^{2} }}{{\phi_{4} \phi_{3} \left| {\kappa_{1}^{2} + \overline{\kappa }_{2}^{1} } \right|^{2} \left| {\kappa_{1}^{1} + \overline{\kappa }_{2}^{2} } \right|^{2} }},\phi_{2}^{jl} = N\phi_{2}^{jj} + \frac{1}{2}\log \frac{{\phi_{1} \phi_{3} \left| {\kappa_{1}^{l} + \overline{\kappa }_{2}^{j} } \right|^{2} \left| {\kappa_{1}^{j} - \kappa_{2}^{l} } \right|^{2} }}{{\phi_{4} \phi_{2} \left| {\kappa_{1}^{l} - \kappa_{2}^{j} } \right|^{2} \left| {\kappa_{1}^{j} + \overline{\kappa }_{2}^{l} } \right|^{2} }}, \hfill \\ \phi_{1} = \left| {\kappa_{1}^{1} - \kappa_{1}^{2} } \right|^{4} ,\phi_{2} = \left| {\kappa_{2}^{1} - \kappa_{2}^{2} } \right|^{4} ,\phi_{3} = \left| {\kappa_{2}^{1} + \overline{\kappa }_{2}^{2} } \right|^{4} ,\phi_{4} = \left| {\kappa_{1}^{1} + \overline{\kappa }_{1}^{2} } \right|^{4} , \hfill \\ j,l = 1,2,j \ne l,m,n = 1,2,m \ne n,N = \left| {\alpha_{j1} } \right|^{2} /\left| {\alpha_{1j} } \right|^{2} ,d = \left\{ {\begin{array}{*{20}c} {1,j = 1} \\ {0,j = 2} \\ \end{array} } \right.. \hfill \\ \end{gathered} $$

The intensity of $S_{1}$ and $S_{2}$ is the same as long as the phase condition $\phi_{m}^{j1} = \phi_{m}^{j2} ,j,m = 1,2$ are satisfied before and after the collision from the above asymptotic analysis. This means that the initial amplitude remains invariant after the collision. It can also be clearly seen from the calculated transition amplitude $T_{j}^{l} = a_{j}^{l + } /a_{j}^{l - } ,j,l = 1,2,$ and $j$ represents two components, and $l \pm$ represents the asymptotic state when $t \to \pm \infty$. The strength of nondegenerate solitons remains unchanged during the collision. And the strength of each soliton is conservative and can be obtained from $\left| {a_{j}^{l - } } \right|^{2} = \left| {a_{j}^{l + } } \right|^{2}$. The strength of each mode is also conservative according to the calculated formula $\left| {a_{j}^{1 - } } \right|^{2} + \left| {a_{j}^{2 - } } \right|^{2} = \left| {a_{j}^{1 + } } \right|^{2} +$$\left| {a_{j}^{2 + } } \right|^{2} ,j,l = 1,2.$

3.2.3 The interaction of nondegenerate two-solitons

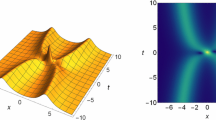
Figure 3 shows the collision of nondegenerate two-solitons. In order to more clearly analyze the energy distribution before and after the soliton collision, we draw a projection map of quasi-intensity in Fig. 3. For the local quantity $q_{1}$, the soliton $S_{1}$($S_{2}$) has a small (large) transition amplitude value before the collision. After the collision, their energy is redistributed, namely the soliton $S_{1}$ is suppressed while soliton $S_{2}$ is increased correspondingly. We observe the opposite situation for the component $q_{2}$. The soliton $S_{1}$ is increased, while the soliton $S_{2}$ is suppressed after the collision. The total energy is conserved after the collision. For two nonlocal quantities $q_{1}^{*}$ and $q_{2}^{*}$, we observe a phenomenon similar to components $q_{1}$ and $q_{2}$. The soliton $S_{1}$ is suppressed, and the soliton $S_{2}$ is increased correspondingly in $q_{1}^{*}$. The soliton $S_{1}$ is increased, while the soliton $S_{2}$ is suppressed in $q_{2}^{*}$. From the previous asymptotic analysis, we can see that the total energy of the whole system is conservative for four components $q_{1} ,q_{2} ,q_{1}^{*} ,q_{2}^{*}$. The situation caused by this collision is not observed in the local NLS equation.

Fig. 3

Quasi-intensity distribution of nondegenerate two-solitons for ${\mathbf{a}}\;q_{1} (x,t),\;{\mathbf{b}}\;q_{2} (x,t),$ ${\mathbf{c}}\;q_{1}^{*} ( - x,t),\;{\mathbf{d}}\;q_{2}^{*} ( - x,t)$ with $\kappa_{1}^{1} = 0.31 + i,\kappa_{1}^{2} = 0.3 - i,\kappa_{2}^{1} = 0.3 + 1.4i,\kappa_{2}^{2} = 0.31 - 1.4i,$$\alpha_{11R} = \alpha_{22R} = 0.5,\alpha_{21R} = \alpha_{12R} = 0.55,\alpha_{ijI} = 1.$

3.3 Interaction between nondegenerate two-solitons and degenerate solitons

In order to make degenerate solitons and nondegenerate solitons exist at the same time in NNLS equation, we limit the wave number of solitons, that is, set one group of wave numbers equal to obtain degenerate solitons, and make the other group of wave numbers different to obtain nondegenerate solitons. Here, we enumerate one of the cases with $\kappa_{1}^{1} = \kappa_{2}^{1} ,\kappa_{1}^{2} \ne \kappa_{2}^{2}$ and $\eta_{1} = \xi_{1} ,\eta_{2} \ne \xi_{2}$ for the limitation. It can be observed from Fig. 4a and b that the intensity of $S_{1}$ is suppressed after the collision of component $q_{1}$, while it is enhanced in component $q_{2}$. As expected, degenerate solitons undergo energy redistribution between components $q_{1}$ and $q_{2}$. For degenerate solitons, the polarization vector $A_{j}^{l} = \alpha_{lj} /(\left| {\alpha_{1j} } \right|^{2} + \left| {\alpha_{2j} } \right|^{2} )^{1/2}$ plays a key role in making it possible to change the shape of solitons.

Fig. 4

Quasi-intensity distribution of nondegenerate two-solitons and degenerate solitons for ${\mathbf{a}}\;q_{1} (x,t),\;{\mathbf{b}}\;q_{2} (x,t),\;{\mathbf{c}}\;q_{1}^{*} ( - x,t),\;{\mathbf{d}}\;q_{2}^{*} ( - x,t)$ with $\kappa_{1}^{1} = 0.5 + i,\kappa_{1}^{2} = 0.5 - i,\kappa_{2}^{1} = 0.5 + i,$$\kappa_{2}^{2} = 0.51 - 1.05i,$$\alpha_{11R} = \alpha_{22R} = 0.5,\alpha_{21R} = \alpha_{12R} = 0.55,\alpha_{ijI} = 1.$

The nondegenerate asymmetric double-peaked soliton $S_{2}$ shows the characteristics of collision as shown in Fig. 4. For two components $q_{1}$ and $q_{2}$, the interaction between nondegenerate soliton $S_{2}$ and degenerate soliton will have a strong impact. As a result, the strength of nondegenerate soliton $S_{2}$ increases after the collision in component $q_{2}$. It is suppressed in the component $q_{1}$. We also note that when nondegenerate solitons interact with degenerate solitons, nondegenerate solitons lose their asymmetric double-peaked structure and become another form of asymmetric double-peaked profile, which is shown by soliton $S_{2}$ in the projection figure of Fig. 4c.

The characteristics of intensity variation in $q_{1}$ and $q_{2}$ are similar to those previously observed in the 2-coupled mixed derivative NLS equation. The expansion of nondegenerate solitons with single peak can be seen as an implementation of signal amplification, in which the degenerate solitons act as pump waves [41]. Soliton $S_{1}$ becomes a double-peaked structure after collision in nonlocal quantities $q_{1}^{*} ( - x,t),q_{2}^{*} ( - x,t)$. This energy sharing collision provides the foundation for the realization of optical logic gates [31].

3.4 Experimental realization of nondegenerate solitons

In order to observe experimentally the existence of nondegenerate solitons, the incoherent process given in [22] can be considered. We use two different laser sources to give two laser beams with different wavelengths, either ordinary laser or special laser. We then use a polarization fraction to split these two different laser beams into four independent incoherent fields. To expand, the first laser source is divided into two different fields $q_{1}$ and $q_{2}$ by the polarization beam splitter. Similarly, the second laser beam given is divided by a beam splitter into two other incoherent fields $q_{1}^{*}$ and $q_{2}^{*}$. The intensity of four fields is different. Two independent nondegenerate solitons are given in $q_{1}$ and $q_{2}$, and another two nondegenerate solitons are formed in $q_{1}^{*}$ and $q_{2}^{*}$. Another beam splitter can be used to couple $q_{1}$ and $q_{1}^{*}$. The same operation applies to $q_{2}$ and $q_{2}^{*}$. Before output to the imaging system, the generated field beam can be focused by two separate cylindrical lenses. It should be noted that the collision angle must be large enough to observe the collision of two nondegenerate solitons [42]. The occurrence of multimode and multipeaked solitons in dispersive nonlinear media can be observed using the experimental program of a single laser [43].

4 Conclusion

In short, we obtain the nondegenerate one- and two-soliton solutions of the NNLS equation by using the nonstandard Hirota bilinear method with auxiliary functions. We show the difference of nondegenerate one-solitons between nonlocal and local equations [25], that is, the velocity of the nondegenerate solitons is not only affected by the imaginary part of the wave number, but also affected by the real part of the wave number in the nonlocal case. The nondegenerate one-solitons with different structures we obtained can be used as the signal carrier proposed in [23] to improve the transmission rate and realize the four stage (00, 01, 10, 11) communication system.

We also study the collision between two nondegenerate two-solitons and find the phenomenon that is not observed in the local state, namely, the local and nonlocal two components have the same intensity change, but the energy of the whole system is conserved. The double-peaked properties of nondegenerate solitons provide the possibility for the realization of information processing. Finally, we investigated that nondegenerate and degenerate solitons can exist together. However, the shape change during the collision of nondegenerate and degenerate solitons indicates that they cannot coexist in communication systems. In the nonlocal quantities, degenerate solitons become double-peaked structures after collisions, and this multipeaked structure can be used to send information about dense data [44]. In future work, we will try to use bilinear residual network method [45] to further study the dynamic behavior between nondegenerate solitons in nonlocal systems and will analyze the phenomenon caused by soliton collisions in more detail.

Appendix parameters in solutions (9) and (11)

1.1 I. Parameters in solution (9)

$$ \eta_{j} = i\kappa_{j} x + i\kappa_{j}^{2} t,\overline{\eta }_{j} = i\overline{\kappa }_{j} x - i\overline{\kappa }_{j}^{2} t,\xi_{j} = i\iota_{j} x + i\iota_{j}^{2} t,\overline{\xi }_{j} = i\overline{\iota }_{j} x - i\overline{\iota }_{j}^{2} t $$

$$ \begin{gathered} \eta_{jR} = - \kappa_{jI} (x + 2\kappa_{jR} t),\eta_{jI} = \kappa_{jR} x + (\kappa_{jR}^{2} - \kappa_{jI}^{2} )t,\xi_{jR} = - \iota_{jI} (x + 2\iota_{jR} t),\xi_{jI} = \iota_{jR} x + (\iota_{jR}^{2} - \iota_{jI}^{2} )t, \hfill \\ A_{1}^{1} = \frac{{\sigma \alpha_{1} \alpha_{2} \overline{\alpha }_{2} ( - \overline{\iota }_{1} - 2\kappa_{1} + \iota_{1} )}}{{(\kappa_{1} + \overline{\iota }_{1} )(\overline{\iota }_{1} + \iota_{1} )^{2} }},A_{{_{1} }}^{2} = \frac{{\sigma \alpha_{1} \alpha_{2} \overline{\alpha }_{1} ( - \overline{\kappa }_{1} - 2\iota_{1} + \kappa_{1} )}}{{(\overline{\kappa }_{1} + \iota_{1} )(\overline{\kappa }_{1} + \kappa_{1} )^{2} }},B_{{_{1} }}^{j} = - \frac{{2\sigma \alpha_{1} \overline{\alpha }_{1} }}{{(\overline{\kappa }_{1} + \kappa_{1} )^{2} }},B_{{_{2} }}^{j} = - \frac{{2\sigma \alpha_{2} \overline{\alpha }_{2} }}{{(\overline{\iota }_{1} + \iota_{1} )^{2} }}, \hfill \\ \end{gathered} $$

$$ \begin{gathered} C_{1}^{1} = \frac{{ - B_{{_{2} }}^{1} B_{{_{1} }}^{1} (\overline{\kappa }_{1} + \kappa_{1} - \overline{\iota }_{1} - \iota_{1} )^{2} - 2(A_{1}^{1} \overline{\alpha }_{1} + A_{{_{1} }}^{2} \overline{\alpha }_{2} + \overline{A}_{1}^{1} \alpha_{1} )}}{{(\overline{\kappa }_{1} + \kappa_{1} + \overline{\iota }_{1} + \iota_{1} )^{2} }},N_{m}^{n} { = } - \frac{{2\sigma \alpha_{mn} \overline{\alpha }_{mn} }}{{(\overline{\kappa }_{n} + \kappa_{m} )^{2} }}{\text{,P}}_{m}^{n} = - \frac{{2\sigma \alpha_{mn} \overline{\alpha }_{mn} }}{{(\overline{\iota }_{n} + \iota_{m} )^{2} }} \hfill \\ C_{{_{1} }}^{2} = \frac{{ - \overline{B}_{{_{2} }}^{1} \overline{B}_{{_{1} }}^{1} (\overline{\kappa }_{1} + \kappa_{1} - \overline{\iota }_{1} - \iota_{1} )^{2} - 2\sigma (A_{1}^{1} \overline{\alpha }_{1} + A_{{_{1} }}^{2} \overline{\alpha }_{2} + \overline{A}_{1}^{1} \alpha_{1} + \overline{A}_{{_{1} }}^{2} \alpha_{2} )}}{{(\overline{\kappa }_{1} + \kappa_{1} + \overline{\iota }_{1} + \iota_{1} )^{2} }}, \hfill \\ \end{gathered} $$

1.2 II. Parameters in solution (11)

$$ \begin{gathered} D_{m}^{n(p)} = \frac{{\sigma ( - 2\kappa_{1n} - \overline{\kappa }_{2p} + \kappa_{2m} )\alpha_{m2} \alpha_{n1} \alpha_{p20} }}{{(\kappa_{2m} + \overline{\kappa }_{2p} )^{2} (\kappa_{1n} + \overline{\kappa }_{2p} )}},d_{m}^{n\left( p \right)} = \frac{{\sigma ( - 2\kappa_{2n} - \overline{\kappa }_{1p} + \kappa_{1m} )\alpha_{m1} \alpha_{n2} \overline{\alpha }_{p1} }}{{(\kappa_{1m} + \overline{\kappa }_{1p} )^{2} (\kappa_{2n} + \overline{\kappa }_{1p} )}} \hfill \\ E_{m}^{n} = - \frac{{2\sigma \alpha_{2n} \alpha_{1n} \overline{\alpha }_{mn} [(\kappa_{n1} + \kappa_{n2} + \overline{\kappa }_{nm} )\overline{\kappa }_{nm} + \kappa_{n1}^{2} + \kappa_{n2}^{2} - \kappa_{n1} \kappa_{n2} ]}}{{(\kappa_{n2} + \overline{\kappa }_{nm} )^{2} (\overline{\kappa }_{nm} + \kappa_{n1} )^{2} }} \hfill \\ \end{gathered} $$

$$ \begin{gathered} F_{1M2N}^{mn} = - \frac{1}{{(\kappa_{1M} + \kappa_{2N} + \overline{\kappa }_{1m} + \overline{\kappa }_{2n} )}}(\sigma d_{M}^{M(m)} d_{N}^{P(N)} (\kappa_{1M} - \kappa_{2N} + \overline{\kappa }_{1m} - \overline{\kappa }_{2n} )^{2} + F + \overline{F}), \hfill \\ F_{n} = - \frac{1}{{(F_{3} + \overline{F}_{3} )}}(\sigma d_{1}^{n(1)} d_{1}^{n(2)} (\kappa_{n1} - \kappa_{n2} + \overline{\kappa }_{n1} - \overline{\kappa }_{n2} )^{2} + F_{4} + \overline{F}_{4} ),F = 2E_{1}^{n} \overline{\alpha }_{2n} + 2E_{2}^{n} \overline{\alpha }_{1n} , \hfill \\ P \ne N,F_{3} = \kappa_{n1} + \kappa_{n2} ,F_{4} = 2D_{N}^{M(n)} \overline{\alpha }_{m1} + 2d_{M}^{N(m)} \overline{\alpha }_{n2} . \hfill \\ \end{gathered} $$

$$ \begin{gathered} J_{1M2m}^{mn} = \frac{1}{{2[(J_{1}^{ + } + \kappa_{2n} + \overline{\kappa }_{1M} )\overline{\kappa }_{1M} + (J_{1}^{ + } + J_{2}^{2 + } + \overline{\kappa }_{1M} )\overline{\kappa }_{2m} + J_{1}^{ + } \kappa_{2n} + \kappa_{11} \kappa_{12} ]}}\sum\limits_{p = 1}^{2} { - 2\{ [J_{2}^{1 + } + ( - 1)^{p - 1} J_{1}^{ - } ]\overline{\kappa }_{2m} + [\kappa_{2n} + ( - 1)^{p - 1} J_{1}^{ - } ]\overline{\kappa }_{1M} } \hfill \\ + \kappa_{2n}^{2} + ( - 1)^{p - 1} J_{1}^{ - } (\kappa_{11} + \kappa_{2n} )\} \alpha_{q1} F_{1p2n}^{Mm} - \sigma^{2} X\sum\limits_{p = 1}^{2} {d_{p}^{p(M)} \alpha_{P1} [(\kappa_{1Q} + \overline{\kappa }_{1M} )^{2} + (J_{2}^{2 + } )^{2} ] - 2\sigma \{ D[ - \frac{1}{2}\overline{\kappa }_{1M}^{2} - \kappa_{11} \kappa_{12} + J_{2}^{2 + } (J_{1}^{ - } + \overline{\kappa }_{2m} - } \hfill \\ \overline{\kappa }_{1M} )] + [(J_{1}^{ + } - J_{2}^{2 + } + \overline{\kappa }_{1M} )\overline{\kappa }_{1M} - (J_{1}^{ + } + \frac{{\overline{\kappa }_{2m} }}{2})\overline{\kappa }_{2m} + (\kappa_{12} - \kappa_{2n} )\kappa_{11} - (\kappa_{12} - \frac{{\kappa_{2n} }}{2})\kappa_{2n} ]E_{M}^{1} X + \frac{1}{2}\sum\limits_{p = 1}^{2} {D_{n}^{P(m)} d_{p}^{p(M)} (\kappa_{1Q}^{2} - 2\kappa_{1P} \overline{\kappa }_{NM} ) + 2} \hfill \\ \overline{D}_{m}^{M(n)} \alpha_{21} \alpha_{11} + \sum\limits_{p = 1}^{2} {D_{n}^{p(m)} \overline{\alpha }_{M1} + \overline{d}_{M}^{m(p)} \alpha_{n2} + d_{p}^{n(M)} \overline{\alpha }_{m2} )\alpha_{q1} \} ,J_{1}^{ \pm } = \kappa_{11} \pm \kappa_{12} ,J_{2}^{p + } = \kappa_{2n} + \overline{\kappa }_{pm} } . \hfill \\ \end{gathered} $$

$$ \begin{gathered} j_{1M2m}^{mn} = \frac{1}{{2[(j_{1}^{ + } + \kappa_{2n} + \overline{\kappa }_{1M} )\overline{\kappa }_{1M} + (j_{1}^{ + } + j_{2}^{2 + } + \overline{\kappa }_{1M} )\overline{\kappa }_{2m} + j_{1}^{ + } \kappa_{2n} + \kappa_{11} \kappa_{12} ]}}\sum\limits_{p = 1}^{2} { - 2\{ [j_{2}^{1 + } + ( - 1)^{p - 1} j_{1}^{ - } ]\overline{\kappa }_{2m} + [\kappa_{2n} + ( - 1)^{p - 1} j_{1}^{ - } ]\overline{\kappa }_{1M} } \hfill \\ + \kappa_{2n}^{2} + ( - 1)^{p - 1} j_{1}^{ - } (\kappa_{11} + \kappa_{2n} )\} \alpha_{q1} F_{1p2n}^{Mm} - \sigma^{2} X\sum\limits_{p = 1}^{2} {d_{p}^{p(M)} \alpha_{P1} [(\kappa_{1Q} + \overline{\kappa }_{1M} )^{2} + (j_{2}^{2 + } )^{2} ] - 2\sigma \{ D[ - \frac{1}{2}\overline{\kappa }_{1M}^{2} - \kappa_{11} \kappa_{12} + j_{2}^{2 + } (j_{1}^{ - } + \overline{\kappa }_{2m} - } \hfill \\ \overline{\kappa }_{1M} )] + [(j_{1}^{ + } - j_{2}^{2 + } + \overline{\kappa }_{1M} )\overline{\kappa }_{1M} - (j_{1}^{ + } + \frac{{\overline{\kappa }_{2m} }}{2})\overline{\kappa }_{2m} + (\kappa_{12} - \kappa_{2n} )\kappa_{11} - (\kappa_{12} - \frac{{\kappa_{2n} }}{2})\kappa_{2n} ]E_{M}^{2} X + \frac{1}{2}\sum\limits_{p = 1}^{2} {d_{n}^{P(m)} D_{p}^{p(M)} (\kappa_{1Q}^{2} - 2\kappa_{1P} \overline{\kappa }_{NM} ) + 2} \hfill \\ \overline{d}_{m}^{M(n)} \alpha_{21} \alpha_{11} + \sum\limits_{p = 1}^{2} {d_{n}^{p(m)} \overline{\alpha }_{M1} + \overline{D}_{M}^{m(p)} \alpha_{n2} + D_{p}^{n(M)} \overline{\alpha }_{m2} )\alpha_{q1} \} ,j_{1}^{ \pm } = \kappa_{11} \pm \kappa_{12} ,j_{2}^{p + } = \kappa_{2n} + \overline{\kappa }_{pm} } . \hfill \\ \end{gathered} $$

$$ D = D_{n}^{M(m)} d_{2}^{2(M)} + D_{n}^{N(m)} d_{1}^{1(M)} ,P = \left\{ {\begin{array}{*{20}c} {M,p = 2} \\ {N,p = 1} \\ \end{array} } \right.,Q \ne P,p \ne q,X = \left\{ {\begin{array}{*{20}c} {d121,m = 1,n = 1} \\ {d212,m = 1,n = 2} \\ \end{array} } \right.o{\text{r }}X = \left\{ {\begin{array}{*{20}c} {d211,m = 2,n = 1} \\ {d122,m = 2,n = 2} \\ \end{array} } \right.. $$

$$ \begin{gathered} H_{mn}^{1} = - \frac{1}{{(\kappa_{11} + \kappa_{12} + \kappa_{2m} + \kappa_{110} + \kappa_{120} + \kappa_{2n0} )}}(\sigma \{ F1[X( - \kappa_{11} - \kappa_{12} + \kappa_{2m} - \kappa_{110} - \kappa_{120} + \kappa_{2n0} )^{2} + 2\alpha_{m2} \overline{\alpha }_{n2} ] + F_{1q2m}^{Nn} \hfill \\ [d_{p}^{p(M)} (\kappa_{11} - \kappa_{12} - ( - 1)^{q} \kappa_{2m} + ( - 1)^{N} (\kappa_{110} - \kappa_{120} ) - ( - 1)^{q} \kappa_{2n0} )^{2} + 2\alpha_{p1} \overline{\alpha }_{M1} ] + Y + \overline{Y} + 2d_{2}^{1(1)} \overline{d}_{2}^{1(1)} + 2d_{1}^{1(2)} \overline{d}_{1}^{1(2)} \} ), \hfill \\ Y = 2\alpha_{12} \overline{j}_{2122}^{1} + 2(\sum\limits_{M = 1}^{2} {} \alpha_{m1} \overline{J}_{1N21}^{11} + \overline{D}_{1}^{M(1)} E_{N}^{1} ) + 2d_{2}^{1(2)} \overline{d}_{1}^{1(1)} ,M \ne N,p \ne q. \hfill \\ \end{gathered} $$

$$ \begin{gathered} H_{mn}^{2} = - \frac{1}{{(\kappa_{21} + \kappa_{1n} + \kappa_{22} + \kappa_{1m0} + \kappa_{210} + \kappa_{220} )}}(\sigma \{ F2[X( - \kappa_{1n} + \kappa_{21} + \kappa_{22} - \kappa_{1m0} + \kappa_{210} + \kappa_{220} )^{2} + 2\alpha_{n1} \overline{\alpha }_{m1} ] + F_{1q2m}^{Nn} \hfill \\ [X(\kappa_{11} - \kappa_{21} - ( - 1)^{q} \kappa_{1n} + ( - 1)^{N} (\kappa_{210} - \kappa_{220} ) - ( - 1)^{q} \kappa_{1m0} )^{2} + 2\alpha_{p2} \overline{\alpha }_{M2} ] + y + \overline{y} + 2D_{2}^{1(1)} \overline{D}_{2}^{1(1)} + 2D_{1}^{1(2)} \overline{D}_{1}^{1(2)} \} ), \hfill \\ y = 2\alpha_{11} \overline{J}_{2122}^{1} + 2(\sum\limits_{M = 1}^{2} {} \alpha_{m2} \overline{j}_{1N21}^{11} + \overline{d}_{1}^{M(1)} E_{N}^{2} ) + 2D_{2}^{1(2)} \overline{D}_{1}^{1(1)} ,M \ne N,p \ne q. \hfill \\ \end{gathered} $$

$\begin{gathered} K_{m} = \sum\limits_{\begin{subarray}{l} m,n, \\ p,q = 1 \end{subarray} }^{2} {} F_{11}^{2n(1m)} \{ - 2d_{m}^{p(q)} \alpha_{21} (k_{2q} + \overline{k}_{2p} )(k_{11} + \overline{k}_{11} + k_{2n} + \overline{k}_{2m} )\sigma - D_{q}^{2(p)} [2(K_{2} - \overline{k}_{11} - \overline{k}_{2m} + \overline{k}_{2p} )\overline{k}_{2p} + 2(K_{2} - \overline{k}_{11} - \overline{k}_{2m} )k_{12} + \hfill \\ 2( - k_{11} - k_{2n} - \overline{k}_{11} - \overline{k}_{2m} )k_{2q} + k_{11}^{2} + k_{2n}^{2} - \overline{k}_{11}^{2} - \overline{k}_{2m}^{2} ]\} + \sum\limits_{\begin{subarray}{l} m,n, \\ p,q = 1 \end{subarray} }^{2} {} F_{12}^{2n(1m)} \{ - 2d_{m}^{p(q)} \alpha_{11} (k_{2q} + \overline{k}_{2p} )(k_{12} + \overline{k}_{11} + k_{2n} + \overline{k}_{2m} )\sigma - D_{q}^{1(p)} [(K_{2} \hfill \\ + \overline{k}_{11} + \overline{k}_{2m} - \overline{k}_{2p} )\overline{k}_{2p} + (k_{12} + k_{21} - k_{22} + \overline{k}_{11} + \overline{k}_{2m} )k_{11} + (k_{12} + k_{2n} + \overline{k}_{11} + \overline{k}_{2m} )k_{2q} + \frac{1}{2}( - k_{12}^{2} - k_{2n}^{2} + \overline{k}_{11}^{2} + \overline{k}_{2m}^{2} )]\} + \sum\limits_{\begin{subarray}{l} m,n, \\ p,q = 1 \end{subarray} }^{2} {} - 2XJ_{11}^{2q(qp)} \hfill \\ \sigma [(K_{2} + \overline{k}_{11} + \overline{k}_{21} - \overline{k}_{22} )\overline{k}_{2p} + ( - k_{11} - k_{12} - k_{2p} - \overline{k}_{11} )\overline{k}_{2n} + K_{1} \overline{k}_{11} + (k_{11} + k_{12} - k_{22} )k_{21} - (k_{11} + k_{12} )k_{22} + k_{11} k_{12} + \frac{1}{2}(k_{2m}^{2} - \overline{k}_{22}^{2} + 2\overline{k}_{11}^{2} )] \hfill \\ /2[(K_{1} + \overline{k}_{11} + \overline{k}_{21} + \overline{k}_{q1}^{2} + \overline{k}_{22} )\overline{k}_{q1} + (K_{1} + \overline{k}_{nm} + \overline{k}_{q2} )\overline{k}_{q2} + (K_{1} + \overline{k}_{nm} )\overline{k}_{nm} + (k_{1n} + k_{12} + k_{22} )k_{q1} + (k_{n1} + k_{n2} )k_{q2} + k_{n1} k_{n2} ], \hfill \\ \end{gathered}$ $\begin{gathered} M = \sum\limits_{\begin{subarray}{l} m,n, \\ p,q = 1 \end{subarray} }^{2} {} - [(k_{11} + k_{12} - k_{21} + k_{22} + \overline{k}_{11} + \overline{k}_{12} + \overline{k}_{21} - \overline{k}_{22} )^{2} d_{q}^{n(m)} + 2\alpha_{np} \overline{\alpha }_{qp} ]\sigma H_{q}^{n(m)} - (k_{11} + k_{12} - k_{21} - k_{22} + \overline{k}_{11} + \overline{k}_{12} - \overline{k}_{21} - \overline{k}_{22} )^{2} F_{1} F_{2} \hfill \\ - 2\sum\limits_{\begin{subarray}{l} m,n,p \\ q,M,N = 1 \end{subarray} }^{2} {} [( - \alpha_{11} d_{n}^{q(M)} \overline{\alpha }_{m1} - \alpha_{M2} d_{n}^{n(n)} \overline{\alpha }_{n2} ) + M_{1} + \overline{M}_{1} ]\sigma F_{12}^{2N(pq)} - 2\sigma [\sum\limits_{\begin{subarray}{l} m,n,p \\ q,M,N = 1 \end{subarray} }^{2} {} (M_{2} + \overline{M}_{2} )] - (k_{11} - k_{12} + k_{21} - k_{22} + \overline{k}_{11} - \overline{k}_{12} + \overline{k}_{21} - \overline{k}_{22} )^{2} F_{12}^{2N(pq)} \hfill \\ - 2\sigma [( - \alpha_{NM} d_{n}^{q(2)} \overline{\alpha }_{pM} - \alpha_{2P} d_{m}^{m(p)} \overline{\alpha }_{qp} )\sigma + M_{3} + \overline{M}_{3} ]F_{11}^{2M(mn)} ,M_{1} = D_{M}^{1(n)} \overline{\alpha }_{m1} + d_{1}^{M(m)} \overline{\alpha }_{n2} ,M_{2} = D_{m}^{n(M)} \overline{J}_{1q}^{2p(pN)} + d_{m}^{n(M)} \overline{j}_{1q}^{2p(pN)} + \overline{E}_{m}^{n} \overline{J}_{21}^{22(p)} . \hfill \\ M_{3} = D_{N}^{2(q)} \overline{\alpha }_{p1} + d_{N}^{N(p)} \overline{\alpha }_{q2} . \hfill \\ \end{gathered}$ $\begin{gathered} L_{m} = \sum\limits_{\begin{subarray}{l} m,n, \\ p,q = 1 \end{subarray} }^{2} {} F_{11}^{2n(1m)} \{ - 2d_{m}^{p(q)} \alpha_{21} (k_{2q} + \overline{k}_{2p} )(k_{11} + \overline{k}_{11} + k_{2n} + \overline{k}_{2m} )\sigma - d_{q}^{2(p)} [2(K_{2} - \overline{k}_{11} - \overline{k}_{2m} + \overline{k}_{2p} )\overline{k}_{2p} + 2( - k_{11} - k_{21} + k_{22} - \overline{k}_{11} - \overline{k}_{2m} )k_{12} \hfill \\ + 2( - k_{11} - k_{2n} - \overline{k}_{11} - \overline{k}_{2m} )k_{2q} + k_{11}^{2} + k_{2n}^{2} - \overline{k}_{11}^{2} - \overline{k}_{2m}^{2} ]\} + \sum\limits_{\begin{subarray}{l} m,n, \\ p,q = 1 \end{subarray} }^{2} {} F_{12}^{2n(1m)} \{ - 2d_{m}^{p(q)} \alpha_{11} (k_{2q} + \overline{k}_{2p} )(k_{12} + \overline{k}_{11} + k_{2n} + \overline{k}_{2m} )\sigma - d_{q}^{1(p)} [(K_{1} + \overline{k}_{11} + \hfill \\ \overline{k}_{2m} - \overline{k}_{2p} )\overline{k}_{2p} + (k_{12} + k_{21} - k_{22} + \overline{k}_{11} + \overline{k}_{2m} )k_{11} + (k_{12} + k_{2n} + \overline{k}_{11} + \overline{k}_{2m} )k_{2q} + \frac{1}{2}( - k_{12}^{2} - k_{2n}^{2} + \overline{k}_{11}^{2} + \overline{k}_{2m}^{2} )]\} + \sum\limits_{\begin{subarray}{l} m,n, \\ p,q = 1 \end{subarray} }^{2} {} - 2Xj_{11}^{2q(qp)} \sigma [(K_{1} + \overline{k}_{11} + \hfill \\ \overline{k}_{21} - \overline{k}_{22} )\overline{k}_{2p} + ( - k_{11} - k_{12} - k_{2p} - \overline{k}_{11} )\overline{k}_{2n} + L_{1} \overline{k}_{11} + (k_{11} + k_{12} - k_{22} )k_{21} - (k_{11} + k_{12} )k_{22} + k_{11} k_{12} + \frac{1}{2}(k_{2m}^{2} - \overline{k}_{22}^{2} + 2\overline{k}_{11}^{2} )]/2[(K_{1} + \overline{k}_{11} + \overline{k}_{21} + \hfill \\ \overline{k}_{q1}^{2} + \overline{k}_{22} )\overline{k}_{q1} + (K_{1} + \overline{k}_{nm} + \overline{k}_{q2} )\overline{k}_{q2} + (K_{1} + \overline{k}_{nm} )\overline{k}_{nm} + (k_{1n} + k_{12} + k_{22} )k_{q1} + (k_{n1} + k_{n2} )k_{q2} + k_{n1} k_{n2} ],m \ne n,p \ne q,K_{1} = k_{11} + k_{12} + k_{21} + k_{22} , \hfill \\ K_{2} = - k_{11} + k_{12} + k_{21} - k_{22} . \hfill \\ \end{gathered}$