Dynamics of high-order solitons in the nonlocal nonlinear Schrödinger equations

Abstract

A study of high-order solitons in three nonlocal nonlinear Schrödinger equations is presented. These include the $\mathcal {PT}$-symmetric, reverse-time, and reverse-space-time nonlocal nonlinear Schrödinger equations. General high-order solitons in three different equations are derived from the same Riemann–Hilbert solutions of the AKNS hierarchy, except for the difference in the corresponding symmetry relations on the “perturbed” scattering data. Dynamics of general high-order solitons in these equations is further analyzed. It is shown that the high-order fundamental-soliton is moving on several different trajectories in nearly equal velocities, and they can be nonsingular or repeatedly collapsing, depending on the choices of the parameters. It is also shown that the high-order multi-solitons could have more complicated wave structures and behave very differently from high-order fundamental-solitons. More interestingly, via the combinations of different size of block matrix in the Riemann–Hilbert solutions, high-order hybrid-pattern solitons are found, which describe the nonlinear interaction between several types of solitons.

1 Introduction

The integrable nonlinear wave equations and soliton theory have been studied for many years [1,2,3,4,5]. They are significant subjects in many branches of nonlinear science. For the integrable nonlinear models, most of them are local equations, i.e., the solutions evolution depends only on the local solution value with its local space and time derivatives. Recently, a number of nonlocal integrable equations were found and triggered renewed interest in integrable systems. The first such nonlocal equation was the $\mathcal {PT}$-symmetric nonlinear Schrödinger (NLS) equation [6, 7]:

$$\begin{aligned} {i} q_t(x,t)=q_{xx}(x,t)+2 q^2(x,t)q^*(-\,x,t), \end{aligned}$$

(1)

where asterisk * represents complex conjugation. For this equation, the evolution of the solution at location x depends both on the local position x and the distant position $-\,x$. This implies that the states of the solution at distant opposite locations are directly related, reminiscent of quantum entanglement in pairs of particles. Mathematically, this nonlocal integrable equation is interesting and distinctly different from local equations. In the view of potential applications, this equation was linked to an unconventional system of magnetics [8]. Moreover, since Eq. (1) is parity-time ($\mathcal {PT}$) symmetric, it is related to the concept of $\mathcal {PT}$-symmetry, which is a hot research area of contemporary physics [9].

For nonlocal Eq. (1), it was actively investigated [6, 7, 10,11,12,13,14,15,16,17,18,19,20]. Meanwhile, many other nonlocal nonlinear integrable equations with different space and/or time coupling were also introduced and studied [10, 21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Indeed, solution properties in several nonlocal equations had been analyzed by the inverse scattering transform method, Darboux transformation, or the bilinear method. These new systems could reproduce solution patterns which had already been discovered in the corresponding local equations. Moreover, interesting behaviors such as blowing-up (i.e., collapsing) solutions [6, 16, 25] and the novel dynamic patterns were also revealed [17, 24, 29,30,31]. In Ref. [25], the connection between nonlocal and local equations was discovered, where it was shown that many nonlocal equations could be converted to local equations through transformations. In addition, this equation-deformation idea could be further applied to broader nonlinear Hamiltonian mathematical models or some fractional-order differential equations [37,38,39].

In this article, we study high-order solitons and their dynamics in the $\mathcal {PT}$-symmetric NLS Equation (1) as well as the reverse-time NLS equation [10]:

$$\begin{aligned} {i}q_t(x,t) = q_{xx}(x,t)+2 q^2(x,t) q(x,-\,t), \end{aligned}$$

(2)

and the reverse-space-time NLS equation [10]:

$$\begin{aligned} {i}q_t(x,t)=q_{xx}(x,t)+2 q^2(x,t) q(-\,x,-\,t). \end{aligned}$$

(3)

Introducing the following coupled Schrödinger equations [1, 2, 5]:

$$\begin{aligned}&{i}q_t=q_{xx}-2q^2r, \end{aligned}$$

(4)

$$\begin{aligned}&{i}r_t=-\,r_{xx}+2r^2q. \end{aligned}$$

(5)

Then, Eqs. (1)–(3) can be, respectively, obtained from coupled systems (4)–(5) under the following nonlocal reductions

$$\begin{aligned}&r(x,t)= -\,q^*(-\,x,t), \end{aligned}$$

(6)

$$\begin{aligned}&r(x,t)= -\,q(x,-\,t), \end{aligned}$$

(7)

$$\begin{aligned}&r(x,t)= -\,q(-x,-\,t). \end{aligned}$$

(8)

As we know, in the framework of inverse scattering transform method, the poles of reflection coefficient (or zeros of the Riemann–Hilbert problem) give rise to the soliton solutions. In Ref. [19], the general N-solitons (corresponding to N-simple poles in the spectral plane) are derived for nonlocal Eqs. (1)–(3) by using the inverse scattering and Riemann–Hilbert method. From this Riemann–Hilbert framework, new types of multi-solitons with novel eigenvalue configurations in the spectral plane are discovered. Therefore, as more general case, the high-order solitons, which correspond to multiple poles in the spectral plane, can be taken into consideration for nonlocal NLS Equations (1)–(3).

The high-order solitons have wide applications. It can not only describe a weak bound state of solitons, but may also appear in the study of train propagation of solitons with nearly equal velocities and amplitudes [40]. High-order soliton for several local equations have been investigated in several studies before, such as the Sine-Gordon, nonlinear Schrödinger, Kadomtsev–Petviashvili I, and Landau–Lifshitz equations [40,41,42,43, 47, 48]. To the best of our knowledge, high-order solitons for nonlocal NLS Eqs. (1)–(3) have never been reported.

In this article, we derive the general high-order solitons in the $\mathcal {PT}$-symmetric, reverse-time, and reverse-space-time nonlocal NLS Eqs. (1)–(3). These solutions are reduced from the same Riemann–Hilbert solutions of the AKNS hierarchy with different symmetry relations on the “perturbed” scattering data, which consist of the “perturbed” eigenvalues as well as the eigenfunctions. Dynamics of these solitons are also explored. We show that a generic feature for high-order solitons in all the three nonlocal equations is repeated collapsing. This feature is firstly reported in Ref. [19] for the general N-solitons of nonlocal NLS Equations (1)–(3). Here, we show that the high-order fundamental-soliton describes several traveling waves move on different trajectories with nearly equal velocities. We also show that the high-order multi-solitons could have more complicated wave and trajectory structures; thus, they behave very differently from the high-order fundamental-soliton. In this case, the configuration of eigenvalues corresponds to equal numbers of zeros with equal order in the upper and lower complex planes. Moreover, we find the high-order hybrid-pattern solitons, which corresponds to novel eigenvalue configurations, i.e., combinations between zeros of unequal order in the upper and lower complex planes. These new patterns describe the nonlinear interaction between several types of solitons, and they exhibit distinctively dynamical patterns which have not been found before.

2 High-order solitons for general coupled Schrödinger equations

To derive high-order solitons in Eqs. (1)–(3), we first need the Riemann–Hilbert solutions of high-order solitons in the coupled Schrödinger equations for given scattering data. Then imposing appropriate symmetry relations on the scattering data, the high-order solitons for each nonlocal equations can be obtained. The coupled systems (4)–(5) admit the following Lax-pair [1, 2]

$$\begin{aligned}&Y_{x}= -\,{i} \zeta \varLambda Y + Q Y, \end{aligned}$$

(9)

$$\begin{aligned}&Y_{t}= 2{i} \zeta ^2 \varLambda Y - 2\zeta Q Y - {i} \varLambda \left( Q_{x}-Q^2 \right) Y, \end{aligned}$$

(10)

where

$$\begin{aligned} \varLambda ={diag}(1,-\,1),\ Q(x,t)=\left( \begin{array}{cc} 0 &{} q(x,t) \\ r(x,t) &{} 0 \\ \end{array} \right) .\nonumber \\ \end{aligned}$$

(11)

For localized functions q(x, t) and r(x, t), the inverse scattering transform and the modern Riemann–Hilbert method was developed [2, 44,45,46]. Following this Riemann–Hilbert treatment, N-solitons in the coupled Schrödinger system can be written as ratios of determinants [3, 5] :

$$\begin{aligned} q(x,t)=2{i}\frac{\left| \begin{array}{cc} M &{} {\overline{Y}}_{2}^\mathrm{T} \\ Y_{1} &{} 0 \\ \end{array} \right| }{\left| M \right| },\quad r(x,t)=-\,2{i}\frac{\left| \begin{array}{cc} M &{} {\overline{Y}}_{1}^\mathrm{T} \\ Y_{2} &{} 0 \\ \end{array} \right| }{\left| M \right| },\nonumber \\ \end{aligned}$$

(12)

where $Y=\left( v_{1}(x,t),\ldots ,v_{N}(x,t)\right) , {\overline{Y}}=({\bar{v}}_{1}(x,t),\ldots ,{\bar{v}}_{N}(x,t))$. $Y_{k}$ and ${\overline{Y}}_{k}$ represents the k-th row of matrix Y and ${\overline{Y}}$, respectively.

Here, $v_{k}(x,t)$ and ${\bar{v}}_{k}(x,t)$ are both column vectors given by

$$\begin{aligned}&v_{k}(x,t)=\exp [-\,i\zeta _{k}\varLambda x + 2i\zeta _{k}^2 \varLambda t]v_{k0}, \end{aligned}$$

(13)

$$\begin{aligned}&{\bar{v}}_{k}(x,t)=\exp [i{\bar{\zeta }}_{k}\varLambda x - 2i{\bar{\zeta }}_{k}^2 \varLambda t]{\bar{v}}_{k0}. \end{aligned}$$

(14)

M is a $N \times N$ matrix defined as:

$$\begin{aligned}&M=\left( M^{(N)}_{j,k}\right) _{1\le j,k \le N},\nonumber \\&M^{(N)}_{j,k}=\frac{{\bar{v}}_{j}^\mathrm{T} v_{k}}{{\bar{\zeta }}_{j}-\zeta _{k}}, \ 1\le j,k \le N, \end{aligned}$$

(15)

here $\zeta _{k} \in {\mathbb {C}}_{+}$ (upper half complex plane), ${\bar{\zeta }}_{k} \in {\mathbb {C}}_{-}$ (lower half complex plane), $v_{k0}$, ${\bar{v}}_{k0}$ are constant column vectors of length two.

Using this formula, the general high-order solitons can be directly obtained through a simple limiting process. For this purpose, setting N discrete spectral in the eigenfunction (13) to be:

$$\begin{aligned}&\zeta _{2}=\zeta _{1}+\epsilon _{1,1}, \ldots , \zeta _{n_{1}}=\zeta _{1}+\epsilon _{1,n_{1}-1},\\&\zeta _{n_{1}+1}=\zeta _{2},\ \zeta _{n_{1}+2}=\zeta _{2}+\epsilon _{2,1},\ldots , \ \zeta _{n_{1}+n_{2}}\\&\qquad =\zeta _{2}+\epsilon _{2,n_{2}-1}, \cdots \\&\zeta _{N-n_{r}+1}=\zeta _{r}, \\&\zeta _{N-n_{r}+2}=\zeta _{r}+\epsilon _{r,1},\ldots , \zeta _{N}=\zeta _{r}+\epsilon _{r,n_{r}-1}. \end{aligned}$$

Similarly, setting another N discrete spectral in the adjoint eigenfunction (14) to be:

$$\begin{aligned}&{\bar{\zeta }}_{2}={\bar{\zeta }}_{1}+{\bar{\epsilon }}_{1,1}, \ldots , {\bar{\zeta }}_{{\bar{n}}_{1}}={\bar{\zeta }}_{1}+{\bar{\epsilon }}_{1,{\bar{n}}_{1}-1},\\&{\bar{\zeta }}_{{\bar{n}}_{1}+1}={\bar{\zeta }}_{2}, \ {\bar{\zeta }}_{{\bar{n}}_{1}+2}={\bar{\zeta }}_{2}+{\bar{\epsilon }}_{2,1},\ldots ,\ {\bar{\zeta }}_{{\bar{n}}_{1}+{\bar{n}}_{2}}\\&\qquad ={\bar{\zeta }}_{1}+{\bar{\epsilon }}_{2,{\bar{n}}_{2}-1},\cdots \\&{\bar{\zeta }}_{N-{\bar{n}}_{s}+1}={\bar{\zeta }}_{s},\\&{\bar{\zeta }}_{N-{\bar{n}}_{1}+2}={\bar{\zeta }}_{s}+{\bar{\epsilon }}_{s,1},\ldots ,\\&{\bar{\zeta }}_{N}={\bar{\zeta }}_{s}+{\bar{\epsilon }}_{s,{\bar{n}}_{s}-1}. \end{aligned}$$

Here, we should have $\sum _{i=1}^{r}n_{i}=\sum _{i=1}^{s}{\bar{n}}_{i}=N,$ and $r,s \in {\mathbb {Z}}_{+}$.

Then, we have the following expansions:

$$\begin{aligned}&v_{j}(\zeta _{j}+\epsilon _{j, k_{j}})=\sum _{k=0}^{\infty } v_{j}^{(k)} \epsilon _{j, k_{j}}^k, \\&{\bar{v}}_{i}({\bar{\zeta }}_{i}+{\bar{\epsilon }}_{i, k_{i}})=\sum _{k=0}^{\infty } {\bar{v}}_{i}^{(k)} {\bar{\epsilon }}_{i, k_{i}}^k, \\&\frac{{\bar{v}}_{i}^\mathrm{T}({\bar{\zeta }}_{i}+{\bar{\epsilon }}_{i, k_{i}}) v_{j}(\zeta _{j}+\epsilon _{j, k_{j}})}{{\bar{\zeta }}_{i}-\zeta _{j}+{\bar{\epsilon }}_{i, k_{i}}-\epsilon _{j, k_{j}}} =\sum _{l=0}^{\infty }\sum _{k=0}^{\infty } M^{[k,l]}_{i,j} {\bar{\epsilon }}_{i, k_{i}}^{\ l} \epsilon _{j, k_{j}}^k. \end{aligned}$$

Therefore, applying these expansions to each matrix element in N-soliton formula (12), performing simple determinant manipulations and taking the limits of $\epsilon _{j, k_{j}}, {\bar{\epsilon }}_{i, k_{i}} \rightarrow 0 \ (k_{j}=1,\ldots , n_{j}-1,\ k_{i}=1,\ldots , {\bar{n}}_{i}-1)$, we derive general high-order solitons for the coupled Schrödinger Eqs. (4)–(5). Those results are summarized in the following theorem.

Theorem 1

The general high-order solitons in the coupled Schrödinger Eqs. (4)–(5) can be formulated as:

$$\begin{aligned} q(x,t)= 2 {i} \frac{\tau _{12}}{\tau _0},\ \ r(x,t)= -\,2 {i} \frac{\tau _{21}}{\tau _0}, \end{aligned}$$

(16)

where

$$\begin{aligned}&\tau _0= \det \left( M\right) ,\ \ \tau _{kj}=\det \left( \begin{array}{cc} M &{} {\bar{\phi }}_{j}^\mathrm{T} \\ \phi _{k} &{} 0 \end{array} \right) ,\\&M=\left( M_{i,j}\right) ^{{1\le i \le s}}_{1\le j \le r}, \ M_{i,j}=\left( M^{[k,l]}_{i,j}\right) ^{0\le k \le {\bar{n}}_{i}-1}_{0\le l \le n_{j}-1,}, \end{aligned}$$

with

$$\begin{aligned}&\phi =\left[ \ v_{1}^{(0)} ,\ldots , v_{1}^{(n_{1}-1)},\ldots , v_{r}^{(0)},\ldots , v_{r}^{(n_{r}-1)} \right] , \\&{\bar{\phi }}=\left[ \ {\bar{v}}_{1}^{(0)}, \ldots , {\bar{v}}_{1}^{({\bar{n}}_{1}-1)},\ldots , {\bar{v}}_{s}^{(0)}, \ldots , {\bar{v}}_{r}^{({\bar{n}}_{s}-1)} \right] . \end{aligned}$$

Here, $\phi _{k}$ and ${\bar{\phi }}_{j}$ stand the k-th row and the j-th row in matrix $\phi$ and ${\bar{\phi }}$, respectively.

This general soliton formula (16) has been reported in [47] (via using dressing method) as well as in [48] (by the generalized Darboux transformation method). So the proof of this theorem can be given along the lines of [47, 48].

3 Symmetry relations of “perturbed” scattering data in the nonlocal NLS equations

First of all, let us recall revelent results on symmetry relations of scattering data for the nonlocal NLS Equations (1)–(3) presented in [19]. For this purpose, we denote:

$$\begin{aligned} v_{k0}=\left[ a_{k}, b_{k} \right] ^\mathrm{T},\ \ {\bar{v}}_{k0}=\left[ {\bar{a}}_{k}, {\bar{b}}_{k} \right] ^\mathrm{T}. \end{aligned}$$

(17)

Next, potential matrix Q(x, t) has the following initial condition:

$$\begin{aligned} Q_{0}:=Q(x,0)=\left( \begin{array}{cc} 0 &{} q(x,0) \\ r(x,0) &{} 0 \\ \end{array} \right) , \end{aligned}$$

(18)

here q(x, 0), r(x, 0) are the initial value of functions q(x, t) and r(x, t) at $t=0$.

Considering the eigenvalue problem

$$\begin{aligned} Y_{x}= -\,{i} \zeta \varLambda Y + Q_{0} Y, \end{aligned}$$

(19)

and its adjoint eigenvalue problem

$$\begin{aligned} K^\mathrm{T}_{x}= {i} \zeta K^\mathrm{T} \varLambda -K^\mathrm{T} Q_{0}. \end{aligned}$$

(20)

By using the symmetry of potential matrix $Q_{0}$ for each nonlocal reduction (6)–(8), along with the large-x asymptotics of $\zeta _{k}$’s eigenfunction $Y_{k}(x)$ as well as ${\bar{\zeta }}_{k}$’s eigenfunction $K_{k}(x)$, Ref. [19] derives the connections between each subset of scattering data $\{\zeta _{k}, a_{k}, b_{k}\}$ and $\{{\bar{\zeta }}_{k}, {\bar{a}}_{k}, {\bar{b}}_{k}\}$ with rigorous proof. Therefore, those important results can be directly used for our purpose.

In the following, we intend to show that: through a simple modification to the original scattering data, more free parameters can be introduced. In that case, the original scattering data can be modified with a perturbation, i.e.,

$$\begin{aligned} \{ \zeta _{k}, a_{k}, b_{k} \} \mapsto \{ \zeta _{k}(\epsilon ), a_{k}(\epsilon ), b_{k}(\epsilon ) \}, \end{aligned}$$

(21)

where $\zeta _{k}(\epsilon ):= \zeta _{k} + \epsilon$, and $a_{k}(\epsilon )$ and $b_{k}(\epsilon )$ can be further defined as:

$$\begin{aligned} a_{k}(\epsilon ):= & {} {\text {e}}^{\phi _{0}+\phi _{1}\epsilon +\phi _{2}\epsilon ^2+\cdots }, \nonumber \\ b_{k}(\epsilon ):= & {} {\text {e}}^{\varphi _{0}+\varphi _{1}\epsilon +\varphi _{2}\epsilon ^2+\cdots }. \end{aligned}$$

(22)

Here $\phi _{k}$, $\varphi _{j}$ are free complex parameters.

According to the theoretical derivation of Theorem 1 in Ref. [19] along with the large-x asymptotics of “perturbed” eigenfunctions, we can obtain symmetry relations of “perturbed” scattering data (21)–(22) for the $\mathcal {PT}$-symmetric NLS Equation (1): for a pair of non-imaginary eigenvalues $(\zeta _{k},\ {\hat{\zeta }}_{k})\in {\mathbb {C}}_{+}$, where ${\hat{\zeta }}_{k}= -\,\zeta ^*_{k}$, the corresponding “perturbed” eigenvalues are defined as $(\zeta _{k}(\epsilon ),\ {\hat{\zeta }}_{k}(\epsilon ))\in {\mathbb {C}}_{+}$, where ${\hat{\zeta }}_{k}(\epsilon ) \equiv -\,\zeta ^*_{k}(\epsilon )$. After scaling the first element $a(\epsilon )$ to 1, the “perturbed” eigenvectors $v_{k0}(\epsilon )$ and ${\hat{v}}_{k0}(\epsilon )$ are related as

$$\begin{aligned} {\hat{v}}_{k0}(\epsilon )= & {} \sigma _{1}v^*_{k0}(\epsilon ),\nonumber \\ v_{k0}(\epsilon )= & {} \left[ 1, {\text {e}}^{\sum _{j=0}^{\infty }b_{k j}\epsilon ^{j}}\right] ^\mathrm{T}, \ \ b_{k j}\in {\mathbb {C}}. \end{aligned}$$

(23)

Repeating above arguments on the adjoint eigenvalue problem, we have: for a pair of non-imaginary $({\bar{\zeta }}_{k},\ \hat{{\bar{\zeta }}}_{k})\in {\mathbb {C}}_{-}$, $\hat{{\bar{\zeta }}}_{k}= -\,{\bar{\zeta }}_{k}^*$, the “perturbed” eigenvalues are defined as $({\bar{\zeta }}_{k}({\bar{\epsilon }}),\ \hat{{\bar{\zeta }}}_{k}({\bar{\epsilon }}))\in {\mathbb {C}}_{-}$, where $\hat{{\bar{\zeta }}}_{k}({\bar{\epsilon }}) \equiv -\,{\bar{\zeta }}_{k}^*({\bar{\epsilon }})$, and the form of their eigenvectors can be similarly obtained as

$$\begin{aligned} \hat{{\bar{v}}}_{k0}({\bar{\epsilon }})= & {} \sigma _{1}{\bar{v}}^*_{k0}({\bar{\epsilon }}),\nonumber \\ {\bar{v}}_{k0}({\bar{\epsilon }})= & {} \left[ 1, {\text {e}}^{\sum _{j=0}^{\infty }{\bar{b}}_{kj}{\bar{\epsilon }}^{j}}\right] ^\mathrm{T},\ \ \ {\bar{b}}_{kj}\in {\mathbb {C}}. \end{aligned}$$

(24)

Especially, if $\zeta _{k}(\epsilon )$ is purely imaginary, from above definition of “perturbed” eigenvalues, we have ${\hat{\zeta }}_{k}(\epsilon )=\zeta _{k}(\epsilon )$. Because $-\zeta _{k}^*=\zeta _{k}$, we have $\epsilon ^*=-\epsilon$. In this case, their “perturbed” eigenvectors are also the same, which can be further scaled into the following form:

$$\begin{aligned} {\hat{v}}_{k0}(\epsilon )= & {} v_{k0}(\epsilon )\nonumber \\= & {} \left[ 1, {\text {e}}^{\sum _{j=0}^{\infty }({i})^{j+1}\theta _{kj}\epsilon ^{j}}\right] ^\mathrm{T}, \ \theta _{kj} \in {\mathbb {R}}. \end{aligned}$$

(25)

Similarly, when ${\bar{\zeta }}_{k}(\epsilon )$ is also purely imaginary, its eigenvector becomes

$$\begin{aligned} \hat{{\bar{v}}}_{k0}({\bar{\epsilon }})= & {} {\bar{v}}_{k0}({\bar{\epsilon }})\nonumber \\= & {} \left[ 1, {\text {e}}^{\sum _{j=0}^{\infty }({i})^{j+1}{\bar{\theta }}_{kj}{\bar{\epsilon }}^{j}}\right] ^\mathrm{T}, \ {\bar{\theta }}_{kj} \in {\mathbb {R}}. \end{aligned}$$

(26)

Next, base on the derivation of Theorem 2 in Ref. [19] as well as the above analysis, we can also derive the symmetry relations of “perturbed” scattering data for the reverse-time NLS Equation (2): for a pair of discrete eigenvalues $(\zeta _{k}, {\bar{\zeta }}_{k})$, where $\zeta _{k} \in {\mathbb {C}}_{+}$ and ${\bar{\zeta }}_{k}=-\zeta _{k} \in {\mathbb {C}}_{-}$. The “perturbed” eigenvalues are defined as $(\zeta _{k}(\epsilon ),\ {\bar{\zeta }}_{k}({\bar{\epsilon }}))$, where $\zeta _{k}(\epsilon ) \in {\mathbb {C}}_{+}$, ${\bar{\zeta }}_{k}({\bar{\epsilon }})\equiv -\zeta _{k}(-{\bar{\epsilon }})\in {\mathbb {C}}_{-}$. Scaling “perturbed” eigenvectors $v_{k0}(\epsilon )$ and ${\bar{v}}_{k0}({\bar{\epsilon }})$ with their first elements become 1, we have

$$\begin{aligned} v_{k0}(\epsilon )= & {} [1, {\text {e}}^{\sum _{j=0}^{\infty }b_{k,j}\epsilon ^{j}} ]^\mathrm{T}, \nonumber \\ {\bar{v}}_{k0}= & {} v_{k0}(-\,{\bar{\epsilon }}),\ \ b_{kj}\in {\mathbb {C}}. \end{aligned}$$

(27)

where $b_{k}$ is an arbitrary complex parameter.

However, for the reverse-space-time NLS Equation (3), according to the symmetry relations on the scattering data given by Theorem 3 in Ref. [19]: the eigenvalues $\zeta _{k}$ can be anywhere in ${\mathbb {C}}_{+}$ and ${\bar{\zeta }}_{k}$ can be anywhere in ${\mathbb {C}}_{-}$, and the corresponding eigenvectors must be of the forms

$$\begin{aligned} v_{k0}= & {} [1,\omega _{k}]^\mathrm{T},\ \omega _{k}=\pm \, 1; \nonumber \\ {\bar{v}}_{k0}= & {} [1,{\bar{\omega }}_{k}]^\mathrm{T},\ {\bar{\omega }}_{k}=\pm \, 1. \end{aligned}$$

(28)

Then, we find that all the parameters in the “perturbed” scattering data can be eliminated in the “perturbed” eigenvectors. Thus, no more parameters can be introduced in (28) so we have $v_{k0}(\epsilon )=v_{k0}, \ {\bar{v}}_{k0}({\bar{\epsilon }})={\bar{v}}_{k0}$.

Therefore, utilizing the above symmetry relations on the “perturbed” scattering data in the high-order Riemann–Hilbert solution (16), we will construct high-order solitons for nonlocal NLS Equations (1)–(3) in the sections below.

4 Dynamics of high-order solitons in the ${\mathcal {PT}}$-symmetric nonlocal NLS equation

To derive the N-th order solitons in the ${\mathcal {PT}}$-symmetric NLS Equation (1), we just need to apply corresponding symmetry relations of “perturbed” scattering data to the high-order soliton formula (16). Then, we investigate solution dynamics in the high-order fundamental (one)-soliton as well as the high-order multi-solitons.

4.1 High-order fundamental-soliton

Firstly, we consider the second-order fundamental-soliton, which corresponds to a single pair of purely imaginary eigenvalues (zero of multiplicity two) $\zeta _{1}=i \eta _{1} \in i{\mathbb {R}}_{+}$, and ${\bar{\zeta }}_{1}=i {\bar{\eta }}_{1} \in i{\mathbb {R}}_{-}$, where $\eta _{1} >0$ and ${\bar{\eta }}_{1}<0$, In this case, symmetry relations on the perturbed eigenfunctions are given by (25)–(26), i.e., $v_{10}(\epsilon )=\left[ 1, {\text {e}}^{i \theta _{10}-\theta _{11}\epsilon }\right] ^\mathrm{T}$, and ${\bar{v}}_{10}({\bar{\epsilon }})=\left[ 1, {\text {e}}^{i {\bar{\theta }}_{10}-{\bar{\theta }}_{11}{\bar{\epsilon }}\ }\right] ^\mathrm{T}$, where $\theta _{10}, \theta _{11}, {\bar{\theta }}_{10}, {\bar{\theta }}_{11}$ are real constants. Substituting these expressions into formula (16) with $N=n_{1}={\bar{n}}_{1}=2$, we obtain the analytic expression for the second-order fundamental-soliton of Eq. (1):

$$\begin{aligned}&q(x,t)\nonumber \\&\quad =\frac{2({\bar{\eta }}_{1}-\eta _{1}) \left[ {\mathcal {G}}(x,t){\text {e}}^{2 {\bar{\eta }}_{1} x-4i {\bar{\eta }}_{1}^2 t+i {\bar{\theta }}_{10}}+\bar{{\mathcal {G}}}(x,t){\text {e}}^{2 \eta _{1} x-4i \eta _{1}^2 t-i \theta _{10}} \right] }{4\cosh ^2\left[ (\eta _{1}-{\bar{\eta }}_{1}) x-2i(\eta _{1}^2-{\bar{\eta }}_{1}^2)t-\frac{i}{2}(\theta _{10}+{\bar{\theta }}_{10})\right] +{\mathcal {F}}(x,t)}, \nonumber \\ \end{aligned}$$

(29)

where ${\mathcal {F}}(x,t)=-\,({\mathcal {G}}+2)(\bar{{\mathcal {G}}}+2)$, with

$$\begin{aligned}&{\mathcal {G}}(x,t)=({\bar{\eta }}_{1}-\eta _{1})(2x-8 i \eta _{1}t+i\theta _{11})-2, \end{aligned}$$

(30)

$$\begin{aligned}&\bar{{\mathcal {G}}}(x,t)=(\eta _{1}-{\bar{\eta }}_{1})(2x-8 i {\bar{\eta }}_{1}t-i {\bar{\theta }}_{11})-2. \end{aligned}$$

(31)

This kind of soliton, which combines exponential functions with algebraic polynomials, has never been reported before in the nonlocal NLS Equation (1). It contains six real parameters: $\eta _{1}, {\bar{\eta }}_{1}, \theta _{10}, {\bar{\theta }}_{10}, \theta _{11}$, and ${\bar{\theta }}_{11}$. The motion trajectory for this solution can be approximatively described by the following two curves

$$\begin{aligned} \varSigma _{\pm }: 2({\bar{\eta }}_{1}-\eta _{1})x \pm \, \ln \left| {\mathcal {F}}(x,t)\right|= & {} 0.\nonumber \\ (\left| {\mathcal {F}}(x,t)\right|\ne & {} 0) \end{aligned}$$

(32)

In this case, two solitons move along the center trajectories $\varSigma _{+}$ and $\varSigma _{-}$. When $|x|\rightarrow \pm \,\infty$, the amplitude |q| of the solution decays exponentially to zero. However, with the development of time, a simple asymptotic analysis with estimation on the leading-order terms shows that: when soliton (29) is moving on $\varSigma _{+}$ or $\varSigma _{-}$, its amplitudes |q| can approximately vary as

$$\begin{aligned} |q(x,t)|\sim \frac{2|\eta _{1}-{\bar{\eta }}_{1}|{\text {e}}^{\left( \eta _{1}+{\bar{\eta }}_{1}\right) z(x,t)}}{|{\text {e}}^{\pm 2i\gamma t -i\tau _{0} \pm i (\theta _{10}+{\bar{\theta }}_{10})}+1|},\quad \ \ t \sim \pm \infty ,\nonumber \\ \end{aligned}$$

(33)

where $z(x,t)=\frac{\ln |{\mathcal {F}}(x,t)|}{\pm \,2\left( \eta _{1} - {\bar{\eta }}_{1}\right) }$, $\gamma =2({\bar{\eta }}_{1}^2-\eta _{1}^2)$, $\tau _{0}= \text {Arg} \left[ {\mathcal {F}}(x,t)\right] +2 k \pi ,\ (k \in {\mathbb {Z}})$, the positive and negative sign in (33), respectively, corresponds to $\varSigma _{+}$ and $\varSigma _{-}$. (It should be noted that estimation (33) is valid only when $|t| \gg \max \{|\theta _{11}|, |{\bar{\theta }}_{11}|\}$. Before this, the amplitudes |q| of solution are unequal when soliton moves on each curve, depending on the value of parameter $\theta _{11}$ and ${\bar{\theta }}_{11}$.)

Fig. 1

Left panel is the second-order one-soliton (29) with parameters (36). Right panel is the corresponding density plot

In the case, when $\eta _{1}=-{\bar{\eta }}_{1}$, solution (29) will be nonsingular or collapsing at certain locations, depending on the values of these parameters. Specifically, this contains two kinds of situations.

• 1. If $\theta _{11}={\bar{\theta }}_{11}$, as long as $\theta _{10}+{\bar{\theta }}_{10} \ne (2k+1)\pi$ for any integer k, this soliton is nonsingular.

• 2. If $\theta _{11}\ne {\bar{\theta }}_{11}$, we first define three different multivariate functions: $c _{0}\equiv \frac{\sin (\theta _{10}+{\bar{\theta }}_{10})}{ \eta _{1}(\theta _{11}-{\bar{\theta }}_{11})}$,

$\varDelta _{1}\equiv \frac{(\theta _{11}-{\bar{\theta }}_{11})^2}{4}-\frac{1+\cos (\theta _{10}-{\bar{\theta }}_{10})}{2\eta _{1}^2}$ and $\varDelta _{2}\equiv -4x_{c}^2+\frac{(\theta _{11}-{\bar{\theta }}_{11})^2}{4}-\frac{1+\cosh (4\eta _{1}x_{c})\cos (\theta _{10}-{\bar{\theta }}_{10})}{2\eta _{1}^2}$, which contain all the parameters. Then, solution (29) will not blow up only when functions $c_{0}$, $\varDelta _{1}$, and $\varDelta _{2}$ satisfy one of the following two critical conditions:

$$\begin{aligned}&\text {(a)} \;\;\ \text {For any} \ \theta _{10}+{\bar{\theta }}_{10}\ne (2k+1)\pi ,\ c _{0} \notin (0,1),\nonumber \\&\text {and} \ \varDelta _{1} <0. \end{aligned}$$

(34)

$$\begin{aligned}&\text {(b)} \;\;\ c _{0} \in (0,1), \ \text {and} \ \varDelta _{1}, \varDelta _{2} <0. \end{aligned}$$

(35)

Otherwise, when $\varDelta _{1}\ge 0$ in condition (a), there will be two (or one) singular points locating at $x=0$, $t=\frac{\pm \sqrt{\varDelta _{1}}}{8\eta _{1}}+t_{0}$, where $t_{0}=\frac{\theta _{11}-{\bar{\theta }}_{11}}{16\eta _{1}}$. Or, when $\varDelta _{2}\ge 0$ with $c_{0}\in (0,1)$ in (b), there would also have two (or one) singular points locating at $x=x_{c}$, $t=\frac{\pm \sqrt{\varDelta _{2}}}{8\eta _{1}}+t_{0}$. Here, $x_{c}$ admits a special transcendental equation $\frac{4\eta _{1}x_{c}}{\sinh (4\eta _{1}x_{c})}=c_{0}$, which can be solved numerically for this given $c_{0}$.

Moreover, for all the nonsingular solution, |q(x, t)| reaches its peak amplitude at $x=0$, $t=t_{0}$ with the value attained as $\left| \frac{8\eta _{1}\left[ \eta _{1}(\theta _{11}-{\bar{\theta }}_{11})\sin (\phi _{0})-2\cos (\phi _{0})\right] }{4\cos ^2(\phi _{0})-\eta _{1}^2(\theta _{11}-{\bar{\theta }}_{11})^2}\right|$, where $\phi _{0}=\frac{\theta _{10}+{\bar{\theta }}_{10}}{2}$. When $t\rightarrow \pm \infty$, according to a logarithmic law for large values of |t|, two solitons move along $\varSigma _{+}$ and $\varSigma _{-}$ with almost equal velocities and amplitudes, and peak amplitude does not exceed $\left| \frac{4\eta _{1}}{1+{\text {e}}^{i(\theta _{1}+{\bar{\theta }}_{1})}}\right|$.

To demonstrate, we choose the following parameters:

$$\begin{aligned}&\eta _{1}=0.5,\ \theta _{10}=\pi /4,\nonumber \\&{\bar{\theta }}_{10}=\pi /6,\ \theta _{11}=0.25,\ {\bar{\theta }}_{11}=0.5. \end{aligned}$$

(36)

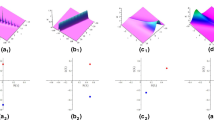
Propagation of this high-order soliton is displayed in Fig. 1. It is shown that two solitons are slowly moving in the spatial orientation. This is quite different from the dynamics of fundamental soliton in Ref. [19], where the soliton cannot move in space. The peak amplitude of |q(x, t)| reaches about 2.65834 at the location (0, 0.09375). Moreover, with the evolution of time, they keep almost identical value of maximum amplitudes, which is no larger than about 1.26047.

Fig. 2

Left panel is the second-order one-soliton (29) in Eq. (1) with parameters (37). Right panel is the corresponding density plot (here, the bright spots shown on the density plot represent the location of singularity)

In a more general case, where $\eta _{1} \ne -{\bar{\eta }}_{1}$, an important feature for this high-order soliton is repeatedly collapsing along two trajectories. This can be clarified from the large time estimation (33). In fact, when $|t|\rightarrow \infty$, a direct calculation shows that $\lim _{|t|\rightarrow \infty }\text {Arg}\left[ {\mathcal {F}}(x,t)\right] =\pi$. Thus, one can repeatedly choose large time point $t_{c}$ s.t. $\cos (2\gamma t_{c} \mp \tau _{0}+(\theta _{10}+{\bar{\theta }}_{10}))=-\,1$. This implies the existence of singularities for the solution at large time.

However, due to the impact of algebraic polynomial terms, the collapsing interval for this high-order soliton is no more a fixed value. Instead, this so-called “period” is slightly varying over time. Besides, amplitudes of solution |q| are unequal when soliton moves on each path, depending on the sign of $\eta _{1}+{\bar{\eta }}_{1}$. To illustrate, we choose parameters as

$$\begin{aligned}&\eta _{1}=0.50,\ \ {\bar{\eta }}_{1}=-\,0.55,\nonumber \\&\theta _{10}={\bar{\theta }}_{10}=0,\ \ \theta _{11}={\bar{\theta }}_{11}=0. \end{aligned}$$

(37)

Graphs of corresponding second-order fundamental-soliton are shown in Fig. 2. Through simple numerical calculation and approximate estimation, the first singularities quartet for this soliton is obtained, which locates approximately at $(\pm \, x_{c}, \pm \, t_{c})$ with $x_{c} \approx 3.9999,\ t_{c} \approx 15.0169$, and the first time interval between two successive singularities $\pm \, t_{c}$ is 30.0338. Afterward, the second singularities quartet approximately appears at $(\pm \,{\tilde{x}}_{c}, \pm \,{\tilde{t}}_{c})$ with ${\tilde{x}}_{c} \approx 5.0369,\ {\tilde{t}}_{c} \approx 44.9041$. So the second time interval between ${\tilde{t}}_{c}$ and $t_{c}$ is about 29.9232. (Here, we illustrate that both Figs. 1 and 2 as well as the following figures are drawn via the Mathematica software. By suitably choosing parameters in the analytic expressions of solitons, and making use of the plotting function in Mathematica, we can derive either 3D plot or density plot for these solutions.)

Generally, the N-th order fundamental-soliton solution can be obtained in the same way by choosing $n_{1}={\bar{n}}_{1}=N$ in formula (16), and the dynamics of N-wave motion on N different asymptote trajectories can be expected.

4.2 High-order multi-solitons

Now, let us consider the high-order multi-solitons for the ${\mathcal {PT}}$-symmetric NLS equation. From the symmetries of scattering data, the eigenvalues in the upper and lower halves of the complex plane are completely independent. This allows for novel eigenvalue configurations, which gives rise to new types of high-order solitons with interesting dynamical patterns. Those results can be divided into the following two cases in principle:

Fig. 3

a The second-order two-solitons with parameters (38)–(39). b The second-order two-solitons with parameters (40)–(41).

4.2.1 The normal pattern: square-matrix blocks

In the most normal pattern, each block $\left( M^{[k,l]}_{i,j}\right) ^{0\le k \le {\bar{n}}_{i}-1}_{0\le l \le n_{j}-1,}$ of $\left( M_{i,j}\right) ^{{1\le i \le s}}_{1\le j \le r}$ in formula(16) is an square matrix. In this case, one has to take the same index $s=r=m$ with $n_{k}={\bar{n}}_{k}=n\ (k=1,2, \ldots ,m)$ and $N=n \times m$ in (16). This yields the normal N-th order m-solitons.

For example, we consider the second-order two-soliton. Especially, choosing a pair of non-purely-imaginary eigenvalues: $\zeta _{1},\ \zeta _{2} \in \{{\mathbb {C}}_{+} \setminus i{\mathbb {R}}_{+}\}$ with $\zeta _{2} =-\zeta _{1}^*$, which belongs to the second type two-solitons for Eq. (1) discussed in [19]. Thus, from above results (23)–(24), their perturbed eigenvalues and eigenvectors are related as

$$\begin{aligned}&\zeta _{2}(\epsilon )= -\,\zeta ^*_{1}(\epsilon ),\\&v_{20}(\epsilon )=\sigma _{1}v^*_{10}(\epsilon ),\ v_{10}(\epsilon )=[1, {\text {e}}^{b_{10}+b_{11}\epsilon \ }]^\mathrm{T}, \end{aligned}$$

where $b_{10}, b_{11}$ are complex constants.

Similarly, for a pair of non-purely-imaginary eigenvalues ${\bar{\zeta }}_{1},\ {\bar{\zeta }}_{2} \in \{{\mathbb {C}}_{-} \setminus i{\mathbb {R}}_{-}\}$, with ${\bar{\zeta }}_{2} =-\,{\bar{\zeta }}_{1}^*$, their perturbed eigenvalues and eigenfunctions are related as

$$\begin{aligned}&{\bar{\zeta }}_{2}({\bar{\epsilon }})=-\,{\bar{\zeta }}_{1}^*({\bar{\epsilon }}),\\&{\bar{v}}_{20}({\bar{\epsilon }})=\sigma _{1} {\bar{v}}_{10}^*({\bar{\epsilon }}),\ {\bar{v}}_{10}(\epsilon )=[1, {\text {e}}^{{\bar{b}}_{10}+{\bar{b}}_{11}\epsilon \ }]^\mathrm{T}, \end{aligned}$$

where ${\bar{b}}_{10}, {\bar{b}}_{11}$ are complex constants. Substituting these data into (16) with $N=4$, $n_{1}=n_{2}=2$ and ${\bar{n}}_{1}={\bar{n}}_{2}=2$. Then, it is found that the corresponding solution can be nonsingular or repeatedly collapse in pairs at spatial locations. In addition, they can move in four opposite directions and exhibit more complex wave-front structures. To demonstrate their dynamics, we choose two sets of parameters:

$$\begin{aligned}&\zeta _{1}=-\,\zeta _{2}^*=0.3+0.8i,\nonumber \\&{\bar{\zeta }}_{1}=-\,{\bar{\zeta }}_{2}^*=0.3-0.8i, \end{aligned}$$

(38)

$$\begin{aligned}&{\text {e}}^{b_{10}}=1+ 0.2i, \ {\text {e}}^{{\bar{b}}_{10}}=1-0.1 i. \nonumber \\&{\text {e}}^{b_{11}}=0.2, \ {\text {e}}^{{\bar{b}}_{11}}=0.25. \end{aligned}$$

(39)

$$\begin{aligned}&\zeta _{1}=-\,\zeta _{2}^*=0.3+i, {\bar{\zeta }}_{1}=-\,{\bar{\zeta }}_{2}^*=0.3 - 1.2i, \end{aligned}$$

(40)

$$\begin{aligned}&{\text {e}}^{b_{10}}=1+ i, \ {\text {e}}^{{\bar{b}}_{10}}=1- i,\ {\text {e}}^{b_{11}}=1, \nonumber \\&{\text {e}}^{{\bar{b}}_{11}}=1. \end{aligned}$$

(41)

Parameters (38)–(39) generate a nonsingular solution which is plotted in the left panel of Fig. 3, while the right panel in Fig. 3 exhibits the blowing-up solution derived from parameter set (40)–(41). Especially, if the real parts of eigenvalues $\zeta _{k}$ and ${\bar{\zeta }}_{k}$ are not equal, the amplitudes of moving waves decrease or increase exponentially with time.

4.2.2 The hybrid pattern: combination of different block types

Secondly, we consider a more general case, where the blocks (sub-matrices) are not required to be square matrices. Instead, different types of blocks can be combined together through formula (16). Specifically, defining two index sets $I_{1}$ and $I_{2}$ for the block matrix:

$$\begin{aligned} I_{1}=\{n_{1},\ldots ,n_{r} \},\ I_{2}=\{ {\bar{n}}_{1},\ldots ,{\bar{n}}_{s} \}. \end{aligned}$$

From above discussion we know that $I_{1}$ and $I_{2}$ are mutually independent. By virtue of this fact, novel solution patterns can be achieved by taking different index values in the sets. These interesting hybrid solitons have not been reported before. They can describe the nonlinear interactions between several one- or multi-solitons with unequal orders.

Taking $N=2$ in formula (16), then index sets have three kinds of combinations (Regardless of other equivalent cases): (a) $I_{1}=I_{2}=\{1, 1\}$; (b) $I_{1}=I_{2}=\{2\}$; (c) $I_{1}=\{1,1\},\ I_{2}=\{2\}$. The first two combinations are the normal case, which corresponding to the two-soliton and second-order fundamental-soliton. For the last combination, there are two simple zeros in ${\mathbb {C}}_{+}$, which locate symmetric about the imaginary axis, and one zero (multiplicity two) locates in ${\mathbb {C}}_{-}$. This interesting configuration of eigenvalues corresponds to a special “two-soliton” solution. Such an example is shown in Fig. 4 with parameters:

$$\begin{aligned} \zeta _{1}= & {} -\zeta _{2}^*=0.1+0.5i,\nonumber \\ \bar{\zeta _{1}}= & {} -0.25i,\ \ b_{10}=0,\ \ {\bar{\theta }}_{10}=0,\ \ {\bar{\theta }}_{11}=0.2. \end{aligned}$$

(42)

This soliton describes two waves travel in opposite directions as they repeatedly collapsing over time. Remarkably, their motion trajectory is no longer on the straight line but certain curves. This is quite different from the normal two-soliton. In addition, the amplitudes |q| of two traveling waves are growing or decreasing exponentially with time, just along the directions of motion.

Fig. 4

Left panel is a hybrid solution with parameters (42). Right panel is the corresponding density plot (here, the collapsing points are shown by the white bright spots, when they are amplifying or shrinking along the line, it means the solutions’ amplitudes are increasing or decreasing correspondingly)

Fig. 5

Left panel is a hybrid solution with parameters (45). Right panel shows a hybrid solution with parameters (43)–(44)

Next, when $N=3$, the corresponding block sets have six combinations: (a). $I_{1}=I_{2}=\{1,1,1\}$; (b). $I_{1}=\{1,1,1\},\ I_{2}=\{1,2\}$; (c). $I_{1}=\{1,1,1\},\ I_{2}=\{3\}$; (d). $I_{1}=\{1,2\},\ I_{2}=\{1,2\}$; (e). $I_{1}=\{1,2\}, \ I_{2}=\{3\}$; (f). $I_{1}=I_{2}=\{3\}$. These sets can feature the interactions of several types of one- or multi-solitons with certain orders, except for the normal case (a) and (f).

Specifically, if we consider combination (b), there will be three simple poles in the upper half plane and one double pole with one simple pole in the lower half plane. This eigenvalue configuration can also bring new hybrid patterns, which features nonlinear superposition between a special “two-soliton” and a fundamental one-soliton. Using parameter values

$$\begin{aligned}&\zeta _{1}=-\,\zeta _{2}^*=0.1+0.6i,\ \zeta _{3}=0.5i,\nonumber \\&\bar{\zeta _{1}}=-\,0.7i, \ \bar{\zeta _{2}}=-\,0.25i, \end{aligned}$$

(43)

$$\begin{aligned}&b_{10}=0, \nonumber \\&\theta _{30}={\bar{\theta }}_{10}={\bar{\theta }}_{20}={\bar{\theta }}_{21}=0. \end{aligned}$$

(44)

The associated solution is plotted in Fig. 5. This soliton features two waves travel in two opposite curves, plus another stationary wave (fundamental soliton) at $x=0$, while they both repeatedly collapse along the directions. Moreover, the amplitudes of the moving waves are changing with time as well.

Considering combination (d) as another example. In this case, there is one simple pole with one double pole in the upper half plane as well as the lower half plane. This eigenvalue configuration could create a new type of hybrid soliton which differs from other patterns. To illustrate its dynamics, we choose parameters

$$\begin{aligned}&\zeta _{1}={\bar{\zeta }}_{1}^*=0.25i,\ \zeta _{2}={\bar{\zeta }}_{2}^*=0.5i, \nonumber \\&\theta _{10}=-\,{\bar{\theta }}_{20}=-\,\pi /6, \end{aligned}$$

(45)

$$\begin{aligned}&{\bar{\theta }}_{10}=-\,\theta _{20}=\pi /4,\ \theta _{21}=1, \ {\bar{\theta }}_{21}=0.5. \end{aligned}$$

(46)

Corresponding graph for this solution is presented in Fig. 5, which features the nonlinear interaction between the second-order one-soliton and a fundamental-soliton.

This soliton does not collapse and the interesting periodic phenomenon can be seen. For the rest of the combinations, we can still utilize formula (16) to generate solitons in other hybrid patterns.

Fig. 6

The second-order one-soliton (48) with parameters: (left panel) $\zeta _{1}=0.1+i, {\text {e}}^{b_{10}}=1+0.1i,\ {\text {e}}^{b_{11}}=1$. (Right panel) $\zeta _{1}=-\,0.1+i, {\text {e}}^{b_{10}}={\text {e}}^{b_{11}}=1$

Therefore, as we could see, solitons with hybrid patterns exhibit rich and novel solution dynamics which have not been observed before. Similarly, the higher-order hybrid solutions can be also investigated in this way and the additional novel phenomenon can be expected.

5 Dynamics of high-order solitons in the reverse-time NLS equation

To derive N-th order solitons for the reverse-time NLS Equation (2), we need to impose corresponding symmetry relations of “perturbed” discrete scattering data in the general soliton formula (16). Normally, for a pair of discrete eigenvalues $(\zeta _{k}, {\bar{\zeta }}_{k})$, where $\zeta _{k} \in {\mathbb {C}}_{+}$ and ${\bar{\zeta }}_{k}=-\,\zeta _{k} \in {\mathbb {C}}_{-}$. From Eq. (27) in Sect. 3, we get the corresponding “perturbed” eigenvectors:

$$\begin{aligned}&v_{k0}(\epsilon )=[1, {\text {e}}^{\sum _{j=0}^{N-1}b_{k,j}\epsilon ^{j}} ]^\mathrm{T},\nonumber \\&{\bar{v}}_{k0}=v_{k0}(-\,{\bar{\epsilon }}),\ \ b_{kj}\in {\mathbb {C}}. \end{aligned}$$

(47)

Hence, the N-th order m-solitons have $m(N+1)$ free complex constants: $\{\zeta _{k},\ b_{k,j},\ 1\le k\le m,\ 0 \le j \le N-1 \}$.

The second-order fundamental-soliton is obtained when we set $N=2, m=1$ with $n_{1}={\bar{n}}_{1}=2$ in (16), and the analytical expression is:

$$\begin{aligned} q(x,t)=\frac{8\zeta _{1} {\text {e}}^{4i\zeta _{1}^2 t} \left[ {\text {e}}^{-2i\zeta _{1}x-\ln b_{10}} f_{1}(x,t)+ {\text {e}}^{2i \zeta _{1}x+\ln b_{10}} {\bar{f}}_{1}(x,t) \right] }{4\cosh ^2\left( 2i\zeta _{1}x+\ln b_{10}\right) + f_{0}(x,t)}.\nonumber \\ \end{aligned}$$

(48)

where $f_{0}(x,t)=4(f_{1}(x,t)+i)({\bar{f}}_{1}(x,t)+i)$, and

$$\begin{aligned} f_{1}(x,t)= & {} \zeta _{1}(2x+8\zeta _{1}t-ib_{11}b_{10}^{-1})-i,\ \\ {\bar{f}}_{1}(x,t)= & {} \zeta _{1}(-2x+8\zeta _{1}t+ib_{11}b_{10}^{-1})-i. \end{aligned}$$

The fundamental soliton in Eq. (2) is found to be stationary [19]. However, for this second-order fundamental-soliton, two solitons move along the path

$$\begin{aligned} \varSigma _{\pm }:\ \ 2 \text {Im} (\zeta _{1}) x \pm \frac{1}{2}\ln \left| f_{0}(x,t)\right| -\ln |b_{1}|=0 \end{aligned}$$

(49)

with almost the same velocity. As $t\rightarrow \pm \infty$, the amplitudes |q| change as

$$\begin{aligned} |q(x,t)|\sim \frac{8|\zeta _{1}|{\text {e}}^{-4\text {Im} (\eta _{1}^2)t}}{|{\text {e}}^{\pm 2i\gamma x-i\tau _{0} \pm 2i\arg (b_{10})}+1|}, \end{aligned}$$

(50)

where $\gamma =2\text {Re}(\zeta _{1})$, $\tau _{0}= \text {Arg} \left[ f_{0}(x,t)\right] +2 k \pi ,\ (k \in {\mathbb {Z}})$.

This soliton would also collapse at certain locations, but not repeatedly collapse with time. Under a suitable choice of parameters, this high-order soliton can be non-collapsing. The amplitudes of two moving waves grows or decays exponentially when $\zeta _{1} \in \{{\mathbb {C}}_{+} \setminus i{\mathbb {R}}_{+}\}$, and it would decay/grow when $\zeta _{1}$ is in the first/second quadrant of the complex plane. As concrete examples, graphs of these solitons are illustrated in Fig. 6 with two sets of parameters.

Normally, the N-th order fundamental-soliton could exhibit analogical features with the second-order fundamental-soliton. There will be N different asymptote trajectories with N waves moving along them in the nearly same velocities. For instance, a decaying third-order one-soliton is displayed in Fig. 7. Moreover, the high-order multi-solitons could exhibit quite different dynamics. For example, the second-order two-solitons move in four opposite directions when $\zeta _{1}$, $\zeta _{2}$ are not both purely imaginary, and the repeated collapsing with “four-way” motion can be observed. Such an high-order two-soliton solution is shown in Fig. 7, which cannot be seen as a simple nonlinear superposition between two second-order fundamental-solitons.

Fig. 7

(Left panel) Density plot for the third-order soliton with parameters: $\zeta _1=0.05+i,\ {\text {e}}^{b_{10}}=1,\ {\text {e}}^{b_{11}}=0.1+0.1i.$ (Right panel) Density plot for the second-order two-solitons with parameters: $\zeta _1=0.2+i,\ \zeta _2=-\,0.1+1.2i,\ {\text {e}}^{b_{10}}=1+0.5i,\ {\text {e}}^{b_{20}}=1,\ {\text {e}}^{b_{11}}={\text {e}}^{b_{21}}=1$

6 Dynamics of high-order solitons in the reverse-space-time NLS equation

To derive the N-th order solitons in the reverse-space-time NLS Eq. (3), we impose symmetry relations of discrete scattering data (28) in the general soliton formula (16). In this case, the normal N-th order m-solitons have 2m free complex constants: $\{ \zeta _{k},\bar{\zeta _{k}}, 1\le k \le m \}$, where $\zeta _{k} \in {\mathbb {C}}_{+}$, and ${\bar{\zeta }}_{k} \in {\mathbb {C}}_{-}$.

For the second-order fundamental-soliton, we choose $m=1$ with $N=n_{1}={\bar{n}}_{1}=2$. So the analytic expression for this solution is

$$\begin{aligned}&q(x,t)=\frac{4 {\bar{\omega }}_1 \left( \zeta _1-{\bar{\zeta }}_1\right) \left[ \omega _1 {\bar{\omega }}_1 {\text {e}}^{-2 i \left( {\bar{\zeta }}_1x -2 {\bar{\zeta }}_1^2 t \right) }f_1(x,t)+ {\text {e}}^{-2 i \left( \zeta _1 x-2 \zeta _1^2 t\right) }{\bar{f}}_1(x,t)\right] }{{\text {e}}^{2 i \left( \bar{\zeta }_1-\zeta _1\right) x+4 i \left( \zeta _1^2-{\bar{\zeta }}_1^2\right) t}+ {\text {e}}^{ -2 i \left( {\bar{\zeta }}_1-\zeta _1\right) x-4 i \left( \zeta _1^2-{\bar{\zeta }}_1^2\right) t}+ \omega _1{\bar{\omega }}_1f_0(x,t)}, \end{aligned}$$

(51)

where $f_{0}(x,t)=4(f_{1}+i)({\bar{f}}_{1}+i)+2$, and

$$\begin{aligned} f_{1}(x,t)= & {} \left( {\bar{\zeta }}_1-\zeta _1\right) (x-4 \zeta _{1} t)-i,\\ {\bar{f}}_{1}(x,t)= & {} \left( \zeta _1-\bar{\zeta }_1\right) (x-4{\bar{\zeta }}_{1}t)-i. \end{aligned}$$

It is found that the above high-order fundamental-soliton (51) has two gradually paralleled center trajectories, which approximatively locate on following two curves in the (x, t) plane:

$$\begin{aligned}&\varSigma _{\pm }:\ \ \text {Im}\left( {\bar{\zeta }}_1-\zeta _1\right) x\nonumber \\&\quad -2\text {Im}\left( {\bar{\zeta }}_1^2 -\zeta _1^2\right) t \pm \frac{1}{2}\ln \left[ \left| f_{0}-2\right| \right] =0. \end{aligned}$$

(52)

Fig. 8

Two second-order one-solitons (51) in the reverse-space-time NLS Equation (3). The parameters for the density plot (a) (b) are given by Eqs. (54) and (55), respectively

Moreover, regardless of the effect brought by the logarithmic part when $t\rightarrow \pm \infty$, two solitons separately move along each curve in a nearly same velocity, which is approximate to

$$\begin{aligned} V \approx V_{c} := 2\text {Im}\left( {\bar{\zeta }}_1^2 -\zeta _1^2\right) /\text {Im}\left( {\bar{\zeta }}_1-\zeta _1\right) , \end{aligned}$$

and the solution’s amplitudes |q| would approximately change as

$$\begin{aligned}&|q(t)|\sim 2|\zeta _{1}-{\bar{\zeta }}_{1}| \ \frac{{\text {e}}^{\beta t \pm \delta _{0}} }{\left| {\text {e}}^{\pm 2i \gamma t-i \tau _{0}} + \omega _{1} {\bar{\omega }}_{1}\right| }, \quad t \sim \pm \infty ,\nonumber \\ \end{aligned}$$

(53)

where

$$\begin{aligned}&\beta = -\,2V_{c} \text {Im}\left( {\bar{\zeta }}_1\right) -4\text {Im}\left( {\bar{\zeta }}_1^2\right) ,\\&\gamma =V_{c}\text {Re}\left( \zeta _1-{\bar{\zeta }}_1\right) -2\text {Re}\left( \zeta _1^2-{\bar{\zeta }}_1^2\right) . \\&\delta _{0}=-\,\text {Im}\left( \zeta _1+{\bar{\zeta }}_1\right) \ln \sqrt{|f_{0}-2|} / \text {Im}\left( {\bar{\zeta }}_1-\zeta _1\right) , \end{aligned}$$

and $\tau _{0}=\text {Arg}\left[ f_{0}(x,t)-2\right] +2k\pi ,\ (k \in {\mathbb {Z}})$.

From this estimation, the soliton’s amplitude is growing or decaying exponentially along the path $\varSigma _{\pm }$ at the rate of ${\text {e}}^{\beta t \pm \delta _{0}}$, which depends mainly on the value of $\beta$ (except for the case when $\text {Re}(\zeta _{1})=\text {Re} ( {{\bar{\zeta }}}_{1})$, where $\beta =0$). There are also some differences in the amplitudes when q(x, t) moves on different trajectories, depending on the sign of $\delta _{0}$. Especially, if $\delta _{0}=0$, both of them will keep the same amplitude.

Another interesting feature for this high-order fundamental-soliton is the repeatedly collapsing phenomenon. And the blowing-up interval $T_{c}$ for this solution admits a “perturbative” varying period, which can be roughly estimated as: $T_{c} = \pi /|\gamma |+\varDelta (t)$, where $\varDelta (t)$ is a time-dependent small error term. Regardless of minor changes in the arguments $\tau _{0}(t)$, the approximately value of $\varDelta (t)$ is attained as $\varDelta (t)\thickapprox \left[ {\bar{\tau }}_{0}(t_{c}+\pi /|\gamma |)-\tau _{0}(t_{c})\right] / 2\gamma$, where $t_{c}$ is the time coordinate for an initial singularity. Examples are given for two sets of parameters:

$$\begin{aligned} \zeta _{1}= & {} -\,0.3+0.9i,\ \ \bar{\zeta _{1}} = -\,0.28-0.6i,\nonumber \\ \omega _1= & {} {\bar{\omega }}_1=1, \end{aligned}$$

(54)

$$\begin{aligned} \zeta _{1}= & {} 0.35+0.9i,\ \ \bar{\zeta _{1}} =0.325-0.6i,\nonumber \\ \omega _1= & {} -\, {\bar{\omega }}_1=1. \end{aligned}$$

(55)

Graphs of the two fundamental solitons are displayed, respectively, in Fig. 8. Apparently, both of these two solitons collapse repeatedly with time. In the former solution, the soliton moves at velocity about $V_{c}\thickapprox -\,1.168$ (to the left). The amplitude |q| exponentially increases along the curve $\varSigma _{\pm }$ at the rate of ${\text {e}}^{\beta t}$ with $\beta \thickapprox 0.0576$. In the latter solution, the soliton moves at velocity $V_{c}\thickapprox 1.36$ (to the right), while |q| decreases exponentially along $\varSigma _{\pm }$ at the rate of ${\text {e}}^{\beta t}$ with $\beta \thickapprox -0.072$.

For the high-order multi-solitons, because the eigenvalues $\zeta _{k} \in {\mathbb {C}}_{+}$ and ${\bar{\zeta }}_{k} \in {\mathbb {C}}_{-}$ are totally independent, they can be arranged in several different configurations, this will give rise to new types of solitons for the reverse-space-time NLS Equation (3). For instance, with symmetry (28) on the eigenvectors, if we take $N=2$ with $I_{1}=\{1,1\}$ and $I_{2}=\{2\}$ in formula (16), certain choice of parameters can produce a high-order “two-soliton.” Choosing $N=4$ with $I_{1}=I_{2}=\{2,2\}$, we can derive a nonlinear superposition between two different second-order one-soliton solutions. (This solution can be also regarded as a second-order two-soliton.) Graphs of these solitons are very similar to those displayed in Figs. 3 and 4, so their novel dynamic behaviors can be expected.

7 Summary and discussion

In summary, we have derived general high-order solitons in the $\mathcal {PT}$-symmetric, reverse-time, and reverse-space-time nonlocal NLS Eqs. (1)–(3) by using a Riemann–Hilbert treatment. Through the symmetry relations on the “perturbed” scattering data for each equation, we have shown that the high-order solitons can be separately reduced from the same Riemann–Hilbert solutions of the AKNS hierarchy. At the same time, novel solution behaviors in these nonlocal equations have been further discussed. We have found that the high-order fundamental-soliton is always moving on several trajectories in nearly equal velocities, while the high-order multi-solitons could have more complicated wave and trajectory structures. In all these nonlocal equations, a generic character in their high-order solitons is repeated collapsing. Moreover, new types of high-order hybrid-pattern solitons are discovered, which can describe a nonlinear superposition between several types of solitons. Our findings reveal the novel and rich structures for high-order solitons in the nonlocal NLS Equations (1)–(3), and they could intrigue further investigations on solitons in the other nonlocal integrable equations.

In addition, it should be noted that by utilizing new symmetry properties of scattering data in these nonlocal equations, some open questions left over in the previous Riemann–Hilbert derivations of solitons have been resolved [19]. Specifically, Ref. [19] pointed out that: when the numbers of eigenvalues (or, known as zeros of the Riemann–Hilbert problem) in the upper and lower complex planes, counting multiplicity, are not equal to each other, it would produce solutions which are unbounded in space (thus never solitons). Therefore, in order to illustrate the validity for this conclusion in the case of multiple zeros, we consider the second-order fundamental-soliton in the $\mathcal {PT}$-symmetric NLS equation by choosing a single pair of eigenvalues $(\zeta _{1}, {\bar{\zeta }}_{1})\in i{\mathbb {R}}_{+}$ in expression (29), then it produces a high-order “fundamental-soliton.” Although it still satisfies Eq. (1), this solution is not localized in space and grows exponentially in the positive x directions.