Chance constrained programming with some non-normal continuous random variables

Abstract

Stochastic or probabilistic programming is a branch of mathematical programming that deals with some situations in which an optimal decision is desired under random uncertainty of some parameters. In this paper, we consider some chance constrained linear programming problems where the right hand side parameters of the chance-constraints follow some non-normal continuous distributions such as power function distribution, triangular distribution and trapezoidal distribution. To find the solution of the stated problems, we first convert the problems in to equivalent deterministic models. Then standard linear programming techniques are used to solve the equivalent deterministic models. Some numerical examples are presented to illustrate the methodology.

1 Introduction

In most of the real-life decision-making problem, decision maker needs to take decision under some uncertain environment. The uncertainty can be found in parameter space as well as in the decision space of a decision making problem. These uncertainties are addressed by using probability distribution or fuzzy value or intervals. Stochastic Programming (SP) is concerned with the decision making problems in which some or all parameters are treated as random variables in order to capture the uncertainty. SP is used in several real world decision making areas such as energy management, financial modeling, supply chain and scheduling, hydro thermal power production planning, transportation, agriculture, defence, environmental and pollution control, production and control management, telecommunications, etc. Several models and methodologies have been developed in the field of stochastic programming. In the literature, there exist two very popular approaches to solve SP problems, namely,

• 1. Chance constrained programming, and

• 2. Two-stage programming.

Chance constrained programming was developed as a means of describing constraints in mathematical programming models in the form of probability levels of attainment. The chance constrained programming (CCP) can be used to solve problems involving chance-constraints, i.e.constraints having violation up to a pre-specified probability level. The use of chance-constraints was initially introduced by Charnes and Cooper [8]. They established three different models for the objective functions with random cost coefficients:

• 1. E-model which maximizes the expected value of the objective function,

• 2. V-model which minimizes the generalized mean square of the objective function, and

• 3. P-model which maximizes the probability of the aspiration level of the objective function.

In the literature of the stochastic linear programming [13, 16, 17], various models have been suggested by several researchers. Bibliographical review is presented by Stancu and Wets [31], Infanger [13]. Most of the applications of the stochastic models assume normal distribution for model coefficients. Apart from the normal distribution, other distributions have been considered for the model coefficients also. Goicoechea et al. [12] presented some probabilistic model involving uniform, exponential, normal and other random variables. Further, Goicoechea and Duckstein [11] presented some deterministic equivalent models for the probabilistic programming with non-normal distributions. Jagannathan [14] has presented a single-objective probabilistic model by considering the parameters as normal random variables. Miller and Wagner [23] presented a method for solving chance constrained programming with joint constraints. Biswal et al. [6] presented some probabilistic linear programming problems by considering some parameters as exponential random variables. Later, Biswal et al. [7] proposed a solution scheme for solving probabilistic constrained programming problems involving log-normal random variables. Sahoo and Biswal [28] have also presented some stochastic programming problems with cauchy and extreme value distributions. Further, they presented some probabilistic linear programming problems by assuming the random parameters as normal and log-normal random variables with joint constraint [27]. Barik et al. [4] presented some stochastic programming problems involving pareto distributions. Agnew et al. [1] applied chance constrained programming to Portfolio Selection in a Casualty Insurance Firm. Sun et al. [32] developed an inexact joint-probabilistic chance-constrained programming method with left-hand-side randomness and applied it to solid waste management. Li et al. [20] proposed chance constrained programming approach to process optimization under uncertainty. Bilsel and Ravindran [5]developed a multi-objective stochastic sequential supplier allocation model to help in supplier selection under uncertainty. Yu and Chung [33] proposed a chance constrained formulation to tackle the uncertainties of load and wind turbine generator in transmission network expansion planning. Shen and Zhu [30] presented a chance-constrained model for uncertain job shop scheduling problem with uncertain processing time and cost. Lejeune and Margot [19] proposed a new and systematic reformulation and algorithmic approach to solve a complex class of stochastic programming problems involving a joint chance constraint with random technology matrix and stochastic quadratic inequalities. Lodi and et al. [21] presented a present a Branch-and-Cut algorithm for a class of nonlinear chance-constrained mathematical optimization problems with applications to hydro scheduling. Recently, Pradhan and Biswal [26] presented a solution procedure based on chance constrained programming technique to solve a multi-choice probabilistic linear programming problem where alternative choices of any multi-choice parameter are considered as random variables.

In the literature of stochastic programming, there is no article on the chance constrained programming problem where some parameters follow power function distribution or triangular distribution or trapezoidal distribution. So, in this paper, we proposed a solution procedure of some chance constrained programming problems where the right hand side parameters follow either power function distribution or triangular distribution or trapezoidal distribution.

2 Stochastic programming problem

Stochastic linear programming is an extension of linear programming problem where some parameters are random variables. Mathematically, a stochastic linear programming problem can be stated as:

$$\begin{aligned} \min : Z = \sum _{j=1}^{n}\ c_{j}x_{j} \end{aligned}$$

(1)

subject to

$$\begin{aligned}&\sum _{j=1}^{n}a_{ij}x_{j} \ge b_{i},\qquad i=1,2,...,s \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{j=1}^{n}a_{ij}x_{j} \le b_{i},\qquad i=s+1,s+2,...,m \end{aligned}$$

(3)

$$\begin{aligned}&x_{j}\ge 0, \qquad \qquad j = 1,2,....n \end{aligned}$$

(4)

where $\mathbf{x}=(x_1,x_2,...,x_n)$ is the decision vector, $a_{ij} \, (i = 1,2,...,m;\,j = 1,2,...,n)$, are the constraint coefficients, $c_{j}\,(j = 1,2,...,n)$ are the coefficients associated with the objective function. Only the right hand side parameters $b_{i} \, (i =1,2,...,m)$ are considered as random variables which follow different distributions with finite mean and variance. Since, $b_i$ are random in nature, we are not able to apply any standard linear programming solution methodology to find the solution of the problem. To overcome this difficulty, first we establish the deterministic model of the problem and then apply the standard methodologies to solve the deterministic model.

2.1 Chance constrained programming problem

Chance Constrained Programming (CCP) and Two-Stage Programming (TSP) are two popular approaches used to establish the deterministic form of a stochastic programming problem. In this paper, we discussed about the hance constrained programming technique only. Using chance constraints for the constraints with random variables, the stochastic programming problem (1)–(4) can be stated as:

$$\begin{aligned} \min : Z = \sum _{j=1}^{n}\ c_{j}x_{j} \end{aligned}$$

(5)

subject to

$$\begin{aligned}&Pr\left( \sum _{j=1}^{n}a_{ij}x_{j} \ge b_{i}\right) \ge (1-\gamma _{i}),\qquad i=1,2,...,s \end{aligned}$$

(6)

$$\begin{aligned}&Pr\left( \sum _{j=1}^{n}a_{ij}x_{j} \le b_{i}\right) \ge (1-\gamma _{i}),\qquad i=s+1,s+2,...,m \end{aligned}$$

(7)

$$\begin{aligned}&0<\gamma _{i}<1,\qquad i=1,2...,m \end{aligned}$$

(8)

$$\begin{aligned}&x_{j}\ge 0, \qquad j = 1,2...,n \end{aligned}$$

(9)

where Pr means probability, $\gamma _i$ is the given probability of the extents to which the i-th constraint violations are admitted. The inequalities given by (6) and (78) are called chance constraints. Here, $a_{ij} \, (i = 1,2,...,m;\,j = 1,2,...,n)$ and $c_{j}\,(j = 1,2,...,n)$ are deterministic constants, and only the right hand side parameters $b_{i}\, (i =1,2,...,m)$ are considered as random variables following either power function distribution or triangular distribution or trapezoidal distribution with finite parameters. Generally in a stochastic transportation problem/ transhipment problem, the coefficients $a_{ij}$ are constants $(\pm 1)$. These two-types of problems are also treated as special type of LPP. However, in the present model $a_{ij} \, (i = 1,2,...,m;\,j = 1,2,...,n)$ are treated as non-negative constants i.e., $a_{ij}\ge 0\, (i = 1,2,...,m;\,j = 1,2,...,n)$. If some of $a_{ij}$ are negative, the linear constraints may not fulfil the requirements. This assumption has been made in all the three cases of the CCP model.

2.1.1 Case I: When $b _i$ follows power function distribution

Power function distribution [2] is a popularly used random variable to estimate the reliability and hazard rates of a electrical component [22]. Let us consider that, $b_{i}\,(i =1,2,...m)$ in the model (5)–(9) are independent random variables which follows power function distribution with positive scale parameter $\alpha _{i}$ and positive shape parameter $\beta _{i}$. The probability density function (pdf) of the i-th random variable $b_{i}\,(i=1,2,...,m)$ is given by:

$$\begin{aligned} f(b_{i})= {\left\{ \begin{array}{ll} \frac{\beta _{i}b_{i}^{\beta _{i}-1}}{\alpha _{i}^{\beta _{i}}},&{} \quad \text{if }\, 0< b_{i} < \alpha _{i},\,\beta _{i}>0\\ 0, &{} \quad \text{otherwise} \end{array}\right. } \end{aligned}$$

(10)

For $\alpha _i=1$, the distribution function of $b_i$ is illustrated by the Fig. 1. The mean and variance of $b_{i}\,(i=1,2,...,m)$ are given by:

$$\begin{aligned} E(b_{i})&= {} \frac{\alpha _{i}\beta _{i}}{1+ \beta _{i}} ,\qquad i =1,2,..,m \end{aligned}$$

(11)

$$\begin{aligned} Var(b_{i})&= {} \frac{\alpha _{i}^{2}\beta _{i}}{(2+\beta _{i})(1+ \beta _{i})^2}, \qquad i = 1,2,...,m, \end{aligned}$$

(12)

respectively.

Fig. 1

Power function distribution with $\alpha _i=1, \,\, \beta _i=0.5,\,\, \beta _i=3$

To establish the equivalent deterministic form of the model (5)–(9), we establish the deterministic form of the chance-constraints. From the chance-constraint (6) we have

$$\begin{aligned}&Pr\left( \sum _{j=1}^{n}a_{ij}x_{j} \ge b_{i}\right) \ge (1-\gamma _{i})\\&\quad \Rightarrow Pr\left( b_{i}\le \sum _{j=1}^{n}a_{ij}x_{j}\right) \ge (1-\gamma _{i})\\&\quad \Rightarrow \int _{0}^{\sum _{j=1}^{n}a_{ij}x_{j}} f(b_{i})db_{i}\ge (1-\gamma _{i})\\ \end{aligned}$$

Integrating above, we obtain,

$$\begin{aligned} \sum _{j=1}^{n}a_{ij}x_{j} \ge \alpha _{i}({1-\gamma _{i}})^{\frac{1}{\beta _{i}}}, \qquad i=1,2,...,s \end{aligned}$$

(13)

Therefore, the equivalent deterministic form of the chance-constraints (6) is given by (13). Similarly, the deterministic form of the chance-constraints (7) is formulated as:

$$\begin{aligned} \sum _{j=1}^{n}a_{ij}x_{j} \le \alpha _{i}\gamma _{i}^{\frac{1}{\beta _{i}}}, \qquad i=s+1,s+2,...,m \end{aligned}$$

(14)

Hence, the equivalent deterministic form of the model (5)–(9) is given by:

$$\begin{aligned} \min {:}\, Z = \sum _{j=1}^{n}\ c_{j}x_{j} \end{aligned}$$

(15)

subject to

$$\begin{aligned}&\sum _{j=1}^{n}a_{ij}x_{j} \ge \alpha _{i}({1-\gamma _{i}})^{\frac{1}{\beta _{i}}},\qquad i=1,2,...,s \end{aligned}$$

(16)

$$\begin{aligned}&\sum _{j=1}^{n}a_{ij}x_{j} \le \alpha _{i}\gamma _{i}^{\frac{1}{\beta _{i}}},\qquad i=s+1,s+2,...,m \end{aligned}$$

(17)

$$\begin{aligned}&0<\gamma _{i}<1, \qquad i=1,2...,m \end{aligned}$$

(18)

$$\begin{aligned}&x_{j}\ge 0, \qquad j = 1,2...,n \end{aligned}$$

(19)

The above model is a linear programming model, using any linear programming technique or LP solver we can solve the problem to obtain the optimal solution.

2.1.2 Case II: When $b _i$ follows triangular distribution

In some real-life situations, we can often estimate the maximum and the minimum values, and the most likely outcome of an event. In these cases, we can represent the corresponding random variable as triangular random variable [3, 15].The triangular distribution is popular for using in modeling estimation of some uncertain quantity in business risk models, oil and gas exploration, business decision making based on simulation of the outcome. The advantages of using triangular distribution over Beta distribution have been discussed by [18]. Let us assume that, in the model (5)–(9), $b_{i}\,(i =1,2,...m)$ are independent random variables which follow triangular distributions with parameters $t_{i1}$ (minimum value), $t_{i2}$ (most likely outcome) and $t_{i3}$ (maximum value). The notation of triangular distribution is given by $b_i=(t_{i1},t_{i2},t_{i3})$. Then the pdf of the random variable $b_{i}$ is given by:

$$\begin{aligned} f(b_{i})= {\left\{ \begin{array}{ll} \frac{2(b_{i}-t_{i1})}{(t_{i3}-t_{i1})(t_{i2}-t_{i1})},&{} \text{if }\qquad t_{i1}< b_{i}< t_{i2}\\ \frac{2(t_{i3}-b_{i})}{(t_{i3}-t_{i1})(t_{i3}-t_{i2})},&{} \text{if }\qquad t_{i2} \le b_{i} < t_{i3} \end{array}\right. } \end{aligned}$$

(20)

The graphical representation of the random variable $b_i$ (with $t_{i1}\ge 0$) is given by the Fig. 2. To establish the deterministic form of the chance constraints, we consider the Eq. (6). Then,

$$\begin{aligned}&Pr\left( \sum _{j=1}^{n}a_{ij}x_{j} \ge b_{i}\right) \ge (1-\gamma _{i})\\&\quad \Rightarrow Pr\left( b_{i}\le \sum _{j=1}^{n}a_{ij}x_{j}\right) \ge (1-\gamma _{i})\\&\quad \Rightarrow \int _{0}^{\sum _{j=1}^{n}a_{ij}x_{j}} f(b_{i})db_{i}\ge (1-\gamma _{i}) \end{aligned}$$

Integrating above, we obtain,

$$\begin{aligned}&\sum _{j=1}^{n}a_{ij}x_{j} \ge t_{i1}+\sqrt{(1-\gamma _{i})(t_{i3}-t_{i1})(t_{i2}-t_{i1})},\,\,when\, \sum _{j=1}^{n}a_{ij}x_{j} \le t_{i2} \end{aligned}$$

(21)

$$\begin{aligned}&\sum _{j=1}^{n}a_{ij}x_{j} \ge t_{i3}-\sqrt{\gamma _{i}(t_{i3}-t_{i1})(t_{i3}-t_{i2})},\,\, when\,\sum _{j=1}^{n}a_{ij}x_{j} \ge t_{i2} \end{aligned}$$

(22)

Similarly, the equivalent deterministic form of the chance-constraint (78) is given by:

$$\begin{aligned}&\sum _{j=1}^{n}a_{ij}x_{j} \le t_{i1}+\sqrt{\gamma _{i}(t_{i3}-t_{i1})(t_{i2}-t_{i1})},\,\,when\, \sum _{j=1}^{n}a_{ij}x_{j} \le t_{i2} \end{aligned}$$

(23)

$$\begin{aligned}&\sum _{j=1}^{n}a_{ij}x_{j} \le t_{i3}-\sqrt{(1-\gamma _{i})(t_{i3}-t_{i1})(t_{i3}-t_{i2})},\,\, when\,\sum _{j=1}^{n}a_{ij}x_{j} \ge t_{i2}\qquad \end{aligned}$$

(24)

In chance-constraint programming, we take the least probability value of the constraint in the range [0.9, 1], usually. In that case, $\gamma _i\in [0,0.1]$. In this situation, $\gamma _i \le Pr(b_i \le t_{i2}) \le 1-\gamma _i$, hence

• 1. $Pr(\sum _{j=1}^{n}a_{ij}x_{j} \ge b_i) \ge 1-\gamma _i \Rightarrow \sum _{j=1}^{n}a_{ij}x_{j} \ge t_{i2}$

• 2. $Pr(\sum _{j=1}^{n}a_{ij}x_{j} \le b_i) \ge 1-\gamma _i \Rightarrow \sum _{j=1}^{n}a_{ij}x_{j} \le t_{i2}$

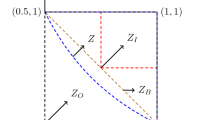
This situation is described by the Fig. 3, where the total area shaded by red lines is $(1-\gamma _i)$ and the area shaded by blue lines is $\gamma _i$. Hence, in this case the equivalent deterministic form of the chance-constraint (6) is given by the Eq. (22) and the equivalent deterministic form of the chance-constraint (78) is given by the Eq. (23).

Fig. 2

Triangular distribution

Fig. 3

$b_i$ Follows triangular distribution

Hence, the equivalent deterministic form of the model (1)–(9) is given as:

$$\begin{aligned} \min : Z = \sum _{j=1}^{n}\ c_{j}x_{j} \end{aligned}$$

(25)

subject to

$$\begin{aligned}&\sum _{j=1}^{n}a_{ij}x_{j} \ge t_{i3}-\sqrt{\gamma _{i}(t_{i3}-t_{i1})(t_{i3}-t_{i2})},\qquad i=1,2,...,s \end{aligned}$$

(26)

$$\begin{aligned}&\sum _{j=1}^{n}a_{ij}x_{j} \le t_{i1}+\sqrt{\gamma _{i}(t_{i3}-t_{i1})(t_{i2}-t_{i1})},\qquad i=s+1,s+2,...,m \end{aligned}$$

(27)

$$\begin{aligned}&0<\gamma _{i}<1, \qquad i=1,2...,m \end{aligned}$$

(28)

$$\begin{aligned}&x_{j}\ge 0, \qquad j = 1,2...,n \end{aligned}$$

(29)

The above model is a linear programming model, using any linear programming technique or LP solver we can solve the problem to obtain the optimal solution.

2.1.3 Case III: When $b _i$ follows trapezoidal distribution

Trapezoidal distributions [10, 15] have been advocated in risk analysis problems by [24] and Powell et al. [25]. They have also found application as membership functions in fuzzy set theory (see, e.g. Chen and Hwang) [9].

In this case, we assume that $b_{i} \, (i =1,2,...m)$ in the model (5)–(9) are independent random variables following trapezoidal distribution with parameters $t_{i1}$ (minimum value), $t_{i4}$ (maximum value), and with two most likely values $t_{i3}$ and $t_{i4}$.The notation of trapezoidal distribution is given by $b_i=(t_{i1},t_{i2},t_{i3},t_{i4})$ The pdf of $b_i$ is given by:

$$\begin{aligned} f(b_{i})= {\left\{ \begin{array}{ll} h_{i}\frac{(b_{i}-t_{i1})}{(t_{i2}-t_{i1})},&{} \text{if }\qquad t_{i1} \le b_{i} \le t_{i2}\\ h_{i}, &{} \text{if }\qquad t_{i2} \le b_{i} \le t_{i3}\\ h_{i}\frac{(t_{i4}-b_{i})}{(t_{i4}-t_{i3})},&{} \text{if }\qquad t_{i3} \le b_{i} \le t_{i4} \end{array}\right. } \end{aligned}$$

(30)

where $h_{i} =\frac{2}{((t_{i4}-t_{i1})+(t_{i3}-t_{i2}))} ,\, i =1,2,..,m.$

Fig. 4

Trapezoidal distribution

The graphical representation of the trapezoidal distribution is given by the Fig. 4. To solve the problem (5)–(9), we establish the deterministic form of the problem by finding the deterministic form of the chance-constraints containing random variables. In this case, right hand side parameter of the chance-constraints follows trapezoidal distribution. Then from chance-constraint (6), we have

$$\begin{aligned}&Pr\left( \sum _{j=1}^{n}a_{ij}x_{j} \ge b_{i}\right) \ge (1-\gamma _{i})\\&\quad \Rightarrow Pr\left( b_{i}\le \sum _{j=1}^{n}a_{ij}x_{j}\right) \ge (1-\gamma _{i})\\&\quad \Rightarrow \int _{a_{i}}^{\sum _{j=1}^{n}a_{ij}x_{j}} f(b_{i})db_{i}\ge (1-\gamma _{i}) \end{aligned}$$

Integrating above, we obtain, when $\sum _{j=1}^{n}a_{ij}x_{j} \le t_{i2}$

$$\begin{aligned} \sum _{j=1}^{n}a_{ij}x_{j} \ge t_{i1}+\sqrt{\frac{2(1-\gamma _i)(t_{i2}-t_{i1})}{h_i}} \end{aligned}$$

(31)

when $t_{i2} \le \sum _{j=1}^{n}a_{ij}x_{j} \le t_{i3}$

$$\begin{aligned} \sum _{j=1}^{n}a_{ij}x_{j} \ge \frac{1}{2}\left( t_{i1}+t_{i2}+\frac{2(1-\gamma _i)}{h_i}\right) \end{aligned}$$

(32)

when $t_{i3} \le \sum _{j=1}^{n}a_{ij}x_{j} \le t_{i4}$

$$\begin{aligned} \sum _{j=1}^{n}a_{ij}x_{j} \ge t_{i4}-\sqrt{\frac{2\gamma _i(t_{i4}-t_{i3})}{h_i}} \end{aligned}$$

(33)

which represent the equivalent deterministic form of the chance-constraint (6).

Similarly, the equivalent deterministic form of the chance-constraint (78) is given by: when $\sum _{j=1}^{n}a_{ij}x_{j} \le t_{i2}$

$$\begin{aligned} \sum _{j=1}^{n}a_{ij}x_{j} \le t_{i1}+\sqrt{\frac{2\gamma _i(t_{i2}-t_{i1})}{h_i}} \end{aligned}$$

(34)

when $t_{i2} \le \sum _{j=1}^{n}a_{ij}x_{j} \le t_{i3}$

$$\begin{aligned} \sum _{j=1}^{n}a_{ij}x_{j} \le \frac{1}{2}\left( t_{i1}+t_{i2}+\frac{2\gamma _i}{h_i}\right) \end{aligned}$$

(35)

when $t_{i3} \le \sum _{j=1}^{n}a_{ij}x_{j} \le t_{i4}$

$$\begin{aligned} \sum _{j=1}^{n}a_{ij}x_{j} \le t_{i4}-\sqrt{\frac{2(1-\gamma _i)(t_{i4}-t_{i3})}{h_i}} \end{aligned}$$

(36)

Similar to the case for triangular distribution, for this case, we consider $\gamma _i \le Pr(b_i \le t_{i2})\le Pr(b_i \le t_{i3}) \le 1-\gamma _i$ also. Then, we have

• 1. $Pr(\sum _{j=1}^{n}a_{ij}x_{j} \ge b_i) \ge 1-\gamma _i \Rightarrow \sum _{j=1}^{n}a_{ij}x_{j} \ge t_{i3}$

• 2. $Pr(\sum _{j=1}^{n}a_{ij}x_{j} \le b_i) \ge 1-\gamma _i \Rightarrow \sum _{j=1}^{n}a_{ij}x_{j} \le t_{i2}$

Fig. 5

First situation

This situation is described by the Fig. 5, where the total area shaded by red lines is $(1-\gamma _i)$ and the area shaded by blue lines is $\gamma _i$. Hence, in this case the equivalent deterministic form of the chance-constraint (6) is given by the Eq. (33). The equivalent deterministic form of the chance-constraint (78) is given by the Eq. (34).

Hence, the equivalent deterministic form of the model (1)–(9) is given by:

$$\begin{aligned} \min : Z = \sum _{j=1}^{n}\ c_{j}x_{j} \end{aligned}$$

(37)

subject to

$$\begin{aligned}&\sum _{j=1}^{n}a_{ij}x_{j} \ge t_{i4}-\sqrt{\frac{2\gamma _i(t_{i4}-t_{i3})}{h_i}},\qquad i=1,2,...,s \end{aligned}$$

(38)

$$\begin{aligned}&\sum _{j=1}^{n}a_{ij}x_{j} \le t_{i1}+\sqrt{\frac{2\gamma _i(t_{i2}-t_{i1})}{h_i}},\qquad i=s+1,s+2,...,m \end{aligned}$$

(39)

$$\begin{aligned}&0<\gamma _{i}<1, \qquad i=1,2...,m \end{aligned}$$

(40)

$$\begin{aligned}&x_{j}\ge 0,\qquad j = 1,2...,n \end{aligned}$$

(41)

where $h_{i} =\frac{2}{((t_{i4}-t_{i1})+(t_{i3}-t_{i2}))} ,\, i =1,2,..,m.$ The above model is a linear programming model, using any linear programming technique or LP solver we can solve the problem to obtain the optimal solution.

3 Numerical examples and result discussion

In the following section, we present some numerical examples to illustrate the models and methodology described in the previous section.

Example 1

In this example, we consider a problem related to a transportation problem where demands and supplies follow independent triangular and trapezoidal distribution. We use our model and methodology to solve the problem.

The ABC Sawmill Company’s CEO asks to see next month’s log hauling schedule to his three sawmills. He wants to make sure he keeps a steady, adequate flow of logs to his sawmills to capitalize on the good lumber market. Secondary, but still important to him, is to minimize the cost of transportation. The harvesting group plans to move to three new logging sites. The distance from each site to each sawmill is in Table 1. The average hauling cost is Rs. 20 per mile for both loaded and empty trucks. Hence, the transportation costs are given by the Table 2. The logging supervisor estimated the number of truckloads of logs coming off each harvest site weekly. The number of truckloads varies because terrain and cutting patterns are not unique for each site. The supply at the harvesting site and the demands at the mills are not unique for every week. From the past data, these values are considered as triangular distributions. The supply and demands are given by the Table 3. Supervisor wants that, the supply from harvesting site 1 should meet at least $99\%$. Similarly, the supply from harvesting site 2 and harvesting site 3 should meet at least $98\%$ and $97\%$, respectively. On the other hand, weekly demand at Mill 1, Mill 2 and Mill 3 should meet at least $96\%$, $95\%$, and $94\%$, respectively.

Table 1 Distances between logging sites and mills

Table 2 Round-trip transportation costs for ABC sawmill company

Table 3 Supply from the logging sites and demand at the mills

We can formulate the problem as a chance constrained model where the hauling costs is minimized and meet each of the sawmills’ daily demand while not exceeding the maximum number of truckloads from each site.

Let $x_{ij} =$ Hauling costs from Site i to Mill j, $i = 1, 2, 3$ (logging sites), $j = 1, 2, 3$ (sawmills)

The mathematical model of the problem is given by:

$$\begin{aligned} \min : Z&= {} 240x_{11}+320x_{12 }+ 400x_{13} \nonumber \\&+280x_{21}+440x_{22 }+ 440x_{23} + 160x_{31}+200x_{32 }+480x_{33} \end{aligned}$$

(42)

subject to

$$\begin{aligned}&Pr(x_{11}+x_{12 }+ x_{13} \le s_{1})\ge 0.99 \end{aligned}$$

(43)

$$\begin{aligned}&Pr(x_{21}+x_{22 }+ x_{23} \le s_{2})\ge 0.98 \end{aligned}$$

(44)

$$\begin{aligned}&Pr(x_{31}+x_{32 }+ x_{33} \le s_{3})\ge 0.97 \end{aligned}$$

(45)

$$\begin{aligned}&Pr(x_{11}+x_{21 }+ x_{31} \ge d_{1})\ge 0.96 \end{aligned}$$

(46)

$$\begin{aligned}&Pr(x_{12}+x_{22 }+ x_{32} \ge d_{2})\ge 0.95 \end{aligned}$$

(47)

$$\begin{aligned}&Pr(x_{13}+x_{23 }+ x_{33} \ge d_{3})\ge 0.94 \end{aligned}$$

(48)

$$\begin{aligned}&x_{ij}\in \{0,1,2,...\}, \qquad i = 1,2,3; \, j = 1,2...,n \end{aligned}$$

(49)

where, $s_{i},\,(i =1,2,3)$ and $d_{i},\,(i =1,2,3)$ are triangular random variables and given by the Table 3. From the given data, we have $\gamma _1=0.01$, $\gamma _2=0.02$, $\gamma _3=0.03$, $\gamma _4=0.04$, $\gamma _5=0.05$, $\gamma _6=0.06$. Now, using (25)–(29), the equivalent deterministic model of (42)–(49) can be formulated as follows:

$$\begin{aligned} \min : Z&= {} 240x_{11}+320x_{12 }+ 400x_{13} \nonumber \\&+280x_{21}+440x_{22 }+ 440x_{23} + 160x_{31}+200x_{32 }+480x_{33} \end{aligned}$$

(50)

subject to

$$\begin{aligned}&x_{11}+x_{12 }+ x_{13} \le 232.828 \end{aligned}$$

(51)

$$\begin{aligned}&x_{21}+x_{22 }+ x_{23} \le 253.464 \end{aligned}$$

(52)

$$\begin{aligned}&x_{31}+x_{32 }+ x_{33} \le 244.899 \end{aligned}$$

(53)

$$\begin{aligned}&x_{11}+x_{21 }+ x_{31} \ge 205.757 \end{aligned}$$

(54)

$$\begin{aligned}&x_{12}+x_{22 }+ x_{32} \ge 113.675 \end{aligned}$$

(55)

$$\begin{aligned}&x_{13}+x_{23 }+ x_{33} \ge 212.254 \end{aligned}$$

(56)

$$\begin{aligned}&x_{ij}\in \{0,1,2,...\},\,\,i = 1,2,3;\,j = 1,2,3 \end{aligned}$$

(57)

Using LINGO 11.0 [29], we obtain the optimal solution. Same result is obtained by using Matlab and Maple software also.The optimal hauling cost is Rs. 149,320 and the optimal solution is given by the Table 4.

Table 4 Optimal solution (triangular case)

Table 5 Supply from the logging sites and demand at the mills

$b_i$ Follows Trapezoidal Distribution Next, we consider the the above problem (Example 1), with the changes that supply parameters $S_i , (i=1,2,3)$ and demand parameters $d_j, (j=1,2,3)$ follow trapezoidal distribution. In this case, the supply and demand are given by the Table 5. Now, using (37)–(41), the equivalent deterministic model of (42)–(49) can be formulated as follows:

$$\begin{aligned} \min : Z&= {} 240x_{11}+320x_{12 }+ 400x_{13} \nonumber \\&+280x_{21}+440x_{22 }+ 440x_{23} + 160x_{31}+200x_{32 }+480x_{33} \end{aligned}$$

(58)

subject to

$$\begin{aligned}&x_{11}+x_{12 }+ x_{13} \le 232.449 \end{aligned}$$

(59)

$$\begin{aligned}&x_{21}+x_{22 }+ x_{23} \le 253.464 \end{aligned}$$

(60)

$$\begin{aligned}&x_{31}+x_{32 }+ x_{33} \le 244.243 \end{aligned}$$

(61)

$$\begin{aligned}&x_{11}+x_{21 }+ x_{31} \ge 206.838 \end{aligned}$$

(62)

$$\begin{aligned}&x_{12}+x_{22 }+ x_{32} \ge 114.523 \end{aligned}$$

(63)

$$\begin{aligned}&x_{13}+x_{23 }+ x_{33} \ge 214 \end{aligned}$$

(64)

$$\begin{aligned}&x_{ij}\in \{0,1,2,...\},\,\,i = 1,2,3;\,j = 1,2,3 \end{aligned}$$

(65)

Using LINGO 11.0, we obtain the optimal solution. Same result is obtained by using Matlab and Maple software also. The optimal hauling cost is Rs. 150,360 and the optimal solution is given by the Table 6.

Table 6 Optimal solution

From the optimal solution of the problem, we observe that the transportation cost is higher for the trapezoidal case (i.e. Rs. 150,360) than the triangular case (i.e. Rs. 149,320). But, for both the cases, the selected source and the destinations are same with variations in the values.

Example 2

In this example, we illustrate the methodology for power function distribution. We consider the following transportation problem:

$$\begin{aligned} \min :Z&= {} 240x_{11}+320x_{12 }+ 400x_{13} \nonumber \\&+280x_{21}+440x_{22 }+ 440x_{23} + 160x_{31}+200x_{32 }+480x_{33} \end{aligned}$$

(66)

subject to

$$\begin{aligned}&Pr(x_{11}+x_{12 }+ x_{13} \le s_{1})\ge 0.99 \end{aligned}$$

(67)

$$\begin{aligned}&Pr(x_{21}+x_{22 }+ x_{23} \le s_{2})\ge 0.98 \end{aligned}$$

(68)

$$\begin{aligned}&Pr(x_{31}+x_{32 }+ x_{33} \le s_{3})\ge 0.97 \end{aligned}$$

(69)

$$\begin{aligned}&Pr(x_{11}+x_{21 }+ x_{31} \ge d_{1})\ge 0.96 \end{aligned}$$

(70)

$$\begin{aligned}&Pr(x_{12}+x_{22 }+ x_{32} \ge d_{2})\ge 0.95 \end{aligned}$$

(71)

$$\begin{aligned}&Pr(x_{13}+x_{23 }+ x_{33} \ge d_{3})\ge 0.94 \end{aligned}$$

(72)

$$\begin{aligned}&x_{ij}\in \{0,1,2,...\}, \qquad i = 1,2,3; \, j = 1,2...,n \end{aligned}$$

(73)

where $s_{i},\,(i =1,2,3)$ and $d_{i},\,(i =1,2,3)$ are random variables and follow power function distribution with known parameters. From the given data, we have $\gamma _1=0.01$, $\gamma _2=0.02$, $\gamma _3=0.03$, $\gamma _4=0.04$, $\gamma _5=0.05$, $\gamma _6=0.06$. The mean and variances of the random variables are given by: $E(s_1)= 150,\, E(s_2)=170,\, E(s_3)=260,\, E(d_1)=195,\, E(d_2)=100,\, E(d_3)=200$; $Var(s_1)=18,\, Var(s_2)=15,\, Var(s_{3})=20,\, Var(d_1)=25,\, Var(d_2)=10,\, Var(d_{3})=60.$

Using Eqs. (11) and (12), the corresponding parameters are calculated as:

• $\alpha _1= 154.3643$, $\beta _1= 34.3694$ (corresponding to $s_1$)

• $\alpha _2= 173.9622$, $\beta _2= 42.9052$ (corresponding to $s_2$)

• $\alpha _3= 264.5497$, $\beta _3= 57.1463$ (corresponding to $s_3$)

• $\alpha _4= 200.0656$, $\beta _4= 38.0128$ (corresponding to $d_1$)

• $\alpha _5= 103.2550$, $\beta _5= 30.6385$ (corresponding to $d_2$)

• $\alpha _6= 208.0517$, $\beta _6= 24.8392$ (corresponding to $d_3$)

Following the model given by (15)–(29), the equivalent deterministic model of (66)–(73) can be formulated as:

$$\begin{aligned} \min : Z&= {} 240x_{11}+320x_{12 }+ 400x_{13} \nonumber \\&+280x_{21}+440x_{22 }+ 440x_{23} + 160x_{31}+200x_{32 }+480x_{33} \end{aligned}$$

(74)

subject to

$$\begin{aligned}&x_{11}+x_{12 }+ x_{13} \le 135.007 \end{aligned}$$

(75)

$$\begin{aligned}&x_{21}+x_{22 }+ x_{23} \le 152.802 \end{aligned}$$

(76)

$$\begin{aligned}&x_{31}+x_{32 }+ x_{33} \le 248.805 \end{aligned}$$

(77)

$$\begin{aligned}&x_{11}+x_{21 }+ x_{31} \ge 199.851 \end{aligned}$$

(78)

$$\begin{aligned}&x_{12}+x_{22 }+ x_{32} \ge 103.082 \end{aligned}$$

(79)

$$\begin{aligned}&x_{13}+x_{23 }+ x_{33} \ge 207.534 \end{aligned}$$

(80)

$$\begin{aligned}&x_{ij}\in \{0,1,2,...\},\,\,i = 1,2,3;\,j = 1,2,3 \end{aligned}$$

(81)

The above deterministic model is solved by using LINGO 11.0 [29]. Same result is obtained by using Matlab and Maple software also. The obtained optimal solution is given by:

$$\begin{aligned} Z^*=145640\, \text{at}\, x^*_{11}= 0,\, x^*_{12}=0,\, x^*_{13}=135 ,x^*_{21}= 56,\, x^*_{22}=73,\, x^*_{23}=0 ,x^*_{31}= 144,\, x^*_{32}=104,\, x^*_{33}=0 . \end{aligned}$$

4 Conclusions

In this paper, we consider a stochastic linear programming problem where some chance-constraints are involved. In these chance-constraints, the right hand side parameters are considered as random variables. By considering the fact that the random variables follows power function distribution or triangular distribution or trapezoidal distribution with known parameters, we establish the equivalent deterministic form of the chance-constraints. Deterministic model for each case has been given and in each case equivalent deterministic models are all linear. It will be interesting to study the chance-constraint problem with technological coefficients and cost coefficients as triangular and trapezoidal distribution. We can apply the result of this study in portfolio optimization. The study can be extended for nonlinear chance-constrained problem and in multi-objective framework.