1 Introduction

Chance constraints appear as a versatile way to model the exposure to uncertainty in optimization. Introduced in [6], they have been used in many applications, such as in energy management [31, 39], in telecommunications [26] or for reinforcement learning [7], to name of few of them. We refer to the seminal book [32], the book chapter [11] for introduction to the theory and to the recent article [37] for a discussion covering recent developments.

We consider a chance-constrained optimization problem of the following form. For a fixed safety probability level \(p \in [0,1)\), we write

$$\begin{aligned} \begin{aligned}&\!\!\min _{x\in \mathop {\mathrm {\mathcal {X}}}\limits }\;\; f(x)\\&\text {s.t.} \;\; {{\,\mathrm{\mathbb {P}}\,}}[g(x, \xi ) \le 0] \ge p, \end{aligned} \end{aligned}$$
(1)

where \(f:\mathop {\mathrm {\mathbb {R}^d}}\limits \rightarrow \mathop {\mathrm {\mathbb {R}}}\limits \) and \(g:\mathop {\mathrm {\mathbb {R}^d}}\limits \times \mathop {\mathrm {\mathbb {R}^m}}\limits \rightarrow \mathop {\mathrm {\mathbb {R}}}\limits \) are two given functions, \(\xi \) is a random vector valued in \(\mathop {\mathrm {\mathbb {R}^m}}\limits \) and \(\mathop {\mathrm {\mathcal {X}}}\limits \subset \mathop {\mathrm {\mathbb {R}^d}}\limits \) is a closed constraint set. We make the following blanket assumptions:

(A1) f and g are convex with respect to \(x\),

(A2) for all \(x \in X\), \(|{{\,\mathrm{\mathbb {E}}\,}}(g(x,\xi ))| < \infty \).

We consider the case of underlying convexity: we assume that f and g are convex (with respect to \(x\)). Even with this underlying convexity, uncertainty may make the chance constrained set non-convex (see e.g. [15]) Though solving chance-constrained problems is difficult, several computational methods have been proposed, regardless of any considerations of convexity and smoothness, and under various assumptions on uncertainty. Let us mention: sample average approximation [24, 29], scenario approximation [5], convex approximation [18, 27], p-efficient points [12], quantile-based reformulation [30] or computation of the efficient frontier [19]; see e.g. [37] for an overview.

In this paper, we propose an original approach for solving chance-constrained optimization problems. First, we present an exact reformulation of (nonconvex) chance-constrained problems as (convex) bilevel optimization problems. This reformulation is simple and natural, involving superquantiles (also called conditional value-at-risk); see e.g., the tutorial [33]. Second, exploiting this bilevel reformulation, we propose a general algorithm for solving chance-constrained problems, and we release an open-source python toolbox implementing it. In the case where we make no assumption on the underlying uncertainty and have only samples of \(\xi \), we propose and analyze a double penalization method, leading to an unconstrained single level DC (Difference of Convex) program. Thus our work mixes a variety of techniques coming from different subdomains of optimization: penalization, error bounds, DC programming, bundle algorithm, Nesterov’s smoothing; relevant references are given along the presentation. The resulting algorithm enables to deal with a fairly large sample of data-points in comparison with state-of-the-art methods based on mixed-integer reformulations, e.g. [1].

This paper is structured as follows. In Sect. 2, we leverage the known link with (super)quantiles and chance-constraint to establish a novel bilevel reformulation of general chance constrained problems. In Sect. 3, we propose and analyze a penalty approach revealing the underlying DC structure. In Sect. 4, we discuss the implementation of this approach in a publicly available toolbox. In Sect. 5, we provide illustrative numerical experiments, as a proof of concept, showing the interest of the method. Technical details on secondary theoretical points and on implementation issues are postponed to appendices.

2 Chance constrained problems seen as bilevel problems

In this section, we derive the reformulation of a chance constraint as a bilevel program wherein both the upper and lower level problems, when taken individually, are convex. We first recall in Sect. 2.1 useful definitions. Our terminology and notations closely follow those of [33].

2.1 Recalls: cumulative distributions functions, quantiles, and superquantiles

In what follows, We consider a probability space and integrable real random variables. Given a random variable \({{\,\textrm{X}\,}}\), its cumulative distribution function is

$$\begin{aligned} F_{{{\,\textrm{X}\,}}}(t) = {{\,\mathrm{\mathbb {P}}\,}}[{{\,\textrm{X}\,}}\le t] \quad \forall t \in \mathop {\mathrm {\mathbb {R}}}\limits . \end{aligned}$$
(2)

This function is known to be non-decreasing and right-continuous. Its jumps occur exactly at the values \(t \in \mathop {\mathrm {\mathbb {R}}}\limits \) at which \({{\,\mathrm{\mathbb {P}}\,}}[{{\,\textrm{X}\,}}= t] > 0\). These properties allow one to define the quantile function \(p \mapsto Q_p({{\,\textrm{X}\,}})\) as the generalized inverse:

$$\begin{aligned} Q_p({{\,\textrm{X}\,}}) = \inf \{t \in \mathop {\mathrm {\mathbb {R}}}\limits : \; F_{{{\,\textrm{X}\,}}}(t) \ge p\}, \quad \forall p \in [0,1). \end{aligned}$$
(3)

If \({{\,\textrm{X}\,}}\) is assumed to belong to \({{\,\mathrm{\mathcal {L}^1}\,}}\), we can additionally define for any \(p \in [0,1)\) its p-superquantile (also called conditional value-at-risk), \(\bar{Q}_p({{\,\textrm{X}\,}})\) as follows:

$$\begin{aligned} \bar{Q}_p({{\,\textrm{X}\,}}) = \frac{1}{1-p} \int _{p' = p}^1 Q_{p'}({{\,\textrm{X}\,}}) dp'. \end{aligned}$$
(4)

As a consequence of [34, Th. 2], one can get from \(F_{{{\,\textrm{X}\,}}}\), both the p-quantile and the p-superquantile functions as functions of p and reciprocally, knowing either the p-quantile (or the p-superquantile) for all \(p \in [0,1]\) suffices to recover \(F_{{{\,\textrm{X}\,}}}\).

From a statistical viewpoint, these three objects are also equally consistent [33, Th. 4] in the sense that convergence in distribution for a sequence of random variables \(({{\,\textrm{X}\,}}_n)_{n \ge 0}\) is equivalent to the pointwise convergence of the two sequences of functions \(p \mapsto Q_p({{\,\textrm{X}\,}}_n)\), \(p \mapsto \bar{Q}_p({{\,\textrm{X}\,}}_n)\). This result is particularly relevant when the distributions are observed through data sampling. We can use the empirical cumulative distribution functions, quantiles and super-quantiles all while upholding asymptotic convergence as the sample size grows.

From an optimization viewpoint though, these three objects are very different. In contrast with the two others, the superquantile has several good properties (including convexity [3, 14, 36]), useful with respect to numerical computation and optimization. In our developments, we use the following key result [35, Th. 1] linking quantiles and superquantile through a one-dimensional problem.

Lemma 1

For an integrable random variable \({{\,\textrm{X}\,}}\) and a probability level p, the superquantile \(\bar{Q}_p({{\,\textrm{X}\,}})\) is the optimal value of the convex problem

$$\begin{aligned} \inf _{\eta \in \mathop {\mathrm {\mathbb {R}}}\limits } ~\eta + \frac{1}{1-p} {{\,\mathrm{\mathbb {E}}\,}}[\max ({{\,\textrm{X}\,}}-\eta , 0)]. \end{aligned}$$
(5)

Moreover, the quantile \(Q_p({{\,\textrm{X}\,}})\) is the left end-point of the solution interval.

Note finally that we consider in this paper with a single inequality system, but the generality of our approach allows to capture several constraint functions with the usual trick formalized in the next remark.

Remark 1

(Joint chance constraints) The extension of our approach to joint chance-constrained problems is straightforward with the usual trick: a chance constraint with \(h:\mathop {\mathrm {\mathbb {R}}}\limits ^d \times \mathop {\mathrm {\mathbb {R}}}\limits ^m \rightarrow \mathop {\mathrm {\mathbb {R}}}\limits ^k\) such that all its components \(h_{i}\, (1\le i \le k)\) are convex with respect to x can be written with convex function \(g(x, \xi )=\max _{{1} \le i \le k} h_i(x, \xi )\), since

$$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}\left[ h(x, \xi ) \le 0\right] \ge p ~\Longleftrightarrow ~ {{\,\mathrm{\mathbb {P}}\,}}\left[ \max _{1 \le i \le k} h_i(x, \xi ) \le 0\right] \ge p. \end{aligned}$$

2.2 Reformulation as a bilevel problem

By definition, the chance constraint in (1) involves the cumulative distribution function: we have, for \(x\in \mathop {\mathrm {\mathbb {R}^d}}\limits \), \({{\,\mathrm{\mathbb {P}}\,}}[g(x, \xi ) \le 0] \ge p \leftrightarrow F_{g(x, \xi )}(0) \ge p\). Following the discussion of the previous section, we easily rewrite this constraint using quantiles, as formalized in the next lemma. This result is well known (see e.g. [27]) and has been used recently in e.g. [30]. We provide here a short proof for completeness.

Lemma 2

For any \(x\in \mathop {\mathrm {\mathbb {R}^d}}\limits \) and \(p \in [0,1)\), we have:

$$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}[g(x, \xi ) \le 0] \ge p \iff Q_p(g(x, \xi )) \le 0. \end{aligned}$$

Proof

By definition of the quantile and the right-continuity of the cumulative function, we have \(p \le {{\,\mathrm{\mathbb {P}}\,}}[g(x, \xi ) \le Q_p(g(x, \xi ))]\). Since the cumulative function is increasing, \(Q_p(g(x, \xi )) \le 0\) implies \({{\,\mathrm{\mathbb {P}}\,}}[g(x, \xi ) \le Q_p(g(x, \xi ))] \le {{\,\mathrm{\mathbb {P}}\,}}[g(x, \xi ) \le 0]\) which implies in turn \(p \le {{\,\mathrm{\mathbb {P}}\,}}[g(x, \xi ) \le 0]\).

Conversely, since \(Q_p(g(x, \xi ))\) is the infimum of \(\{t\in \mathop {\mathrm {\mathbb {R}}}\limits : {{\,\mathrm{\mathbb {P}}\,}}[g(x, \xi ) \le t] \ge p\}\), if \(Q_p(g(x, \xi )) > 0\), then it holds \({{\,\mathrm{\mathbb {P}}\,}}[g(x, \xi ) \le 0] < p\).\(\square \)

Compared to the empirical cumulative distribution function, the p-quantile function \(x\mapsto Q_p(g(x,\xi ))\) is continuous with respect to x, whenever g is. However, it remains non-convex and non-smooth in general. So we propose to use yet another reformulation in terms of superquantiles, as follows.

Together with (5), we obtain from the previous lemma a bilevel formulation of the general chance-constrained problem (7). The idea is simple: introducing an auxiliary variable \(\eta \in \mathop {\mathrm {\mathbb {R}^d}}\limits \) to recast the potentially non-convex chance constraint of (1) as two constraints, a simple bound constraint and a difficult optimality constraint, forming a lower subproblem. Introducing the jointly convex function \(G: \mathop {\mathrm {\mathcal {X}}}\limits \times \mathop {\mathrm {\mathbb {R}}}\limits \rightarrow \mathop {\mathrm {\mathbb {R}}}\limits \)

$$\begin{aligned} G(x, s) = s + \frac{1}{1-p} {{\,\mathrm{\mathbb {E}}\,}}[\max (g(x,\xi ) - s, 0)], \end{aligned}$$
(6)

we indeed have the following exact reformulation.

Theorem 1

Under assumptions (A1) and (A2), Problem (1) is equivalent to the bilevel problem:

$$\begin{aligned} \left\{ \displaystyle \begin{array}{ll} \min _{x\in \mathop {\mathrm {\mathcal {X}}}\limits , \eta \in \mathop {\mathrm {\mathbb {R}}}\limits } &{} f(x) \\ \text {s.t.} &{} \eta \le 0 \\ &{} \eta \in S(x) = \mathop {\mathrm {arg\,min}}\limits _{s \in \mathop {\mathrm {\mathbb {R}}}\limits } G(x,s).\\ \end{array} \right. \end{aligned}$$
(7)

More precisely, if \(x^\star \) is an optimal solution of (1), then \((x^\star , Q_p(g(x^\star , \xi )))\) is an optimal solution of the above bilevel problem, and conversely.

Proof

By Lemma 2, we have that (1) is equivalent to

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \min _{x\in \mathop {\mathrm {\mathcal {X}}}\limits , \eta \in \mathop {\mathrm {\mathbb {R}}}\limits } &{} f(x) \\ \text {s.t.} &{} \eta \le 0 \\ &{} \eta = Q_p(g(x, \xi )). \end{array} \right. \end{aligned}$$
(8)

By Lemma 1, \(Q_p(g(x, \xi )) \in S(x)\) for any \(x\in \mathop {\mathrm {\mathbb {R}}}\limits ^d\). Hence, any solution \((x,\eta )\) of (8) is feasible for (7). Conversely, any solution \((x^{\star }, \eta ^{\star })\) of (7) satisfies: \(Q_p(g({x}^{\star }, \xi )) \le \eta ^{\star } \le 0\) which implies that \((x^\star , Q_p(g({x}^{\star }, \xi ))\) is a feasible point of (8). Since both problems have the same objective, they are equivalent.\(\square \)

The first constraint \(\eta \le 0\) is an easy one-dimensional bound constraint which does not involve the decision variable \(x\). The second constraint, which constitutes the lower level problem is more difficult; when this constraint is satisfied, \(\eta \) is an upper-bound on the p-quantile of \(g(x, \xi )\).

This bilevel reformulation is nice, natural, and seemingly new; we believe that it opens the door to new approaches for solving chance-constrained problems with underlying convexity. We propose such an approach, in the next section.

Remark 2

Bilevel formulation vs sampled approximation Let us emphasize that Theorem 1 provides an exact reformulation of the problem (1). This is in contrast with sampling methods, such as  [5], which approximate the chance constraint through sampling. Note also that, though [5] provides theoretical guarantees, it also presents limitations when the sampled constraint remains infeasible, as explained in [5, Section 4.2]. This infeasibility for the sampled problem occurs frequently in practice (see e.g. [38]), as well as in the illustrative examples of Sect. 5.

Remark 3

(Bilevel formulation vs bilevel approximation) Our bilevel formulation is exact, as opposed to the recent bilevel approach of [18]. This paper proposes indeed a reformulation that approximates the chance constraint with better guarantees than the CVaR approximation from [27]. In contrast, we leverage here the variational properties of the CVaR to enforce exactly the probabilistic constraint.

3 A double penalization scheme for chance constrained problems

In this section, we explore one possibility offered by the bilevel formulation of chance-constrained problems, presented in the previous section. We propose a (double) penalization approach for solving the bilevel optimization problem, with a different treatment of the two constraints: a basic penalization of the easy constraint together with an exact penalization of the hard constraint formalized as the lower problem.

We first derive in Sect. 3.1, some growth properties of the lower problem. We then show in Sect. 3.2 to what extent these properties help to provide an exact penalization of the “hard” constraint. We finally present the double penalty scheme in Sect. 3.3.

From the bilevel problem (7), we derive the two following penalized problems, associated with two penalization parameters \(\mu , \lambda > 0\) and

$$\begin{aligned} (P_{\mu }) \quad \left\{ \begin{array}{ll} \displaystyle \min _{(x,\eta ) \in \mathop {\mathrm {\mathcal {X}}}\limits \times \mathop {\mathrm {\mathbb {R}}}\limits } &{} f(x) + \mu \max (\eta , 0) \\ \text{ s.t. } &{} \eta \in \mathop {\mathrm {arg\,min}}\limits _{s\in \mathop {\mathrm {\mathbb {R}}}\limits } G(x, s) \end{array} \right. \end{aligned}$$
(9)

and

$$\begin{aligned} (P_{\lambda , \mu })\quad \min _{(x, \eta ) \in \mathop {\mathrm {\mathcal {X}}}\limits \times \mathop {\mathrm {\mathbb {R}}}\limits } f(x) + \lambda \left( G(x,\eta ) - \min _{s \in \mathop {\mathrm {\mathbb {R}}}\limits } G(x, s)\right) + \mu \max (\eta , 0). \end{aligned}$$
(10)

We consider a general data-driven situation where the uncertainty \(\xi \) is just known through a sample (or, said alternatively, follows an equiprobable discrete distribution over arbitrary values):

(A3) We assume that there exists \(n \in \mathop {\mathrm {\mathbb {N}}}\limits ^*\) and n different scenarios

$$\begin{aligned} \xi _1, \xi _2, \dots , \xi _n \in \mathop {\mathrm {\mathbb {R}^m}}\limits \quad \text {such that}\, {{\,\mathrm{\mathbb {P}}\,}}[\xi = \xi _i] = \frac{1}{n}\hbox { for all }i \in \{1, \dots , n\}. \end{aligned}$$
(11)

Under this assumption, the objective (6) of the lower level problem writes:

$$\begin{aligned} G(x, s) = s + \frac{1}{{n}(1-p)} \sum ^n_{i=1}\max (g(x,\xi _i) - s, 0). \end{aligned}$$
(12)

We then define the set \(\mathcal {I}_n= \left\{ \frac{i}{n}, ~ i \in \{0,...,n-1\} \right\} \) which will play a special role in our developments. In particular, we denote the distance to \(\mathcal {I}_n\) by \(d_{\mathcal {I}_n}(p)= \inf \{|p - \frac{i}{m}|, 0\le i \le n-1\}\), and we define the key quantity

$$\begin{aligned} \delta = \left\{ \begin{array}{ll} \displaystyle \frac{1}{n(1-p)} &{} \text{ if } p \in \mathcal {I}_n\\ \displaystyle \frac{d_{\mathcal {I}_n}(p)}{(1-p)} &{} \text{ otherwise, }\\ \end{array} \right. \end{aligned}$$
(13)

which depends implicitly on the number of samples n and the fixed safety parameter p.

Remark 4

(Penalization choice) We study in this paper a double penalization approach with a penalization of the easy constraint (which is proved to be exact in forthcoming Proposition 1) followed by a penalization of the difficult constraint, which thus gives \((P_{\lambda , \mu })\) in (10). Other approaches to solve the bilevel problem could be worth investigating as well, and are left for future research in this direction. Note that the alternative penalization that would consist in penalizing only the difficult constraint \(\eta \in \text{ argmin}_{s\in \mathbb {R}} G(x,s)\) and leave the easy bound constraint \(\eta \le 0\) would suffer from the objective function not being Lipschitz. This extra difficulty might be tackled by more advanced penalization techniques, as e.g. [2] and [13] (in a framework of Nash Equilibrium). We use here the standard approach and focus on analyzing it and showing how it leads to an efficient algorithm.

3.1 Analysis of the value function

In view of the forthcoming exact penalization, we study here the value function \(h: \mathop {\mathrm {\mathcal {X}}}\limits \times \mathop {\mathrm {\mathbb {R}}}\limits \rightarrow \mathop {\mathrm {\mathbb {R}}}\limits \) defined, from G in (12), as

$$\begin{aligned} h(x,\eta ) = G(x, \eta ) - \min _{s\in \mathop {\mathrm {\mathbb {R}}}\limits } G(x,s). \end{aligned}$$
(14)

Observe that, for a fixed \(x\), the function \(h(x,\cdot )\) is a polyedral, in the data-driven situation (11). Similarly, the solution set \(S(x)\) of the lower level problems in (7) is polyedral as well. This yields that there is a steep increase of the value function with respect to \(\eta \) outside of S(x). In accordance with the terminology of [4], the set S(x) is said to be a weak sharp minima for the lower-level problem. In terms of function values, this declines as h being lower-bounded by \(d_{S(x)}(\cdot )\), the distance function to \(S(x)\). In the next result, we establish this property by a direct proof, providing, as a by-product, a specific estimation of the lower-bound.

Theorem 2

Let \(p\in [0,1)\) be fixed but arbitrary. Under assumptions (A1), (A2), and (A3), the function h defined in (14) satisfies for any \((x, \eta ) \in \mathop {\mathrm {\mathcal {X}}}\limits \times \mathop {\mathrm {\mathbb {R}}}\limits \):

$$\begin{aligned} h(x,\eta ) \ge \delta \;d_{S(x)}(\eta ) \end{aligned}$$
(15)

with \(\delta \) and S(x) respectively defined by (13) and (7).

Proof

Let us fix \(x\in \mathop {\mathrm {\mathcal {X}}}\limits \). Note first that, the function \(\psi : s \mapsto h(x, s)\) is continuous and convex, since so is G, as defined in 12. As a result S(x) is a closed interval.

Since h is non-negative, (15) is immediate if \(S(x) = (-\infty , +\infty )\). Furthermore it clearly appears that \(h(x,s)=0\) for all \(s \in S(x)\). We thus assume that S(x) is lower-bounded or upper-bounded. Let us introduce \(q_p^+ = \sup S(x)\), and assume \(q_p^+ < \infty \). By standard subdifferential calculus [16, 4.4.2], we have

$$\begin{aligned} \partial \psi (s)&= \left\{ 1 - \frac{1}{n(1-p)} \sum _{i=1}^n \mathbb {1}_{s< g(x, \xi _i)} + \alpha _i \mathbb {1}_{s = g(x, \xi _i)}, \text {s.t.} (\alpha _i, \ldots , \alpha _n)\in [0, 1]^n \right\} \nonumber \\&= \left[ 1 - \frac{1}{1-p} \mathbb {P}[g(x, \xi ) \ge s], 1 - \frac{1}{1-p} \mathbb {P}[g(x, \xi ) > s] \right] \nonumber \\&= \left[ \frac{\mathbb {P}[g(x, \xi ) < s]}{1-p} , \frac{\mathbb {P}[g(x, \xi ) \le s]}{1-p}\right] - \frac{p}{1-p}. \end{aligned}$$
(16)

Therefore,

$$\begin{aligned} {0 \in \partial \psi (s) \leftrightarrow p \in \left[ \mathbb {P}[g(x, \xi ) < s], \mathbb {P}[g(x, \xi ) \le s] \right] \leftrightarrow s \in S(x).} \end{aligned}$$

By the convexity of \(\psi \), for any s, u and \(g_u \in \partial \psi (u)\):

$$\begin{aligned} h(x,s) - h(x,u) \ge g_u^\top (s-u). \end{aligned}$$
(17)

As a consequence for any \(u \notin S(x)\), since \(0 \notin \partial \psi (u)\), we obtain from (16) that \({{\,\mathrm{\mathbb {P}}\,}}(g(x, \xi ) \le u) \ne p\). Moreover, since \({{\,\mathrm{\mathbb {P}}\,}}(g(x, \xi ) \le u) \in \mathcal {I}_n\), we necessarily have

$$\begin{aligned} |{{\,\mathrm{\mathbb {P}}\,}}(g(x, \xi ) \le u) - p| \ge \left| \begin{array}{ll} \displaystyle \frac{1}{n} &{} \text{ if } p \in \mathcal {I}_n\\ \displaystyle d_{\mathcal {I}_n}(p) &{} \text{ otherwise. }\\ \end{array} \right. \end{aligned}$$

Hence, for any \(s> u > q_p^+\), we use the subgradient inequality (17) with \(g_u = \frac{{{\,\mathrm{\mathbb {P}}\,}}(g(x, \xi ) \le u) - p}{1-p}\) to obtain:

$$\begin{aligned} h(x,s) - h(x,u) \ge \frac{{{\,\mathrm{\mathbb {P}}\,}}(g(x, \xi ) \le u) - p}{1-p} (s-u) \ge \delta (s-u), \end{aligned}$$

where we have used \(g_u > 0\), since \(u> q_p^+\). Now, by letting u approach \(q_p^+\) from above, upon using continuity of \(h(x,\cdot )\) in u, together with \(h(x,q_p^+)=0\) (since \(q_p^+ \in S(x)\)), we derive \(h(x, s) \ge \delta (s - q_p^+)\). Since clearly \((s - q_p^+) \ge d_{S(x)}(s)\) the result follows.

Similarly, if \(q_p \triangleq \inf S(x) > -\infty \), then for any \(s< u < q_p\), we may leverage the subgradient inequality to derive:

$$\begin{aligned} \begin{aligned} h(x,s) - h(x,u)&\ge \frac{{{\,\mathrm{\mathbb {P}}\,}}(g(x, \xi ) \le u) - p}{1-p} (s-u) \\&= \frac{p - {{\,\mathrm{\mathbb {P}}\,}}(g(x, \xi ) \le u)}{1-p}(u - s) = \frac{| {{\,\mathrm{\mathbb {P}}\,}}(g(x, \xi ) \le u) - p|}{1-p}(u - s) \\&\ge \delta (u-s) \\ \end{aligned} \end{aligned}$$

since \(u< q_p \implies {{\,\mathrm{\mathbb {P}}\,}}(g(x, \xi ) \le u) < p\).

Now letting u approach \(q_p\) from below, using continuity of h in the second argument, \(q_p \in S(x)\), \(h(x,q_p)=0\) and \((q_p - s) \ge d_{S(x)}(s)\), we get \(h(x, s) \ge \delta d_{S(x)}(s)\) as desired. \(\square \)

Following the terminology of [41], this theorem shows that h is a uniform parametric error bound and provides the modulus of uniformity. We note here that the quality of the lower bound depends on the number n of data points considered, as \(\delta \) depends on d. This dependence is a drawback which turns out to “pass to the limit”, in the sense that the lower bound of fails to be a uniform parametric error bound when \(\xi \) follows a continuous distribution; this is an interesting but secondary result that we prove in Appendix 1.

3.2 Exact penalization for the hard constraint

We show here that \((P_{\lambda , \mu })\) is an exact penalization of \((P_{\mu })\), when \(\lambda \) is large enough. The proof of this result follows usual rationale (see e.g., [8, Prop. 2.4.3]); the main technicality is the sharp growth of h established in Theorem 2.

Proposition 1

Let \(\mu > 0\) be given and assume that there is a solution to \((P_{\mu })\) defined in (9). Then, under assumptions (A1),  (A2), and (A3), for any \(\lambda > \mu /\delta \) with \(\delta \) defined in (13), the solution set of \((P_{\mu })\) coincides with the one of \((P_{\lambda , \mu })\) defined in (10).

Proof

Take \(\mu >0\), define \(\lambda _\mu = \mu /\delta \), and take \(\lambda > \lambda _{\mu }\) arbitrary but fixed. Let us first take a solution \(({x}^{\star }, \eta ^{\star }) \in \mathop {\mathrm {\mathcal {X}}}\limits \times \mathop {\mathrm {\mathbb {R}}}\limits \) of \((P_{\mu })\) and show by contradiction that it is also a solution of \((P_{\lambda , \mu })\). Indeed, to the contrary, assume there exists some \(\varepsilon > 0\) and \(({x}', \eta ') \in \mathop {\mathrm {\mathcal {X}}}\limits \times \mathop {\mathrm {\mathbb {R}}}\limits \) such that:

$$\begin{aligned} f({x}') + \mu \max (0, \eta ') + \lambda h_{{x}'}(\eta ') \le f({x}^{\star }) + \mu \max (0, \eta ^{\star }) + \lambda \; h_{{x}^{\star }}(\eta ^{\star }) - \varepsilon . \end{aligned}$$

Let then \(\eta _p' \in S({x}')\) be such that: \(|\eta _p' - \eta '| \le d_{S({x}')}(\eta ') + \frac{\varepsilon }{2 \mu }\). Then the point \(({x}', \eta _p')\) is a feasible for \(P_{\mu }\) (recall \(\eta _p' \in S({x}')\)) and since \(\eta \mapsto \mu \max (0, \eta )\) is \(\mu \)-Lipschitz, we first have

$$\begin{aligned} \begin{aligned} f({x}') + \mu \max (0, \eta _p')&\le f({x}') + \mu \max (\eta ',0) + \mu |\eta _p' - \eta '|\\&\le f({x}') + \mu \max (\eta ',0) + \mu \left( d_{S({x}')}(\eta ') + \frac{\varepsilon }{2 \mu } \right) . \end{aligned}{} \end{aligned}$$

Using Theorem 2, we then have

$$\begin{aligned} \begin{aligned} f({x}') + \mu \max (0, \eta _p')&\le f({x}') + \mu \max (\eta ',0) + \mu \left( \frac{1}{\delta } h(x',\eta ') + \frac{\varepsilon }{2 \mu }\right) \\&\le f({x}') + \mu \max (\eta ',0) + \lambda _{\mu }\; h({x}',\eta ') + \frac{\varepsilon }{2}\\&\le f({x}^{\star }) + \mu \max (\eta ^{\star },0) - \frac{\varepsilon }{2}\\ \end{aligned}{} \end{aligned}$$

which gives the contradiction. Hence any solution of \((P_\mu )\) is also a solution to problem \((P_{\lambda , \mu })\).

Let now \((\bar{x}, \bar{\eta })\) be a solution of \((P_{\lambda , \mu })\) and let us show that it is actually a solution for \(P_{\mu }\). Let again \(({x}^{\star }, \eta ^{\star })\) be an arbitrary solution of \((P_{\mu })\). We first note that, by the optimality result of \((\bar{x}, \bar{\eta })\) for \((P_{\lambda , \mu })\), we have:

$$\begin{aligned} f(\bar{x}) + \mu \max (0,\bar{\eta }) + \lambda \underbrace{h(\bar{x}, \bar{\eta })}_{\ge 0} \le f({x}^\star ) + \mu \max (0,\eta ^\star ) + \lambda \underbrace{h({x}^\star , \eta ^\star )}_{=0}, \end{aligned}$$

which by positivity of the function h and feasibility for \((P_{\mu })\), i.e., \(h(x^\star , \eta ^\star )=0\) of \(({x}^{\star }, \eta ^{\star })\) yields:

$$\begin{aligned} f(\bar{x}) + \mu \max (0,\bar{\eta }) \le f({x}^\star ) + \mu \max (0, \eta ^\star ). \end{aligned}$$

It remains to show that \((\bar{x}, \bar{\eta })\) is a feasible point for \((P_\mu )\). By the first point, \(({x}^{\star }, \eta ^{\star })\) is both a solution of \((P_{\lambda , \mu })\) and \((P_{\frac{\lambda + \lambda _{\mu }}{2}, \mu })\). Hence, we have:

$$\begin{aligned} \begin{aligned} f(\bar{x}) + \mu \max (0, \bar{\eta }) + \lambda h(\bar{x}, \bar{\eta })&\le f({x}^{\star }) + \mu \max (0, {\eta }^{\star }) \\&= f({x}^{\star }) + \mu \max (0, {\eta }^{\star }) + \frac{\lambda + \lambda _\mu }{2} h(x^\star ,\eta ^\star ) \\&\le f(\bar{x}) + \mu \max (0, \bar{\eta }) + \frac{\lambda + \lambda _\mu }{2} h(\bar{x},\bar{\eta })\\ \end{aligned} \end{aligned}$$

But since \(\lambda > \lambda _\mu \) we necessarily have: \(h(\bar{x},\bar{\eta }) = 0\) which implies by the properties of the value function that \((\bar{x}, \bar{\eta })\) is a feasible point for \((P_{\mu })\).\(\square \)

We note that the above result is a consequence, in our specific case, of [41, Theorem 2.6] which is meant for generalized bilevel programs. Based on the terminology of [41] and references therein, we have that \(P_\mu \) satisfies the partial calmness property, as the value function h is a uniform parametric error bound.

3.3 Double penalization scheme

From the previous results, we get that solving the sequence of penalized problems gives approximations of the solution of the initial problem. We formalize this in the next proposition suited for our context of double penalization. The proof of this result follows standard arguments; see e.g. [25, Ch. 13.1].

Proposition 2

Assume (A1), (A2), and (A3) are satisfied, and Problem (7) has a non-empty feasible set. Let \((\mu _k)_{k \ge 0}\) be an increasing sequence such that \({\mu _k \nearrow \infty }\), and \((\lambda _k)_{k \ge 0}\) be taken such that \(\lambda _k > \frac{\mu _k}{\delta }\) with \(\delta \) as defined in (13). If, for all k, there exists a solution of \((P_{\lambda _k, \mu _k})\) (denoted by \((x_k, \eta _k)\)), then any cluster point of the sequence \(({x}_k, \eta _k)\) is an optimal solution of (1).

Proof

The fact that \((x_k,\eta _k)\) is an optimal solution of \((P_{\lambda _k,\mu _k})\) implies that

$$\begin{aligned} f({x}_k) + \mu _k \max (0, \eta _k)&+ \lambda _k h(x_k,\eta _k)\\&\le f(x_{k+1}) + \mu _k \max (0, \eta _{k+1}) + \lambda _k h(x_{k+1},\eta _{k+1}) \nonumber \end{aligned}$$
(18)

Similarly for \((x_{k+1},\eta _{k+1})\), we get

$$\begin{aligned} f(x_{k+1}) + \mu _{k+1} \max (0, \eta _{k+1})&+ \lambda _{k+1} h(x_{k+1},\eta _{k+1}) \\&\le f(x_k) + \mu _{k+1} \max (0, \eta _k) + \lambda _{k+1} h(x_k,\eta _k). \nonumber \end{aligned}$$
(19)

By Proposition 1, \(\eta _k\) (resp. \(\eta _{k+1}\)) is feasible for \((P_{\mu _k})\) (resp. \((P_{\mu _{k+1}})\)); in other words, we have \(h(x_k,\eta _k) = h(x_{k+1},\eta _{k+1}) = 0\). Hence summing up these two inequalities yields

$$\begin{aligned} \max (\eta _k, 0) \ge \max (\eta _{k+1}, 0). \end{aligned}$$

Using this last inequality with (18) gives:

$$\begin{aligned} \begin{aligned} f({x}_k) - f({x}_{k+1}) \le \mu _k \left( \max (\eta _{k+1}, 0) - \max (\eta _{k}, 0)\right) \le 0, \end{aligned} \end{aligned}$$

and as a consequence the sequence \(\{f({x}_k)\}_{k \ge 0}\) increases. Let \((x', \eta ')\) be an arbitrary feasible solution for (P). By definition of the sequence \(({x}_k, \eta _k)\), for any \(k \in \mathop {\mathrm {\mathbb {N}}}\limits \), we have:

$$\begin{aligned} f({x}_k) \le f({x}_k) + \mu _k \max (\eta _k, 0) \le f({x}') + \mu _k \max (\eta ', 0) \le f({x}'). \end{aligned}$$
(20)

Therefore for any cluster point \((\bar{x}, \bar{\eta })\) of the sequence \(\{({x}_k, \eta _k)\}_{k \ge 0}\), we have \(f(\bar{x}) \le f(x')\). In order to show that \((\bar{x}, \bar{\eta })\) is a a solution of (7), it remains to show its feasibility. With the right hand side inequality of (20), we obtain

$$\begin{aligned} \max (\eta _k, 0) \le \frac{f(x') - f({x}_k)}{\mu _k} \le \frac{f(x') - f(x_0)}{\mu _k} \xrightarrow [k \rightarrow \infty ]{} 0, \end{aligned}$$

so that we may deduce that, \(\bar{\eta } \le 0\). Moreover, continuity of h ensures that \(h(\bar{x}, \bar{\eta })=0\) which completes the proof.\(\square \)

In words, cluster points of a sequence of solutions obtained as \(\mu \) grows to \(+\infty \) are feasible solutions of the initial chance-constrained problem. In practice though, we have observed that taking a fixed \(\mu \) is enough for reaching good approximations of the solution with increasing \(\lambda \)’s; see the numerical experiments of Sect. 5. In the next section, we discuss further the practical implementation of the conceptual double penalization scheme.

We finish this section by a note about the assumption of existence of a solution to \((P_{\lambda , \mu })\), in Proposition 2. Asserting the existence of a (global) solution for a difference of convex program is obviously difficult in general. For our doubly penalized problem, we can still get a specific result, under standard “compactness” assumptions giving existence of a solution for the problem without the chance-constraint.

Proposition 3

Assume that the constraint function \(g(\cdot , z)\) is continuous for all \(z \in \mathop {\mathrm {\mathbb {R}^m}}\limits \). Assume also that the objective function f is coercive or that the constraint set \(\mathop {\mathrm {\mathcal {X}}}\limits \) is compact. Then, for any \(\lambda , \mu > 0\), the penalized problem \((P_{\lambda , \mu })\) admits a global solution.

Proof

For \(\lambda , \mu \ge 0\) fixed, introduce \(\varphi \) the DC objective function of \((P_{\lambda , \mu })\)

$$\begin{aligned} \varphi (x, \eta ) = f(x) +\lambda h(x, \eta ) + \mu \max (\eta , 0) \quad \text {as well as}\quad \varphi ^\star = \!\inf _{x\in \mathop {\mathrm {\mathcal {X}}}\limits , \eta \in \mathop {\mathrm {\mathbb {R}}}\limits } \varphi (x, \eta ), \end{aligned}$$

and observe that we have

$$\begin{aligned} \varphi (x,\eta )&\ge f(x) + \mu \max (\eta , 0) \ge f(x). \end{aligned}$$
(21)

Consider \((x_n, \eta _n)_{n\ge 0}\) to be such that \({\varphi (x_n, \eta _n) \swarrow \varphi ^\star }\). By either the compactness of \(\mathop {\mathrm {\mathcal {X}}}\limits \) or (21) combined with the coercivity of f, we have that \((x_n)\) necessarily admits a finite cluster point \(\bar{x}\). We assume without loss of generality that \(x_n \rightarrow \bar{x}\). Let us show the existence of some \(\bar{\eta }\) such that \((\bar{x}, \bar{\eta })\) is a solution of \((P_{\lambda , \mu })\). Note that, if \(\eta _n\) is bounded, then the proof is done. So the interesting cases are \(\eta _n \rightarrow +\infty \) and \(\eta _n \rightarrow -\infty \) (up to a subsequence extraction)

  • If \(\eta _n \rightarrow +\infty \), then, by (21)

    $$\begin{aligned} \begin{aligned} \varphi (x_n, \eta _n) \ge f(x_n) + \mu \max (0, \eta _n) \ge \min _x f(x) + \mu \max (0, \eta _n) \rightarrow +\infty \end{aligned} \end{aligned}$$

    which is absurd.

  • If \(\eta _n \rightarrow -\infty \), the sequence becomes eventually negative, and we can write

    $$\begin{aligned} \varphi (x_{n}, \eta _{n}) = f(x_{n}) + \lambda h(x_{n}, \eta _{n}) \ge f(x_{n}) + \lambda h(x_{n}, Q_{p}(g(x_{n}, \xi )))\ge \varphi ^\star . \end{aligned}$$

    By continuity of \(g(\cdot , \xi )\) and \(Q_p\) we have convergence of \(Q_{p}(g(x_{n}, \xi ))\) toward \(\tilde{\eta }= Q_{p}(g(\bar{x}, \xi ))\). We conclude that \((\bar{x}, \tilde{\eta })\) is a minimum of \(\varphi \). \(\square \)

4 Double penalization in practice

In this section, we propose a practical version of the double penalization scheme for solving chance-constrained optimization problems. First, we present in Sect. 4.1 how to tackle the inner penalized problem \((P_{\lambda , \mu })\) by leveraging its difference-of-convex (DC) structure. Then we quickly describe, in Sect. 4.2, the python toolbox that we release, implementing this bundle algorithm and efficient oracles within the double penalization method.

4.1 Solving penalized problems by a bundle algorithm

We discuss an algorithm for solving \((P_{\lambda , \mu })\) by revealing the DC structure of the objective function. Notice indeed that, introducing the convex functions

$$\begin{aligned} \varphi _1(x, \eta ) = f(x) + \lambda G(x, \eta ) + \mu \max (\eta , 0) \quad \text {and}\quad \varphi _2(x, \eta ) = \lambda \min _{s\in \mathop {\mathrm {\mathbb {R}}}\limits } G(x, s) \end{aligned}$$

we can write \((P_{\lambda , \mu })\) as the DC problem

$$\begin{aligned} \min _{(x,\eta ) \in \mathop {\mathrm {\mathcal {X}}}\limits \times \mathop {\mathrm {\mathbb {R}}}\limits } \varphi (x, \eta ) = \varphi _1(x, \eta ) - \varphi _2(x, \eta ). \end{aligned}$$
(22)

We then propose to solve this problem by the bundle algorithm of [9], which has shown to be a method of choice for DC problems. This bundle algorithm interacts with first-order oracles for \(\varphi _1\) and \(\varphi _2\); in our situation, there exist computational procedures to compute subgradients of \(\varphi _1\) and \(\varphi _2\) from output of oracles of f and g, as formalized in the next proposition. The proof of this proposition is deferred to Appendix 1. Note that at the price of more heavy expressions, we could derive the whole subdifferential.

Proposition 4

Let \((x, \eta ) \in \mathop {\mathrm {\mathcal {X}}}\limits \times \mathop {\mathrm {\mathbb {R}}}\limits \) be fixed. Let \(s_f\) be a subgradient of f at x and \({s_g}_1, \dots , {s_g}_n\) be respective subgradients of \(g(\cdot , \xi _1),\dots , g(\cdot , \xi _n)\) at x. For a given \(t\in \mathop {\mathrm {\mathbb {R}}}\limits \), denote by \(I_{>t}\) the set of indices such that \(g(x, \xi _i) > t\) and by \(I_{=t}\) the set of indices such that \(g(x, \xi _i) = t\). Let finally \(\alpha = \frac{{{\,\mathrm{\mathbb {P}}\,}}[g(x,\xi ) \le Q_p(g(x, \xi )] - p}{\#(I_{=Q_p(g(x, \xi ))})}\). Then, \(s_{\varphi _1}\) and \(s_{\varphi _2}\) defined as:

$$\begin{aligned}{} & {} \begin{aligned} s_{\varphi _1} =&\left( s_f + \frac{\lambda }{n(1-p)} \sum _{i \in I_{>\eta }}^n {s_g}_i ~,~ 1 + \mu \mathbb {1}_{\eta> 0} - \lambda \frac{\#(I_{>\eta })}{n(1-p)} \right) \\ \end{aligned}\\{} & {} s_{\varphi _2} = \left( \frac{\lambda }{n(1-p)} \left( \sum _{i \in I_{>Q_{p}(g(x,\xi ))}} \!\!{s_g}_i + \alpha \!\!\sum _{i \in I_{=Q_{p}(g(x,\xi ))}} \!\! {s_g}_i \right) ~,~ 0 \right) \end{aligned}$$

are respectively subgradients of \(\varphi _1\) and \(\varphi _2\) at \((x, \eta )\).

Thus we can use the bundle algorithm to tackle \((P_{\lambda , \mu })\) written as (22). Notice, though, that this algorithm is not guaranteed to converge towards optimal solutions: the convergence result [9, Th. 1] establishes convergence towards a point \(\bar{u} = (\bar{x},\bar{\eta }\)) satisfying

$$\begin{aligned} \partial \varphi _2(\bar{u}) \cap \partial \varphi _1(\bar{u}) \ne \emptyset , \end{aligned}$$
(23)

which is a weak notion of criticality. We then follow the suggestion of [10] to replace \(\varphi _2\) in (22) by a smooth approximation of it, denoted by \(\widetilde{\varphi }_2\). The reason is that the bundle method minimizing \(\widetilde{\varphi } = \varphi _1 - \widetilde{\varphi }_2\) then reaches a Clarke-stationary point: indeed, (23) reads \(\nabla \widetilde{\varphi }_2(\bar{u}) \subset \partial \varphi _1(\bar{u})\), which in turn gives that

$$\begin{aligned} 0 \in \partial \varphi (\bar{u}) = \partial \varphi _1(\bar{u}) - \nabla \widetilde{\varphi }_2(\bar{u}), \end{aligned}$$

i.e., that \(\bar{u}\) is Clarke-stationary (for the smoothed problem). Quantifying the approximation of the true optimal solutions by the obtained points is completely out of the scope of this paper; we refer to preliminary discussions in [9, 10]. In particular, [10] mentions that this smoothing technique helps in computing (approximate) critical points of good quality.

In practice, to smooth \(\varphi _2\), we use the efficient smoothing procedure of [21] for superquantile-based functions (implementing the Nesterov’s smoothing technique [28]). More precisely, [21, Prop. 2.2] reads as follows.

Proposition 5

Assume that g is differentiable. For a smoothing parameter \(\rho > 0\), the function

$$\begin{aligned} \widetilde{\varphi }_2(x, \eta ) = \lambda \sup _{\begin{array}{c} 0\le q_i \le \frac{1}{n(1-p)} \\ q_1 + \dots + q_n = 1 \end{array}} \sum _{i=1}^n \left\{ q_i\; g(x, \xi _i) - \frac{\rho }{2} (q_i - \tfrac{1}{n})^2\right\} \end{aligned}$$
(24)

is a global approximation of \(\varphi _2\), such that \(\widetilde{\varphi }_2(x, \eta ) \le \varphi _2(x, \eta ) \le \widetilde{\varphi }_2(x, \eta ) + \frac{\lambda \rho }{2}\) for all \((x, \eta ) \in {\mathop {\mathrm {\mathbb {R}}}\limits }^{d+1}\). Moreover, the function is differentiable and its gradient writes, with \(S = ({s_g}_i)_{1 \le i \le n}\) the Jacobian of \(x \mapsto (g(x, \xi _1),\dots , g(x, \xi _n))\), as

$$\begin{aligned} \nabla \widetilde{\varphi }_2 (x, \eta ) = (\lambda \; S\; \tilde{q},\;0) \end{aligned}$$

where \(\tilde{q}\) is the (unique) optimal solution.Footnote 1 of (24).

Let us conclude about our approach to tackle \((P_{\lambda , \mu })\). We implement an existing advanced bundle algorithm, together with efficient subroutines, to solve a smooth approximation of \((P_{\lambda , \mu })\). There is a convergence result of this algorithm towards a critical point of the approximated problem, but no convergence guarantee towards the optimal solution of the approximated problem or of \((P_{\lambda , \mu })\) itself. In practice, though, we observe satisfying empirical convergence to near optimal solutions, confirming the good results presented in [9, Sec. 6]. We illustrate the correct empirical convergence of the resulting algorithm in Sect. 5.2 on problems for which we have explicit optimal solutions.

4.2 A python toolbox for chance constrained optimization

We release TACO, an open-source python toolbox for solving chance constrained optimization problems (1). The toolbox implements the penalization approach outlined in Sect. 3 together with the bundle method [9] for the inner penalized subproblems. TACO routines rely on just-in-time compilation supported by Numba [23]. The routines are optimized to provide fast performances on reasonably large datasets. Documentation is available at: https://yassine-laguel.github.io/taco We provide here basic information on TACO; for further information, we refer to Sect. 2 in appendix and the online documentation.

The python class Problem wraps up all information about the problem to be solved. This class possesses an attribute data which contains the values of \(\xi \) and is formatted as a numpy array in 64-bit float precision. The class also implements two methods giving first-order oracles: objective_func and objective_grad for the objective function f, and constraint_func and constraint_grad for the constraint function g.

Let us take a simple quadratic problem in \(\mathop {\mathrm {\mathbb {R}}}\limits ^2\) to illustrate the instantiation of a problem. We consider

$$\begin{aligned}&\!\!\min _{x\in \mathop {\mathrm {\mathbb {R}}}\limits ^2}\;\; \Vert x - a\Vert ^2&a = [1.0, 2.0]^\top \\&\text {s.t.} \;\; {{\,\mathrm{\mathbb {P}}\,}}[{x}^\top \xi \le 0] \ge 0.9,&\text { with}\,1000\hbox { samples of }\xi \sim \mathcal {N}(0,1) . \end{aligned}$$

The instance of Problem is in this case:

figure a

TACO handles the optimization process with a python class named Optimizer. Given an instance of Problem and hyper-parameters provided by the user, the class Optimizer runs an implementation of the bundle method of [9] on the penalized problem (10). The toolbox gives the option to update the penalization parameters \(\mu , \lambda \) along the running process to escape possible stationary points for the DC objective that are non-feasible for the chance constraint.

figure b

Customizable parameters are stored in a python dictionary, called params, and designed as an attribute of the class Optimizer. The main parameters to tune are: the safety level of probability p, the starting penalization parameters \(\mu =\texttt {pen1}\) and \(\lambda =\texttt {pen2}\), the starting point of the algorithm and the starting value for the proximal parameter of the bundle method. We underline in particular the importance of the two starting penalization parameters: an initial tuning of \(\mu =\texttt {pen1}\) and \(\lambda =\texttt {pen2}\) is often required to get a satisfying solutions for the problem considered. See for instance the experimental setup of our numerical illustrations in 3 and codes on the toolbox website for the specific tuning used there. Others parameters are filled with default values when instantiating an Optimizer; for instance:

figure c

Some important parameters (such as the safety probability level, or the starting penalization parameters) may also be given directly to the constructor of the class Optimizer, when instantiating the object; as in the first example.

5 Numerical illustrations

We illustrate our double penalisation approach implemented in the toolbox TACO on three problems: a 2-dimensional quadratic problem with a non-convex chance constraint (in Sect. 5.1), a family of problems with explicit solutions (in Sect. 5.2), and a case study from [27] (in Sect. 5.3). These proof-of-concept experiments are not meant to be extensive but to show that our approach is viable. These experiments are reproducible: the experimental framework is available on the toolbox’s website.

5.1 Visualization of convergence on a 2d problem

We consider a two-dimensional toy quadratic problem in order to track the convergence of the iterates on the sublevel sets. We take [22, Ex. 4.1] which considers an instance of problem (1) with

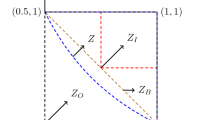
$$\begin{aligned} \begin{aligned} f(x)&= \frac{1}{2} (x-a)^\top Q (x-a) \quad \;\text {with}\;a = \begin{pmatrix} 2. \\ 2. \end{pmatrix}, Q=\begin{pmatrix} 5.5 &{} 4.5 \\ 4.5 &{} 5.5 \end{pmatrix}\\ g(x,z)&= z^\top W(x) z + w^\top z \quad \text {with}\; W\!(x)\!=\!\begin{pmatrix} x_1^2 + 0.5\! &{} 0. \\ 0. &{} \!|x_2 - 1|^3 \!+\! 1 \end{pmatrix}\\ \xi&\sim \mathcal {N}(\mu , \Sigma ) \qquad 10^4\text { samplings with}\, \mu = \begin{pmatrix} 1. \\ 1. \end{pmatrix}, \Sigma = \begin{pmatrix} 20. &{} 0. \\ 0. &{} 20. \end{pmatrix}. \end{aligned} \end{aligned}$$
(25)

For this example, [22] shows that the chance constraint is convex for large enough probability levels, but here we take a low probability level \(p=0.008\) to have a non-convex chance-constraint. We can see this on Fig. 1, ploting the level sets of the objective function and the constraint function: the chance-constrained region for \(p=0.008\) is delimited by a black dashed line; the optimal value of this problem is located at the star.

Fig. 1
figure 1

Trajectory of the iterates (in blue) on the plot of the level sets of the chance-constraint and the objective for the 2d problem with data (25)

Full size image

We apply our double penalization method to solve this problem, with the setting described in Appendix 3 and available on the TACO website. We plot on the sublevel sets of Fig. 1 the path (in deep blue) taken by the sequence of iterates starting from the point [0.5, 1.5] moving towards the solution. We observe that the sequence of iterates, after a exploration of the functions landscape, gets rapidly close to the optimal solution. At the end of the convergence, we also see a zigzag behaviour around the frontier of the chance constraint. This can be explained by the penalization term which is activated asymptotically whenever the sequence leaves the feasible region of the chance constraint.

5.2 Experiments on a family of problems with explicit solutions

We consider the family of d-dimensional problems of [17, section 5.1]. For a given dimension d, the problem writes as an instance of (1) with

$$\begin{aligned} f(x) = - \sum ^d_{i=1}x_i, \quad \mathop {\mathrm {\mathcal {X}}}\limits = \mathbb {R}_+^d, \quad g(x, Z) = \!\!\!\! \max _{i \in \{ 1,\dots , 10 \}} \sum _{j=1}^d Z_{i,j}^2 x_j^2 - 100 \end{aligned}$$
(26)

and \(\xi \) is random \(10\times d\)-matrix satisfying for all i, j, \(\xi _{i,j} \sim \mathcal {N}(0,1)\). The interest of this family of problems is that they have explicit solutions: for given d, the optimal value is

$$\begin{aligned} f^\star = -\frac{10\,d}{\sqrt{F_{\chi _d^2}^{(-1)}(p^{\frac{1}{10}})}} \end{aligned}$$

where \(F_{\chi _d^2}\) is \(\chi ^2\) cumulative distribution with d degrees of freedom. We consider four instances of this problem with dimension d from 2 to 200 and the safety probability threshold p set to 0.8. We consider a rich information on uncertainty: \(\xi \) is sampled 10000 times. In this case, a direct approach consisting in solving the standard mixed-integer quadratic reformulations (see e.g. [1]) with efficient MINLP solvers (we used Juniper [20]) does not provide reasonable solutions; see basic information in Appendix 3.

Fig. 2
figure 2

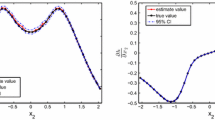
Convergence of the algorithm on four problems (26) with \(d=2,10,50,200\)

Full size image

We solve these instances with our double penalization approach, parameterized as described in Appendix 3. Figure 2 plots the relative suboptimality \( (f(x_k) - f^\star )/|f^\star | \) along iterations. The green (resp. red) regions represent iterates that, respectively, satisfy (resp. do not satisfy) the chance constraint.

In the four instances, we take an initial iterate well inside the feasible region. We then observe an initial decrease of the objective function down to global optimal value. The chance constraint starts to be violated later, only when the threshold is reached, and therefore the last part of convergence deals with local improvement of precision and feasibility. Let us underline that the convergence to the global optimal solution, observed here, is specific to this particular situation, and not guaranteed in the general setting.

Table 1 reports the final suboptimality and satisfaction of the probabilistic constraint. The probability constraint is evaluated for 100 sampled points out of the total \(N=10000\) points. We give the resulting probability; the standard deviation is 0.004 for the four instances.

We observe that the algorithm reaches an accuracy of order of \(10^{-3}\). Regarding satisfaction of the constraint \({{\,\mathrm{\mathbb {P}}\,}}[g(x,\xi ) \le 0] \ge 0.8 \), it is achieved to a \(10^{-4}\) precision for \(d= 2\) but it slightly degrades as the dimension grows.

Table 1 Final suboptimality and feasibility for (26) (where \(p=0.8\))
Full size table

5.3 Experiments on a classic case study

We consider the chance-constrained portfolio optimization problem from [27]. The problem writes as maximizing the superquantile/value-at-risk of a portfolio over \(d=65\) assets (with respective random returns \(r_i\)):

$$\begin{aligned} \left\{ \displaystyle \begin{array}{ll} \max _{x\ge 0, t \in \mathop {\mathrm {\mathbb {R}}}\limits } &{} t-1\\ \text {s.t.} &{} {{\,\mathrm{\mathbb {P}}\,}}[\sum _{j=0}^d r_j x_j \le t] \ge 0.95 \\ &{} \sum _{j=1}^d x_j = 1.\\ \end{array} \right. \end{aligned}$$
(27)

We follow [27] for the modeling of randomness and the generation of instances of this problem; see details in Appendix 3. We consider several samplings of the \(r_i\), yielding several instances of the problem.

Our reference instance uses a sampling of \(n=14684\) points; this sample size corresponds to the theoretical size for which the solution obtained by a scenario approximation satisfies the intrinsic chance constraint in (27) with probability \(1 - 10^{-3}\); see [5, 27]. We also generate instances with smaller sample sizes (\(n \in \{500, 1000, 2000, 5000, 10000\}\)) to illustrate the out-of-sample performance of solutions computed by our algorithm.

Fig. 3
figure 3

Convergence, trade-off quality, and out-of-sample performance of our algorithm for various parameters solving (27) with different sample size

Full size image

We report the computational results in Fig. 3, highlighting three aspects. In the left-hand plot, we illustrate the empirical convergence of our algorithm on the reference instance. We report the values of the DC objective (22) along the iterations of our algorithm. Vertical lines correspond to updates of the penalty parameters. Between two such updates, the DC objective decreases along the iterates of the inner bundle algorithm. In contrast, at each update, there is an increase, as expected in theory (see (19) in the proof of Proposition 2). After approximately 1600 iterations, no more updates on the penalization parameter occur and we observe an empirical convergence.

In the middle plot in Fig. 3, we illustrate the trade-off between maximization of the objective and satisfaction of the approximated chance-constraint. More precisely, here is the set-up of this experiment. For each sample size, we generate independently 5 instances of the approximated problem, that we solve several times with our algorithm using different penalization parametersFootnote 2. For each sample size (that has an associated color) and each run of the algorithm, we report the averages over the 5 instances of the final objective values and the chance-constraint satisfaction.Footnote 3 We observe, on the figure, a better satisfaction of the chance constraint as n grows, which comes at the price of lower objective values. We also note a bigger sensitivity to penalization parameters for the instances with small n (as cloud of colors points are more scattered).

Finally, in the right-hand plot of Fig. 3, we illustrate fluctuations on the out-of-sample performances of computed solutions. More precisely, in the same set-up as above, we select the couple of starting penalization parameters providing the best averageFootnote 4 As in the previous illustration, we observe that the constraint satisfaction improves when the sample size grows. We also see that the variance of the constraint satisfaction significantly improve as n grows.

6 Conclusions, perspectives

In this paper, we bring to light a nice bilevel reformulation of chance-constrained optimization problems. We then leverage it to propose a double penalization algorithm, discuss its theoretical properties, and illustrate it on three non-convex case studies. We also release an open-source python toolbox implementing the algorithm and the numerical experiments.

This work opens the door to various possible extensions. First, the applicability of the approach can be widened. For instance, we consider here a convex objective function, but the approach generalizes to difference-of-convex functions, with the same algorithm. Further theoretical guarantees as well as numerical illustrations would then be necessary. Second, note that all ingredients of the algorithm could be improved. For instance, we could try another approach or a better tuning of hyper-parameters, with the help of Lagrangian duality. We could also investigate the use of specific first-order methods, rather than a generic bundle method, to solve the inner penalized problems. Finally, beyond the preliminary computational experiments (illustrating the ease-of-use of the toolbox, the heuristic convergence of the algorithm, and the out-of-sample performance of the approach), a study of the sensitivity of the algorithm to the parameters, the adaptivity to special instances, and the comparison to other approaches (other than MINLP) would be of interest. All this is out of the scope of this paper and deserves thorough investigations.