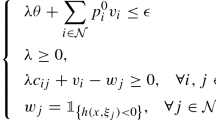Optimized Bonferroni approximations of distributionally robust joint chance constraints

Abstract

A distributionally robust joint chance constraint involves a set of uncertain linear inequalities which can be violated up to a given probability threshold $\epsilon$, over a given family of probability distributions of the uncertain parameters. A conservative approximation of a joint chance constraint, often referred to as a Bonferroni approximation, uses the union bound to approximate the joint chance constraint by a system of single chance constraints, one for each original uncertain constraint, for a fixed choice of violation probabilities of the single chance constraints such that their sum does not exceed $\epsilon$. It has been shown that, under various settings, a distributionally robust single chance constraint admits a deterministic convex reformulation. Thus the Bonferroni approximation approach can be used to build convex approximations of distributionally robust joint chance constraints. In this paper we consider an optimized version of Bonferroni approximation where the violation probabilities of the individual single chance constraints are design variables rather than fixed a priori. We show that such an optimized Bonferroni approximation of a distributionally robust joint chance constraint is exact when the uncertainties are separable across the individual inequalities, i.e., each uncertain constraint involves a different set of uncertain parameters and corresponding distribution families. Unfortunately, the optimized Bonferroni approximation leads to NP-hard optimization problems even in settings where the usual Bonferroni approximation is tractable. When the distribution family is specified by moments or by marginal distributions, we derive various sufficient conditions under which the optimized Bonferroni approximation is convex and tractable. We also show that for moment based distribution families and binary decision variables, the optimized Bonferroni approximation can be reformulated as a mixed integer second-order conic set. Finally, we demonstrate how our results can be used to derive a convex reformulation of a distributionally robust joint chance constraint with a specific non-separable distribution family.

1 Introduction

1.1 Setting

A linear chance constrained optimization problem is of the form:

$$\begin{aligned} \min&\ \ c^{\top }x, \end{aligned}$$

(1a)

$$\begin{aligned} \mathrm{s.t. }&\ \ x \in S, \end{aligned}$$

(1b)

$$\begin{aligned}&\ \ {\mathbb {P}}\left\{ \varvec{\xi }:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x), \forall i\in [I]\right\} \ge 1-\epsilon . \end{aligned}$$

(1c)

Above, the vector $x \in {{\mathbb {R}}}^n$ denotes the decision variables; the vector $c \in {{\mathbb {R}}}^n$ denotes the objective function coefficients; the set $S \subseteq {{\mathbb {R}}}^n$ denotes deterministic constraints on x; and the constraint (1c) is a chance constraint involving I inequalities with uncertain data specified by the random vector $\varvec{\xi }$ supported on a closed convex set $\varXi \subseteq {{\mathbb {R}}}^m$ with a known probability distribution ${\mathbb {P}}$. We let $[R]:=\{1,2,\ldots ,R\}$ for any positive integer R, and for each uncertain constraint $i \in [I]$, $a_i(x) \in {{\mathbb {R}}}^{m_i}$ and $b_i(x) \in {{\mathbb {R}}}$ denote affine mappings of x such that $a_i(x)=A^i x+a^i$ and $b_i(x)=B^i x+b^i$ with $A^i\in {{\mathbb {R}}}^{m_i\times n}$, $a^i\in {{\mathbb {R}}}^{m_i}$, $B^i\in {{\mathbb {R}}}^{n}$, and $b^i\in {{\mathbb {R}}}$, respectively. The uncertain data associated with constraint i is specified by $\varvec{\xi }_i$ which is the projection of $\varvec{\xi }$ to a coordinate subspace $\mathcal {S}_i\subseteq {{\mathbb {R}}}^{m}$, i.e., $\mathcal {S}_i$ is a span of $m_i$ distinct standard bases with $\dim (\mathcal {S}_i)=m_i$. The support of $\varvec{\xi }_i$ is $\varXi _i={{\,\mathrm{Proj}\,}}_{\mathcal {S}_i}(\varXi )$. The chance constraint (1c) requires that all I uncertain constraints are simultaneously satisfied with a probability or reliability level of at least $(1-\epsilon )$, where $\epsilon \in (0,1)$ is a specified risk tolerance. We call (1c) a single chance constraint if $I = 1$ and a joint chance constraint if $I \ge 2$.

Remark 1

The notation above might appear to indicate that the uncertain data is separable across the inequalities. However, note that $\varvec{\xi }_i$ is a projection of $\varvec{\xi }$. For example, we may have $\varvec{\xi }_i = \varvec{\xi }$ and $\mathcal {S}_i = {{\mathbb {R}}}^m$ for all i, when each inequality involves all uncertain coefficients $\varvec{\xi }$.

In practice, the decision makers often have limited distributional information on $\varvec{\xi }$, making it challenging to commit to a single ${\mathbb {P}}$. As a consequence, the optimal solution to (1a)–(1c) can actually perform poorly if the (true) probability distribution of $\varvec{\xi }$ is different from the one we commit to in (1c). In this case, a natural alternative of (1c) is a distributionally robust chance constraint of the form

$$\begin{aligned}&\ \ \inf _{{\mathbb {P}}\in {{\mathcal {P}}}} {\mathbb {P}}\left\{ \varvec{\xi }:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x), \forall i\in [I]\right\} \ge 1-\epsilon , \end{aligned}$$

(1d)

where we specify a family ${{\mathcal {P}}}$ of probability distributions of $\varvec{\xi }$, called an ambiguity set, and the chance constraint (1c) is required to hold for all the probability distributions ${\mathbb {P}}$ in ${{\mathcal {P}}}$. We call formulation (1a)–(1b), (1d) a distributionally robust joint chance constrained program (DRJCCP) and denote the feasible region induced by (1d) as

$$\begin{aligned} Z:=\left\{ x\in {{\mathbb {R}}}^n:\inf _{{\mathbb {P}}\in {{\mathcal {P}}}}{\mathbb {P}}\left\{ \varvec{\xi }:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x), \forall i\in [I]\right\} \ge 1-\epsilon \right\} . \end{aligned}$$

(2)

In general, the set $Z$ is nonconvex and leads to NP-hard optimization problems [16]. This is not surprising since the same conclusion holds even when the ambiguity set ${{\mathcal {P}}}$ is a singleton [25, 27]. The focus of this paper is on developing tractable convex approximations and reformulations of set $Z$.

1.2 Related literature

Recently, distributionally robust optimization (DRO) has received increasing attention in the literature [10, 12, 14, 16, 19, 42]. Various ambiguity sets have been investigated, including moment-based ambiguity sets (see, e.g., [10, 16, 42]) and distance-based ambiguity sets (see, e.g., [12, 14, 19]). Historical data can be used to calibrate the ambiguity sets so that they contain the true probability distribution with a high confidence (see, e.g., [10, 12]). In this paper, we will focus on DRJCCP.

Existing literature has identified a number of important special cases where $Z$ is convex. In the non-robust setting, i.e. when ${{\mathcal {P}}}$ is a singleton, the set $Z$ is convex if $A^i = 0$ for all $i \in [I]$ (i.e. the uncertainties do not affect the variable coefficients) and either (i) the distribution of the vector $[(a^1)^{\top }\varvec{\xi }_1, \ldots , (a^I)^{\top }\varvec{\xi }_I]^{\top }$ is quasi-concave [29, 40, 41] or (ii) the components of vector $[(a^1)^{\top }\varvec{\xi }_1, \ldots , (a^I)^{\top }\varvec{\xi }_I]^{\top }$ are independent and follow log-concave probability distributions [30]. Much less is known about the case $A^i \ne 0$ (i.e. with uncertain coefficients), except that $Z$ is convex if $I = 1$, $\epsilon \le 1/2$, and $\varvec{\xi }$ has a symmetric and non-degenerate log-concave distribution [22], of which the normal distribution is a special case [20]. In the robust setting, when ${{\mathcal {P}}}$ consists of all probability distributions with given first and second moments and $I = 1$, the set $Z$ is second-order cone representable [6, 11]. Similar convexity results hold when $I = 1$ and ${{\mathcal {P}}}$ also incorporates other distributional information such as the support of $\varvec{\xi }$ [8], the unimodality of ${\mathbb {P}}$ [16, 23], or arbitrary convex mapping of $\varvec{\xi }$ [44]. For distributionally robust joint chance constraints, i.e. $I \ge 2$ and ${{\mathcal {P}}}$ is not a singleton, conditions for convexity of $Z$ are scarce. To the best of our knowledge, [17] provides the first convex reformulation of $Z$ in the absence of coefficient uncertainty, i.e. $A^i = 0$ for all $i \in [I]$, when ${{\mathcal {P}}}$ is characterized by the mean, a positively homogeneous dispersion measure, and a conic support of $\varvec{\xi }$. For the more general coefficient uncertainty setting, i.e. $A^i\ne 0$, [44] identifies several sufficient conditions for $Z$ to be convex (e.g., when ${{\mathcal {P}}}$ is specified by one moment constraint), and [43] shows that $Z$ is convex when the chance constraint (1d) is two-sided (i.e., when $I = 2$ and $a_1(x)^{\top }\varvec{\xi }_1=-a_2(x)^{\top }\varvec{\xi }_2$) and ${{\mathcal {P}}}$ is characterized by the first two moments.

Various approximations have been proposed for settings where $Z$ is not convex. When ${{\mathcal {P}}}$ is a singleton, i.e. ${{\mathcal {P}}}=\{{\mathbb {P}}\}$, [27] propose a family of deterministic convex inner approximations, among which the conditional-value-at-risk (CVaR) approximation [34] is proved to be the tightest. A similar approach is used to construct convex outer approximations in [1]. Sampling based approaches that approximate the true distribution by an empirical distribution are proposed in [5, 24, 28]. When the probability distribution ${\mathbb {P}}$ is discrete, [2] develop Lagrangian relaxation schemes and corresponding primal linear programming formulations. In the distributionally robust setting, [7] propose to aggregate the multiple uncertain constraints with positive scalars in to a single constraint, and then use CVaR to develop an inner approximation of $Z$. This approximation is shown to be exact for distributionally robust single chance constraints when ${{\mathcal {P}}}$ is specified by first and second moments in [46] or, more generally, by convex moment constraints in [44].

1.3 Contributions

In this paper we study the set $Z$ in the distributionally robust joint chance constraint setting, i.e. $I \ge 2$ and ${{\mathcal {P}}}$ is not a singleton. In particular, we consider a classical approximation scheme for joint chance constraint, termed Bonferroni approximation [7, 27, 46]. This scheme decomposes the joint chance constraint (1d) into I single chance constraints where the risk tolerance of constraint i is set to a fixed parameter $s_i \in [0,\epsilon ]$ such that $\sum _{i\in [I]}s_i\le \epsilon$. Then, by the union bound, it is easy to see that any solution satisfying all I single chance constraints will satisfy the joint chance constraint. Such a distributionally robust single chance constraint system is often significantly easier than the joint constraint. To optimize the quality of the Bonferroni approximation, it is attractive to treat $\{s_i\}_{i \in [I]}$ as design variables rather than as fixed parameters. However, this could undermine the convexity of the resulting approximate system and make it challenging to solve. Indeed, [27] cites the tractability of this optimized Bonferroni approximation as “an open question” (see Remark 2.1 in [27]). In this paper, we make the following contributions to the study of optimized Bonferroni approximation:

• 1. We show that the optimized Bonferroni approximation of a distributionally robust joint chance constraint is in fact exact when the uncertainties are separable across the individual inequalities, i.e., each uncertain constraint involves a different set of uncertain parameters and corresponding distribution families.

• 2. For the setting when the ambiguity set is specified by the first two moments of the uncertainties in each constraint, we establish that the optimized Bonferroni approximation, in general, leads to strongly NP-hard problems; and go on to identify several sufficient conditions under which it becomes tractable.

• 3. For the setting when the ambiguity set is specified by marginal distributions of the uncertainties in each constraint, again, we show that while the general case is strongly NP-hard, there are several sufficient conditions leading to tractability.

• 4. For moment based distribution families and binary decision variables, we show that the optimized Bonferroni approximation can be reformulated as a mixed integer second-order conic set.

• 5. Finally, we demonstrate how our results can be used to derive a convex reformulation of a distributionally robust joint chance constraint with a specific non-separable distribution family.

2 Optimized Bonferroni approximation

In this section we formally present the optimized Bonferroni approximation of the distributionally robust joint chance constraint set $Z$, compare it with alternative single chance constraint approximations, and provide a sufficient condition under which it is exact.

2.1 Bonferroni and Fréchet inequalities

In this subsection, we review Bonferroni and Fréchet inequalities.

Definition 1

(Bonferroni inequality, or union bound) Let $(\varXi ,{{\mathcal {F}}}, {\mathbb {P}})$ be a probability space, where $\varXi \subseteq {{\mathbb {R}}}^m$ is a sample space, ${{\mathcal {F}}}$ is a $\sigma$-algebra of $\varXi$, and ${\mathbb {P}}$ is a probability measure on $(\varXi ,{{\mathcal {F}}})$. Given I events $\{E_i\}_{i\in [n]}$ with $E_i\in {{\mathcal {F}}}$ for each $i\in [I]$, the Bonferroni inequality [3] is:

$$\begin{aligned} {\mathbb {P}}\left\{ \bigcup \limits _{i\in [I]}E_i\right\} \le \min \left\{ \sum _{i\in [I]}{\mathbb {P}}\left\{ E_i\right\} , 1\right\} . \end{aligned}$$

Definition 2

(Fréchet inequality) Let $\{(\varXi _i,{{\mathcal {F}}}_i, {\mathbb {P}}_i): \ i \in [I]\}$ be a finite collection of probability spaces, where for $i \in [I]$, $\varXi _i\subseteq \mathcal {S}_i$ is a sample space, ${{\mathcal {F}}}_i$ is a $\sigma$-algebra of $\varXi _i$, and ${\mathbb {P}}_i$ is a probability measure on $(\varXi _i,{{\mathcal {F}}}_i)$. Consider the product space $(\varXi ,{{\mathcal {F}}}) = \prod _{i \in [I]} (\varXi _i,{{\mathcal {F}}}_i)$, and let ${{\mathcal {M}}}(\varXi ,{{\mathcal {F}}})$ denote the set of all probability measures on $(\varXi ,{{\mathcal {F}}})$. Let ${{\mathcal {M}}}({\mathbb {P}}_1,\ldots ,{\mathbb {P}}_I)$ denote the set of joint probability measures on $(\varXi ,{{\mathcal {F}}})$ generated by $({\mathbb {P}}_1,\ldots ,{\mathbb {P}}_I)$, i.e.

$$\begin{aligned} {{\mathcal {M}}}({\mathbb {P}}_1,\ldots ,{\mathbb {P}}_I) = \left\{ {\mathbb {P}}\in {{\mathcal {M}}}(\varXi ,{{\mathcal {F}}}): \ {{\,\mathrm{Proj}\,}}_i({\mathbb {P}}) = {\mathbb {P}}_i \ \forall \ i \in [I]\right\} , \end{aligned}$$

where ${{\,\mathrm{Proj}\,}}_i: \varXi \rightarrow \varXi _i$ denotes the i-th projection operation. For any ${\mathbb {P}}\in {{\mathcal {M}}}({\mathbb {P}}_1,\ldots ,{\mathbb {P}}_I)$ and event $E_i\in {{\mathcal {F}}}_i$ for each $i\in [I]$, the Fréchet inequality [13] is:

$$\begin{aligned} \left[ \sum _{i\in [I]} {\mathbb {P}}_i\left\{ E_i\right\} - (I-1) \right] _+ \le {\mathbb {P}}\left\{ \displaystyle {\prod _{i \in [I]}} E_i \right\} , \end{aligned}$$

where $[a]_+ = \max \{0,a\}$.

Remark 2

Note that in the special case of $\varXi _i=\varXi$ for all $i \in [I]$, the above Fréchet inequality is

$$\begin{aligned} \left[ \sum _{i\in [I]} {\mathbb {P}}_i\left\{ E_i\right\} - (I-1) \right] _+ \le {\mathbb {P}}\left\{ \displaystyle {\bigcap _{i \in [I]}} E_i \right\} , \end{aligned}$$

which is essentially the Bonferroni inequality complemented. Indeed, let ${\bar{E}}_i=\varXi {\setminus }E_i$ for all $i\in [I]$, then we have

$$\begin{aligned} {\mathbb {P}}\left\{ \displaystyle {\bigcap _{i \in [I]}} E_i \right\}= & {} 1-{\mathbb {P}}\left\{ \displaystyle {\bigcup _{i \in [I]}} {{\bar{E}}}_i \right\} \\\ge & {} 1-\min \left\{ \sum _{i\in [I]} {\mathbb {P}}_i\left\{ {{\bar{E}}}_i\right\} ,1 \right\} =\max \left\{ \sum _{i\in [I]} {\mathbb {P}}_i\left\{ E_i\right\} -I+1,0\right\} , \end{aligned}$$

where the inequality is due to the Bonferroni inequality.

2.2 Single chance constraint approximations

Recall that the uncertain data associated with constraint $i \in [I]$ is specified by $\varvec{\xi }_i$ which is the projection of $\varvec{\xi }$ to a coordinate subspace $\mathcal {S}_i\subseteq {{\mathbb {R}}}^{m}$ with $\dim (\mathcal {S}_i)=m_i$, and the support of $\varvec{\xi }_i$ is $\varXi _i={{\,\mathrm{Proj}\,}}_{\mathcal {S}_i}(\varXi )$. For each $i \in [I]$, let ${{\mathcal {D}}}_i$ denote the projection of the ambiguity set ${{\mathcal {P}}}$ to the coordinate subspace $\mathcal {S}_i$, i.e., ${{\mathcal {D}}}_i = {{\,\mathrm{Proj}\,}}_{\mathcal {S}_i}({{\mathcal {P}}})$. Thus ${{\mathcal {D}}}_i$ denotes the projected ambiguity set associated with the uncertainties appearing in constraint i. The following two examples illustrate ambiguity set ${{\mathcal {P}}}$ and its projections $\{{{\mathcal {D}}}_i\}_{i\in [I]}$.

Example 1

Consider

$$\begin{aligned} Z = \left\{ x \in {{\mathbb {R}}}^2: \inf _{{\mathbb {P}}\in {{\mathcal {P}}}} {\mathbb {P}}\left\{ \varvec{\xi }: \begin{array}{c} \widehat{\xi }_{1} x_1 + \widehat{\xi }_2 x_2 \le 0 \\ \widehat{\xi }_2 x_1 + \widehat{\xi }_3 x_2 \le 1 \end{array}\right\} \ge 0.75 \right\} , \end{aligned}$$

where $\varvec{\xi }= [\widehat{\xi }_1, \widehat{\xi }_2, \widehat{\xi }_3]^{\top }$, $\varvec{\xi }_1 = [\widehat{\xi }_1, \widehat{\xi }_2]^{\top }$, $\varvec{\xi }_2 = [\widehat{\xi }_2, \widehat{\xi }_3]^{\top }$, and ${{\mathcal {P}}}= \{\mathbb {P}: {{\mathbb {E}}}_{{\mathbb {P}}}[\varvec{\xi }] = 0, {{\mathbb {E}}}_{{\mathbb {P}}}[\varvec{\xi }\varvec{\xi }^{\top }] = \varSigma \}$ with

$$\begin{aligned} \varSigma \ = \ \begin{bmatrix} 1&\quad 0&\quad 1.2 \\ 0&\quad 0.5&\quad 0.5 \\ 1.2&\quad 0.5&\quad 2 \end{bmatrix}. \end{aligned}$$

In this example, $m = 3$, $m_1 = m_2 = 2$, $\mathcal {S}_1 = \{\widehat{\xi }\in {{\mathbb {R}}}^3: \widehat{\xi }_3=0\}$, $\mathcal {S}_2 = \{\widehat{\xi }\in {{\mathbb {R}}}^3: \widehat{\xi }_1=0\}$, and ${{\mathcal {D}}}_i = \{\mathbb {P}: {{\mathbb {E}}}_{{\mathbb {P}}}[\varvec{\xi }_i] = 0, {{\mathbb {E}}}_{{\mathbb {P}}}[\varvec{\xi }_i\varvec{\xi }_i^{\top }] = \varSigma _i\}$ for $i = 1, 2$, where

$$\begin{aligned} \varSigma _1 \ = \ \begin{bmatrix} 1&\quad 0 \\ 0&\quad 0.5 \end{bmatrix} \ \text{ and } \ \varSigma _2 \ = \ \begin{bmatrix} 0.5&\quad 0.5 \\ 0.5&\quad 2 \end{bmatrix}. \ \ \ \ \end{aligned}$$

$\square$

Example 2

Consider

$$\begin{aligned} Z = \left\{ x\in {{\mathbb {R}}}^I: \inf _{{\mathbb {P}}\in {{\mathcal {P}}}} {\mathbb {P}}\left\{ \varvec{\xi }: \varvec{\xi }_i \le x_i, \forall i \in [I] \right\} \ge 0.9 \right\} , \end{aligned}$$

where $\varvec{\xi }\sim \mathcal {N}(\mu , \varSigma )$, i.e. ${{\mathcal {P}}}$ is a singleton containing only an I-dimensional multivariate normal distribution with mean $\mu \in \mathbb {R}^I$ and covariance matrix $\varSigma \in \mathbb {R}^{I\times I}$. In this example, $m = I$, and for all $i \in [I]$, $m_i = 1$, $\mathcal {S}_i = \{\varvec{\xi }\in {{\mathbb {R}}}^I: \xi _j=0, j\ne i, \forall j\in [I]\}$, and ${{\mathcal {D}}}_i$ is a singleton containing only a 1-dimensional normal distribution with mean $\mu _i$ and variance $\varSigma _{ii}$. $\square$

Consider the following two distributionally robust single chance constraint approximations of $Z$:

$$\begin{aligned} Z_{O}:=\left\{ x\in {{\mathbb {R}}}^n:\inf _{{\mathbb {P}}_i\in {{\mathcal {D}}}_i}{\mathbb {P}}_i\left\{ \varvec{\xi }_i:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x)\right\} \ge 1-\epsilon , \forall i\in [I]\right\} , \end{aligned}$$

(3)

and

$$\begin{aligned} Z_{I}:=\left\{ x\in {{\mathbb {R}}}^n:\inf _{{\mathbb {P}}_i\in {{\mathcal {D}}}_i}{\mathbb {P}}_i\left\{ \varvec{\xi }_i:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x)\right\} \ge 1-\frac{\epsilon }{I}, \forall i\in [I]\right\} . \end{aligned}$$

(4)

Both $Z_O$ and $Z_I$ involve I distributionally robust single chance constraints, and they differ by the choice of the risk levels. The approximation $Z_O$ relaxes the requirement of simultaneously satisfying all uncertain linear constraints, and hence is an outer approximation of $Z$. In $Z_I$, each single chance constraint has a risk level of $\epsilon /I$, and it follows from the union bound (or Bonferroni inequality [3]), that $Z_I$ is an inner approximation of $Z$. The set $Z_I$ is typically called the Bonferroni approximation. We consider an extension of $Z_I$ where the risk level of each constraint is not fixed but optimized [27]. The resulting optimized Bonferroni approximation is:

$$\begin{aligned} Z_B&:=\left\{ x:{\exists s\in {{\mathbb {R}}}_+^I \ \text{ such } \text{ that }} \ \inf _{{\mathbb {P}}_i\in {{\mathcal {D}}}_i}{\mathbb {P}}_i\left\{ \varvec{\xi }_i:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x)\right\} \nonumber \right. \\&\left. \ge 1 - s_i, \ \forall i\in [I], \sum _{i\in [I]}s_i\le \epsilon \right\} . \end{aligned}$$

(5)

Note that the set $Z_B$ depends on the projected ambiguity sets $\{{{\mathcal {D}}}_i\}_{i\in [I]}$. For notational brevity, we will use $Z_B$ to denote the feasible region of the optimized Bonferroni approximation for all ambiguity sets. It should be clear from the context which ambiguity set $Z_B$ is associated with.

Finally, we review the CVaR approximation of the set $Z$ (see, e.g., [27, 46]). We note that $Z$ can be recast in the following form of a distributionally robust single chance constraint:

$$\begin{aligned} Z=\left\{ x\in {{\mathbb {R}}}^n:\sup _{{\mathbb {P}}\in {{\mathcal {P}}}}{\mathbb {P}}\left\{ \varvec{\xi }:\max _{i\in [I]}\left[ a_i(x)^{\top }\varvec{\xi }_i -b_i(x)\right] > 0\right\} \le \epsilon \right\} . \end{aligned}$$

(6)

Then, applying the ${\text{ CVaR }}$ approximation to the chance constraint in (6) for any probability distribution ${\mathbb {P}}\in {{\mathcal {P}}}$ yields the following approximation:

$$\begin{aligned} Z_{C}:=\left\{ x\in {{\mathbb {R}}}^n:\sup _{{\mathbb {P}}\in {{\mathcal {P}}}}\inf _{\beta }\left\{ -\epsilon \beta +{{\mathbb {E}}}\left[ \max _{i\in [I]}\left[ a_i(x)^{\top }\varvec{\xi }_i -b_i(x)\right] +\beta \right] _+\right\} \le 0\right\} . \nonumber \\ \end{aligned}$$

(7)

We note that (i) set $Z_{C}$ is convex and $Z_C\subseteq Z$ because CVaR is a convex and conservative approximation of the chance constraint and (ii) to compute the worst-case ${\text{ CVaR }}$ in (7), we often switch the $\sup$ and $\inf$ operators, yielding a potentially more conservative approximation set, ${\widehat{Z}}_{C}$. Nevertheless, $Z_{C} = {{\widehat{Z}}}_C$ in many cases, e.g., when ${{\mathcal {P}}}$ is weakly compact (cf. Theorem 2.1 in [37]).

2.3 Comparison of approximation schemes

From the previous discussion we know that $Z_O$ is an outer approximation of $Z$, while both $Z_B$ and $Z_I$ are inner approximations of $Z$ and that $Z_B$ is at least as tight as $Z_I$. In addition, for the single chance constraint, we note that all the above four sets are equivalent to each other, and is less conservative than the ${\text{ CVaR }}$ approximation $Z_C$. We formalize this observation in the following result (see [32] for parallel results with respect to classical chance-constrained programs).

Theorem 1

• (i) $Z_{O} \supseteq Z\supseteq Z_B \supseteq Z_{I}$; and

• (ii) if $I=1$, then $Z_{O} =Z=Z_B = Z_{I}\supseteq Z_{C}$.

Proof

• (i) By construction, $Z_{O} \supseteq Z$. To show that $Z\supseteq Z_B$, we pick $x \in Z_B$. For all ${\mathbb {P}}\in {{\mathcal {P}}}$ and $i \in [I]$, $x \in Z_B$ implies that ${\mathbb {P}}\{\varvec{\xi }:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x)\} = {\mathbb {P}}_i\{\varvec{\xi }_i:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x)\} \ge 1 - s_i$, or equivalently, $\sup _{{\mathbb {P}}\in {{\mathcal {P}}}} {\mathbb {P}}\{\varvec{\xi }:a_i(x)^{\top }\varvec{\xi }_i > b_i(x)\} \le s_i$. Hence,

  $$\begin{aligned} \inf _{{\mathbb {P}}\in {{\mathcal {P}}}} {\mathbb {P}}\{\varvec{\xi }:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x), \forall i \in [I]\} \ =&\ 1 - \sup _{{\mathbb {P}}\in {{\mathcal {P}}}} {\mathbb {P}}\{\varvec{\xi }: \exists i \in [I], \text{ s.t. } a_i(x)^{\top }\varvec{\xi }_i \\&> b_i(x) \} \\ \ge&\ 1 - \sup _{{\mathbb {P}}\in {{\mathcal {P}}}}\sum _{i \in [I]}{\mathbb {P}}\{\varvec{\xi }: a_i(x)^{\top }\varvec{\xi }_i> b_i(x) \} \\ \ge&\ 1 - \sum _{i \in [I]} \sup _{{\mathbb {P}}\in {{\mathcal {P}}}}{\mathbb {P}}\{\varvec{\xi }: a_i(x)^{\top }\varvec{\xi }_i > b_i(x) \} \\ \ge&\ 1 - \sum _{i \in [I]} s_i \ \ge \ 1 - \epsilon , \end{aligned}$$

  where the first inequality is due to the Bonferroni inequality or union bound, the second inequality is because the supremum over summation is no larger than the sum of supremum, and the final inequality follows from the definition of $Z_B$. Thus, $x \in Z$. Finally, note that $Z_I$ is a restriction of $Z_B$ by setting $s_i = \epsilon /I$ for all $i \in [I]$ and so $Z_B \supseteq Z_I$.

• (ii) $Z_{O} =Z=Z_B = Z_{I}$ holds by definition. The conservatism of the ${\text{ CVaR }}$ approximation follows from [27].

$\square$

The following example shows that all inclusions in Theorem 1 can be strict.

Example 3

Consider

$$\begin{aligned} Z = \left\{ x\in {{\mathbb {R}}}^2: \inf _{{\mathbb {P}}\in {{\mathcal {P}}}} {\mathbb {P}}\left\{ \varvec{\xi }: \begin{array}{c} \varvec{\xi }_1\le x_1\\ \varvec{\xi }_2\le x_2\\ x_1\le 1\\ x_2\le 1 \end{array}\right\} \ge 0.5 \right\} , \end{aligned}$$

where ${{\mathcal {P}}}$ is a singleton containing the probability distribution that $\varvec{\xi }_1$ and $\varvec{\xi }_2$ are independent and uniformly distributed on [0, 1]. It follows that

$$\begin{aligned} Z_{O}=&\left\{ x\in [0,1]^2:x_1 \ge 0.5,x_2 \ge 0.5 \right\} , \\ Z=&\left\{ x\in [0,1]^2:x_1x_2 \ge 0.5\right\} , \\ Z_B=&\left\{ x\in [0,1]^2:x_1+x_2 \ge 1.5\right\} , \text{ and } \\ Z_I=&\left\{ x\in [0,1]^2:x_1 \ge 0.75,x_2 \ge 0.75\right\} . \end{aligned}$$

We display these four sets in Fig. 1, where the dashed lines denote the boundaries of $Z_{O},Z,Z_B , Z_{I}$.

For set $Z_C$, we are unable to obtain a closed-form formulation in the space of $(x_1,x_2)$. Nevertheless, we can show that it is a strict subset of $Z_I$. Indeed,

$$\begin{aligned} Z_C&=\left\{ x\in [0,1]^2:\inf _{\beta }\left\{ -\epsilon \beta +{{\mathbb {E}}}\left[ \max \left\{ \varvec{\xi }_1- x_1, \varvec{\xi }_2- x_2\right\} +\beta \right] _+\right\} \le 0 \right\} \\&=\left\{ x\in [0,1]^2:\exists \beta , \ {{\mathbb {E}}}\left[ \max \left\{ (\varvec{\xi }_1- x_1+\beta )_+, (\varvec{\xi }_2- x_2+\beta )_+\right\} \right] \le \epsilon \beta \right\} \\&\subseteq \left\{ x\in [0,1]^2:\exists \beta , \ \max \left\{ {{\mathbb {E}}}(\varvec{\xi }_1- x_1+\beta )_+, {{\mathbb {E}}}(\varvec{\xi }_2- x_2+\beta )_+\right\} \le \epsilon \beta \right\} \\&\subseteq \left\{ x\in [0,1]^2:\exists \beta _1,\beta _2, \ {{\mathbb {E}}}(\varvec{\xi }_1- x_1+\beta _1)_+\le \epsilon \beta _1, \ {{\mathbb {E}}}(\varvec{\xi }_2- x_2+\beta _2)_+\le \epsilon \beta _2 \right\} \\&=\left\{ x\in [0,1]^2:x_1 \ge 0.75,x_2 \ge 0.75\right\} =Z_I, \end{aligned}$$

where the second equality is because the infimum can be obtained by a finite $\beta \in [-1, 1]$, the first inclusion is due to the Jensen’s inequality, and the second inclusion is because we further relax the constraint $\beta _1=\beta _2$. In addition, it can be shown that $(0.75,1)\notin Z_C$. It follows that $Z_{C} \subsetneq Z_{I}$.

Therefore, in this example, we have $Z_{O} \supsetneq Z\supsetneq Z_B \supsetneq Z_{I}\supsetneq Z_{C}$. $\square$

Fig. 1

Illustration of Example 3

2.4 Exactness of optimized Bonferroni approximation

In this section we use a result from [36] to establish a sufficient condition under which the optimized Bonferroni approximation is exact.

The following result establishes a tight version of the Fréchet inequality.

Theorem 2

(Theorem 6 in [36]) Let $\{(\varXi _i,{{\mathcal {F}}}_i): \ i \in [I]\}$ be a finite collection of Polish spaces with associated probability measures $\{{\mathbb {P}}_1,\ldots ,{\mathbb {P}}_I\}$. Then for all ${E_i} \in {{\mathcal {F}}}_i$ with $i \in [I]$ it holds that

$$\begin{aligned} \left[ \sum _{i\in [I]} {\mathbb {P}}_i\left\{ {E_i}\right\} - (I-1) \right] _+ = \inf \left\{ {\mathbb {P}}\left\{ \displaystyle {\prod _{i \in [I]}} {E_i} \right\} : \ {\mathbb {P}}\in {{\mathcal {M}}}({\mathbb {P}}_1,\ldots ,{\mathbb {P}}_I) \right\} . \end{aligned}$$

Next we use the above result to show that the optimized Bonferroni approximation $Z_B$, consisting in single chance constraints, is identical to $Z$ consisting of a joint chance constraint when the uncertainties in each constraint are separable, i.e. each uncertain constraint involves a different set of uncertain parameters and associated ambiguity sets. Recall that uncertain data in $Z$ is described by the random vector $\varvec{\xi }$ supported on a closed convex set $\varXi \subseteq {{\mathbb {R}}}^m$, and the uncertain data associated with constraint i is specified by $\varvec{\xi }_i$ which is the projection of $\varvec{\xi }$ to a coordinate subspace $\mathcal {S}_i\subseteq {{\mathbb {R}}}^{m}$ with $\dim (\mathcal {S}_i)=m_i$. The support of $\varvec{\xi }_i$ is $\varXi _i={{\,\mathrm{Proj}\,}}_{\mathcal {S}_i}(\varXi )$. Furthermore, the ambiguity set associated with the uncertainties appearing in constraint i, ${{\mathcal {D}}}_i$, is the projection of the ambiguity set ${{\mathcal {P}}}$ to the coordinate subspace $\mathcal {S}_i$, i.e., ${{\mathcal {D}}}_i = {{\,\mathrm{Proj}\,}}_{\mathcal {S}_i}({{\mathcal {P}}})$. The separable uncertainty condition can then be formalized as follows:

• (A1) $\varXi = \prod _{i \in [I]} \varXi _i$ and ${{\mathcal {P}}}=\prod _{i\in [I]}{{\mathcal {D}}}_i$, i.e., ${\mathbb {P}}\in {{\mathcal {P}}}$ if and only if $\text{ Proj }_{i}{({\mathbb {P}})} \in {{\mathcal {D}}}_i$ for all $i \in [I]$.

Note that Assumption (A1) does not imply that $\{\varvec{\xi }_i\}_{i\in [I]}$ are mutually or jointly independent. That is, $\{\varvec{\xi }_i\}_{i\in [I]}$ are allowed to be positively or negatively correlated as long as the marginal distribution $\text{ Proj }_{i}{({\mathbb {P}})}$ is in ${{\mathcal {D}}}_i$. The following example illustrates Assumption (A1).

Example 4

Consider

$$\begin{aligned} Z = \left\{ x\in {{\mathbb {R}}}^2: \inf _{{\mathbb {P}}\in {{\mathcal {P}}}} {\mathbb {P}}\left\{ \varvec{\xi }: \begin{array}{c} \varvec{\xi }_{1} \le x_1 \\ 2\varvec{\xi }_2 \le x_1+x_2 \end{array}\right\} \ge 0.75 \right\} , \end{aligned}$$

where $\varXi _1={{\mathbb {R}}},\varXi _2={{\mathbb {R}}}, \varXi ={{\mathbb {R}}}^2$ and

$$\begin{aligned}&{{\mathcal {P}}}= \{\mathbb {P}: {{\mathbb {E}}}_{{\mathbb {P}}}[\varvec{\xi }_1] = 0, {{\mathbb {E}}}_{{\mathbb {P}}}[\varvec{\xi }_1^2] = \sigma _1^2,{{\mathbb {E}}}_{{\mathbb {P}}}[\varvec{\xi }_2] = 0, {{\mathbb {E}}}_{{\mathbb {P}}}[\varvec{\xi }_2^2] = \sigma _2^2\}\\&{{\mathcal {D}}}_1 = \{\mathbb {P}_1: {{\mathbb {E}}}_{{\mathbb {P}}_1}[\varvec{\xi }_1] = 0, {{\mathbb {E}}}_{{\mathbb {P}}_1}[\varvec{\xi }_1^2] = \sigma _1^2\}\\&{{\mathcal {D}}}_2 = \{\mathbb {P}_2: {{\mathbb {E}}}_{{\mathbb {P}}_2}[\varvec{\xi }_2] = 0, {{\mathbb {E}}}_{{\mathbb {P}}_2}[\varvec{\xi }_2^2] = \sigma _2^2\}. \end{aligned}$$

Clearly, $\varXi =\varXi _1\times \varXi _2$ and ${{\mathcal {P}}}={{\mathcal {D}}}_1\times {{\mathcal {D}}}_2$. Note that $\varvec{\xi }_1$ and $\varvec{\xi }_2$ are not assumed to be independent. $\square$

We are now ready to establish the exactness of optimized Bonferroni approximation under the above condition.

Theorem 3

Under Assumption (A1), $Z=Z_B$.

Proof

We have $Z_B\subseteq Z$ by Theorem 1. It remains to show that $Z\subseteq Z_B$. Given an $x \in Z$, we rewrite the left-hand side of (1d) as

$$\begin{aligned}&\ \inf _{{\mathbb {P}}\in {{\mathcal {P}}}}{\mathbb {P}}\left\{ \varvec{\xi }:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x), \forall i\in [I]\right\} \end{aligned}$$

(8a)

$$\begin{aligned}&\quad = \ \ \inf _{{\mathbb {P}}_i \in {{\mathcal {D}}}_{i},\forall i \in [I]} \ \inf _{{\mathbb {P}}\in {{\mathcal {M}}}({\mathbb {P}}_1, \ldots , {\mathbb {P}}_I)} \ {\mathbb {P}}\left\{ \varvec{\xi }:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x), \forall i\in [I]\right\} \end{aligned}$$

(8b)

$$\begin{aligned}&\quad = \ \ \inf _{\begin{array}{c} {\mathbb {P}}_i \in {{\mathcal {D}}}_i,\forall i\in [I] \end{array}} \ \left[ \sum _{i\in [I]} {\mathbb {P}}_i\left\{ \varvec{\xi }_i:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x)\right\} - (I-1) \right] _+, \end{aligned}$$

(8c)

where equality (8b) decomposes the optimization problem in (8a) into two layers: the outer layer searches for optimal (i.e., worst-case) marginal distributions ${\mathbb {P}}_i \in {{\mathcal {D}}}_i$ for all $i\in [I]$, while the inner layer searches for the worst-case joint probability distribution that admits the given marginals ${\mathbb {P}}_i$. Equality (8c) follows from Theorem 2. Note that our sample space is Euclidean and is hence a Polish space. Since $x \in Z$, the right-hand-side of (8c) is no smaller than $1-\epsilon$. It follows that (8c) is equivalent to

$$\begin{aligned}&\ \inf _{\begin{array}{c} {\mathbb {P}}_i \in {{\mathcal {D}}}_i,\forall i\in [I] \end{array}} \ \left[ \sum _{i\in [I]} {\mathbb {P}}_i\left\{ \varvec{\xi }_i:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x)\right\} - (I-1) \right] \nonumber \\&\quad = \ \sum _{i\in [I]}\inf _{{\mathbb {P}}_i \in {{\mathcal {D}}}_i} \ {\mathbb {P}}_i\left\{ \varvec{\xi }_i:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x)\right\} - (I-1), \end{aligned}$$

(8d)

where equality (8d) is because the ambiguity sets ${{\mathcal {D}}}_i$, $i \in [I]$, are separable by Assumption (A1). Finally, let $s_i: = 1-\inf _{{\mathbb {P}}_i \in {{\mathcal {D}}}_i} \ {\mathbb {P}}_i\left\{ \varvec{\xi }_i:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x)\right\}$ and so $s_i\ge 0$ for all $i \in [I]$. Since $x \in Z$, by (8d), we have

$$\begin{aligned} \sum _{i\in [I]}(1-s_i) - (I-1) \ge 1-\epsilon \end{aligned}$$

which implies $\sum _{i\in [I]} s_i \le \epsilon$. Therefore, $x\in Z_B$. $\square$

The above result establishes that if the ambiguity set of a distributionally robust joint chance constraint is specified in a form that is separable over the uncertain constraints, then the optimized Bonferroni approximation involving a system of distributionally robust single chance constraints is exact. In the next two sections, we investigate two such settings.

3 Ambiguity set based on the first two moments

In this section, we study the computational tractability of optimized Bonferroni approximation when the ambiguity set is specified by the first two moments of the projected random vectors $\{\varvec{\xi }_i\}_{i\in [I]}$. More specifically, for each $i \in [I]$, we make the following assumption on ${{\mathcal {D}}}_i$, the projection of the ambiguity set ${{\mathcal {P}}}$ to the coordinate subspace $\mathcal {S}_i$:

• (A2) The projected ambiguity sets $\{{{\mathcal {D}}}_i\}_{i\in [I]}$ are defined by the first and second moments of $\varvec{\xi }_i$:

  $$\begin{aligned} {{{\mathcal {D}}}_i=\left\{ {\mathbb {P}}_i: {{\mathbb {E}}}_{{\mathbb {P}}_i}[\varvec{\xi }_i]=\mu _i,{{\mathbb {E}}}_{{\mathbb {P}}_i}[(\varvec{\xi }_i-\mu _i)(\varvec{\xi }_i-\mu _i)^{\top }]= \varSigma _i\right\} }, \end{aligned}$$

  (9)

  where $\varSigma _i\succ 0$ for all $i\in [I]$.

Distributionally robust single chance constraints with moment based ambiguity sets as above have been considered in [10, 11].

Next we establish that, in general, it is strongly NP-hard to optimize over set $Z_B$. We will need the following result which shows that set $Z_B$ can be recast as a bi-convex program. This confirms the statement in [27] that for the general joint chance constraints, optimizing variables $s_i$ in Bonferroni approximation “destroys the convexity.”

Lemma 1

Under Assumption (A2), $Z_B$ is equivalent to

$$\begin{aligned}&Z_B = \left\{ x:a_i(x)^{\top }\mu _i +\sqrt{\frac{1-s_i}{s_i}}\sqrt{a_i(x)^{\top }\varSigma _ia_i(x)}\le b_i(x), \forall i\in [I],\sum _{i\in [I]}s_i\le \epsilon , s\ge 0\right\} . \end{aligned}$$

(10)

Proof

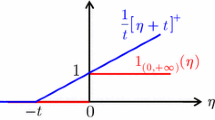
From [11, 39], the chance constraint $\inf _{{\mathbb {P}}_i \in {{\mathcal {D}}}_i} \ {\mathbb {P}}_i\{\varvec{\xi }:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x)\} \ge 1-s_i$ is equivalent to

$$\begin{aligned} a_i(x)^{\top }\mu _i +\sqrt{\frac{1-s_i}{s_i}}\sqrt{a_i(x)^{\top }\varSigma _ia_i(x)}\le b_i(x) \end{aligned}$$

for all $i \in [I]$. Then, the conclusion follows from the definition of $Z_B$.$\square$

Theorem 4

It is strongly NP-hard to optimize over set $Z_B$.

Proof

We prove by using a transformation from the feasibility problem of a binary program. First, we consider set ${\bar{S}}:=\{x\in \{0,1\}^n:Tx\ge d\}$, with given matrix $T \in {\mathbb {Z}}^{\tau \times n}$ and vector $d\in {\mathbb {Z}}^n$, and the following feasibility problem:

$$\begin{aligned} \text{(Binary } \text{ Program): } \text{ Does } \text{ there } \text{ exist } \text{ an } x \in \{0,1\}^n \text{ such } \text{ that } x \in {\bar{S}}\text{? } \end{aligned}$$

(11)

Second, we consider an instance of $Z_B$ with a projected ambiguity set in the form of (9) as

where

$$\begin{aligned} {{\mathcal {D}}}_i=\{{\mathbb {P}}_i: {{\mathbb {E}}}_{{\mathbb {P}}_i}[\varvec{\xi }_i]=0,{{\mathbb {E}}}_{{\mathbb {P}}_i}[\varvec{\xi }_i^2]=1\}, \forall i \in [2n+\tau ], \end{aligned}$$

and $T_{j}$ denotes the jth row of matrix T. It follows from Lemma 1 and Fourier–Motzkin elimination of variables $\{s_i\}_{i\in [2n+\tau ]{\setminus }[2n]}$ that

It is clear that $x_i \in [0, 1]$ for all $x \in Z_B$. Then, by discussing whether $x_i > 0$ and $x_i < 1$ for each $i \in [n]$, we can further recast $Z_B$ as

(12)

Third, for $x \in Z_B$, let $I_1=\{i\in [n]: 1> x_i>0\}$, $I_2=\{i\in [n]: x_i=0\}$, and $I_3=\{i\in [n]: x_i=1\}$, where $|I_1|+|I_2|+|I_3|=n$. Then,

$$\begin{aligned}0.5\ge \sum _{i\in [2n]}s_i \ge \sum _{i \in [n]} \left( \frac{1}{2n}\mathbb {I}(x_i>0) + \frac{1}{2n}\mathbb {I}(x_i<1) \right) = \frac{2|I_1|+|I_2|+|I_3|}{2n} =0.5+\frac{|I_1|}{2n}, \end{aligned}$$

where the first two inequalities are due to (12) and the third equality is due to the definitions of sets $I_1$, $I_2$, and $I_3$. Hence, $|I_1| = 0$ and so $x \in \{0, 1\}^n$ for all $x \in Z_B$. It follows that ${\bar{S}} \supseteq Z_B$. On the other hand, for any $x\in {\bar{S}}$, by letting $s_i= \frac{1}{2n}\mathbb {I}(x_i>0), s_{n+i}= \frac{1}{2n}\mathbb {I}(x_i<1)$, clearly, (x, s) satisfies (12). Thus, ${\bar{S}}=Z_B$, i.e., ${\bar{S}}$ is feasible if and only if $Z_B$ is feasible. Then, the conclusion follows from the strong NP-hardness of (Binary Program). $\square$

Although $Z_B$ is in general computationally intractable, there exist important special cases where $Z_B$ is convex and tractable. In the following theorems, we provide two sufficient conditions for the convexity of $Z_B$. The first condition requires a relatively small risk parameter $\epsilon$ and applies to the setting of uncertain constraint coefficients (i.e., $A^i\ne 0$ for some $i\in [I]$).

Theorem 5

Suppose that Assumption (A2) holds and $B^i=0$ for all $i\in [I]$ and $\epsilon \le \frac{1}{1+(2\sqrt{\eta }+\sqrt{4\eta +3})^2}$, where $\eta =\max _{i\in [I]}\mu _i^{\top }\varSigma _i^{-1}\mu _i$. Then set $Z_B$ is convex and is equivalent to

$$\begin{aligned}&Z_B=\left\{ x:a_i(x)^{\top }\mu _i \le b^i, s_i\ge \frac{a_i(x)^{\top }\varSigma _ia_i(x)}{a_i(x)^{\top }\varSigma _ia_i(x)+\left( b^i-a_i(x)^{\top }\mu _i\right) ^2},\nonumber \right. \\&\left. \quad \forall i\in [I],\sum _{i\in [I]}s_i\le \epsilon , s\ge 0\right\} . \end{aligned}$$

(13)

Proof

First, $b_i(x)=b^i$ because $B^i=0$ for all $i\in [I]$. The reformulation (13) follows from Lemma 1.

Hence, $a_i(x)^{\top }\varSigma _ia_i(x)/[a_i(x)^{\top }\varSigma _ia_i(x)+\left( b^i-a_i(x)^{\top }\mu _i\right) ^2] \le s_i \le \epsilon \le 1/[ 1+(2\sqrt{\eta }+\sqrt{4\eta +3})^2]$. Since $(b^i-a_i(x)^{\top }\mu _i) \ge 0$, we have

$$\begin{aligned} \frac{b^i-a_i(x)^{\top }\mu _i}{\sqrt{a_i(x)^{\top }\varSigma _ia_i(x)}} \ge 2\sqrt{\eta }+\sqrt{4\eta +3}. \end{aligned}$$

(14a)

Hence, to show the convexity of $Z_B$, it suffices to show that the function $a_i(x)^{\top }\varSigma _ia_i(x)/[a_i(x)^{\top }\varSigma _ia_i(x)+\left( b^i-a_i(x)^{\top }\mu _i\right) ^2]$ is convex when x satisfies (14a). To this end, we let $z_i:=\varSigma _i^{1/2}a_i(x)$, $q_i:=\varSigma _i^{-1/2}\mu _i$, and $k_i := (b^i-a_i(x)^{\top }\mu _i)/\sqrt{a_i(x)^{\top }\varSigma _ia_i(x)} = (b^i-q_i^{\top }z_i)/\sqrt{z_i^{\top }z_i}$. Then, $k_i \ge 2\sqrt{\eta }+\sqrt{4\eta +3}$. Since $a_i(x)$ is affine in the variables x, it suffices to show that the function

$$\begin{aligned} f_i(z_i)=\frac{z_i^{\top }z_i}{z_i^{\top }z_i+\left( b^i-z_i^{\top }q_i\right) ^2} \end{aligned}$$

is convex in variables $z_i$ when $k_i :=(b^i-q_i^{\top }z_i)/\sqrt{z_i^{\top }z_i} \ge 2\sqrt{\eta }+\sqrt{4\eta +3}$. To this end, we consider the Hessian of $f_i(z_i)$, denoted by $Hf_i(z_i)$, and show that $r^{\top }Hf_i(z_i)r \ge 0$ for an arbitrary $r \in \mathbb {R}^{m_i}$. Standard calculations yield

$$\begin{aligned} r^{\top }Hf_i(z_i)r&= \ 2\left( z_i^{\top }z_i+\left( b^i-z_i^{\top }q_i\right) ^2\right) ^{-3}\left\{ z_i^{\top }z_i\left[ \left( b^i-z_i^{\top }q_i\right) ^2 r^{\top }r-z_i^{\top }z_i(q_i^{\top }r)^2\right. \right. \nonumber \\&\quad \left. \left. -4\left( b^i-z_i^{\top }q_i\right) (q_i^{\top }r) (z_i^{\top }r)+3\left( b^i-z_i^{\top }q_i\right) ^2(q_i^{\top }r)^2\right] \right. \nonumber \\&\quad \left. +\left( b^i-z_i^{\top }q_i\right) ^2\left[ r^{\top }r\left( b^i-z_i^{\top }q_i\right) ^2-4(z_i^{\top }r)^2\nonumber \right. \right. \\&\quad \left. \left. +4\left( b^i-z_i^{\top }q_i\right) (q_i^{\top }r) (z_i^{\top }r)\right] \right\} \nonumber \\&= \ 2\left( z_i^{\top }z_i+\left( b^i-z_i^{\top }q_i\right) ^2\right) ^{-3}\bigl [ (k_i^4 + k_i^2) (z_i^{\top }z_i)^2 (r^{\top }r) - 4k_i^2 (z_i^{\top }z_i)(z_i^{\top }r)^2 \nonumber \\&\quad + (3k_i^2-1)(z_i^{\top }z_i)^2 (q_i^{\top }r)^2 + (4k_i^3 - 4k_i) (z_i^{\top }z_i)^{3/2} (q_i^{\top }r) (z_i^{\top }r) \bigr ] \end{aligned}$$

(14b)

$$\begin{aligned}&\ge \quad 2\left( z_i^{\top }z_i+\left( b^i-z_i^{\top }q_i\right) ^2\right) ^{-3}\Bigl [ (k_i^4 + k_i^2) (z_i^{\top }z_i)^2 (r^{\top }r) - 4k_i^2 (z_i^{\top }z_i)^2(r^{\top }r) \nonumber \\&\quad - (4k_i^3 - 4k_i)\sqrt{q_i^{\top }q_i} (z_i^{\top }z_i)^2(r^{\top }r) \Bigr ] \end{aligned}$$

(14c)

$$\begin{aligned}&\ge \quad 2\left( z_i^{\top }z_i+\left( b^i-z_i^{\top }q_i\right) ^2\right) ^{-3} (z_i^{\top }z_i)^2 (r^{\top }r) {k_i^2}\left( k_i^2 -4k_i\sqrt{q_i^{\top }q_i}-3\right) \end{aligned}$$

(14d)

$$\begin{aligned}&\ge \ 0 \end{aligned}$$

(14e)

for all $r \in \mathbb {R}^{m_i}$. Above, equality (14b) is from the definition of $k_i$; inequality (14c) follows from $3k_i^2 \ge 1,(4k_i^3 - 4k_i)\ge 0$ and the Cauchy-Schwarz inequalities $z_i^{\top }r \le \sqrt{z_i^{\top }z_i}\sqrt{r^{\top }r}$ and $q_i^{\top }r \le \sqrt{q_i^{\top }q_i}\sqrt{r^{\top }r}$; inequality (14d) is due to the fact $k_i \ge 0$; and inequality (14e) is because $k_i \ge 2\sqrt{\eta }+\sqrt{4\eta +3} \ge 2\sqrt{q_i^{\top }q_i}+\sqrt{4q_i^{\top }q_i+3}$. $\square$

The second condition does not require a small risk parameter $\epsilon$ but is only applicable when the constraint coefficients are not affected by the uncertain parameters (right-hand side uncertainty), i.e. $A^i= 0$ for all $i\in [I]$.

Theorem 6

Suppose that Assumption (A2) holds. Further assume that $A^i=0$ for all $i\in [I]$ and $\epsilon \le 0.75$. Then the set $Z_B$ is convex and is equivalent to

$$\begin{aligned}&Z_B=\left\{ x:(a^i)^{\top }\mu _i +\sqrt{\frac{1-s_i}{s_i}}\sqrt{(a^i)^{\top }\varSigma _ia^i}\le b_i(x), \forall i\in [I],\sum _{i\in [I]}s_i\le \epsilon , s\ge 0\right\} . \end{aligned}$$

(15)

Proof

For all $i \in [I]$, $a_i(x) = a^i$ because $A^i = 0$. Thus, the reformulation (15) follows from Lemma 1. Hence, to show the convexity of $Z_B$, it suffices to show that function $\sqrt{(1 - s_i)/s_i}$ is convex in $s_i$ for $0 \le s_i \le \epsilon$. This follows from the fact that

$$\begin{aligned} \frac{d^2}{ds_i^2}\left( \sqrt{\frac{1 - s_i}{s_i}} \right) = \frac{0.75-s_i}{(1-s_i)^{3/2}s_i^{5/2}} \ \ge \ 0 \end{aligned}$$

because $0 \le s_i \le \epsilon \le 0.75$. $\square$

The following example illustrate that $Z_B$ is convex when condition of Theorem 5 holds and becomes non-convex when this condition does not hold.

Example 5

Consider set $Z_B$ with regard to a projected ambiguity set in the form of (9),

$$\begin{aligned} Z_B = \left\{ x: \begin{array}{c}\inf _{{\mathbb {P}}_1 \in {{\mathcal {D}}}_1} {\mathbb {P}}_1\left\{ \varvec{\xi }_1: x_1\varvec{\xi }_1\le 1\right\} \ge 1-s_1\\ \inf _{{\mathbb {P}}_2 \in {{\mathcal {D}}}_2} {\mathbb {P}}_2\left\{ \varvec{\xi }_2: x_2\varvec{\xi }_2\le 1\right\} \ge 1-s_2\\ s_1+s_2\le \epsilon \\ s_1,s_2\ge 0 \end{array}\right\} \end{aligned}$$

where

$$\begin{aligned} {{\mathcal {D}}}_1 = \left\{ {\mathbb {P}}_1: {{\mathbb {E}}}_{{\mathbb {P}}_1}[\varvec{\xi }_1]=0, {{\mathbb {E}}}_{{\mathbb {P}}_1}[\varvec{\xi }_1^2]=1\right\} , {{\mathcal {D}}}_2 = \left\{ {\mathbb {P}}_2: {{\mathbb {E}}}_{{\mathbb {P}}_2}[\varvec{\xi }_2]=0, {{\mathbb {E}}}_{{\mathbb {P}}_2}[\varvec{\xi }_2^2]=1\right\} \end{aligned}$$

Projecting out variables $s_1,s_2$ yields

$$\begin{aligned} Z_B=\left\{ x\in {{\mathbb {R}}}^2:\frac{x_1^2}{x_1^2+1}+\frac{x_2^2}{x_2^2+1}\le \epsilon \right\} . \end{aligned}$$

We depict $Z_B$ in Fig. 2 with $\epsilon = 0.25$, 0.50, and 0.75, respectively, where the dashed line denotes the boundary of of $Z_B$ for each $\epsilon$. Note that $Z_B$ is convex when $\epsilon = 0.25$ and becomes non-convex when $\epsilon = 0.50, 0.75$. As $\eta = \max _{i \in [I]}\mu _i^{\top } \varSigma _i \mu _i = 0$, this figure confirms the sufficient condition of Theorem 5 that $Z_B$ is convex when $\epsilon \le \frac{1}{1+(2\sqrt{\eta }+\sqrt{4\eta +3})^2} = 0.25$. $\square$

Fig. 2

Illustration of Example 5

Finally, we note that when either conditions of Theorems 5 or 6 hold, $Z_B$ is not only convex but also computationally tractable. This observation follows from the classical result in [15] on the equivalence between tractable convex programming and the separation of a convex set from a point.

Theorem 7

Under Assumption (A2), suppose that set S is closed and compact, and it is equipped with an oracle that can, for any $x \in \mathbb {R}^n$, either confirm $x \in S$ or provide a hyperplane that separates x from S in time polynomial in n. Additionally, suppose that either conditions of Theorems 5 or 6 holds. Then, for any $\alpha \in (0, 1)$, one can find an $\alpha$-optimal solution to the optimized Bonferroni approximation of $Z$, i.e., formulation $\min _x\{c^{\top }x: x \in S \cap Z_B\}$, in time polynomial in $\log (1/\alpha )$ and the size of the formulation.

Proof

We prove the conclusion when condition of Theorem 5 holds. The proof for the condition of Theorem 6 is similar and is omitted here for brevity.

Since S is convex by assumption and $Z_B$ is convex by Theorem 5, the conclusion follows from Theorem 3.1 in [15] if we can show that there exists an oracle that can, for any $x \in \mathbb {R}^n$, either confirm $x \in Z_B$ or provide a hyperplane that separates x from $Z_B$ in time polynomial in n. To this end, from the proof of Theorem 5, we note that $Z_B$ can be recast as

$$\begin{aligned} Z_B=\left\{ x:a_i(x)^{\top }\mu _i \le b^i, \ \forall i \in [I], \ \sum _{i \in [I]} \frac{a_i(x)^{\top }\varSigma _ia_i(x)}{a_i(x)^{\top }\varSigma _ia_i(x)+\left( b^i-a_i(x)^{\top }\mu _i\right) ^2} \le \epsilon \right\} . \nonumber \\ \end{aligned}$$

(17)

All constraints in (17) are linear except $\sum _{i\in [I]} g_i(x) \le \epsilon$, where $g_i(x) := a_i(x)^{\top }\varSigma _ia_i(x)/[a_i(x)^{\top }\varSigma _ia_i(x)+\left( b^i-a_i(x)^{\top }\mu _i\right) ^2]$. On the one hand, whether $\sum _{i \in [I]} g_i(x) \le \epsilon$ can be confirmed by a direct evaluation of $g_i(x)$, $i \in [I]$, in time polynomial in n. On the other hand, for an ${\widehat{x}}$ such that $\sum _{i \in [I]} g_i({\widehat{x}}) > \epsilon$, the following separating hyperplane can be obtained in time polynomial in n:

$$\begin{aligned} \epsilon \ge \sum _{i \in [I]} \left\{ g_i({\widehat{x}}) + \frac{2(b^i - q_i^{\top }{\widehat{z}}_i)}{[{\widehat{z}}_i^{\top }{\widehat{z}}_i + (b^i - q_i^{\top }{\widehat{z}}_i)^2]^2} \left[ (b^i - q_i^{\top }{\widehat{z}}_i) {\widehat{z}}_i + ({\widehat{z}}_i^{\top }{\widehat{z}}_i) q_i \right] ^{\top } \varSigma _i^{1/2} A^i (x - {\widehat{x}}) \right\} , \end{aligned}$$

where ${\widehat{z}}_i = \varSigma ^{1/2}_i (A^i{\widehat{x}} + a^i)$ and $q_i = \varSigma ^{-1/2}_i \mu _i$. $\square$

4 Ambiguity set based on marginal distributions

In this section, we study the computational tractability of the optimized Bonferroni approximation when the ambiguity set is characterized by the (known) marginal distributions of the projected random vectors. More specifically, we make the following assumption on ${{\mathcal {D}}}_i$.

• (A3) The projected ambiguity sets $\{{{\mathcal {D}}}_i\}_{i\in [I]}$ are characterized by the marginal distributions of $\varvec{\xi }_i$, i.e., ${{\mathcal {D}}}_i = \{{\mathbb {P}}_i\}$, where ${\mathbb {P}}_i$ represents the probability distribution of $\varvec{\xi }_i$.

We first note that ${{\mathcal {D}}}_i$ is a singleton for all $i \in [I]$ under Assumption (A3). By the definition of Bonferroni approximation (5), $Z_B$ is equivalent to

$$\begin{aligned} Z_B=\left\{ x:{\mathbb {P}}_i\left\{ \varvec{\xi }_i:a_i(x)^{\top }\varvec{\xi }_i\le b_i(x)\right\} \ge 1-s_i, \forall i\in [I],\sum _{i\in [I]}s_i\le \epsilon , s\ge 0\right\} .\nonumber \\ \end{aligned}$$

(18)

Next, we show that optimizing over $Z_B$ in the form of (18) is computationally intractable. In particular, the corresponding optimization problem is strongly NP-hard even if $m_i = 1$, $A^i = 0$, and $a^i = 1$ for all $i \in [I]$, i.e., only right-hand side uncertainty.

Theorem 8

Under Assumption (A3), suppose that $m_i = 1$, $A^i = 0$, and $a^i = 1$ for all $i \in [I]$. Then, it is strongly NP-hard to optimize over set $Z_B$.

Proof

Similar to the proof of Theorem 4, we consider set ${\bar{S}}=\{x\in \{0,1\}^n:Tx\ge d\}$, with given matrix $T \in \mathbb {Z}^{\tau \times n}$ and vector $d \in \mathbb {R}^n$, and show the reduction from (Binary Program) defined in (11). Second, we consider an instance of $Z_B$ with a projected ambiguity set satisfying Assumption (A3) as

where

$$\begin{aligned} {{\mathcal {D}}}_i=\{{\mathbb {P}}_i: \varvec{\xi }\sim \mathcal {B}(1,1/(2n))\}, \forall i \in [2n+\tau ], \end{aligned}$$

and $\mathcal {B}(1,p)$ denotes Bernoulli distribution with probability of success equal to p. It follows from (18) and Fourier–Motzkin elimination of variables $\{s_i\}_{i\in [2n+\tau ]{\setminus }[2n]}$ that

Following a similar proof as that of Theorem 4, we can show that ${\bar{S}} = Z_B$, i.e., ${\bar{S}}$ is feasible if and only if $Z_B$ is feasible. Then, the conclusion follows from the strong NP-hardness of (Binary Program) in (11). $\square$

Next, we identify two important sufficient conditions where $Z_B$ is convex. Similar to Theorem 5, the first condition holds for left-hand uncertain constraints with a small risk parameter $\epsilon$.

Theorem 9

Suppose that Assumption (A3) holds and $B^i=0$ and $\varvec{\xi }_i\sim {{\mathcal {N}}}(\mu _i,\varSigma _i)$ for all $i\in [I]$ and $\epsilon \le \frac{1}{2}-\frac{1}{2}{{\,\mathrm{erf}\,}}\left( \sqrt{\eta }+\sqrt{\eta +0.75}\right)$, where $\eta =\max _{i\in [I]}\mu _i^{\top }\varSigma _i^{-1}\mu _i$ and ${{\,\mathrm{erf}\,}}(\cdot ),{{\,\mathrm{erf}\,}}^{-1}(\cdot )$ denote the error function and its inverse, respectively. Then the set $Z_B$ is convex and is equivalent to

Proof

First, $b_i(x)=b^i$ because $B^i=0$ for all $i\in [I]$. Since $\varvec{\xi }_i\sim {{\mathcal {N}}}(\mu _i,\varSigma _i)$ for all $i\in [I]$, it follows from (18) that $Z_B$ is equivalent to (19).

Let $f_i(x):=a_i(x)^{\top }\varSigma _ia_i(x)/[a_i(x)^{\top }\varSigma _ia_i(x)+(b^i-a_i(x)^{\top }\mu _i)^2]$. Since $\epsilon \le \frac{1}{2}-\frac{1}{2}{{\,\mathrm{erf}\,}}\left( \sqrt{\eta }+\sqrt{\eta +0.75}\right)$ and $s_i\le \epsilon$, thus we have $f_{i}(x)\le 1/[1+(2\sqrt{\eta }+\sqrt{4\eta +3})^2]$. Hence, from the proof of Theorem 5, $f_i(x)$ is convex in $x\in Z_B$. Hence, it remains to show that $G(s_i):=1/[1+2\left( {{\,\mathrm{erf}\,}}^{-1}(1-2s_i)\right) ^2]$ is concave in variable $s_i$ when $s_i \in [0,\epsilon ]$. This is indeed so because

$$\begin{aligned} \frac{d^2G(s_i)}{ds_i^2}=-\frac{4\pi e^{2 {{\,\mathrm{erf}\,}}^{-1}(1 - 2 s_i)^2} \left[ 1 - 2 {{\,\mathrm{erf}\,}}^{-1}(1 - 2 s_i)^2\right] ^2}{\left[ 1 + 2 {{\,\mathrm{erf}\,}}^{-1}(1 - 2 s_i)^2\right] ^3} \le 0 \end{aligned}$$

for all $0 \le s_i \le \epsilon$. $\square$

Note that if $\mu _i=0$ for each $i\in [I]$, then $\eta =0$ and the threshold in Theorem 9 is $\frac{1}{2}-\frac{1}{2}{{\,\mathrm{erf}\,}}\left( \sqrt{0.75}\right) \approx 0.11$.

Similar to Theorem 6, the second condition only holds for right-hand uncertain constraints with a relatively large risk parameter $\epsilon$. We need the notion “concave point” (see [31]) for the next result. If $F(\cdot )$ represents the cumulative distribution function of a random variable $\varvec{\xi }$, then the concave point r of F represents the minimal value such that F is concave in the domain $[r,\infty )$. Please see Table 1 in [9] for examples of the concave points of some commonly used distributions.

Theorem 10

Suppose that Assumption (A3) holds and $m_i = 1$, $A^i = 0$, $a^i = 1$ for all $i\in [I]$ and $\epsilon \le \min _{i\in [I]}\{1-F_i(r_i)\}$, where $F_i(\cdot )$ represents the cumulative distribution function of $\varvec{\xi }_i$ and $r_i$ represents its concave point. Then the set $Z_B$ is convex and is equivalent to

$$\begin{aligned}&Z_B=\left\{ x: F_i(b_i(x))\ge 1-s_i, \forall i\in [I],\sum _{i\in [I]}s_i\le \epsilon , s\ge 0\right\} . \end{aligned}$$

(20)

Proof

By assumption, $\varvec{\xi }_i$ is a 1-dimensional random variable and so $Z_B$ is equivalent to (20). Since $s_i \le \epsilon$, $\epsilon \le 1 - F_i(r_i)$ by assumption, and $b_i(x)$ is affine in x, it follows that the constraint $F_i(b_i(x))\ge 1-s_i$ is convex. Thus $Z_B$ is convex.$\square$

Similar to Theorem 7, we note that when either the condition of Theorem 9 holds or that of Theorem10 holds, the set $Z_B$ is not only convex but also computationally tractable. We summarize this result in the following theorem and omit its proof.

Theorem 11

Under Assumption (A3), suppose that set S is closed and compact, and it is equipped with an oracle that can, for any $x \in \mathbb {R}^n$, either confirm $x \in S$ or provide a hyperplane that separates x from S in time polynomial in n. Additionally, suppose that either condition of Theorem 9 or that of Theorem10 holds. Then, for any $\alpha \in (0, 1)$, one can find an $\alpha$-optimal solution to the problem $\min _x\{c^{\top }x: x \in S \cap Z_B\}$, in time polynomial in $\log (1/\alpha )$ and the size of the formulation.

When modeling constraint uncertainty, besides the (parametric) probability distributions mentioned in Table 1 in [9], a nonparametric alternative employs the empirical distribution of $\varvec{\xi }$ that can be directly established from the historical data. In the following theorem, we consider right-hand side uncertainty with discrete empirical distributions and show that the optimized Bonferroni approximation can be recast as a mixed-integer linear program (MILP).

Theorem 12

Suppose that Assumption (A3) holds and $m_i=1$, $A^i=0$, and $a^i=1$ for all $i \in [I]$. Additionally, suppose that ${\mathbb {P}}\{\varvec{\xi }_i = \xi _i^{j}\} = p_i^j$ for all $j \in [N_i]$ such that $\sum _{j\in [N_i]}p_i^j = 1$ for all $i \in [I]$, and $\{\xi _i^j\}_{j \in [N_i]} \subset {{\mathbb {R}}}_+$ is sorted in the ascending order. Then,

Proof

By (18), $x \in Z_B$ if and only if there exists an $s_i \ge 0$ such that ${\mathbb {P}}_i\{\varvec{\xi }_i \le B^ix + b^i\} \ge 1 - s_i$, $i \in [I]$, and $\sum _{i\in [I]} s_i \le \epsilon$. Hence, it suffices to show that ${\mathbb {P}}_i\{\varvec{\xi }_i \le B^ix + b^i\} \ge 1 - s_i$ is equivalent to constraints (21a)–(21d).

To this end, we note that nonnegative random variable $\varvec{\xi }_i$ takes value $\xi _i^j$ with probability $p_i^j$, and so ${\mathbb {P}}_i\{\varvec{\xi }_i \le \xi _i^j\} = \sum _{t\in [j]}p_i^{t}$ for all $j \in [N_i]$. It follows that ${\mathbb {P}}_i\{\varvec{\xi }_i \le B^ix + b^i\} \ge 1 - s_i$ holds if and only if $1 - s_i \le \sum _{t\in [j]}p_i^{t}$ whenever $B^ix+b^i \ge \xi _i^j$. Then, we introduce additional binary variables $\{z_i^j\}_{j \in [N_i],i\in [N]}$ such that $z_i^j = 1$ when $B^ix+b^i\ge \xi _i^j$ and $z_i^j = 0$ otherwise. It follows that ${\mathbb {P}}_i\{\varvec{\xi }_i \le B^ix + b^i\} \ge 1 - s_i$ is equivalent to constraints 21a–21d. $\square$

Remark 3

The nonegativity assumption of $\{\xi _i^j\}_{j \in [N_i]}$ for each $i\in [I]$ can be relaxed. If not, then for each $i\in [I]$ we can subtract $M_i$, where $M_i:=\min _{j \in [N_i]}\xi _i^j$, from $\{\xi _i^j\}_{j \in [N_i]}$ and the right-hand side of uncertain constraint $B^ix + b^i$, i.e., $\xi _i^j:=\xi _i^j-M_i$ for each $j\in [N_i]$ and $B^ix + b^i:=B^ix + b^i-M_i$.

We close this section by demonstrating that $Z_B$ may not be convex when the condition of Theorem 10 does not hold.

Example 6

Consider set $Z_B$ with regard to a projected ambiguity set satisfying Assumption (A3),

$$\begin{aligned}Z_B = \left\{ x\in {{\mathbb {R}}}^2: \begin{array}{c} \inf _{{\mathbb {P}}_1 \in {{\mathcal {D}}}_1} {\mathbb {P}}_1\left\{ \varvec{\xi }_1: \varvec{\xi }_1\le x_1\right\} \ge 1-s_1\\ \inf _{{\mathbb {P}}_2 \in {{\mathcal {D}}}_2} {\mathbb {P}}_2\left\{ \varvec{\xi }_2: \varvec{\xi }_2\le x_1\right\} \ge 1-s_2\\ \inf _{{\mathbb {P}}_3 \in {{\mathcal {D}}}_3} {\mathbb {P}}_3\left\{ \varvec{\xi }_3: \varvec{\xi }_3\le x_2\right\} \ge 1-s_3\\ s_1+s_2+s_3\le \epsilon \\ s_1,s_2,s_3\ge 0 \end{array}\right\} \end{aligned}$$

where

$$\begin{aligned} {{\mathcal {D}}}_1 = \left\{ {\mathbb {P}}_1: \varvec{\xi }_1\sim {{\mathcal {N}}}(0,1)\right\} , {{\mathcal {D}}}_2 = \left\{ {\mathbb {P}}_2: \varvec{\xi }_2\sim {{\mathcal {N}}}(0,1)\right\} , \ \text { and } \ {{\mathcal {D}}}_3 = \left\{ {\mathbb {P}}_3: \varvec{\xi }_3\sim {{\mathcal {N}}}(0,1)\right\} \end{aligned}$$

with standard normal distribution ${{\mathcal {N}}}(0,1)$. Projecting out variables $s_1,s_2,s_3$ yields

$$\begin{aligned} Z_B=\left\{ x\in {{\mathbb {R}}}^2:2{{\,\mathrm{erf}\,}}\left( \frac{x_1}{\sqrt{2}}\right) +{{\,\mathrm{erf}\,}}\left( \frac{x_2}{\sqrt{2}}\right) \ge 2-2\epsilon \right\} . \end{aligned}$$

We depict $Z_B$ in Fig. 3 with $\epsilon = 0.25$, 0.50, and 0.75, respectively, where the dashed line denotes the boundary of $Z_B$ for each $\epsilon$. Note that this figure confirms condition of Theorem 10 that for normal random variables $\{\varvec{\xi }_i\}$, $Z_B$ is convex if $\epsilon \le 0.5$ but may not be convex otherwise. $\square$

Fig. 3

Illustration of Example 6

5 Binary decision variables and moment-based ambiguity sets

In this section, we focus on the projected ambiguity sets specified by first two moments as in Assumption (A2) and also assume that all decision variables x are binary, i.e., $S \subseteq \{0,1\}^n$. Distributionally robust joint chance constrained optimization involving binary decision variables arise in a wide range of applications including the multi-knapsack problem (cf. [8, 44]) and the bin packing problem (cf. [38, 45]). In this case, $Z_B$ is naturally non-convex due to the binary decision variables. Our goal, however, is to recast $S\cap Z_B$ as a mixed-integer second-order conic set (MSCS), which facilitates efficient computation with commercial solvers like GUROBI and CPLEX.

First, we show that $S \cap Z_B$ can be recast as an MSCS in the following result.

Theorem 13

Under Assumption (A2), suppose that $S \subseteq \{0, 1\}^n$. Then, $S\cap Z_B=S\cap \widehat{Z}_B$, where

Proof

By Lemma 1, we recast $Z_B$ as

It is sufficient to linearize $(b_i(x) -a_i(x)^{\top }\mu _i )^2+a_i(x)^{\top }\varSigma _ia_i(x)$ in the extended space for each $i\in [I]$. To achieve this, we introduce additional continuous variables $t_i:=(b_i(x) -a_i(x)^{\top }\mu _i )^2+a_i(x)^{\top }\varSigma _ia_i(x)$, $i \in [I]$, as well as additional binary variables $w:=xx^{\top }$ and linearize them by using McCormick inequalities (see [26]), i.e.,

$$\begin{aligned} w_{jk} \ge x_{j}+x_{k}-1,0\le w_{jk}\le x_{j},w_{jk}\le x_{k},\forall j,k\in [n] \end{aligned}$$

which lead to reformulation (22). $\square$

The reformulation of $S\cap Z_B$ in Theorem 13 incorporates $n^2$ auxiliary binary variables $\{w_{jk}\}_{j, k \in [n]}$. Next, under an additional assumption that $\epsilon \le 0.25$, we show that it is possible to obtain a more compact reformulation by incorporating $n\times I$ auxiliary continuous variables when $I<n$.

Theorem 14

Under Assumption (A2), suppose that $S \subseteq \{0, 1\}^n$ and $\epsilon \le 0.25$. Then, $S\cap Z_B=S\cap \bar{Z}_B$, where

where vector $q_{i\cdot } := [q_{i1}, \ldots , q_{in}]^{\top }$ for all $i \in [I]$.

Proof

By Lemma 1, we recast $Z_B$ as

We note that nonlinear constraints (24b) hold if and only if there exist $\{r_i\}_{i \in [I]}$ such that $0 \le r_i \le \sqrt{s_i/(1-s_i)}$ and $\sqrt{a_i(x)^{\top }\varSigma _ia_i(x)}\le r_i(b_i(x) -a_i(x)^{\top }\mu _i)$ for all $i \in [I]$. Note that $s_i \in [0, \epsilon ]$ and so $r_i \le \sqrt{s_i/(1-s_i)} \le \sqrt{\epsilon /(1-\epsilon )}$. Defining n-dimensional vectors $q_{i\cdot } := r_i x$, $i \in [I]$, we recast constraints (24b) as (23b), (23d)–(23f), where constraints (23e) are McCormick inequalities that linearize products $r_i x$. Note that constraints (23d) characterize a convex feasible region because $0 \le s_i \le \epsilon \le 0.25$ and so $\sqrt{s_i/(1-s_i)}$ is concave in $s_i$. $\square$

Remark 4

When solving the optimized Bonferroni approximation as a mixed-integer convex program based on reformulation (23), we can incorporate the supporting hyperplanes of constraints (23d) as valid inequalities in a branch-and-cut algorithm. In particular, for given ${\widehat{s}} \in [0, \epsilon ]$, the supporting hyperplane at point $({\widehat{s}}, \sqrt{{\widehat{s}}/(1-{\widehat{s}})})$ is

$$\begin{aligned} r_i \le \left[ \frac{1}{2}{\widehat{s}}^{-1/2}(1-{\widehat{s}})^{-3/2}\right] s_i + {\widehat{s}}^{1/2} (1-{\widehat{s}})^{-3/2} \Bigl (\frac{1}{2}-{\widehat{s}}\Bigr ). \end{aligned}$$

(25a)

Remark 5

We can construct inner and outer approximations of reformulation (23) by relaxing and restricting constraints (23d), respectively. More specifically, constraints (23d) imply $r_i \le \sqrt{s_i/(1-\epsilon )}$ because $s_i \le \epsilon$ for all $i\in [I]$. It follows that constraints (23d) imply the second-order conic constraints

$$\begin{aligned}&\left| \left| \begin{bmatrix} r_i \\ \frac{s_i-(1 - \epsilon )}{2(1 - \epsilon )} \end{bmatrix} \right| \right| \le \frac{s_i+(1 - \epsilon )}{2(1 - \epsilon )}, \forall i \in [I] . \end{aligned}$$

(25b)

In the branch-and-cut algorithm, we could start by relaxing constraints (23d) as (25b) and then iteratively incorporate valid inequalities in the form of (25a). In contrast to (25b), we can obtain a conservative approximation of constraints (23d) by noting that these constraints hold if $r_i \le \sqrt{s_i}$. It follows that constraints (23d) are implied by the second-order conic constraints

$$\begin{aligned}&\left| \left| \begin{bmatrix} r_i \\ \frac{s_i-1}{2} \end{bmatrix} \right| \right| \le \frac{s_i+1}{2}, \forall i \in [I]. \end{aligned}$$

(25c)

Hence, we obtain an inner approximation of Bonferroni approximation by replacing constraints (23d) with (25c).

5.1 Numerical study

In this subsection, we present a numerical study to compare the MCSC reformulation in Theorem 13 with another MCSC reformulation proposed by [44] on the distributionally robust multidimensional knapsack problem (DRMKP) [8, 38, 44]. In DRMKP, there are n items and I knapsacks. Additionally, $c_j$ represents the value of item j for all $j \in [n]$, $\varvec{\xi }_i := [\xi _{i1}, \ldots , \xi _{in}]^{\top }$ represents the vector of random item weights in knapsack i, and $b^i$ represents the capacity limit of knapsack i, for all $i \in [I]$. The binary decision variable $x_j=1$ if the jth item is picked and 0 otherwise. We suppose that the ambiguity set is separable and satisfies Assumption (A2). DRMKP is formulated as

$$\begin{aligned} v^* = \max _{x\in \{0,1\}^n} \quad&c^{\top }x,\nonumber \\ \mathrm{s.t.}\quad&\inf _{{\mathbb {P}}\in {{\mathcal {P}}}}{\mathbb {P}}\left\{ \varvec{\xi }_i^{\top }x\le b^i,{\forall i\in [I]}\right\} \ge 1-\epsilon . \end{aligned}$$

(26)

We generate 10 random instances with $n=20$ and $I=10$. For each $i \in [I]$ and each $j \in [n]$, we independently generate $\mu _{ij}$ and $c_j$ from the uniform distribution on the interval [1, 10]. Additionally, for each $i \in [I]$, we set $b^i := 100$ and $\varSigma _i := 10I_{20}$, where $I_{20}$ represents the $20\times 20$ identity matrix. We test these 10 random instances with risk parameter $\epsilon \in \{0.05,0.10\}$.

Our first approach is to solve the MCSC reformulation of DRMKP in Theorem 13, which reads as follows:

$$\begin{aligned} v^* = \max _{x\in \{0,1\}^n} \quad&c^{\top }x,\nonumber \\ \mathrm{s.t.}\quad&\mu _i^{\top }x\le b^i,i\in [I],\nonumber \\&\left| \left| \begin{bmatrix} 2\varSigma _i^{1/2}x \\ s_i - t_i \end{bmatrix} \right| \right| \le s_i + t_i, i \in [I], \nonumber \\&t_i \le \left( b^i\right) ^2 -2b^i\mu _i^{\top }x+ \langle \mu _i\mu _i^{\top }+\varSigma _i, w\rangle , i \in [I], \nonumber \\&\sum _{i\in [I]}s_i\le \epsilon ,\nonumber \\&w_{jk} \ge x_{j}+x_{k}-1,0\le w_{jk}\le x_{j},w_{jk}\le x_{k},\forall j,k\in [n],\nonumber \\&s_i\ge 0, t_i \ge 0, \forall i\in [I]. \end{aligned}$$

(27)

We compare our approach with another MCSC reformulation of DRMKP proposed by [44] (see Example 4 in [44]), which is as follows:

$$\begin{aligned} v^* = \max _{x\in \{0,1\}^n}&c^{\top }x,\nonumber \\ \text {s.t. }&\lambda -\sum _{j\in [I]}\left<\varSigma _{j},w_{\cdot \cdot j}\right>\ge 1-\epsilon ,\nonumber \\&\lambda +\sum _{j\in [I]}t_{0j}\le 1,\nonumber \\&\lambda +\sum _{j\in [I]}t_{ij}\le \alpha _i b^i- \mu _i^{\top }y^i,\forall i \in [I],\nonumber \\&\gamma _{1j}^2\le 4 t_{ij}\gamma _{2j} ,\forall i\in [I],j\in [I]{\setminus } \{i\},\nonumber \\&(\gamma _{1i}-\alpha _i)^2\le 4 t_{ii}\gamma _{2i}, \forall i \in [I],\nonumber \\&\gamma _{1j}^2\le 4t_{0j}\gamma _{2j} ,\forall j\in [I],\nonumber \\&0\le y^i_j\le M_{i}x_j,\alpha _i-M_{i}(1-x_j)\le y^i_j\le \alpha _i,\forall i\in [I],j\in [n],\nonumber \\&0\le w_{ikj}\le \frac{\epsilon }{\underline{\delta }\eta }x_i,0\le w_{ikj}\le \frac{\epsilon }{\underline{\delta }\eta }x_k,\nonumber \\&\gamma _{2j}-\frac{\epsilon }{\underline{\delta }\eta }(2-x_i-x_k)\le w_{ikj}\le \gamma _{2j},\forall i,k\in [n],j\in [I]\nonumber \\&\gamma _{2i} \ge 0, \alpha _i\ge 0, \forall i\in [I], \end{aligned}$$

(28)

where

$$\begin{aligned} M_i= \frac{4\epsilon }{\underline{\delta }\eta }\left[ (b^i+\Vert \mu _i\Vert _1)+\sqrt{(b^i+\Vert \mu _i\Vert _1)^2+\underline{\delta }\eta -\frac{\underline{\delta }\eta }{2\epsilon }}\right] \end{aligned}$$

for each $i\in [I]$ with $\eta =\min _{x\in \{0,1\}^n: x\ne 0}\Vert x\Vert _2^2=1$ and $\underline{\delta }$ the smallest eigenvalue of matrices $\{\varSigma _{j}\}_{j\in [I]}$. Note that [44] did not explore the separability of the formulation and the ambiguity set, leading to the MCSC reformulation (28) with big-M coefficients and more variables.

We use the commercial solver Gurobi (version 7.5, with default settings) to solve all the instances to optimality using both formulations. The results are displayed in Table 1. We use Opt. Val. and Time to denote the optimal objective value and the total running time, respectively. All instances were executed on a MacBook Pro with a 2.80 GHz processor and 16 GB RAM.

Table 1 Performance comparison of Model (27) and Model (28)

From Table 1, we observe that the overall running time of our new MCSC reformulation (27) significantly outperforms that of (28) proposed in [44]. The main reasons are two-fold: (i) Model (28) involves $\mathcal {O}(n^2I)$ continuous variables and $\mathcal {O}(I^2)$ second-order conic constraints, while model (27) involves $\mathcal {O}(I+n^2)$ continuous variables and $\mathcal {O}(I)$ second-order conic constraints; and (ii) Model (28) contains big-M coefficients, while model (27) is big-M free. We also observe that, as the risk parameter increases, both models take longer to solve but model (27) still significantly outperforms model (28). These results demonstrate the effectiveness our proposed approaches.

6 Extension: ambiguity set with one linking constraint

In previous sections, we have shown that $Z=Z_B$ under the separability condition of Assumption (A1) and established several sufficient conditions under which the set $Z_B$ is convex. In this section, we demonstrate that these results may help establish new convexity results for the set $Z$ even when the ambiguity set is not separable.

In this section, we consider an ambiguity set specified by means of random vectors $\{\varvec{\xi }_i\}_{i\in [I]}$ and a bound on the overall deviation from mean. In particular, the ambiguity set is as follows.

• (A4) The ambiguity set ${{\mathcal {P}}}$ is given as

  $$\begin{aligned} {{\mathcal {P}}}=\left\{ {\mathbb {P}}:{{\mathbb {E}}}_{{\mathbb {P}}}[\varvec{\xi }]=\mu ,\sum _{i\in [I]}{{\mathbb {E}}}_{{\mathbb {P}}}[\Vert \varvec{\xi }_i-\mu _i\Vert ]\le \varDelta \right\} . \end{aligned}$$

  (29)

Note that we can equivalently express ${{\mathcal {P}}}$ as follows:

$$\begin{aligned} {{\mathcal {P}}}=\left\{ {\mathbb {P}}:\text{ Proj }_i({\mathbb {P}}) = {\mathbb {P}}_i \in {{\mathcal {D}}}_i(\delta _i), \forall i\in [I], \forall \delta \in {{\mathcal {K}}}\right\} , \end{aligned}$$

(30a)

where ${{\mathcal {K}}}:=\{\delta :\delta \ge 0,\sum _{i\in [I]} \delta _i \le \varDelta \}$ and for each $i\in [I]$ and $\delta \in {{\mathcal {K}}}$. The marginal ambiguity sets $\{{{\mathcal {D}}}_i(\delta _i)\}_{i\in [I]}$ are defined as

$$\begin{aligned} {{\mathcal {D}}}_i(\delta _i)=\left\{ {\mathbb {P}}:{{\mathbb {E}}}_{{\mathbb {P}}}[\varvec{\xi }_i]=\mu _i,{{\mathbb {E}}}_{{\mathbb {P}}}[\Vert \varvec{\xi }_i-\mu _i\Vert ]\le \delta _i\right\} , \end{aligned}$$

(30b)

where $\varXi _i={{\mathbb {R}}}^{m_i}$ for all $i\in [I]$.

The following theorem shows that under Assumption (A4), the set $Z$ can be reformulated as a convex program.

Theorem 15

Suppose that the ambiguity set ${{\mathcal {P}}}$ is defined as (30a) and $\varXi =\prod _{i\in [I]}\varXi _i$, then the set $Z$ is equivalent to

$$\begin{aligned}&Z=\left\{ x:\frac{\varDelta }{2\epsilon }\Vert a_i(x)\Vert _*+a_i(x)^{\top }\mu _i\le b_i(x),\forall i\in [I]\right\} , \end{aligned}$$

(31)

where $\Vert \cdot \Vert _{*}$ is the dual norm of $\Vert \cdot \Vert$.

Proof

We can reformulate $Z$ as

$$\begin{aligned} Z=\{x: x\in Z(\delta ), \forall \delta \in {{\mathcal {K}}}\} \end{aligned}$$

(32a)

where ${{\mathcal {K}}}:=\{\delta :\delta \ge 0,\sum _{i\in [I]} \delta _i \le \varDelta \}$ and

$$\begin{aligned} Z(\delta ):=\left\{ x\in {{\mathbb {R}}}^n:\inf _{{\mathbb {P}}\in {{\mathcal {P}}}(\delta )}{\mathbb {P}}\left\{ \varvec{\xi }:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x), \forall i\in [I]\right\} \ge 1-\epsilon \right\} \end{aligned}$$

(32b)

with

$$\begin{aligned} {{\mathcal {P}}}(\delta )=\left\{ {\mathbb {P}}:\text{ Proj }_i({\mathbb {P}}) = {\mathbb {P}}_i \in {{\mathcal {D}}}_i(\delta ), \forall i\in [I] \right\} . \end{aligned}$$

By Theorem 3, we know that $Z(\delta )$ is equivalent to its Bonferroni Approximation $Z_B(\delta )$ for any given $\delta \in {{\mathcal {K}}}$, i.e.,

$$\begin{aligned}&Z(\delta )=Z_B(\delta )\\&\quad =\left\{ x:\inf _{{\mathbb {P}}_i\in {{\mathcal {D}}}_i(\delta _i)}{\mathbb {P}}_i\left\{ \varvec{\xi }_i:a_i(x)^{\top }\varvec{\xi }_i \le b_i(x)\right\} \ge 1-s_i, \forall i\in [I],\sum _{i\in [I]}s_i\le \epsilon , s\ge 0\right\} . \end{aligned}$$

Let $\{\gamma _{1i},\gamma _{2i}\}_{i\in [I]}$ be the dual variables corresponding to the moment constraints in (30b). Thus, by Theorem 4 in [44], set $Z_B(\delta )$ is equivalent to

where by convention, $0\cdot \infty =0$. By solving the inner supremums, $Z_B(\delta )$ is equivalent to

Now let

Note that $Z_B(\delta )\subseteq \tilde{Z_B}(\delta )$. This is because for each $i\in [I]$, by aggregating $\Vert \gamma _{1i}\Vert _*\le \gamma _{2i},\Vert \gamma _{1i}+a_i(x)\Vert _*\le \gamma _{2i}$ and using triangle inequality, we have

$$\begin{aligned} \Vert a_i(x)\Vert _*\le 2\gamma _{2i}. \end{aligned}$$

On the other hand, by letting $\gamma _{1i}=-\frac{1}{2}a_i(x)$ in (32c), we obtain set $\tilde{Z_B}(\delta )$, thus $\tilde{Z_B}(\delta )\subseteq Z_B(\delta )$. Hence $\tilde{Z_B}(\delta )=Z_B(\delta )$.

By projecting out $\{\gamma _{2i}\}_{i\in [I]}$, (32d) yields

$$\begin{aligned}&Z_B(\delta )=\left\{ x:\frac{\delta _i\Vert a_i(x)\Vert _*}{2s_i}\le b_i(x)-a_i(x)^{\top }\mu _i,\forall i\in [I],\sum _{i\in [I]}s_i\le \epsilon , s\ge 0\right\} . \end{aligned}$$

(32e)

Finally, by projecting out variables s, (32e) is further reduced to

$$\begin{aligned}&Z_B(\delta )=\left\{ x:b_i(x)\ge a_i(x)^{\top }\mu _i,\forall i\in [I],\sum _{i\in [I]}\frac{\delta _i\Vert a_i(x)\Vert _*}{2(b_i(x)- a_i(x)^{\top }\mu )}\le \epsilon \right\} . \end{aligned}$$

Therefore,

$$\begin{aligned}&Z=\left\{ x:b_i(x)\ge a_i(x)^{\top }\mu _i,\forall i\in [I],\sum _{i\in [I]}\frac{\delta _i\Vert a_i(x)\Vert _*}{2(b_i(x)- a_i(x)^{\top }\mu )}\le \epsilon ,\forall \delta \in {{\mathcal {K}}}\right\} , \end{aligned}$$

with ${{\mathcal {K}}}=\{\delta :\delta \ge 0,\sum _{i\in [I]} \delta _i \le \varDelta \}$, which is equivalent to

$$\begin{aligned}&Z=\left\{ x:b_i(x)\ge a_i(x)^{\top }\mu _i,\forall i\in [I],\sum _{i\in [I]}\frac{\delta _i\Vert a_i(x)\Vert _*}{2(b_i(x)- a_i(x)^{\top }\mu )}\le \epsilon ,\forall \delta \in {\mathbf {ext}}({{\mathcal {K}}})\right\} , \end{aligned}$$

(32f)

with ${\mathbf {ext}}({{\mathcal {K}}}):=\{0\}\cup \{\varDelta \mathbf {e}_i\}_{i\in [I]}$ denoting the set of extreme points of ${{\mathcal {K}}}$. Thus, (32f) leads to (31). $\square$

Remark 6

The technique for proving Theorem 15 is quite general and may be applied to other settings. For example, if the ambiguity set ${{\mathcal {P}}}$ is defined by known mean and sum of component-wise standard deviations, then we can reformulate $Z$ as a second-order conic set.

Next we consider the optimized Bonferroni approximation of $Z$.

Theorem 16

Suppose that the ambiguity set ${{\mathcal {P}}}$ is defined as (30a) and $\varXi =\prod _{i\in [I]}\varXi _i$, then the set $Z_B$ is equivalent to

$$\begin{aligned}&Z_B=\left\{ x:\frac{\varDelta }{2}\sum _{i\in [I]}\frac{\Vert a_i(x)\Vert _*}{b_i(x)-a_i(x)^{\top }\mu _i}\le \epsilon ,a_i(x)^{\top }\mu _i\le b_i(x), \forall i\in [I]\right\} , \end{aligned}$$

(33)

where $\Vert \cdot \Vert _{*}$ is the dual norm of $\Vert \cdot \Vert$.

Proof

The optimized Bonferroni approximation of set $Z$ is

$$\begin{aligned}&Z_B=\left\{ x:\inf _{{\mathbb {P}}_j\in {{\mathcal {D}}}_j(\varDelta )}{\mathbb {P}}_j\left\{ \varvec{\xi }_j:a_j(x)^{\top }\varvec{\xi }_j \le b_j(x)\right\} \ge 1-s_j, \forall j\in [I],\sum _{j\in [I]}s_j\le \epsilon , s\ge 0\right\} \end{aligned}$$

i.e.,

$$\begin{aligned}&Z_B=\left\{ x:\inf _{{\mathbb {P}}_j\in {{\mathcal {D}}}_j(\varDelta )}{\mathbb {P}}_j\left\{ \varvec{\xi }_j:a_j(x)^{\top }\varvec{\xi }_j \le b_j(x)\right\} \ge 1-s_j, \forall j\in [I],\sum _{j\in [I]}s_j\le \epsilon , s\ge 0\right\} . \end{aligned}$$

By letting $I=1$ in Theorem 15, we know that $\inf _{{\mathbb {P}}_j\in {{\mathcal {D}}}_j(\varDelta )}{\mathbb {P}}_j\{\varvec{\xi }_j:a_j(x)^{\top }\varvec{\xi }_j \le b_j(x)\} \ge 1-s_j$ is equivalent to

$$\begin{aligned} \frac{\varDelta }{2\epsilon }\Vert a_j(x)\Vert _*+a_j(x)^{\top }\mu _j\le b_j(x) \end{aligned}$$

for each $j\in [I]$. Thus, set $Z_B$ is further equivalent to

$$\begin{aligned}&Z_B=\left\{ x:\frac{\varDelta }{2s_j}\Vert a_j(x)\Vert _*+a_j(x)^{\top }\mu _j\le b_j(x), \forall j\in [I],\sum _{j\in [I]}s_j\le \epsilon , s\ge 0\right\} , \end{aligned}$$

which leads to (33) by projecting out s. $\square$

Remark 7

The constraints defining (33) are not convex in general. Thus even if $Z$ is convex (Theorem 15), its optimized Bonferroni approximation $Z_B$ may not be convex.

Remark 8

The constraints defining (33) are convex in case of only right-hand side uncertainties, i.e. $A^i=0$ for all $i\in [I]$.

We conclude by demonstrating the limitations of the optimized Bonferroni approximation by an example illustrating that, unless the established conditions hold, the distance between sets $Z$ and $Z_B$ can be arbitrarily large.

Example 7

Consider $Z$ with regard to a projected ambiguity set in the form of (30a)

$$\begin{aligned} Z= \left\{ x\in {{\mathbb {R}}}^I: \inf _{{\mathbb {P}}\in {{\mathcal {P}}}} {{\mathcal {P}}}\left\{ \varvec{\xi }: \varvec{\xi }_ix_i\le 1,\forall i\in [I]\right\} \ge 1-\epsilon \right\} \end{aligned}$$

where

$$\begin{aligned} {{\mathcal {P}}}= \left\{ {\mathbb {P}}: {{\mathbb {E}}}_{{\mathbb {P}}}[\varvec{\xi }]=0, {{\mathbb {E}}}_{{\mathbb {P}}}[\Vert \varvec{\xi }\Vert ]\le \varDelta \right\} . \end{aligned}$$

Thus, (31) and (33) yield

$$\begin{aligned} Z=\left\{ x\in {{\mathbb {R}}}^I:|x_i|\le \frac{2\epsilon }{\varDelta },\forall i\in [I]\right\} , \end{aligned}$$

and

$$\begin{aligned} Z_B=\left\{ x\in {{\mathbb {R}}}^I:\sum _{i\in [I]}|x_i|\le \frac{2\epsilon }{\varDelta }\right\} . \end{aligned}$$

These two sets are shown in Fig. 4 with $\frac{2\epsilon }{\varDelta } =2$ and $I=2$, where the dashed lines denote the boundaries of $Z,Z_B$. Indeed, simple calculation shows that the Hausdorff distance (c.f. [35]) between sets $Z_B$ and $Z$ is $\frac{I-1}{\sqrt{I}}\frac{2\epsilon }{\varDelta }$, which tends to be infinity when $\varDelta \rightarrow 0$ and $I, \epsilon$ are fixed, or $I\rightarrow \infty$ and $\varDelta , \epsilon$ are fixed. $\square$

Fig. 4

Illustration of Example 7 with $\frac{2\epsilon }{\varDelta } =2$ and $I=2$

7 Conclusion

In this paper, we study optimized Bonferroni approximations of distributionally robust joint chance constrained problems. We first show that when the uncertain parameters are separable in both uncertain constraints and ambiguity sets, the optimized Bonferroni approximation is exact. We then prove that optimizing over the optimized Bonferroni approximation set is NP-hard, and establish various sufficient conditions under which the optimized Bonferroni approximation set is convex and tractable. Finally, we extend our results to a distributionally robust joint chance constrained problem with one linking constraint in the ambiguity set. One future direction is to study ambiguity sets containing more distributional information (e.g., bivariate marginal distributions). Another possible direction is to study other bounding schemes for joint chance constraints (see, e.g., [4, 18, 21, 33]) in the distributionally robust setting and their convex reformulations.