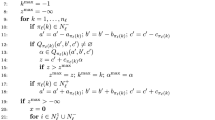1 Introduction

In this paper, we investigate chance constrained optimization problems (CCP). Such problems were introduced in [1] and nowadays cover numerous applications: among other portfolio selection [2, 3], hydro reservoir management [4], logistics [5], energetics [6] or insurance [7, 8]. Since the feasible region is generally nonconvex even for convex data and the evaluation of the chance constraints leads to a computation of multivariate integrals, these problems are usually difficult to solve.

In this paragraph, we present an overview of several approaches for solving CCP. A general approach called sample (empirical) approximation is based on substituting the underlying continuous distribution by a finite sample and reformulating it as a mixed-integer programming problem, see [9]. For linear constraints and finite discrete distribution, algorithms based on cutting planes for mixed-integer reformulations are available, cf. [10, 11]. For joint chance constraints under discrete distribution, where the random parts of the constraints are separated from the decision variables, we can use p-level efficient points (pLEPs) to obtain a deterministic reformulation, see [12]. A bundle method for this special case was recently proposed by [13]. Optimality conditions for these problems were derived by [14] under convexity assumptions. Boolean reformulation framework was introduced by [15, 16]. Additionally, a recent extension [17] of this method was proposed for nonlinear chance constraints. Nonlinear programming algorithms were suggested for general chance constrained problems by [18, 19]. A wide class of approaches is based on approximating the indicator function by a more tractable function. Approximation based on conditional value at risk has been deeply investigated by [2, 20]. A similar idea was used by [21] who employed the so-called integrated chance constraints. Bernstein approximation has been introduced by [22] for constraints affine in random coefficients. Recently, algorithmic approaches based on representation using difference of convex functions appeared in the literature, see [3, 23]. A second-order cone programming reformulation was obtained by [24] for problems with linear constraints under normally distributed random coefficient. For these linear Gaussian problems, [25] provided an explicit gradient formula and derived an efficient solution procedure.

Our approach relies on distributional assumptions where we consider finite discrete distributions only. However, apart from differentiability we require no further assumption on the data apart from standard constraint qualifications (which are naturally satisfied in the linear case). Thus, we allow nonlinear, possibly nonconvex, functions not only in the random constraints, but also in the deterministic constraints and in the objective. We use the usual reformulation via additional binary decision variables, which enable to identify whether the random constraint is fulfilled for particular scenario or not. Then we relax these binary variables into continuous ones to obtain a relaxed nonlinear programming problem. We derive necessary optimality conditions for both the original and the relaxed problem and then show the relations between local minima and stationary points of both problems.

We prove that any local solution of the original problem can be extended to become a local solution of the relaxed problem. On the other hand, if we obtain a solution of the relaxed problem, still some verification regarding the relaxed binary variables is necessary to decide whether the solution is or is not a local solution of the original problem. We make use of this observation and propose an iterative algorithm which solves the relaxed problem. The algorithm either determines that the obtained point is a solution of the original problem or provides another point which can be used as a starting point for the solution process for the relaxed problem.

Since this approach has certain disadvantages, such as violated standard constraint qualifications, we derive a second algorithm. To this aim, we approach the relaxed problem from the viewpoint of mathematical programs with complementarity constraints (MPCC). Using standard techniques from this field, we regularize the relaxed problem, i.e., we enlarge the feasible set in a proper way, derive necessary optimality conditions and show that the stationary points of the regularized problem converge to the stationary points of the relaxed problem. Coupling this with the previous paragraph, we obtain stationarity for the original CCP. We would like to emphasize that the obtained stationary is the strong S–stationarity; hence, we work only with Fréchet objects and do not have to pass to weaker conditions based on limiting or Clarke objects.

Based on the results of this paper, a solver CCP-SIR (Chance Constraint Problems: Successive Iterative Regularization) was developed. It may be freely distributed and is available online.Footnote 1 We believe that its main strength lies in finding stationary points of nonconvex medium-sized problems, where the sources of nonconvexity can be the random and deterministic functions in the constraints as well as the objective function.

The paper is organized as follows. In Sect. 2, we derive the relaxed problem mentioned above and obtain necessary optimality conditions for both the original and relaxed problem. In Sect. 3, we regularize the relaxed problem and show that stationary points of the regularized problem converge to a stationary point of the relaxed problem. Finally, in Sect. 4 we verify the theoretical results on a nontrivial numerical example.

2 Problem Reformulations and Necessary Optimality Conditions

The problem may be formulated as follows:

(1)

Here \(x\in {\mathbb R}^n\) is the decision variable, \(0\le \varepsilon <1\) is a prescribed probabilistic level, \(f:{\mathbb R}^n\rightarrow {\mathbb R}\), \(g:{\mathbb R}^n\times {\mathbb R}^d\rightarrow {\mathbb R}\) and \(h_j:{\mathbb R}^n\rightarrow {\mathbb R}\) are functions which are continuously differentiable in variable x and finally \(\xi \in {\mathbb R}^d\) is a random vector with known probability distribution P.

In this paper, we assume that \(\xi \) has known discrete distribution and enumerate all possible realizations by \(\xi _1,\dots ,\xi _S\) and the corresponding positive probabilities by \(p_1,\dots ,p_S\). We may then reformulate problem (1) into

(2)

where \(\chi \) stands for the characteristic function which equals to 1 if \(g(x,\xi _i)\le 0\) and 0 otherwise. Introducing artificial binary variable \(y\in \{0,1\}^S\) to deal with \(\chi \), we obtain the following mixed-integer nonlinear problem

(3)

To avoid the problematic constraint \(g(x,\xi _i)y_i\le 0\), usually this constraint is replaced by \(g(x,\xi _i)\le M (1-y_i)\), where M is a sufficiently large constant. This leads to the following problem

(4)

This reformulation was proposed by [26] and will be used in the numerical analysis in Sect. 4 for mixed-integer programming solvers.

Since this problem is difficult to tackle by mixed-integer (nonlinear) programming techniques in any of the previous forms, we relax binary constraint \(y_i\in \{0,1\}\) into \(y_i\in [0,1]\) to obtain nonlinear programming problem

(5)

In the subsequent text, we will denote problem (5) as the relaxed problem. Even though problems (2) and (5) are not equivalent, see Example 2.1 below, there are close similarities between them, see Lemmas 2.1 and 2.2 below.

For notational simplicity, we define the following index sets

$$\begin{aligned} I_{00}(x,y):= & {} {\left\{ i:g(x,\xi _i) = 0,\ y_i=0\right\} },\qquad \quad \qquad \; I_0(x) := {\left\{ i:g(x,\xi _i) = 0\right\} },\nonumber \\ I_{0+}(x,y):= & {} {\left\{ i:g(x,\xi _i) = 0,\ 0<y_i<1\right\} },\quad \qquad J_0(x) := {\left\{ j:h_j(x) = 0\right\} },\nonumber \\ I_{01}(x,y):= & {} {\left\{ i:g(x,\xi _i) = 0,\ y_i=1\right\} }. \end{aligned}$$
(6)

Further, we define sets which will be extensively used later in the manuscript

$$\begin{aligned} \hat{\mathcal {I}}(x)&:= {\left\{ \tilde{I}\subset \{1,\dots ,S\}:\sum _{i\in \tilde{I}}p_i\ge 1-\varepsilon , \begin{array}{lll} g(x,\xi _i)&{}< 0\implies i\in \tilde{I}\\ g(x,\xi _i)&{}> 0\implies i\notin \tilde{I}\end{array} \right\} },\nonumber \\ \mathcal {I}(x)&:= \text {minimal elements of }\hat{\mathcal {I}}(x)\text { with respect to set inclusion}, \end{aligned}$$
(7)
$$\begin{aligned} Y(x)&:= {\left\{ y\in \{0,1\}^S: \exists I\in \mathcal {I}(x)\text { s.t. } y_i=1\text { if }i\in I;\ y_i=0\text { if }i\notin I\right\} }. \end{aligned}$$
(8)

The purpose of the definition of these sets is that the union of \(\{x:\ g(x,\xi _i)\le 0,\ i\in I\}\) with respect to \(I\in \hat{\mathcal {I}}(\bar{x})\) or with respect to \(I\in \mathcal {I}(\bar{x})\) has the same shape as the feasible set of problem (2) on the neighborhood of \(\bar{x}\).

2.1 Necessary Optimality Conditions for CCP and Its Relaxation

In this subsection, we derive optimality conditions for both the CCP (2) and the nonlinear problem (5). To be able to do so, we impose the following assumption which will be used throughout the whole paper.

Assumption 2.1

Let \(\bar{x}\) be a feasible point of problem (2). Assume that at least one of the following two conditions is satisfied:

  • Functions \(g(\cdot ,\xi _i)\) and \(h_j\) are affine linear.

  • The following implication is satisfied for all \(I\in \mathcal {I}(\bar{x})\)

    $$\begin{aligned} \left. \begin{array}{lll} &{}\displaystyle \sum _{i\in I_0(\bar{x}) } \lambda _i\nabla _x g(\bar{x},\xi _i) + \sum _{j\in J_0(\bar{x})}\mu _j\nabla h_j(\bar{x}) = 0 \\ &{}\lambda _i=0,\ i\in I_0(\bar{x}) {\setminus } I\\ &{}\lambda _i \ge 0,\ i\in I_0(\bar{x}) \cap I \\ &{}\mu _j \ge 0,\ j\in J_0(\bar{x})\\ \end{array}\right\} \implies \begin{array}{ll} \lambda _i=0,\ i\in I_0(\bar{x}) ,\\ \mu _j=0,\ j\in J_0(\bar{x}). \end{array} \end{aligned}$$

We will comment on this assumption more in Remark 2.1, where we show that this assumption is rather standard. For reader’s convenience, we provide two basic definitions here. For a set \(Z\subset {\mathbb R}^n\) and a point \(\bar{x}\in Z\), we define the tangent and (Fréchet) normal cones to Z at \(\bar{x}\), respectively, as

$$\begin{aligned} T_Z(\bar{x}):= & {} {\left\{ d\in {\mathbb R}^n:\exists d^k\rightarrow d\ \exists t^k\searrow 0: \bar{x}+t^kd^k\in Z\right\} },\\ \hat{N}_Z(\bar{x}):= & {} {\left\{ x^*\in {\mathbb R}^n:\langle x^*,d\rangle \le 0\text { for all }d\in T_Z(\bar{x})\right\} }. \end{aligned}$$

Theorem 2.1

Let Assumption 2.1 be satisfied. If \(\bar{x}\) is a local minimum of CCP (2), then for every \(I\in \mathcal {I}(\bar{x})\) there exist multipliers \(\lambda _i,\ i\in I_0(\bar{x}) \) and \(\mu _j,\ j\in J_0(\bar{x})\) such that

$$\begin{aligned}&\nabla f(\bar{x})+\sum _{i\in I_0(\bar{x}) } \lambda _i\nabla _x g(\bar{x},\xi _i)\ + \sum _{j\in J_0(\bar{x})}\mu _j\nabla h_j(\bar{x}) = 0, \nonumber \\&\quad \lambda _i= 0,\ i\in I_0(\bar{x}) {\setminus } I,\nonumber \\&\quad \lambda _i \ge 0,\ i\in I_0(\bar{x}) \cap I,\nonumber \\&\quad \mu _j\ge 0,\ j\in J_0(\bar{x}). \end{aligned}$$
(9)

Proof

Denote the feasible set of problem (2) by Z and consider a point \(\bar{x}\in Z\). Then Z coincides locally around \(\bar{x}\) with

$$\begin{aligned} \bigcup _{I\in \mathcal {I}(\bar{x})} Z_I := \bigcup _{I\in \mathcal {I}(\bar{x})} {\left\{ x:g(x,\xi _i) \le 0,\ i\in I_0(\bar{x})\cap I,\ h_j(x) \le 0,\ j=1,\dots ,J \right\} }, \end{aligned}$$

which means that

$$\begin{aligned} \hat{N}_Z(\bar{x}) = (T_Z(\bar{x}))^* = \left( \bigcup _{I\in \mathcal {I}(\bar{x})}T_{Z_I}(\bar{x})\right) ^{*} = \bigcap _{I\in \mathcal {I}(\bar{x})}\hat{N}_{Z_I}(\bar{x}). \end{aligned}$$

By [27, Theorem 6.12], we obtain that \(0\in \nabla f(\bar{x})+\hat{N}_Z(\bar{x})\) is a necessary optimality condition for CCP (2). To obtain the theorem statement, it suffices to use chain rule [27, Theorem 6.14]. \(\square \)

In the next theorem, we derive necessary optimality conditions for the relaxed problem (5).

Theorem 2.2

Assume that \((\bar{x}, \bar{y})\) with \(\bar{y}\in Y(\bar{x})\) is a local minimum of problem (5) and that Assumption 2.1 is satisfied at \(\bar{x}\). Then there exist multipliers \(\lambda _i,\ i\in I_0(\bar{x}) \) and \(\mu _j,\ j\in J_0(\bar{x})\) such that

$$\begin{aligned}&\nabla f(\bar{x})+\sum _{i\in I_0(\bar{x}) }\lambda _i\nabla _x g(\bar{x},\xi _i)\ + \sum _{j\in J_0(\bar{x})} \mu _j\nabla h_j(\bar{x}) =0,\nonumber \\&\quad \lambda _i= 0,\ i\in I_{00}(\bar{x},\bar{y}),\nonumber \\&\quad \lambda _i\ge 0,\ i\in I_{01}(\bar{x},\bar{y})\cup I_{0+}(\bar{x},\bar{y}),\nonumber \\&\quad \mu _j\ge 0,\ j\in J_0(\bar{x}). \end{aligned}$$
(10)

Proof

Due to [27, Theorem 6.12], the necessary optimality conditions for problem (5) read

$$\begin{aligned} 0\in \begin{pmatrix}\nabla f(\bar{x})\\ 0\end{pmatrix}+ \hat{N}_Z(\bar{x},\bar{y}) = \begin{pmatrix}\nabla f(\bar{x}) + N_1(\bar{x})\\ N_2(\bar{y})\end{pmatrix}, \end{aligned}$$

where Z is the feasible set of problem (2) and \(N_1(\bar{x})\) and \(N_2(\bar{y})\) are computed in Lemma 6.1 proposed in Appendix. Observing that \(0\in N_2(\bar{y})\), we obtain the desired result. \(\square \)

We conclude this subsection by a remark concerning Assumption 2.1 and its relation to standard constraint qualifications.

Remark 2.1

It can be shown that standard constraint qualifications such as linear independence constraint qualification (LICQ) or Mangasarian–Fromovitz constraint qualification (MFCQ) do not hold for the feasible set of problem (5) at all points where at least one probabilistic constraint is violated. Based on Lemma 6.1, it can be shown that the Guignard constraint qualification (GCQ), see [28], is satisfied under Assumption 2.1.

Now, we will show that the constraint qualification imposed in Assumption 2.1 is reasonable. Consider the following set

$$\begin{aligned} \tilde{Z}:={\left\{ x:g(x,\xi _i)\le 0,\ i=1,\dots ,S,\ h_j(x) \le 0,\ j=1,\dots ,J\right\} }. \end{aligned}$$

Then MFCQ for \(\tilde{Z}\) at \(\bar{x}\) implies Assumption 2.1. Moreover, the second part of Assumption 2.1 is closely related to CC-MFCQ, see [29, 30] for stationarity concepts for a similar problem.

2.2 Relations Between Solutions of CCP and Its Relaxation

In this subsection, we will investigate relations between global and local minima and stationary points of problems (2) and (5). Recall that a point is stationary if it satisfies the necessary optimality of Theorems 2.1 and 2.2, respectively.

Lemma 2.1

A point \(\bar{x}\) is a global minimum of problem (2) if and only if there exists \(\bar{y}\) such that \((\bar{x},\bar{y})\) is a global minimum of problem (5). A point \(\bar{x}\) is a local minimum of problem (2) if and only if for all \(\bar{y}\in Y(\bar{x})\) the point \((\bar{x},\bar{y})\) is a local minimum of problem (5).

Proof

Assume that \(\bar{x}\) is a global minimum of (2) and define \(\bar{y}\) componentwise as \(\bar{y}_i:=1\) when \(g(\bar{x},\xi _i)\le 0\) and \(\bar{y}_i:=0\) otherwise. Then it is not difficult to verify that \((\bar{x},\bar{y})\) is a global minimum of (5). On the other hand, assume that \((\bar{x},\bar{y})\) is a global minimum of (5) and define \(\hat{y}\) which is equal to \(\bar{y}\) with the difference that all positive components of \(\hat{y}\) are replaced by 1. Then \((\bar{x},\hat{y})\) is also a global minimum of (5) and \(\bar{x}\) is a global minimum of (2).

Assume now that \(\bar{x}\) is a local minimum of (2) and for contradiction assume that there exists \(\bar{y}\in Y(\bar{x})\) such that \((\bar{x},\bar{y})\) is not a local minimum of (5). Then there exists a sequence \((x^k,y^k)\rightarrow (\bar{x},\bar{y})\) such that \((x^k,y^k)\) is a feasible point of (5) and \(f(x^k)<f(\bar{x})\). But this means that \((x^k,\bar{y})\) is also feasible for (5) and thus \(\bar{x}\) is not a local minimum of (2).

Finally, assume that \((\bar{x},\bar{y})\) is a local minimum of (5) for all \(\bar{y}\in Y(\bar{x})\) and for contradiction assume that \(\bar{x}\) is not a local minimum of (2). Then there exists \(x^k\rightarrow \bar{x}\) such that \(x^k\) is feasible for (2) and \(f(x^k)<f(\bar{x})\). Similarly as in the first case define \(y^k\) as \(y_i^k:=1\) if \(g(x^k,\xi _i)\le 0\) and \(y_i^k:=0\) otherwise. Since \(y^k\) is bounded, we can select a constant subsequence, denoted by the same indices, such that \(y^k=\hat{y}\) and thus \((x^k,\hat{y})\) and \((\bar{x},\hat{y})\) are feasible points of problem (5) for all k. Since \(f(x^k)<f(\bar{x})\), this means that \((\bar{x},\hat{y})\) is not a local minimum of (5). As \(g(\cdot ,\xi _i)\) are continuous functions by assumption, we have \(\hat{y}\in Y(\bar{x})\), which is a contradiction. \(\square \)

Lemma 2.2

Consider a feasible point \(\bar{x}\) of problem (2). Then \(\bar{x}\) satisfies the necessary optimality conditions (9) if and only if \((\bar{x},\bar{y})\) satisfies the necessary optimality conditions (10) for all \(\bar{y}\in Y(\bar{x})\).

Proof

This lemma follows directly from Theorems 2.1 and 2.2 and the coincidence with \(\mathcal {I}(\bar{x})\) with all possible \(I_{01}(\bar{x},\bar{y})\) corresponding to \(\bar{y}\in Y(\bar{x})\). \(\square \)

Fig. 1
figure 1

Possible partitions of the set from Example 2.1. a Local minima of problem (2). b Local minimum of problem (5)

Full size image

We intend to solve problem (5) and based on its solution \((\bar{x},\bar{y})\) derive some information about a solution of problem (2). Lemma 2.2 states that if \((\bar{x},\bar{y})\) is a stationary point of problem (5), we cannot say whether \(\bar{x}\) is a stationary point of problem (2). To be able to do so, we would have to go through all \(y\in Y(\bar{x})\) and verify that \((\bar{x},y)\) is also a stationary point of problem (5). However, if it happens that \(Y(\bar{x})\) is a singleton, we have equivalence between local minima of both problems. We show this behavior in the following example.

Example 2.1

Consider functions

$$\begin{aligned} f(x):=(x_1-0.3)^2+(x_2-2)^2,\ g(x,\xi ):=(x_1-\xi )^2+x_2^2-1, \end{aligned}$$

number of scenarios \(S=2\) with probabilities \(p_1=p_2=\frac{1}{2}\), realizations \(\xi _1=\frac{1}{2}\), \(\xi _2=-\frac{1}{2}\) and probability level \(\varepsilon =\frac{1}{2}\). Since \(\varepsilon =\frac{1}{2}\), at least one of the probabilistic constraints has to be satisfied. The feasible solution of problem (2) is union of two circles and is depicted in Fig. 1a. It is obvious that problem (2) admits one local minimum \(\bar{x}^1\) and one global minimum \(\bar{x}^2\).

Problem (5) contains additional local minima. Consider point \(\bar{x}=(0,\frac{\sqrt{3}}{2})\) and \(\bar{y}=(1,1)\). Since both components of \(\bar{y}\) are positive, when we consider a point (x, y) close to \((\bar{x},\bar{y})\), then both (and not only one) probabilistic constraints have to be satisfied at x. This changes the feasible set from the union into the intersection of two circles and thus \((\bar{x},\bar{y})\) is indeed a local minimum of problem (5). This situation is depicted in Fig. 1b. However, since \(\bar{x}\) is not a local solution to (2), there has to exist some \(\hat{y}\in Y(\bar{x})\) such that \((\bar{x},\hat{y})\) is not a local minimum of problem (5). This point can be obtained by choosing either \(\hat{y}=(1,0)\) or \(\hat{y}=(0,1)\).

Based on Lemma 2.2, we propose Algorithm 1 to solve problem (2). First, we solve problem (5) to obtain \((\bar{x},\bar{y})\), then we find all \(y\in Y(\bar{x})\) and for all of them we verify whether they are stationary points of problem (5). If so, then \((\bar{x},\bar{y})\) is a stationary point of problem (2) due to Lemma 2.2. In the opposite case, there exists some \(y\in Y(\bar{x})\) such that \((\bar{x},y)\) is not a stationary point of problem (5), and thus \(\bar{x}\) is not a stationary point of problem (2). Thus, we choose this point as a starting one and continue with a new iteration. Note that by changing \((\bar{x},\bar{y})\) to \((\bar{x},y)\), the objective value stays the same.

figure a

3 Regularized Problem

Algorithm 1 may suffer from two drawbacks. The first one is the verification of necessary optimality conditions (10) which may be time-consuming. The second one is that MFCQ is generally not satisfied as noted in Remark 2.1. For these reasons, we propose additional technique similar to regularizing MPCCs, see [31]. This technique enlarges the feasible set and solves the resulting regularized problem while driving the regularization parameter to infinity. Thus, we consider regularized problem

(11)

where \(\phi _t:{\mathbb R}\rightarrow {\mathbb R}\) are continuously differentiable decreasing functions which depend on a parameter \(t>0\) and which satisfy the following properties:

$$\begin{aligned} \phi _t(0)=1,&\end{aligned}$$
(12)
$$\begin{aligned} \phi _t(z)>0,&\quad \text {for }z\in {\mathbb R}, \end{aligned}$$
(13)
$$\begin{aligned} \phi _t(z^t)\rightarrow 0,&\quad \text {whenever }z^t\mathop {\rightarrow }\limits ^{t\rightarrow \infty }\bar{z}>0, \end{aligned}$$
(14)
$$\begin{aligned} \frac{\phi _t'(z^t)}{\phi _t'(\tilde{z}^t)}\rightarrow 0,&\quad \text {whenever }\phi _t(z^t)\searrow 0\text { and }\phi _t(\tilde{z}^t)\rightarrow \bar{z}>0. \end{aligned}$$
(15)

As an example of such regularizing function, we may consider \(\phi _t(z) = e^{-tz}.\)

We show the differences in problems (3), (5) and (11) in Fig. 2. We can see the main reason for regularizing the feasible set of problem (5). Consider the case of \(g(\bar{x},\xi _i)=0\) and \(\bar{y}>0\). While in Fig. 2a or b it is not possible to find a feasible point (x, y) in the vicinity of \((\bar{x},\bar{y})\) such that \(g(x,\xi _i)>0\), this is possible in Fig. 2c.

Fig. 2
figure 2

Feasible sets of problems (3), (5) and (11). a \(g(x_i)y_i\le 0\), \(y_i\in \{0,1\}\), b \(g(x_i)y_i\le 0\), \(y_i\in [0,1]\), c \(y_i\le \phi _t(g(x_i))\), \(y_i\in [0,1]\)

Full size image

The necessary optimality conditions for problem (11) at a point \((\bar{x}^t,\bar{y}^t)\) read as follows: There exist multipliers \(\alpha ^t\in {\mathbb R}\), \(\beta ^t\in {\mathbb R}^S\), \(\gamma ^t\in {\mathbb R}^S\) and \(\mu ^t\in {\mathbb R}^J\) such that the optimality conditions

$$\begin{aligned} 0&= \nabla f(\bar{x}^t) - \sum _{i=1}^S\gamma _i^t \phi _t'(g(\bar{x}^t,\xi _i))\nabla _x g(\bar{x}^t,\xi _i) + \sum _{j\in J_0(\bar{x})}\mu _j^t\nabla h_j(\bar{x}^t), \end{aligned}$$
(16)
$$\begin{aligned} 0&= -\alpha ^t p_i + \beta _i^t + \gamma _i^t,\ i=1,\dots ,S \end{aligned}$$
(17)

and the complementarity conditions and multiplier signs

$$\begin{aligned}&\alpha ^t(1-\varepsilon -p^\top \bar{y}^t) = 0, \end{aligned}$$
(18)
$$\begin{aligned}&\beta _i^t \left\{ \begin{array}{ll} \ge 0, &{} \quad \text {if }\, \bar{y}_i^t = 1,\\ = 0, &{}\quad \text {if }\, 0<\bar{y}_i^t<1,\\ \le 0, &{}\quad \text {if }\,\bar{y}_i^t = 0, \end{array} \right. \end{aligned}$$
(19)
$$\begin{aligned}&\gamma _i^t\left( \bar{y}_i^t-\phi _t(g(\bar{x}^t,\xi _i))\right) = 0, \end{aligned}$$
(20)
$$\begin{aligned}&\alpha ^t\ge 0,\ \beta _i^t\in {\mathbb R},\ \gamma _i^t\ge 0,\ \mu _j^t \ge 0. \end{aligned}$$
(21)

are satisfied. Since in the rest of the paper we will work only with stationary conditions, we do not derive a constraint qualification under which they are satisfied.

In the next theorem, we show that stationary points of problems (11) converge to a stationary point of problem (5). Since we will need boundedness of certain multipliers, we need to assume the second part of Assumption 2.1. First, we state two auxiliary lemmas. For notational simplicity, we write only t instead of the more correct \(t^k\) and denote all subsequences by the same indices.

Lemma 3.1

Assume that \((\bar{x}^t,\bar{y}^t)\) is a stationary point of problem (11). Then the following assertions hold true:

  1. 1.

    \(g(\bar{x}^t,\xi _i)<0\implies \gamma _i^t=0;\)

  2. 2.

    \(\alpha ^t = 0 \implies \beta _i^t=\gamma _i^t=0\) for all i;

  3. 3.

    \(\bar{y}_i^t < \min \{1,\phi _t(g(\bar{x}^t,\xi _i))\}\) for some \( i\implies \alpha ^t = 0\).

Proof

The statements follow directly from an analysis of system (16)–(21). \(\square \)

Lemma 3.2

If for all t we have \(p^\top \bar{y}^t = 1-\varepsilon \) and for some i we have \(\phi _t(g(\bar{x}^t,\xi _i)) = \bar{y}_i^t\searrow 0\), then there exists a subsequence in t such that \(\gamma _i^t=0\) for all t or such that there exists an index j such that

$$\begin{aligned} \frac{ -\gamma _i^t \phi _t'(g(\bar{x}^t,\xi _i))}{ -\gamma _j^t \phi _t'(g(\bar{x}^t,\xi _j))} \rightarrow 0. \end{aligned}$$
(22)

Proof

Due to the assumptions, there exists index j, and possibly a subsequence in t, such that \(\bar{y}_j^t\) is strictly increasing. This implies that \(0<\bar{y}_j^t<1\) and \(\beta _i^t=\beta _j^t=0\) for all t. If \(\gamma _i^t=0\), then the proof is finished. In the opposite case, we have \(\alpha ^t>0\) and

$$\begin{aligned} \frac{- \gamma _i^t \phi _t'(g(\bar{x}^t,\xi _i))}{- \gamma _j^t \phi _t'(g(\bar{x}^t,\xi _j))} = \frac{- \alpha ^tp_i \phi _t'(g(\bar{x}^t,\xi _i))}{- \alpha ^tp_j \phi _t'(g(\bar{x}^t,\xi _j))} = \frac{p_i}{p_j}\frac{\phi _t'(g(\bar{x}^t,\xi _i))}{\phi _t'(g(\bar{x}^t,\xi _j))}\rightarrow 0, \end{aligned}$$

where the first equality follows from (17) and the convergence follows from \(\phi _t(g(\bar{x}^t,\xi _j)) \ge \bar{y}_j^t\), the fact that \(\bar{y}_j^t\) is a strictly increasing sequence and assumption (15). \(\square \)

Theorem 3.1

Consider \((\bar{x}^t,\bar{y}^t)\) to be stationary points of problem (11). Assume that the second part of Assumption 2.1 is satisfied at \(\bar{x}\) and that \((\bar{x}^t,\bar{y}^t) \rightarrow (\bar{x},\bar{y})\) as \(t\rightarrow \infty \). Then \((\bar{x},\bar{y})\) is a stationary point of problem (5).

Proof

We will show first that \((\bar{x},\bar{y})\) is a feasible solution to (5). Due to continuity, it is sufficient to show that \(g(\bar{x},\xi _i)\bar{y}_i\le 0\). Since this relation is obvious whenever \(g(\bar{x},\xi _i)\le 0\), we consider \(g(\bar{x},\xi _i)>0\). But then \(g(\bar{x}^t,\xi _i)>0\) for sufficiently large t and thus \(0\le \bar{y}_i^t\le \phi _t(g(\bar{x}^t,\xi _i))\). But since \(g(\bar{x}^t,\xi _i)\rightarrow g(\bar{x},\xi _i)>0\), formula (14) implies that \(\bar{y}_i=0\), and thus \((\bar{x},\bar{y})\) is a feasible point of problem (5).

For notational simplicity, we assume in the rest of the proof that \(J_0(\bar{x})=\emptyset \). Define now

$$\begin{aligned} \lambda _i^t := - \gamma _i^t \phi _t'(g(\bar{x}^t,\xi _i)) \ge 0, \end{aligned}$$

where the nonnegativity follows from the property that \(\phi _t\) is decreasing. Then for a subsequence in t, optimality condition (16) reads

$$\begin{aligned} 0= & {} \nabla f(\bar{x}^t) + \sum _{i=1}^S\lambda _i^t\nabla _x g(\bar{x}^t,\xi _i) \nonumber \\= & {} \nabla f(\bar{x}^t) + \sum _{{\left\{ i:g(\bar{x},\xi _i)=0,\, \bar{y}_i>0\right\} }}\lambda _i^t \nabla _x g(\bar{x}^t,\xi _i) + \sum _{{\left\{ i:g(\bar{x},\xi _i)\ge 0,\ \bar{y}_i=0\right\} }}\lambda _i^t\nabla _x g(\bar{x}^t,\xi _i). \end{aligned}$$
(23)

Here, we can omit indices with \(g(\bar{x},\xi _i) <0\) due to Lemma 3.1.

We claim now that \(\lambda _i^t\) is uniformly bounded in i and t. If this is not the case, then we have

$$\begin{aligned} \lambda _\mathrm{max}^t:= \max _{i=1,\dots ,S}\lambda _i^t \rightarrow \infty . \end{aligned}$$

Then dividing equation (23) by \(\lambda _\mathrm{max}^t\) yields

$$\begin{aligned} 0= & {} \frac{1}{\lambda _\mathrm{max}^t}\nabla f(\bar{x}^t) + \sum _{{\left\{ i:g(\bar{x},\xi _i)=0,\, \bar{y}_i>0\right\} }}\frac{\lambda _i^t}{\lambda _\mathrm{max}^t} \nabla _x g(\bar{x}^t,\xi _i) \\&+ \sum _{{\left\{ i:g(\bar{x},\xi _i)\ge 0,\ \bar{y}_i=0\right\} }}\frac{\lambda _i^t}{\lambda _\mathrm{max}^t}\nabla _x g(\bar{x}^t,\xi _i). \end{aligned}$$

When taking limit \(t\rightarrow \infty \), the last term vanishes due to Lemma 3.2. Since the first term also converges to zero, we obtain

$$\begin{aligned} 0 = \sum _{{\left\{ i:g(\bar{x},\xi _i)=0,\, \bar{y}_i>0\right\} }}\lim _{t\rightarrow \infty }\frac{\lambda _i^t}{{\lambda _\mathrm{max}^t}} \nabla _x g(\bar{x}^t,\xi _i). \end{aligned}$$

Since \(\frac{\lambda _i^t}{\lambda _\mathrm{max}^t}\in [0,1]\) and at least one of them equals to 1 due to the definition of \(\lambda _\mathrm{max}^t\), this contradicts Assumption 2.1 and thus \(\lambda _i^t\) is indeed bounded.

This means that we may pass to a converging subsequence, say \(\lambda _i^t\rightarrow \lambda _i\). Since \(\lambda _i^t\ge 0\) for all t, the same property holds for \(\lambda _i\). In the light of (23), to finish the proof it suffices to show that \(\lambda _i=0\) for all i such that \(g(\bar{x},\xi _i)\ge 0\) and \(\bar{y}_i=0\). Fix any such i. If \(p^\top \bar{y}^t > 1-\varepsilon \) or \(\phi _t(g(\bar{x}^t,\xi _i)) > \bar{y}_i^t\), then from Lemma 3.1 we have \(\lambda _i^t=0\). In the opposite case, we may use Lemma 3.2 to obtain that \(\lambda _i^t=0\) or there exists j such that \(\frac{\lambda _i^t}{\lambda _j^t}\rightarrow 0\). But the second possibility implies \(\lambda _i^t\rightarrow 0\) due to the boundedness of \(\lambda _j^t\). Thus \((\bar{x},\bar{y})\) is indeed a stationary point of problem (5). \(\square \)

We summarize the previous results in Algorithm 2. We have added several modifications to the core result presented in Theorem 3.1 mainly to increase the performance of the algorithm. We start with regularization parameters \(0<t_1<\dots <t_K\) and possibly with a starting point \((x_0,y_0)\). Provided that f, all \(g(\cdot ,\xi _i)\) and \(h_j\) are convex, we may start with \(\phi _1(z)=1-\frac{1}{M}z\), where M should at least approximately satisfy \(g(\bar{x},\xi _i)\le M\). By doing so, we obtain the “big M” formulation (4), where the binary variables \(y_i\in \{0,1\}\) are relaxed in continuous ones \(y_i\in [0,1].\)

figure b

After potentially solving the convex problem, in step 5 we are looking for a point which satisfies the necessary optimality conditions (16)–(17) with given \(t^k\). In step 6, we may terminate the loop if \((\bar{x}^t,\bar{y}^t)\) is feasible for problem (5) and thus increasing t cannot provide additional benefits or if a stopping criterion is satisfied. After doing so, we select the best solution and check in step 11 whether \(\bar{x}\) is a stationary point of problem (2). If this is not the case, we propose to switch to Algorithm 1. Numerical experience suggests that Algorithm 2 is able to find a stationary point of problem (2) almost in all cases and thus this switching of algorithms did not happen almost at all. We believe that this is linked with the behavior that by regularizing the problem, we reduce the set of stationary points. We present this behavior in the following example.

Example 3.1

Consider the same data as in Example 2.1. From Fig. 1, it can be computed that

$$\begin{aligned} \bar{x}^1 = \frac{1}{\sqrt{4.64}}\begin{pmatrix}0.8\\ 2\end{pmatrix}-\begin{pmatrix}0.5\\ 0\end{pmatrix}\doteq \begin{pmatrix}-0.1286 \\ 0.9285\end{pmatrix}\end{aligned}$$

Since Assumption 2.1 is satisfied at \(\bar{x}^1\), it is a stationary point of this problem. We will show that there is a neighborhood of \(\bar{x}^1\) such that for every \(t>0\), this point is not a stationary point of problem (11). We consider \(\phi _t(z)=e^{-tz}\).

Optimality conditions (16) for (x, y) take form

$$\begin{aligned} \begin{pmatrix}0\\ 0\end{pmatrix}= \begin{pmatrix}2x_1 - 0.6 \\ 2x_2-4\end{pmatrix}- \gamma _1 \phi _t'(g(x,\xi _1))\begin{pmatrix}2x_1 - 1 \\ 2x_2 \end{pmatrix}- \gamma _2 \phi _t'(g(x,\xi _2))\begin{pmatrix}2x_1 + 1 \\ 2x_2 \end{pmatrix}\\ \end{aligned}$$

Since we are interested in a neighborhood of \(\bar{x}^1\), we may consider only x with \(x_2>0\). Then it may be computed that

$$\begin{aligned} \gamma _1 = \frac{2x_1 - 0.8x_2 + 1}{x_2t e^{-tg(x,\xi _1)}},\quad \gamma _2 = -\frac{2x_1 + 0.2x_2 - 1}{x_2te^{-tg(x,\xi _2)}}. \end{aligned}$$
(24)

Since \(\nabla f(x)\ne 0\), Lemma 3.1 combined with (16) implies \(\alpha >0\). Combining this with (18) yields \(y_1+y_2=1\). Using again Lemma 3.1, we see that \(0<y_i=\phi _t(g(x,\xi _i))<1\), which subsequently implies \(\beta _i=0\) and (17) then implies that \(\gamma _1=\gamma _2\). Plugging this back into (24), we see that

$$\begin{aligned} \frac{2x_1-0.8x_2+1}{2x_1+0.2x_2-1} = -\frac{e^{tg(x,\xi _2)}}{e^{tg(x,\xi _1)}}. \end{aligned}$$
(25)

But when we are close to \(\bar{x}^1\), the left-hand side is close to 0 and the right-hand one is close to infinity. This shows that there are indeed no stationary points of the regularized problem in the vicinity of \(\bar{x}^1\).

As we have already mentioned, this means that problem (11) is able to ignore stationarity points of the original problem (2). This phenomenon is depicted in Fig. 3, where we show the path taken by the regularized problem with starting point \(\bar{x}^1\). The circles depict optimal points for certain regularization parameters t. Thus, Algorithm 2 is able to find global minimum (2) even when starting from its local minimum.

Fig. 3
figure 3

Algorithm 2 is able to converge from a local optimum \(\bar{x}^1\) of problem (2) to its global minimum \(\bar{x}^2\). The circles denote updates of t

Full size image

4 Numerical Results

In this section, we compare the proposed algorithms. We have implemented both Algorithm 1 based on relaxed problem (5) and Algorithm 2 for regularized problem (11). For solving mixed-integer program (4), we have used CPLEX and BONMIN solvers with GAMS 24.3.3. Otherwise, the codes were run in MATLAB 2015a and are freely available on authors’ webpage.

It is well known that the choice of M in problem (4) can significantly influence the quality of solutions and the computational time, see [32]. Too big M leads to constraints which are not tight and thus difficult to handle for mixed-integer solvers. In all problems, we considered \(\phi _t(z)=e^{-tz}\). Further, we have chosen \(t^1=1\) and \(t^{k+1}=2.5t^k\).

In the test problem, we consider the \(l_1\) norm maximization problem with nonlinear random budget constraints which can be formulated as follows

(26)

The problem has been already solved by [20, 23, 33] using CVaR and difference of convex approximations. However, the codes were not made available by the authors; thus, we do not attach any comparison with our techniques. We consider samples from standard normal distribution with realizations \(\xi _{ji}\) with \(j = 1, \dots , n\) and \(i = 1, \dots , S\), which leads to \(g(x,\xi _i) = \sum _{j=1}^{n} \xi _{ji}^2 x_j^2 - b\).

We considered the following data: \(S \in \{100, 500\}\), \(b = 10\), \(\varepsilon = 0.05\) and \(n = 10\). For result robustness, we have run the above problem, with different random vector realizations, multiple times, specifically 100 times for \(S=100\) and 10 times for \(S=500\). We have employed eight different algorithm modifications, based on both continuous and mixed-integer reformulation. For the continuous solvers, we have solved relaxed problem (5) via Algorithm 1 and regularized problem (11) via Algorithm 2 with and without convex start. For the mixed-integer reformulation, we have solved problem (4) and used CPLEX and BONMIN with both \(M=50\) and \(M=1000\). Since BONMIN had time issues for \(M=1000\), we imposed time limit T.

We summarize the obtained results in Table 1. The used algorithms were described in the previous paragraph. Column success denotes the percentage for which the obtained point is a stationary point of the original problem (2). Columns objective, reliability and time then denote the average objective value, the reliability (percentage of satisfied constraints \(g(x,\xi _i)\le 0\)) and the elapsed time in seconds, respectively.

Table 1 Comparison of various algorithms for problem (26) with \(S=100\) scenarios
Full size table

We see that the regularized problem performs much better than the relaxed problem. If we run CPLEX or BONMIN with a good initial estimate for M, then these mixed-integer algorithms perform comparable with our solvers. However, if we decrease the precision of the initial estimate of M, then the objective value gets worse and the computation time explodes. If we impose on BONMIN the time limit of one minute, which is still about 30 times greater than the average time for the regularized problem, the quality of the solution decreases even more.

Results for \(S=500\) are given in Table 2. In one of the problems, CPLEX was not able to solve the problem and returned zeros as the optimal solution. We have omitted this run from the results for all solvers. Note that all solvers were comparable with the exception of elapsed time. While the average of regularized solver was below ten minutes, neither of the mixed-integer solvers was able to converge under one hour in any single case. This can be seen in the column reliability, where the mixed-integer solvers were not able to identify the correct \(95\,\%\) precisely. Moreover, even though the objective was rather good for BONMIN, it was not able to identify a local minimum in any run.

Table 2 Comparison of various algorithms for problem (26) with \(S=500\) scenarios
Full size table

5 Conclusions

We have developed new numerical methods for solving chance constrained problems. These methods are based on necessary optimality conditions which have been derived for the original CCP, and both relaxed and regularized problems. The first algorithm is based on modification of the auxiliary variables in the relaxed problem. Using this approach, we are able to move toward a stationary point of the original problem. The second algorithm is based on the proved convergence of a sequence of stationary points of the regularized problem to a stationary point of the relaxed problem. Numerical experiments suggest a very good behavior of the proposed methods on medium-sized nonconvex problems.