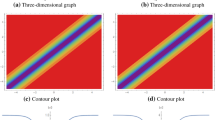
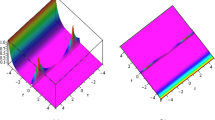
Abstract
The current paper recovers soliton solutions in magneto-optic waveguides having generalized form of Kudryashov’s self-phase modulation structure. The retrieval of soliton solutions is achieved by the well-known and primitive \(G^{\prime }/G\)-expansion scheme. The intermediary functions that made this retrieval possible are Jacobi’s elliptic functions and Weierstrass’ elliptic functions. The parameter constraints for the solitons to exist are also presented.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
One of the inherent hurdles for soliton propagation through fibers and other waveguides is the clutter they form [1,2,3,4,5]. Therefore to circumvent this problem is to introduce magneto-optic waveguides [6,7,8,9,10]. Such form of waveguides transforms the solitons state of clutter to a state of separation so that a smooth and laminar flow of solitons is ensured through the fibers for intercontinental distances [11,12,13,14,15]. The current paper is about the transmission of solitons through a magneto-optic waveguide that comes with Kudryashov’s form of self-phase modulation structure [16,17,18,19,20]. This is the model that is being considered for the first time in this paper. The model is integrated by the aid of generalized \(G^{\prime }/G\)-expansion scheme [21,22,23,24,25]. This is an efficient scheme that yielded a full spectrum of optical solitons through magneto-optic waveguides through a couple of intermediary function. These are Jacobi’s elliptic functions [26,27,28,29,30] and Weierstrass’ elliptic functions [31,32,33,34,35]. In both cases optical soliton solutions emerged as special cases when the modulus approached unity in its limit or as a special case of the Weierstrass’ elliptic functions. These solitons came with their respective parameter constraints that are also presented in the work. The results are exhibited after a detailed introduction to the model. The details are jotted in the rest of the paper.
Governing model
Considering the variables \(a_{l}, b_{l}, c_{l}, d_{l}, e_{l}, f_{l}, g_{l}, h_{l}, k_{l}, Q_{l}, \beta _{l}, \lambda _{l}, \gamma _{l},\) and \(\theta _{l}\) for \(l=1,2\) as real-valued constants and \(i=\sqrt{-1}\), this framework encompasses Eqs. (1) and (2) that focus on the complex-valued soliton profiles represented by the dependent variables q(x, t) and r(x, t). These equations, set against the backdrop of spatial and temporal dimensions denoted by x and t, outline the linear temporal evolutions through their first terms. Within this setup, \(a_{l}\) coefficients are chromatic dispersions, managing the spread of light in a spectrum, while \(b_{l}\), \(c_{l}\), \(d_{l},\) and \(e_{l}\) correspond to self-phase modulation, impacting the light beam’s phase. The coefficients \(f_{l}\), \(g_{l}\), \(h_{l}\), and \(k_{l}\) are related to cross-phase modulation, indicating interactions among multiple light waves. Additionally, \(Q_{l}\) and \(\beta _{l}\) stand for magneto-optic parameters and inter-modal dispersions (IMD), critical in light propagation dynamics. The terms \(\lambda _{l}\) are associated with preventing shock waves through self-steepening (SS), while \(\gamma _{l}\) and \(\theta _{l}\) account for nonlinear dispersion (ND), crucial in the phase velocity’s intensity-dependent variation. This study also supplements its results with those obtained through the unified auxiliary equation method and the new mapping method, as discussed in references [24] and [25], enriching the analysis with diverse methodological perspectives.
Mathematical preliminaries
In order to solve Eqs. (1) and (2), we assume that the solutions of Eqs. (1) and (2) have the following forms:
where the real functions \(\psi _{j}(\zeta )\) for \(j=1,2\) represent the amplitude portion of the soliton and \(\digamma \left( x,t\right)\) is the phase component of the pulse, v is the speed of the wave, k is the frequency, \(\omega\) is the wave number and \(\theta _{0}\) is the phase constant. Next, insert (3) with (4) into Eqs. (1) and (2), and then the real parts are:
and
where \({}^{\prime }=\frac{d}{d\zeta }.\) The imaginary parts are:
The linearly independent principle is applied on Eqs. (8) and (9) to obtain:
where \(j=1,~2.\)
Let us set
where \(\mho\) is a nonzero constant, such that \(\mho \ne 1.\) As a results Eqs. (6) and (7) reduce to
Equations (13) and (14) have the same form under the following constraint conditions:
From (18), the wave number \(\omega\) is given by
Balancing \(\psi _{1}^{2n-1}\psi _{1}^{\prime \prime }\) and \(\psi _{1}^{4n}\) in Eq. (13) gives \(N=\frac{1}{n}\). Therefore, the new wave transformation
changes Eq. (13) to the following new nonlinear ordinary differential equation:
where \(\phi (\zeta )\) is a new function of \(\ \zeta\), such that \(\phi (\zeta )>0\) for \(n>0\), and
Generalized \(\left( G^{\prime }/G\right)\)-expansion
By balancing \(\phi \phi ^{\prime \prime }\) and \(\phi ^{4}\) in Eq. (23), one obtains \(N=1.~\)The \(\left( G^{\prime }/G\right)\) expansion method [26,27,28] assumes the formal solution of Eq. (23) as:
and the function \(G(\zeta )\) satisfies the following Jacobi elliptic equation:
where \(A_{0},~A_{1},~R,~Q\) and P are constants, with the condition \(A_{1}\ne 0\). It is well-known that Eq. (26) gives many explicit solutions in terms of Jacobi elliptic functions and Weierstrass-elliptic functions [26,27,28,29,30] as the following tables:
By differentiating Eq. (25) and successively applying Eq. (26), one can obtain the following derivatives:
By substituting (25) and (27) into Eq. (23) and collecting all the coefficients of \(\left( \tfrac{G^{\prime }(\zeta )}{G(\zeta )} \right) ^{i},~(i=0,~1,~2,~3,~4)\) and setting them equal to zero, we obtain the following algebraic equations:
On solving the algebraic equations \(\left( \tfrac{G^{\prime }(\zeta )}{G(\zeta )} \right) ^{0}-\left( \tfrac{G^{\prime }(\zeta )}{G(\zeta )}\right) ^{4}\) using Maple or Mathematica, we have the following result:
via the restrictions
provided \(a_{1}\Delta _{4}<0\) and \(\Delta _{4}\left( n^{2}\Delta _{2}-2Qa_{1}\right) >0.\)
By substituting (28) into (25), the general exact solution of Eq. (23) obtains as follows:
Now, according to Tables 1 and 2. and the general formal solution (30), we deduce the following set of optical solitons of Eqs. (1) and (2):
Case-1: If \(P=\tau ^{2},~Q=-(\tau ^{2}+1),~R=1,~0<\tau <1\) and \(G(\zeta )=\textrm{ sn}\left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}+2a_{1}(\tau ^{2}+1)}{\Delta _{4}}>0.\)
In particular, if \(\tau \rightarrow 1\), then Eqs. (1) and (2) have the straddled solitons
Case-2: If \(P=\tau ^{2},~Q=-\left( 1+\tau ^{2}\right) ,~R=1,~0<\tau <1\) and \(G(\zeta )=\textrm{cd}\left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}+2a_{1}\left( 1+\tau ^{2}\right) }{\Delta _{4}} >0.\)
Case-3: If \(P=-\tau ^{2},~Q=2\tau ^{2}-1,~R=1-\tau ^{2},~0<\tau <1\) and \(G(\zeta )= \mathrm {\text {cn}}\left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-2a_{1}\left( 2\tau ^{2}-1\right) }{\Delta _{4}} >0.\)
In particular, if \(\tau \rightarrow 1\), then Eqs. (1) and (2) have the dark solitons
provided \(\tfrac{n^{2}\Delta _{2}-2a_{1}}{\Delta _{4}}>0.\)
Case-4: If \(P=-1,~Q=2-\tau ^{2},~R=\tau ^{2}-1,~0<\tau <1\) and \(G(\zeta )=\mathrm { \text {dn}}\left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-2a_{1}\left( 2-\tau ^{2}\right) }{\Delta _{4}} >0.\)
In particular, if \(\tau \rightarrow 1\), then Eqs. (1) and (2) have the same dark solitons (39) and (40).
Case-5: If \(P=1-\tau ^{2},~Q=2-\tau ^{2},~R=1,~0<\tau <1\) and \(G(\zeta )=\textrm{ sc}\left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-2a_{1}\left( 2-\tau ^{2}\right) }{\Delta _{4}} >0.\)
In particular, if \(\tau \rightarrow 1\), then Eqs. (1) and (2) have the singular solitons
provided \(\tfrac{n^{2}\Delta _{2}-2a_{1}}{\Delta _{4}}>0.\)
Case-6: If \(P=-\tau ^{2}\left( 1-\tau ^{2}\right) ,~Q=2\tau ^{2}-1,~R=1,~0<\tau <1\) and \(G(\zeta )=\textrm{sd}\left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-2a_{1}\left( 2\tau ^{2}-1\right) }{\Delta _{4}} >0.\)
In particular, if \(\tau \rightarrow 1\), then Eqs. (1) and (2) have the same singular solitons (45) and (46).
Case-7: If \(P=\frac{1}{4},~Q=\frac{1-2\tau ^{2}}{2},~R=\frac{1}{4},~0<\tau <1\) and \(G(\zeta )=\mathrm {\text {ns}}\left( \zeta ,\tau \right) \pm \textrm{cs} \left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-a_{1}\left( 1-2\tau ^{2}\right) }{6n^{2}\Delta _{4}}>0.\)
In particular, if \(\tau \rightarrow 1\), then Eqs. (1) and (2) have the singular solitons
provided \(\tfrac{n^{2}\Delta _{2}+a_{1}}{\Delta _{4}}>0.\)
Case-8: If \(P=\frac{1-\tau ^{2}}{4},~Q=\frac{1+\tau ^{2}}{2},~R=\frac{ 1-\tau ^{2}}{4},~0<\tau <1\) and \(G(\zeta )=\mathrm {\text {nc}}\left( \zeta ,\tau \right) \pm \textrm{sc}\left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-a_{1}\left( 1+\tau ^{2}\right) }{\Delta _{4}} >0.\)
Case-9: If \(P=\frac{\tau ^{2}}{4},~Q=\frac{\tau ^{2}-2}{2},~R=\frac{\tau ^{2}}{4 },~0<\tau <1\) and \(G(\zeta )=\mathrm {\text {ns}}\left( \zeta ,\tau \right) \pm \mathrm { \text {ds}}\left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-a_{1}\left( \tau ^{2}-2\right) }{\Delta _{4}} >0.\)
In particular, if \(\tau \rightarrow 1\), then Eqs. (1) and (2) have the same singular solitons (51) and (52).
Case-10: If \(P=\frac{\tau ^{2}}{4},~Q=\frac{\tau ^{2}-2}{2},~R=\frac{\tau ^{2} }{4},~0<\tau <1\) and \(G(\zeta )=\sqrt{\tau ^{2}-1}\mathrm {\text {sd}}\left( \zeta ,\tau \right) \pm \textrm{cd}\left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-a_{1}\left( \tau ^{2}-2\right) }{\Delta _{4}} >0.\)
Case-11: If \(P=\frac{\tau ^{2}-1}{4},~Q=\frac{1+\tau ^{2}}{2},~R=\frac{ \tau ^{2}-1}{4},~0<\tau <1\) and \(G(\zeta )=\tau \mathrm {\text {sd}}\left( \zeta ,\tau \right) \pm \textrm{nd}\left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-a_{1}\left( 1+\tau ^{2}\right) }{\Delta _{4}} >0.\)
Case-12: If \(P=\frac{\tau ^{2}}{4},~Q=\frac{\tau ^{2}-2}{2},~R=\frac{\tau ^{2}}{ 4},~0<\tau <1\) and \(G(\zeta )=\mathrm {\text {dc}}\left( \zeta ,\tau \right) \pm \sqrt{ 1-\tau ^{2}}\textrm{nc}\left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-a_{1}\left( \tau ^{2}-2\right) }{\Delta _{4}} >0.\)
Case-13: If \(P=1,~Q=2\left( 1-2\tau ^{2}\right) ,~R=1,~0<\tau <1\) and \(G(\zeta )=\mathrm {\text {sc}}\left( \zeta ,\tau \right) \mathrm {\text {dn}}\left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-4a_{1}\left( 1-2\tau ^{2}\right) }{\Delta _{4}} >0.\)
In particular, if \(\tau \rightarrow 1\), then Eqs. (1) and (2) have the same straddled solitons (33) and (34).
Case-14: If \(P=\tau ^{4},~Q=2\left( \tau ^{2}-2\right) ,~R=1,~0<\tau <1\) and \(G(\zeta )=\mathrm {\text {sd}}\left( \zeta ,\tau \right) \mathrm {\text {cn}}\left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-4a_{1}\left( \tau ^{2}-2\right) }{\Delta _{4}} >0.\)
In particular, if \(\tau \rightarrow 1\), then Eqs. (1) and (2) have the same straddled solitons (33) and (34).
Case-15: If \(P=1,~Q=2\left( \tau ^{2}+1\right) ,~R=1-2\tau ^{2}+\tau ^{4},~0<\tau <1\) and \(G(\zeta )=\text {cs}\left( \zeta ,\tau \right) \mathrm {\text {dn}}\left( \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-4a_{1}\left( \tau ^{2}+1\right) }{\Delta _{4}} >0.\)
In particular, if \(\tau \rightarrow 1\), then Eqs. (1) and (2) have the straddled solitons
provided \(\tfrac{n^{2}\Delta _{2}-8a_{1}}{\Delta _{4}}>0.\)
Case-16: If \(R=\frac{\tau ^{2}Q^{2}}{\left( \tau ^{2}+1\right) ^{2}P},~Q<0,~P>0,~0<\tau <1\) and \(G(\zeta )=\sqrt{-\tfrac{\tau ^{2}Q}{\left( \tau ^{2}+1\right) ^{2}P}}\text {sn}\left( \sqrt{-\tfrac{Q}{\left( \tau ^{2}+1\right) }}\zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-2a_{1}Q}{\Delta _{4}}>0.\)
In particular, if \(\tau \rightarrow 1\), then Eqs. (1) and (2) have the straddled solitons
Case-17: If \(R=\frac{\left( 1-\tau ^{2}\right) Q^{2}}{\left( \tau ^{2}-2\right) ^{2}P},~Q>0,~P<0,~0<\tau <1\) and \(G(\zeta )=\sqrt{-\tfrac{Q}{\left( 2-\tau ^{2}\right) P}}\text {dn}\left( \sqrt{\tfrac{Q}{\left( 2-\tau ^{2}\right) }} \zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-2a_{1}Q}{\Delta _{4}}>0.\)
In particular, if \(\tau \rightarrow 1\), then Eqs. (1) and (2) have the dark solitons
Case-18: If \(R=\frac{\tau ^{2}\left( \tau ^{2}-1\right) Q^{2}}{\left( 2\tau ^{2}-1\right) ^{2}P},~Q>0,~P<0,~0<\tau <1\) and \(G(\zeta )=\sqrt{-\frac{\tau ^{2}Q}{ \left( 2\tau ^{2}-1\right) P}}\text {cn}\left( \sqrt{\frac{Q}{\left( 2\tau ^{2}-1\right) }}\zeta ,\tau \right) ,\) we have the Jacobi elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-2a_{1}Q}{\Delta _{4}}>0.\)
In particular, if \(\tau \rightarrow 1\), then Eqs. (1) and (2) have the same dark solitons (77) and (78).
Case-19: If \(g_{2}=\frac{4\left( Q^{2}-3PR\right) }{3},~g_{3}=\frac{ 4Q\left( -2Q^{2}+9PR\right) }{27}\) and \(G(\zeta )=\sqrt{\frac{1}{P}\left( \wp \left( \zeta ;g_{2},g_{3}\right) -\frac{Q}{3}\right) },\) we have the Weierstrass-elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-2a_{1}Q}{\Delta _{4}}>0.\)
Case-20: If \(g_{2}=\frac{4\left( Q^{2}-3PR\right) }{3},~g_{3}=\frac{ 4Q\left( -2Q^{2}+9PR\right) }{27}\) and \(G(\zeta )=\sqrt{\frac{3R}{3\wp \left( \zeta ;g_{2},g_{3}\right) -Q}},\) we have the Weierstrass-elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-2a_{1}Q}{\Delta _{4}}>0.\)
Case-21: If \(g_{2}=\frac{Q^{2}}{12}+PR,~g_{3}=\frac{Q\left( 36PR-Q^{2}\right) }{216}\) and \(G(\zeta )=\frac{\sqrt{R}\left[ 6\wp \left( \zeta ;g_{2},g_{3}\right) +Q\right] }{3\wp ^{\prime }\left( \zeta ;g_{2},g_{3}\right) },\) we have the Weierstrass-elliptic function solutions
provided \(\frac{n^{2}\Delta _{2}-2a_{1}Q}{6n^{2}\Delta _{4}}>0.\)
Case-22: If \(g_{2}=\frac{Q^{2}}{12}+PR,~g_{3}=\frac{Q\left( 36PR-Q^{2}\right) }{216}\) and \(G(\zeta )=\tfrac{3\wp ^{\prime }\left( \zeta ;g_{2},g_{3}\right) }{\sqrt{P\,}\left[ 6\wp \left( \zeta ;g_{2},g_{3}\right) +Q \right] },\) we have the Weierstrass-elliptic function solutions
provided \(\frac{n^{2}\Delta _{2}-2a_{1}Q}{\Delta _{4}}>0.\)
Case-23: If \(g_{2}=\frac{2Q^{2}}{9},~g_{3}=\frac{Q^{3}}{54},~R= \frac{5Q^{2}}{36P}\) and \(G(\zeta )=\tfrac{Q\sqrt{-\frac{15Q}{2P}}\wp \left( \zeta ;g_{2},g_{3}\right) }{3\wp \left( \zeta ;g_{2},g_{3}\right) +Q},\) we have the Weierstrass-elliptic function solutions
provided \(\tfrac{n^{2}\Delta _{2}-2a_{1}Q}{6n^{2}\Delta _{4}}>0.\)
Remark-1: All the results obtained in this article satisfy Eq. (23) under the given constraints outlined in (29).
Remark-2: The above solutions (31)–(90) are new and not found in [24, 25] or elsewhere.
Conclusions
This paper recovered a complete spectrum of optical solitons propagating through magneto-optic waveguides that comes with Kudryashov’s form of self-phase modulation structure. The integration scheme is the age-old version of the then-popular, although not robust, \(G^{\prime }/G\)-expansion scheme. The recovered results are a complete spectrum of optical solitons that emerged through a couple of intermediary functions. These are the Jacobi’s elliptic functions and the Weierstrass’ elliptic functions. The soliton solutions came with parameter constraints that are also presented in the entire paper. It is not out of place to point out that the adopted integration scheme fails to recover soliton radiation. Thus the integration algorithm carries a gigantic loophole. Therefore, the results of this manuscript are indeed technically incorrect with no soliton radiation components in them. In future, this will be rectified with the implementation of the inverse scattering transform [36,37,38,39] or so. This work is therefore an eye-opener !!!
References
G.P. Agrawal, Nonlinear Fiber Optics, 3rd edn. (Academic Press, 2001)
Y.S. Kivshar, G.P. Agrawal, Optical Solitons: From Fibers to Photonic Crystals (Academic Press, 2003)
M.J. Ablowitz, P.A. Clarkson, Solitons, Nonlinear Evolution Equations and Inverse Scattering (Cambridge University Press, 1991)
A. Biswas, D. Milovic, M. Edwards, Mathematical Theory of Dispersion-Managed Optical Solitons (Springer, 2010)
S.K. Turitsyn, B.G. Bale, M.P. Fedoruk, Dispersion-managed solitons in fibre systems and lasers. Phys. Rep. 521, 135–203 (2012)
N. Raza, A. Javid, Generalization of optical solitons with dual dispersion in the presence of Kerr and quadratic-cubic law nonlinearities. Mod. Phys. Lett. B 33, 1850427 (2019)
M. Mirzazadeh, M. Eslami, B.F. Vajargah, A. Biswas, Optical solitons and optical Rogons of generalized resonant dispersive nonlinear Schr ödinger’s equation with power law nonlinearity. Optik 125, 4246–4256 (2014)
E.M.E. Zayed, R.M. Shohib, M.E. Alngar, New extended generalized Kudryashov method for solving three nonlinear partial differential equations. Nonlinear Anal. Model. Control 25, 598–617 (2020)
E.M.E. Zayed, M. El-Shater, K.A.E. Alurrfi, A.H. Arnous, N.A. Shah, J.D. Chung, Dispersive optical soliton solutions with the concatenation model incorporating quintic order dispersion using three distinct schemes. AIMS Math. 9, 8961–8980 (2024)
S.A. Durmus, N. Ozdemir, A. Secer, M. Ozisik, M. Bayram, Bright soliton of the third-order nonlinear Schrödinger equation with power law of self-phase modulation in the absence of chromatic dispersion. Opt. Quantum Electron. 56, 1–17 (2024)
M.A.S. Murad, Analyzing the time-fractional (3+1)-dimensional nonlinear Schrödinger equation: a new Kudryashov approach and optical solutions. Int. J. Comput. Math. 1–14 (2024)
S.A. Durmus, N. Ozdemir, A. Secer, M. Ozisik, M. Bayram, Examination of optical soliton solutions for the perturbed Schrö dinger-Hirota equation with anti-cubic law in the presence of spatiotemporal dispersion. Eur. Phys. J. Plus 139, 464 (2024)
N. Kudryashov, S. Lavrova, D. Nifontov, Analytical solutions and conservation laws of the generalized model for propagation pulses with four powers of nonlinearity. Opt. Quantum Electron. 56, 1110 (2024)
E.M.E. Zayed, K.A.E. Alurrfi, A.H. Arnous, M.S. Hashemi, M. Bayram, Effects of high dispersion and generalized non-local laws on optical soliton perturbations in magneto-optic waveguides with sextic-power law refractive index. Nonlinear Dyn. 112, 8507–8525 (2024)
E.M.E. Zayed, K.A.E. Alurrfi, M. Elshater, Y. Yildirim, Dispersive optical solitons with stochastic Radhakrishnan-Kundu-Lakshmanan equation in magneto-optic waveguides having power law nonlinearity and multiplicative white noise. Ukr. J. Phys. Opti. 25, S1086–S1112 (2024)
E.M.E. Zayed, A.-G. Al-Nowehy, A.H. Arnous, M.S. Hashemi, M.A.S. Murad, M. Bayram, Investigating the generalized Kudryashov’s equation in magneto-optic waveguide through the use of a couple integration techniques. J. Opt. (2024) https://doi.org/10.1007/s12596-024-01857-3
E.M.E. Zayed, M.E. Alngar, R.M. Shohib, Optical solitons in magneto-optic waveguides for perturbed NLSE with Kerr law nonlinearity and spatio-temporal dispersion having multiplicative noise via Itô calculus. Optik 276, 170682 (2023)
N.A. Kudryashov, A generalized model for description of propagation pulses in optical fiber. Optik 189, 42–52 (2019)
S. Arshed, A. Arif, Soliton solutions of higher-order nonlinear Schrödinger equation (NLSE) and nonlinear Kudryashov’s equation. Optik 209, 164588 (2020)
A. Biswas, A.H. Arnous, M. Ekici, A. Sonmezoglu, A.R. Seadawy, Q. Zhou et al., Optical soliton perturbation in magneto-optic waveguides. J. Nonlinear Opt. Phys. Mater. 27, 1850005 (2018)
A. Biswas, Solitons in magneto-optic waveguides. Appl. Math. Comput. 153, 87–93 (2004)
M. Savescu, A.H. Bhrawy, E.M. Hilal, A.A. Alshaery, A. Biswas, Optical solitons in magneto-optic waveguides with spatio-temporal dispersion. Frequenz 68, 445–51 (2014)
M.I. Asjad, N. Ullah, H.U. Rehman, M. Inc, Construction of optical solitons of magneto-optic waveguides with anti-cubic law nonlinearity. Opt. Quantum Electron. 53, 646 (2021)
E.M.E. Zayed, M.E. Alngar, A. Biswas, M. Asma, M. Ekici, A.K. Alzahrani, M.R. Belic, Solitons in magneto-optic waveguides with Kudryashov’s law of refractive index. Chaos Solitons Fractals 140, 110129 (2020)
E.M.E. Zayed, K.A.E. Alurrfi, R.A. Alshbear, On application of the new mapping method to magneto-optic waveguides having Kudryashov’s law of refractive index. Optik 287, 171072 (2023)
E.M.E. Zayed, New traveling wave solutions for higher dimensional nonlinear evolution equations using a generalized \(\left( G^{\prime }/G\right)\)-expansion method. J. Phys. A Math. Theor. 42, 195202 (2009)
E.M.E. Zayed, K.A.E. Alurrfi, Extended generalized \(\left( G^{\prime }/G\right)\)-expansion method for solving the nonlinear quantum Zakharov-Kuznetsov equation. Ricerche Mat. 65, 235–254 (2016)
Y. Yang, Y. He, A. Feng, New Jacobi elliptic function solutions for coupled KdV-mKdV equation. In Proceedings of the World Congress on Engineering and Computer Science (WCECS 2014), vol. 2 (2014)
A. Ebaid, E.H. Aly, Exact solutions for the transformed reduced Ostrovsky equation via the F-expansion method in terms of Weierstrass-elliptic and Jacobian-elliptic functions. Wave Motion 49, 296–308 (2012)
A.H. Arnous, M.S. Hashemi, K.S. Nisar, M. Shakeel, J. Ahmad, I. Ahmad, R. Jan, A. Ali, M. Kapoor, N.A. Shah, Investigating solitary wave solutions with enhanced algebraic method for new extended Sakovich equations in fluid dynamics. Results Phys. 57, 107369 (2024)
M.E. Alngar, A.M. Mostafa, S.A. AlQahtani, R.M. Shohib, P. Pathak. Highly dispersive eighth-order embedded solitons with cubic-quartic \(\chi\) (2) and \(\chi\) (3) nonlinear susceptibilities under the influence of multiplicative white noise using Itô calculus. Mod. Phys. Lett. B 2450474 (2024).
M.E. Alngar, A.M. Alamri, S.A. AlQahtani, R.M. Shohib, P. Pathak. Exploring optical soliton solutions in highly dispersive couplers with parabolic law nonlinear refractive index using the extended auxiliary equation method. Mod. Phys. Lett. B 2450350 (2024)
Y. Chahlaoui, R.M. Shohib, M.E. Alngar, Perturbed Biswas-Milovic equation with Kudryashov’s law of refractive index: analysis and solutions for nonlinear optical systems. Opt. Quantum Electron. 56(7), 1108 (2024)
S.A. AlQahtani, M.E. Alngar, Soliton solutions of perturbed NLSE-CQ model in polarization-preserving fibers with cubic-quintic-septic-nonic nonlinearities. J. Opt. (2023). https://doi.org/10.1007/s12596-023-01526-x
S.A. AlQahtani, M.E. Alngar, R.M. Shohib, A.M. Alawwad, Enhancing the performance and efficiency of optical communications through soliton solutions in birefringent fibers. J. Opt. (2024). https://doi.org/10.1007/s12596-023-01490-6
S.A. AlQahtani, M.E. Alngar, Soliton solutions for coupled nonlinear generalized Zakharov equations with anti-cubic nonlinearity using various techniques. Int. J. Appl. Comput. Math. 10(1), 9 (2024)
S.A. AlQahtani, M.E. Alngar, R.M. Shohib, P. Pathak, Highly dispersive embedded solitons with quadratic \(\chi\) (2) and cubic \(\chi\) (3) non-linear susceptibilities having multiplicative white noise via Itô calculus. Chaos Solitons Fractals 171, 113498 (2023)
M. Savescu, E.M. Hilal, A.A. Alshaery, A.H. Bhrawy, L. Moraru, A. Biswas, Optical solitons with quadratic nonlinearity and spatio-temporal dispersion. J. Optoelectron. Adv. Mater. 16, 619–623 (2014)
Y. Yıldırım, A. Biswas, M. Ekici, O. Gonzalez-Gaxiola, S. Khan, H. Triki, M.R. Belic, Optical solitons with Kudryashov’s model by a range of integration norms. Chin. J. Phys. 66, 660–672 (2020)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors claim there is no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zayed, E.M.E., Alurrfi, K.A.E., Alshbear, R.A. et al. Solitons in magneto-optic waveguides with generalized Kudryashov’s form of self-phase modulation structure. J Opt (2024). https://doi.org/10.1007/s12596-024-02188-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12596-024-02188-z