Construction of optical solitons of magneto-optic waveguides with anti-cubic law nonlinearity

Abstract

Two efficient integration schemes, new extended hyperbolic function and generalized tanh are employed to discover optical soliton solutions to magneto-optic waveguides that retains anti-cubic form of nonlinear refractive index. Bright, dark, periodic singular, singular, and combo soliton solutions have created. These solutions expose the comprehensive variety of soliton solutions.

1 Introduction

Optical solitons have a variety of applications in different optoelectronic tools such as optical couplers, birefringent fibers, polarization-preserving fibers, magneto-optic waveguides (MOW), metasurfaces and metamaterials as well as in wavelength division multiplexed structures and photonic crystal fibers. An abundant of results have been stated in all of these areas (Khater et al. 2020; Akinyemi 2021; Ali Akbar et al. 2021; Akinyemi et al. 2020; Akinyemi 2019; Raza 2020; Dotsch et al. 2005; Fedele et al. 2003; Guzman et al. 2014; Haider 2017; Hasegawa and Miyazaki 1992; Raza and Arshed 2020; Rehman et al. 2021a; b; c; Khan 2020; Kudryashov 2019; Qiu et al. 2019; Shoji and Mizumoto 2018; Wazwaz 2008; Yan et al. 2009; Zayed et al. 2020; Imran et al. 2020; Rehman et al. 2019; Zayed et al. 0000; Dai et al. 2017; Dai et al. 2020; Wang et al. 2018; Dai et al. 2019; Younas and Ren 2021; Bilal et al. 2021a; Bilal et al. 2021b; Bilal et al. 2021c; Bilal et al. 2021d). This paper describes dynamics behavior of solitons for MOW that retains anti-cubic (AC) form of nonlinear refractive index (NLRI). The RI law was first suggested during 2003 and far ahead it was considered all across (Fedele et al. 2003). In this paper the construction of optical solitons solutions is made by using new extended hyperbolic function method (EHFM) and generalized tanh methods. In this work, purpose is to construct dark, singular and bright soliton solutions along with trigonometric and hyperbolic functions solutions for MOW with AC form of nonlinear RI. It is important that these discovered results are novel, correct and are being stated earliest in this paper. Likewise, it should be noted that the solitons discovered to MOW with AC law nonlinearity will be highly favorable in the fiber-optic communication technology.

This paper is structured as: Sect. 2 contains the governing medel. New extended hyperbolic function method and its application for MOW with AC nonlinearity are described in Sect. 3. Section 4 consists generalized tanh method and its application for the MOW with AC nonlinearity. Section 5 contains results and discussion and Sect. 6 occupys the conclusion of this work.

2 Governing model

A set of two nonlinear Schrödinger equations (NLSEs) in MOW with AC law nonlinearity is stated as

$$\begin{aligned}&\iota q_t+a_1q_{xx}+\bigg (\frac{b_{11}}{|q|^4}+b_{12}|q|^2+b_{13}|q|^4+\frac{c_{11}}{|r|^4} +c_{12}|r|^2+c_{13}|r|^4\bigg )q=Q_{1}r+\iota [\alpha _1q_x\nonumber \\&\quad +\lambda _1(|q|^2q)_x+\theta _1|q|^2 q_{x}+v_1(|q|^2)_x q], \end{aligned}$$

(1)

$$\begin{aligned}&\iota r_t+a_2r_{xx}+\bigg (\frac{b_{21}}{|r|^4}+b_{22}|r|^2 +b_{23}|r|^4+\frac{c_{21}}{|q|^4}+c_{22}|q|^2 +c_{23}|q|^4\bigg )r=Q_{2}q+\iota [\alpha _2r_x\nonumber \\&\quad +\lambda _2(|r|^2r)_x+\theta _2|r|^2 r_{x}+v_2(|q|^2)_x r], \end{aligned}$$

(2)

where $a_1, ~b_{11},~ b_{12},~ b_{13},~ c_{11},~ c_{12},~ c_{13},~ Q_1,~ \alpha _1,~ \lambda _1,~ \nu _1$ and $\theta _1$ are constants, for $l = 1, 2$, while $\iota =\sqrt{-1}$. Where q(x, t) and r(x, t) are dependent variables of complex valued while x and t are spatial and temporal independent variables. Here $a_1$ is the coefficients of chromatic dispersion (CD), while coefficients of SPM are $b_{11}$, $b_{12}$ and $b_{13}$, whetre $c_{11}$, $c_{12}$ and $c_{13}$ are the terms of XPM. On the right side, $\alpha _1$ and $Q_1$ are the coefficients of inter-modal dispersions (IMD) and magneto-optic parameters while $\lambda _1$ gives the self-steepening (SS) terms. Lastly, $\nu _1$ and $\theta _1$ are the coefficients of nonlinear dispersion.

2.1 Mathematical analysis

From (1) and (2), we choose the supposition as follows

$$\begin{aligned} q(x,t)= & {} P_1(\eta ) e^{\iota Y}, \end{aligned}$$

(3)

$$\begin{aligned} r(x,t)= & {} P_2(\eta ) e^{\iota Y}, \end{aligned}$$

(4)

and

$$\begin{aligned} \eta =x-vt,~~~Y= -kx+wt+\theta _0. \end{aligned}$$

(5)

where k, v, $\theta _0$ and w are the frequency, speed, phase constant, and wave number, respectively. Replacing (3) and (4) as well as (5) into (1) and (2). Real parts obtain

$$\begin{aligned}&a_1P''_1+\frac{b_{11}}{P_1^3}+b_{13}P_1^5+\frac{c_{11}}{P_2^4}P_1 +c_{12}P_1P_2^2+[b_{12}-k(\lambda _1+\theta _1)]P_1^3 \nonumber \\&\quad +c_{13}P_1P_2^4-[w+\alpha _1k+a_1k^2]P_1-Q_1P_2=0, \end{aligned}$$

(6)

$$\begin{aligned}&a_2P''_2+\frac{b_{21}}{P_2^3}+b_{23}P_2^5+\frac{c_{21}}{P_1^4}P_2 +c_{22}P_2P_1^2+[b_{22}-k(\lambda _2+\theta _2)]P_2^3 \nonumber \\&\quad +c_{23}P_2P_1^4-[w+\alpha _2k+a_2k^2]P_2-Q_2P_1=0, \end{aligned}$$

(7)

imaginary parts give

$$\begin{aligned}&(v+2a_1k+\alpha _1)P'_1+(3\lambda _1+2v_1+\theta _1)P_1^2P'_1=0, \end{aligned}$$

(8)

$$\begin{aligned}&(v+2a_2k+\alpha _2)P'_2+(3\lambda _2+2v_2+\theta _2)P_2^2P'_2=0. \end{aligned}$$

(9)

Using linearly independent principle, we obtain from (8) and (9).

$$\begin{aligned}&v=-(2a_1k+\alpha _1), \end{aligned}$$

(10)

$$\begin{aligned}&3\lambda _1+2v_1+\theta _1=0, \end{aligned}$$

(11)

and

$$\begin{aligned}&v=-(2a_2k+\alpha _2), \end{aligned}$$

(12)

$$\begin{aligned}&3\lambda _2+2v_2+\theta _2=0, \end{aligned}$$

(13)

we get frequency of soliton using (10) and (12),

$$\begin{aligned} k=\frac{(\alpha _2-\alpha _1)}{2(a_1-a_2)}, \end{aligned}$$

(14)

provided

$$\begin{aligned} a_1\ne a_2,~~~\alpha _2\ne \alpha _1. \end{aligned}$$

(15)

Set

$$\begin{aligned} P_2(\eta )=\chi P_1(\eta ), \end{aligned}$$

(16)

here $\chi$ is a constant and $\chi \ne 1$. Next, (6) and (7) convert to

$$\begin{aligned}&a_1P_1^3P''_1+\bigg (b_{11}+\frac{c_{11}}{\chi ^4}\bigg )-(w+\alpha _1 k+a_1k^2+Q_1\chi )P_1^4\nonumber \\&\quad +[c_{12}\chi ^2+b_{12}-k(\lambda _1+\theta _1)]P_1^6+(b_{13}+c_{13}\chi ^4)P_1^8=0, \end{aligned}$$

(17)

$$\begin{aligned}&a_2P_1^3P''_1+\bigg (\frac{b_{21}}{\chi ^3}+c_{21}\chi \bigg )-[(w+\alpha _2 k+a_2k^2)\chi +Q_2]P_1^4\nonumber \\&\quad +{c_{22}\chi ^2+[b_{22}-k(\lambda _2+\theta _2)\chi ^3]}P_1^6+(b_{23}\chi ^5+c_{23}\chi )P_1^8=0. \end{aligned}$$

(18)

Using the constraint conditions

$$\begin{aligned}&a_2=a_1\chi , \end{aligned}$$

(19)

$$\begin{aligned}&b_{11}+\frac{c_{11}}{\chi ^4}+\frac{b_{21}}{\chi ^3}+c_{21}\chi , \end{aligned}$$

(20)

$$\begin{aligned}&w+\alpha _1k+a_1k^2+Q_1\chi =[w+\alpha _2k+a_2k^2]\chi +Q_2, \end{aligned}$$

(21)

$$\begin{aligned}&c_{12}\chi ^2+b_{12}-k(\lambda _1+\theta _1)=c_{22}\chi +[b_{22}-k(\lambda _2+\theta _2)]\chi ^3, \end{aligned}$$

(22)

$$\begin{aligned}&b_{13}+c_{13}\chi ^4=b_{23}\chi ^5+c_{23}\chi , \end{aligned}$$

(23)

(17) and (18) are similar to see. Next, the wave number w is attained from (19) and (21),

$$\begin{aligned} w=\frac{\chi Q_1-Q_2-k(\chi \alpha _2-\alpha _1)}{\chi _1}, \end{aligned}$$

(24)

Balancing $P_1^3P''_1~ and ~P_1^8$ in Eq. (17), yields $N=\frac{1}{2}$,

$$\begin{aligned} P_1(\eta )=[U(\eta )]^\frac{1}{2}. \end{aligned}$$

(25)

(17) converts to

$$\begin{aligned} 4(\Lambda _0+\Lambda _2U^2+\Lambda _3U^3+\Lambda _4U^4)+a_1(2UU''-U'^2)=0, \end{aligned}$$

(26)

where

$$\begin{aligned} \Lambda _0= & {} b_{11}+\frac{c_{11}}{\chi ^4},\nonumber \\ \Lambda _2= & {} -(w+\alpha _1k+a_1k^2+Q_1\chi ),\nonumber \\ \Lambda _3= & {} c_{12}\chi ^2+b_{12}-k(\lambda _1+\theta _1),\nonumber \\ \Lambda _4= & {} b_{13}+c_{13}\chi ^4. \end{aligned}$$

(27)

3 New EHFM

The new EHFM (Shang 2008; Shang et al. 2008; Nestor et al. 2020) have some phases as follows

Form 1: Let PDE as given in (1)-(2) with the wave transformation in (4)-(5) along with (6) using wave transformation ODE is obtained as in (26). We assume that (26) has a solution in the next form

$$\begin{aligned} U(\eta )=\sum ^{N}_{i=0}F_i \Phi ^i(\eta ), \end{aligned}$$

(28)

where $F_i(i = (1, 2, 3, .....N))$ are constants and $\Phi (\eta )$ admits the ODE in next form, as

$$\begin{aligned} \frac{d \Phi }{d \eta }=\Phi \sqrt{\tau +\Theta \Phi ^2},~ \tau , \Theta \in R. \end{aligned}$$

(29)

By using balancing rule in (26) the value of N is found. Replacing (28) into (26) with (29), offers a set of equations for $F_i(i = (0, 1,2, 3, ....N))$. On solving this set, we yield set of solutions that admits (29), so

• Set 1: When $\tau > 0$  and  $\Theta > 0$,

  $$\begin{aligned} \Phi (\eta )=- \sqrt{\frac{\tau }{\Theta }}csch(\sqrt{\tau }(\eta +\eta _0)). \end{aligned}$$

  (30)

• Set 2: When $\tau < 0$  and $\Theta > 0$,

  $$\begin{aligned} \Phi (\eta )= \sqrt{\frac{-\tau }{\Theta }}sec(\sqrt{-\tau }(\eta +\eta _0)). \end{aligned}$$

  (31)

• Set 3: When $\tau > 0$ and $\Theta < 0$,

  $$\begin{aligned} \Phi (\eta )= \sqrt{\frac{\tau }{-\Theta }}sech(\sqrt{\tau }(\eta +\eta _0)). \end{aligned}$$

  (32)

• Set 4: When $\tau < 0$  and  $\Theta > 0$,

  $$\begin{aligned} \Phi (\eta )= \sqrt{\frac{-\tau }{\Theta }}\csc (\sqrt{-\tau }(\eta +\eta _0)). \end{aligned}$$

  (33)

• Set 5: When $\tau > 0$  and  $\Theta = 0$,

  $$\begin{aligned} \Phi (\eta )= \exp (\sqrt{\tau }(\eta +\eta _0)). \end{aligned}$$

  (34)

• Set 6: When $\tau < 0$  and  $\Theta = 0$,

  $$\begin{aligned} \Phi (\eta )= \cos (\sqrt{-\tau }(\eta +\eta _0))+\iota sin(\sqrt{-\tau }(\eta +\eta _0)). \end{aligned}$$

  (35)

• Set 7: When $\tau = 0$  and  $\Theta > 0$,

  $$\begin{aligned} \Phi (\eta )= \pm \frac{1}{(\sqrt{\Theta }(\eta +\eta _0))}. \end{aligned}$$

  (36)

• Set 8: When $\tau = 0$  and  $\Theta < 0$,

  $$\begin{aligned} \Phi (\eta )= \pm \frac{\iota }{(\sqrt{-\Theta }(\eta +\eta _0))}. \end{aligned}$$

  (37)

Form 2: Using the same pattern as previous, we adopt that $\Phi (\eta )$ admits the ODE as follows

$$\begin{aligned} \frac{d\Phi }{d\eta }= \tau +\Theta \Phi ^2,~ \tau ,\Theta \in R. \end{aligned}$$

(38)

Substituting (28) into (26) along with (38) along value of N, makes a set of equations as well the values of $F_i(i=1,2,3,\ldots N)$ .

Let the (38) accepts the solutions, so

• Set 1: When  $\tau \Theta >0$,

  $$\begin{aligned} \Phi (\eta )=sgn(\tau ) \sqrt{\frac{\tau }{\Theta }}tan(\sqrt{\tau \Theta }(\eta +\eta _0)). \end{aligned}$$

  (39)

• Set 2:  When  $\tau \Theta >0$,

  $$\begin{aligned} \Phi (\eta )=-sgn(\tau ) \sqrt{\frac{\tau }{\Theta }}cot(\sqrt{\tau \Theta }(\eta +\eta _0)). \end{aligned}$$

  (40)

• Set 3:  When  $\tau \Theta <0$,

  $$\begin{aligned} \Phi (\eta )=sgn(\tau ) \sqrt{\frac{\tau }{-\Theta }}tanh(\sqrt{-\tau \Theta }(\eta +\eta _0)). \end{aligned}$$

  (41)

• Set 4:  When  $\tau \Theta <0$,

  $$\begin{aligned} \Phi (\eta )=sgn(\tau ) \sqrt{\frac{\tau }{-\Theta }}coth(\sqrt{-\tau \Theta }(\eta +\eta _0)). \end{aligned}$$

  (42)

• Set 5:  When $\tau =0$  and  $\Theta >0$,

  $$\begin{aligned} \Phi (\eta )=-\frac{1}{\Theta (\eta +\eta _0)}. \end{aligned}$$

  (43)

• Set 6:  When $\tau \in R$  and  $\Theta =0$,

  $$\begin{aligned} \Phi (\eta )=\tau (\eta +\eta _0). \end{aligned}$$

  (44)

Note: sgn is the famous sign functions.

3.1 Application of the new EHFM

Form 1: Here, we employ the new EHFM for the MOW with AC form of NLRI to construct the optical solitons solutions. Using balancing method in (26), gives $N=1$, so (28) gives

$$\begin{aligned} U(\eta )=F_0+F_1\Phi (\eta ) , \end{aligned}$$

(45)

where $F_0$ and $F_2$ are constants. Replacing (45) into (26) and equating the coefficients polynomials of $\Phi (\eta )$ to zero, we get a set of equations in $F_0,~F_1,~\tau ,~\Theta ~ and~ \Lambda _0$.

On resolving the set of equations, we attain

$$\begin{aligned} F_0= & {} -\frac{3 ~\Lambda _3}{8~\Lambda _4},~~~F_1=F_1,\nonumber \\ \tau= & {} \frac{-32~ \Lambda _2+\frac{9~ \Lambda _3^2}{\Lambda _4}}{8~ a_1},~\Theta =-\frac{4~ F_1^2~ \Lambda _4}{3~ a_1}.\nonumber \\ \Lambda _0= & {} -\frac{9~(15~\Lambda _3^4+64~\Lambda _2~\Lambda _3^2~\Lambda _4 )}{4096 ~\Lambda _4^3}. \end{aligned}$$

(46)

• Set 1: When $\tau > 0$ and $\Theta > 0$,

  $$\begin{aligned}&q_1(x,t)=\bigg (-\frac{3 ~\Lambda _3}{8~\Lambda _4}+F_1\bigg (- \sqrt{\frac{3(-9~\Lambda _3^2+32~\Lambda _2~\Lambda _4)}{32~F_1^2~\Lambda _4^2}}\nonumber \\&\quad csch(\sqrt{\frac{-32~ \Lambda _2+\frac{9~ \Lambda _3^2}{\Lambda _4}}{8~ a_1}}(\eta +\eta _0))\bigg )\bigg )^{\frac{1}{2}}\times e^{\iota (-kw+wt+\theta _0)}. \end{aligned}$$

  (47)
  $$\begin{aligned} r_{1}=\chi q_{1}(x,t). \end{aligned}$$

  (48)

• Set 2: When $\tau < 0$ and $\Theta > 0$,

  $$\begin{aligned}&q_2(x,t)=\bigg (-\frac{3 ~\Lambda _3}{8~\Lambda _4}+F_1\bigg ( \sqrt{-\frac{3(-9~\Lambda _3^2+32~\Lambda _2~\Lambda _4)}{32~F_1^2~\Lambda _4^2}}\nonumber \\&\quad sec(\sqrt{-\frac{-32~ \Lambda _2+\frac{9~ \Lambda _3^2}{\Lambda _4}}{8~ a_1}}(\eta +\eta _0))\bigg )\bigg )^{\frac{1}{2}}\times e^{\iota (-kw+wt+\theta _0)}. \end{aligned}$$

  (49)
  $$\begin{aligned}&r_{2}=\chi q_{2}(x,t). \end{aligned}$$

  (50)

• Set 3: When $\tau > 0$ and $\Theta < 0$,

  $$\begin{aligned} q_{3} (x,t) = & \left( { - \frac{{3~\Lambda _{3} }}{{8~\Lambda _{4} }} + F_{1} \left( {\sqrt { - \frac{{3( - 9~\Lambda _{3}^{2} + 32~\Lambda _{2} ~\Lambda _{4} )}}{{32~F_{1}^{2} ~\Lambda _{4}^{2} }}} } \right.} \right. \\ & \text{sech} \left( {\sqrt { - \frac{{ - 32~\Lambda _{2} + \frac{{9~\Lambda _{3}^{2} }}{{\Lambda _{4} }}}}{{8~a_{1} }}} (\eta + \eta _{0} )))} \right)^{{\frac{1}{2}}} \times e^{{\iota ( - kw + wt + \theta _{0} )}} . \\ \end{aligned}$$

  (51)
  $$\begin{aligned} r_{3}= & {} \chi q_{3}(x,t). \end{aligned}$$

  (52)

• Set 4: When $\tau < 0$ and $\Theta < 0$,

  $$\begin{aligned} q_4(x,t)= & {} \bigg (-\frac{3 ~\Lambda _3}{8~\Lambda _4}+F_1\bigg (\sqrt{-\frac{3(-9~\Lambda _3^2+32~\Lambda _2~\Lambda _4)}{32~F_1^2~\Lambda _4^2}}\nonumber \\&csc(\sqrt{-\frac{-32~ \Lambda _2+\frac{9~ \Lambda _3^2}{\Lambda _4}}{8~ a_1}}(\eta +\eta _0))\bigg )\bigg )^{\frac{1}{2}}\times e^{\iota (-kw+wt+\theta _0)}. \end{aligned}$$

  (53)
  $$\begin{aligned} r_{4}= & {} \chi q_{4}(x,t). \end{aligned}$$

  (54)

• Set 5: When $\tau = 0$ and $\Theta > 0$,

  $$q_{5} (x,t) = {\text{ }}\left( { - \frac{{3~\Lambda _{3} }}{{8~\Lambda _{4} }} + F_{1} \left( { \pm \frac{1}{{\sqrt { - \frac{{4~F_{1}^{2} ~\Lambda _{4} }}{{3~a_{1} }}} (\eta + \eta _{0} )}}} \right)} \right)^{{\frac{1}{2}}} \times e^{{\iota ( - kw + wt + \theta _{0} )}} .$$

  (55)
  $$\begin{aligned} r_{5}= & {} \chi q_{5}(x,t). \end{aligned}$$

  (56)

• Set 6: When $\tau = 0$ and $\Theta < 0$,

  $$q_{6} (x,t) = {\text{ }}\left( { - \frac{{3~\Lambda _{3} }}{{8~\Lambda _{4} }} + F_{1} \left( { \pm \frac{\iota }{{\sqrt {\frac{{4~F_{1}^{2} ~\Lambda _{4} }}{{3~a_{1} }}} (\eta + \eta _{0} )}}} \right)} \right)^{{\frac{1}{2}}} \times e^{{\iota ( - kw + wt + \theta _{0} )}} ,$$

  (57)
  $$\begin{aligned} r_{6}= & {} \chi q_{6}(x,t). \end{aligned}$$

  (58)

where $\eta =(x-vt),~~and~~ Y=-kx + wt +\theta _0$.

Form 2:

Operating balancing rule in (26), gives $N=1$, so (28) brings to

$$\begin{aligned} U(\eta )=F_0+F_1\Phi (\eta ), \end{aligned}$$

(59)

where $F_0$ and $F_1$ are constants. Replacing (59) into (26) and equating the coefficients of polynomials of $\Phi (\eta )$ to zero, we get a set of equations in $F_0,~F_1,~\tau ,~\Theta ,~and~\Lambda _0$.

On resolving the set of equations, we attain

$$\begin{aligned} F_0= & {} -\frac{3 ~\Lambda _3}{8 ~\Lambda _4},~~~F_1=F_1,~~a_1=-\frac{4~F_1^2~\Lambda _4}{3~\Theta ^2},\nonumber \\ \tau= & {} \frac{3~\Theta (-9~\Lambda _3^2+32~\Lambda _2~\Lambda _4)}{64~F_1^2~\Lambda _4^2},~~\Theta =\Theta , \end{aligned}$$

(60)

$$\begin{aligned} \Lambda _0= & {} -\frac{3(9~\Lambda _3^2-96~\Lambda _2~\Lambda _3^2~\Lambda _4+256~\Lambda _2^2~\Lambda _4^2)}{1024\Lambda _4^3}. \end{aligned}$$

(61)

• Set 1: When $\tau \Theta >0$,

  $$\begin{aligned} q_{7} (x,t) = & \left( { - \frac{{3~\Lambda _{3} }}{{8~\Lambda _{4} }} + F_{1} \left( {\Gamma \sqrt {\frac{{3~( - 9~\Lambda _{3}^{2} + 32~\Lambda _{2} ~\Lambda _{4} )}}{{64~F_{1}^{2} ~\Lambda _{4}^{2} }}} } \right.} \right. \\ & \left. {\left. {\tan \left( {\sqrt {\frac{{3~\Theta ^{2} ( - 9~\Lambda _{3}^{2} + 32~\Lambda _{2} ~\Lambda _{4} )}}{{64~F_{1}^{2} ~\Lambda _{4}^{2} }}} (\eta + \eta _{0} )} \right)} \right)} \right)^{{\frac{1}{2}}} \times e^{{\iota ( - kw + wt + \theta _{0} )}} . \\ \end{aligned}$$

  (62)
  $$\begin{aligned} r_{7}= & {} \chi q_{7}(x,t). \end{aligned}$$

  (63)

• Set 2: When $\tau \Theta >0$,

  $$\begin{aligned} q_{8}(x,t)= & {} \bigg (-\frac{3 ~\Lambda _3}{8 ~\Lambda _4}+F_1\bigg (-\Gamma \sqrt{\frac{3~(-9~\Lambda _3^2+32~\Lambda _2~\Lambda _4)}{64~F_1^2~\Lambda _4^2}}\nonumber \\&cot(\sqrt{\frac{3~\Theta ^2(-9~\Lambda _3^2+32~\Lambda _2~\Lambda _4)}{64~F_1^2~\Lambda _4^2}}(\eta +\eta _0))\bigg )\bigg )^{\frac{1}{2}}\times e^{\iota (-kw+wt+\theta _0)}. \end{aligned}$$

  (64)
  $$\begin{aligned} r_{8}= & {} \chi q_{8}(x,t). \end{aligned}$$

  (65)

• Set 3: When $\tau \Theta <0$,

  $$\begin{aligned} q_{9} (x,t) = & \left( { - \frac{{3~\Lambda _{3} }}{{8~\Lambda _{4} }} + F_{1} \left( {\Gamma \sqrt { - \frac{{3~( - 9~\Lambda _{3}^{2} + 32~\Lambda _{2} ~\Lambda _{4} )}}{{64~F_{1}^{2} ~\Lambda _{4}^{2} }}} } \right.} \right. \\ & \left. {\left. {\tanh \left( {\sqrt { - \frac{{3~\Theta ^{2} ( - 9~\Lambda _{3}^{2} + 32~\Lambda _{2} ~\Lambda _{4} )}}{{64~F_{1}^{2} ~\Lambda _{4}^{2} }}} (\eta + \eta _{0} )} \right)} \right)} \right)^{{\frac{1}{2}}} \times e^{{\iota ( - kw + wt + \theta _{0} )}} . \\ \end{aligned}$$

  (66)
  $$\begin{aligned} r_{9}= & {} \chi q_{9}(x,t). \end{aligned}$$

  (67)

• Set 4: When $\tau \Theta <0$,

  $$\begin{aligned} q_{{10}} (x,t) = & \left( { - \frac{{3~\Lambda _{3} }}{{8~\Lambda _{4} }} + F_{1} \left( {\Gamma \sqrt { - \frac{{3~( - 9~\Lambda _{3}^{2} + 32~\Lambda _{2} ~\Lambda _{4} )}}{{64~F_{1}^{2} ~\Lambda _{4}^{2} }}} } \right.} \right. \\ & \left. {\left. {\coth \left( {\sqrt { - \frac{{3~\Theta ^{2} ( - 9~\Lambda _{3}^{2} + 32~\Lambda _{2} ~\Lambda _{4} )}}{{64~F_{1}^{2} ~\Lambda _{4}^{2} }}} (\eta + \eta _{0} )} \right)} \right)} \right)^{{\frac{1}{2}}} \times e^{{\iota ( - kw + wt + \theta _{0} )}} . \\ \end{aligned}$$

  (68)
  $$\begin{aligned} r_{10}= & {} \chi q_{10}(x,t). \end{aligned}$$

  (69)

• Set 5: When $\tau =0$ and $\Theta >0$,

  $$\begin{aligned} q_{11}(x,t)= & {} \bigg (-\frac{3 ~\Lambda _3}{8 ~\Lambda _4}+F_1\bigg (-\frac{1}{\Theta (\eta +\eta _0)} \bigg )\bigg )^{\frac{1}{2}}\times e^{\iota (-kw+wt+\theta _0)}. \end{aligned}$$

  (70)
  $$\begin{aligned} r_{11}= & {} \chi q_{11}(x,t). \end{aligned}$$

  (71)

4 The generalized Tanh method Ullah et al. (2020)

Let the PDE, as given in (1)-(2) with the wave transformation in (3)-(4) along with (5) using wave transformation ODE is obtained as in (26). We assume that (26) has a solution, as

$$\begin{aligned} U(\eta )=\sum ^{N}_{i=0}F_i \Phi ^i(\eta ), \end{aligned}$$

(72)

here, $F_i(i = (1, 2, 3,\ldots N))$ are constants and $\Phi (\eta )$

$$\begin{aligned} \frac{d \Phi }{d \eta }= h+\Phi ^2(\eta ) \end{aligned}$$

(73)

By using balancing rule in (26) the value of N is found. Replacing (72) into (26) with (73), offers a set of equations for $F_i(i = (0, 1,2, 3,\ldots N))$. On solving this set, we yield set of solutions that admits (73), as follows

Consider the solutions of (21) are, as

• Case 1. If $h<0$, then

  $$\begin{aligned} \Phi (\eta )=-\sqrt{-h}~~tanh(\sqrt{-h}\eta ), \end{aligned}$$

  (74)

  and

  $$\begin{aligned} \Phi (\eta )=-\sqrt{-h}~~ coth(\sqrt{-h}\eta ). \end{aligned}$$

  (75)

• Case 2. If $h=0$, then

  $$\begin{aligned} \Phi (\eta )=-\frac{1}{\eta }. \end{aligned}$$

  (76)

• Case 3. If $h>0$, then

  $$\begin{aligned} \Phi (\eta )=\sqrt{h}~~tan(\sqrt{h}\eta ), \end{aligned}$$

  (77)

  and

  $$\begin{aligned} \Phi (\eta )=-\sqrt{h}~~ cot(\sqrt{h}\eta ). \end{aligned}$$

  (78)

4.1 Application of the generalized Tanh method

According the balancing rule in (26), we get, $N=1$, (72) reduces to

$$\begin{aligned} U(\eta )=F_0+ F_1 \Phi (\eta ), \end{aligned}$$

(79)

Putting (79) and (73) in (26) produces a polynomial in form of $\Phi (\eta )$. We get a system on making a comparison of the coefficients of $\Phi (\eta )$ to zero, after solving it, we get solutions as

$$\begin{aligned} F_0= & {} -\frac{3 ~\Lambda _3}{8 ~\Lambda _4},~~~F_1=F_1,~~a_1=-\frac{4}{3}F^2_1\Lambda _4,\nonumber \\ \Lambda _2= & {} -\frac{9\lambda ^2_3}{32\Lambda _4 }+\frac{2}{3}h~F^2_1~\Lambda _4,~~~\Lambda _0 =-\frac{(9~\Lambda ^2_3+64~h~F^2_1~\Lambda ^2_4)^2}{12288~\Lambda ^3_4}. \end{aligned}$$

(80)

If $h<0$, then

$$\begin{aligned} q_{1}(x,t)= & {} \bigg ( (-\frac{3 ~\Lambda _3}{8 ~\Lambda _4}+F_1\sqrt{-h}~~tanh(\sqrt{-h}\eta ))\bigg )^{\frac{1}{2}}\times e^{\iota (-kw+wt+\theta _0)}, \end{aligned}$$

(81)

$$\begin{aligned} r_{1}= & {} \chi q_{1}(x,t), \end{aligned}$$

(82)

or

$$\begin{aligned} q_{2}(x,t)= & {} \bigg ((-\frac{3 ~\Lambda _3}{8 ~\Lambda _4}+F_1\sqrt{-h}~~ coth(\sqrt{-h}\eta ))\bigg )^{\frac{1}{2}}\times e^{\iota (-kw+wt+\theta _0)}. \end{aligned}$$

(83)

$$\begin{aligned} r_{2}= & {} \chi q_{2}(x,t). \end{aligned}$$

(84)

If $h=0$, then

$$\begin{aligned} q_{3}(x,t)= & {} \bigg (-\frac{3 ~\Lambda _3}{8 ~\Lambda _4}+F_1(-\frac{1}{\eta })\bigg )^{\frac{1}{2}}\times e^{\iota (-kw+wt+\theta _0)}. \end{aligned}$$

(85)

$$\begin{aligned} r_{3}= & {} \chi q_{3}(x,t). \end{aligned}$$

(86)

If $h>0$, then

$$q_{4} (x,t) = \left( {\left( { - \frac{{3~\Lambda _{3} }}{{8~\Lambda _{4} }} + F_{1} \sqrt h ~~\tan (\sqrt h \eta )} \right)} \right)^{{\frac{1}{2}}} \times e^{{\iota ( - kw + wt + \theta _{0} )}} ,$$

(87)

$$\begin{aligned} r_{4}= & {} \chi q_{4}(x,t). \end{aligned}$$

(88)

or

$$q_{5} (x,t) = {\text{ }}\left( {\left( { - \frac{{3~\Lambda _{3} }}{{8~\Lambda _{4} }} + F_{1} \sqrt h ~~\cot (\sqrt h \eta )} \right)} \right)^{{\frac{1}{2}}} \times e^{{\iota ( - kw + wt + \theta _{0} )}} .$$

(89)

$$\begin{aligned} r_{5}= & {} \chi q_{5}(x,t). \end{aligned}$$

(90)

where $\eta =(x-vt),~~and~~ Y=-kx + wt +\theta _0$.

5 Results and discussions

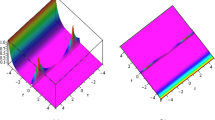
The results of this paper will be valuable for researchers to study the most noticeable applications of the MOW equation in optic fibers. Figures 1, 2, 3, 4, 5, 6 clearly reveals the surfaces of the solution acquired for 3-dim and 2-dim plots, with selection of suitable parameters for the MOW equation. Likewise, 3D plots provide us to model and exhibit accurate physical behavior. Through this study, we consider the optical soliton solutions to the nonlinear MOW model using new EHFM and tanh method. The authors proposed different analytic approach in newly issued article and reported some fascinating findings. The authors can understand from all the graphs that the new EHFM and generalized tanh are very effectual and more specific in assessing the equation under consideration. Figures 1 and 2 designate the solutions stated by (47) and (51) which are bright and singular respectively. Figures3 and 4 are the graphical representations of the solutions stated by (62) and (64) which are dark and singular solitons respectively. While Figures 5 and 6 present the solutions stated by (81) and (89) which are combined dark-bright and periodic singular solitons respectively.

Fig. 1

a 3-d graph of (47)  with  $a_1=1.75$, $\Lambda _2=-1.3$, $\Lambda _3=1.4$, $\Lambda _4=-0.9$, $v=0.65$, $k=0.8$, $\theta _1=0.56$, $\Lambda _1=1.2$, $F_1=0.6$,  $w=2$. (a-1) 2-d plot of (47) with $t=1$

Fig. 2

b 3-d graph of (51) with  $a_1=1.77$,  $\Lambda _2=-1.2$,  $\Lambda _3=1.6$, $\Lambda _4=-0.9$,  $v=0.65$,  $k=0.8$, $\theta _1=0.86$, $\Lambda _1=1.2$, $F_1=0.6$,  $w=2$. (b-1) 2-d plot of (51) with $t=1$

Fig. 3

c 3-d graph of (62)  with  $\Lambda _2=1.1$,  $\Lambda _3=1.3$,  $\Lambda _4=1.9$,$\Theta =1.75$, $v=0.65$, $k=0.9$, $\theta _1=0.56$, $\Lambda _1=1.3$, $F_1=1.6$,  $w=2$,  $\Gamma =0.44$. (c-1) 2-d plot of (64) with $t=1$

Fig. 4

d 3-d graph of (64)  with  $\Lambda _2=2.1$,  $\Lambda _3=1.7$,  $\Lambda _4=-1.9$,$\Theta =0.75$, $v=0.65$,  $k=0.7$, $\theta _1=1.66$, $\Lambda _1=1.1$, $F_1=0.6$,  $w=2$,  $\Gamma =0.35$. (d-1) 2-d plot of (64) with $t=1$

Fig. 5

e 3-d graph of (81)  with  $h=-0.75$,  $\Lambda _3=1.5$,  $\Lambda _4=0.8$,  $v=0.65$, $k=0.9$, $\theta _1=0.57$,  $w=2$, $F_1=0.5$. (e-1) 2-d plot of (81) with $t=1$

Fig. 6

f 3-d graph of (89)  with  $h=0.76$,  $\Lambda _3=1.3$,  $\Lambda _4=0.9$, $v=0.66$,  $k=0.7$, $\theta _1=0.59$,  $w=2$, $F_1=0.7$. (f-1) 2-d plot of (89) with $t=1$

6 Conclusion

This article includes a comprehensive variety of optical soliton solutions that are discovered for magneto-optic waveguides with AC form of nonlinear refractive index. The outcomes are in the form of bright, singular, dark and combo solitons solutions. These solutions have wide applications in the arena of optoelectronics. As stated in the introduction section, the bright soliton solutions will be a vast advantage in controlling the soliton disorder. This shows that the solitons can be transformed to a shape of parting from a shape of magnetism which would mean clearing the clutter. Consequently, this would carry a factor of “easiness” to the internet bottleneck that is an increasing problem to the present day communications industry where the internet is an important tool for existence. For the period of the present pandemic time of COVID-19, where all trade happenings are supervised online, it is bossy to have a flat and continuous flow of pulses for continuous Internet communications. Also, dark solitons are also beneficial for soliton communication when a background wave is exict. Although, singular soliton solutions are only elaborate the shape of solitons and show a total spectrum of soliton solutions created from the model. Furthermore, these novel solutions have many applications in physics and other branches of applied sciences. Further, these solutions may be suitable for understanding the procedure of the nonlinear physical phenomena in wave propagation. We will report these results in future research studies.