Analytical solutions and conservation laws of the generalized model for propagation pulses with four powers of nonlinearity

Abstract

Analytical solutions of the generalized nonlinear Schrödinger with four powers of nonlinearity for description of propagating pulses in optical fiber are presented. Optical solitons corresponding to the mathematical model are given. Conservation laws of the generalized model for propagation pulses with four powers of nonlinearity are written. To the best of our knowledge, the conservation laws obtained have not yet been presented in literature. The equation investigated generalizes several well-known models, which allows us to evaluate the influence of various processes on pulse propagation. Conservative quantities for the bright optical soliton, corresponding to its power, momentum and energy, are calculated. The analytical expressions for conservative quantities obtained can be applied to check whether numerical schemes for the explored equation are conservative.

1 Introduction

In this paper we study the equation in the form (Kudryashov 2019)

$$\begin{aligned} i\,q_t+a\,q_{xx}+\left( b_1\,|q|^{2n}+b_2\,|q|^{n}+b_3\,|q|^{-n}+b_4\,|q|^{-2n}\right) \,q=0, \end{aligned}$$

(1)

where q(x, t) is a complex function, $i^2=-1$, $n\in {\mathbb {Z}},$ a, $b_1$, $b_2$, $b_3$ and $b_4$ are parameters of Eq. (1). $n \ne -1$ (if $b_1 \ne 0$), $n \ne -2$ (if $b_2 \ne 0$), $n \ne 2$ (if $b_3 \ne 0$), $n \ne 1$ (if $b_4 \ne 0$).

Equation (1) has been proposed by Kudryashov in (2019) and it is known as the Kudryashov model (Biswas et al. 2020d; Raheel et al. 2023; Sonmezoglu et al. 2022; Yıldırım et al. 2020; Zayed et al. 2020a, 2020c). Equation (1) does not pass the Painlevé test (Kudryashov 2019) and the Cauchy problem for this equation cannot be solved by the inverse scattering transform. However, taking into account the traveling wave reduction (for more recent examples of the search for soliton solutions of PDEs see, for instance, Biswas et al. 2018; Triki et al. 2022a, 2022b; Yıldırım 2019a, 2019b, 2021; Yıldırım and Yaşar 2017) one can find periodic and solitary wave solutions of Eq. (1) in the form of optical solitons, which have recently been found in a number of papers (see, for example, Arnous et al. 2021; Arshed and Arif 2020; Arshed et al. 2021, 2022; Biswas et al. 2019, 2020a, 2020b, 2020e; Hu and Yin 2022; Kai and Li 2023; Kudryashov 2020b, 2020d, 2020f, 2021d, 2021e; Kudryashov and Antonova 2020; Kumar et al. 2020; Li and Wang 2022; Raheel et al. 2022a; Raza et al. 2021; Zayed and Alngar 2021; Zayed et al. 2020d, 2021b, 2021e). Without stopping at a detailed analysis of optical solitons, which are solutions of Eq. (1), we note that Eq. (1) generalizes a number of well-known equations used to describe impulses in optical media. It is obvious that Eq. (1) at $n=1$, $b_2=0$, $b_3=0$ and $b_4=0$ is the famous non-linear Schrödinger equation, which was the first mathematical model that was proposed to describe the optical solitons (Hasegawa and Tappert 1973a, b; Tai et al. 1986).

As we have previously mentioned, optical soliton solutions described by Eq. (1) are currently well-investigated. However, to the best of our knowledge, conservation laws corresponding to Eq. (1) have not been studied yet to date. Conservative quantities of partial differential equations are often applied to check whether numerical schemes used for solving partial differential equations are conservative (see, for example, Bayramukov and Kudryashov (2024). To analytically calculate conservative quantities for the solitary wave one must first find an explicit expression for the solitary wave solution and the conservation law of the equation, therefore we also present them in this work. The aforementioned discussion explains why it is significant to look for conservation laws of the proposed equation. Thus, the main purpose of this paper is to present conservation laws of Eq. (1) by means of direct calculations and find conserved quantities corresponding to its soliton solution.

It is well known that we say there exists the conservation law corresponding to Eq. (1), if we can write this equation in the form

$$\begin{aligned} \frac{\partial T_j}{\partial t}+\frac{\partial X_j}{\partial x}=0, \qquad (j=1,\,2,\,3), \end{aligned}$$

(2)

where $T\equiv T_j(u,u_x,u_t,\ldots ,x,t)$ is the density and $X_j\equiv X(u,u_x,u_t,\ldots ,x,t)$ is the flux.

Integrating Eq. (2) with respect to x, we get the conservative quantity of the density as follows (Alshehri et al. 2022a, Alshehri et al. 2022b; Alshehri and Biswas 2022; Arnous et al. 2022; Biswas et al. 2020c, 2021a, 2021b; Kivshar and Agrawal 2003; Kivshar and Malomed 1989; Kivshar and Pelinovsky 2000; Kudryashov et al. 2022; Olver 1993; Serkin and Belyaeva 2018; Vega-Guzman et al. 2021; Yıldırım et al. 2021; Zayed et al. 2020b, 2021a, 2021c2021d, 2021f)

$$\begin{aligned} I_j=\int _{-\infty }^{\infty }{T_j}\,dx=Constant. \end{aligned}$$

(3)

One can see that $I_j$ is the conservative quantity for the solution q(x, t).

This paper is organized as follows. Periodic and solitary wave solutions of Eq. (1) are given in Sect. 2. Bifurcations of phase portraits of the traveling wave reduction of Eq.(1) are presented in Sect. 3. In Sects. 4, 5 and 6 we obtain conservation laws corresponding to Eq. (1). In Sect. 7 conservative quantities of optical soliton of Eq. (1) are calculated.

2 Optical solitons of equation

The Cauchy problem for Eq. (1) cannot be soled by the inverse scattering transform (Kudryashov 2019). However the optical soliton of Eq. (1) can be found using the traveling wave solutions. These solutions can be found using special methods (see, for example, (Alotaibi 2021; Biswas et al. 2021c, 2022; Ege 2022; Ekici 2022; Eldidamony et al. 2022a, 2022b; González-Gaxiola 2022; Kudryashov 1990, 1991, 2005, 2009, 2012, 2020a, 2020c, 2020e, 2021a, 2021b, 2021c, 2022a,2022b, 2022c; Ozisik et al. 2022; Raheel et al. 2022b; Vitanov 2010, 2011a, 2011b; Vitanov and Dimitrova 2010; Vitanov et al. 2010; Wang 2022a, 2022b; Zayed et al. 2022).

We take into account traveling wave solutions in the form

$$\begin{aligned} q(x,t)=y(z)\,e^{i\,(\psi (z)-\omega \,t)}, \end{aligned}$$

(4)

where y(z), $\psi (z)$ are new functions and $z=x-C_0\,t$.

Substituting (4) into Eq. (1), we obtain the system of equations for imaginary and real part as the following (Kudryashov 2019)

$$\begin{aligned} 2\,a\,y_z\,\psi _z+a\,y\,\psi _{zz}-C_0\,y_z=0 \end{aligned}$$

(5)

and

$$\begin{aligned}{} & {} \omega \,y+C_0\,\psi _z\,y+a\,y_{zz}-a\,y\,\psi _z^2\nonumber \\{} & {} \quad \quad +b_1\,y^{2\,n+1}+b_2\,y^{n+1}+b_3\,y^{1-n}+b_4\,y^{1-2\,n}=0. \end{aligned}$$

(6)

Equation (5) can be integrated after being multiplyed by y(z). We have

$$\begin{aligned} \psi _z=\frac{C_0}{2\,a}-\frac{C_1}{a\,y^2}, \end{aligned}$$

(7)

where $C_1$ is an arbitrary constant.

Substituting $\psi _z$ into (6), we get the second-order differential equation for y(z) in the form

$$\begin{aligned}{} & {} a\,y_{zz}+\left( \omega +\frac{C_0^2}{4\,a}\right) \,y-\frac{C_1^2}{a\,y^3}+b_1\,y^{2\,n+1}+b_2\,y^{n+1}+\nonumber \\{} & {} \quad \quad + b_3\,y^{1-n}+b_4\,y^{1-2\,n}=0 \end{aligned}$$

(8)

Multiplying Eq. (8) by $y_z$ and integrating the resulting expression with respect to z, we have at $n \ne -1$, $n \ne -2$, $n \ne 1$ and $n \ne 2$ the first integral as follows (Kudryashov 2019)

$$\begin{aligned}{} & {} y_z^2+\left( \frac{\omega }{a}+\frac{C_0^2}{4\,a^2}\right) \,y^2+\frac{b_1}{a\,(n+1)}\,y^{2\,n+2}+\frac{2\,b_2}{a\,(n+2)}\,y^{n+2}-\nonumber \\{} & {} \quad \quad - \frac{2\,b_3}{a\,(n-2)}\,y^{2-n}-\frac{b_4}{a\,(n-1)}\,y^{2-2\,n}+\frac{C_1^2}{a^2\,y^2}=C_2. \end{aligned}$$

(9)

Some partial cases of Eq. (9) were considered in the paper by Kudryashov in 2019). Here, let us consider Eq. (9) at $C_1=0$ and $C_2=0$ using the new variable in the form (Kudryashov 2019)

$$\begin{aligned} y(z)=V(z)^{\frac{1}{n}} \end{aligned}$$

(10)

Substituting the expression (4) into Eq. (9), we have the equation

$$\begin{aligned} V_{z}^2-\delta +\alpha \,V-\mu \,V^2+\beta \,V^3-\nu \,V^4=0, \end{aligned}$$

(11)

where $\mu$, $\beta$, $\nu$, $\alpha$ and $\delta$ are determined as follows

$$\begin{aligned}{} & {} \alpha =\frac{2\,b_3\,n^2}{a(2-n)},\quad \beta =\frac{2\,b_2\,n^2}{a\,(n+2)},\quad \mu =-\frac{\omega \,n^2}{a}-\frac{C_0^2\,n^2}{4\,a^2},\nonumber \\{} & {} \nu =-\frac{b_1\,n^2}{a(n+1)},\quad \delta =\frac{b_4\,n^2}{a(n-1)}. \end{aligned}$$

(12)

The general solution of Eq. (11) is expressed via the Jacobi elliptic sine in the form (Kudryashov 2020b, 2020d, 2020f, 2021d, 2021e)

$$\begin{aligned} V(z)=V_3+\frac{(V_4-V_3)(V_3-V_1)}{V_3-V_1+(V_1-V_4)\,\mathrm{sn^2}{\left\{ \sqrt{\chi }(z-z_1);S\right\} }}, \end{aligned}$$

(13)

where

$$\begin{aligned} \chi =\frac{\nu }{4}\,(V_3-V_1)(V_4-V_2),\quad S^2=\frac{(V_1-V_4)(V_2-V_3)}{(V_2-V_4)(V_1-V_3)} \end{aligned}$$

(14)

and $V_1$, $V_2$, $V_3$ and $V_4$ are roots of the following algebraic equation

$$\begin{aligned} \nu \,V^4-\beta \,V^3+\mu \,V^2-\alpha \,V+\delta =0. \end{aligned}$$

(15)

These real roots satisfy the following constraints

$$\begin{aligned}{} & {} V_1\,V_2\,V_3\,V_4=\frac{\delta }{\nu }, \end{aligned}$$

(16)

$$\begin{aligned}{} & {} V_1\,V_2\,V_3+V_1\,V_2\,V_4+V_1\,V_3\,V_4+V_2\,V_3\,V_4=\frac{\alpha }{\nu } \end{aligned}$$

(17)

$$\begin{aligned}{} & {} V_1\,V_2+V_1\,V_3+V_1\,V_4+V_2\,V_3+V_2\,V_4+V_3\,V_4=\frac{\mu }{\nu }, \end{aligned}$$

(18)

$$\begin{aligned}{} & {} V_1+V_2+V_3+V_4=\frac{\beta }{\nu }. \end{aligned}$$

(19)

Taking into account (4), (10) and (13), we get the periodic solution of Eq. (1) in the form

$$\begin{aligned} q(x,t)=\left[ V_3+\frac{(V_4-V_3)(V_3-V_1)}{V_3-V_1+(V_1-V_4)\,\textrm{sn}^2{\left\{ \sqrt{\chi }(x-C_0 t-z_1);S\right\} }}\right] ^{\frac{1}{n}}\,e^{i\,(\psi (z)-\omega \,t)}, \end{aligned}$$

(20)

In the case of $V_1=V_2$, we have $S^2=1$ and the elliptic sine is reduced to the hyperbolic tangent. From the solution (13) we obtain the solitary wave solution in the form

$$\begin{aligned} V(z)=V_3+\frac{(V_4-V_3)(V_3-V_1)}{V_3-V_1+(V_1-V_4)\,\mathrm{\tanh ^2}{\left\{ \sqrt{\chi }(z-z_1)\right\} }}. \end{aligned}$$

(21)

Using (4), (10) and (21), we have the bright and dark soliton of Eq. (1) as follows

$$\begin{aligned} q(x,t)=\left[ V_3+\frac{(V_4-V_3)(V_3-V_1)}{V_3-V_1+(V_1-V_4)\,\mathrm{\tanh ^2}{\left\{ \sqrt{\chi }(x-C_0 t-z_1)\right\} }}\right] ^{\frac{1}{n}}\,e^{i\,(\psi (z)-\omega \,t)}. \end{aligned}$$

(22)

In particular, the optical soliton of Eq. (1) can be found by looking for the solution of Eq. (9) at $b_3=b_4=C_1=C_2=0$ in the form (see E_{{{\text{MP}}}} 2020c, 2020e, 2021c, 2022a)

$$\begin{aligned} q(x,t)=\left[ \frac{4\,\mu }{2\,\beta +(\beta ^2-4\,\mu \,\nu )\,{\textrm{e}}^{-\sqrt{\mu }(x-C_0 t-z_0)}+{\textrm{e}}^{\sqrt{\mu }(x-C_0 t-z_0)}}\right] ^{\frac{1}{n}}\,e^{i\,(\psi (z)-\omega \,t)}, \end{aligned}$$

(23)

where $z_0$ is a constant and parameters $\mu$, $\beta$ and $\nu$ are determined by (12). Some other optical solitons have been obtained in the paper by Kudryashov in (2019).

3 Bifurcations of phase portraits of the system (8)

In this section we plot several partial cases of phase portraits of the studied system (8). In rewrite it as

$$\begin{aligned} y_z = v,\hspace{5.0pt}v_z = -\frac{b_1}{a}y^{2n+1} - \frac{b_2}{a}y^{n+1} - \left( \omega +\frac{C_0^2}{4a}\right) y - \frac{C_1}{a}\frac{1}{y^3} - \frac{b_3}{a}\frac{1}{y^{n+1}} - \frac{b_4}{a}\frac{1}{y^{2n+1}}. \end{aligned}$$

(24)

Let us observe the first partial case. We write the equation explored at $n=1$, $C_1=0$ and $b_4=0$

$$\begin{aligned} y_z=v, \hspace{5.0pt}v_{z}=-\frac{b_1}{a}y^3-\frac{b_2}{a}y^2-\left( \frac{\omega }{a}+\frac{C_0^2}{4a}\right) y-\frac{b_3}{a} \equiv f_1(y). \end{aligned}$$

(25)

The first integral of the system (25) is written in a following way

$$\begin{aligned} H_1(y,v) = \frac{v^2}{2} + \frac{b_1}{a}\frac{y^4}{4} + \frac{b_2}{a}\frac{y^3}{3} + \left( \frac{\omega }{a}+\frac{C_0^2}{4a}\right) \frac{y^2}{2} + \frac{b_3}{a}y. \end{aligned}$$

(26)

Equilibrium points of Eq. (25) are located on the v axis and with the coordinate defined by the following cubic equation

$$\begin{aligned} \frac{b_1}{a}y^3+\frac{b_2}{a}y^2+\left( \frac{\omega }{a}+\frac{C_0^2}{4a}\right) y+\frac{b_3}{a} \equiv -f_1(y) = 0 \end{aligned}$$

(27)

Fig. 1

Phase portraits for the first case

Fig. 2

Phase portraits for the first case

Equation (27) may have at most three roots. Let us denote them as $y_{1s}, \ y_{2s}, \ y_{3s}$. Provided that the root $y_{is}$ is real, the stability of an equilibrium point $(y_{is},0)$ is determined by the eigenvalues of the following matrix

$$\begin{aligned} \begin{pmatrix} 0 &{} 1\\ -\frac{df_1}{dy}\big |_{y_{is}} &{} 0 \end{pmatrix}, \hspace{5.0pt}i=1..3. \end{aligned}$$

(28)

The eigenvalues of (28) are as follows

$$\begin{aligned} \lambda _{1,2} = \pm \sqrt{\frac{df}{dy}\Big |_{y_{is}}}, \hspace{5.0pt}i=1..3. \end{aligned}$$

(29)

Thus, if $f_1(y)$ increases at the point $y_{is}$, then an equilibrium is a saddle, if it decreases at that point, then it is a center, otherwise it is a degenerate equilibrium. Having said that, we can propose the following classification of equilibria, depending on the parameter values and the sign of the discriminant $D_1$ of Eq. (27):

• 1. $D_1>0, \hspace{5.0pt}-{b_1}/{a}>0$. Equation (25) has three equilibria on the v axis with coordinates $y_{1\,s},\ y_{2\,s}, \ y_{3\,s}$ (we assume $y_{1\,s}<y_{2\,s}<y_{3\,s}$), out of which left and right equilibria are saddles and the middle one is a center (Fig. 1a-b).

• 2. $D_1>0, \hspace{5.0pt}-{b_1}/{a}<0$. Equation (25) has three equilibria on the v axis with coordinates $y_{1\,s},\ y_{2\,s}, \ y_{3\,s}$ (we assume $y_{1\,s}<y_{2\,s}<y_{3\,s}$), out of which left and right equilibria are centers and the middle one is a saddle.

• 3. $D_1<0, \hspace{5.0pt}-{b_1}/a>0$. Equation (25) has one equilibrium on the v axis with the coordinate $y_{1s}$, which is a saddle.

• 4. $D_1<0, \hspace{5.0pt}-{b_1}/a<0$. Equation (25) has one equilibrium on the v axis with the coordinate $y_{1s}$, which is a center.

• 5. $D_1=0, \hspace{5.0pt}-{b_1}/a > 0$. Equation (25) has two equilibria $y_{1s}$ and $y_{2s}$ out of which one is a saddle and one is degenerate. On the curve $D_1=0$ in the parameter space a pitchfork bifurcation occurs, where two equilibria of Eq. (25) either appear or vanish.

• 6. $D_1=0, \hspace{5.0pt}-{b_1}/a < 0$. Equation (25) has two equilibria $y_{1s}$ and $y_{2s}$ out of which one is a center and one is degenerate. On the curve $D_1=0$ in the parameter space a pitchfork bifurcation occurs, where two equilibria of Eq. (25) either appear or vanish.

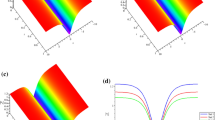
The phase portraits for the above cases are shown in Figs. 1-2. The pitchfork bifurcationw occur in the last two instances of the phase portraits.

Next, we write the equation studied for $n=1$, $C_1=0$, $b_2=0$ and $b_3=0$

$$\begin{aligned} y_z = v, \hspace{5.0pt}v_z = -\frac{b_1}{a}y^3 - \left( \frac{\omega }{a} + \frac{C_0^2}{4a}\right) y - \frac{b_4}{ay}. \end{aligned}$$

(30)

Fig. 3

Phase portraits for the second case

Fig. 4

Phase portraits for the second case

The right hand side of the system of Eq. (30) is not continuous at $y=0$. To get the regular system associated to (30), we use the following variable transformation

$$\begin{aligned} dz = ayd\xi . \end{aligned}$$

(31)

Therefore, the regular system assosiated with (30) is written as follows

$$\begin{aligned} y_{\xi } = ayv, \hspace{5.0pt}v_{\xi } = -b_1y^4 - \left( \omega +\frac{C_0^2}{4}\right) y^2 - b_4 \equiv f_2(y) \end{aligned}$$

(32)

Systems of equations (30) and (32) have the same first integral

$$\begin{aligned} H_2(y,v) = \frac{v^2}{2} + \frac{b_1}{a}\frac{y^4}{4} + \left( \frac{\omega }{a} + \frac{C_0^2}{4a} \right) \frac{y^2}{2} + \frac{b_4}{a}\ln {y}, \end{aligned}$$

(33)

therefore their orbits are topologically the same, with the exception of the line $y=0$. Thus, we can investigate the stability of equilibria of (32), which will match the stability of equilibria of (30). Every equilibrium of (32) is located on the v axis with the coordinate determined by the following equation

$$\begin{aligned} b_1y^4 + \left( \omega + \frac{C_0^2}{4} \right) y^2 + b_4 = -f_2(y) = 0. \end{aligned}$$

(34)

This equation can have at most four roots. Let us denote them as $y_{1s}, \ y_{2s}, \ y_{3s}, \ y_{4s}$. Provided that the root is real, the stability of an equilibrium point $(y_{is},0)$ is determined by the eigenvalues of the matrix

$$\begin{aligned} \begin{pmatrix} 0 &{} ay_{is}\\ -\frac{df_2}{dy}\big |_{y_{is}} &{} 0 \end{pmatrix}, \hspace{5.0pt}i=1..3. \end{aligned}$$

(35)

Accordingly, if $f_2(y)$ increases at the point $y_s$ and $y_s>0$, or decreases at the point $y_s$ and $y_s<0$, then an equilibrium is a saddle; if $f_2(y)$ decreases at $y_s$ and $y_s>0$, or $f_2(y)$ increases at $y_s$ and $y_s<0$, then it is a center, otherwise it is a degenerate equilibrium (this works for $a>0$, in the case of $a<0$ the situation is reversed). Thus, we present the following classification for equilibrium points in this case (in all the cases we assume that the discriminant of Eq. (34) is nonnegative $D_2\ge 0$, except for the last one)

• 1. $b_1>0, \hspace{5.0pt}b_4>0, \hspace{5.0pt}\omega +C_0^2/4\ge 0$. Equation (32) has no equilibria (Fig. 3a).

• 2. $b_1>0, \hspace{5.0pt}b_4>0, \hspace{5.0pt}\omega +C_0^2/4 < 0$. Equation (32) has four equilibria in a sequence: (center, saddle, saddle, center) (Fig. 3b).

• 3. $b_1>0, \hspace{5.0pt}b_4<0$. Equation (32) has two center equilibria (Fig. 3c).

• 4. $b_1<0, \hspace{5.0pt}b_4>0$. Equation (32) has two saddle equilibria (Fig. 3d).

• 5. $b_1<0, \hspace{5.0pt}b_4<0, \hspace{5.0pt}\omega +C_0^2/4>0$. Equation (32) has four equilibria in a sequence: (saddle, center, center, saddle) (Fig. 3e).

• 6. $b_1<0, \hspace{5.0pt}b_4<0, \hspace{5.0pt}\omega +C_0^2/4<0$. Equation (32) has no equilibria (Fig. 3f).

• 7. $b_1\cdot (\omega +C_0^2/4)>0, \hspace{5.0pt}b_4=0$. Equation (32) has a degenerate zero equilibrium (Fig. 4a-b).

• 8. $b_1>0, \hspace{5.0pt}\omega +C_0^2/4<0, \hspace{5.0pt}b_4=0$. Equation (32) has three equilibria in a sequence: (center, degenerate, center) (Fig. 4c).

• 9. $b_1<0, \hspace{5.0pt}\omega +C_0^2/4>0, \hspace{5.0pt}b_4=0$. Equation (32) has three equilibria in a sequnce: (saddle, degenerate, saddle) (Fig. 4d).

• 10. $b_1\cdot (\omega +C_0^2/4)<0, \hspace{5.0pt}D_2=0$. Equation (32) has two degenerate equilibria (Fig. 4e).

4 The first conservation law corresponding to Eq. (1)

Let us write Eq. (1) as the system of equations in the form

$$\begin{aligned} i\,q_t+a\,q_{xx}+\left( b_1\,|q|^{2n}+b_2\,|q|^{n}+b_3\,|q|^{-n}+b_4\,|q|^{-2n}\right) \,q=0, \end{aligned}$$

(36)

and

$$\begin{aligned} -i\,q_t^{*}+a\,q_{xx}^{*}+\left( b_1\,|q|^{2n}+b_2\,|q|^{n}+b_3\,|q|^{-n}+b_4\,|q|^{-2n}\right) \,q^{*}=0. \end{aligned}$$

(37)

Multiplying Eq. (36) by $q^{*}$ and Eq. (37) by $-q$ and adding the resulting expressions, we obtain the equation

$$\begin{aligned} i\,(q^{*}\,q_t+q\,q_t^{*})+a\,(q^{*}q_{xx}-q\,q_{xx}^{*})=0. \end{aligned}$$

(38)

Equation (38) can be presented in the form

$$\begin{aligned} \frac{\partial {T_1}}{\partial t}+\frac{\partial {X_1}}{\partial x}=0. \end{aligned}$$

(39)

where $T_1$ and $X_1$ take the form

$$\begin{aligned} T_1=i\,{|q|^2},\qquad X_1=a\,(q^{*}q_{x}-q\,q_{x}^{*}). \end{aligned}$$

(40)

From Eq. (39) follows the conservative quantity

$$\begin{aligned} P=\int _{-\infty }^{\infty }\,{|q|^2}\,dx=Const. \end{aligned}$$

(41)

The conservative quantity (41) correspons to the impulse power.

5 The second conservation law corresponding to Eq. (1)

The second conservation law can be found by multiplying Eq. (36) by $q_x^{*}$ and Eq. (37) by $q_x$ and adding the resulting equations. We get

$$\begin{aligned}{} & {} i\,(q_x^{*}\,q_t-q_x\,q_t^{*})+a\,(q_x^{*}\,q_{xx}+q_x\,q_{xx}^{*})+b_1\,|q|^{2n}\,(q_x^{*}\,q+q_x\,q^{*})+\nonumber \\{} & {} \quad \quad + b_2\,|q|^{n}\,(q_x^{*}\,q+q_x\,q^{*})+b_3\,|q|^{-n}\,(q_x^{*}\,q+q_x\,q^{*})+b_4\,|q|^{-2n}\,(q_x^{*}\,q+q_x\,q^{*})=0. \end{aligned}$$

(42)

Taking into account the following formulas

$$\begin{aligned}{} & {} q_x^{*}\,q_t-q_x\,q_t^{*}=\frac{1}{2}\,\frac{\partial }{\partial t}\,(q_x^{*}q-q^{*}q_x)-\frac{1}{2}\,\frac{\partial }{\partial x}\,(q_t^{*}q-q^{*}q_{t}), \end{aligned}$$

(43)

$$\begin{aligned}{} & {} q_x^{*} q+q^{*}q_x=\frac{\partial }{\partial x}\,(|q|^2), \end{aligned}$$

(44)

$$\begin{aligned}{} & {} q_x^{*}q_{xx}+q_{xx}^{*}q_x=\frac{\partial }{\partial x}\,(|q_x|^2), \end{aligned}$$

(45)

we can write Eq. (42) in the form

$$\begin{aligned}{} & {} \frac{i}{2}\,\frac{\partial }{\partial t}\,(q_x^{*}q-q^{*}q_x)-\frac{i}{2}\,\frac{\partial }{\partial x}\,(q_t^{*}q-q^{*}q_{t})+a\,\frac{\partial }{\partial x}\,(|q_x|^2)+\nonumber \\{} & {} \quad \quad + \frac{2 b_1}{2n+2}\frac{\partial }{\partial x}|q|^{2n+2}+\frac{2 b_2}{n+2}\frac{\partial }{\partial x} |q|^{n+2}+\nonumber \\{} & {} \quad \quad + \frac{2 b_3}{2-n} \frac{\partial }{\partial x} |q|^{2-n}+\frac{2 b_4}{2-2n} \frac{\partial }{\partial x} |q|^{2-2n}. \end{aligned}$$

(46)

The last equation can be presented as the conservation law

$$\begin{aligned} \frac{\partial T_2}{\partial t}+\frac{\partial X_2}{\partial x}\,=0, \end{aligned}$$

(47)

where $T_2$ and $X_2$ are determined by formulas

$$\begin{aligned} T_2= & {} \frac{i}{2}\,(q_x^{*}q-q^{*}q_x), \end{aligned}$$

(48)

$$\begin{aligned} X_2= & {} \frac{i}{2}\,(q^{*}q_{t}-q_t^{*}q)+a\,|q_x|^2 +\frac{2 b_1}{2n+2}\,|q|^{2n+2}+\frac{2 b_2}{n+2}\,|q|^{n+2}\nonumber \\{} & {} + \frac{2 b_3}{2-n}\,|q|^{2-n}+\frac{2 b_4}{2-2n}\,|q|^{2-2n}. \end{aligned}$$

(49)

From Eq. (47) we obtain the conservative quantity in the form

$$\begin{aligned} M=\frac{i}{2}\,\int _{-\infty }^{\infty }\left( q_x^{*}q-q^{*}q_x\right) =Const. \end{aligned}$$

(50)

Conservative quantity (50) corresponds to the conservation of the momentum of the solution q(x, t).

6 The third conservation law corresponding to Eq. (1)

At the first step we multiply Eq. (36) by $|q|^{2n}\,q^{*}$ and Eq. (37) by $-|q|^{2n}\,q$. After that we add the equations obtained. As a result we have the following equation

$$\begin{aligned} \frac{2\,i}{2n+2}\,\frac{\partial \,|q|^{2n+2}}{\partial t}+a\,|q|^{2n}\,(q^{*}\,q_{xx}-q\,q_{xx}^{*})=0. \end{aligned}$$

(51)

We also have the following equation after multiplying Eq. (36) by $|q|^{n}\,q^{*}$ and Eq. (37) by $-|q|^{n}\,q$ and then adding them. We get

$$\begin{aligned} \frac{2\,i}{n+2}\,\frac{\partial \,|q|^{n+2}}{\partial t}+a\,|q|^{n}\,(q^{*}\,q_{xx}-q\,q_{xx}^{*})=0. \end{aligned}$$

(52)

The two following equations can be obtained by multiplying Eq. (36) by $|q|^{-n}\,q^{*}$ and by $|q|^{-2n}\,q^{*}$, consequently, and Eq. (37) by $-|q|^{-n}\,q$, and bt $-|q|^{-2n}\,q$. Adding these expressions yields two following equations

$$\begin{aligned} \frac{2\,i}{2-n}\,\frac{\partial \,|q|^{2-n}}{\partial t}+a\,|q|^{-n}\,(q^{*}\,q_{xx}-q\,q_{xx}^{*})=0 \end{aligned}$$

(53)

and

$$\begin{aligned} \frac{2\,i}{2-2n}\,\frac{\partial \,|q|^{2-2n}}{\partial t}+a\,|q|^{-2n}\,(q^{*}\,q_{xx}-q\,q_{xx}^{*})=0. \end{aligned}$$

(54)

From Eqs. (51)–(54) one can see that we need other equations to find the third conservation law of Eq. (1). At the second step, first of all, we multiply Eq. (36) by $q_{xx}^{*}$ and Eq. (37) by $-q_{xx}$. Adding the expressions obtained, we have the equation

$$\begin{aligned}{} & {} i\,\frac{\partial \,}{\partial x}\left( q_x^{*}\,q_t+q_x\,q_t^{*}\right) -i\,\frac{\partial \,|q_x|^2}{\partial t}+\left( q\,q_{xx}^{*}-q_{xx}\,q^{*}\right) (b_1\,|q|^{2n}+\nonumber \\{} & {} \quad \quad + b_2\,|q|^{n}+b_3\,|q|^{-n}+b_4\,|q|^{-2n})=0. \end{aligned}$$

(55)

At the third step, we, first of all, multiply Eqs. (51), (52), (53) and (54) by $b_1$, $b_2$, $b_3$ and $b_4$, respectively. Then, Eq. (55) is multiplied by a. Adding five equations obtained yields the equation in the form

$$\begin{aligned}{} & {} \frac{2\,i\,b_1}{2n+2}\,\frac{\partial \,|q|^{2n+2}}{\partial t}+\frac{2\,i\,b_2}{n+2}\,\frac{\partial \,|q|^{n+2}}{\partial t}+\frac{2\,i\,b_3}{2-n}\,\frac{\partial \,|q|^{2-n}}{\partial t}+\nonumber \\{} & {} \quad \quad + \frac{2\,i\,b_4}{2-2n} \frac{\partial \,|q|^{2-2n}}{\partial t}-i\,a \frac{\partial \,|q_x|^2}{\partial t}+i\,a\,\frac{\partial \,}{\partial x}\left( q_x^{*}\,q_t+q_x\,q_t^{*}\right) . \end{aligned}$$

(56)

The last equation can be written as the conservation law

$$\begin{aligned} \frac{\partial \,T_3}{\partial t}+\frac{\partial \,X_3}{\partial x}=0, \end{aligned}$$

(57)

where $T_3$ and $X_3$ take the form

$$\begin{aligned} T_3=\frac{2\,b_1\,|q|^{2n+2}}{2n+2}+\frac{2\,b_2\,|q|^{n+2}}{n+2}+ \frac{2\,b_3\,|q|^{2-n}}{2-n}+\frac{2\,b_4\,|q|^{2-2n}}{2-2n} - a\,|q_x|^2 \end{aligned}$$

(58)

and

$$\begin{aligned} X_3=a\,\left( q_x^{*}\,q_t+q_x\,q_t^{*}\right) . \end{aligned}$$

(59)

From (57) we obtain the conservative quantity in the form

$$\begin{aligned}{} & {} H=\int _{-\infty }^{\infty }\left( \frac{2\,b_1}{2\,n+2}\,|q|^{2n+2}+\frac{2\,b_2}{n+2}\,|q|^{n+2}+\frac{2\,b_3}{2-n}\,|q|^{2-n}+\right. \nonumber \\{} & {} \quad + \left. \frac{2\,b_4}{2-2n}\,|q|^{2-2n} - a\,|q_x|^2 \right) \,dx=Const. \end{aligned}$$

(60)

Expression (60) corresponds to the conservation of energy for the optical soliton of Eq. (1).

7 Conservative quantities corresponding to the soliton (23) of Eq. (1)

Using the conservation laws we can calculate conservative quantities of solutions of Eq. (1). Without loss of generality, let us calculate the conservative quantities of optical soliton (23) corresponding to Eq. (1).

Let us note that to calculate the conservative quantity we use the following integral (Hammer 1953)

$$\begin{aligned} \Omega (\rho ,m,k)= & {} \int _{0}^{\infty }\,\frac{x^{2k-1}}{\left( {1+2\,\rho \,x+x^2}\right) ^{2m}}\,dx \nonumber \\= & {} (\rho - \sqrt{\rho ^2 - 1})^{2\,k}\,B(4m-2k,2k)\,F(2\,k,2\,m,4\,m,\frac{2\,\sqrt{\rho ^2 - 1})}{\rho + \sqrt{\rho ^2 - 1})}), \end{aligned}$$

(61)

where B(x, y) is the beta function and F(a, b, c, z) is the Gaussian hypergeometric function, and $2m>k$.

Substituting (23) into (41), we obtain the power of optical soliton (23) in the form

$$\begin{aligned} P=\int _{-\infty }^{\infty }\,{\left[ \frac{4\,\mu }{2\,\beta +(\beta ^2-4\,\mu \,\nu )\,{\textrm{e}}^{-\sqrt{\mu }z}+{\textrm{e}}^{\sqrt{\mu }z}}\right] }^{\frac{2}{n}}\,dz. \end{aligned}$$

(62)

Using the new variable $\xi =\frac{1}{\sqrt{\mu }}\,\ln (z)$, the integral (41) is reduced to the following

$$\begin{aligned} P= & {} \frac{(4\,\mu )^{\frac{2}{n}}}{\sqrt{\mu }}\,\int _{0}^{\infty }\,\frac{\xi ^{\frac{2}{n}-1}}{ \left( \beta ^2-4\,\mu \,\nu +2\,\beta \,\xi +\xi ^2\right) ^{\frac{2}{n}}}\,d \xi =\nonumber \\= & {} \frac{(4\,\mu )^{\frac{2}{n}}}{\sqrt{\mu }\,(\beta ^2-4\mu \nu )^{\frac{1}{n}}} \Omega \left( \frac{\beta }{\sqrt{\beta ^2-4\,\mu \,\nu }},\,\frac{1}{n},\frac{1}{n}\right) . \end{aligned}$$

(63)

The conservative quantity corresponding to the momentum is found by substituting solution (23) into expression (50). As a result we have

$$\begin{aligned} M=\frac{C_0\,(4\,\mu )^{\frac{2}{n}}}{2\,a\,\sqrt{\mu }\,(\beta ^2-4\,\mu \,\nu )^{\frac{1}{n}}}\,\Omega \left( \frac{\beta }{\sqrt{\beta ^2-4\,\mu \,\nu }},\,\frac{1}{n},\frac{1}{n}\right) . \end{aligned}$$

(64)

Conservative quantity of solution (23) corresponding to Eq. (1) can be calculated by substituting solution (23) into (60) and taking into account integral (61) at $b_3=0$ and $b_4=0$. This yields the conservative quantity in the form

$$\begin{aligned} H= & {} \frac{2\,b_1\,(4\,\mu )^{\frac{2n+2}{n}}}{(2n+2)\sqrt{\mu }\,(\beta ^2-4\mu \nu )^{\frac{n+1}{n}}}\,\,\Omega \left( \frac{\beta }{\sqrt{\beta ^2-4\,\mu \,\nu }},\,1+\frac{1}{n},\,1+\frac{1}{n}\right) \nonumber \\{} & {} + \frac{2\,b_2\,(4\,\mu )^{\frac{n+2}{n}}}{(n+2)\sqrt{\mu }\,(\beta ^2-4\mu \,\nu )^{\frac{n+2}{2n}}}\,\,\Omega \left( \frac{\beta }{\sqrt{\beta ^2-4\,\mu \,\nu }},\,\frac{1}{2}+\frac{1}{n},\,\frac{1}{2}+\frac{1}{n}\right) \nonumber \\{} & {} - \frac{C^2_0}{4\,a}\frac{(4\,\mu )^{\frac{2}{n}}}{\sqrt{\mu }\,(\beta ^2-4\mu \nu )^{\frac{1}{n}}}\,\Omega \left( \frac{\beta }{\sqrt{\beta ^2-4\,\mu \,\nu }},\,\frac{1}{n},\,\frac{1}{n}\right) \nonumber \\{} & {} - \frac{4^{\frac{2}{n}}\,\mu ^{\frac{2}{n} + \frac{1}{2}}\,a}{n^2\,(\beta ^2-4\mu \nu )^{\frac{1}{n}}}\,(\Omega (\frac{\beta }{\sqrt{\beta ^2-4\,\mu \,\nu }},\,1+\frac{1}{n},\,2+\frac{1}{n}) \nonumber \\{} & {} - 2\,\Omega (\frac{\beta }{\sqrt{\beta ^2-4\,\mu \,\nu }},\,1+\frac{1}{n},\,1+\frac{1}{n})\nonumber \\{} & {} + \Omega (\frac{\beta }{\sqrt{\beta ^2-4\,\mu \,\nu }},\,1+\frac{1}{n},\,\frac{1}{n})). \end{aligned}$$

(65)

This conservative quantity (65) corresponds to the energy of the optical soliton (23).

8 Conclusion

In this paper we have studied the mathematical model for propagation pulses with four powers of nonlinearity. This nonlinear partial differential equation is the generalization of the nonlinear Schrödiner equation and some other well-known mathematical models for description of propagation pulses in optical medium, therefore it may help us evaluate the influence of various processes on pulse propagation. The main objective of this paper was to construct conservation laws of Eq. (1). There have been derived three conservation laws corresponding to Eq. (1) by means of direct calculations. To present analytical expressions of conserved quantites for the explored equation, analytical optical soliton solutions corresponding to the mathematical model have also been given. Conservative quantities for the bright optical soliton have been calculated. We suppose that the analytical expressions for conservative quantities obtained can be applied to verify whether numerical schemes for the studied equation are conservative.