1 Introduction

Investigations on nonlinear partial differential equations (NLPDEs) are crucial and significant because these equations describe numerous different tendencies in a variety of scientific fields, including bioengineering, molecular biology, hydrodynamics, fluid mechanics, biogenetics, physiology, fiber optics and many more (Malik et al. 2023; Lin and Wen 2023; Abdulwahhab 2021; Shen et al. 2022; Perumalsamy et al. 2020). NLPDEs in a fluid mechanic describe the movement of neutrally buoyant plumes in a curving absorbent media, the authors of Adeyemo et al. (2022), Wen and Yan (2017, 2018) researched it. The solutions like solitons, breathers, rogue waves and semi-rational solutions on periodic backgrounds for the coupled Lakshmanan–Porsezian–Daniel equations was investigated by Li and Guo (2023). The generalized Korteweg–de Vries–Zakharov–Kuznetsov equation was also researched in Khalique and Adeyemo (2020). In particular, the authors in Gao et al. (2021) investigated a (3+1)-dimensional generalized varying Kadomtsev–Petviashvili (KP)-Burgers-type equation for several forms of interstellar dust plasma screens that was supported by observational and experimental data. One of the galactic or laboratory dust plasmas could be described by this equation as having an acceptor, subatomic or dust-ion-acoustic wave. Further examples are available for the reader in Raza et al. (2023), Zahran et al. (2023). In addition to the aforementioned, there has been a significant increase in mathematicians and physicists discovering efficient methods to find an exact solution to NLPDEs in recent times. Many of these methods include, the theory of the Lie groups (Yao et al. 2023), the generalized Riccati equation expansion method (Cakicioglu et al. 2023), the complicated hyperbolic function technique (Leonenko and Phillips 2023), the kather method (Ali et al. 2023), the \(\tan -\cot\) technique (Muatjetjejaa et al. 2023), the non-classical strategy (Raza et al. 2023), the variational transform (Golovnev 2023), the transformations (Singh and Ray 2023), the F-expansion technique (Rezazadeh et al. 2023), the extended simplest approach (Rehman et al. 2022), the Hirota bilinear technique (Ma and Fan 2011), the bifurcation technique (Ding et al. 2023), the \(\frac{G'}{G^2}\)-expansion technique (Walls and Stein 1973), the Darboux transformation (DT) (Li et al. 2020), the sine-Gordon equation expansion method approach (Kheaomaingam et al. 2023), the Kudryashov technique (Barman et al. 2021), the exp-function technique (Shakeel et al. 2023) and so on (Ahmad 2023, 2022).

It has been demonstrated in recent publications (Gilson et al. 1996) that multidimensional NLPDEs can be divided into a few (1+1)-dimensional NLPDEs. As a result, the latter can be used to deduce accurate solutions. Of the numerous methods, the DT is well recognized for being successful at identifying soliton solutions for NLPDEs. Geng has provided a new method for breaking down a YTSF equation into three (1+1)-dimensional Ablowitz–Kaup–Newell–Segur (AKNS) spectral equations.

It is observed that the YTSF equation is frequently employed to study the dynamics of solitons together with nonlinear waves that occur in fluid mechanics, hydrodynamics and weakly scattering media. Consider the YTSF equation (Dong et al. 2019)

$$\begin{aligned} -4v_{xt}+v_{xxxz}+4v_{x}v_{xz}+2v_{xx}v_{z}+3v_{yy}=0, \end{aligned}$$
(1)

this is a counterpart of the (3+1)-dimensional NLPDEs of the dynamic type defined as

$$\begin{aligned} \begin{aligned}&{[}-4u_{t}+\varPsi (u)u_{z}]_{x}+3u_{yy}=0,\\&\varPsi (u)=\partial ^{2}_{x}+4u+2u_{x}+2u_{x} \partial ^{-1}_{x}, \end{aligned} \end{aligned}$$
(2)

which contains the integro-differential component in Eq. (2) was primarily proposed by Ma et al. (2009) by the use of strong symmetry when creating the three-dimensional extension from the (2+1)-dimensional Calogero–Bogoyavlenkii–Schiff equation (Wazwaz 2017)

$$\begin{aligned} \begin{aligned}&-4u_{t}+\varPsi (u) u_{z}=0,\\&\varPsi (u)=\partial ^{2}_{x}+4u+2u_{x}\partial ^{-1}_{x}, \end{aligned} \end{aligned}$$
(3)

similar to the manner in which the KdV equation was used to derive the KP equation. System of Eq. (2) converts to the YTSF Eq. (1), which is an auxiliary of the Bogoyavlenskii–Schiff equation by taking \(u=v_{x}\). Furthermore, we see that Eq. (1) becomes the KP equation if \(z=x\) is assumed and it also reduces to the KdV equation if \(v_{y}=0\) is assumed. It is worth noting that the YTSF equation Eq. (1) is a hugely important higher dimensional nonlinear evolution equation (NLEE) capable of describing several dynamic processes as well as key phenomena encountered in both physics and engineering. The authors of Verma and Kaur (2021) used the exp-\((\psi (z))\)-expansion approach in conjunction with a sophisticated method to obtain some approximations to the Eq. (1). Furthermore, they were able to derive five different sorts of solutions, including exponentially, hyperbolic, rational, elliptical function and trigonometric solutions. Feng introduced a Bernoulli sub-ODE approach in Yang et al. (2015) to get certain accurate wave solutions of Eq. (1). The authors of Kristiansen (2004) used the \(\frac{G'}{G}\)-expansion approach to obtain several generalized solitary solutions of various physical structures for the YTSF Eq. (1). Adeyemo et al. (2023) used the transformations of undefined functions to change Eq. (1) into an integrated equation with two unique bilinear forms. Furthermore, the authors used Darvishi’s strategy to get certain modern multi-solutions by the use of homoclinic test technique and three wave techniques. Additionally, the non-traveling wave solution was realized by way of auto-B\(\ddot{a}\)cklund transformation, as well as the extended projective Riccati equation approaches (Li and Chen 2003). Additionally, several periodic solutions, as well as soliton solutions for the YTSF equation, were obtained using the Hirota bilinear, exp-function, homoclinic, \(\tanh -\coth\) and extended homoclinic tests. Recently, Darvishi employed the modified of the homoclinic testing method to secure certain closed-form solutions to the YTSF in Eq. (1) (Naidoo et al. 2023). In a similar spirit, Zayed and Arnous used the improved simple equation technique to obtain specific closed-form approximations to the YTSF equation (Wazwaz 2022). Also, by using the multiple \((\frac{G'}{G},\frac{1}{G})\)-expansion technique, Zayed and Hoda Ibrahim both succeeded in finding some analytical traveling wave solutions to the YTSF equation (Feng 2012). By using the \(\tanh\) approach, new closed-form solutions to the problem were derived after engaging in symmetry reduction of Eq. (1) (Gonze et al. 2020). Zayed and Arnous (2012) recently introduced

$$\begin{aligned} -4v_{xt}-v_{xxxx}-6v^{2}_{x}-6vv_{xx}+3v_{yy}=0, \end{aligned}$$
(4)

the equation is also known as the (2+1)-dimensional YTSF equation. Using symbolic computation and the Hirota bilinear approach, the authors got several closed-form solutions to Eq. (4) and some lump solutions.

In our study, we used a generalized YTSF equation

$$\begin{aligned} -2\epsilon v_{tx}+\epsilon v_{z}v_{xx}+2\epsilon v_{x}v_{xz}+\delta v_{yy}+\alpha v_{xxxz}=0, \end{aligned}$$
(5)

where parameters \(\epsilon ,~\delta ~and~\alpha\) are considered real constants with nonzero values. If \(\epsilon =2,~\delta =3~and~\alpha =1\), the YTSF Eq. (5) may be connected to the totally generalized YTSF Eq. (1). In this study, an explicit N-fold DT (Wen et al. 2015; Guo and Xie 2023) of the AKNS spectral equations is developed and the DT and decomposition are used to provide the multi-soliton, resonant and complex soliton solution to the YTSF equation. As an example, we get the solutions to a variety of solutions interactions. In contrast to the other approaches, DT is completely algebraic and offers a logical process for creating soliton solutions for nonlinear equations. By using DT to iteratively combine the solutions to the associated spectrum problem and nonlinear equation, one is able to generate solutions like resonant, complex, and multi-soliton solutions.

The article’s layout is set up as follows: Sect. 2 presents the decomposition of the YTSF equation to the three (1+1)-dimensional ANKS equation. Section 3 implements the DT technique. Sect. 4 represents the multi-soliton, along with the subsections of resonant and complex soliton solutions to the YTSF equation. Results and discussions are presented in Sect. 5 and concluding observations are made in Sect. 6.

2 The decomposition of a (3+1)-dimensional nonlinear YTSF equation to the (1+1)-dimensional AKNS equations

Assume that the AKNS spectral equation

$$\begin{aligned} \varphi _{x}=W\varphi ,\qquad W=\begin{pmatrix} \gamma &{} n\\ m &{} -\gamma \end{pmatrix}, \end{aligned}$$
(6)

and the adjunct problem

$$\begin{aligned} \varphi _{{t}_{r}}=L^{(r)}\varphi ,\qquad L^{(r)}=\begin{pmatrix} L^{(r)}_{11} &{} L^{(r)}_{12}\\ \\ L^{(r)}_{21} &{} -L^{(r)}_{11} \end{pmatrix}, \end{aligned}$$
(7)

where

$$\begin{aligned} L^{(r)}_{11}=\beta \gamma ^{(r)}+\sum _{i=0}^{r-1}c_{i}\gamma ^{i},\qquad L^{(r)}_{12}=\sum _{i=0}^{r-1}d_{i}\gamma ^{i},\qquad L^{(r)}_{21}=\sum _{i=0}^{r-1}e_{i}\gamma ^{i}, \end{aligned}$$

where \(c_{i},~d_{i}~and ~e_{i} ~(i = 0, 1,\ldots , r-1)\) being function of x and \(t_{r}\), \(\gamma\) is a constant spectral component and \(\beta\) is a constant. The zero distortion equation \(W_{{t}_{r}}-L^{(r)}_{x}+[W,~L^{(r)}]=0\), which is equal to the AKNS hierarchical, is the compatibility prerequisite of Eqs. (6) and (7).

$$\begin{aligned} \left( {\begin{array}{c}n\\ -m\end{array}}\right) _{{t}_{r}}=2\beta \phi ^{r}\left( {\begin{array}{c}n\\ m\end{array}}\right) , \end{aligned}$$
(8)

where

$$\begin{aligned}{} & {} \phi =\begin{pmatrix} \frac{1}{2}\partial _{x}-n\partial ^{-1}_{x}m &{} n\partial ^{-1}_{x}n\\ \\ -m\partial ^{-1}_{x}m &{} -\frac{1}{2}\partial _{x}+m\partial ^{-1}_{x}n \end{pmatrix}, \end{aligned}$$
(9)
$$\begin{aligned}{} & {} \left( {\begin{array}{c}d_{i-1}\\ e_{i-1}\end{array}}\right) =\phi \left( {\begin{array}{c}d_{i}\\ e_{i}\end{array}}\right) , \end{aligned}$$
(10)

and

$$\begin{aligned} d_{r-1}=\beta n,\qquad e_{r-1}=\beta m. \end{aligned}$$
(11)

The three major AKNS hierarchical members are provided by Eq. (8).

The AKNS equation is given for \(r = 2,~ t_{2} = y~and~\beta =-2\) is

$$\begin{aligned} n_y =-n_{xx}+2n^{2}m,\qquad m_{y}=m_{xx}-2nm^{2}, \end{aligned}$$
(12)

and the associated adjunct problem,

$$\begin{aligned} L^{(2)}=\begin{pmatrix} -2\gamma ^{(2)}+mn &{} -2\gamma n-n_{x}\\ \\ -2\gamma m +m_{x} &{} 2\gamma ^{(2)}-mn \end{pmatrix}. \end{aligned}$$
(13)

We obtain the AKNS equation for \(r = 3,~ t_{3} = t~ and~\beta = 4\) is,

$$\begin{aligned} n_{t}=n_{xxx}-6nmn_{x},\qquad m_{t}=m_{xxx}-6nmm_{x}, \end{aligned}$$
(14)

and the associated adjunct problem,

$$\begin{aligned} L^{(3)}=\begin{pmatrix} 4\gamma ^3-2\gamma nm-mn_{x}+nm_{x} &{} 4\gamma ^2 n+2\gamma n_x +n_{xx} -2n^2m\\ \\ 4\gamma ^2m-2\gamma m_{x}+m_{xx}-2nm^2 &{} -4\gamma ^3+2\gamma nm+mn_{x}-nm_{x} \end{pmatrix}. \end{aligned}$$
(15)

We obtain the AKNS equation for \(r = 4,~ t_{4} = z~ and~\beta = -8\) is,

$$\begin{aligned} \begin{aligned} n_z&=-n_{xxxx}+8nmn_{xx}+6n^{2}_{x}m+4nn_{x}m_{x}+2n^{2}m_{xx}-6n^3m^2, \\ m_z&=m_{xxxx}-8nmm_{xx}-6m^{2}_{x}n-4mn_{x}m_{x}-2m^{2}n_{xx}+6n^2m^3, \end{aligned} \end{aligned}$$
(16)

and the associated adjunct problem,

$$\begin{aligned} L^{(4)}=\begin{pmatrix} L^{(4)}_{11} &{} L^{(4)}_{12}\\ \\ L^{(4)}_{21} &{} -L^{(4)}_{11} \end{pmatrix}, \end{aligned}$$
(17)

where

$$\begin{aligned} \begin{aligned} L^{(4)}_{11}&=+4\gamma ^2mn-8\gamma ^4-2\gamma (nm_{x}-mn_{x})-n_xm_x-3n^2m^2+mn_{xx}+nm_{xx},\\ L^{(4)}_{12}&=-n_{xxx}-4\gamma ^2 n_x-8\gamma ^3n+6nmn_{x}+\gamma (4n^2m-2n_{xx}),\\ L^{(4)}_{21}&=6nmm_{x}+m_{xxx}-8\gamma ^3m+4\gamma ^2m_{x}+\gamma (4nm^2-2m_{xx}). \end{aligned} \end{aligned}$$

Considering the constraint, Geng recently published a novel decomposition of the (3+1)-dimensional NEE of Eq. (1)

$$\begin{aligned} v(x,y,t,z)=3nm. \end{aligned}$$
(18)

It is noteworthy that the reduction is perfectly connected to the (1+1)-dimensional AKNS Eqs. (12), (14) and (16).

Proposition (i)

Considering that the (1+1)-dimensional AKNS Eqs. (12), (14) and (16) have a corresponding solution of (n,  m). Then, the (3+1)-dimensional NEE of Eq. (1) is solved by the function of (18).

By creating an exact N-fold DT of the Eqs. (12), (14) and (16). The interoperable solutions (n,  m) of Eqs. (12), (14) and (16) as well as the constraint provide the multi-soliton, resonant and complex soliton solution to the (3+1)-dimensional NEE.

3 Darboux transformation

The DT of the spectral Eq. (6) and (7) (with Eqs. (12), (14) and (16)) will be discussed. In actuality, the DT is a gauge transformation.

$$\begin{aligned} {\overline{\varphi }}={\textbf{U}} \varphi {.} \end{aligned}$$
(19)

of the Eqs. (13), (15) and (17) from the spectrum Eqs. (6) and (7). It is necessary that \({\overline{\varphi }}\) also meets the same criteria as spectral difficulties.

$$\begin{aligned} {\overline{\varphi }}_{x}= & {} {\overline{W}}{\overline{\varphi }}, \qquad {\overline{W}}=\left( {\textbf{U}}_{x}+{\textbf{U}} W\right) {\textbf{U}}^{-1},\end{aligned}$$
(20)
$$\begin{aligned} {\overline{\varphi }}_{y}= & {} {\overline{L}}^{(2)}{\overline{\varphi }}, \qquad {\overline{L}}^{(2)}=\left( {\textbf{U}}_{y}+{\textbf{U}} L^{(2)}\right) {\textbf{U}}^{-1},\end{aligned}$$
(21)
$$\begin{aligned} {\overline{\varphi }}_{t}= & {} {\overline{L}}^{(3)}{\overline{\varphi }}, \qquad {\overline{L}}^{(3)}=\left( {\textbf{U}}_{t}+{\textbf{U}} L^{(3)}\right) {\textbf{U}}^{-1},\end{aligned}$$
(22)
$$\begin{aligned} {\overline{\varphi }}_{z}= & {} {\overline{L}}^{(4)}{\overline{\varphi }}, \qquad {\overline{L}}^{(4)}=\left( {\textbf{U}}_{z}+{\textbf{U}} L^{(4)}\right) {\textbf{U}}^{-1}. \end{aligned}$$
(23)

The previous potentials n and m in \(W,~ L ^{(2)},~ L ^{(3)} and L^{(4)}\) must be replaced with the new potentials \({\overline{n}}~ and~ {\overline{m}}\), which implies we must discover a matrix \({\textbf{U}}\) that accomplishes this goal.

Now assume that

$$\begin{aligned} {\textbf{U}}={\textbf{U}}(\gamma )=\begin{pmatrix} G(\gamma ) &{}Q(\gamma ) \\ \\ R(\gamma )&{} H(\gamma ) \end{pmatrix}, \end{aligned}$$
(24)

where

$$\begin{aligned} G(\gamma )= & {} \gamma ^{M}+\sum _{j=0}^{M-1}G{j}\gamma ^{j},\qquad Q(\gamma )=\sum _{j=0}^{M-1}Q{j}\gamma ^{j},\end{aligned}$$
(25)
$$\begin{aligned} R(\gamma )= & {} \sum _{j=0}^{M-1}R{j}\gamma ^{j},\qquad H(\gamma )=\gamma ^{M}+\sum _{j=0}^{M-1}H{j}\gamma ^{j}, \end{aligned}$$
(26)

with \(G(\gamma ),~Q(\gamma ),~R(\gamma )~and~H(\gamma ) ~(0\le j\le M-1)\) are functions of x,  y,  z and t.

\(\varphi (\gamma _{i})=(\varphi _{1}(\gamma _{i}),\varphi _{2}(\gamma _{i}))^{{\textbf{U}}}\) and \(\varPsi (\gamma _{i})=(\varPsi _{1}(\gamma _{i}),\varPsi _{2}(\gamma _{i}))^{{\textbf{U}}}\) are two fundamental solution to Eqs. (6) and (7), including Eqs. (13), (15) and (17). Constants \(p_{i}~ (1 \le i \le 2M)\), which fulfill Eq. (19), exist.

$$\begin{aligned}{} & {} \left[ G(\gamma _{i})\varphi _{1}(\gamma _{i})+Q(\gamma _{i}) \varphi _{2}(\gamma _{i}) \right] -p_{i}\left[ G(\gamma _{i})\varPsi _{1}(\gamma _{i})+Q(\gamma _{i}) \varPsi _{2}(\gamma _{i})\ \right] =0,\end{aligned}$$
(27)
$$\begin{aligned}{} & {} \left[ R(\gamma _{i})\varphi _{1}(\gamma _{i})+H(\gamma _{i}) \varphi _{2}(\gamma _{i}) \right] -p_{i}\left[ R(\gamma _{i})\varPsi _{1}(\gamma _{i})+H(\gamma _{i}) \varPsi _{2}(\gamma _{i})\ \right] =0. \end{aligned}$$
(28)

The Eqs. (27) and (28) can also be expressed as a linear algebraic problems.

$$\begin{aligned} G(\gamma _{i})+\sigma _{i}Q(\gamma _{i})=0,\qquad R(\gamma _{i})+\sigma _{i}H(\gamma _{i})=0, \end{aligned}$$
(29)

or

$$\begin{aligned} \sum _{j=0}^{M-1}(G_{j}+\sigma _{j}Q_{j})\gamma _{i}^{j}=-\gamma _{i}^{M},\qquad \sum _{j=0}^{M-1}(R_{j}+\sigma _{j}H_{j})\gamma _{i}^{j}=-\sigma _{i} \gamma _{i}^{M}, \end{aligned}$$
(30)

with

$$\begin{aligned} \sigma _{i}=\frac{\varphi _{2}(\gamma _{i})-p_{i}\varPsi _{2}(\gamma _{i})}{\varphi _{1}(\gamma _{i})-p_{i}\varPsi _{1}(\gamma _{i})},\quad 1 \le i \le 2M. \end{aligned}$$
(31)

The consideration of the constants \(\gamma _{i}~(\gamma _{j}\ne \gamma _{i}~as~j\ne i)\) and \(p_{i}\) ensures that the determinant of the coefficients in Eq. (30) is non-zero. As a result, determines \(G_{j},~Q_{j},~R_{j}~and~H_{j}~(0 \le j\le M-1)\) exclusively in Eq. (30). The Eqs. (25) and (26) illustrate that \(\det ({\textbf{U}}(\gamma ))\) is a second order polynomial in \(\gamma\),

$$\begin{aligned} \det {\textbf{U}}(\gamma _{i})=G(\gamma _{i})H(\gamma _{i})-Q(\gamma _{i})R(\gamma _{i}), \end{aligned}$$
(32)

from Eq. (29), we obtain

$$\begin{aligned} G(\gamma _{i})=-\sigma _{i}Q(\gamma _{i}),\qquad R(\gamma _{i})=-\sigma _{i}H(\gamma _{i}). \end{aligned}$$
(33)

As a result, it asserts that

$$\begin{aligned} \det {\textbf{U}}(\gamma _{i})=0. \end{aligned}$$
(34)

This suggest that \(\gamma _{i}~ (1 \le ~i \le ~ 2M)\) are 2M root of \(\det {\textbf{U}}(\gamma )\), which is

$$\begin{aligned} \det {\textbf{U}}(\gamma )=\alpha \prod _{i=1}^{2M}(\gamma -\gamma _{i}),\quad \therefore \alpha ~not~depend~in~\gamma . \end{aligned}$$
(35)

Proposition (ii)

The matrix \({\overline{W}}\) obtained from Eq. (20) possesses the same structure as W, which is

$$\begin{aligned} {\overline{W}}=\begin{pmatrix} \gamma &{} {\overline{n}}\\ {\overline{m}}&{} -\gamma \end{pmatrix}, \end{aligned}$$

where the transformation between n, m and \({\overline{n}}\), \({\overline{m}}\) is obtained by

$$\begin{aligned} {\overline{n}}=n-2Q_{M-1},\quad {\overline{m}}=m+2R_{N-1}, \end{aligned}$$
(36)

and

$$\begin{aligned} G_{{M-f}_{x}}= & {} R_{M-f}(n-2Q_{M-1})-mQ_{M-f},\end{aligned}$$
(37)
$$\begin{aligned} Q_{{M-f}_{x}}= & {} 2Q _{M-f-1}-nG_{M-f}+H_{M-f}(n-2Q_{M-1}),\end{aligned}$$
(38)
$$\begin{aligned} R_{{M-f}_{x}}= & {} -2R_{M-f-1}-mH_{M-f}+G_{M-f}(m+2R_{M-1}),\end{aligned}$$
(39)
$$\begin{aligned} H_{{M-f}_{x}}= & {} -nR_{M-f}+Q_{M-f}(m+2R_{M-1}), \end{aligned}$$
(40)

that is \(1~\le ~f\le ~ M,~G_{-1}=~Q_{-1}=~R_{-1}=~H_{-1}=~0.\)

Proof

Suppose \({\textbf{U}}^{-1}={\textbf{U}}^{*}/\det {\textbf{U}}\) and

$$\begin{aligned} ({\textbf{U}}_{x}+{\textbf{U}}W){\textbf{U}}^{*}=\begin{pmatrix} g_{11}(\gamma ) &{}g_{12}(\gamma ) \\ \\ g_{21}(\gamma )&{} g_{22}(\gamma ) \end{pmatrix}. \end{aligned}$$
(41)

It is unambiguous that \(g_{11}(\gamma )\) and \(g_{22}(\gamma )\) are polynomials of \((2M + 1)th\) order in \(\gamma\), whereas \(g_{12}(\gamma )\) and \(g_{21}(\gamma )\) are polynomials of 2Nth order in \(\gamma\). We explore Eqs. (6) and (31).

$$\begin{aligned} \sigma _{ix}=m-2\gamma _{i}\sigma _{i}-n\sigma _{i}^{2}. \end{aligned}$$
(42)

All \(\gamma _{i}~(0 ~\le ~i ~2M)\) are roots of \(g_{cd}(\gamma )~(c,d=1,2)\), according to Eqs. (33) and (42). Explored with Eqs. (35) and (41), yield us

$$\begin{aligned} ({\textbf{U}}_{x}+{\textbf{U}}W){\textbf{U}}^{*}=(\det {\textbf{U}})B(\gamma ), \end{aligned}$$
(43)

where

$$\begin{aligned} B(\gamma )= \begin{pmatrix} b_{11}^{(1)}(\gamma )+b_{11}^{(0)} &{}b_{12}^{(0)} \\ \\ b_{21}^{(0)}&{} b_{22}^{(1)}(\gamma )+b_{22}^{(0)} \end{pmatrix}, \end{aligned}$$
(44)

\(b_{ed}^{k}~ (e,~ d = 1, 2, ~k = 0, 1)\) are unrelated by the variable \(\gamma\). Equation (43) may now be expressed as

$$\begin{aligned} {\textbf{U}}_{x}+{\textbf{U}}W=B(\gamma ){\textbf{U}}, \end{aligned}$$
(45)

observations are made by contrasting the coefficients of \(\gamma ^{M+1}\) and \(\gamma ^{M}\) in Eq. (45) and observing Eq. (36).

$$\begin{aligned} b_{11}^{(1)}= & {} -b_{22}^{(1)}=1,\quad b_{11}^{(0)}=b_{22}^{(0)}=0,\end{aligned}$$
(46)
$$\begin{aligned} b_{12}^{(0)}= & {} n-2Q_{M-1}={\overline{n}},\quad b_{21}^{(0)}=m+2R_{M-1}={\overline{m}}. \end{aligned}$$
(47)

Hence, we proved that \(B(\gamma )={\overline{W}}\), with the help of Eqs. (20) and (45). \(\square\)

Proposition (iii)

The only difference between the matrix \({\overline{L}}^{(2)}\) and the matrix \(L^{(2)}\) described by Eq. (21) is the substitution of \({\overline{n}}\) and \({\overline{m}}\) for n and m. The identical DT in Eq. (19) are used to transfer the existing potentials (n, m) into new ones Eq. (36).

Proof

We write \({\textbf{U}}^{-1}={\textbf{U}}^{*}/\det {\textbf{U}}\), in a similar manner to proposition (ii) and

$$\begin{aligned} ({\textbf{U}}_{y}+{\textbf{U}}L^{(2)}){\textbf{U}}^{*}=\begin{pmatrix} q_{11}^{(2)}(\gamma ) &{}q_{12}^{(2)}(\gamma ) \\ \\ q_{21}^{(2)}(\gamma )&{} q_{22}^{(2)}(\gamma ) \end{pmatrix}. \end{aligned}$$
(48)

It is noteworthy that \(q_{11}^{(2)}\) and \(q_{22}^{(2)}\) are polynomial of \((2M + 2)th\) order in \(\gamma\), whereas \(q_{12}^{(2)}\) and \(q_{21}^{(2)}\) are polynomial of \((2M + 1)th\) order in \(\gamma\). Using Eqs. (7), (13), (31) and (33), we derive that

$$\begin{aligned} \sigma _{iy}= & {} -2\gamma m +m_{x}+2(2\gamma ^{2}-nm)\sigma _{i}+(2\gamma n+n_{x})\sigma _{i}^{2},\end{aligned}$$
(49)
$$\begin{aligned} G_{y}(\gamma _{i})= & {} -Q_{y}(\gamma _{i})\sigma _{i}-Q(\gamma _{i})\sigma _{iy},\end{aligned}$$
(50)
$$\begin{aligned} R_{y}(\gamma _{i})= & {} -H_{y}(\gamma _{i})\sigma _{i}-H(\gamma _{i})\sigma _{iy}. \end{aligned}$$
(51)

By using Eqs. (33) and (49–51), we can demonstrate that all \(\gamma _{i}~ (1 ~\le ~ i~ 2M)\) are roots of \(q_{cd}^{(2)}(\gamma ) (c,d = ~1, ~2).\) Eqs. (35) and (48), together with

$$\begin{aligned} ({\textbf{U}}_{y}+{\textbf{U}}L^{(2)}){\textbf{U}}^{*}=(\det {\textbf{U}})A(\gamma ), \end{aligned}$$
(52)

where

$$\begin{aligned} A(\gamma )=\begin{pmatrix} a_{11}^{(2)}\gamma ^{2}+a_{11}^{(1)}\gamma +a_{11}^{(0)}&{}a_{12}^{(1)}(\gamma )+a_{12}^{(0)} \\ \\ a_{21}^{(1)}(\gamma )+a_{21}^{(0)} &{} a_{22}^{(2)}\gamma ^{2}+a_{22}^{(1)}\gamma +a_{22}^{(0)} \end{pmatrix}, \end{aligned}$$
(53)

\(a_{ed}^{(k)}~(e,d=~0,~1,~k=0,~1,~2)\) are not dependent on \(\gamma\). Equation (52) is now represented as

$$\begin{aligned} {\textbf{U}}_{y}+{\textbf{U}}L^{(2)}=A(\gamma ){\textbf{U}}, \end{aligned}$$
(54)

using Eqs. (36–40) and contrasting the coefficients of \(\gamma ^{M+2},~ \gamma ^{M+1}\) and \(\gamma ^{M}\) in Eq. (54), we obtain

$$\begin{aligned} -a_{11}^{(2)}= & {} a_{22}^{(2)}=2,\quad a_{11}^{(1)}=a_{22}^{(1)}=a_{22}^{(1)}=0,\end{aligned}$$
(55)
$$\begin{aligned} a_{12}^{(1)}= & {} 2(2Q_{M-1}-n)=-2{\overline{n}},\nonumber \\ a_{21}^{(1)}= & {} -2(m+2R_{M-1})=-2{\overline{m}},\end{aligned}$$
(56)
$$\begin{aligned} a_{11}^{(0)}= & {} -a_{22}^{(0)}=-(2Q_{M-1}-n)(m+2R_{M-1})={\overline{n}}{\overline{m}},\end{aligned}$$
(57)
$$\begin{aligned} a_{12}^{(0)}= & {} -2nG_{M-1}+4Q_{M-2}+2nH_{M-1}-4Q_{M-1}H_{M-1}-n_{x} =(2Q_{M-1}-n)_{x}=-{\overline{n}}_{x},\end{aligned}$$
(58)
$$\begin{aligned} a_{21}^{(0)}= & {} 2mG_{M-1}-2mH_{M-1}+4G_{M-1}R_{M-1}-4R_{M-2}+m_{x} =(2R_{M-1}+m)_{x}={\overline{m}}_{x}. \end{aligned}$$
(59)

Hence, we proved that \(A(\gamma )={\overline{L}}^{(2)}\), with the help of Eqs. (21) and (54). \(\square\)

Proposition (iv)

The difference between \(L^{(3)]}\) and the matrix \({\overline{L}}^{(3)}\) described in Eq. (22) is the substitution of \({\overline{n}}\) and \({\overline{m}}\) for n and m. The similar DT are used to transfer the existing potentials n,  m into new ones of Eqs. (19) and (36).

Proof

From Eq. (19)

$$\begin{aligned} {\textbf{U}}_{t}+{\textbf{U}}L^{(3)}=C(\gamma ){\textbf{U}}, \end{aligned}$$
(60)

where

$$\begin{aligned} C(\gamma )=\begin{pmatrix} c_{11}^{(3)}\gamma ^{3}+c_{11}^{(2)}\gamma ^{2}+c_{11}^{(1)}\gamma +c_{11}^{(0)} &{} c_{12}^{(2)}\gamma ^{2}+c_{12}^{(1)}\gamma +c_{12}^{(0)} \\ \\ c_{21}^{(2)}\gamma ^{2}+c_{21}^{(1)}\gamma +c_{21}^{(0)} &{} c_{22}^{(3)}\gamma ^{3}+c_{22}^{(2)}\gamma ^{2}+c_{22}^{(1)}\gamma +c_{22}^{(0)} \end{pmatrix}, \end{aligned}$$
(61)

\(c_{ed}^{(k)}~(e,d=~0,~1,~k=0,~1,~2,~3)\) are not dependent on \(\gamma\). According to Eqs. (7), (15), (31) and (33), we obtain

$$\begin{aligned} \sigma _{it}= & {} 4\gamma ^{2}m-2\gamma m_{x}-2nm^{2}+m_{xx}-2(4\gamma ^{3} -2nm-mn_{x}+nm_{x})\sigma _{i}\nonumber \\{} & {} -4(\gamma ^{2}n+2\gamma n_{x}-2n^{2} m +n_{xx})\sigma _{i}^{2},\end{aligned}$$
(62)
$$\begin{aligned} G_{t}(\gamma _{i})= & {} -Q_{t}(\gamma _{i})\sigma _{i}-Q(\gamma _{i})\sigma _{it},\end{aligned}$$
(63)
$$\begin{aligned} R_{t}(\gamma _{i})= & {} -H_{t}(\gamma _{i})\sigma _{i}-H(\gamma _{i})\sigma _{it}, \end{aligned}$$
(64)

using Eqs. (36–40) and contrasting the coefficients of \(\gamma ^{M+3},~\gamma ^{M+2},~\gamma ^{N+1}\) and \(\gamma ^{M}\) in Eq. (60), we have

$$\begin{aligned} c_{11}^{(3)}= & {} -c_{22}^{(3)}=4,\quad c_{11}^{(2)}=c_{22}^{(2)}=0\end{aligned}$$
(65)
$$\begin{aligned} c_{12}^{(2)}= & {} 4(n-2Q_{M-1})=4{\overline{m}},\quad c_{21}^{(2)}=4(m+2R-{M-1})=4{\overline{m}},\end{aligned}$$
(66)
$$\begin{aligned} c_{11}^{(1)}= & {} -c_{22}^{(1)}=-2(n-2Q_{M-1})(m+2R_{M-1}) =-2{\overline{m}}~{\overline{n}},\end{aligned}$$
(67)
$$\begin{aligned} c_{12}^{(1)}= & {} -2(4Q_{M-2}-4Q_{M-1}H_{M-1}-2nG_{M-1}+2nH_{M-1}-n_{x}) =-2(2Q_{M-1}-n)_{x}=2{\overline{n}}_{x},\end{aligned}$$
(68)
$$\begin{aligned} c_{21}^{(1)}= & {} -2(m_{x}+4G_{M-1}R_{M-1}-4R_{M-2}+2mG_{M-1}-2mH_{M-1}) =-2(m+2R_{M-1})_{x}=-2{\overline{m}}_{x},\end{aligned}$$
(69)
$$\begin{aligned} c_{11}^{(0)}= & {} -c_{22}^{(0)}=nm_{x}-8G_{M-1}Q_{M-1}R_{M-1}+8Q_{M-2} R_{M-1}+8Q_{M-1}R_{M-2}-8Q_{M-1}R_{M-1}H_{M-1}\nonumber \\{} & {} -4nR_{M-2}+4nR_{M-1}H_{M-1}-4mG_{M-1}Q_{M-1}+4mQ_{M-2}-2n_{x}R_{M-1} -mn_{x}-2m_{x}Q_{M-1} \nonumber \\= & {} -(2R_{M-1}+m)(n-2Q_{M-1})_{x}+(n-2Q_{M-1})(2R_{M-1}+m)_{x} =-{\overline{m}}~{\overline{n}}_{x}+{\overline{n}}~{\overline{m}}_{x},\end{aligned}$$
(70)
$$\begin{aligned} c_{12}^{(0)}= & {} n_{xx}-8G_{M-3}-8QQ_{M-1}^{2}R_{M-1}+8Q_{M-2}H_{M-1} -8Q_{M-1}H_{M-1}^{2}+8Q_{M-1}H_{M-2}+4nG_{M-2}+4nG_{M-1}\nonumber \\{} & {} R_{M-1}-4nG_{M-1}H_{M-1}+4nH_{M-1}^{2}-4nH_{M-2}-4mQ_{M-1}^{2} +4nmQ_{M-1}+2n^{2}m+2n_{x}G_{M-1}-2n_{x}H_{M-1}\nonumber \\= & {} -2(n-2Q_{M-1})^{2}(m+2R_{M-1})+(n-2Q_{M-1})_{xx} =-2{\overline{n}}^{2}~{\overline{m}}+{\overline{n}}_{xx},\end{aligned}$$
(71)
$$\begin{aligned} c_{21}^{(0)}= & {} m_{xx}-8G_{M-2}R_{M-1}+8G_{M-1}^{2}R_{M-1}+8Q_{M-1} R_{M-1}^{2}-8G_{M-1}R_{M-2}+8R_{M-3}-4nR_{M-1}^{2}+4mG_{M-1}^{2}\nonumber \\{} & {} -4mG_{M-2}+4mQ_{M-1}R_{M-1}-4mG_{M-1}H_{M-1}+4mH_{M-2}-4nmR_{M-1} -2nm^{2}+2m_{x}G_{M-1}-2m_{x}H_{M-1}\nonumber \\= & {} -2(n-2Q_{M-1})(m+2R_{M-1})^{2}+(m+2R_{M-1})_{xx}=-2{\overline{n}} ~{\overline{m}}^{2}+{\overline{m}}_{xx}. \end{aligned}$$
(72)

Hence, we proved that \(C(\gamma )={\overline{L}}^{(3)}\), with the help of Eqs. (22) and (60). \(\square\)

Proposition (v)

The only difference between the matrix \({\overline{L}}^{(4)}\) and the matrix \(L^{(4)}\) described by Eq. (23) is the substitution of \({\overline{n}}\) and \({\overline{m}}\) for n and m. The identical DT of Eqs. (19) and (36) are used to transfer the existing potentials n,  m into new ones.

Proof

From Eq. (19)

$$\begin{aligned} {\textbf{U}}_{z}+{\textbf{U}}L^{(4)}=S(\gamma ){\textbf{U}}, \end{aligned}$$
(73)

where

$$\begin{aligned} S(\gamma )=\begin{pmatrix} s_{11}^{(4)}\gamma ^{4}+s_{11}^{(3)}\gamma ^{3}+s_{11}^{(2)}\gamma ^{2}+s_{11}^{(1)}\gamma +s_{11}^{(0)} &{} s_{12}^{(3)}\gamma ^{3}+s_{12}^{(2)}\gamma ^{2}+s_{12}^{(1)}\gamma +s_{12}^{(0)} \\ \\ s_{21}^{(3)}\gamma ^{3}+s_{21}^{(2)}\gamma ^{2}+s_{21}^{(1)}\gamma +s_{21}^{(0)} &{} s_{22}^{(4)}\gamma ^{4}+s_{22}^{(3)}\gamma ^{3}+s_{22}^{(2)}\gamma ^{2}+s_{22}^{(1)}\gamma +s_{22}^{(0)} \end{pmatrix}, \end{aligned}$$
(74)

\(s_{ed}^{(k)}~(e,d=~0,~1,~k=0,~1,~2,~3,~4)\) are not dependent on \(\gamma\). According to Eqs. (7), (17), (31) and (33), we obtain

$$\begin{aligned} \sigma _{iz}= & {} m_{xxx}-8\gamma ^{3}m+4\gamma ^{2}m_{x}-6nmm_{x} +2\gamma (2nm^{2}-m_{xx})\nonumber \\{} & {} -2[-8\gamma ^{4}+4\gamma ^{2}nm-3n^{2}m^{2}-n_{x}m_{x}\nonumber \\{} & {} -2\gamma (nm_{x}-mn_{x})+mn_{xx}+nm_{xx}]\sigma _{i}-[-8\gamma ^{3}n- 4\gamma ^{2}n_{x}\nonumber \\{} & {} +2\gamma (2n^{2}m-n_{xx}+6nmn_{xx}-n_{xxx}]\sigma _{i}^{2},\end{aligned}$$
(75)
$$\begin{aligned} G_{z}(\gamma _{i})= & {} -Q_{z}(\gamma _{i})\sigma _{i}-Q(\gamma _{i})\sigma _{iz},\end{aligned}$$
(76)
$$\begin{aligned} R_{z}(\gamma _{i})= & {} -H_{z}(\gamma _{i})\sigma _{i}-H(\gamma _{i})\sigma _{iz}, \end{aligned}$$
(77)

using Eqs. (36–40) and contrasting the coefficients of \(\gamma ^{M+4},~\gamma ^{M+3},~\gamma ^{M+2},~\gamma ^{N+1}\) and \(\gamma ^{M}\) in Eq. (73), we have

$$\begin{aligned} s_{22}^{(4)}= & {} -s_{11}^{(4)}=8,\quad s_{11}^{(3)}=s_{22}^{(3)}=0,\end{aligned}$$
(78)
$$\begin{aligned} s_{12}^{(3)}= & {} -8(n-2Q_{M-1})=-8{\overline{n}},\quad s_{21}^{(3)}=-8(m+2R_{M-1})=-8{\overline{m}},\end{aligned}$$
(79)
$$\begin{aligned} s_{11}^{(2)}= & {} -s_{22}^{(2)}=4(n-2Q_{M-1})(m+R_{M-1})=4{\overline{n}}~{\overline{m}},\end{aligned}$$
(80)
$$\begin{aligned} s_{12}^{(2)}= & {} 4(-n_{x}+4Q_{M-2}-4Q_{M-1}H_{M-1}-2nG_{M-1}+2nH_{M-1})\nonumber \\= & {} -4(n-2Q_{M-1})_{x}=-4{\overline{n}}_{x},\end{aligned}$$
(81)
$$\begin{aligned} s_{21}^{(2)}= & {} 4(m_{x}+4G_{M-1}R_{M-1}-4R_{M-2}+2mG_{M-1}-2mH_{M-1}\nonumber \\= & {} 4(m+2R_{M-1})_{x}=4{\overline{m}}_{x}\end{aligned}$$
(82)
$$\begin{aligned} s_{11}^{(1)}= & {} -s_{22}^{(1)}=-2[nm_{x}-8G_{M-1}Q_{M-1}R_{M-1}\nonumber \\{} & {} +8Q_{M-2}R_{M-1}+8Q_{M-1}R_{M-2}-8Q_{M-1}R_{M-1}H_{M-1}\nonumber \\{} & {} -4mR_{M-2}+4mR_{M-1}H_{M-1-2}-4mG_{M-1}Q_{M-1}+4mQ_{M-2}\nonumber \\{} & {} -2n_{x}R_{M-1}-mn_{x}-2m_{x}Q_{M-1}] \nonumber \\= & {} -2[-(m+2R_{M-1})(n-2Q_{M-1})_{x}+(n-2Q_{M-1})(2R_{M-1}+m)_{x}]\nonumber \\{} & {} =-2(-{\overline{m}}~{\overline{n}}_{x}+{\overline{n}}~{\overline{m}}_{x}),\end{aligned}$$
(83)
$$\begin{aligned} s_{12}^{(1)}= & {} 2[-n_{xx}+8G_{M-3}+8Q_{M-1}^{2}R_{M-1}-8Q_{M-2}H_{M-1}\nonumber \\{} & {} +8Q_{M-1}H_{M-1}^{2}-8Q_{M-1}H_{M-2}-4nG_{M-2}\nonumber \\{} & {} -4nQ_{M-1}R_{M-1}+4mG_{M-1}H_{M-1}-4nH_{M-1}^{2}+4nH_{M-2}\nonumber \\{} & {} +4mQ_{M-1}^{2}-4nmQ_{M-1}+2n^{2}m-2n_{x}G_{M-1}\nonumber \\{} & {} +2n_{x}H_{M-1}] =4(n-2Q_{M-1})^{2}(m+2R_{M-1})-2(n-2Q_{M-1})_{xx}\nonumber \\= & {} 4{\overline{n}}^{2}{\overline{m}}-2{\overline{n}}_{xx},\end{aligned}$$
(84)
$$\begin{aligned} s_{21}^{(1)}= & {} -2[m_{xx}+8G_{M-1}^{2}R_{M-1}-8G_{M-2}R_{M-1}\nonumber \\{} & {} +8Q_{M-1}R_{M-1}^{2}-8G_{M-1}R_{M-1}+8R_{M-3}-4nR_{M-1}^{2}\nonumber \\{} & {} +4mG_{M-1}^{2}-4mG_{M-2}+4mQ_{M-1}R_{M-1}-4mG_{M-1}H_{M-1}\nonumber \\{} & {} +4mH_{M-2}-4nmR_{M-1}-2nm^{2}+2m_{x}G_{M-1}\nonumber \\{} & {} -2m_{x}H_{M-1}]=4(n-2Q_{M-1})(m+2R_{M-1})^{2}-2(m+2R_{M-1})_{xx}\nonumber \\= & {} 4{\overline{n}}~{\overline{m}}^{2}-2{\overline{m}}_{xx},\end{aligned}$$
(85)
$$\begin{aligned} s_{11}^{(0)}= & {} -s_{22}^{(0)}=-3(n-2Q_{M-1})^{2}-(n-2Q_{M-1})_{x}(m +2Q_{M-1})_{x}+(m+2R_{M-1})(n-2Q_{M-1})\nonumber \\{} & {} {}_{xx}+(n-2Q_{M-1})(m+2R_{M-1})_{xx}\nonumber \\= & {} -3{\overline{n}}^{2}{\overline{m}}^{2} -{\overline{n}}_{x}~{\overline{m}}_{x}+{\overline{n}}~{\overline{m}}_{xx} +{\overline{n}}~{\overline{m}}_{xxx},\end{aligned}$$
(86)
$$\begin{aligned} s_{12}^{(0)}= & {} 6(n-2Q_{M-1})(m+2R_{M-1})(n-2Q_{M-1})_{x}-(n-2Q_{M-1})_{xxx}\nonumber \\= & {} -6{\overline{n}}~{\overline{m}}~{\overline{n}}_{x}-{\overline{n}}_{xxx},\end{aligned}$$
(87)
$$\begin{aligned} s_{21}^{(0)}= & {} 6(-n+2Q_{M-1})(m+2R_{M-1})(m+2R_{M-1})_{x}+(m+2R_{M-1})_{xxx}\nonumber \\= & {} {\overline{m}}_{xxx}-6{\overline{n}}~{\overline{m}}~{\overline{m}}_{x}. \end{aligned}$$
(88)

Hence, we proved that \(S(\gamma )={\overline{L}}^{(4)}\), with the help of Eqs. (23) and (74).

The modifications of Eqs. (19) and (36), turn the lax pair of Eqs. (6), (13), (15) and (17) into additional lax pair of the Eqs. (20–23), as shown by propositions \((ii)-(v)\). It follows that both Lax pair of Eqs. (6), (13) and Eqs. (20), (21) lead to the same AKNS equation of Eq. (12), both Lax pairs of Eqs. (6), (15) and Eqs. (20, 22) lead to the same AKNS Eq. (14) and both Lax pairs of Eqs. (6), (17) and Eqs. (20), (23), lead to the same AKNS Eq. (16). The DT of the AKNS Eqs. (12), (14) and (36), are the transformation of Eqs. (19) and (36). \(\square\)

4 Soliton solutions

In accordance with the proposition (i)–(v), we will create the fundamental solution of Eqs. (6) and (7) (such as Eqs. (13), (15) and (17) and the DT of Eqs. (19) and (36) for the (1 + 1)-dimensional AKNS equations of Eqs. (12), (14) and (16). Start by substituting \(n=m=0\) into the spectral Eqs. (6) and (7) (such as Eqs. (13), (15) and (17)). Then select one of the two simple solutions,

$$\begin{aligned} \varphi (\gamma _{i})=\left( {\begin{array}{c}\exp (\zeta _{i})\\ 0\end{array}}\right) ,\quad \varPsi (\gamma _{i})=\left( {\begin{array}{c}0\\ \exp (-\zeta _{i})\end{array}}\right) , \end{aligned}$$
(89)

that is \(\zeta _{i}=\gamma _{i}x-2\gamma ^{2}_{i}y-8\gamma _{i}^{4}z+4\gamma _{i}^{3}t~~(1\le ~i\le ~2\,M).\) Eq. (31) implies that,

$$\begin{aligned} \sigma _{i}=-p_{i}\exp (-2\zeta _{i}),\quad (1 \le ~i\le ~2M). \end{aligned}$$
(90)

Proposition (vi)

We may derive a novel solution for the (3+1)-dimensional NEE of Eq. (1) using DT of Eqs. (19) and (36) and constraints of Eq. (18),

$$\begin{aligned} v[M]=-12Q_{M-1}R_{M-1}=-12\frac{\varDelta _{Q_{M-1}}\varDelta _{R_{M-1}}}{\varDelta _{M-1}^{2}}, \end{aligned}$$
(91)

where

$$\begin{aligned} \varDelta _{M-1}=\begin{vmatrix} 1&\sigma _1&\gamma _{1}&\sigma _{1}\gamma _{1}&...&\gamma _{1}^{M-1}&\sigma _{1}\gamma _{1}^{M-1}\\ \\ 1&\sigma _2&\gamma _{2}&\sigma _{2}\gamma _{2}&...&\gamma _{2}^{M-1}&\sigma _{2}\gamma _{2}^{M-1} \\...&...&...&...&...&...&... \\ 1&\sigma _{2M-1}&\gamma _{2M-1}&\sigma _{2m-1}\gamma _{2M-1}&...&\gamma _{2M-1}^{M-1}&\sigma _{2M-1}\gamma _{2M-1}^{M-1}\\ \\ 1&\sigma _{2M}&\gamma _{2M}&\sigma _{2M}\gamma _{2M}&...&\gamma _{2M}^{M-1}&\sigma _{2M}\gamma _{2m}^{M-1} \end{vmatrix}, \end{aligned}$$

Now, we discuss following cases for different values for M.

Case (i). \((M=1)\)

Suppose that \(\gamma _{i},~p_{i}~(i=1,~2),\) solve the algebraic Eq. (30),

$$\begin{aligned} \begin{aligned} G_0=\frac{\sigma _{1}\gamma _{2}-\sigma _{2}\gamma _{1}}{\sigma _{2}-\sigma _{1}}, \quad Q_{0}=\frac{\gamma _{1}-\gamma _{2}}{\sigma _{2}-\sigma _{1}}, \quad R_{0}=\frac{\sigma _{1}\sigma _{2}(\gamma _{2}-\gamma _{1})}{\sigma _{2}-\sigma _{1}}, \quad H_{0}\frac{\sigma _{1}\gamma _{1}-\sigma _{2}\gamma _{2}}{\sigma _{2}-\sigma _{1}}. \end{aligned} \end{aligned}$$
(92)

A one-soliton solution of Eq. (1) is derived by inserting Eq. (92) into Eq. (91),

$$\begin{aligned} v[1]=3{\overline{n}}[1]{\overline{m}}[1]=-12Q_{0}R_{0} =\frac{12p_{1}p_{2}(\gamma _{1}-\gamma _{2})^{2}}{[p_{1}\exp (\theta _{1})-p_{2} \exp (-\theta _{1})]^{2}}, \end{aligned}$$
(93)

that is \(\theta _{1}=\zeta _{1}-\zeta _{2}.\)

Case (ii). \((M=2)\)

Suppose that \(\gamma _{i},~p_{i}~(i=1,~2,~3,~4),\) solve the algebraic Eq. (30),

$$\begin{aligned} Q_{1}=\frac{\varDelta _{Q_{1}}}{\varDelta _{1}},\quad R_{1}=\frac{\varDelta _{R_{1}}}{\varDelta _{1}}, \end{aligned}$$
(94)

where

$$\begin{aligned} \varDelta _{1}=\begin{vmatrix} 1&\sigma _{1}&\gamma _1&\sigma _{1}\gamma _1\\ 1&\sigma _{2}&\gamma _2&\sigma _{2} \gamma _2\\ 1&\sigma _{3}&\gamma _3&\sigma _{3} \gamma _3\\ 1&\sigma _{4}&\gamma _4&\sigma _{4}\gamma _4 \end{vmatrix},~~~ \varDelta _{Q_{1}}=\begin{vmatrix} 1&\sigma _{1}&\gamma _1&-\gamma _1^2\\ 1&\sigma _{2}&\gamma _2&-\gamma _2^2\\ 1&\sigma _{3}&\gamma _3&-\gamma _3^2\\ 1&\sigma _{4}&\gamma _4&-\gamma _4^2 \end{vmatrix},~~~ \varDelta _{R_{1}}=\begin{vmatrix} 1&\sigma _{1}&-\sigma _{1}\gamma _1^{2}&\sigma _{1}\gamma _1\\ 1&\sigma _{2}&-\sigma _{2}\gamma _2^{2}&\sigma _{2}\gamma _2\\ 1&\sigma _{3}&-\sigma _{3}\gamma _3^{2}&\sigma _{3}\gamma _3\\ 1&\sigma _{4}&-\sigma _{4}\gamma _4^{2}&\sigma _{4}\gamma _4 \end{vmatrix}. \end{aligned}$$

A two-soliton solution of Eq. (1) is derived by using Eq. (91),

$$\begin{aligned} v[2]=-12Q_{1}R_{1}=-12\frac{\varDelta _{Q_{1}}\varDelta _{R_{1}}}{\varDelta _{1}^{2}}. \end{aligned}$$
(95)

Case (iii). \((M=3)\)

Suppose that \(\gamma _{i},~p_{i}~(i=1,~2,~3,~4,~5,~6),\) solve the algebraic Eq. (30),

$$\begin{aligned} Q_{2}=\frac{\varDelta _{Q_{2}}}{\varDelta _{2}},\quad R_{2}=\frac{\varDelta _{R_{2}}}{\varDelta _{2}}, \end{aligned}$$
(96)

where

$$\begin{aligned} \varDelta _{2}= & {} \begin{vmatrix} 1&\sigma _1&\gamma _1&\sigma _1\gamma _1&\gamma _1^2&\sigma _{1}\gamma _{1}^{2}\\ 1&\sigma _2&\gamma _2&\sigma _2\gamma _2&\gamma _2^2&\sigma _{2}\gamma _{2}^{2} \\ 1&\sigma _3&\gamma _3&\sigma _3\gamma _3&\gamma _3^2&\sigma _{3}\gamma _{3}^{2}\\ 1&\sigma _4&\gamma _4&\sigma _4\gamma _4&\gamma _4^2&\sigma _{4}\gamma _{4}^{2} \\ 1&\sigma _5&\gamma _5&\sigma _5\gamma _5&\gamma _5^2&\sigma _{5}\gamma _{5}^{2}\\ 1&\sigma _6&\gamma _6&\sigma _6\gamma _6&\gamma _6^2&\sigma _{6}\gamma _{6}^{2} \end{vmatrix},\quad \varDelta _{Q_{2}}=\begin{vmatrix} 1&\sigma _1&\gamma _1&\sigma _1\gamma _1&\gamma _1^2&-\gamma _{1}^{3}\\ 1&\sigma _2&\gamma _2&\sigma _2\gamma _2&\gamma _2^2&-\gamma _{2}^{3}\\ 1&\sigma _3&\gamma _3&\sigma _3\gamma _3&\gamma _3^2&-\gamma _{3}^{3}\\ 1&\sigma _4&\gamma _4&\sigma _4\gamma _4&\gamma _4^2&-\gamma _{4}^{3}\\ 1&\sigma _5&\gamma _5&\sigma _5\gamma _5&\gamma _5^2&-\gamma _{5}^{3}\\ 1&\sigma _6&\gamma _6&\sigma _6\gamma _6&\gamma _6^2&-\gamma _{6}^{3} \end{vmatrix},\\ \varDelta _{R_{2}}= & {} \begin{vmatrix} 1&\sigma _1&\gamma _1&\sigma _1\gamma _1&-\sigma _{1}\gamma _1^3&\sigma _{1}\gamma _{1}^{2}\\ 1&\sigma _2&\gamma _2&\sigma _2\gamma _2&-\sigma _{2}\gamma _2^3&\sigma _{2}\gamma _{2}^{2} \\ 1&\sigma _3&\gamma _3&\sigma _3\gamma _3&-\sigma _{3}\gamma _3^3&\sigma _{3}\gamma _{3}^{2}\\ 1&\sigma _4&\gamma _4&\sigma _4\gamma _4&-\sigma _{4}\gamma _4^3&\sigma _{4}\gamma _{4}^{2} \\ 1&\sigma _5&\gamma _5&\sigma _5\gamma _5&-\sigma _{5}\gamma _5^3&\sigma _{5}\gamma _{5}^{2}\\ 1&\sigma _6&\gamma _6&\sigma _6\gamma _6&-\sigma _{6}\gamma _6^3&\sigma _{6}\gamma _{6}^{2} \end{vmatrix}. \end{aligned}$$

A three-soliton solution of Eq. (1) is derived by using Eq. (91),

$$\begin{aligned} v[3]=-12Q_{2}R_{2}=-12\frac{\varDelta _{Q_{2}}\varDelta _{R_{2}}}{\varDelta _{2}^{2}}. \end{aligned}$$
(97)

and a four-soliton solution of Eq. (1) is derived by using Eq. (91), when substitute \(M=4\),we get

$$\begin{aligned} v[4]=-24Q_{2}R_{2}=-24\frac{\varDelta _{Q_{2}}^{2}\varDelta _{R_{2}}}{\varDelta _{2}^{2}}. \end{aligned}$$
(98)

4.1 Resonant solution

In order to solve the spectrum Eqs. (6) and (7) (such as Eqs. (13), (15) and (17)), we first start with the simple solutions \(v(x, y, t, z) = v\) (a non-zero constant), \(u(x, y, t, z) = 0\), then select one of the two simple solutions.

$$\begin{aligned} \varphi (\gamma _{i})=\left( {\begin{array}{c}\cosh \\ \frac{\gamma _{i}}{n}\sinh \theta _{i} -\frac{\gamma _{i}}{n}\cosh \theta _{i}\end{array}}\right) ,\quad \varPsi (\gamma _{i}) =\left( {\begin{array}{c}\sinh \\ \frac{\gamma _{i}}{n}\cosh \theta _{i}-\frac{\gamma _{i}}{n}\sinh \theta _{i}\end{array}}\right) , \end{aligned}$$
(99)

that is \(\theta _{i}=\gamma _{i}x-2\gamma _{i}^{2}y+4\gamma _{i}^{3}t-8\gamma _{i}^{4}z~~~(1\le ~i~\le ~2M).\) From Eq. (31), we derive

$$\begin{aligned} \sigma _{i}=\frac{\gamma _{i}(\tanh \theta _{i}}{n(1-p_{i}\tanh \theta _{i}} -\frac{\gamma _{i}}{n},\quad (1\le ~i~\le ~2M). \end{aligned}$$
(100)

We can provide a resonant solution of Eq. (1), when Eqs. (99) is used in place of Eq. (90). A resonant solutions of Eq. (1) is

$$\begin{aligned} v[5]=12(\gamma _{1}-\gamma _{2})^{2}\frac{[\frac{\gamma _{1} (\tanh \theta _{1}-p_{1})}{1-p_{1}\tanh \theta _{1}}-\gamma _{1}] [\frac{\gamma _{2}(\tanh \theta _{2}-p_{2})}{1-p_{2}\tanh \theta _{2}} -\gamma _{2}]}{[\frac{\gamma _{2}(\tanh \theta _{2}-p_{2})}{1-p_{2} \tanh \theta _{2}}-\gamma _{2}-\frac{\gamma _{1}(\tanh \theta _{1} -p_{1})}{1-p_{1}\tanh \theta _{1}}-\gamma _{1}]}. \end{aligned}$$
(101)

4.2 Complex solitons

The complex solution for the Eq. (1) will be created using Eq. (91). We will cover the exceptional dynamic to keep problems simple of Eq. (95). Suppose we set \(n = m = 0\),

$$\begin{aligned} \gamma _{1}=\beta _{1}+i\alpha _{1},\quad \gamma _{2}=\beta _{1}+i\alpha _{1},\quad \gamma _{3}=\beta _{1}+i\alpha _{1},\quad \gamma _{4}=\beta _{1}+i\alpha _{1}, \end{aligned}$$
(102)

now, from spectral Eqs. (6) and (7), are

$$\begin{aligned} \varphi (\gamma _{1})= & {} \left( {\begin{array}{c}\phi _{1}(\gamma _{1})\\ \phi _{2}(\gamma _{1})\end{array}}\right) =\left( {\begin{array}{c}\exp (\theta _{-})(\cos (\zeta _{-})+i\sin (\zeta _-))\\ \exp (-\theta _{-}) (\cos (\zeta _{-})-i\sin (\zeta _-))\end{array}}\right) ,\end{aligned}$$
(103)
$$\begin{aligned} \varphi (\gamma _{2})= & {} \left( {\begin{array}{c}\phi _{1}(\gamma _{2})\\ \phi _{2}(\gamma _{2})\end{array}}\right) =\left( {\begin{array}{c}\exp (\theta _{+})(\cos (\zeta _{+})-i\sin (\zeta _+))\\ \exp (-\theta _{+}) (\cos (\zeta _{+})+i\sin (\zeta _+))\end{array}}\right) ,\end{aligned}$$
(104)
$$\begin{aligned} \varphi (\gamma _{3})= & {} \left( {\begin{array}{c}\phi _{1}(\gamma _{3})\\ \phi _{2}(\gamma _{3})\end{array}}\right) =\left( {\begin{array}{c}\exp (\theta _{-})(\cos (\zeta _{-})-i\sin (\zeta _-))\\ \exp (-\theta _{-}) (\cos (\zeta _{-})+i\sin (\zeta _-))\end{array}}\right) ,\end{aligned}$$
(105)
$$\begin{aligned} \varphi (\gamma _{4})= & {} \left( {\begin{array}{c}\phi _{1}(\gamma _{4})\\ \phi _{2}(\gamma _{4})\end{array}}\right) =\left( {\begin{array}{c}\exp (\theta _{+}(\cos (\zeta _{+})+i\sin (\zeta _+))\\ \exp (-\theta _{+} (\cos (\zeta _{+})-i\sin (\zeta _+))\end{array}}\right) , \end{aligned}$$
(106)

where

$$\begin{aligned} \begin{aligned} \theta _{-}&=\beta _{1}x-2(\beta _{1}^{2}-\alpha _{1}^{2})y-8(\beta _{1}^{4} -6\beta _{1}^{2}\alpha _{1}^{2}+\alpha _{1}^{4})z-4\beta (3\alpha _{1}^{2}-\beta _{1}^{2})t,\\ \theta _{+}&=-\beta _{1}x+2(\beta _{1}^{2}+\alpha _{1}^{2})y+8(\ \beta _{1}^{4} -6\beta _{1}^{2}\alpha _{1}^{2}- \alpha _{1}^{4})z+4\beta (3\alpha _{1}^{2}-\beta _{1}^{2})t,\\ \zeta _{-}&= \alpha _{1}(x-4\beta _{1}+32\beta _{1}(\alpha _{1}^{2}+\beta _{1}^{2})z +2(3\beta _{1}^{2}-\alpha _{1}^{2})t),\\ \zeta _{+}&=\alpha _{1}(x-4\beta _{1}+32\beta _{1}(\alpha _{1}^{2}+\beta _{1}^{2})z +2(3\beta _{1}^{2}-\alpha _{1}^{2})t), \end{aligned} \end{aligned}$$

and \(\beta _{1}\) and \(\alpha _{1}\) are constants, from Eq. (31)

$$\begin{aligned} \sigma _{1}= & {} \exp (-2\theta _{-})[\cos 2\alpha _{1}(\zeta _{-}) -i\sin 2\alpha _{1}(\zeta _{-})],\end{aligned}$$
(107)
$$\begin{aligned} \sigma _{2}= & {} \exp (-2\theta _{+})[\cos 2\alpha _{1}(\zeta _{+}) +i\sin 2\alpha _{1}(\zeta _{+})],\end{aligned}$$
(108)
$$\begin{aligned} \sigma _{3}= & {} \exp (-2\theta _{-})[\cos 2\alpha _{1}(\zeta _{-}) +i\sin 2\alpha _{1}(\zeta _{-})],\end{aligned}$$
(109)
$$\begin{aligned} \sigma _{4}= & {} \exp (-2\theta _{+})[\cos 2\alpha _{1}(\zeta _{+}) -i\sin 2\alpha _{1}(\zeta _{+})]. \end{aligned}$$
(110)

Inserting Eq. (102) and Eqs. (107–110), to Eq. (95), we get

$$\begin{aligned} \begin{aligned} v[6]&=-12Q_{1}R_{1}=-12[16\beta _{1}\alpha _{1}\exp (\omega _-) (\alpha _{1}\cos (2\zeta _+)+\beta _{1}\sin (2\zeta _+))\\&\quad +16\beta _{1}\alpha _{1}\exp (\omega _{+})(-\alpha _{1}\cos (2\zeta _-) +\beta _{1}\sin (2\zeta _-))][16\beta _1\alpha _1\exp (\varOmega _+)\\&\quad (\alpha _1\cos (2\zeta _+)-\beta _1\sin (2\zeta _+))-16\beta _{1} \alpha _1\exp (\varOmega _-)(\alpha _1\cos (\zeta _-)+\beta _1\sin (\zeta _-))]\\&\quad /[6\exp (\xi )(\alpha _1]^2\cosh (\epsilon )-(\alpha _1^2\cos (2\zeta _+) \cos (2\zeta _-)+(2\beta _{1}^2+\alpha _{1}^2\sin (2\zeta _+)\sin (2\zeta _-))))], \end{aligned} \end{aligned}$$
(111)

and

$$\begin{aligned} \begin{aligned} v[7]&=-12Q_{1}R_{1}=-12[16\beta _{1}\alpha _{1}\exp (\omega _-) (\alpha _{1}\cos (2\zeta _+)+\beta _{1}\sin (2\zeta _+))\\&\quad +16\beta _{1}\alpha _{1}\exp (\omega _{+})(-\alpha _{1}\cos (2\zeta _-) +\beta _{1}\sin (2\zeta _-))][16\beta _1\alpha _1\exp (\varOmega _+)\\&\quad (\alpha _1\cos (2\zeta _+)-\beta _1\sin (2\zeta _+))-16\beta _{1}\alpha _1 \exp (\varOmega _-)(\alpha _1\cos (\zeta _-)+\beta _1\sin (\zeta _-))]\\&\quad /\sqrt{[6\exp (\xi )(\alpha _1]^2\cosh (\epsilon )-(\alpha _1^2\cos (2\zeta _+) \cos (2\zeta _-)+(2\beta _{1}^2+\alpha _{1}^2\sin (2\zeta _+)\sin (2\zeta _-))))]}, \end{aligned} \end{aligned}$$
(112)

where

$$\begin{aligned} \begin{aligned} \omega _-&=8\beta _1(4\alpha _1^2-\beta _1^2)t+28(\beta _1^3-7\beta _{1}^2 \alpha _1^2+\beta _1^5)z+8(\beta _{1}^3-\alpha _{1}^4)y-2\beta _1x,\\ \omega _+&=-8\beta _1(4\alpha _1^2-\beta _1^2)t-28(\beta _1^3-7\beta _{1}^2 \alpha _1^2+\beta _1^5)z=8(\beta _{1}^3-\alpha _{1}^4)y+2\beta _1x,\\ \varOmega _-&=7\beta _1(3\alpha _1^2-\beta _1^2)t+18(\beta _1^3-9\beta _{1}^2 \alpha _1^2+\beta _1^5)z+2(\beta _{1}^3-\alpha _{1}^3)y-4\beta _1x,\\ \varOmega _+&=-7\beta _1(3\alpha _1^2-\beta _1^2)t-18(\beta _1^3-9\beta _{1}^2 \alpha _1^2+\beta _1^5)z-2(\beta _{1}^3-\alpha _{1}^3)y+4\beta _1x,\\ \xi&=7(\beta _{1}^3-\alpha _{1}^3)y+23(\beta _{3}-7\beta _{1}^4+\alpha _1^3)z,\quad \epsilon =5\beta _1x+15\beta _1(\beta _{1}-2\alpha _1)t. \end{aligned} \end{aligned}$$

5 Results and discussion

This section thoroughly contrasts the evaluated results with the previously computed outcomes to demonstrate the uniqueness of the present investigation. It can be illustrated that (Adeyemo and Khalique 2022) calculated a relatively small number of solutions by employing Lei symmetry analysis. However, by utilizing the Darboux transformation, we have acquired a large number of solutions in this article. We obtain the multi-soliton, resonant and complex soliton solution to the YTSF Eq. (5) in the preceding sections using the DT. The AKNS hierarchy simplifies all solutions for solving a linear algebraic system, which is appropriate for generating solutions. Multi-solitons are a type of soliton solution that can be found in nonlinear wave equations. These solitons are characterized by the presence of several waves that move at various speeds and engage in nonlinear interactions. The YTSF equation is one such nonlinear wave equation that accepts multiple solitons. The DT approach has lately been employed by researchers to look into the dynamics of multi-solitons. By leveraging existing solutions, the DT method is a mathematical technique that enables the construction of new solutions for NLPDEs. This approach has allowed researchers to examine the behavior of multi-solitons. With the use of DT, we explore unique multi-soliton, resonant, and complicated solutions in this study. Complex interactions between these solitons can result in phenomena. The analysis of multi-solitons and the YTSF equation using DT has, all in all, yielded important insights into the dynamics of nonlinear wave equations. These discoveries are crucial for industries like optics, where soliton solutions are essential for the movement of light through optical fibers.

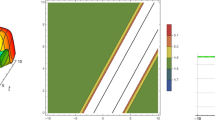
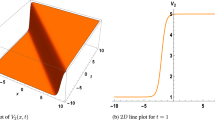
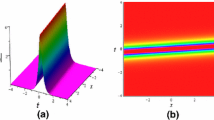
The wavelength and frequency of a wave are determined by its period, which is the duration of time it takes for a cycle to complete, and its soliton solution, which is a wave with a repeating continuous pattern. Here, we plotted a number of wave profiles that were taken from the solutions to Eq. (5) and Solutions in the YTSF equation can be represented graphically in a 3-dimensional plot along with the projection of a contour plot and a 2-dimensional plot. A single, localized wave-like structure is represented by a one-soliton solution. Two solitons, which are frequently depicted as peaks or waves, are combined to form a two-soliton solution. Three solitons can travel at once in a three-soliton solution. Through particular restrictions or mechanisms, such as velocity resonance, resonant soliton solutions are attained. Solitons with additional characteristics, such as fluctuating amplitudes or phases, are referred to as complex soliton solutions. The one-soliton solution of Eq. (93) is depicted in Fig. (1) by applying appropriate parameter values. Equation (95) two-soliton solution is shown in Fig. (2). The three-soliton solution of Eq. (97) is shown in Fig. (3). The hyperbolic solutions to Eq. (98) are shown in Fig. (4). The resonances of Eq. (101) are shown in Fig. (5). The complex soliton solution of Eqs. (111) and (112) are shown in Figs. (6 and 7).

These graphical interpretations can be used to examine the propagation and interaction of solitons in a variety of physical systems and are crucial for comprehending the dynamics and behavior of the YTSF equation and its solutions.

Fig. 1
figure 1

Physical depiction of Eq. (93) at \(p_1=1.2,~p_2=1.1,~\gamma _{1}=0.22~and~\gamma _2=0.13\)

Full size image
Fig. 2
figure 2

Physical depiction of Eq. (95) at \(\sigma _1=2.1,~\sigma _2=2,~\gamma _{1}=1.2,~\gamma _2=1.23.,~\sigma _3=1-.4,~\gamma _{3}=1.2~and~~\sigma _4=1.2,~\gamma _{4}=0.6\)

Full size image
Fig. 3
figure 3

Physical depiction of Eq. (97) at \(\sigma _1=2,~\sigma _2=1,~\gamma _{1}=0.2,~\gamma _2=0.23,~\sigma _3=1.4,~\gamma _{3}=0.2,~\sigma _4=1.5,\)\(\gamma _{4}=0.4,~\sigma _5=1.6,~\gamma _{5}=0.9~and~\sigma _6=1.2,~\gamma _{6}=0.6\)

Full size image
Fig. 4
figure 4

Physical depiction of Eq. (99) at \(\sigma _1=2.2,~\sigma _2=2.1,~\gamma _{2}=2.3,~\gamma _2=2.23,~\sigma _3=2.4,~\gamma _{3}=2.25,~\sigma _4=2.5,~\gamma _{4}=2.4,~\sigma _5=1.26,~\gamma _{5}=1.9~and~\sigma _6=-0.2,~\gamma _{6}=0.7\)

Full size image
Fig. 5
figure 5

Physical depiction of Eq. (102) at \(p_1=1.2,~\gamma _2=0.21,~\gamma _{1}=1.2,~p_2=1.23\)

Full size image
Fig. 6
figure 6

Physical depiction of Eq. (111) at \(\alpha _1=0.42,~\beta _1=0.9\)

Full size image
Fig. 7
figure 7

Physical depiction of Eq. (112) at \(\alpha _1=1.42,~\beta _1=2.4\)

Full size image

6 Conclusions

The YTSF equation has multi-soliton, resonant, and complex soliton solutions, which we obtain in this work. The DT technique, which is based on the Lax pair, can be used to find these solutions. The study of nonlinear wave dynamics in a variety of physical systems, such as fluid mechanics, plasma physics and nonlinear optics, will be significantly impacted by these results. With a few graphical illustrations, the characteristics of the derived solutions were explored. Through carefully choosing the parameter values, the different dynamical behaviors of derived solutions were explored in order to comprehend the physical difficulties. Several soliton features have been thoroughly described by modifying arbitrary functions. Overall, the paper contributes to ongoing research efforts to understand the behavior of nonlinear wave phenomena in various physical systems.