1 Introduction

Large areas spiraling circulations of water in ocean are called gyres, which are mainly driven by the winds and the Coriolis force (due the rotations of the Earth). Gyres are widely existing all over the world’s major ocean regions and controlled by land masses and bottom topography (see [1]). The winds mostly only act on the surface of the water, while the landmasses and the Coriolis force act beneath the surface (see [22]). Due to Coriolis force, gyres in the Northern Hemisphere rotate predominantly clockwise and gyres in the Southern Hemisphere rotate anticlockwise. Note that, due to the vanishing of the meridional component of the Coriolis force, gyres are not cross the equator (see [6, 16, 17]). There are three types of gyres. Tropical gyres are near the Equator but confined strictly to the Northern or Southern hemispheres (see [9,10,11, 20, 21]). Subtropical gyres are situated between polar and equatorial regions, where exists a gigantic ocean areas with thousands of kilometers of diameter (see [8]). Subpolar gyres are the smallest ones on the Earth and are situated in the polar regions (see [18]). In this paper, we will set our eyes on arctic gyres, which are distributed in the Arctic ocean. Arctic ocean is a semi-enclosed ocean almost completely surrounded by landmasses and is covered by permanent ice with thickness exceeding 2 m. The permanent ice floats on the ocean, slowly rotating clockwise, roughly centered on the North Pole (see [1,2,3,4,5, 24]). It is worth mentioning that the Antarctic is very different from the Arctic: the Antarctic is a single landmass encircled by a very powerful current known as the Antarctic Circumpolar Current (ACC). We refer to [7, 14, 18,19,20, 25,26,27,28] for the ACC.

In order to study the related properties of gyres, some simplifications are made to reduce its complexity. The horizontal velocity of gyres is \(10^{4}\) larger than the vertical velocity (see [23]). Ignoring the vertical velocity, a model of gyres in spherical coordinates as shallow-water flow on a rotating sphere is obtained (see [8]). In [2], this model is transformed into a plane semi-linear elliptic equation boundary value problem by stereographic projection, and then it is reduced to second-order ordinary differential equation by neglecting the change of azimuthal variations. Haziot replaces the stereographic projection by the Mercator projection, which reduces the model in [8] to a semi-linear elliptic equation that is simpler than the equation obtained recently in [2] (see [15]). Then Haziot uses a conformal map to map the semi-linear elliptic equation from the unbounded strip into the unit circle and considers the existence of solutions for constant vorticity and linear vorticity (see [14]).

In this paper, inspired by Haziot’s work in [14], we derive a second-order ordinary differential equation by considering the radial solutions for the semi-linear elliptic equation model of gyres and introducing exponential transformation, which acts as a new model for the ocean flow in arctic gyres. With the suitable asymptotic conditions and boundary conditions, we study the solutions of constant vorticity, linear vorticity and nonlinear vorticity in this model.

2 Preliminaries

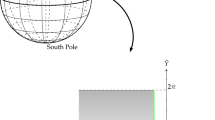
As we know, the classical model of arctic gyres is derived by Constantin and Johnson, which is a model of gyres in spherical coordinates as shallow-water flow on a rotating sphere (see [8]). One can set \(\theta \in [0,\pi )\) the polar angle and \(\theta =0\) corresponds to the South Pole. Let \(\varphi \in [0,2\pi )\) be the azimuthal angle. Considering the model for gyres in spherical coordinates, the polar and azimuthal velocity components of the flow on the Earth are given by

$$\begin{aligned} \frac{1}{\sin (\theta )}\psi _{\varphi },~~-\psi _{\theta }, \end{aligned}$$

respectively, where \(\psi (\theta ,\varphi )\) represents the stream function in spherical coordinates. Furthermore, the governing equation for gyres is given by

$$\begin{aligned} \frac{1}{\sin (\theta )}\Psi _{\varphi \varphi }+\Psi _{\theta }\cot (\theta )+\Psi _{\theta \theta }=F(\Psi -\omega \cos (\theta )), \end{aligned}$$
(1)

where \(\Psi (\theta ,\varphi )=\psi (\theta ,\varphi )+\omega \cos (\theta )\) is associated with the vorticity of the underlying motion of the ocean relative to the Earth’s surface, \( 2\omega \cos (\theta )\) represents the spin vorticity due the rotation of the Earth and \(F(\Psi -\omega \cos (\theta )) \) represents the ocean vorticity.

Using Mercator projection (see [13]), the change of variables are given by

$$\begin{aligned} {\tilde{x}}=-\ln \left[ \tan \left( \frac{\theta }{2}\right) \right] ,~~{\tilde{y}}=\varphi . \end{aligned}$$
(2)

Then the North Pole \((\theta =\pi )\) corresponds to \( {\tilde{x}}=-\infty \) and the equator \(\theta =\frac{\pi }{2} \) corresponds to \( {\tilde{x}} = 0\), where \( {\tilde{x}}<0 \) is in the Northern Hemisphere. Setting \( U({\tilde{x}},{\tilde{y}})=\psi (\theta ,\varphi ), \) one can reformulate the governing equation (1) as the following semi-linear elliptic equation

$$\begin{aligned} \Delta U({\tilde{x}},{\tilde{y}})=\frac{F(U({\tilde{x}},{\tilde{y}}))}{\cosh ^{2}({\tilde{x}})}+2\omega \frac{\sinh ({\tilde{x}})}{\cosh ^{3}({\tilde{x}})} \end{aligned}$$
(3)

with boundary condition

$$\begin{aligned} U({\tilde{x}}_{0},{\tilde{y}})=U_{0}({\tilde{y}}), \end{aligned}$$
(4)

where \({\tilde{x}}_{0}<0\) is a constant. In the North Pole, the asymptotic conditions are given by

$$\begin{aligned} \lim _{{\tilde{x}}\rightarrow -\infty }U({\tilde{x}},{\tilde{y}})=\psi _{0},~~ \lim _{{\tilde{x}}\rightarrow -\infty } \{(U_{{\tilde{x}}}({\tilde{x}},{\tilde{y}}),U_{{\tilde{y}}}({\tilde{x}},{\tilde{y}})\}\cosh ({\tilde{x}})=(0,0), \end{aligned}$$
(5)

where \(\psi _{0}\in \mathbb {R}\) is a constant, which is the value of the stream function \(\psi \) at the North Pole. In fact, the second asymptotic condition of (5) means that the flow is stagnant at the North Pole.

Haziot uses a conformal map to project (3) into a unit circle (see [6]). In order to map from the unbounded strip on the plane into the unit circle, setting \(\xi ={\tilde{x}}-{\tilde{x}}_{0}+\imath {\tilde{y}}, \) and then one can use the conformal map \(\Re =\exp (\xi )\) to get it into the unit circle. Let x and y be the new variables in the unit circle, which are defined by

$$\begin{aligned} x=e^{{\tilde{x}}-{\tilde{x}}_{0}}\cos ({\tilde{y}}),~~y=e^{{\tilde{x}}-{\tilde{x}}_{0}}\sin ({\tilde{y}}), \end{aligned}$$
(6)

and u(x, y) in the circle, such that \( u(x,y)=U({\tilde{x}},{\tilde{y}})\). Therefore, we have by (3) that

$$\begin{aligned} \Delta u(x,y)= & {} \frac{4F(u)(x^{2}+y^{2})}{[e^{{\tilde{x}}_{0}}(x^{2}+y^{2})+e^{-{\tilde{x}}_{0}}]^{2}}\nonumber \\{} & {} +8\omega \frac{[e^{{\tilde{x}}_{0}}(x^{2}+y^{2})-e^{-{\tilde{x}}_{0}}](x^{2}+y^{2})}{[e^{{\tilde{x}}_{0}}(x^{2}+y^{2})+e^{-{\tilde{x}}_{0}}]^{3}},~~0<x^{2}+y^{2}\le 1, \end{aligned}$$
(7)

and boundary condition (4) becomes

$$\begin{aligned} u_{0}(x,y)=u\Big (\arctan \Big (\frac{y}{x}\Big )\Big ), \end{aligned}$$
(8)

where \(x^{2}+y^{2}=1\).

Consider \(u_{0}(x,y)=u_{0} \), where \( u_{0}\) is a constant that the boundary is a streamline. Similarly as in (5), the asymptotic conditions can be given by

$$\begin{aligned} \lim \limits _{x^{2}+y^{2}\rightarrow 0}u(x,y)=\psi _{0}, \lim \limits _{x^{2}+y^{2}\rightarrow 0}\{u_{x},u_{y}\}=\{0,0\}. \end{aligned}$$
(9)

Note that the second condition of (9) is necessary and sufficient for the North Pole to be a stagnation point. Now we turn to consider the radial solutions of (7) and set \(r=(x^{2}+y^{2})^{\frac{1}{2}}\). From (7), we have

$$\begin{aligned} u_{rr}+\frac{u_{r}}{r}=\frac{4F(u)r^{2}}{(e^{{\tilde{x}}_{0}}r^{2}+e^{-{\tilde{x}}_{0}})^{2}}+8\omega \frac{(e^{{\tilde{x}}_{0}}r^{2}-e^{-{\tilde{x}}_{0}})r^{2}}{(e^{{\tilde{x}}_{0}}r^{2}+e^{-{\tilde{x}}_{0}})^{3}},~~0<r\le 1. \end{aligned}$$
(10)

Setting \(r=e^{t}\), we obtain by (10) that

$$\begin{aligned} u''(t)=\frac{4F(u)e^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{2}}+8\omega \frac{(e^{{\tilde{x}}_{0}}e^{2t}-e^{-{\tilde{x}}_{0}})e^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{3}},\quad -\infty <t\le 0. \end{aligned}$$
(11)

Meanwhile, the boundary condition (8) becomes

$$\begin{aligned} u(0)=u_{0}, \end{aligned}$$
(12)

and (9) reduces to

$$\begin{aligned} \lim \limits _{r\rightarrow 0}u(r)= \lim \limits _{t\rightarrow -\infty }u(t)=\psi _{0},~~\lim \limits _{r\rightarrow 0}u'(r)= \lim \limits _{t\rightarrow -\infty }e^{-t}u'(t)=0. \end{aligned}$$
(13)

In addition, we consider

$$\begin{aligned} u'(0)=0, \end{aligned}$$
(14)

which represents no jet flow phenomenon.

3 Constant Vorticity Case

Constant vorticity represents specific gyres. In particular, the case of \(F=0\) is corresponding to precisely with the classical irrotational flow in two-dimensional (see [8]).

3.1 \(F=0\)

Considering (11) with \(F=0\) and (12) and the second equation of (13), one has

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=8\omega \frac{(e^{{\tilde{x}}_{0}}e^{2t}-e^{-{\tilde{x}}_{0}})e^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{3}},\quad -\infty <t\le 0,\\&\lim \limits _{t\rightarrow -\infty }e^{-t}u'(t)=0,\\&u(0)=u_{0}. \end{aligned} \right. \end{aligned}$$
(15)

Now we are ready to state the first result.

Theorem 3.1

The explicit solution of (15) is written as

$$\begin{aligned} \begin{aligned} u(t)&=-2\omega e^{-2{\tilde{x}}_{0}}\Big [\frac{1}{e^{2{\tilde{x}}_{0}}e^{2t}+1}+2\ln (e^{2{\tilde{x}}_{0}}e^{2t}+1)+dilog(e^{2{\tilde{x}}_{0}}e^{2t}+1)\Big ] \\&\qquad +u_{0}+2\omega e^{-2{\tilde{x}}_{0}}\Big [\frac{1}{e^{2{\tilde{x}}_{0}}+1}+2\ln (e^{2{\tilde{x}}_{0}}+1)+dilog(e^{2{\tilde{x}}_{0}}+1)\Big ],\\&\qquad -\infty <t\le 0, \end{aligned} \end{aligned}$$
(16)

where \(dilog(x)=\int _{1}^{x}\frac{\ln (s)}{1-s}ds\).

Proof

Integrating the first equation of (15), we obtain

$$\begin{aligned} u'(t)=8\omega \left[ \frac{\frac{3}{2}e^{2t}+e^{-2{\tilde{x}}_{0}}}{(e^{2t}e^{2{\tilde{x}}_{0}}+1)^{2}}+\frac{1}{2}e^{-2{\tilde{x}}_{0}}\ln (e^{2t}e^{2{\tilde{x}}_{0}}+1)\right] +c_{0}. \end{aligned}$$
(17)

Using (17) and the second equation of (15), we have

$$\begin{aligned} c_{0}=-8\omega e^{-2{\tilde{x}}_{0}}. \end{aligned}$$
(18)

Then putting (18) into (17) and integrating it, we have

$$\begin{aligned} \begin{aligned} u(t)=&-2\omega e^{-2{\tilde{x}}_{0}}\left[ \frac{1}{e^{2{\tilde{x}}_{0}}e^{2t}+1}+2\ln (e^{2{\tilde{x}}_{0}}e^{2t}+1)+dilog(e^{2{\tilde{x}}_{0}}e^{2t}+1)\right] +c_{1}. \end{aligned} \end{aligned}$$
(19)

By (19) and the third equation of (15), we obtain

$$\begin{aligned} \begin{aligned} \ c_{1}=&u_{0}+2\omega e^{-2{\tilde{x}}_{0}}\left[ \frac{1}{e^{2{\tilde{x}}_{0}}+1}+2\ln (e^{2{\tilde{x}}_{0}}+1)+dilog(e^{2{\tilde{x}}_{0}}+1)\right] . \end{aligned} \end{aligned}$$
(20)

Linking (19) and (20), one can obtain (16). This proof is completed. \(\square \)

Considering (11) with \(F=0\) and (12) and (14), one has

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=8\omega \frac{(e^{{\tilde{x}}_{0}}e^{2t}-e^{-{\tilde{x}}_{0}})e^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{3}},\quad -\infty <t\le 0,\\&u'(0)=0,\\&u(0)=u_{0}. \end{aligned} \right. \end{aligned}$$
(21)

Now we are ready to state the second result.

Theorem 3.2

The explicit solution of (21) is written as

$$\begin{aligned} \begin{aligned} u(t)&=-2\omega e^{-2{\tilde{x}}_{0}}\left[ 2\ln (e^{2{\tilde{x}}_{0}}e^{2t}+1)+\frac{1}{e^{2{\tilde{x}}_{0}}e^{2t}+1}+dilog(e^{2{\tilde{x}}_{0}}e^{2t}+1)\right] \\&\quad +8\omega e^{-2{\tilde{x}}_{0}}\left[ 1-\frac{\frac{3}{2}+e^{-2{\tilde{x}}_{0}}}{e^{-2{\tilde{x}}_{0}}(e^{2{\tilde{x}}_{0}}+1)^{2}}-\frac{1}{2}\ln (e^{2{\tilde{x}}_{0}}+1)\right] t+u_{0}\\&\quad +2\omega e^{-2{\tilde{x}}_{0}}\left[ \frac{1}{e^{2{\tilde{x}}_{0}}+1}+2\ln (e^{2{\tilde{x}}_{0}}+1)+dilog(e^{2{\tilde{x}}_{0}}+1)\right] ,\\&\quad -\infty <t\le 0. \end{aligned} \end{aligned}$$

The calculation is similar to that of Theorem 3.1. Here, we omit it.

3.2 \(F=c~(c\ne 0)\)

Considering (11) with \(F=c\) and (12) and the second equation of (13), one has

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=\frac{4ce^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{2}}+8\omega \frac{(e^{{\tilde{x}}_{0}}e^{2t}-e^{-{\tilde{x}}_{0}})e^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{3}},\quad -\infty <t\le 0,\\&\lim \limits _{t\rightarrow -\infty }e^{-t}u'(t)=0,\\&u(0)=u_{0}. \end{aligned} \right. \end{aligned}$$
(22)

Now we are ready to state the third result.

Theorem 3.3

The explicit solution of (22) is written as

$$\begin{aligned} \begin{aligned} u(t)&=-(2\omega +c)e^{-2{\tilde{x}}_{0}}\left[ dilog(e^{2{\tilde{x}}_{0}}e^{2t}+1)+2\ln (e^{2{\tilde{x}}_{0}}e^{2t}+1)\right] -2\omega \frac{e^{-2{\tilde{x}}_{0}}}{e^{2{\tilde{x}}_{0}}e^{2t}+1}\\&\quad +u_{0}+(2\omega +c)e^{-2{\tilde{x}}_{0}}\left[ dilog(e^{2{\tilde{x}}_{0}}+1)+2\ln (e^{2{\tilde{x}}_{0}}+1)\right] \\&\quad +2\omega \frac{e^{-2{\tilde{x}}_{0}}}{e^{2{\tilde{x}}_{0}}+1},~~-\infty <t\le 0. \end{aligned} \end{aligned}$$

The calculation is similar to that of Theorem 3.1. Here, we omit it.

Considering (11) with \(F=c\) and (12) and (14), one has

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=\frac{4ce^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{2}}+ 8\omega \frac{(e^{{\tilde{x}}_{0}}e^{2t}-e^{-{\tilde{x}}_{0}})e^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{3}},\quad -\infty <t\le 0,\\&u'(0)=0,\\&u(0)=u_{0}. \end{aligned} \right. \end{aligned}$$
(23)

Now we are ready to state the fourth result.

Theorem 3.4

The explicit solution of (23) is written as

$$\begin{aligned} \begin{aligned} u(t)&=-(2\omega +c)e^{-2{\tilde{x}}_{0}}\left[ dilog(e^{2{\tilde{x}}_{0}}e^{2t}+1)+2\ln (e^{2{\tilde{x}}_{0}}e^{2t}+1)\right] \\&\quad -2\omega \frac{e^{-2{\tilde{x}}_{0}}}{e^{2{\tilde{x}}_{0}}e^{2t}+1}+2ce^{-2{\tilde{x}}_{0}}\left[ 1-\ln (e^{2{\tilde{x}}_{0}}+1)-\frac{1}{e^{2{\tilde{x}}_{0}}+1}\right] t\\&\quad +8\omega e^{-2{\tilde{x}}_{0}}\left[ 1-\frac{\frac{3}{2}+e^{-2{\tilde{x}}_{0}}}{e^{-2{\tilde{x}}_{0}}(e^{2{\tilde{x}}_{0}}+1)^{2}}-\frac{1}{2}\ln (e^{2{\tilde{x}}_{0}}+1)\right] t+u_{0}\\&\quad +2\omega \frac{e^{-2{\tilde{x}}_{0}}}{e^{2{\tilde{x}}_{0}}+1}+(2\omega +c)e^{-2{\tilde{x}}_{0}}[dilog(e^{2{\tilde{x}}_{0}}+1)+2\ln (e^{2{\tilde{x}}_{0}}+1)],~~\\&\quad -\infty <t\le 0. \end{aligned} \end{aligned}$$

The calculation is similar to that of Theorem 3.1. Here, we omit it.

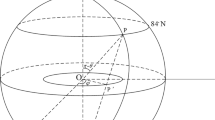
To end this section, we apply our results to deal with the arctic gyres, which are located between the North Pole and \(84^{\circ }\) N (which is approximately equal to \(\frac{14}{15}\pi \)). From the Mercator projection, we have \({\tilde{x}}_{0}=-\ln (\tan (\frac{14\pi }{30}))\approx -2.253.\) In particular, we can take a typical approximation of \(\omega \) that is 4650 (see [8]). Without lose of generality, we can set \(u_{0}=0\). In terms of the original spherical variables \((\theta ,\varphi )\), we have by (2) and (6) that

$$\begin{aligned} x=\frac{\tan \frac{\theta _{0}}{2}}{\tan \frac{\theta }{2}}\cos (\varphi ),~~y=\frac{\tan \frac{\theta _{0}}{2}}{\tan \frac{\theta }{2}}\sin (\varphi ). \end{aligned}$$

Recalling \(t=\ln (r)=\ln (x^{2}+y^{2})^{\frac{1}{2}}\), we have

$$\begin{aligned} t=\ln \bigg [\frac{\tan \frac{\theta _{0}}{2}}{\tan \frac{\theta }{2}}(\cos ^{2}(\varphi )+\sin ^{2}(\varphi ))^{\frac{1}{2}}\bigg ]. \end{aligned}$$

Then \(\psi (\theta ,\varphi )=u(t)=\psi (\theta )\) is independent of \(\varphi \). Fixed \(\theta =\theta _{1}\), \(\psi (\theta _{1},\varphi )\) is a streamline, where \(\theta \in [\frac{14}{15}\pi ,\pi )\) and \(\varphi \in [0,2\pi )\) (see Fig. 1).

Fig. 1
figure 1

Under \(F=0\) and the asymptotic conditions specified by (5), the change trend of stream function \(\psi \) is monotonic increasing with respect to variable \(\theta \) from \(84^{\circ }\) N to the North Pole and independent of \(\varphi \). It shows that the North Pole is a stagnation point and the center for the arctic gyres

Full size image

4 Linear Vorticity Case

Linking (13), we assume

$$\begin{aligned} \lim \limits _{t\rightarrow -\infty }u(t)=u(-N)=\psi _{0}, ~~ \lim \limits _{t\rightarrow -\infty }e^{-t}u'(t)=e^{N}u'(-N)=0, \end{aligned}$$
(24)

where \(N>0\) is chosen large enough.

Now considering (11) with \(F=au+b\) (where a, b \(\in {\mathbb {R}}\)) and (24), one has

$$\begin{aligned} \left\{ \begin{aligned}&u''(t)=A(t)u+B(t),\quad -N\le t\le 0,\\&u(-N)=\psi _{0},\\&u'(-N)=0, \end{aligned} \right. \end{aligned}$$
(25)

where

$$\begin{aligned} \begin{aligned} A(t):&=\frac{4ae^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{2}},\\ B(t):&=\frac{4be^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{2}} +8\omega \frac{(e^{{\tilde{x}}_{0}}e^{2t}-e^{-{\tilde{x}}_{0}})^{2}e^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{3}},~~-N\le t\le 0. \end{aligned} \end{aligned}$$

Set \( U(t)=(u'(t),u(t))^\textrm{T}\), then \(U(-N)=(u'(-N),u(-N))^\textrm{T}=(0,\psi _{0})^\textrm{T}\).

Therefore, (25) can be written as the following form

$$\begin{aligned} U'(t)={\tilde{A}}(t)U(t)+{\tilde{B}}(t),~~-N\le t\le 0, \end{aligned}$$
(26)

with the constraint condition \(U(-N),\) where

$$\begin{aligned} {\tilde{A}}(t)=\left( \begin{array}{cc} 0 &{}\quad A(t) \\ 1 &{}\quad 0\\ \end{array} \right) , ~~{\tilde{B}}(t)= \left( \begin{array}{c} B(t)\\ 0 \end{array} \right) . \end{aligned}$$

From [20], the following matrix function

$$\begin{aligned} \begin{aligned} \Phi (t,-N)&=I+\int _{-N}^{t}{\tilde{A}}(\tau )d\tau +\int _{-N}^{t}{\tilde{A}}(\tau _{1})\left[ \int _{-N}^{\tau _{1}}{\tilde{A}}(\tau _{2})d\tau _{2}\right] d\tau _{1}+\cdot \cdot \cdot , \end{aligned} \end{aligned}$$

solves \(\Phi '(t,-N)={\tilde{A}}(t)\Phi (t,-N),~~-N\le t\le 0,\quad \Phi (-N,-N)=I\), where I denotes the identity matrix.

Therefore, the solution of (26) can be written as (see [29])

$$\begin{aligned} U(t)=\Phi (t,-N)U(-N)+\int _{-N}^{t}\Phi (t,\tau ){\tilde{B}}(\tau )d\tau ,~~t\in [-N,0]. \end{aligned}$$

Finally, the solution of (25) can be derived

$$\begin{aligned} \begin{aligned} u(t)&=\left( 1+\int _{-N}^{t}\int _{-N}^{\tau _{1}} A(\tau _{2})d\tau _{2}d\tau _{1}\right. \\&\quad \left. +\int _{-N}^{t}\int _{-N}^{\tau _{1}} A(\tau _{2})\int _{-N}^{\tau _{2}}\int _{-N}^{\tau _{3}}A(\tau _{4})d\tau _{4}d\tau _{3}d\tau _{2}d\tau _{1}+\cdot \cdot \cdot \right) \psi _{0}\\&\quad +\int _{-N}^{t}\left[ (t-\tau )+\int _{\tau }^{t}\int _{\tau }^{\tau _{1}}A(\tau _{2})(\tau _{2}-\tau )d\tau _{2}d\tau _{1}+\cdot \cdot \cdot \right] \nonumber \\&\quad \times B(\tau )d\tau ,~~t\in [-N,0]. \end{aligned} \end{aligned}$$

Considering (11) with (13), we have

$$\begin{aligned} u(t)= & {} \psi _0+\int _{-\infty }^t(t-s)\left( \frac{4F(u(s))e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}+8\omega \frac{(e^{{\tilde{x}}_{0}}e^{2s} -e^{-{\tilde{x}}_{0}})e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{3}}\right) ds\nonumber \\= & {} \psi _0-2\omega e^{2{\tilde{x}}_{0}}\Big [dilog\left( e^{2{\tilde{x}}_{0}} e^{2 t}+1\right) +\frac{1}{e^{2{\tilde{x}}_{0}} e^{2 t}+1}+2 \ln \left( e^{2{\tilde{x}}_{0}} e^{2 t}+1\right) -1\Big ] \nonumber \\{} & {} \quad +\int _{-\infty }^t\frac{4(t-s)e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}F(u(s))ds. \end{aligned}$$
(27)

We consider again the linear case \(F(u)=au+b\). Then (27) has a form

$$\begin{aligned} u(t)=aAu(t)+bh_1(t)+\omega h_2(t)+\psi _0, \end{aligned}$$
(28)

for

$$\begin{aligned} Au(t)= & {} \int _{-\infty }^t\frac{4(t-s)e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}u(s)ds,\\ h_1(t)= & {} \int _{-\infty }^t\frac{4(t-s)e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds=-e^{2{\tilde{x}}_{0}}[dilog\left( e^{2{\tilde{x}}_{0}} e^{2 t}+1\right) \\{} & {} \quad +2\ln \left( e^{2{\tilde{x}}_{0}}e^{2 t}+1\right) ],\\ h_2(t)= & {} -2e^{2{\tilde{x}}_{0}}\Big [dilog\left( e^{2{\tilde{x}}_{0}} e^{2 t}+1\right) +\frac{1}{e^{2{\tilde{x}}_{0}} e^{2 t}+1}+2 \ln \left( e^{2{\tilde{x}}_{0}} e^{2 t}+1\right) -1\Big ]. \end{aligned}$$

We solve (28) on a Banach space \(X=C_b(\mathbb {R}_-)\) of all bounded functions \(u:\mathbb {R}_-\rightarrow \mathbb {R}\) with a norm \(\Vert u\Vert =\sup \nolimits _{t\in \mathbb {R}_-}|u(t)|\). Note

$$\begin{aligned} \begin{aligned} |Au(t)|&\le \Vert u\Vert \int _{-\infty }^t4(t-s)e^{4s}ds=\frac{e^{4t}}{4}\Vert u\Vert \le \frac{1}{4}\Vert u\Vert ,\\ |(Au)'(t)|&\le \Vert u\Vert \int _{-\infty }^t4e^{4s}ds=e^{4t}\Vert u\Vert \le \Vert u\Vert ,\\ |h_1(t)|&\le \int _{-\infty }^t4(t-s)e^{4s}ds=\frac{e^{4t}}{4}\le \frac{1}{4},\quad |h_1'(t)|\le \int _{-\infty }^t4e^{4s}ds=e^{4t}\le 1,\\ |h_2(t)|&\le \int _{-\infty }^t8(t-s)(1+e^{-{\tilde{x}}_{0}})e^{4s}ds=(1+e^{-{\tilde{x}}_{0}})\frac{e^{4t}}{2}\le \frac{1+e^{-{\tilde{x}}_{0}}}{2},\\ |h_2'(t)|&\le \int _{-\infty }^t8(1+e^{-{\tilde{x}}_{0}})e^{4s}ds=2(1+e^{-{\tilde{x}}_{0}})e^{4t}\le 2(1+e^{-{\tilde{x}}_{0}}). \end{aligned} \end{aligned}$$

We see that any solution \(u\in X\) of (28) satisfies \(\lim \nolimits _{t\rightarrow -\infty }u(t)=\psi _0\) and \(\lim \nolimits _{t\rightarrow -\infty }e^{-t}u'(t)=0\) with a rate \(e^{4t}\). Moreover, \(A: X\rightarrow X\) is a bounded linear operator mapping the unit ball \(\{u\in X: \Vert u\Vert \le 1\}\) into the set

$$\begin{aligned} A(\{u\in X: \Vert u\Vert \le 1\})\subset \{v\in X: \Vert v(t)\Vert \le e^{4t},~\forall t\in \mathbb {R}_-,~\, \Vert v'\Vert \le 1\}. \end{aligned}$$

Applying the Arzelà-Ascoli theorem, we can see that the set

$$\begin{aligned} \{v\in X: \Vert v(t)\Vert \, \le e^{4t},~\forall t\in \mathbb {R}_-,\, \Vert v'\Vert \le 1\} \end{aligned}$$

is precompact in X. Thus A is compact. Next, if \(\lambda \ne 0\) is an eigenvalue of A with an eigenfunction u, then for any \(t_0<0\), we have

$$\begin{aligned} |\lambda |\sup _{t\le t_0}|u(t)|=\sup _{t\le t_0}|Au(t)|\le \frac{e^{4t_0}}{4}\sup _{t\le t_0}|u(t)|. \end{aligned}$$

So, if \(|\lambda |>\frac{e^{4t_0}}{4}\), then \(\sup \nolimits _{t\le t_0}|u(t)|=0\), and noting

$$\begin{aligned} \lambda u''(t)=\frac{4e^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{2}}u(t), \end{aligned}$$

we have \(u(t)=0\) on \(\mathbb {R}_-\). This leads, since A is compact, to the fact that the spectrum of A is \(\{0\}\) and thus the spectral radius of A is 0. Consequently, (28) is uniquely solvable

$$\begin{aligned} u(t)&=[(I-aA)^{-1}(bh_1+\omega h_2+\psi _0)](t)\nonumber \\&=b[(I-aA)^{-1}h_1](t)+\omega [(I-aA)^{-1}h_2](t)+\psi _0[(I-aA)^{-1}](t). \end{aligned}$$
(29)

Moreover, the Neumann lemma gives

$$\begin{aligned} (I-aA)^{-1}=I+aA+a^2A^2+\cdots , \end{aligned}$$
(30)

so we can solve (29) approximately. An alternative way is to use an iteration procedure

$$\begin{aligned} u_{n+1}(t)=aAu_n(t)+bh_1(t)+\omega h_2(t)+\psi _0,n\ge 1,\, u_1(t)=0. \end{aligned}$$
(31)

In summary, we have the following result.

Theorem 4.1

(11) with (13) for \(F(u)=au+b\), \(a,b\in \mathbb {R}\) has a unique solution given by (29). Moreover, (12) or (14) hold if and only if

$$\begin{aligned} b[(I-aA)^{-1}h_1](0)+\omega [(I-aA)^{-1}h_2](0)+\psi _0[(I-aA)^{-1}](0)-u_0=0,\nonumber \\ \end{aligned}$$
(32)

or

$$\begin{aligned} b[(I-aA)^{-1}h_1]'(0)+\omega [(I-aA)^{-1}h_2]'(0)+\psi _0[(I-aA)^{-1}]'(0)=0, \end{aligned}$$
(33)

respectively.

Remark 4.2

(32) and (33) are linear in \((b,\omega ,\psi _0,u_0)\) while nonlinear but analytic in a. They give surfaces in the parametric space \((a,b,\omega ,\psi _0,u_0)\) that the unique solution from Theorem 4.1 satisfies also either (12) or (14). These surfaces can be approximately computed for a concrete value of \({\tilde{x}}_0\) by using either (30) or (31). Applying (31), we have approximated surfaces \(u_{n}(0)-u_0=0\) and \(u_n'(0)=0\), respectively. For fixed \((\omega ,\psi _0,u_0)\), we have functions

$$\begin{aligned} b=\Psi _1(a)=\frac{u_0-\omega [(I-aA)^{-1}h_2](0)-\psi _0[(I-aA)^{-1}](0)}{\omega [(I-aA)^{-1}h_2](0)+\psi _0[(I-aA)^{-1}](0)}, \end{aligned}$$

and

$$\begin{aligned} b=\Psi _2(a)=-\frac{\omega [(I-aA)^{-1}h_2]'(0)+\psi _0[(I-aA)^{-1}]'(0)}{[(I-aA)^{-1}h_1]'(0)}, \end{aligned}$$

respectively.

5 Nonlinear Vorticity Case

In this section, we study the existence and uniqueness of continuous solutions for (11) with suitable asymptotic conditions and boundary conditions.

5.1 Lipschitz-Type Nonlinear Vorticity Case

Firstly, we show the existence and uniqueness of continuous solution for (11) with asymptotic conditions by the Banach’s fixed-point theorem. Linking the second condition in (13) and integrating (11), we obtain

$$\begin{aligned} \begin{aligned} u'(t)&=8\omega \Big [\frac{\frac{3}{2}e^{2t}+e^{-2{\tilde{x}}_{0}}}{(e^{2t}e^{2{\tilde{x}}_{0}}+1)^{2}}+\frac{1}{2}e^{-2{\tilde{x}}_{0}}\ln (e^{2t}e^{2{\tilde{x}}_{0}}+1)\Big ]-8\omega e^{-2{\tilde{x}}_{0}}\\&\quad +\int _{-\infty }^{t}\frac{4e^{4s}F(u(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds,~~t\le 0. \end{aligned} \end{aligned}$$
(34)

Integrating (34), we have

$$\begin{aligned} \begin{aligned} u(t)&=\psi _{0}+2\omega e^{-2{\tilde{x}}_{0}}-2\omega e^{-2{\tilde{x}}_{0}}\\&\quad \times \Bigg [\frac{1}{e^{2{\tilde{x}}_{0}}e^{2t}+1}+2\ln (e^{2{\tilde{x}}_{0}}e^{2t}+1)+dilog(e^{2{\tilde{x}}_{0}}e^{2t}+1)\Bigg ]\\&\quad +\int _{-\infty }^{t}(t-s)\frac{4e^{4s}F(u(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds,~~t\le 0, \end{aligned} \end{aligned}$$
(35)

in view of the first condition in (13). Linking (34) and the second condition in (13), by L’Hospital rule, we have

$$\begin{aligned} \begin{aligned} \lim \limits _{t\rightarrow -\infty }\left\{ e^{-t}\int _{-\infty }^{t}\frac{4e^{4s}F(u(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\right\}&=\lim \limits _{t\rightarrow -\infty }\frac{\frac{4e^{4t}F(u(t))}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{2}}}{e^{t}}\\&=\lim \limits _{t\rightarrow -\infty }\frac{4F(u(t))}{e^{-3t}(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{2}}=0, \end{aligned} \end{aligned}$$
(36)

which implies that u(t) is a bounded function on \((-\infty ,0]\) (see (38)).

Next, we investigate the existence and uniqueness of continuous solution for integral equation (35).

Theorem 5.1

Assume that \(F:\mathbb {R}\rightarrow \mathbb {R}\) is Lipschitz continuous, i.e., there exists a constant \(M>0\) such that

$$\begin{aligned} |F(u)-F(v)|\le M|u-v|,~~u,v\in \mathbb {R}, \end{aligned}$$
(37)

then integral equation (35) has a unique continuous solution \(u:(-\infty ,0]\rightarrow \mathbb {R}\), which is a unique solution of (11) with (13).

Proof

Choose \(t_{0}\le 0\) such that \(\frac{e^{2{\tilde{x}}_{0}}}{dilog(e^{2{\tilde{x}}_{0}}e^{2t_{0}}+1)+2\ln (e^{2{\tilde{x}}_{0}}e^{2t_{0}}+1)}>M\). For all bounded functions \(u\in X\), we consider the Banach space X defined above.

Consider the operator \({\mathcal {T}}: X\rightarrow X\) as follows

$$\begin{aligned} \begin{aligned} ({\mathcal {T}}u)(t)&=\psi _{0}+2\omega e^{-2{\tilde{x}}_{0}}-2\omega e^{-2{\tilde{x}}_{0}}\\&\quad \times \Big [\frac{1}{e^{2{\tilde{x}}_{0}}e^{2t}+1}+2\ln (e^{2{\tilde{x}}_{0}}e^{2t}+1)+dilog(e^{2{\tilde{x}}_{0}}e^{2t}+1)\Big ]\\&\quad +\int _{-\infty }^{t}(t-s)\frac{4e^{4s}F(u(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds,~~t\le 0. \end{aligned} \end{aligned}$$

Firstly, we check that \({\mathcal {T}}\) is well-defined with X. For each \(t\in (-\infty ,0]\), linking (36), we have

$$\begin{aligned} \int _{-\infty }^{t}(t-s)\frac{4e^{4s}F(u(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds&\le \int _{-\infty }^{t}\frac{-4e^{4s}s|F(u(s))|}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\nonumber \\&\le \int _{-\infty }^{t}\frac{-4s}{e^{-s}}ds=4e^t-4te^t\le 4, \end{aligned}$$
(38)

which shows that \({\mathcal {T}}: X\rightarrow X\).

Then for any \(u,v\in X\), we obtain that

$$\begin{aligned} \begin{aligned} \Vert {\mathcal {T}}u-{\mathcal {T}}v\Vert&\le \sup \limits _{t\le t_{0}}\int _{-\infty }^{t}(t-s)\frac{4e^{4s}|F(u(s))-F(v(s))|}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\&\le \sup \limits _{t\le t_{0}}\int _{-\infty }^{t}(t-s)\frac{4e^{4s}M|u(s)-v(s)|}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\&\le M\Vert u-v\Vert \sup \limits _{t\le t_{0}}\int _{-\infty }^{t}\frac{4e^{4s}(t-s)}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\&=e^{-2{\tilde{x}}_{0}}[dilog(e^{2{\tilde{x}}_{0}}e^{2t_{0}}+1)+2\ln (e^{2{\tilde{x}}_{0}}e^{2t_{0}}+1)]M\Vert u-v\Vert \\&<\Vert u-v\Vert , \end{aligned} \end{aligned}$$

where we use the fact

$$\begin{aligned} \begin{aligned} \int _{-\infty }^{t}\frac{4e^{4s}(t-s)}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds&=\int _{-\infty }^{t}\int _{-\infty }^{s}\frac{4e^{4\tau }}{(e^{{\tilde{x}}_{0}}e^{2\tau }+e^{-{\tilde{x}}_{0}})^{2}}d\tau ds\\&=\int _{-\infty }^{t}2e^{-2{\tilde{x}}_{0}}\Big [\ln (e^{2s}e^{2{\tilde{x}}_{0}}+1)-\frac{e^{2s}e^{2{\tilde{x}}_{0}}}{e^{2s}e^{2{\tilde{x}}_{0}}+1}\Big ]ds\\&=e^{-2{\tilde{x}}_{0}}[dilog(e^{2{\tilde{x}}_{0}}e^{2t}+1)+2\ln (e^{2{\tilde{x}}_{0}}e^{2t}+1)]. \end{aligned} \end{aligned}$$

By using the contraction principle, \({\mathcal {T}}\) has a unique fixed-point on X. This fixed-point is the unique solution to (35) on \((-\infty ,t_{0}]\). If \(t_{0}=0\), then result holds. If \(t_{0}<0\), then the linear growth rate of \(F(\cdot )\) prevents blow-up in finite time, so that we may extend the solution from \((-\infty ,t_{0}]\) to \((-\infty ,0]\). Assume that \(F(\cdot )\) is Lipschitz continuous, we obtain the uniqueness of solution to (35) on \((-\infty ,0]\). The proof is completed. \(\square \)

Theorem 5.2

In the sense of supremum norm, the solution of Theorem 5.1 (on the infinite interval \((-\infty ,0]\)) is stable with respect to variations of \(\psi _{0}\).

Proof

Let \(u\in X\) and \({\tilde{u}}\in X\) be two solutions of (35) with \(\lim \nolimits _{t\rightarrow -\infty }u(t)=\psi _{0}\) and \(\lim \nolimits _{t\rightarrow -\infty }{\tilde{u}}(t)={\tilde{\psi }}_{0}\), respectively. Choose \(t_{0}\le 0\) such that

$$\begin{aligned} e^{-2{\tilde{x}}_{0}}[dilog(e^{2{\tilde{x}}_{0}}e^{2t_{0}}+1)+2\ln (e^{2{\tilde{x}}_{0}}e^{2t_{0}}+1)]\le \frac{1}{1+M}. \end{aligned}$$
(39)

Setting \(\Vert u\Vert =\sup \nolimits _{t\le t_{0}}{|u(t)|}\), we have

$$\begin{aligned} \begin{aligned} |u(t)-{\tilde{u}}(t)|&\le |\psi _{0}-{\tilde{\psi }}_{0}|+\Big |\int _{-\infty }^{t}(t-s)\frac{4e^{4s}(F(u(s))-F({\tilde{u}}(s)))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\Big |\\&\le |\psi _{0}-{\tilde{\psi }}_{0}|+\sup \limits _{t\le t_{0}}\int _{-\infty }^{t}(t-s)\frac{4e^{4s}|F(u(s))-F({\tilde{u}}(s))|}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\&\le |\psi _{0}-{\tilde{\psi }}_{0}|+M\sup \limits _{t\le t_{0}}\int _{-\infty }^{t}(t-s)\frac{4e^{4s}|u(s)-{\tilde{u}}(s)|}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\&\le |\psi _{0}-{\tilde{\psi }}_{0}|+M\Vert u-{\tilde{u}}\Vert \sup \limits _{t\le t_{0}}\int _{-\infty }^{t}\frac{4(t-s)e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\&= |\psi _{0}-{\tilde{\psi }}_{0}|+M\Vert u-{\tilde{u}}\Vert e^{-2{\tilde{x}}_{0}}[dilog(e^{2{\tilde{x}}_{0}}e^{2t_{0}}+1)\\&\quad +2\ln (e^{2{\tilde{x}}_{0}}e^{2t_{0}}+1)],~~t\le t_{0}. \end{aligned} \end{aligned}$$
(40)

By (39) and (40), we have

$$\begin{aligned} \Vert u-{\tilde{u}}\Vert \le |\psi _{0}-{\tilde{\psi }}_{0}|+\frac{M}{M +1}\Vert u-{\tilde{u}}\Vert , \end{aligned}$$

so that

$$\begin{aligned} \Vert u-{\tilde{u}}\Vert \le (1+M)|\psi _{0}-{\tilde{\psi }}_{0}|. \end{aligned}$$
(41)

Using (40) and (41), we obtain that

$$\begin{aligned} |u'(t)-{\tilde{u}}'(t)|\le & {} \int _{-\infty }^{t}\frac{4e^{4s}|F(u(s))-F({\tilde{u}}(s))|}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\\le & {} \int _{-\infty }^{t}\frac{4e^{4s}M|u(s)-{\tilde{u}}(s)|}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\\le & {} M\Vert u-{\tilde{u}}\Vert \int _{-\infty }^{t}\frac{4e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\\le & {} M(1+M)|\psi _{0}-{\tilde{\psi }}_{0}|\int _{-\infty }^{t}\frac{4e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\= & {} M(1+M)|\psi _{0}-{\tilde{\psi }}_{0}|2e^{-2{\tilde{x}}_{0}}\Big [\ln (e^{2t}e^{2{\tilde{x}}_{0}}+1)-\frac{e^{2t}}{e^{2t}e^{2{\tilde{x}}_{0}}+1}\Big ],~~t\le t_{0}. \end{aligned}$$

Then, by (39), we have

$$\begin{aligned} |u'(t_{0})-{\tilde{u}}'(t_{0})|\le M|\psi _{0}-{\tilde{\psi }}_{0}|, \end{aligned}$$
(42)

since

$$\begin{aligned} \begin{aligned} 0&\le 2e^{-2{\tilde{x}}_{0}}\Big [\ln (e^{2t}e^{2{\tilde{x}}_{0}}+1)-\frac{e^{2t}}{e^{2t}e^{2{\tilde{x}}_{0}}+1}\Big ]\\&\le 2e^{-2{\tilde{x}}_{0}}\ln (e^{2t}e^{2{\tilde{x}}_{0}}+1)\\&\le 2e^{-2{\tilde{x}}_{0}}\ln (e^{2t_{0}}e^{2{\tilde{x}}_{0}}+1)\\&\le \frac{1}{1+M},~~t\le t_{0}. \end{aligned} \end{aligned}$$

Due to \(|u(t_{0})-{\tilde{u}}(t_{0})|\le \Vert u-{\tilde{u}}\Vert \), from (41), we have

$$\begin{aligned} \begin{aligned} |u(t_{0})-{\tilde{u}}(t_{0})|&\le (1+M)|\psi _{0}-{\tilde{\psi }}_{0}|.\\ \end{aligned} \end{aligned}$$
(43)

If \(t_{0}=0\), then the proof is completed. Otherwise, for \(t_{0}<0\), we see that \(u(t_{0})\) is the value for (35) at \(t=t_{0}\), starting with data \(u(t_{0})\) and \(u'(t_{0})\) at \(t=t_{0}\). Let

$$\begin{aligned} s=t-t_{0},~~v(s)=u(s+t_{0}),~~t_{0}\le t\le 0, \end{aligned}$$
(44)

then we have

$$\begin{aligned} v''(s)=\frac{4e^{4(s+t_{0})}F(v(s))}{(e^{{\tilde{x}}_{0}}e^{2(s+t_{0})}+e^{-{\tilde{x}}_{0}})^{2}}+8\omega \frac{(e^{{\tilde{x}}_{0}}e^{2(s+t_{0})}-e^{-{\tilde{x}}_{0}})e^{4(s+t_{0})}}{(e^{{\tilde{x}}_{0}}e^{2(s+t_{0})}+e^{-{\tilde{x}}_{0}})^{3}},~~~0\le s\le -t_{0},\nonumber \\ \end{aligned}$$
(45)

with initial data

$$\begin{aligned} v(0)=u(t_{0}),~~v'(0)=u'(t_{0}). \end{aligned}$$
(46)

Linking the second condition of (46) and integrating (45) on [0, s], we obtain

$$\begin{aligned} v'(s)&=v'(0)+\int _{0}^{s}\frac{4e^{4(\tau +t_{0})}F(v(s))}{(e^{{\tilde{x}}_{0}}e^{2(\tau +t_{0})}+e^{-{\tilde{x}}_{0}})^{2}}d\tau \nonumber \\&\quad +\int _{0}^{s}8\omega \frac{(e^{{\tilde{x}}_{0}}e^{2(\tau +t_{0})}-e^{-{\tilde{x}}_{0}})e^{4(\tau +t_{0})}}{(e^{{\tilde{x}}_{0}}e^{2(\tau +t_{0})}+e^{-{\tilde{x}}_{0}})^{3}}d\tau ,~~0\le s\le -t_{0}. \end{aligned}$$
(47)

Using the first condition of (46), then integrating both sides of (47) on [0, s], which yields

$$\begin{aligned} v(s)&=v(0)+v'(0)s+\int _{0}^{s}(s-\tau )\frac{4e^{4(\tau +t_{0})}F(v(\tau ))}{(e^{{\tilde{x}}_{0}}e^{2(\tau +t_{0})}+e^{-{\tilde{x}}_{0}})^{2}}d\tau \nonumber \\&\quad +\int _{0}^{s}8\omega (s-\tau )\frac{(e^{{\tilde{x}}_{0}}e^{2(\tau +t_{0})}-e^{-{\tilde{x}}_{0}})e^{4(\tau +t_{0})}}{(e^{{\tilde{x}}_{0}}e^{2(\tau +t_{0})}+e^{-{\tilde{x}}_{0}})^{3}}d\tau ,~~0\le s\le -t_{0}. \end{aligned}$$
(48)

Let \({\tilde{v}}\in X\) also be a solution of the integral equation (48), then we have

$$\begin{aligned} \begin{aligned}&|v(s)-{\tilde{v}}(s)|\le |v(0)-{\tilde{v}}(0)|+s|(v'(0)-{\tilde{v}}'(0)|\\&\qquad +\Big |\int _{0}^{s}(s-\tau )\frac{4e^{4(\tau +t_{0})}(F(v(\tau ))-F({\tilde{v}}(\tau )))}{(e^{{\tilde{x}}_{0}}e^{2(\tau +t_{0})}+e^{-{\tilde{x}}_{0}})^{2}}d\tau \Big |\\&\le |v(0)-{\tilde{v}}(0)|-t_{0}|v'(0)-{\tilde{v}}'(0)| +\int _{0}^{s}(s-\tau )\frac{4e^{4(\tau +t_{0})}|F(v(\tau ))-F({\tilde{v}}(\tau ))|}{(e^{{\tilde{x}}_{0}}e^{2(\tau +t_{0})}+e^{-{\tilde{x}}_{0}})^{2}}d\tau \\&\le |v(0)-{\tilde{v}}(0)|-t_{0}|v'(0)-{\tilde{v}}'(0)|\\&\quad +M\int _{0}^{s}(s-\tau )\frac{4e^{4(\tau +t_{0})}|v(\tau )-{\tilde{v}}(\tau )|}{(e^{{\tilde{x}}_{0}}e^{2(\tau +t_{0})}+e^{-{\tilde{x}}_{0}})^{2}}d\tau ,~~ 0\le s \le -t_{0}. \end{aligned} \end{aligned}$$

Taking (42) and (43) into account, we obtain that

$$\begin{aligned} |v(s)-{\tilde{v}}(s)|&\le (1+M-t_{0}M)|\psi _{0}-{\tilde{\psi }}_{0}|+M\int _{0}^{s}(s-\tau )\\&\quad \times \frac{4e^{4(\tau +t_{0})}|v(\tau )-{\tilde{v}}(\tau )|}{(e^{{\tilde{x}}_{0}}e^{2(\tau +t_{0})}+e^{-{\tilde{x}}_{0}})^{2}}d\tau ,~~ 0\le s \le -t_{0}. \end{aligned}$$

By the Gronwall’s inequality (see [12]), we have

$$\begin{aligned} \begin{aligned} |v(s)-{\tilde{v}}(s)|&\le (1+M-t_{0}M)|\psi _{0}-{\tilde{\psi }}_{0}|\exp (4M\int _{0}^{s}\frac{(s-\tau )e^{4(\tau +t_{0})}}{(e^{{\tilde{x}}_{0}}e^{2(\tau +t_{0})}+e^{-{\tilde{x}}_{0}})^{2}}d\tau ), \end{aligned}\nonumber \\ \end{aligned}$$
(49)

where

$$\begin{aligned} \begin{aligned} \int _{0}^{s}\frac{4(s-\tau )e^{4(\tau +t_{0})}}{(e^{{\tilde{x}}_{0}}e^{2(\tau +t_{0})}+e^{-{\tilde{x}}_{0}})^{2}}d\tau&=\int _{0}^{s}\int _{0}^{\tau }\frac{4e^{4(\sigma +t_{0})}}{(e^{{\tilde{x}}_{0}}e^{2(\sigma +t_{0})}+e^{-{\tilde{x}}_{0}})^{2}}d\sigma d\tau \\&=\int _{0}^{s}2e^{-2{\tilde{x}}_{0}}\Bigg [\ln \frac{(e^{2(t_{0}+\tau )}e^{2{\tilde{x}}_{0}}+1)}{e^{2t_{0}}e^{2{\tilde{x}}_{0}}+1}\\&\quad +\frac{e^{2(t_{0}+\tau )}e^{2{\tilde{x}}_{0}}-e^{2t_{0}}e^{2{\tilde{x}}_{0}}}{(e^{2(t_{0}+\tau )}e^{2{\tilde{x}}_{0}}+1)(e^{2t_{0}}e^{2{\tilde{x}}_{0}}+1)}\Bigg ]d\tau \\&=\gamma _{1}(s)-\gamma _{2},~~ 0\le s \le -t_{0}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \gamma _{1}(s)=e^{-2{\tilde{x}}_{0}}[dilog(e^{2{\tilde{x}}_{0}}e^{2(s+t_{0})}+1)+2\ln (e^{2{\tilde{x}}_{0}}e^{2(s+t_{0})}+1)], \\ \gamma _{2}=e^{-2{\tilde{x}}_{0}}[dilog(e^{2{\tilde{x}}_{0}}e^{2t_{0}}+1)+2\ln (e^{2{\tilde{x}}_{0}}e^{2t_{0}}+1)]. \end{aligned}$$

Thus, (49) reduces to

$$\begin{aligned} |u(t)-{\tilde{u}}(t)| \le (1+M-t_{0}M)|\psi _{0}-{\tilde{\psi }}_{0}|\exp (M(\gamma _{1}(s)-\gamma _{2})). \end{aligned}$$
(50)

Then linking (44) and (50), we obtain

$$\begin{aligned} |u(t)-{\tilde{u}}(t)| \le (1+M-t_{0}M)|\psi _{0}-{\tilde{\psi }}_{0}|\exp (M({\tilde{\gamma }}_{1}(t)-\gamma _{2})),~~t_{0}\le t \le 0,\nonumber \\ \end{aligned}$$
(51)

where \({\tilde{\gamma }}_{1}(t)=e^{-2{\tilde{x}}_{0}}[dilog(e^{2{\tilde{x}}_{0}}e^{2t}+1)+2\ln (e^{2{\tilde{x}}_{0}}e^{2t}+1)],~t_{0}\le t \le 0\). Linking (43) and (51), u(t), which is the solution obtained in Theorem 5.1, continuously depends on the variations of \(\psi _{0}\). The proof is completed. \(\square \)

5.2 General Nonlinear Vorticity Case

Next, we will focus on studying the existence a continuous solution for the nonlinear second-order ordinary differential equation (11) with boundary conditions by Schauder’s fixed-point theorem (see [21]). Using (14) and integrating (11) on [t, 0], then we obtain

$$\begin{aligned} -u'(t)=\int _{t}^{0}q(s)F(s,u(s))ds+\int _{t}^{0}p(s)ds,~~t\le 0, \end{aligned}$$
(52)

where

$$\begin{aligned} q(t):=\frac{4e^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{2}},~~p(t):=8\omega \frac{(e^{{\tilde{x}}_{0}}e^{2t}-e^{-{\tilde{x}}_{0}})e^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{3}},~~t\le 0. \end{aligned}$$

Integrating both sides of (52) on [t, 0] and using (12), we have

$$\begin{aligned} u(t)=u_{0}+\int _{t}^{0}(s-t)q(s)F(s,u(s))ds+\int _{t}^{0}(s-t)p(s)ds,~~t\le 0, \end{aligned}$$
(53)

Next, we show the existence a continuous solution for integral equation (53).

Theorem 5.3

Assume that \(q(\cdot ),~p(\cdot ):(-\infty ,0]\rightarrow \mathbb {R}\) and \(F(\cdot ): \mathbb {R}\rightarrow \mathbb {R}\) are continuous. Denoted by

$$\begin{aligned} C_{1}=\int _{-T}^{0}q(s)ds,~~C_{2}=\int _{-T}^{0}|p(s)|ds,~~\text{ for } \text{ some }~ T\ge 0, \end{aligned}$$

we suppose that there exists a constant \(h>0\) such that for

$$\begin{aligned} M_{h}=\max _{u(t)\in [u_{0}-h,u_{0}+h]}|F(u(t))|,~t\in [-T,0], \end{aligned}$$

it holds \(M_{h}\le \frac{h}{2TC_{1}},~C_{2}\le \frac{h}{2T}\). Then (53) has at least one continuous solution u on \([-T,0]\).

Proof

Consider the Banach space

$$\begin{aligned} U_{0}=\{u \mid u\in C^{2}([-T,0],\mathbb {R})\} \end{aligned}$$

endowed with the maximum norm

$$\begin{aligned} \Vert u\Vert =\max _{t\in [-T,0]}|u(t)|. \end{aligned}$$

Set

$$\begin{aligned} K=\{u\mid u\in U_{0}:u_{0}-h\leqslant u(t)\leqslant u_{0}+h,~t\in [-T,0]\} \end{aligned}$$

and the operator \({\mathcal {F}}: K\rightarrow K\) is defined by

$$\begin{aligned} ({\mathcal {F}}u)(t)=u_{0}+\int _{t}^{0}(s-t)q(s)F(u(s))ds+\int _{t}^{0}(s-t)p(s)ds. \end{aligned}$$
(54)

Then we prove that \({\mathcal {F}}\) defined in (54) has a fixed-point on K by the following four steps.

Step 1. Let \(u_{n}(t)\in K,~n=1,2,...\), and \(u_{n}(t)\rightarrow u_{*}(t)\in U_{0},~n\rightarrow \infty \). We have

$$\begin{aligned} |u_{*}(t)-u_{0}|\le |u_{*}(t)-u_{n}(t)|+|u_{n}(t)-u_{0}|\le h,~~n\rightarrow \infty , \end{aligned}$$

which shows that K is closed. Let \(u_{i}(t)\in K,~i=1,2,...,m,~m\in \mathbb {N^{*}}\) and \(\sum \nolimits _{i=1}^{m}\lambda _{i}=1,~\lambda _{i}\geqslant 0\). Then we obtain

$$\begin{aligned} \left| \sum \limits _{i=1}^{m} \lambda _{i}u_{i}(t)-u_{0}\right| =\left| \sum \limits _{i=1}^{m} \lambda _{i}(u_{i}(t)-u_{0})\right| \le \sum \limits _{i=1}^{m} \lambda _{i}|u_{i}(t)-u_{0}|\le \sum \limits _{i=1}^{m}\lambda _{i}h=h, \end{aligned}$$

so that

$$\begin{aligned} \sum \limits _{i=1}^{m} \lambda _{i}u_{i}(t)\in K, \end{aligned}$$

which means that K is convex. Obviously, K is a closed and convex subset on \(U_{0}\).

Step 2. We check that \({\mathcal {F}}\) is well-defined with K. For each \(t\in [-T,0]\), we have

$$\begin{aligned} |({\mathcal {F}}u)(t)-u_{0}|\le & {} \int _{t}^{0}(s-t)|q(s)F(u(s))+p(s)|ds\\\le & {} \int _{-T}^{0}(s-t)q(s)|F(u(s))|ds+\int _{-T}^{0}(s-t)|p(s)|ds\\\le & {} \int _{-T}^{0}(s+T)q(s)|F(u(s))|ds+\int _{-T}^{0}(s+T)|p(s)|ds\\\le & {} TM_{h}\int _{-T}^{0}q(s)ds+T\int _{-T}^{0}|p(s)|ds\\\le & {} h, \end{aligned}$$

which shows that \({\mathcal {F}}(K)\subset K\).

Step 3. Let us now prove that \( {\mathcal {F}}(K)\) is relatively compact in \(U_{0}\). Differentiating both sides of (54) with respect to t, we have

$$\begin{aligned} ({\mathcal {F}}u)'(t)=\int _{t}^{0}q(s)F(u(s))ds+\int _{t}^{0}p(s)ds,~~t\in [-T,0]. \end{aligned}$$

For all \(t\in [-T,0]\), we obtain

$$\begin{aligned} \begin{aligned} |({\mathcal {F}}u)'(t)|&\le \Big |\int _{t}^{0}q(s)F(u(s))ds\Big |+\Big |\int _{t}^{0}p(s)ds\Big |\\&\le \int _{t}^{0}|q(s)F(u(s))|ds+\int _{t}^{0}|p(s)|ds\\&\le \int _{-T}^{0}q(s)|F(u(s))|ds+\int _{-T}^{0}|p(s)|ds\\&\le M_{h}\int _{-T}^{0}q(s)ds+\int _{-T}^{0}|p(s)|ds\\&\le \frac{h}{T}. \end{aligned} \end{aligned}$$

Then let \(\{u_{n}\}\) be an arbitrary sequence in K, by the mean value theorem yields

$$\begin{aligned} |({\mathcal {F}}u_{n})(t_{1})-({\mathcal {F}}u_{n})(t_{2})|\le \frac{h}{T}|t_{1}-t_{2}|,~\forall t_{1},t_{2}\in [-T,0],~n\in \mathbb {N^{*}}, \end{aligned}$$

which implies that \(\{{\mathcal {F}}u_{n}\}\) is equicontinuous function in \(U_{0}\). Linking Step 2, \(\{{\mathcal {F}}u\}\) is uniformly bounded in \(U_{0}\). Therefore the Arzelà-Ascoli theorem guarantees that \(\{{\mathcal {F}}u\}\) is relatively compact in \(U_{0}\).

Step 4. We confirm that \({\mathcal {F}}:K\rightarrow K\) is continuous. Given a fixed \(\varepsilon >0\), due to \(F:[u_{0}-h,u_{0}+h]\rightarrow \mathbb {R}\) is uniformly continuous, therefore there exists a constant such that if \(u,~{\bar{u}}\in [u_{0}-h,u_{0}+h]\) with \(|u-{\bar{u}}|<\delta \), then

$$\begin{aligned} |F(u)-F({\bar{u}})|\le \frac{2\varepsilon }{q_{*}T^{2}}, \end{aligned}$$

where \(q_{*}=\max \nolimits _{t\in [-T,0]}q(t)\). For arbitrary \(u_{1},~u_{2}\in K\) with \(\Vert u_{1}-u_{2}\Vert <\delta \), we have

$$\begin{aligned} \begin{aligned} |({\mathcal {F}}u_{1})(t_{1})-({\mathcal {F}}u_{2})(t_{1})|=&\left| \int _{t}^{0}(s-t)q(s)F(u_{1}(s))ds-\int _{t}^{0}(s-t)q(s)F(u_{2}(s))ds\right| \\&\le \int _{t}^{0}(s-t)q(s)|F(u_{1}(s))-F(u_{2}(s))|ds\\&\le q_{*}\frac{2\varepsilon }{q_{*}T^{2}}\int _{-T}^{0}(s-t)ds\\&\le \frac{2\varepsilon }{T^{2}}\int _{-T}^{0}(s+T)ds\\&=\frac{2\varepsilon }{T^{2}}\cdot \frac{T^{2}}{2}\\&=\varepsilon . \end{aligned} \end{aligned}$$

Therefore, we have \(\Vert {\mathcal {F}}u_{1}-{\mathcal {F}}u_{2}\Vert \le \varepsilon \). Then the operator \({\mathcal {F}}:K \rightarrow K\) is continuous.

We have verified that all assumptions of the Schauder’s fixed-point theorem are satisfied. There exists at least one \(u\in K\) such that \({\mathcal {F}}u=u\), which corresponds to a continuous solution of (53) on \([-T,0]\). \(\square \)

Remark 5.4

Applying our results to deal with the arctic gyres, one can determine uniform upper bounds for \(C_{1}\) and \(C_{2}\) as follow

$$\begin{aligned} \begin{aligned} \int _{-\infty }^{0}q(s)ds&=\int _{-\infty }^{0}\frac{4e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\&=2e^{-2{\tilde{x}}_{0}}\Big [\ln (e^{2{\tilde{x}}_{0}}+1)-\frac{e^{2{\tilde{x}}_{0}}}{e^{2{\tilde{x}}_{0}}+1}\Big ]\approx 181.118,\\ \int _{-\infty }^{0}|p(s)|ds&=\int _{-\infty }^{0}8\omega \Big |\frac{(e^{{\tilde{x}}_{0}}e^{2s}-e^{-{\tilde{x}}_{0}})e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{3}}\Big |ds\\&=8\omega e^{-2{\tilde{x}}_{0}}\Big |\frac{\frac{3}{2}e^{2{\tilde{x}}_{0}}+1}{(e^{2{\tilde{x}}_{0}}+1)^{2}}+\frac{1}{2}\ln (e^{2{\tilde{x}}_{0}}+1)-1\Big |\approx 0.021\omega , \end{aligned} \end{aligned}$$

where \({\tilde{x}}_{0}\approx -2.253\).

To end this section, we present a simple but rather general existence and uniqueness result.

Theorem 5.5

Set

$$\begin{aligned} \begin{aligned} \zeta ^+({\tilde{x}}_0)=&\sup _{t\le 0}\left( 2e^{-2{\tilde{x}}_{0}}-2e^{-2{\tilde{x}}_{0}}\Big [\frac{1}{e^{2{\tilde{x}}_{0}}e^{2t}+1}+2\ln (e^{2{\tilde{x}}_{0}}e^{2t}+1)+dilog(e^{2{\tilde{x}}_{0}}e^{2t}+1)\Big ]\right) ,\\ \zeta ^-({\tilde{x}}_0)=&\inf _{t\le 0}\left( 2e^{-2{\tilde{x}}_{0}}-2e^{-2{\tilde{x}}_{0}}\Big [\frac{1}{e^{2{\tilde{x}}_{0}}e^{2t}+1}+2\ln (e^{2{\tilde{x}}_{0}}e^{2t}+1)+dilog(e^{2{\tilde{x}}_{0}}e^{2t}+1)\Big ]\right) ,\\ \xi ({\tilde{x}}_0)=&\sup _{t\le 0}e^{-2{\tilde{x}}_{0}}[dilog(e^{2{\tilde{x}}_{0}}e^{2t}+1)+2\ln (e^{2{\tilde{x}}_{0}}e^{2t}+1)]. \end{aligned} \end{aligned}$$

If there are constants \(\kappa _1<\kappa _2\) such that

$$\begin{aligned} \begin{aligned} \psi _0+\omega \zeta ^+({\tilde{x}}_0)+\xi ({\tilde{x}}_0)\max \left\{ 0,\max _{u\in [\kappa _1,\kappa _2]}|F(u)|\right\}&\le \kappa _2,\\ \psi _0+\omega \zeta ^-({\tilde{x}}_0)+\xi ({\tilde{x}}_0)\min \left\{ 0,\min _{u\in [\kappa _1,\kappa _2]}|F(u)|\right\}&\ge \kappa _1,\ \end{aligned} \end{aligned}$$
(55)

then (11) with (13) has a solution with \(\kappa _1\le u(t)\le \kappa _2\) for all \(t\le 0\). In addition, if \(F(\cdot )\) is Lipschitz continuous on \([\kappa _1,\kappa _2]\), i.e.

$$\begin{aligned} \sup _{u_1,u_2\in [\kappa _1,\kappa _2],u_1\ne u_2}\frac{|F(u_1)-F(u_2)|}{|u_1-u_2|}<\infty , \end{aligned}$$

then this solution is unique.

Proof

We consider the above operator

$$\begin{aligned} \begin{aligned} ({\mathcal {T}}u)(t)&=\psi _{0}+2\omega e^{-2{\tilde{x}}_{0}}-2\omega e^{-2{\tilde{x}}_{0}}\\&\quad \times \Big [\frac{1}{e^{2{\tilde{x}}_{0}}e^{2t}+1}+2\ln (e^{2{\tilde{x}}_{0}}e^{2t}+1)+dilog(e^{2{\tilde{x}}_{0}}e^{2t}+1)\Big ]\\&\quad +\int _{-\infty }^{t}(t-s)\frac{4e^{4s}F(u(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds,~~t\le 0. \end{aligned} \end{aligned}$$

It is to check, that inequalities of (55) implies

$$\begin{aligned} {\mathcal {T}}(W_{\kappa _1,\kappa _2})\subset W_{\kappa _1,\kappa _2}=\{u|u\in \kappa _1\le u(t)\le \kappa _2,~ \forall t\le 0\}. \end{aligned}$$

Clearly \(W_{\kappa _1,\kappa _2}\) is a convex, bounded and closed subset of X. Since we already know that \({\mathcal {T}}\) is a compact mapping, we can apply the Schauder’s fixed-point theorem for the existence part of our theorem. The uniqueness follows from the proof Theorem 5.1. This proof is finished. \(\square \)

Remark 5.6

(55) is equivalent to

$$\begin{aligned} \begin{aligned} \max \left\{ 0,\max _{u\in [\kappa _1,\kappa _2]}|F(u)|\right\}&\le \frac{\kappa _2-\psi _0-\omega \zeta ^+({\tilde{x}}_0)}{\xi ({\tilde{x}}_0)},\\ \min \left\{ 0,\min _{u\in [\kappa _1,\kappa _2]}|F(u)|\right\}&\ge \frac{\kappa _1-\psi _0-\omega \zeta ^-({\tilde{x}}_0)}{\xi ({\tilde{x}}_0)}.\ \end{aligned} \end{aligned}$$
(56)

Since always it holds

$$\begin{aligned} \min \{0,\min _{u\in [\kappa _1,\kappa _2]}|F(u)|\}\le \max \{0,\max _{u\in [\kappa _1,\kappa _2]}|F(u)|\}, \end{aligned}$$

(56) implies that we need

$$\begin{aligned} \omega (\zeta ^+({\tilde{x}}_0)-\zeta ^+({\tilde{x}}_0))\le \kappa _2-\kappa _1. \end{aligned}$$
(57)

On the other hand, if (57) is satisfied, then (55) is equivalent to

$$\begin{aligned} \begin{aligned} \frac{\kappa _1-\psi _0-\omega \zeta ^-({\tilde{x}}_0)}{\xi ({\tilde{x}}_0)}&\le \min \left\{ 0,\min _{u\in [\kappa _1,\kappa _2]}|F(u)|\right\} \\&\le \max \left\{ 0,\max _{u\in [\kappa _1,\kappa _2]}|F(u)|\right\} \\&\le \frac{\kappa _2-\psi _0-\omega \zeta ^+({\tilde{x}}_0)}{\xi ({\tilde{x}}_0)}. \end{aligned} \end{aligned}$$
(58)

Clearly (58) is more readable and applicable than (55).

6 Ulam–Hyers Type Stability

In this section, we consider the Ulam–Hyers type stability of the equation (11) with asymptotic conditions (13).

Let \(\varepsilon , \lambda _{\mu }\) be two positive real numbers and let \(\mu : (-\infty ,t_{0}]\rightarrow [0,+\infty ),\ t_0\le 0\) be a continuous and nondecreasing function satisfying

$$\begin{aligned} \int _{-\infty }^{t}(t-s)\mu (s)ds\le \lambda _{\mu }\mu (t),~~t\in (-\infty ,t_0]. \end{aligned}$$
(59)

For example, we set \(\mu (t)=\rho e^{\alpha t}, ~-\infty < t \le 0,\) where \(\rho >0\) and \(\alpha \ge 1\). Then (59) holds. In fact,

$$\begin{aligned} \int _{-\infty }^{t}(t-s)\mu (s)ds= & {} \int _{-\infty }^{t}\int _{-\infty }^{s}\rho e^{\alpha \tau }d \tau ds\\= & {} \frac{\rho }{\alpha }\int _{-\infty }^{t}e^{\alpha \tau }\mid ^{s}_{-\infty } ds\\= & {} \frac{\rho }{\alpha } \int _{-\infty }^{t}e^{\alpha s} ds = \frac{\rho }{\alpha ^2} e^{\alpha t}. \end{aligned}$$

Consider

$$\begin{aligned} \Big |u''(t)-\frac{4e^{4t}F(u(t))}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{2}}-8\omega \frac{(e^{{\tilde{x}}_{0}}e^{2t}-e^{-{\tilde{x}}_{0}})e^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{3}}\Big |\le \varepsilon \mu (t),~~t\in (-\infty ,t_{0}],~t_{0}\le 0,\nonumber \\ \end{aligned}$$
(60)

and

$$\begin{aligned} \Big |u''(t)-\frac{4e^{4t}F(u(t))}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{2}}-8\omega \frac{(e^{{\tilde{x}}_{0}}e^{2t}-e^{-{\tilde{x}}_{0}})e^{4t}}{(e^{{\tilde{x}}_{0}}e^{2t}+e^{-{\tilde{x}}_{0}})^{3}}\Big |\le \varepsilon ,~~ t\in [t_{0},0]. \end{aligned}$$
(61)

Definition 6.1

(see [30]) For \(\forall ~ \varepsilon >0\), if there exists a real number \(C_{1}>0\) such that for any solution \({\hat{u}}\in C^{2}([t_{0},0],\mathbb {R})\) of (61) with asymptotic conditions (13), there exists a solution \(u\in C^{2}([t_{0},0],\mathbb {R})\) of (11) with asymptotic conditions (13) and

$$\begin{aligned} \mid {\hat{u}}(t)-u(t)\mid \le C_{1}\varepsilon ,~~\forall ~t\in [t_{0},0], \end{aligned}$$

then the equation (11) with asymptotic conditions (13) is Ulam–Hyers stable.

Definition 6.2

(see [30]) For \(\forall ~ \varepsilon >0\), if there exists a real number \(C_{\mu }>0\) such that for any solution \({\hat{u}}\in C^{2}((-\infty ,t_{0}],\mathbb {R})\) of (60) with asymptotic conditions (13), there exists a solution \(u\in C^{2}((-\infty ,t_{0}],\mathbb {R})\) of (11) with asymptotic conditions (13) and

$$\begin{aligned} \mid {\hat{u}}(t)-u(t)\mid \le C_{\mu }\varepsilon \mu (t),~~\forall ~t\in (-\infty ,t_{0}], \end{aligned}$$

then the equation (11) with asymptotic conditions (13) is Ulam–Hyers–Rassias stable.

Theorem 6.3

Assume that the conditions of Theorem 5.1 hold, then the equation (11) with asymptotic conditions (13) is Ulam–Hyers–Rassias stable on \((-\infty ,t_{0}]\).

Proof

Let \({\hat{u}}\in C^{2}((-\infty ,t_{0}],\mathbb {R})\) be a solution of (60) with asymptotic conditions (13). From (59) and (60), we have

$$\begin{aligned} \begin{aligned} |{\hat{u}}(t)-u(t)| =&\left| {\hat{u}}(t)-g(t)-\int _{-\infty }^{t}(t-s)\frac{4e^{4s}F(u(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\right| \\ \le&\left| {\hat{u}}(t)-g(t)-\int _{-\infty }^{t}(t-s)\frac{4e^{4s}F({\hat{u}}(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\right| \\&\quad +\left| \int _{-\infty }^{t}(t-s)\frac{4e^{4s}F({\hat{u}}(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds-\int _{-\infty }^{t}(t-s)\frac{4e^{4s}F(u(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\right| \\ \le&\left| {\hat{u}}(t)-g(t)-\int _{-\infty }^{t}(t-s)\frac{4e^{4s}F({\hat{u}}(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\right| \\&\quad +\int _{-\infty }^{t}(t-s)\frac{4e^{4s}| F({\hat{u}}(s)-F(u(s))|}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\ \le&\lambda _{\mu }\varepsilon \mu (t)+\int _{-\infty }^{t}(t-s)\frac{4e^{4s}| F({\hat{u}}(s)-F(u(s))|}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\ \le&\lambda _{\mu }\varepsilon \mu (t)+\int _{-\infty }^{t}(t-s)\frac{4e^{4s}M|{\hat{u}}(s)-u(s)|}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds,~~-\infty < t\le t_{0}.\\ \end{aligned} \end{aligned}$$

where \(g(t)=\psi _{0}+2\omega e^{-2{\tilde{x}}_{0}}\Big [\frac{1}{e^{2{\tilde{x}}_{0}}e^{2t}+1}+2\ln (e^{2{\tilde{x}}_{0}}e^{2t}+1)+dilog(e^{2{\tilde{x}}_{0}}e^{2t}+1)-1\Big ],~-\infty < t\le t_{0}.\)

By the Gronwall’s inequality, we obtain that

$$\begin{aligned} \begin{aligned} |{\hat{u}}(t)-u(t)|&\le \lambda _{\mu }\varepsilon \mu (t)\exp \Big (\int _{-\infty }^{t}\frac{4M(t-s)e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\Big )\\&\le \lambda _{\mu }\varepsilon \mu (t)\exp \Big (\sup \limits _{t\le t_0}\int _{-\infty }^{t}\frac{4M(t-s)e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\Big )\\&=\lambda _{\mu }\exp \Big (Me^{-2{\tilde{x}}_{0}}[dilog(e^{2{\tilde{x}}_{0}}e^{2t_{0}}+1)+2\ln (e^{2{\tilde{x}}_{0}}e^{2t_{0}}+1)]\Big )\\ \varepsilon \mu (t)&:=C_{\mu }\varepsilon \mu (t),~~-\infty < t\le t_{0}, \end{aligned} \end{aligned}$$

i.e., the equation (11) with asymptotic conditions (13) is Ulam–Hyers–Rassias stable. The proof is completed. \(\square \)

Theorem 6.4

Assume that the conditions of Theorem 5.1 hold, then the equation (11) with asymptotic conditions (13) is Ulam–Hyers stable on \([t_{0},0]\).

Proof

Linking (44) and (48), we obtain that

$$\begin{aligned} \begin{aligned} u(t)&=u(t_{0})+u'(t_{0})(t-t_{0})+\int _{t_{0}}^{t}(t-s)\frac{4e^{4s}F(u(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\&\quad +\int _{t_{0}}^{t}(t-s)8\omega \frac{(e^{{\tilde{x}}_{0}}e^{2s}-e^{-{\tilde{x}}_{0}})e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{3}}ds,~~t_{0}\le t\le 0. \end{aligned} \end{aligned}$$
(62)

Let \({\hat{u}}\in C^{2}((-\infty ,t_{0}],\mathbb {R})\) be a solution of (61) with asymptotic conditions (13). From (61) and (62) we have

$$\begin{aligned} \begin{aligned} |{\hat{u}}(t)-u(t)| =&\left| {\hat{u}}(t)-h(t)-\int _{t_{0}}^{t}(t-s)\frac{4e^{4s}F(u(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\right| \\ \le&\left| {\hat{u}}(t)-h(t)-\int _{t_{0}}^{t}(t-s)\frac{4e^{4s}F({\hat{u}}(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\right| \\&\quad +\left| \int _{t_{0}}^{t}(t-s)\frac{4e^{4s}F({\hat{u}}(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds-\int _{t_{0}}^{t}(t-s)\frac{4e^{4s}F(u(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\right| \\ \le&\left| {\hat{u}}(t)-h(t)-\int _{t_{0}}^{t}(t-s)\frac{4e^{4s}F(u(s))}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\right| \\&\quad +\int _{t_{0}}^{t}(t-s)\frac{4e^{4s}|F({\hat{u}}(s))-F(u(s))|}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\ \le&\, \frac{(t-t_{0})^{2} }{2}\varepsilon +\int _{t_{0}}^{t}(t-s)\frac{4e^{4s}|F({\hat{u}}(s))-F(u(s))|}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\\ \le&\, \frac{t_{0}^{2} }{2}\varepsilon +\int _{t_{0}}^{t}(t-s)\frac{4e^{4s}M|{\hat{u}}(s)-u(s)|}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds,~~t_{0}\le t\le 0,\\ \end{aligned} \end{aligned}$$

where \(h(t)=u(t_{0})+u'(t_{0})(t-t_{0})+\int _{t_{0}}^{t}(t-s)8\omega \frac{(e^{{\tilde{x}}_{0}}e^{2\,s}-e^{-{\tilde{x}}_{0}})e^{4\,s}}{(e^{{\tilde{x}}_{0}}e^{2\,s}+e^{-{\tilde{x}}_{0}})^{3}}ds,~~t_{0}\le t\le 0.\)

By the Gronwall’s inequality, we have

$$\begin{aligned} \begin{aligned} |{\hat{u}}(t)-u(t)|&\le \frac{t_{0}^{2}}{2} \exp \left( \int _{t_{0}}^{t}\frac{4M(t-s)e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\right) \varepsilon \\&\le \frac{t_{0}^{2} }{2} \exp \left( \sup \limits _{t_{0}\le t\le 0}\int _{t_{0}}^{0}\frac{4M(t-s)e^{4s}}{(e^{{\tilde{x}}_{0}}e^{2s}+e^{-{\tilde{x}}_{0}})^{2}}ds\right) \varepsilon :=C_{1}\varepsilon ,~~t_{0}\le t\le 0, \end{aligned} \end{aligned}$$

i.e., the equation (11) with asymptotic conditions (13) is Ulam–Hyers stable. This proof is finished. \(\square \)

7 Conclusion

We study a new second-order ordinary differential equation model of arctic gyres, which is derived by considering the radial solutions for the semi-linear elliptic equation model of gyres in [15] and introducing exponential transformation. With the suitable asymptotic conditions and boundary conditions, we provide explicit solutions of constant vorticity and linear vorticity. Then we study the existence and uniqueness of continuous solutions for the nonlinear vorticity with the fixed-point techniques. Finally, we show that Lipschitz-type nonlinear vorticity with asymptotic conditions for arctic gyres is Ulam–Hyers stable on finite interval and Ulam–Hyers–Rassias stable on infinite interval.