1 Introduction

Realistic computer simulations in engineering, non-engineering, physics, and mathematics can incur an increasing computing strain. Model order reduction (MOR) is gaining popularity because it may extract essential insights from complicated simulations while removing computationally costly and unneeded elements. MOR provides an identical subsystem with a minor acceptance deviation that keeps system features such as stability, passivity, positivity, and a good approximation of input-output dynamics [1,2,3]. Reduced-order systems offer various advantages, including being more accessible to understand, using less computational power, requiring less hardware complexity, and assisting in the design of a feasible controller [1,2,3]. MOR is now being used in many technological and scientific fields. As in power systems [4, 5], chemical processes [6], controller design [7,8,9,10,11,12,13,14,15,16,17], and references therein.

Many approaches for order reduction of original plants are presented in the frequency domain [18,19,20,21]. To mention a few, are the Pade approximation method (PAM), Routh approximation method (RAM), stability equation method (SEM), Mikhailov stability criterion (MSC), factor division method (FDM), dominant mode retention (DMR) and pole clustering technique (PCT). These methodologies give simplified models that mimic the plant’s current dynamics and input-output behavior. These techniques have certain drawbacks, including the PAM may generate unstable reduced models for an existing stable plant, the RAM requires the application of reciprocal and inverse transformations and needs to form two separate Routh tables, the SEM is only applicable to minimum phase systems, DMR is considered only poles near origin as a dominant, and the PCT requirement for tuning and gain correction factors. New mixed approaches combine the prior strategies; the reader can refer to [22,23,24,25,26] and the references therein to solve these deficiencies. Most of these techniques correspond to the retention of stability and the first few moments in the reduced model. But in general, maintaining a few moments and a few Markov parameters is required for an excellent overall response approximation of the original system [27,28,29,30,31].

The concept of order reduction by balancing transformation may be traced back to Kalman’s first publication on canonical system decomposition in 1963, i.e., the uncontrollable or unobservable system modes do not exist in the system transfer function. As a result, the authors of [32, 33] conclude that system modes that are both weakly controlled and weakly observable have minimal effects on system dynamics and can be discarded. However, those modes that are weakly controllable and well observable, as well as those that are highly controllable and weakly observable, cannot be ignored—they may become crucial for the closed-loop system performance. The reduced-order system produces an excellent approximation of the original system (with good spectra approximation on higher frequencies) subject to impulse input. Still, it displays considerable steady-state inaccuracy for step input application (bad spectra approximation on lower frequencies) [34]. This issue occurs because the steady state gains of the original and lower-order systems differ, as the simplified model is generated by removing the spectra component at lower frequencies (the system’s disregarded part-state variables \(x_{2} (t)\)).

The literature provides a variety of methods [35,36,37,38,39] to improve the balance truncated-reduced model’s steady state approximation. In [35], the balanced truncation method (BTM) is integrated with the Pade approximation method. In [36], the BTM is combined with the factor division method. At the same time, [37] uses the BTM and elementary mathematical equations to build the numerator of the simplified model. The paper [38] uses the balanced truncation to generate a lower-order model. Next, a gain factor is added to the model to enhance the steady-state performance. [39] Utilizes the benefits of the balanced truncation approach in addition to the modified Cauer continuous fraction expansion. The merits and limitations of these techniques are detailed in table 1. Nevertheless, these strategies [35,36,37,38] do not account for the high-order system’s Markov parameters (MPs) in the simplified model. Time moments (TMs) and MPs are essential for getting close approximations of system responses. Keeping track of TMs will offer a reasonable estimate of the system’s responsiveness in a steady state. Keeping track of MPs will provide a good approximation of the system’s responsiveness during transients. Even though there are a few different ways to order reduction, they still need to offer satisfactory results across the board for any of the systems. Consequently, research into the efficiency of new algorithms is now receiving much attention.

Table 1 Moore’s balanced truncation-based reduction methods with steady-state gain approximation.
Full size table
Table 2 Performance comparison of the original plant and various abated models from recent literature for test system 1.
Full size table

It is common practice in model simplification strategies to use optimization techniques to calculate lower-order models by minimizing the difference in transient responses between the full-scale system and the simplified plant. Based on this idea, many methods for reducing and weighted equation errors have been developed [42, 43]. The most recent optimization development is using a metaheuristic algorithm inspired by nature. Available metaheuristic approaches are also used to reduce complexity in the transfer function of dynamic systems [44,45,46,47,48,49]. Parameters for the simplified model have been optimized using metaheuristic processes inspired by natural phenomena. Minimizing the error-index, such as integral square error (ISE), H∞ norm, H2 norm, and integral time absolute error (ITAE), is a few.

Advanced controller design approaches such as linear-quadratic-Gaussian (LQG), H∞ control design, micro-synthesis, and linear matrix inequality (LMI) provide controller orders that are at least equal to or greater than the system order [8, 9]. Hence, all system states are unavailable for measurement; therefore, state estimation involves using a Kalman filter or a state observer, increasing the control rule’s complexity and cost [8, 9]. As a result, a low-complexity controller is frequently required. Numerous approaches exist for developing simpler controllers for large-scale order networks [7,8,9,10,11,12,13,14,15,16,17]. One option is to decrease the plant’s order and then use the reduced model as a predictive model to develop a reduced-order controller. Another approach is constructing a high-order controller for a real-world high-order plant and then decreasing the controller order using reduction techniques.

This article proposes a unique approach for retrieving simplified models of complicated order plants. The reduced model denominator was obtained using the balanced truncation method. The lessened model numerator coefficients are retrieved using a simple mathematical procedure in the proposed scenario by comparing the reduced model's initial TMs and MPs with the original plant. In contrast, most existing approaches maintain initial TMs, but the intended method retains TMs and MPs. The proposed method is simple, accurately approximates the precise system response over the whole frequency range, and ensures the stability of the simplified system for the given stable original system. The study’s second purpose is to provide a strategy for developing a controller for a large-scale system based on a reduced-order model. This method is used to design controllers for any sophisticated real-time system. Finally, the controller created using a simplified model is integrated into the original plant. The proposed method is validated using a ninth-order system, a sixth-order stable, practical open-loop helicopter engine with a fuel controller system, an eighth-order flexible-missile control model, and a two-input, two-output (TITO) tenth-order linear dynamical model of a SMIB power system network. The simulation results demonstrate that the suggested approach outperforms the most recent community-released model reduction solutions.

The remainder of the document is organized as follows: in Section 2; The general statement of the problem is discussed in Section 3, the suggested technique for computing the reduced scheme is discussed. Section 4 describes PID controller design and compensators using original and reduced models. The utility of the recommended method is shown in Section 5 using a few typical and real-life examples from the literature. Section 6 concludes with the future scope of the proposed work.

2 Problem statement

Consider a high-dimensional minimal, asymptotically stable, minimal, linear time-invariant in state space form

(1)

here \(x(t) \in \Re^{n} ,u(t) \in \Re^{p} ,y(t) \in \Re^{q}\) are the state vector, input vector, and output vector with n states, p inputs, and q outputs. The system matrix (A), output matrix(C), input matrix (B), and feed-forward matrix (D) are constant, with appropriate dimensions. For single input single output (SISO) case \(p = q = 1\).

Definition 1

A linear time-invariant system (1) is realizable if the pair \(\left( {C,A} \right)\) is entirely observable and the pair \(\left( {A,B} \right)\) controllable [1, 2, 33]. The equivalent transfer function of the system (1) for the SISO case is

$$ G(s) = \frac{N(s)}{{D(s)}} = \frac{{f_{0} + f_{1} s + \cdots + f_{m} s^{m} }}{{h_{0} + h_{1} s + \cdots + h_{n} s^{n} }} $$
(2)

Where \(m \le n;\) \(h_{j} ;j = 0,1, \ldots ,n\) and \(f_{i} ;i = 0,1, \ldots ,m\) are the coefficients of the numerator and denominator polynomials of a given original plant (2), respectively, scalar constants. For the MIMO case, the dynamics of the system (1) in the frequency domain are represented by the transfer function matrix as follows:

$$ [G(s)] = [g_{ij} (s)]_{q \times p} = \frac{1}{D(s)}\left[ {\begin{array}{*{20}c} {A_{11} (s)} & {A_{12} (s)} & {\ldots.} & {A_{1p} (s)} \\ {A_{21} (s)} & {A_{22} (s)} & {\ldots} & {A_{2p} (s)} \\ \vdots & \vdots & \vdots & \vdots \\ {A_{q1} (s)} & {A_{q2} (s)} & {\ldots} & {A_{qp} (s)} \\ \end{array} } \right] $$
(3)

where \(i = 1,2,..,q\) and \(j = 1,2,..,p\).

The basic form of entries \(g_{ij} (s)\) of (3) is defined as a transfer function for i output to jth input, represented by

$$ g_{ij} (s) = \frac{{A_{ij} (s)}}{D(s)} = \frac{{\hat{f}_{0} + \hat{f}_{1} s + \cdots+ \hat{f}_{m} s^{m} }}{{\hat{h}_{0} + \hat{h}_{1} s +\cdots + \hat{h}_{n} s^{n} }} $$
(4)

The objective is to find an equivalent kth order reduced model of the original system (1) of the form

(5)

where \(x_{k} (t) \in \Re^{k} ,u(t) \in \Re^{p} ,y(t) \in \Re^{q}\) are the state vector, input vector, and output vector with k states, p inputs, and q outputs. The system matrix (Ak), output matrix (Ck), input matrix (Bk), and feed-forward matrix (Dk) are constant, with appropriate dimensions. The rational system function (5) for the SISO case is described as

$$ R_{k} (s) = C_{k} (sI_{k} - A_{k} )^{ - 1} B_{k} + D_{k} = \frac{{w_{0} + \cdots + w_{k - 1} s^{k - 1} }}{{z_{0} + \cdots + z_{k} s^{k} }} $$
(6)

where \(w_{i} ;i = 0,1,\ldots,k - 1\) and \(z_{j} ;j = 0,1,\ldots,k\) are unknown coefficients of reduced model numerator and denominator polynomial of (6), respectively, which are scalar constants. For the MIMO case

$$ [R_{k} (s)] = [r_{ij} (s)]_{q \times p} = \frac{1}{{\overline{{D_{k} }} (s)}}\left[ {\begin{array}{*{20}c} {B_{11} (s)} & {B_{12} (s)} & {..} & {B_{1p} (s)} \\ {B_{21} (s)} & {B_{22} (s)} & {..} & {B_{2p} (s)} \\ \vdots & \vdots & \vdots & \vdots \\ {B_{q1} (s)} & {B_{q2} (s)} & {..} & {B_{qp} (s)} \\ \end{array} } \right] $$
(7)

The basic form of entries \(r_{ij} (s)\) of (7) is defined as a transfer function for ith output to jth input, represented by

$$ r_{ij} (s) = \frac{{B_{ij} (s)}}{{\overline{D}_{k} (s)}} = \frac{{c_{0} + c_{1} s + \cdots + c_{k - 1} s^{k - 1} }}{{d_{0} + d_{1} s + \cdots + d_{k} s^{k} }} $$
(8)

2.1 Selection of reduced model order

In this article, the order in which the original system is to be reduced is not random, and the reduced order is selected based on the original system’s Hankel singular values (HSV).

Select the reduced order ‘k’ such that.

$$ \sigma_{k} > \sum\limits_{i = k + 1}^{n} {\sigma_{i} } $$
(9)

here \(\sigma_{i}\) is the ith HSV of the original system.

3 Proposed reduction procedure

3.1 Procedure to determine abated model denominator by Balanced Truncation [32, 33, 48]

Consolidating the principal component analysis and singular value decomposition, Moore [1] introduced the balanced realization approach by employing the system controllability and observability gramians. The BTM involves two stages, namely Lyapunov balancing and state truncation.


3.1a Lyapunov balancing: 1. Compute the controllability gramian \(\left( {P_{c} } \right)\) and observability gramian \(\left( {Q_{o} } \right)\) of the original system (1) using (10), which is a positive semi-definite and unique solution to the following algebraic Lyapunov equations

$$ \left. \begin{gathered} AP_{c} + P_{c} A^{T} = - BB^{T} \hfill \\ Q_{o} A + A^{T} Q_{o} = - C^{T} C \hfill \\ \end{gathered} \right\} $$
(10)

2. Transform the original system into a balanced form. Do Choleskey factorizations of \(P_{c}\) and \(Q_{o}\) as follows:

\(P_{c} = XX^{T}\); \(Q_{0} = YY^{T}\).

Here \(X,Y \in \Re^{n \times n}\) are lower triangular matrices.

3. Now compute the singular value decomposition (SVD) of the Hankel matrix \(X^{T} Y\).

4. \(SVD(X^{T} Y) = U\sum V^{T}\).

Where \(U,V \in \Re^{n \times n}\) are unitary (orthogonal) matrices. \(\sum \in \Re^{n \times n}\) is a singular value matrix.

5. Balancing requires changing the basis for the states of the system (1) using a similarity transformation matrix.

\(x(t) = T\tilde{x}(t)\), \(\tilde{x}(t) = T^{ - 1} x(t)\).

Here \(T \in \Re^{n \times n}\) is an invertible matrix.

6. The transformation matrix \(T = XV\sum^{{\frac{ - 1}{2}}}\) transforms the system (1) into a balanced form

(11)

7. The controllability and observability gramians of the

system in balanced form (11) are

$$ \tilde{P}_{c} = \tilde{Q}_{0} = \sum = \left[ {\begin{array}{*{20}c} {\sum_{1} } & 0 \\ 0 & {\sum_{2} } \\ \end{array} } \right] = diag(\sigma_{1} ,.,\sigma_{k} ,.,\sigma_{n} ) $$
(12)

3.1b Concept of State Truncation: Partition the balanced system of (11) into blocks corresponding to the block partition of the singular value matrix \(\sum_{i} ;i = 1,2\) as in (12).

(13)

where subscripts 1 and 2 denote the dimensions k and n - k, respectively.

\(\sum_{1} = diag(\sigma_{1} ,\sigma_{2} , \ldots ,\sigma_{k} )\) It gives singular values corresponding to strongly reachable and observable states.

\(\sum_{2} = diag(\sigma_{k + 1} ,\sigma_{k + 2} , \ldots ,\sigma_{n} )\) It gives singular values corresponding to weakly reachable and observable states, which decay rapidly and become insignificant.

The k-dimensional abated model was obtained by truncating the weakly controllable and weakly observable states as follows:

(14)

The transfer function of the diminished model (14) is

$$ R_{k} (s) = C_{k} (sI_{k} - A_{k} )^{ - 1} B_{k} = C_{1} (sI_{k} - A_{11} )^{ - 1} B_{1} $$
(15)

The characteristic or denominator polynomial of the abated model is

$$ d{}_{k}(s) = \left| {sI_{k} - A_{11} } \right| = z_{0} + z_{1} s + \cdots + z_{k} s^{k} $$
(16)

3.2 Determination of reduced model numerator using a factor division-like method [50]

The reduced model denominator is obtained using the balanced truncation approach, and the reduced model numerator is created by matching the high-order system’s first “k” moments with the reduced-order model. In certain instances, this results in a subpar transient response approximation. In general, a simplified model should keep a few initial time moments (for steady-state response accuracy) and a few Markov parameters (for transient response accuracy) from the higher-order dynamic system to give a decent approximation of the overall response of the original system [27,28,29,30,31, 38]. The goal is to find a ROM that approximates HOS's overall reaction (transient and steady-state). A factor division-like approach retains initial ‘T’ time moments and ‘M’ Markov parameters in the reduced model [50].

\(D_{k} (s)\) Being predetermined by the algorithm discussed in section 3.1, the reduced model numerator \(N_{k} (s)\) is obtained by retaining the initial ‘T’ time moments and ‘M’ Markov parameters of the HOS (1). Such that \(T + M = k\). Let (2) be approximated by (6), and then decompose the HOS numerator polynomial as follows:

$$ N(s) = N_{M} (s) + N_{r} (s) + N_{T} (s) $$
(17)

Remark 1

We need only the first ‘T’ terms of N(s) starting from s0 to sT-1 to retain ‘T’ time moments of HOS in ROM, and to retain ‘M’ Markov parameters of HOS in ROM, it requires only ‘M’ terms of N(s) starting from sn-1 to sn-M. The remaining terms, starting from sT to sn-M-1 of N(s), are not required in order reduction.

Consider the polynomials defined as follows:

$$ N_{M} (s) = f_{n - 1} s^{n - 1} + f_{n - 2} s^{n - 2} + \cdots + f_{n - M} s^{n - M} $$
(18)
$$ N_{r} (s) = f_{n - M - 1} s^{n - M - 1} + \cdots + f_{T + 1} s^{T + 1} + f_{T} s^{T} $$
(19)
$$ N_{T} (s) = f_{T - 1} s^{T - 1} + \cdots + f_{1} s + f_{0} $$
(20)

Then from (2) \(G(s)\) can be written as follows:

$$ G\left( s \right) = \frac{{N_{M} (s)}}{D(s)} + \frac{{N_{r} (s)}}{D(s)} + \frac{{N_{T} (s)}}{D(s)} $$
(21)

Note 1: In (13), only the expressions \(\frac{{N_{T} (s)}}{D(s)}\) and \(\frac{{N_{M} (s)}}{D(s)}\) contributions to the first ‘T’ time moments and ‘M’ Markov parameters, respectively, are to be reserved in the reduced model. So, the effect of \(\frac{{N_{r} (s)}}{D(s)}\) can be ignored for model order reduction.

The reduced model numerator coefficients, determined as follows such that it closely approximate (2)

$$ \begin{gathered} R_{k} \left( s \right) = \frac{{N_{k} (s)}}{{D_{k} (s)}} = \frac{{N_{M} (s)D_{k} (s)/D(s)}}{{D_{k} (s)}} + \frac{{N_{T} (s)D_{k} (s)/D(s)}}{{D_{k} (s)}} \hfill \\ \cong G(s) \hfill \\ \end{gathered} $$
(22)
$$ N_{k} (s) = \frac{{N_{M} (s)D_{k} (s)}}{D(s)} + \frac{{N_{T} (s)D_{k} (s)}}{D(s)} = N_{k}^{M} (s) + N_{k}^{T} (s) $$
(23)

where

$$ N_{k}^{M} (s) = w_{k - 1} s^{k - 1} + w_{k - 2} s^{k - 2} + \cdots + w_{k - M} s^{k - M} $$
$$ N_{k}^{T} (s) = w_{T - 1} s^{T - 1} + w_{T - 2} s^{T - 2} + \cdots + w_{1} s + w_{0} $$

Case (i): The coefficients \(w_{T - 1} , \ldots w_{0}\) are determined by the following procedure that retains ‘T’ time moments. It requires performing polynomial multiplication up to sT-1 terms from s0 in \(N_{T} (s)D_{k} (s)\) and the first ‘T’ terms of \(D(s)\) from s0 to sT-1.

The direct truncation of the Taylor series expansion of \(\frac{{N_{T} (s)D_{k} (s)}}{D(s)}\) about \(s = 0\) obtains the coefficients

$$ \left. {\frac{{N_{T} (s)D_{k} (s)}}{D(s)}} \right|_{s = 0} = w_{0} + w_{1} s + \cdots + w_{T - 1} s^{T - 1} $$
(24)

where

$$ \frac{{N_{T} (s)D_{k} (s)}}{D(s)} = \frac{{e_{0} + e_{1} s + \cdots + e_{T - 1} s^{T - 1} }}{{h_{0} + h_{1} s + \cdots + h_{T - 1} s^{T - 1} }} $$
(25)

Case (ii): The coefficients \(w_{k - 1} , \ldots w_{k - M}\) are determined by the following procedure that retains ‘M’ Markov parameters. It requires performing polynomial multiplication up to sn+k-1 terms from sn+k-M in \(N_{M} (s)D_{k} (s)\) and the first ‘M’ terms from sn to sn-M+1 in \(D(s)\).

The direct truncation of the Taylor series expansion of \(\frac{{N_{M} (s)D_{k} (s)}}{D(s)}\) about \(s = \infty\) obtains the coefficients

$$ \left. {\frac{{N_{M} (s)D_{k} (s)}}{D(s)}} \right|_{s = \infty } = w_{k - 1} s^{k - 1} + \cdots + w_{k - M} s^{k - M} $$
(26)

where

$$ \frac{{N_{M} (s)D_{k} (s)}}{D(s)} = \frac{{s^{k} (l_{1} s^{n - 1} + \cdots + l_{M} s^{n - M} )}}{{h_{n} s^{n} + \cdots + h_{n - M + 1} s^{n - M + 1} }} $$
(27)

4 Controller and compensator design algorithm

Designing and simulating a controller/compensator is challenging for large plants. The difficulty and the expense of the controller architecture rise in tandem with the order of the system [7,8,9]. This problem can be handled by locating a roughly similar reduced framework for the high-order paradigm and designing the controller using a reduced model.

4.1 The control design problem can be illustrated as follows

Suppose the original open-loop model has poor dynamic behavior, like high overshoot and slow oscillatory response about a step input. In that case, the controller must be designed such that the controlled system performance must mimic the performance of the selected closed-loop reference model. The construction of the reference model is based on the open loop behavior of the plant (either time or frequency) [51,52,53,54,55,56]. The closed-loop characteristics of the controlled plant with unity feedback fully match those of the estimated reference model. The following stages demonstrate the controller design algorithm based on approximate model matching in Pade’s sense. The block diagrams of the closed-loop control systems design are presented in figures 1, 2, 3, and 4.

Figure 1
figure 1

Block diagram of open loop original model.

Full size image
Figure 2
figure 2

Block diagram of open loop system with controller.

Full size image
Figure 3
figure 3

Block diagram of closed loop system with controller.

Full size image
Figure 4
figure 4

Block diagram of closed loop reference model.

Full size image

Step 1: Built a closed-loop reference model M(s) based on the original system’s specified requirements for obtaining the expected characteristics, such that the closed-loop feature of the controlled system with unity feedback resembles that of the reference system. The detailed procedure to construct a reference model from the given specifications is explained in [51,52,53,54,55,56]. The general form of the unity feedback closed-loop reference model is selected as follows:

$$ M(s) = \frac{{\omega_{n}^{2} }}{{s^{2} + 2\varsigma \omega_{n} s + \omega_{n}^{2} }} $$
(28)

Based on the plant's desired closed-loop performance, the closed-loop reference model may be under-damped or critically damped.

Step 2: The equivalent open loop reference model is obtained as follows:

$$ M_{open} (s) = \frac{M(s)}{{1 - M(s)}} \Rightarrow \frac{{\omega_{n}^{2} }}{{(s + 2\varsigma \omega_{n} )s}} $$
(29)

Step 3: Consider the following arbitrary transfer function of a controller, which produces the necessary closed-loop response:

$$ \begin{gathered} \frac{{Y_{1} (s)}}{X(s)} = \frac{C(s)G(s)}{{1 + C(s)G(s)}} \approx \frac{{Y_{2} (s)}}{X(s)} = \frac{{M_{open} (s)}}{{1 + M_{open} (s)}} \hfill \\ \Rightarrow C(s)G(s) = M_{open} (s) \hfill \\ \end{gathered} $$
(30)
$$ C(s) = \frac{{M_{open} (s)}}{G(s)} \Rightarrow \frac{1}{s}H(s) $$
(31)

where, \(C(s)\) is the arbitrary transfer function of the controller, \(G(s)\) represents the open loop plant model, \(H(s)\) the polynomial obtained from the ratio \(\frac{{M_{open} (s)}}{G(s)}\).

$$ H(s) = \frac{{x_{0} + x_{1} s + \cdots + x_{T - 1} s^{T - 1} + \cdots + x_{q} s^{q} }}{{y_{0} + y_{1} s + \cdots + y_{T - 1} s^{T - 1} + \cdots + y_{p} s^{p} }} $$
(32)

Step 4: Unknown controller or compensator parameters, calculated by assuming that the output of the open-loop controlled system followed that of the open-loop reference prototype.

4.2 To design the PID controller

Let the PID controller structure have the following form:

$$ C_{PID} (s) = \frac{{K_{i} + K_{p} s + K_{d} s^{2} }}{s} $$
(33)

To determine the unknown PID controller parameters, it is required to match the initial three-time moments (T) of (31) with (33) as follows:

$$ \frac{{K_{i} + K_{p} s + K_{d} s^{2} }}{s} = \frac{1}{s}H^{\prime}(s) $$
(34)
$$ K_{i} + K_{p} s + K_{d} s^{2} = H^{\prime}(s) $$
(35)

where \(H^{\prime}(s) = \frac{{x_{0} + x_{1} s + x_{2} s^{2} }}{{y_{0} + y_{1} s + y_{2} s^{2} }}\) is obtained from the eq. (32).

The power series expansion of \(H^{\prime}(s)\) about \(s = 0\) gives the time moments of \(H^{\prime}(s)\).

$$ \left. {H^{\prime}(s)} \right|_{s = 0} = v_{0} + v_{1} s + v_{2} s^{2} $$
(36)

Now, from eq. (35) and (36)

$$ K_{i} + K_{p} s + K_{d} s^{2} = v_{0} + v_{1} s + v_{2} s^{2} $$
(37)

Now, compare identical powers of ‘s’ in eq. (37) from \(s^{0}\) to \(s^{2}\).

$$ K_{i} = v_{0} ,K_{p} = v_{1} ,K_{d} = v_{2} $$
(38)

4.3 To design a compensator controller

Let the compensator structure have the following form:

$$ C_{com} (s) = \frac{{K_{1} (1 + K_{2} s)}}{{s(1 + K_{3} s)}} $$
(39)

To determine the unknown controller parameters, it is required to match the initial three-time moments (T) of (31) with (39) as follows:

$$ \frac{{K_{1} (1 + K_{2} s)}}{{s(1 + K_{3} s)}} = \frac{1}{s}H^{\prime}(s) $$
(40)
$$ \frac{{K_{1} (1 + K_{2} s)}}{{(1 + K_{3} s)}} = H^{\prime}(s) $$
(41)

The power series expansion of \(H^{\prime}(s)\) about \(s = 0\) gives the time moments of \(H^{\prime}(s)\).

$$ \left. {H^{\prime}(s)} \right|_{s = 0} = v^{\prime}_{0} + v^{\prime}_{1} s + v^{\prime}_{2} s^{2} $$
(42)

Now, from eq. (41) and (42).

$$ \frac{{K_{1} (1 + K_{2} s)}}{{(1 + K_{3} s)}} = v^{\prime}_{0} + v^{\prime}_{1} s + v^{\prime}_{2} s^{2} $$
(43)

Now, cross multiply Eq. (43) and compare identical powers of ‘s’ from \(s^{0}\) to \(s^{2}\).

$$ K_{1} = v^{\prime}_{0} $$
(44)
$$ K_{1} K_{2} = v^{\prime}_{0} K_{3} + v^{\prime}_{1} $$
(45)
$$ K_{3} v^{\prime}_{1} + v^{\prime}_{2} = 0 $$
(46)

By solving eq. (44), (45), and (46), the compensator controller parameters are determined.

Step 5: The closed-loop transfer function of a controlled system with the controller designed using the original system is represented as follows:

$$ G_{cl}^{G} (s) = \frac{{G_{c} (s)G(s)}}{{1 + G_{c} (s)G(s)}} $$
(47)

\(G_{c} (s)\) refer to the PID controller or compensator designed using the original system.

Step 6: Decrease the original system \(G(s)\) to use the aimed process. Later, repeat steps 3 and 4. The closed-loop transfer function of a controlled system with the controller designed via the diminished model is represented as follows:

$$ G_{cl}^{R} = \frac{{R_{cr} (s)G(s)}}{{1 + R_{cr} (s)G(s)}} $$
(48)

\(R_{cr} (s)\) refer to a controller or compensator designed using the reduced model.

5 Test systems and validation of results

The performance of the proposed technique is assessed and compared to existing reduction strategies by computing error indexes such as integral square error (ISE), H∞ norm, root mean square error (RMSE), integral absolute error (IAE), and impulse response energy (IRE). The suggested approach’s utility and efficacy are investigated in different case studies from the literature. The practical application of the proposed technique is demonstrated by building a PID controller and compensator controller for an eighth-order flexible-missile control model and a sixth-order realistic open-loop helicopter engine with a fuel control system to achieve the desired closed-loop behavior. The lower the value of the error indices for a specific simplified model, the better the approximation of the original plant. The comparative analysis of the presented algorithm and other reduction algorithms is conducted based on several error indices. The findings indicate that the proposed approach exhibits superior performance and is on par with different widely-used model reduction strategies.

5.1 The performance error indexes are considered as follows

$$ ISE = \int\limits_{0}^{\infty } {[y(t) - y_{k} (t)]^{2} } dt $$
(49)
$$ IRE = \int\limits_{0}^{\infty } {[h(t)]^{2} } dt $$
(50)
$$ IAE = \int\limits_{0}^{\infty } {\left| {y(t) - y_{k} (t)} \right|} dt $$
(51)

Let the error system function is defined as follows:

\(E(s) = G(s) - R_{k} (s)\).

Then, the \(H_{\infty }\) norm of the error system is defined as follows:

$$ \left\| {E(s)} \right\|_{\infty } = \left\| {G(s) - R_{k} (s)} \right\|_{\infty } $$
(52)

where \(y(t);y_{k} (t)\) are unit step responses of the existing system abated model, respectively, and \(h(t)\) is the impulse response of a system, \(G(s)\) is the original system function in the s-domain, and \(R_{k} (s)\) is the reduced model transfer function in the s-domain. The RMSE of Bode’s response of existing and reduced systems at each frequency \(\omega\) in a given frequency range of interest \(\omega = [\omega_{Low} ,\omega_{High} ]\) is computed concerning the number of frequency samples N as follows:

$$ RMSE_{Gain} = \sqrt {\frac{{\sum\limits_{i = 1}^{N} {\left( {\left| {G(j\omega_{i} )} \right|_{dB} - \left| {R_{k} (j\omega_{i} )} \right|_{dB} } \right)^{2} } }}{N}} $$
(53)

where \(\left| {G(j\omega_{i} )} \right|_{dB}\) and \(\left| {R_{k} (j\omega_{i} )} \right|_{dB}\) are the magnitude of the original higher-order system and reduced model, respectively.

Test System 1: A 9th-order system that is extensively studied in engineering and sciences by several researchers is adopted from the literature [39] as

$$ G(s) = \frac{{s^{4} + 35s^{3} + 291s^{2} + 1093s + 1700}}{{s^{9} + 9s^{8} + 66s^{7} + 294s^{6} + 1029s^{5} + 2541s^{4} + 4684s^{3} + 5856s^{2} + 4620s + 1700}} $$
(54)

The Hankel singular values of the original system are

0.8277 0.4769 0.1971 0.0613 0.0151 0.0032 0.00151 0.00048 0.0005]. The first three singular values are significantly larger than the remaining ones, so a reduced model is retrieved via truncating states corresponding to those, as these states decay more quickly and become insignificant. The state-space model of the abated model retrieved via conventional balanced truncation [32, 33] was obtained as follows:

$$ R_{BTM} (s) = \frac{{0.1405s^{2} - 0.8492s + 1.8814}}{{s^{3} + 1.575s^{2} + 3.5235s + 1.7169}} $$
(55)

The steady-state gain of the original plant (54) is computed as 1, and the steady-state gain of the abated model (55) via balanced truncation is 1.0958.

To achieve an accurate overall response (transient and steady-state) approximation of the original system, the reduced model should maintain a few starting time moments (for excellent steady-state accuracy) and a few Markov parameters (for good transient accuracy). The abated model numerator polynomial is obtained by matching the initial moments as discussed in Section 3.2, such that the model retains the first-time moment and few Markov parameters. Now, using eq. (17–27), the abated model numerator polynomials are obtained as follows:

\(n_{2} (s) = - 0.8492s + 1.7169\) with \(T = 1,M = 1\).

\(n_{2} (s) = 1.7169\) with \(T = 1,M = 2\).

Corresponding diminished models are obtained as follows (figures 5, 6):

$$ R_{BTM\_MM}^{T = 1,M = 1} (s) = \frac{ - 0.8492s + 1.7169}{{s^{3} + 1.575s^{2} + 3.5235s + 1.7169}} $$
(56)
$$ R_{BTM\_MM}^{T = 1,M = 2} (s) = \frac{1.7169}{{s^{3} + 1.575s^{2} + 3.5235s + 1.7169}} $$
(57)
Figure 5
figure 5

Step response comparisons of the original plant and abated models by recent proposals for test system 1.

Full size image
Figure 6
figure 6

Frequency response comparisons of the original plant and abated models by recent proposals for test system.

Full size image

Discussion: Figure 5 compares the step response of the original plant, diminished models returned from the suggested method, and models recovered from newly proposed algorithms [11, 32, 37, 38, 40, 41] in the literature. Similarly, figure 6 compares the frequency responses. Figures 5 and 6 show that the suggested reduced model closely mimics the plant time and frequency responses across the entire frequency range. Table 2 compares the findings of the recommended strategy to various standard techniques in the literature [11, 25, 32, 35, 37–39, 40, 41] in terms of numerous performance indices such as ISE, IAE, IRE, RMSE, and H∞ error. This table indicates that the proposed technique yields the lowest error indices, which are lower than the error values produced by most technologies in the recent past.

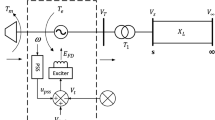
Test System-2: The practical viability of the proposed approach is illustrated using the single-machine infinite-bus (SMIB) power system model from [45,46,47,48,49]. The SMIB power system’s detailed block diagram, mathematical model, and parameter values for different operating points are considered from [45, 49].

The \(x_{T}\) and \(x_{L}\) in the figure 7 represent the reactance of the transformer and the transmission line, respectively. The \(V_{T}\) and \(V_{L}\) are the generator terminal and infinite bus voltages, respectively. The system comprises a three-phase 160-MVA synchronous machine with an automatic excitation control system. The Hankel singular values of the SMIB power system model are [12.1598 10.6553 2.4869 1.0555 0.1337 0.0052 0.0018 0.0007 0.0002 0.0000]

$$ \sum\limits_{i = 5}^{10} {\sigma_{i} = 0.1416 < \sigma_{4} = 1.0555} $$
(58)
Figure 7
figure 7

Single-machine infinite-bus (SMIB) power system.

Full size image

The fourth-order reduced model gives a good approximation of the original system.

$$ R_{4} (s) = \frac{1}{{\overline{{D_{4} (s)}} }}\left[ {\begin{array}{*{20}c} {B_{11} (s)} & {B_{12} (s)} \\ {B_{21} (s)} & {B_{22} (s)} \\ \end{array} } \right] $$
(59)

The fourth-order reduced models obtained using the proposed reduction technique are obtained as follows.

$$ B_{11} (s) = 2.519s^{2} - 9.0997s - 66.4711 $$
$$ B_{12} (s) = 29.09s^{2} + 57.9743s + 79.3593 $$
$$ B_{21} (s) = 2.6906s^{2} + 2.9673s + 29.9846 $$
$$ B_{22} (s) = - 1.0969s^{2} - 7.7939s - 2.3767 $$

The common denominator is obtained as follows:

$$ \overline{{D_{4} (s)}} = s^{4} + 1.9889s^{3} + 14.1829s^{2} + 17.3303s + 30.9775 $$

Discussion: The relative Bode graphs of the original two-area power system output 1 and 2, the retrieved diminished models via the proposed method, and reduced models attained using [32, 36, 38, 46,47,48, 57] are exemplified in figures 8 and 9, respectively. In table 3, the root mean squared error between Bode’s graph of abated models and the existing system is given, and the integral squared error between the original system and diminished models subject to a step input is also provided. It is evident from the Bode graph comparisons of the reduction methodologies that the suggested method applied to a given power system retrieves a diminished system that closely matches the frequency response of the original system in the low and medium frequency ranges and approximately in the high-frequency range. The error measures in table 3 validate the persuasiveness of the proposed approach, which gives the lowest error values, so the proposed conventional method can be considered an alternative to system order reduction compared to some standard techniques.

Figure 8
figure 8

Bode magnitude diagram of the original system and 4th order reduced models for system output1.

Full size image
Figure 9
figure 9

Bode magnitude diagram of the original system and 4th order reduced models for system output 2.

Full size image
Table 3 Performance comparison of the original plant and various abated models from recent literature for test system 2.
Full size table

Test System-3: Consider a sixth-order stable, practical open-loop helicopter engine, including a fuel control system for the compensator design discussed in [16].

$$ G(s) = \frac{{248.05s^{4} + 1483.3s^{3} + 91931s^{2} + 468730s + 634950}}{{s^{6} + 26.24s^{5} + 1363.1s^{4} + 26803s^{3} + 326900s^{2} + 859170s + 528050}} $$
(60)

The closed-loop reference model to design a compensator controller is considered from [16, 51,52,53]

$$ M(s) = \frac{4}{{s^{2} + 4s + 4}} $$
(61)

Open loop reference model computed using (29) as follows:

$$ M_{open} (s) = \frac{4}{s(s + 4)} $$
(62)

5.2 Design of compensator using the original system

The arbitrary controller transfer function is

$$ C(s) = \frac{{M_{{open}} (s)}}{{G(s)}} = \frac{{2.112e06 + 3.437e06s + 1.308e06s^{2} + 107212s^{3} + 5452s^{4} + 105s^{5} + 4s^{6} }}{{s(2.54e06 + 2.51e06s + 836454s^{2} + 9.786e04s^{3} + 2476s^{4} + 248.1s^{5} )}} $$
(63)

The general structure of the compensator is

$$ C_{COM} (s) = \frac{{K_{1} (1 + K_{2} s)}}{{s(1 + K_{3} s)}} $$
(64)

To determine the unknown controller parameters, it is required to match the initial three-time moments (T) of (63) with (64) as follows:

$$ \frac{{K_{1} (1 + K_{2} s)}}{{s(1 + K_{3} s)}} = \frac{{2.112e06 + 3.437e06s + 1.308e06s^{2} }}{{s(2.54e06 + 2.51e06s + 836454s^{2} )}} $$
(65)
$$ \frac{{K_{1} (1 + K_{2} s)}}{{(1 + K_{3} s)}} = 0.8316 + 0.5313s - 0.2841s^{2} $$
(66)

Now, by cross multiplying eq. (66) and comparing identical powers of ‘s’ from \(s^{0}\) to \(s^{2}\) the compensator parameters, they are computed as follows:

\(K_{1} = 0.8316\), \(K_{2} = 1.1735\) and \(K_{3} = 0.5347\).

The compensator transfer function is obtained as follows:

$$ G_{COM} (s) = \frac{0.976s + 0.8316}{{s(0.5347s + 1)}} $$
(67)

The transfer function of a closed-loop controlled system with the compensator is designed using an original plant and can be obtained as

$$ G_{cl}^{G} (s) = \frac{{G_{COM} (s)G(s)}}{{1 + G_{COM} (s)G(s)}} $$
(68)

\(G_{COM} (s)\) is the compensator designed using the original system.

5.3 Design of compensator using the proposed reduced model

The third-order reduced model via the proposed BTM and matching moments was computed as follows:

$$ R_{\Pr op} (s) = \frac{{356.0219s^{2} - 93.9535s + 1484.0947}}{{s^{3} + 2.1561s^{2} + 1018.9077s + 1234.2329}} $$
(69)

The arbitrary controller transfer function is computed as

$$ C(s) = \frac{{M_{open} (s)}}{{R_{\Pr op} (s)}} = \frac{{4937 + 4076s + 8.624s^{2} + 4s^{3} }}{{s(5936 + 1108s + 1330s^{2} + 356s^{3} )}} $$
(70)

To determine the unknown controller parameters, it is required to match the initial three-time moments (T) of (63) with (70) as follows:

$$ \frac{{K_{1} (1 + K_{2} s)}}{{s(1 + K_{3} s)}} = \frac{{4937 + 4076s + 8.624s^{2} }}{{s(5936 + 1108s + 1330s^{2} )}} $$
(71)
$$ \frac{{K_{1} (1 + K_{2} s)}}{{(1 + K_{3} s)}} = 0.8316 + 0.5313s - 0.2841s^{2} $$
(72)

Now, by cross-multiplying eq. (72) and comparing identical powers of ‘s’ from \(s^{0}\) to \(s^{2}\) the compensator parameters, they are computed as follows:

\(K_{1} = 0.8316\), \(K_{2} = 1.1735\) and \(K_{3} = 0.5347\).

The compensator transfer function is obtained as follows:

$$ R_{COM} (s) = \frac{0.976s + 0.8316}{{s(0.5347s + 1)}} $$
(73)

The transfer function of a closed-loop controlled system with the compensator is designed using an abated model obtained by using

$$ G_{cl}^{R} (s) = \frac{{R_{COM} (s)G(s)}}{{1 + R_{COM} (s)G(s)}} $$
(74)

\(R_{COM} (s)\) is the compensator designed using the proposed reduced system.

Discussion: The figure 10 displays the closed-loop system plant’s step response, incorporating compensators created by various model reduction methods. These compensators are computed using the natural plant and decreased models; it is evident that the characteristics of the closed-loop regulated systems closely reflect those of the reference model in transient and steady-state areas. Table 4 displays the time-domain characteristics of the closed-loop plants with compensators. The time-domain properties of the closed-loop plant with the compensator developed using the presented reduced model are nearly identical to those of the closed-loop system with the compensator obtained using the original plant, and these specifications are almost similar to those of the reference model. As a result, the proposed approach generates lower-order models and controllers, which are especially valuable for quick comprehension of large-scale systems, simplifying controller design, cutting computing complexity, allowing for faster simulations, and reducing storage space requirements.

Figure 10
figure 10

Comparison of step responses of closed-loop controlled systems for test system 3.

Full size image
Table 4 Qualitative comparison of closed-loop controlled system.
Full size table

Test System 4: Consider the flexible-missile control model and the rigid body loop given by an eighth-order transfer function for the design of the PID controller design so that it provides a natural frequency of 10 rad/sec and a damping ratio of 20 [40]

$$ \begin{aligned} G(s) = & \frac{{ - s^{6} + 306s^{5} - 4.96 \times 10^{4} s^{4} + 3.577 \times 10^{6} s^{3} - 6.303 \times 10^{7} s^{3} }}{{s^{8} + 53s^{7} + 3.05 \times 10^{4} s^{6} + 1.375 \times 10^{6} s^{5} + 1.839 \times 10^{8} s^{4} + 5.232 \times 10^{9} s^{3} + 3.422 \times 10^{{11}} s^{3} }} \\ & \frac{{ - 1.246 \times 10^{{10}} s^{2} + 5.906 \times 10^{{11}} }}{{ + 2.823 \times 10^{{12}} s^{2} + 1.442 \times 10^{{14}} }} \\ \end{aligned} $$
(75)

The closed-loop reference model to design a PID controller is considered from [40]

$$ M(s) = \frac{100}{{s^{2} + 400s + 100}} $$
(76)

The open-loop reference model is computed using (29) as follows:

$$ M_{open} (s) = \frac{100}{{s(s + 400)}} $$
(77)

5.4 PID controller design using the original system

The arbitrary PID controller transfer function was obtained using eq. (75) and (77) as follows:

$$ C(s) = \frac{{M_{{open}} (s)}}{{G(s)}} = \frac{{ - 1.442e16 - 2.823e14s - 3.422e13s^{2} - 5.232e11s^{3} - 1.839e10s^{4} - 1.375e08s^{5} - 3.05e06s^{6} - 5299s^{7} - 100s^{8} }}{{s( - 2.362e14 - 4.393e12s + 3.767e10s^{2} - 1.368e09s^{3} + 1.626e07s^{4} - 72800s^{5} + 94s^{6} + s^{7} )}} $$
(78)

The general structure of the PID controller is

$$ C_{PID} (s) = \frac{{K_{i} + K_{p} s + K_{d} s^{2} }}{s} $$
(79)

To determine the unknown controller parameters, it is required to match the initial three-time moments (T) of (78) with (79) as follows:

$$ \frac{{K_{i} + K_{p} s + K_{d} s^{2} }}{s} = \frac{{ - 1.442e16 - 2.823e14s - 3.422e13s^{2} }}{{s( - 2.362e14 - 6.167e11s + 7.775e10s^{2} )}} $$
(80)
$$ K_{i} + K_{p} s + K_{d} s^{2} = 61.039 + 2.3293s + 60.1985s^{2} $$
(81)

Now, comparing the identical powers of ‘s’ from \(s^{0}\) to \(s^{2}\) the PID controller parameters are computed as follows:

\(K_{p} = 2.3293\), \(K_{i} = 61.0396\) and \(K_{d} = 0.1985\).

The PID controller transfer function is obtained as

$$ G_{PID} (s) = \frac{{61.0396 + 2.3293s + 0.1985s^{2} }}{s} $$
(82)

The transfer function of a closed-loop controlled system with a PID controller is designed using the original system as follows:

$$ G_{cl}^{G} (s) = \frac{{G_{PID} (s)G(s)}}{{1 + G_{PID} (s)G(s)}} $$
(83)

\(G_{PID} (s)\) is the controller designed using the original system.

5.5 PID controller design using the proposed reduced system

The second-order diminished model via the proposed method, as discussed in Sections 3.1 and 3.2, was computed as follows:

$$ R_{Prop} (s) = \frac{ - 0.0970s + 2.4796}{{s^{2} + 0.9322s + 605.4218}} $$
(84)

The arbitrary PID controller transfer function was obtained using eq. (75) and (84) as follows:

$$ \frac{{K_{i} + K_{p} s + K_{d} s^{2} }}{s} = \frac{{ - 6.054e - 04 - 93.22s - 100s^{2} }}{{s(991.8 + 36.32s + 0.097s^{2} )}} $$
(85)
$$ K_{i} + K_{p} s + K_{d} s^{2} = 61.0403 + 2.3292s + 0.1921s^{2} $$
(86)

Now, comparing the identical powers of ‘s’ from \(s^{0}\) to \(s^{2}\) the PID controller parameters are computed as follows:

\(K_{p} = 2.3292\), \(K_{i} = 61.0403\) and \(K_{d} = 0.1921\)

The PID controller transfer function is obtained as

$$ R_{PID} (s) = \frac{{0.1921s^{2} + 2.3292s + 61.0403}}{s} $$
(87)

The transfer function of a closed-loop controlled system with a PID controller is designed using the original system as follows:

$$ G_{cl}^{R} (s) = \frac{{R_{PID} (s)G(s)}}{{1 + R_{PID} (s)G(s)}} $$
(88)

\(R_{PID} (s)\) is the controller designed using the reduced system.

Discussion: The figure 11 compares the temporal response of the closed-loop transfer function of the original plant with PID controllers that were calculated by approximated systems with the reference system. It is evident that the features of the closed-loop controlled systems closely reflect those of the reference model in both transient and steady-state areas. Table 5 displays the time-domain characteristics of the closed-loop plants with controllers. The time-domain properties of the closed-loop plant with the controller created using the presented reduced model are nearly identical to those of the closed-loop system with the controller designed using the original plant, and these specifications are roughly equivalent to the reference models. Consequently, the proposed approach produces lower-order models and controllers, which are particularly effective for rapid comprehension of high-dimensional plants, controller design reduction, computation complexity reduction, allowing for better simulations, and memory space reduction.

Figure 11
figure 11

Closed-loop controlled system step response comparison of different techniques for test system 4.

Full size image
Table 5 Qualitative comparison of closed-loop controlled system.
Full size table

6 Conclusion and future scope

A novel approach has been put forward for simplifying complex systems on a large scale. The suggested methodology maintains the benefits of the balanced truncation strategy while also considering the static and transient reactions of the smaller plant’s higher-order system (HOS). Furthermore, it effectively overcomes the constraints imposed by the balanced truncation methods. The proposed approach demonstrates improved accuracy in analyzing real-time plant data compared to current methodologies. Furthermore, the analysis of reaction times indicates that the simplified models generated by the proposed technology provide a very accurate estimation of the behavior of large-scale systems. It is evident that the suggested methodology is suitable for single-input, single-output (SISO) models and yields favorable results for higher-order multi-variable systems. The use of the proposed reduced-order model extends to the construction of controllers for plants of significant size. It has been observed that the time domain specifications of the closed-loop system derived from the reduced-order model closely resemble those obtained from the higher-order system. The use of simplified order systems in controller design renders it more approachable compared to the utilization of large-scale systems in controller design. Hence, the suggested methodology can optimize controllers’ designs for many categories of expansive real-time systems. Furthermore, the approach described herein may include Order reduction of multi-input and multi-output systems, Discrete-time systems, linear interval systems, and Controller implementation.