1 Introduction

The exact analysis of large-order system is actually very complex and tedious. The reduction of any higher order system is basically making the analysis, synthesis along with simulation much easier for any real system. Model order reduction [MOR] theory plays an important role in case of mathematical modeling of a physical system, such as for designing various power system components like AVR or power stabilizers etc. The basic guidelines are that working with original mathematical model of any physical system, which have higher order system controller, compensators, or analysis of stability is difficult and the total scenario becomes simple and easier if anyone deal with reduce model of the original system. Bendjeghaba [1] proposed a reduction method which is based on optimization technique of the actual system and its lower order model. But this method has a disadvantage that the higher system is stable but the obtained reduced order model may not be stable. For overcoming the challenge associated with stability problem and Ahmed in their paper [2], Chen [3], Choudhary [4] also implement different methods based on optimization and stability criteria. Some other methods have been illustrated by Shamash [5] and Chen [6] describes about stability equation method, Gutman et al. [7] for reduction of model order which always confirms the stability of the reduced system without proposing any stability criteria. Later on, some combined techniques are also involved in the field of reduction such as denomination reduction by stability criteria is proposed by Shamesh [7], Chen et al. [8], Wan [9] and numerator is lowered by other techniques [7,8,9]. The Routh stability method initially developed by Shamesh describes the limitation that the dominant poles are unable to preserve stability for non-minimum-phase-system [10]. In later stage, it is shown that the reduction method by using stability equations is also inapplicable for non-minimum phase systems [11, 12].

In this context, moment matching algorithm is a popular approach described in [11]. Routh approximation becomes one of the most popular methods in terms of MOR [12, 13]. In comparison with other reduction procedures, Routh approximation is featured with simplicity in terms of computation, prosperity of access and the potential to hold the stability of original model. To overwhelm the above-mentioned limitations, numerous collective techniques are projected based on these methods [14,15,16,17,18,19]. The Routh approximation is much authenticated method but still it fails to maintain stability sometimes, in particular, for working with large order systems. Differential technique [20] is mathematically very simple and computationally very easy to develop the reduced model. The stability problem associated with differential technique can be overcome by using Pole clustering techniques [21]. For pole-clustering technique the order can be reduced up to third-order or more and second-order model not possible to develop and this limitation can be overcome by using modified pole clustering techniques [22]. Another method of model order reduction is developed with factor division algorithm and Eigen values of system matrix [23]. The drawback of this technique is that the obtained reduced model sometimes became unstable. Later on, balance truncation and Markov parameters-based algorithms are also successfully implemented in the model reduction theory [24]. The kind of limitation associated with truncation technique is such as its unsteadiness for large model with order higher than three.

In recent days’ research, various optimization techniques are being used [25]. Popular optimization techniques increase the mathematical complexity and also, they have a time bound factor. During last few decades, numerous methods for reduction of model in larger-order systems are designed in the time domain, such as method of aggregation [26], singular norms-perturbation [27], Arnoldi [28], Krylov identified subspace [29, 30], and Hankel norm approximation method [31]. Classically, these methods suggest good estimate but these approaches also have some limitations such as gain difference in steady-state between the actual plant and its reduced models, sometimes it fails to keep the constancy of the actual model and error boundaries.

In existing power system, the primary concern of reactive power generation using an alternator is related to generator excitation control with the help of AVR. The AVR in an alternator basically regulates the output terminal voltage at a certain level. In this context, the damping of output terminal voltage following instabilities is of highly alarming because it can really affect the safety of the whole power system. The alternator excitation system is in directive to preserve alternator voltage and to control the flow of reactive power using AVR. Hence, with the development in the design of reduced order controller for AVRs as well as the growing difficulty of huge interconnected power system, fluctuations may endure for a prolonged period and uncertainty may arise subsequent system disturbances [32]. The authors in [9, 16] have highlighted that AVR model design and further its reduced model developed with improved model-order-reduction [MOR] technique in simple way using optimization techniques.

The first objective of this paper is to design the reduce order model using proposed technique and other objective of this research paper is to design an algorithm for controller for the large AVR system using its proposed stable reduced order model. In literature there are various controller design available based on Routh & Mihailov criteria, Balanced truncation method reduction approaches [12, 33]. But these methods have limitations such as rising simulation time or storage memory requirements more. These limitations may overcome by using several mixed techniques balanced state representation, modified pole clustering, Pade approximation [34,35,36], Ibrahim Kaya [37] paper describes the application of reduce order model technique and controller design in domain of power system. Sikandara and Prasad [40] paper involves differentiation-based khartinov theorem application and optimization techniques for reduction and Gupta [33] uses hybrid approach for developing reduced models. Proposed technique involves large computational complexity and also time consuming due to large iteration process of optimization.

The features of this work are as follows: (i) a unique method with derivation of a generalized formula by combining Differential and Routh techniques is developed for reduction of a higher order system to a lower order system; (ii) the developed method is computationally simple, less time-consuming compare to other approximation techniques; (iii) the proposed method reduces the steady-state error of the reduced model in comparison with other existing ones; (iv) the combined method enhances the stability of the reduced model. (v) The proposed method is applied to an AVR system for its functionality checking and performance evaluation is made by comparing with other existing methods. The uniqueness of the work is that a combined order reduction scheme is devised such that the higher order system is reduced to second-order one and requires only two variables to evaluate online.

2 Brief overview of order reduction techniques

2.1 Requirement of order reduction from generalized higher order models

A generalized transfer function model of a typical higher order system with mth and nth order of numerator and denominator, respectively, is represented by Eq. (1) as

$$G(s) = \frac{{a_{1} + a_{2} s + a_{3} s^{2} + \cdots + a_{m} s^{m} }}{{b_{1} + b_{2} s + b_{3} s^{2} + \cdots + b_{n} s^{n} }}$$
(1)

where the behavior of the system depends on the values of each of the coefficients a1, a2… am and b1, b2, …, bn and the m and n values are large enough for higher order complex system. In general, these coefficients need not always remain constant with respect to time, accordingly processing all of these large coefficients and designing their values for interacting different scenarios of changing input to produce the desired output is a very tedious and computationally intensive job, and all these require a high-end processor. Thus, as an alternative, different model order reduction techniques are proposed so that the system can be realized, maintained and processed in an efficient and less computational way.

2.2 Brief description of different reduced order techniques

2.2.1 Differential approach

The differential approach is first introduced by Gutman [7]. The procedure is based on reduction of the order of polynomials of numerator and denominator with help of differentiation. The numerator and denominator polynomials of any higher order system is differentiated consecutively until the transfer function in terms of its coefficients for the desired reduced order model is produced.

2.2.2 Routh array technique

The Routh stability criterion is the foundation of the Routh array (RA) approach. This method of lowering the model order of a high order system depends only on the array, expressed in the following format, starting with the coefficients of the provided polynomial.

$$a_{1} + a_{2} s + a_{3} s^{2} + \cdots + a_{m} s^{m}$$
(2)

The Routh matrices for the polynomials that make up the numerator and denominator of Eq. (2) are formed as per general Routh table formation.

In Routh table odd coefficients are made up the first, third, fifth, etc. rows, while even coefficients are made with the second, fourth, sixth, etc. rows. The first two rows are produced using the provided transfer function, and the other rows are calculated using the provided equation [21]

$$C_{ij} = \, \frac{{C_{i \, - 2,j + 2} {-}\left( {C_{i - 2,1} x \, C_{i - 1,j + 1} } \right)}}{{C_{i + 1,1} }}\quad {\text{For }}i \ge m \,$$
(3)

2.2.3 Pole clustering technique

Higher-order systems are divided into two distinct clusters using a combination of actual poles and imaginary poles in pole clustering approaches. A new cluster centre is then established with the aid of some numerical operations, and a new reduced order model of a third-order system is created while maintaining the original system characteristics. The details of splitting of polynomials into clusters and their reduction schemes are elaborated in [28].

2.2.4 Optimization techniques

Particle swarm optimization (PSO), Big-bang algorithm, Genetic algorithm, simulated annealing approach etc. various optimization techniques are adopted for model order reduction approach. Using different optimization technique approximates the coefficients of reduced model to provide stable response. But optimization techniques rely on large number of iterations which makes the analysis of reduction techniques complex and more over time consuming. Though optimization techniques are latest observations still it is not popular in case of reduction technique due its overburdening system feature.

2.3 Derivation of reduced order model using proposed differential-Routh technique

The advantages of both differential approach and Routh array technique are extracted and are utilized in this proposed technique. Differential method is simplest technique in the field of MOR, but this method also suffers from serious limitation of steady-state error. Routh approximation offers stability of MOR. But this method becomes complicated for nonlinear systems and for very large systems. The proposed technique combines the advantages of both methods having less complexity. By virtue, differential technique has the capability to reduce the order of the system from high to lower and Routh technique can improve system stability. The properties of both these techniques are extracted in this proposed work where initial steps are associated with differential technique to reduce computational complexity while later steps utilizes Routh technique to move the system more stable one without steady state error.

Let us consider a system having transfer function G(s) of same order as described in Eq. (1). The proposed method is applicable to systems having order of numerator (n) greater than four (minimum one step of differentiation and One step Routh for getting stable reduced model for stable reduced order) than that of its denominator. In order to realize the proposed Differential-Routh (DR) method, the following equations are derived and described in stepwise manner.

Rearranging the denominator polynomials of G(s) of Eq. (1) in reciprocate form, Eq. (2) can be derived as

$$\begin{gathered} D\left( s \right) \, = b_{n} + b_{n - 1} s^{n - n + 1} \cdots + b_{3} s^{n - 2} + b_{2} s^{n - 1} + b_{1 } s^{n} \hfill \\ D\left( s \right) = b_{1} + b_{2} s^{2} + b_{3} s^{3} + \cdots + b_{n} s^{n} \hfill \\ \end{gathered}$$
(4)

Differentiating the reciprocated denominator 2 times, Eqs. (5) and (6) are obtained

$$D1(s) = 0 + b_{n - 1} (1)s^{0} \cdots + b_{3} (n - 2)s^{n - 3} + b_{2} (n - 1)s^{n - 2} + b_{1 } (n)s^{n - 1}$$
(5)
$$D2(s) = 0 + 0 \cdots + b_{3} (n - 2)(n - 3)s^{n - 4} + b_{2} (n - 1)(n - 2)s^{n - 3} + b_{1 } n(n - 1)s^{n - 2}$$
(6)

Simplifying Eqs. (4)–(6) the generalized equation to get the denominator polynomial upto 4th order is derived as –

$$D^{\prime}(n - 4)(s) = \frac{{b_{1 } n!s^{0} }}{(n - 4)!} + \frac{{b_{2} (n - 1)!s^{1} }}{(n - 5)!} + \frac{{b_{3} (n - 2)!s^{2} }}{(n - 6)!} + \frac{{b_{4} (n - 3)!s^{3} }}{(n - 7)!} + \cdots + \frac{{b_{n - 4} (3)!s^{n - 4} }}{1!}$$
(7)

Further rearranging Eq. (6) in normalization form, it can be re-written as

$$D(n - 4)(s) = 0 + \frac{{b_{n - 4} (3)!s}}{1!} + \cdots + \frac{{b_{3} (n - 2)!s^{n - 6} }}{(n - 6)!} + \frac{{b_{2} (n - 1)!s^{n - 5} }}{(n - 5)!} + \frac{{b_{1 } n!s^{n - 4} }}{(n - 4)!}$$
(8)

Rearranging the denominator of Eq. (8) and applying Routh-array technique, Routh table having second-order denominator is formed as represented in Table 1 format.

Table 1 Routh-array for denominator
Full size table

The first, third, fifth, etc. rows consist of odd coefficients while the second, fourth, sixth, etc. rows are with even coefficients. The coefficients of first two rows are generated from Eq. (8) and remaining rows are calculated using row 1 and 2:

$$C_{ij} = \, \frac{{C_{i \, - 2,j + 2} {-}\left( {C_{i - 2,1} x \, C_{i - 1,j + 1} } \right)}}{{C_{i + 1,1} }}\quad {\text{For }}i \ge 3\quad {\text{and}}\quad i \, \le \left[ {\frac{{\left( {n - 1 + 3} \right)}}{2}} \right]$$

In a very similar manner, the numerator polynomial is reduced to represent in the form of Eq. (8) as

$$N^{\prime}(m - 4)(s) = \frac{{b_{1 } m!s^{0} }}{(m - 4)!} + \frac{{b_{2} (m - 1)!s^{1} }}{(m - 5)!} + \frac{{b_{3} (m - 2)!s^{2} }}{(m - 6)!} + \frac{{b_{4} (m - 3)!s^{3} }}{(m - 7)!} + \cdots + \frac{{b_{n - 4} (3)!s^{m - 4} }}{1!}$$
(9)

Thus, the reduced transfer function of the system is represented as follows:

$$R\left( S \right) = \frac{{c_{0} + c_{1} s}}{{d_{0} + d_{1} s^{{}} + d_{2} s^{2} }}$$
(10)

where the coefficients \(c_{0}\), \(c_{1}\) and \(d_{0} ,d_{1} ,d_{2}\) are obtained from Routh table for numerator and denominator part in the conventional way, respectively. Thus, a larger order system, represented by Eq. (1), is reduced to a lower order model as represented by Eq. (10) using differential-Routh method.

The performance of the derived lower order model is to be checked now with various stability analysis methods. The errors are to be estimated and to be compared with other existing reduction techniques in order to prove its efficacy.

2.3.1 Case study 1

If the numerator of a transfer function in a control system has only a constant term (i.e., no s-term, where s is the Laplace variable), it indicates that the transfer function has a DC gain or steady-state gain. In this case, the transfer function can be represented as:

$$\begin{gathered} {\text{Numerator}}: \, k{\text{ and Denominator}}: \, \left( {s + a} \right)\left( {s + b} \right)\left( {s + c} \right)\hfill \\ \qquad \cdots \left( {s \, + \, n} \right), \hfill \\ {\text{Where }}{\prime} k{\prime} {\text{ is the constant gain and }}\hfill\\ \qquad \left( {s + a} \right)\left( {s + b} \right)\left( {s + c} \right)\quad \left( {s + n} \right)\hfill\\ \qquad {\text{ represents the poles of the system}}{.} \hfill \\ \end{gathered}$$

If the numerator of the transfer function only contains a constant term, the reduced numerator polynomial using the differentiation method will be zero. This is because the differentiation of a constant results in zero, and setting s to zero in the resulting polynomial yields the steady-state response of zero. So, it is another limitation of differential method of reduction.

2.3.2 Case study 2

If a row in the Routh-Hurwitz array becomes all zeros, it indicates that there are roots of the characteristic equation with real parts equal to or larger than zero. In control system analysis, this situation could imply that the system is marginally stable or unstable. When working with reduced-order modeling in control systems, the intention is to capture dominant behavior of the system ignoring less significant dynamics.

Here's a general process to determine a reduced-order model when a row in the Routh-Hurwitz array becomes all zeros:

  • Identify the problematic pole: the row of zeros in the Routh-Hurwitz array corresponds to a pole of the system's transfer function that has a real part equal to zero or greater. This pole is a cause of instability or marginal stability.

  • Remove the dominant unstable/marginal mode: the unstable or marginally stable mode is generally the dominant mode causing the instability. If you're looking to create a reduced-order model, you can neglect this mode and consider the rest of the modes.

  • Formulate the reduced-order transfer function: the reduced-order transfer function will include all poles except the dominant unstable/marginal mode. This can be done by factoring out the problematic pole from the original transfer function.

  • Create the reduced-order state-space model (if needed): if you're working with state-space representations, you'll need to derive the reduced-order state-space model from the reduced-order transfer function. This involves finding a state-space realization that corresponds to the reduced-order transfer function. Remember that the reduced-order model might not capture all aspects of the original system's behavior, especially if the neglected poles contribute significantly in certain operating conditions or frequency ranges. It's a trade-off between model complexity and accuracy.

Finally, always consider the context of your specific control system and its requirements when determining a reduced-order model. In some cases, it might be better to address the instability directly rather than relying on a reduced-order approximation.

3 MOR applied to automatic voltage regulator (AVR) of an alternator

3.1 Generalized schematic of an automatic voltage regulator (AVR)

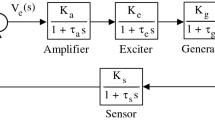
The role of AVR in synchronous generator is fundamentally to regulate the voltage magnitude of a synchronous generator at a specific level. The schematic diagram of AVR system is shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of automatic voltage regulator system of an alternator

Full size image

The terminal voltage of an alternator varies in proportion with the change in reactive-power and is sensed using potential transformer (PT). The PT output is rectified and compared with reference voltage to generate error in voltage. This error is then processed and fed to the excitation controller of the AVR system. The generation of reactive-power is controlled to a new equilibrium by changing the output voltage of the alternator to the desired value.

3.2 Derivation of transfer function for AVR model

For developing the general model of AVR, major components like amplifier, exciter, generator and sensor etc. are used, as shown in Fig. 2. For simplicity, considering four basic components of the AVR system like (i) amplifier, (ii) exciter, (iii) generator, (iv) sensor, the transfer function model of AVR is represented as.

Fig. 2
figure 2

Block diagram of AVR

Full size image

Considering stabilizer part, the closed-loop transfer function became-

$$\frac{{V_{t} (s)}}{{V_{{\rm ref}} (s)}} = \frac{{K_{A} K_{E} K_{G} K_{R} K_{F} (1 + sT_{R} )(1 + sT_{F} )}}{{[(1 + sT_{A} )(1 + sT_{E} )(1 + sT_{G} )(1 + sT_{R} )(1 + sT_{F} ) + K_{A} K_{E} K_{G} K_{R} K_{F} ]}}$$
(11)

It is seen for many cases that small amplifier gain is not satisfactory and for increasing the relative stability, a zero is needed to be added to the AVR open loop TF. With proper adjustment of \(K_{F}\) and TF, a satisfactory response can be obtained.

The developed model is of 5th order which is as given below:

$$\frac{{V_{t} (s)}}{{V_{{\rm ref}} (s)}} = \frac{{K_{A} K_{E} K_{G} K_{R} K_{F} (1 + sT_{R} )(1 + sT_{F} )}}{{[(1 + sT_{A} )(1 + sT_{E} )(1 + sT_{G} )(1 + sT_{R} )(1 + sT_{F} ) + K_{A} K_{E} K_{G} K_{R} K_{F} ]}}$$

Let us consider, \(K = K_{A} K_{E} K_{G} K_{R} K_{F}\)

$$\begin{gathered} \frac{{V_{t} (s)}}{{V_{{\rm ref}} (s)}} = \frac{{K(1 + sT_{R} )(1 + sT_{F} )}}{{[(1 + sT_{A} )(1 + sT_{E} )(1 + sT_{G} )(1 + sT_{R} )(1 + sT_{F} ) + K]}} \hfill \\ N\left( s \right) = k \, T_{2}^{\iota } s^{2} + \, k \, T_{1}^{\iota } s \, + k, \hfill \\ G_{AVR} = \frac{{k \, T_{2}^{\iota } s^{2} + \, k \, T_{1}^{\iota } s \, + k}}{{T_{5} s^{5} + T_{4} s^{4} + T_{3} s^{3} + T_{2} s^{2} + T_{1} s + \left( {k + 1} \right)}} \hfill \\ \end{gathered}$$

Considering the given values of a practical AVR [1]:

$$\begin{gathered} K_{A} = {1}0,\quad T_{A} = 0.{1},\quad K_{E} = {1},\quad T_{E} = 0.{5},\hfill\\ K_{F} = {2}.0,\quad T_{F} = 0.0{\text{4}}s,\quad K = {25}0,\quad T_{2}^{\iota } = {1}, \hfill \\ T_{1}^{\iota } = {\text{45}}s,\quad T_{5} = {1},\quad T_{4} = {58}.{4},\quad T_{3} = {13645},\hfill\\ T_{2} = 270962.{5},\quad T_{1} = {274875},\quad k = {137499}, \hfill \\ H = {3},\quad K_{G} = 0,\quad \omega_{0} = {377},\quad K_{R} = {1}\quad {\text{and}}\quad T_{R} = 0.0 \hfill \\ \end{gathered}$$
$${\text{G}}_{{{\text{AVR}}}} = \frac{{\Delta V_{t} (s)}}{{\Delta V_{{{\text{ref}}}} (s)}} = \frac{{{\text{250(}}s^{2} {\text{ + 45s + 500)}}}}{{{\text{ }}s^{5} { + 58}{\text{.5}}s^{4} {\text{ + 13,645}}s^{3} { + 270,962}{\text{.5}}s^{2} {\text{ + 274,875s + 137,500}}}}$$
(12)

Equation (12) represents the 5th order model of AVR system on which the proposed MOR is to be applied for its performance testing.

3.3 Error analysis

The effectiveness and accuracy of the developed algorithm are studied by applying it to AVR model. For screening the practicability and usefulness of the newly developed algorithm with some prevailing algorithms, numerous performance errors are calculated. The low-order models designed by the proposed MOR algorithms and other techniques are compared in terms of various performance error indices such as relative integral square error (RISE), integral absolute error (IAE), integral square error (ISE), and integral time-weighted absolute error (ITAE).

In this evaluation, a variety of performance error indices were employed to quantitatively measure the discrepancies between the low-order models generated by the proposed Model Order Reduction (MOR) algorithm and those derived from other established techniques. These error indices encompassed the following key metrics:

  • Relative integral square error (RISE): this index quantifies the cumulative squared differences between the actual system responses and the desired responses, normalized to the integral of the squared desired responses. It provides insight into the overall system performance over time.

  • Integral absolute error (IAE): IAE computes the integral of the absolute differences between the actual and desired responses. It offers a measure of the cumulative error magnitude over the entire response duration.

  • Integral square error (ISE): similar to IAE, ISE calculates the integral of the squared differences between actual and desired responses. It emphasizes larger errors more prominently due to the squaring operation.

  • Integral time-weighted absolute error (ITAE): ITAE combines the error magnitude with a time weighting factor, reflecting the idea that errors occurring earlier in the response have a greater impact on system performance. This index is particularly sensitive to early-time errors.

By employing these performance error indices, the researchers were able to comprehensively evaluate the performance of the proposed algorithm in comparison with existing algorithms. This allowed for a detailed understanding of the strengths and weaknesses of the developed approach across different aspects of system behavior.

In conclusion, the study involved assessing the effectiveness and accuracy of a newly developed algorithm for model order reduction by applying it to an AVR model. The researchers systematically compared the performance of low-order models generated by their algorithm with models obtained from other techniques, using various performance error indices. This comprehensive analysis provided valuable insights into the practicality and utility of the proposed algorithm within the context of AVR control and beyond. Here, with help of MATLAB simulation process various errors has been calculated.

The performance error indices are described in [9, 16, 32, 33] as:

$${\text{ISE}} = \int\limits_{0}^{\infty } {\left[ {g\left( t \right) \, - {\text{ g}}_{r} \left( t \right)} \right] \, ^{2} } \;{\text{d}}t$$
(13)
$${\text{RISE}} = \frac{{\int\limits_{0}^{\infty } {\left[ {g\left( t \right) \, - {\text{ g}}_{r} \left( t \right)} \right]^{2} } \;{\text{d}}t}}{{\int\limits_{0}^{\infty } {\widehat{[g(t)]}^{2} } }}$$
(14)
$${\text{IAE}} = \int\limits_{0}^{\infty } {\left| {g\left( t \right) - {\text{g}}_{r} \left( t \right)} \right|^{2} } \;{\text{d}}t$$
(15)
$${\text{ITAE }} = \int\limits_{0}^{\infty } {t\left| {g\left( t \right) - {\text{g}}_{r} \left( t \right)} \right|} \;{\text{d}}t$$
(16)

where g(t) and gr(t) are the unit step responses of the original AVR and the abated system, respectively. In addition, \(\widehat{g(t)}\) is the impulse response of the original AVR. The minimum values of the performance error indices of a reduced AVR system indicate that the lower order AVR system is improved approximant to the original AVR model and equivalent reduction-method is a better method compared to other existing methods.

3.4 Controller design for AVR

One of the important objectives of order reduction is to design the controller with MOR which has actually to control the original larger order system so that the overall mathematical calculations and computational burden are reduced. Automatic voltage regulators (AVRs) are primarily used to address unstable power system conditions. AVR is essential for electrical equipment, particular high-technology item with stringent voltage requirements and imported precision electrical equipment. This has led to the development of more sophisticated and high-tech voltage regulators to meet the demand for various types of precision equipment.

3.4.1 Controller schematic for AVR system

From Fig. 3, it can be clearly understood that for designing a controller for AVR system can be approached two ways-firstly with using original higher order system which will develop higher order controller and secondly with reduce order AVR system reduce order controller can be developed. Here, the problem is to design a controller Gc(S) for AVR system, G(S) for getting desired voltage output such that the closed-loop response with unity feedback is stable and has desired quick response.

Fig. 3
figure 3

Approaches for controller design

Full size image

In Fig. 4a shows closed-loop higher-order system with higher order controller. Figure 4b shows reduced order system including reduce order controller in closed-loop formation. Figure 4c shows reference model which close loop model can approximate the original response of the system. Figure 4 describes that reduce order controller design with help of reference model M(s).

Fig. 4
figure 4

Closed-loop configuration with reference model

Full size image

3.4.2 General algorithm for controller-design

Step1: Reference model M(S) constructed on the base of requirements whose close loop system principally approximate to that of the original response of close loop.

$$M(s) = \frac{{a_{0} + a_{1} s + \cdots + a_{m} s^{m} }}{{b_{0} + b_{1} s + \cdots + b_{n} s^{n} }}$$
(17)

Step 2: Determine an equivalent open loop specific model

$$\tilde{M}(s) = \frac{M(s)}{{1 - M(s)}}$$
(18)

Step 3: Specification of the structure of the controller:

$$G_{c} (s) = \frac{{p_{0} + p_{1} s + \cdots .... + p_{k} s^{k} }}{{q_{0} + q_{1} s + \cdots + q_{l} s^{l} }}$$
(19)

Step 4: For defining the unidentified control parameters, the characteristics of closed-loop system is match with that reference:

$$\begin{gathered} G_{c} (s)G(s) = \tilde{M}(s) \hfill \\ G_{c} (s) = \frac{{\tilde{M}(s)}}{G(s)} = \mathop \Sigma \limits_{i = 0}^{\alpha } e_{i} s^{i} \hfill \\ \end{gathered}$$
(20)

where ei is basically the power series coefficients at s = 0. Now, the controller parameters pi and qi are evaluated by comparing the equation in well-known mathematical approach, i.e., pade [41] sense.

Step 5: Comparing equation step 4 the desired controller parameter can be obtained.

Step 6: The transfer function of the closed-loop system can be obtained as-

$$G_{cl} (s) = \frac{{G_{c} (s)G(s)}}{{1 + G_{c} (s)G(s)}}$$
(21)

Step 7: Using the reduced model of AVR by repeating steps 4 and 5 the closed-loop transfer function for reduced model can be determined as follows-

$$R_{cl} (s) = \frac{{R_{c} (s)R(s)}}{{1 + R_{c} (s)R(s)}}$$
(22)

Equation (22) represents the controller for the reduced plant.

3.4.2.1 Example of controller parameter calculations

The transfer function of the full order model of AVR [1]:

$$G_{{{\text{AVR}}}} = \frac{{\Delta V_{t} (s)}}{{\Delta V_{{\rm ref}} (s)}} = \frac{{250(s^{2} + 45s \, + \, 500)}}{{ \, s^{5} + 58.5s^{4} \, + \, 13645s^{3} \, + \, 270962.5s^{2} \, + \, 274875s \, + \, 137500}}.$$

and that with the proposed DR method can be represented as:

$$R_{{{\text{AVR}}}} = \frac{0.01777 \, s \, + \, 0.4873}{{ \, s^{2} + 1.043s + 0.536}}$$
(23)

Now, for this 2nd order model the reference model has been chosen using damping ratio ζ and natural frequency (ωn) (as it gives the approximately similar response of the original system)

$$M(s) = \frac{0.536}{{s^{2} + 0.7123s + 0.536}}$$
(24)

Now open loop transfer function of the reduced model using reference model obtained as-

$$\tilde{M}(s) = \frac{{0.536s^{2} + 0.3818s + 0.2873}}{{s^{4} + 1.425s^{3} + 1.043s^{2} + 0.3818s}}$$
(25)

The controller structure is given by:

$$\begin{aligned} R_{c} (s) & = \frac{{\tilde{M}(s)}}{R(s)}\\ &= \frac{{0.536s^{4} + 0.9408s^{3} + 0.9728s^{2} + 0.5043s + 0.154}}{{0.01955s^{5} + 0.564s^{4} + 0.7841s^{3} + 0.5668s^{2} + 0.2047s}} \\ &= \frac{1}{s}(0.7523 + 0.8897s + 1.24s^{2} - 1.668s^{3} - \cdots ) \\ \end{aligned}$$
(26)

Now, consider the generalized structure of PID controller:

$$R_{c} (s) = k_{p} + \frac{{k_{i} }}{s} + k_{D} s$$
(27)

Comparing Eqs. (26) and (27) we get:

$$\begin{array}{*{20}c} \begin{gathered} k_{p} = 0.8897 \hfill \\ k_{i} = 0.7523 \hfill \\ k_{D} = 1.24 \hfill \\ \end{gathered} & , & {R_{c} (s) = 0.8897 + \frac{0.7523}{s} + 1.24s} \\ \end{array}$$

The closed-loop transfer function of Reduced AVR with controller obtained as:

$$R_{cl} (s) = \frac{{0.02388s^{6}{+}0.6968s^{5}{+}1.198s^{4}{+}1.263s^{3}{+}0.6739s^{2}{+}0.2129s}}{{0.9941s^{6}{+}2.721s^{5}{+}3.293s^{4}{+}2.347s^{3}{+}0.9527s^{2}{+}0.2129s}}$$
(28)

3.4.3 Stability analysis of MOR AVR controller

For understanding the stability of the proposed system, few stability checking methods such as step responses, bode plots, response behavior with sinusoidal inputs are utilized. The stability aspects AVR system are analyzed in time domain by means of step and sinusoidal response and in frequency domain by implementing Bode plot of reduced model.

Following Eq. (1), if K > 0 exists and the system G(s) is stable, then:

$$\left\| {G\left. u \right\|} \right._{L2} \le K\left\| u \right\|_{L2}$$

Regardless of the fact that this is the correct definition for systems with transfer functions, it is infrequently applied. Bound output follows from bounded input. When \(y(t) \to 0_{{}} {\text{and}}^{{}} u(t) \to 0\), a system is stable.

4 Experimental result

4.1 Case studies with reduced AVR model

Considering original AVR system where the system parameters are expressed as

$$N\left( s \right) = k \, T_{2}^{\iota } s^{2} + \, k \, T_{1}^{\iota } s \, + k,\quad G_{{{\text{AVR}}}} = \frac{{k \, T_{2}^{\iota } s^{2} + \, k \, T_{1}^{\iota } s \, + k}}{{T_{5} s^{5} + T_{4} s^{4} + T_{3} s^{3} + T_{2} s^{2} + T_{1} s + \left( {k + 1} \right)}}$$

Considering the system parameters from literature [1] of a practical AVR system

$$\begin{gathered} K_{A} = {1}0,\quad T_{A} = 0.{1},\quad K_{E} = {1},\quad T_{E} = 0.{5},\hfill \\ K_{F} = {2}.0,\quad T_{F} = 0.0{\text{4}}s,\quad K = {25}0,\quad T_{2}^{\iota } = {1}, \hfill \\ T_{1}^{\iota } = {\text{45}}s,\quad T_{5} = {1},\quad T_{4} = {58}.{4},\quad T_{3} = {13,645},\hfill \\ T_{2} = { 27}0,{962}.{5},\quad T_{1} = {274,875},\quad k = {137,499}, \hfill \\ H = {3},\quad K_{G} = 0,\quad \omega_{0} = {377},\quad K_{R} = {1}\quad {\text{and}}\quad T_{R} = 0.0 \hfill \\ \end{gathered}$$
$$\begin{aligned} G_{{{\text{AVR}}}} &= \frac{{\Delta V_{t} (s)}}{{\Delta V_{{\rm ref}} (s)}} \\ &= \frac{{250(s^{2} + 45s \, + \, 500)}}{{ \, s^{5} + 58.5s^{4} \, + \, 13645s^{3} \, + \, 270962.5s^{2} \, + \, 274875s \, + \, 137500}} \end{aligned}$$
(29)

4.1.1 Case 1: reduced order AVR system using DR method without controller

This 5th order system is reduced to a 2nd order system where the coefficients are calculated from Routh table following Eq. (8). In a similar way, numerator is reduced using differential-Routh technique. After simplifying reduced transfer function by dividing numerator and denominator coefficients, the 2nd order reduced model thus takes the form like:

$$\frac{0.01777 \, s \, + \, 0.4873}{{ \, s^{2} + 1.043s + 0.536}}$$

Here, Fig. 5a shows the step input behaviors of the original system without controller and proposed reduction technique along with various existing reduction schemes. Figure 5a shows the comparison of terminal voltage variation (AVR). So, it showing the comparison with original system response with different reduced order techniques along with proposed method (DR). Referring to Fig. 5a, the reference values are varied for the regulation. Table 2 describes parameters obtained from step responses. It has been easily seen from Fig. 5a and from Tables 2 and 3 that obtained result of error analysis of different methods indicates that proposed method is much closer to actual system.

Fig. 5
figure 5

a Step response for change in terminal voltage of an AVR system without controller. b Comparison of sinusoidal input responses of AVR system and its reduced models. c Bode response of original system with its reduced models with phase offset adjustments

Full size image
Table 2 Comparisons of different Parameters of Reduced order Model of AVR
Full size table
Table 3 Comparisons of different Error Calculations
Full size table

Figure 5b shows the sinusoidal behaviors of original system and reduced models while Fig. 5c gives us the exposure to frequency domain stability obtained analysis using bode plot along with phase offset adjustment. Table 4 indicates the phase margin, gain margin, and stability aspects obtained using bode analysis. As per this first case study, higher order AVR system is reduced using proposed DR method. Furthermore, error analysis is performed to realize the deviation from original system and its reduced model. From Tables 2 and 3, comparing the parameters of the original system and reduced models of different existing techniques along with proposed method, it is obtained that proposed method showing better results compare to other existing techniques.

Table 4 Comparison of Bode Plot parameters
Full size table

4.1.2 Case 2: reduced controller design for AVR

As it is well known that design of controller for higher order system is a tedious job, a reduced order controller for AVR system is developed in this case study. It is very easy to understand that calculating controller parameters became easy, less time consuming and complexity of mathematics when the calculations are done using lower order models. The transfer function of the full order model of AVR-

$$\begin{aligned} G_{{{\text{AVR}}}} &= \frac{{\Delta V_{t} (s)}}{{\Delta V_{{\rm ref}} (s)}} \\ &= \frac{{250(s^{2} + 45s \, + \, 500)}}{{ \, s^{5} + 58.5s^{4} \, + \, 13645s^{3} \, + \, 270962.5s^{2} \, + \, 274875s \, + \, 137500}} \end{aligned}$$

and that with the proposed DR method can be represented as:

$$R_{{{\text{AVR}}}} = \frac{0.01777 \, s \, + \, 0.4873}{{ \, s^{2} + 1.043s + 0.536}}$$

Using Eq. (28), the closed-loop transfer function of Reduced AVR with controller is obtained as-

$$R_{cl} (s) = \frac{{0.02388s^{6}{+}0.6968s^{5}{+}1.198s^{4}{+}1.263s^{3}{+}0.6739s^{2}{+}0.2129s}}{{0.9941s^{6}{+}2.721s^{5}{+}3.293s^{4}{+}2.347s^{3}{+}0.9527s^{2}{+}0.2129s}}.$$

Considering the same values of PID controller parameter the original AVR with controller transfer function obtained as-

$$G_{cl} (s) = \frac{\begin{gathered} 281.8s^{10} + 2.937 \times 10^{04} s^{9} + 4.748 \times 10^{06} s^{8} + 2.61 \times 10^{08} s^{7} + 5.623 \times 10^{09} s^{6} + 4.576 \times 10^{10} s^{5} \hfill \\ + 7.37 \times 10^{10} s^{4} + 7.372 \times 10^{10} s^{3} + 3.846 \times 10^{10} s^{2} + 1.175 \times 10^{10} s \hfill \\ \end{gathered} }{\begin{gathered} 0.8263s^{12} + 96.68s^{11} + 2.565 \times 10^{04} s^{10} + 1.796 \times 10^{06} s^{9} + 1.852 \times 10^{08} s^{8} + 6.396 \times 10^{09} s^{7} \hfill \\ + 7.25 \times 10^{10} s^{6} + 1.72 \times 10^{11} s^{5} + 1.977 \times 10^{11} s^{4} + 1.362 \times 10^{11} s^{3} + 5.408 \times 10^{10} s^{2} + 1.175 \times 10^{10} s \hfill \\ \end{gathered} }.$$

4.2 Stability analysis with controller

Here, Fig. 6a compares the step response attributes of the proposed reduction technique with those of the original system and many other reduction schemes with controllers. Figure 6b shows its sinusoidal behaviors and Fig. 6c frequency domain behaviors. All the parameters of PID controller have been calculated and shown in Table 5 using the same technique of controller design as per proposed method. The parameters derived from time domain analysis are shown in Table 5.

Fig. 6
figure 6

a Comparison of Step Response closed-loop system performance including reduced model controllers. b Comparison of Sinusoidal Response of closed-loop system performance including reduced model controllers. c Comparison of Bode Response closed-loop system performance including reduced model controllers

Full size image
Table 5 Comparisons of different Parameters of Reduced order Model of AVR
Full size table

It is clear from Fig. 6 and from Table 6 that the proposed method of controller design with combined differential and Routh approach perform better than existing other method of literature. From the analysis of Tables 6 and 7 results of PID controller, it indicates that the obtained results of the suggested method are significantly more similar to the actual system and its performance also shown better compare to other existing methods. The sinusoidal behaviors of the original system and the reduced models are depicted in Fig. 6b. The frequency domain stability analysis shown in Fig. 6c. After adding controller with the reduced second-order model of AVR system has been designed. So, step and sinusoidal responses obtained from transfer function model to understand stability in time-domain and Bode plot has been considered for frequency domain analysis. After comparing with proposed method and other existing methods it is clearly seen that proposed technique gives us better performance.

Table 6 Comparisons of different Error Calculations including controller
Full size table
Table 7 Comparison of Bode Plot parameters
Full size table

5 Conclusions

The article emphasizes the pivotal role of a controller in maintaining stability and desired output in an Automatic Voltage Regulator (AVR) system. It proposes a novel reduction scheme that combines enhanced differential approximation with the Routh array, offering several key advantages. (i) It ensures stability preservation in higher-order systems, a critical aspect of system design. (ii)It eliminates the need for gain adjustment or extensive tuning, simplifying the reduction process. (iii) It is computationally simple, enhancing efficiency and practicality. (iv) It addresses steady-state error problems associated with traditional differential reduction methods. (v) It simplifies controller development, boosting computational efficiency in AVR systems. (vi) It is easy to apply in AVR systems, streamlining calculations without requiring complex mathematical approaches. (vii) It underscores the importance of AVR systems in power technology, advocating for simpler mathematical models for enhanced controller design. (viii) It holds potential for wider applications in multiple-input, multiple-output (MIMO) systems and hybrid methods, providing a foundation for advanced compensator or controller design. Lastly, the proposed technique offers a more effective and straightforward solution compared to existing reduced controller design methods.

However, the article acknowledges certain limitations: first, the validity of assumptions made by the Differential Reduction (DR) method may lead to discrepancies if not universally applicable. Second, the reduction process may oversimplify complex interactions within the system. Third, sensitivity to initially neglected system parameters can limit its applicability. Lastly, the DR method is strictly for linear time-invariant systems, restricting its use in analyzing nonlinear or time-varying systems.