1 Introduction

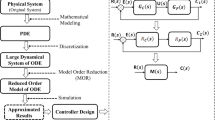
The approximation of linear time-invariant large scale dynamical (LSD) systems is important in many engineering problems, particularly in the design of control systems, where the engineer is confronted with the control of a physical system whose analytical model is described as a high order linear time-invariant (LTI) system. LSD systems can be used to model a wide range of practical systems. It is critical to investigate the control problem of LSD systems to enhance the control performance of such systems [1, 2]. LSD systems, which have been made up of a series of connected subsystems are widely used in practical applications [3, 4]. The development of a mathematical model begins with the investigation of all physical systems, such as aircraft, chemical plants, refineries, electrical grids, traffic congestion networks, digital communication, and control systems, etc. In many practical situations, a complex, HOS is derived from theoretical considerations [5, 6]. Realistic systems have often been observed to consist of many interactive subsystems with their characteristics, and the resulting system size may be too large to be conveniently handled when such subsystems are interconnected. A typical example of this situation is the dynamic stability studies of modern interconnected power systems. System equations are linear under dynamic conditions, but the total number of differential equations describing system performance increases rapidly as the number of interconnected machines increases. Special numerical techniques for calculations are required for a system of a high order. The analysis of such a HOS is not only time-consuming but also not cost-effective for online implementation.

The complexity of the system also makes it difficult to gain a thorough understanding of its behavior. An uncomfortably HOS may present difficulties in its analysis, synthesis, or identification. Preliminary design and optimization of such systems can often be accomplished more easily if a ROM is derived that provides a good approximation of the system. It is thus preferable to replace a high order system with a low order system while retaining the main qualitative features of the original system, such as the constant time, damping ratio, natural frequency, and stability ratio. Thus, the MOR method contributes to a better understanding of the system. The model must also be mathematically simple so that it can be easily analyzed, and the results studied. In short, the main goals of obtaining ROMs are to develop a better understanding of the higher order of the original system, to reduce computational complexity, to reduce hardware complexity, to make designs feasible, and to obtain simpler control legislation.

This paper is split into six parts. The first part provides an overview and detailed summary of the literature review for large-scale systems. Section 2 defines the Problem Statement. Theoretical Perspective for MOR is described in Sect. 3. Section 4 describes the application of the MOR method for LTI large-scale dynamical systems to reduce, followed by numerical experiments and results that are compared to methods from the literature to determine the validity of the proposed method in Sect. 5. Finally, Sect. 6 discusses the premise and future scope of the work.

2 Problem Statement

Let us consider an nth order SISO linear time-invariant higher-order system represented by the following transfer state-space representation by Eq. (1):

(1)

where \(x\) \(\in\) \({\mathbb{R}}^{n}\), \(u \in {\mathbb{R}}^{p}\), \(y\) \(\in\) \({\mathbb{R}}^{p}\) with ‘p’ inputs and ‘q’ outputs and A ∈ \({\mathbb{R}}^{n \times n}\), B ∈ \({\mathbb{R}}^{n \times m}\), C ∈ \({\mathbb{R}}^{p \times n}\) and \(D \in {\mathbb{R}}^{p \times m}\) are constant matrices of appropriate size. p = q = 1, the original system is referred to as the SISO system, otherwise, it will be called the multi-dimensional system. The MOR problem consists of finding an approximate system of order ‘r’ \(r( \ll n)\) described by

(2)

Such a dimensional SISO Dynamic system and order model are similar in the important aspects of their characteristics and \(x_{r}\) \(\in\) \({\mathbb{R}}^{r}\), \(u \in {\mathbb{R}}^{p}\), \(y_{r}\) \(\in\) \({\mathbb{R}}^{p}\) and A ∈ \({\mathbb{R}}^{r \times r}\), B ∈ \({\mathbb{R}}^{r \times m}\), C ∈ \({\mathbb{R}}^{p \times r}\) and \(D \in {\mathbb{R}}^{p \times m}\) are constant matrices of reduced-order model and reduced output \(y_{r}\) should be a close approximation of \(y\) for a given set of inputs [7, 8]. The transfer function associated with original system Eq. (1) representations may be expressed by

$$G(s) = D + C\left[ {sI_{n} - A} \right]^{ - 1} B$$
(3)
$$G(s) = \frac{N(s)}{{D(s)}} = \frac{{n_{0} + n_{1} s + n_{2} s^{2} + \cdot \cdot \cdot n_{m - 1} s^{m - 1} }}{{d_{0} + d_{1} s + d_{2} s^{2} + \cdot \cdot \cdot + d_{n} s^{n} }}$$
(4)

or

$$G(s) = \frac{{\sum\limits_{i = 0}^{m - 1} {n_{i} s^{i} } }}{{\sum\limits_{i = 0}^{n} {d_{i} s^{i} } }}$$
(5)

where \(G(s)\) is expressed as and \(n_{i} ,d_{i}\) are scalar constants of the HOS system.

The challenge is to design a ROM (5) that retains the important properties of the original and approximates the output as closely as possible [9, 10], The ROM is expressed as \(G_{r} (s)\) and obtained is described as follows:where

$$G_{r} (s) = R_{r} (s) = D_{r} + C_{r} (sI_{r} - A_{r} )^{ - 1} B_{r}$$
(6)
$$G_{r} (s) = \frac{{N_{r} (s)}}{{D_{r} (s)}} = \frac{{\hat{n}_{0} + \hat{n}_{1} s + \hat{n}_{2} s^{2} + \cdot \cdot \cdot \hat{n}_{r - 1} s^{r - 1} }}{{\hat{d}_{0} + \hat{d}_{1} s + \hat{d}_{2} s^{2} + \cdot \cdot \cdot + \hat{d}_{r} s^{r} }}$$
(7)

or

$$R_{r} (s) = \frac{{\sum\limits_{j = 0}^{r - 1} {\hat{n}_{j} s^{j} } }}{{\sum\limits_{j = 0}^{r} {\hat{d}_{j} s^{j} } }}$$
(8)

where suffix ‘r’ is denoted and \(m_{j} ,n_{j}\) are a scalar constant of the ROM [11].

3 Theoretical Perspective for MOR

Simplicity while preserving the features of interest will be one of the most desirable features of such models. Since the models can be developed with different goals and objectives or with different points of view, a given system can have more than one model, each satisfying some predefined goals. Dissimilar people progress different models for the same system; if their perception or point of view changes over time, the same individual may develop dissimilar models for the same system. The model's usability is a crucial aspect, especially in online controls. Simpler models commonly give a better feel of the original system [12,13,14]. The approximation method theoretical survey is provided in Tables 1 and 2. Several researchers have proposed a wide variety of MOR methods over the past few decades. The goal of MOR can be summarised as follows:

  1. (i)

    The prominent points that should always be taken care of while deriving the ROM, are as follows [15]

    • Stability should be preserved.

    • Passivity should also be maintained or preserved.

    • The method should be reliable and effective in computation.

    • The method should be reliable and effective in computation.

    • The methods must adopt some specific requirements for error tolerance.

    • High fidelity representation of the original large-scale system.

    • A considerable difference between the size of the ROM and the original system.

    • Lesser approximation error and existence of global error bound.

    • Numerically stable and efficient procedure.

    • Economize in terms of hardware while synthesizing the system.

  2. (ii)

    Some of the reasons for MOR are as follows

    • Fast and ease in the understanding of the system Reduced computational burden.

    • Reduced computational burden

    • Reduced Controller synthesis

    • Controller procedure making reasonable designs.

    • Improving the computer-aided system design approach.

    • All of the above results in the best cost-effective solution.

Table 1 A summary of investigation for MOR
Full size table
Table 2 A summary of general comparisons of approximation techniques
Full size table

3.1 A Systematic Literature Review of Inference Strategies for MOR

  • Researchers are either developing new algorithms or improving the existing algorithms for MOR.

  • Control design can be done after the approximation of a system or even approximation-based control design can be achieved.

  • Mixed methods (a combination of two existing methods) are widely available in the literature.

  • MOR for real-time systems such as the power system model is the focus of many researchers.

  • Much attention has been given to stability preserving ROM.

  • Structure and passivity preserving ROM is a new shift in this research area.

  • Work on MOR for parametric systems, interval systems, and hybrid systems can be found and still work on it is going on.

  • Researchers are also developing nonlinear balancing methods, but so far these can only be used for systems of very limited size (< 100).

3.2 MOR From Mathematics to Innovative Applications

MOR was initially being developed in system theory and control engineering, which studies the properties of dynamic systems in application to reduce their complexity while preserving as much of their input–output behavior as possible. Numerical Mathematicians have also taken up the field, particularly after publishing methods such as PVL (Padé via Lanczos). MOR is a multidisciplinary topic of great interest over the past 40 years. This is because engineering problems often involve large-scale systems or very complex processes that have to be controlled using low-order controllers. The ROMs are required to minimize the computational effort during analysis, simulation and controller design of high order practical systems [16,17,18]. ROMs are valuable for the following reasons: ROM are neither robust concerning parameter changes nor cheap to generate. A scheme based on a ROM database dramatically reduces the cost of computing aeroelastic forecasts while maintaining good accuracy.

  • Analysis and synthesis of the system

  • Predicting transient response sensitivities of high order systems using ROMs

  • Design of controllers and observers

  • Advanced applications in the area of integrated circuits, microfluidic devices, innovative materials, etc.

  • Innovative methods to reliable MOR in networks.

  • Development of online simulators of system

  • They are predicting transient response sensitivities of high-order systems using ROMs.

  • The area of economic and financial systems.

  • Control system design

  • New mathematical tools for ROM

  • Adaptive control design with the help of low order models.

  • Suboptimal control derived by simplified models.

  • Power system stability

  • Providing that a guideline for online interactive modeling

3.3 Key Challenges of MOR

Rethinking about the linear/nonlinear MOR problem, a few prominent and significant challenges in MOR has been pointed out which are as follows:

  • Modeling uncertain mechanical systems is challenging and necessitates the careful analysis of an enormous amount of data- Uncertain mechanical systems [19, 20].

  • Multi-disciplinary optimization in MOR [14, 21]

  • Stability preservation for large scale dynamical systems [22,23,24,25,26,27,28,29,30]

  • Passivity Preservation [31,32,33,34,35,36]

  • MOR for nonlinear complex systems & dimensionality reduction [12, 37,38,39,40,41]

  • Challenges in MOR for industrial problems [21, 42,43,44]

  • VLSI devices and layout optimization [27, 45, 46]

  • Optimization technology and device modeling in micro and nano-electronics [47,48,49,50,51,52]

  • Optimization of the electrical power system and smart city [14, 53]

  • A Posteriori error estimation [54,55,56,57]

  • Projection-based ROM [58,59,60]

  • Aeroelasticity loads analysis [61]

  • The financial and economic system in MOR [62]

4 MOR of LTI Large-Scale Dynamical System

The most important problem in the appearance of complex activities of a higher dimension system is that it occurs in many areas, including complicated transport, ecological systems, electrical equipment, aeronautics, hydraulics, etc. [5, 143,144,145].

All these complex and large systems with conventional techniques are difficult to model. The combination of these is also considered to be big (large) if it wishes to be detached for each numerical measurement to many structured machineries or small structures for practical purposes [16, 146, 147]. Then perhaps a system is complex and wide enough to fail to generate the proper solutions with realistic computational efforts by conventional modeling, analysis, device design, and approximation strategies [148, 149]. Studying this physical system [17] starts with structuring the model, which can be considered as an enthusiastic example of this kind of structure, which is motivated by a task of control in preparing and evaluating a model [149,150,151]. We are presenting a high stage of negotiation on computing in this first segment, which is important for detailed incident model observations in perspective and industry implementation [16, 152].

Several MOR solutions were mainly provided in two ways, namely frequency and time domain [155]. Researchers' reduction techniques have both benefits and inconveniences. One common weakness in the methods is that even if the HOS is stable, the reduced-order system is unstable [5, 149, 153] and steady-state matching. The other drawbacks are the low precision in average ranges as well as high frequency and the non-minimum phase characteristics [136, 154]. Based upon the dominant poles method, numerous mixed methods have been suggested by [155, 156], the continued method and time matching fraction expansion can produce stable systems models. In the literature search, there are numerous approaches for reducing models of LSD system, such as a ROM algorithm, which was presented with a Pade´ approximation [63, 157, 158] and MOR of state linear time-invariant system based on the theory of balanced realization was initially firstly suggested by [159] in which the realization term balanced is selected for the system state configuration and partitions of the modes [160]. If the steady-state matches the balanced truncation of the steady-state value and the steady-state error of the LSD system is not kept, the BT reduction models obtained after truncation would have a less controllable and less measurable status. Addressed that the weak subsystem removed can be used to maintain the steady-state BT gain using the SPA approach [137, 161,162,163,164,165,166]. Preserving the ratio of steady-state output to steady-state input of the BT model for the minimal system using the SPA approach, which can be used to reduce the system to stable, minimal, and internal balancing [137].

The contribution of the work is that, with the traditional BT method, it is easy to derive a ROM that may fit well with the original system, but in most cases, it may be possible to observe a steady-state value mismatch. Although various researchers have used SPA to prevent such demerits from occurring. We, too, have successfully applied this concept in one of our works. The interesting part of the present work is that, with simple algorithmic modifications, it leads to a new modified algorithm based on a hybrid approach with the BT method and the SPA approach. It is referred to as a balanced singular perturbation approximation (BSPA) method. The advantage of the methodology lies not only in its steady-state matching, but also in its applicability to LSD systems, as shown by some of the examples derived from the published work, and also in comparison with the existing methods available in the literature to validate the effectiveness and superiority of the proposed method.

4.1 Balanced Truncation Method

A systems realization is balanced if its observability and controllability gramians are equal, meaning each state is controllable and observable. When this is done, one finds a reduced-order model by deleting those states that are least controllable and observable (as measured by the size of HSVs) provides a measure of energy for each state in a system structure in control theory. They are the basis for a balanced reduction of the system, which retains high energy states while discarding low energy states. The ROM obtained via this method has significant characteristics of the original systems [92, 167, 168].

The main idea is that the singular values of the controllability gramians correspond to the amount of energy required to move the corresponding states in the system. This balanced truncation process is a very interesting and powerful generalization of minimal realization theory, which only eliminates the completely unobservable and uncontrollable states from a given system model to furnish a minimal realization. This paper aims to construct a new model order reduction strategy to simplify a large-scale linear dynamical (LSLD) system.

In Table 3, the Balanced Realization (BR) Algorithm to derive ROM from higher-dimensional systems has been presented. In the BR process, a higher dimensional stable structure may be controllable and observable at once. However, as reported in the literature, a transformation still needs to be established in many situations [159]. Then, it is transformed into a unique form of controllability and observability gramians, which are further equal. This leads to a diagonal matrix \(\sum\), consisting of Hankel singular values at its diagonal, ultimately ordered in their dominance. Such kind of realization is called BR or internally balanced realization. This balancing of a given system is the first step into a category of methods for MOR, referred to as the BT method [159, 169].

Table 3 Balanced realization algorithm
Full size table

4.2 Proposed Hybrid Method for Approximation

The proposed algorithm is the result of the hybridization of the Balanced truncation and Singular perturbation approximation approach. It consists of two steps as follows:

Step 1 The ROM obtained using the balanced truncation method [141, 148] algorithm has been discussed in Table 3 of Sect. 4.1.

The Steps of the order reduction algorithm using the Balanced Truncation Method may be described as followed.

To understand the balanced truncation method, we need to introduce two characteristics of a state: controllability and observability.

The controllability gramian (\(G_{C}\)) and observability gramian of the system is defined as follows:

$$G_{C} = \int_{0}^{\infty } {e^{A\tau } BB^{T} e^{{A^{T} \tau }} d\tau }$$
(9)
$$G_{O} = \int_{0}^{\infty } {e^{A\tau } C^{T} Ce^{A\tau } d\tau }$$
(10)

The matrix \(G_{c} ,G_{o}\) is a symmetric positive-semidefinite matrix called controllability and observability gramian, respectively. It is a solution of the following Lyapunov equation

$$\left. \begin{gathered} AG_{C} + G_{C} A^{T} = - BB^{T} \hfill \\ A^{T} G_{O} + G_{O} A = - CC^{T} \hfill \\ \end{gathered} \right\}$$
(11)

Assumption: The nth-order dimensional system is an asymptotically stable system and also minimal. Moreover, the state-space equation of the original system or the pair (A0, B0) states controllable if and only if the n × nm state controllability matrix and pair (A0, C0) is observable if the np × n observability matrix [159].

By assumption, both gramians \(G_{C}\) and \(G_{O}\) are a positive definite and unique symmetric matrix explanation to the couple of gramians. Since their implementation is minimal.

Both gramians satisfy the following linear Lyapunov equations [170, 171].

In control philosophy, eigenvalues express system stability, although HSV describes the “energy” of each state in the system.

Again, G, eigenvectors (as well as eigenvalues) are completely dependent on the choice of basis. Therefore, one may speak of dominant controllable states only relative to a certain basis.

Numerically we express as a stable state-space system Eq. (1), its HSV are well-defined as the square roots of the eigenvalues of P Q, ordered non increasingly, are called Hankel Singular Values: \(\sigma_{i} = \sqrt {\lambda_{i} (G_{C} G_{C} }\), respectively. For simplicity, such singular values (SV) are generally ordered downward to truncate states that match smaller Hankel singular values as follows.

$$\sigma_{1} \ge \sigma_{2} \ge \sigma_{3} \ge \sigma_{4} \ge \sigma_{r} \ge \sigma_{r + 1} \ge \cdots \sigma_{n} > 0$$
(12)

The Hankel singular values are also the singular values of the (infinite-dimensional, but finite rank) Hankel operator, which maps past inputs to future system outputs.

This is also a significant action of the minimality of realization of the original system is the diminishing positive number such that

$$P_{c} = P_{0} = \sum = Diagonal\left\{ {\sigma_{1} ,\sigma_{2}, \sigma_{3}, \sigma_{4} \ldots \sigma_{n} } \right\}$$
(13)

The diagonal matrix (\(\sum\)) if such a matrix realization exists [170, 172, 173].

$$\sigma (\omega ) = \left\| {G_{o} (j\omega )} \right\|^{2}$$
(14)

Any symmetric positive definite matrix may be decomposed into a product.

Compute (Cholesky) factors (CF) of the gramians are often obtained by this factorization according to [146, 174]. The lower triangular matrix (CF) Qc and Qo of both gramians Pc and Po is obtained as [146, 161].

$$P_{c} = Q_{c} Q_{c}^{T}$$
(15)
$$P_{o} = Q_{o} Q_{o}^{T}$$
(16)

Compute SVD, the \(Q_{o} Q_{c}^{T}\) is singular value decomposition of gramians, also known as SVD of the system, found as follows:

$$SVD\left( {Q_{o}^{T} Q_{c} } \right) = U\sum V^{*}$$
(17)

where U and V are a vector, define as left and right singular. Also, unitary matrices (orthogonal).

This system matric may be transformed into the balanced model by a similarity transformation matrices W, which may be achieved as follows [146, 171, 175].

ROM is (\(WAW^{ - 1}\), \(WB\), \(CW^{ - 1}\)).where W is a transformation matrix

$$W = Q_{c} V{\sum}^{{ - \frac{1}{2}}}$$
(18)

The original system has been completely balanced, which is partitioned as:

(19)
(20)

where the singular value \(\sum_{1} = diag(\sigma_{1} , \ldots ,\sigma_{r} )\) and \(\sum_{2} = diag(\sigma_{r + 1} , \ldots ,\sigma_{n} )\). It is seen that \(\sum_{1}\) corresponds to the “strong” sub-systems to be retained and \(\sum_{2}\) the “weak” sub-systems to be deleted.

$$\left. \begin{gathered} A_{B} = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } \\ {A_{21} } & {A_{22} } \\ \end{array} } \right],B_{B} = \left[ {\begin{array}{*{20}c} {B_{1} } \\ {B_{2} } \\ \end{array} } \right], \hfill \\ C_{B} = \left[ {\begin{array}{*{20}c} {C_{1} } & {C_{2} } \\ \end{array} } \right],D_{B} = D \hfill \\ \end{gathered} \right\}:\underbrace {Strong\;Subsystem}_{{({\text{to}}\;{\text{be}}\;{\text{retained}})}}\, + \underbrace {Weak\;Subsystem}_{{({\text{to}}\;{\text{be}}\;{\text{retained}})}} \Leftrightarrow \sum$$
(21)

Hence, the reduced-order model is defined as

$$A_{r} = A_{11} ,\;B_{r} = B_{1} ,\;C_{r} = C_{1}$$

where A11 is part of a strong subsystem and \(\sum_{1}\) are \(r \times r(r < n)\) matrixes. We call this ROM a balanced system approximation of direct-truncation (DT). There are some well-known results on approximation. There are some well-known results on the approximation [137, 176].

Lemma 1

(Pernebo et al. 1982) The subsystem matrix \(A_{ii} ,B_{i} ,C_{i}\) is the minimal and internally balanced realization through Grammian \(\sum_{i} (i = 1,2)\) (i = 1, 2).

Lemma 2

(Pernebo et al. 1982) The subsystem matrix Aii (i = 1, 2) is asymptotically stable if \(\sum_{1}\) and \(\sum_{2}\) has no common diagonal component. Furthermore, the subsystem (A11, B1, C1) (i = 1, 2) is both completely controllable and observable [177].

Step 2 Now, let us focus on applying the SPA derived from the ROM of an LTI system [177, 178].

In numerous engineering, the system's steady-state gain, usually referred to as DC gain value (the system gains at an infinitive time, equivalent to \(G(0)\), plays an essential role in evaluating system performance. It is, therefore, restored to preserve the DC gain value in the ROM, i.e., \(G_{r} (0) = G(0)\), The balanced truncation approach introduced in the preceding subsection does not retain the DC gain value unchanged [179].

Suppose that \((A,B,C,D)\) is compatible with minimal and balanced truncation of the stable system and the partitioned system as in the previous subsection. Then, it can be demonstrated that stable is \({\text{A}}_{{{22}}}\).

In this section, we address the order reducing procedure for higher-dimensional systems resulting in a hybrid approach using BT and balanced SPA. In the BT method, all balanced systems are separated into two parts as a slow and fast mode by defining the lower Hankel singular values (HSV) as fast mode, with the others defined as a slow mode. First, the derivative of all states equal to zero in fast mode may be obtained by defining a reduced system. The main aim of structure preservation in the ROM is to preserve the dominant frequencies of the original system. Hence, to preserve dominant dynamic modes in the reduced system. This work introduces a new MOR algorithm applied for a linear large-scale dynamical system, based on the idea of preserving the dominant poles of the original system during the order reduction. The notion of Hankel singular values is a superior criterion for deciding the order of ROM verified and validated with various test problems. The approach is based on retaining the dominant eigenvalues or modes of the system and truncating the less significant eigenvalues comparatively.

Equation (22) has been attained as a minimal realized model containing strong and weak subsystems. Thus, SPA may be effortlessly applied on subsystems of Eq. (3.39). In the BT model, reduced (r) balanced states are retained, which are completely controllable and observable, so balanced states are preserved and remaining weakly controllable and observable states are truncated. SPA is used to maintain the DC gain of the original system in the model [139, 180]. The concerned researcher may refer to [177, 178] for more indications of the method.

The portioned form as above may be used to construct a singular perturbation approximation. As the balanced realized system determine, it can be re-written in the form of given as

$$\left. \begin{gathered} \left[ {\begin{array}{*{20}c} {\frac{{dx_{1} }}{dt}} \\ {\frac{{dx_{2} }}{dt}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } \\ {A_{21} } & {A1_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {B_{1} } \\ {B_{2} } \\ \end{array} } \right]u(t) \hfill \\ y = \left[ {\begin{array}{*{20}c} {C_{1} } & {C_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \right] + Du(t) \hfill \\ \end{gathered} \right\}:Balanced\;Model$$
(22)

Again, re-write is equation form

$$\frac{{d\dot{x}_{1} }}{dt} = A_{11} x_{1} + A_{12} x_{2} + B_{1} u\;(Slower)$$
(23)
$$\mu \frac{{d\dot{x}_{2} }}{dt} = A_{21} x_{1} + A_{22} x_{2} + B_{2} u\;(Faster)$$
(24)

where, \(\mu\) is a positive small perturbational parameter of singular perturbation approximation approach [181, 182].

By comparing the derivative of the weakly subsystem to zero below, the BSPA model may be achieved [138, 139].

Now the final system (\(\hat{A}_{BSPA} ,\hat{B}_{BSPA} ,\hat{C}_{BSPA} ,\hat{D}_{BSPA}\)) conformally as in (25).

(25)

In the preceding section, the technique will be verified, and the proposed method will be successfully validated.

To compare the effectiveness and performance of the proposed methodology with other existing reduced models available in the literature review. The Accuracy and performance of the proposed method are also validated by calculating performance indices such as an integral square error (ISE), integral absolute error (IAE), relative integral square error (RISE), integral time-weighted absolute error (ITAE) [8, 145, 183, 184], in between the original system and its reduced-order model will be calculated and these are defined as

$$ISE = \int\limits_{0}^{\infty } {[y_{1} (t) - y_{2} (t)]^{2} } dt$$
(26)
$$IAE = \int\limits_{0}^{\infty } {\left| {y_{1} (t) - y_{2} (t)} \right|} \,dt$$
(27)
$$ITAE = \int\limits_{0}^{\infty } {t\left| {y_{1} (t) - y_{2} (t)} \right|} \,dt$$
(28)
$$RISE = \int\limits_{0}^{\infty } {\left( {y_{1} (t) - y_{2} (t)} \right)^{2} dt/\int\limits_{0}^{\infty } {(g(t)} } )^{{2}} {\text{dt}}$$
(29)

where \({\text{y}}_{1} ({\text{t}})\) and \({\text{y}}_{2} ({\text{t}})\) are the outputs of the original system and ROM [63].

The reduced system's RISE values should be nearby (close) the original system, and ISE should be as small as possible. Respectively, \({\text{y}}_{1} ({\text{t}})\) and \({\text{y}}_{2} ({\text{t}})\) are system under the consideration and the ROM step responses obtained respectively from the proposed method. \({\text{g}}({\text{t}})\) is the impulse response of the system [5, 76, 185,186,187] To obtain a lower-order model from the more complex model is an issue in control systems like stability, realizability, and large-order capability. Thus, there is significant interest in investigating new algorithms that work faster and with greater precision. To find out which results come from the proposed method, which results are used, which ones are given, and which ones are used in place of these, the ISE, IAE, and ITAE and RISE known methods are different, are evaluated for accuracy.

5 Numerical Experiments and Results

Example 1

Consider the following 4th order system [63].

$${\text{G}}_{4} ({\text{s}}) = \frac{{{\text{s}}^{3} + 7.00{\text{s}}^{2} + 24.00{\text{s}} + 24.00}}{{{\text{s}}^{4} + 10.00{\text{s}}^{3} + 35.00{\text{s}}^{2} + 50.00{\text{s}} + 24.00}}$$
(30)

The HSVs of the original system are calculated as \(\upsigma\) is given by

$$\upsigma = \left[ {0.5179,0.0309,0.0124,0.0006} \right]$$
(31)

The first–second singular values are important here \(\upsigma_{2} \gg \upsigma_{3}\), and the third singular values quickly decay, as can be seen from the matrix, Eq. (31). As a result, the second-order reduction order has been chosen.

The ROM matrices obtained by using BSPA, are given as

$$\left. \begin{gathered} {\text{A}}_{{{\text{BSPA}}}} = \left[ {\begin{array}{*{20}c} { - 0.7417} & {0.7286} \\ { - 0.7286 \, } & { - 2.656} \\ \end{array} } \right],{\text{B}}_{{{\text{BSPA}}}} = \left[ {\begin{array}{*{20}c} { - 0.8765} \\ { - 0.4049} \\ \end{array} } \right], \hfill \\ {\text{C}}_{{{\text{BSPA}}}} = \left[ {\begin{array}{*{20}c} { - 0.8765} & {0.4049 \, } \\ \end{array} } \right],{\text{D}}_{{{\text{BSPA}}}} = 0.02597 \hfill \\ \end{gathered} \right\}$$
(32)

Finally, the ROM of representation in the form of the transfer function is expressed as \({\text{R}}_{2} ({\text{s}})\) of test system 2.

$${\text{R}}_{2} ({\text{s}}) = \frac{{0.02597s^{2} + 0.6925{\text{s}} + 2.501}}{{{\text{s}}^{2} + 3.98{\text{s}} + 2.501}}$$
(33)

The results of the simulation are shown in Fig. 1. The second-order ROM obtained by the suggested method is very close to the original system to the other methods available in the literature review for the same step unit, respectively. Also, the performance indices error values are calculated to check the modeling error and the closeness of the original system, as shown in Table 4. The proposed method shows that the ISE value is much lower than the value obtained from other literature. It has been seen that the ISE values are calculated to be, for Example 2 is that 4.427e–05. whereas the least value of ISE, using Moore (1981), Suman et al. (2019), Pal (1980), and Pati et al. (2014), and others are shown in the literature. Furthermore, in Table 5, a comparison analysis of the time-domain specifications between the various second-order model and the original system with help of literature has been presented. The response is to demonstrate the exact representation and effectiveness of the proposed method. The results of the proposed method were compared with existing ROM methods which show an improvement in performance error indices, time response characteristics, and time domain specifications with the same DC gain as the original system. This response allows an accurate approximation and confirms the efficacy of the technique.

Fig. 1
figure 1

Qualitative comparison of the proposed method and original system with other ROM methods in terms of step response for Example 1

Full size image
Table 4 Performance analysis of the proposed method and other existing ROM methods for Example 1
Full size table
Table 5 A Comparison of time-domain specification with Other available ROM Methods according to literature for Example 1
Full size table

Example 2

Let us consider the eighth order system represented by the following transfer function, which many researchers have previously considered [73, 195]

$${\text{G}}_{8} ({\text{s}}) = \frac{{18{\text{s}}^{7} + 514{\text{s}}^{6} + 5982{\text{s}}^{5} + 36380{\text{s}}^{4} + 12264{\text{s}}^{3} + 222088{\text{s}}^{2} + 185760{\text{s}} + 40320}}{{{\text{s}}^{8} + 36{\text{s}}^{7} + 546{\text{s}}^{6} + 4536{\text{s}}^{5} + 22449{\text{s}}^{4} + 67284{\text{s}}^{3} + 118124{\text{s}}^{2} + 109584{\text{s}} + 40320}}$$
(34)

The HSVs of the original system is calculated as \({\upsigma }\) is given by

$$\begin{gathered} \upsigma = [1.216652465935050,0.746403486833304,0.027915998321307,0.001940648946887, \hfill \\ 0.000107069466391,0.000001588964686,0.000000145817410,0.000000000050828] \hfill \\ \end{gathered}$$
(35)

From the matrix \(\upsigma\), it can be proved that \(\upsigma_{2} \gg \upsigma_{3}\). The first and second singular values are extremely important, and the third singular values quickly disappear away. As a result, the reduction order has been chosen as the second order.

The ROM matrices obtained by using BSPA, are given as

$$\left. \begin{gathered} {\text{A}}_{{{\text{BSPA}}}} = \left[ {\begin{array}{*{20}c} { - 6.644} & { \, - 2.201} \\ { \, 2.201 \, } & { - 0.0444} \\ \end{array} } \right],{\text{B}}_{{{\text{BSPA}}}} = \left[ {\begin{array}{*{20}c} { - 4.021} \\ {0.2575} \\ \end{array} } \right], \hfill \\ {\text{C}}_{{{\text{BSPA}}}} = \left[ {\begin{array}{*{20}c} { \, - 4.021} & { - 0.2575 \, } \\ \end{array} } \right],{\text{D}}_{{{\text{BSPA}}}} = 0.0595 \hfill \\ \end{gathered} \right\}$$
(36)

Finally, the ROM of representation in the form of the transfer function is expressed as \(R_{2} (s)\) of Example 2.

$${\text{R}}_{2} ({\text{s}}) = \frac{{ \, 0.0595{\text{s}}^{2} + 16.5{\text{s + }}5.141}}{{{\text{s}}^{2} + 6.688{\text{s}} + 5.141}}$$
(37)

It is shown in Fig. 2 that The ROM obtained by the proposed method is very close to the original system, compared with other methods also available in the literature. As well, the comparative analyses of ROMs in terms of ISE, IAE, ITAE, and RISE, are given in Table 6 for illustration. From this comparison, it can be observed that the proposed method obtained a good result and gives the closest approximation to the original system with less error than other ROM models. It has been seen that the ISE values are calculated to be, for example, 2, 0.0005563, whereas the least value of ISE, by other methods and recently published work by Moore (1981), Suman et al. (2019), Afzal Sikander et al. (2015) and Narwal et al. (2016) and others are depicted in Table 6. Furthermore, in Table 7, the comparison of time-domain specifications between different 2nd order models and the original system has been presented. The response is to illustrate the exact representation and effectiveness of the proposed method. The results of the proposed method have been compared with existing ROM methods which show an improvement in performance error indices, time response characteristics, and time-domain specifications with the same DC gain or steady-state value as the original system. This response allows for an accurate approximation and confirms the efficacy of the technique. Hence, it is clear that the proposed method is much better than the other well-known methods available in the literature review.

Fig. 2
figure 2

Qualitative comparison of the proposed method and original system with other ROM methods in terms of step response for Example 2

Full size image
Table 6 Performance analysis of the proposed method and other existing ROM methods for Example 2
Full size table
Table 7 A Comparison of time-domain specification with Other available ROM Methods according to literature for Example 2
Full size table

6 Conclusion and Future Scope

In this contribution, the various MOR methods for the LSD system have been thoroughly and comprehensively reviewed. It has been focused on methods with their detailed theoretical background as applied to the system. We have also discussed similarities and differences between several approaches along with their merits and demerits which may be useful to the research community. Two numerical comparisons show the advantages and disadvantages of these approaches. There are a few new viewpoints to this area which has been elaborated. We have also, highlighted the impressive improvements made over the last few years with respect to MOR applied to linear systems, although several key challenges remain to be investigated and further developments in numerical methods are, yet to be addressed. In addition, an application to my previous work for reducing the order of the large-scale dynamic LTI system has been further investigated in this paper. The hybrid technique applied was found to be superior to the conventional method (BT) or other existing methods. This hybridization approach using BT and SPA Approach has been found to effectively compensate for the demerits of each other. Furthermore, the same technique has been illustrated with a couple of very promising examples of a continuous LTI system. The step response comparison shows that the ROM obtained by the method applied provides a close approximation to the HOS. In addition, the accuracy, validation, and superior performance of the presented method have been demonstrated by comparing the performance indices with various similar outcomes existing in the literature. Applicability to large-scale systems may increase the benefits of the method however it which is a matter of further investigation. Some of them are currently ongoing at the present. This procedure can be extended to the design of the state feedback controller, optimum, H-infinity controller, etc.