An EPQ model for three-layer supply chain with partial backordering and disruption: Triangular dense fuzzy lock set approach

Abstract

This article deals with three-echelon supply chain (SC) network involving flow of raw materials with imperfect quality, the manufacturer and multiple retailers under the effect of learning experiences in fuzzy decision-making process. Existing literature explores the SC model under full backordering and disruption. Thus, in this study we first develop a production-inventory control problem accompanied with partial backlogging and random disruptions. Any batch received from the supplier is inspected by the manufacturer and if any of them are found to be flawed then all the goods in the inspected batch are rejected. However, we present a case study for problem definition and to comprehend the model into practical applicability. To minimize the aggregate cost of the SC we have utilized the Triangular dense fuzzy lock set for controlling the cost vector of the proposed objective function of the model. Utilizing new defuzzification method and applying the proper keys, chosen by the decision maker, it is possible to minimize the average system cost exclusively. Finally, graphical illustrations and sensitivity analysis are made to justify the model.

1 Introduction

The traditional decision-making problem of a supply chain was determined by a single decision maker (DM). At the early stage, a classical economic order quantity (EOQ) model was introduced by Harris [1]. Taft [2] extended his work and studied the basic economic production quantity (EPQ) model. Many researchers have been considered EPQ models (Li et al. [3], Zhang [4], Chiu and Tink [5], Sana [6]). Shortage is one of the wide spread assumptions in several inventory problems. Customers’ behaviors in the shortage situation have led to another assumption in formulating different model. Montgomery [7] considered one of those behaviors and extended the EOQ pattern through partial backordering (EOQ-PBO). The EOQ-PBO problem has been studied by several researchers (Hsieh and Dye [8], Taleizadeh et al. [9], Pentico et al. [10], Zhang et al. [11], Sicilia et al. [12], San-José et al. [13, 14], Karimi-Nasab and Wee [15], San-José et al. [16]). Mak [17] developed an EPQ-PBO model with time dependent-backorder cost and constant unit lost sale cost. Pentico and Drake [18] spread the Mak’s program greatly and proposed a new method to optimize the objective function. San-José et al. [16] studied an EPQ-PBO model with a combination between the dispatching policies LIFO and FIFO. By relaxing perfect quality of the supply process, the inventory models with disruption (EOQD), were studied (Parlar and Berkin [19], Wee et al. [20], Chang and Ho [21], Salehi et al. [22]).

However, disruptions in supply chains can occur due to natural reasons, labor strikes, machine break downs, supplier stock outs or quality problems. Chiu et al. [23] considered disruptions due to machine breakdowns. They developed an EPQ model with disruption (EPQD) when some machine-breakdowns occurred according to a Poisson process. They also proposed an EPQD problem through unplanned machine failures and developed an optimal replenishment policy. Paul et al. [24] modeled an imperfect production inventory system and provided a genetic algorithm based search technique to solve the mathematical model. Some studies have been considered inventory in supply chain decisions. Hu et al. [25] studied the ordering decisions in a situation of the PBO in two-echelon supply chain.

In addition, the article of Skouri et al. [26] was a part of EOQ problem for single-echelon inventory. The demand rate, all cost components are constant and the shortages are fully backordered. Furthermore, Konstantaras et al. [27] studied over an EOQ model for independent endogenous supply disruption. In this article they developed a news vendor problem of fully backordered single-echelon supply chain model where the demand rate is assumed to be cumulative time dependent function. Ritha and Nishandhi [28] developed a single vendor multi-buyer’s model for rejection of supply batches for nonstandard items. Model for exogenous disruption was studied by Heiman and Waage [29], Snyder [30], Snyder et al. [31], Bark and Arreola-Risa [32]. Atan and Synder [33] studied a detailed review of supply disruption in inventory management problems where the concepts of ‘dry’ and ‘wet’ period backlogging demand are extensively discussed.

To study with nonrandom and uncertain environment we must trust the fuzzy system. Numerous articles have been found in fuzzy system. Some notable recent works in fuzzy system are discussed as follows: Kumar and Goswami [34, 35] proposed a fuzzy random EPQ model for imperfect quality items with possibility and necessity constraints. Mahata [36] investigated the learning effect of the unit production time on optimal lot size for the imperfect production process with partial backlogging of shortage quantity in fuzzy random environments. He assumed that the set-up cost, the average holding cost, the backorder cost, the raw material cost and the labor cost are characterized as fuzzy variables and the elapsed time until the machine shifts from “in-control” state to “out-of-control” state is characterized as a fuzzy random variable. Articles on learning effect have been discussed wisely by Shekarian et al. [37]. Alternatively, De and Beg [38, 39] introduced dense fuzzy approach to capture the measure of learning experiences recent times. After that the idea of dense fuzzy number was extended by De and Mahata [40]. To do this they have developed a cloud type fuzzy number incorporating the inventory cycle time to the measure of fuzziness. To resolve the difficulties and to defuzzify the cloud type fuzzy number they invented a new defuzzification method also. Recently, Karmakar et al. [41] first established a pollution sensitive dense fuzzy economic production quantity model with cycle time dependent production rate. Concurrently, De and Sana [42] developed a backlogging model implementing a phi coefficient test for pentagonal fuzzy number. Beyond this, researchers like De and Sana [43, 44], Karmakar et al. [45] have kept a remarkable destination over the fuzzy backlogging models. Chakraborty et al. [46] investigated a supply chain model with stock dependent demand under fuzzy random and bifuzzy environments.

However, in the field of trade credit models researchers like Mahata and Goswami [47, 48], Mahata and Mahata [49] have applied fuzzy decision theory to optimize the model. In addition, if we consider the cases of group decision making under fuzzy as well as the intuitionistic fuzzy environment of modern times then Xu and Zhou [50], Wang and Xu [51], Ding et al. [52] will come under the subject domain itself. Thus, in fuzzy domain we see none of the researchers have studied with fuzzy lock environment over supply chain production inventory model. Basically, in fuzzy system the role of DM is quite inactive; in dense fuzzy system the DM gains learning experiences to implement it to the inventory process. In fact, the existing models are studied with single judgement by single DM, though some fuzzy extension (cases of soft hesitant fuzzy, etc.) where the group DM has been incorporated wisely but in learning fuzzy system the concept of closed formed multiple DM has not yet been studied.

Based on these discussions, we may summarize that, the supply chain disruption models have been studied by several researcher in which most of the articles belong to single-layer EOQ models with fixed cost components, demand functions are deterministic or function of time alone, shortages are fully backlogged, rejection of supply batches covers ‘all or none’ policy. However, in fuzzy domain articles of disruption SC model is not found yet. The main contribution of this article in the light of managerial insights is thus stated as follows:

• (i) First of all, we have analyzed a three-echelon SC model. The quality of raw materials of the supplier is imperfect, and the “all or none” inspection policy is used by the manufacturer. The production rate of the manufacturer is stable and retailer’s surplus demand is partially backordered. An EPQ problem through random disruption and partial backordering (EPQD-PBO) is extended. The cost function of the mathematical model includes holding, backlogging and missing sales (or goodwill loss) costs. Applying these cost components, we developed a three-layer SC model to optimize its expected total average objective function.

• (ii) Considering a case study, incorporating flexibility of several cost parameters as triangular lock fuzzy we have analyzed the fuzzy objective function for further investigation.

• (iii) We have introduced the concept of group decision making by means of application of multiple keys in fuzzy lock for a DM in the three-layer SC model.

• (iv) Finally, numerical study, sensitivity analysis, graphical illustrations are performed for model validation.

The major findings in the related literature are summarized in table 1 which indicates that this paper was different from previous study.

Table 1 Gap analysis for major related literature.

2 Preliminaries

2.1 Triangular dense fuzzy set (TDFS) (De and Beg [38, 39])

Definition 1

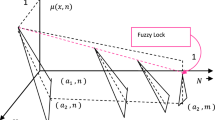
Let $\tilde{A}$ be the fuzzy number whose components are the elements of ${\mathcal{R}} \times N$, ${\mathcal{R}}$ being the set of real numbers and $N$ being the set of natural numbers with the membership grade satisfying the functional relation $\mu :{\mathcal{R}} \times N \to \left[ {0,1} \right]$. Now as $n \to \infty$ if $\mu \left( {x,n} \right) \to 1$ for some $x \in {\mathcal{R} }\,{\text{and}}\, n \in N$ then we call the set $\tilde{A}$ as dense fuzzy set. If $\tilde{A}$ is triangular then it is called TDFS. Now, if for some n in N, $\mu \left( {x,n} \right)$ attains the highest membership degree 1 then the set itself is called “Normalized Triangular Dense Fuzzy Set” or NTDFS.

Example 1

As per definition let us assume the NTDFS as

$$ \tilde{A} = \left\langle {a_{2} \left( {1 - \frac{\rho }{1 + n}} \right), a_{2} , a_{2} \left( {1 + \frac{\sigma }{1 + n}} \right)} \right\rangle , for\; 0 < \rho , \sigma < 1 , n \ge 0 $$

(1)

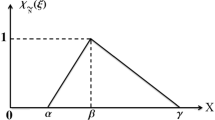
and the corresponding memberships function is defined by (2) with thephical iustration (shown in figure 1) stated below:

$$ \mu \left( {x,n} \right) = \left\{ {\begin{array}{ll} 0 & {\text{if}\; x< {a_{2} \left( {1 - \frac{\rho }{1 + n}} \right) \;{\text{and}}\; x} > a_{2} \left( {1 + \frac{\sigma }{1 + n}} \right)} \\ {\left\{ {\frac{{x - a_{2} \left( {1 - \frac{\rho }{1 + n}} \right)}}{{\frac{{\rho a_{2 } }}{1 + n}}}} \right\}} & {\begin{array}{ll} {\text{if}\; a_{2} \left( {1 - \frac{\rho }{1 + n}} \right) \le x \le a_{2 } } \\ \end{array} } \\ {\left\{ {\frac{{a_{2} \left( {1 + \frac{\sigma }{1 + n}} \right) - x}}{{\frac{{\sigma a_{2 } }}{1 + n}}}} \right\}} & {\begin{array}{ll} {\begin{array}{ll} { \text{if}\;a_{2 } \le x \le a_{2} \left( {1 + \frac{\sigma }{1 + n}} \right)} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right. $$

(2)

Figure 1

Membership function of NTDFS.

2.2 Triangular Dense Fuzzy Lock Sets(TDFLS) (De [53])

Definition 2

Let $\tilde{A} = a_{1} ,a_{2} ,a_{3}$ be the TDFS whose components are the elements of ${\mathcal{R}} \times N$, then if its membership function $\mu :{\mathcal{R}} \times N \to \left[ {0,1} \right]$ satisfies as $n \to \infty$ if $\mu \left( {x,n} \right){ \nrightarrow }1$ for some $x \in {\mathcal{R} }\,{\text{and}}\, n \in N$ and in this case the index value $I(\tilde{A}){ \nrightarrow } a_{2}$ then the TDFS $\tilde{A}$ is called Triangular dense fuzzy lock set. It is also normal by its initial assumptions over NTDFS.

Definition 3

Let the TDFS $\tilde{A} = \left\langle {a\left\{ {1 - \rho f_{n} } \right\}, a,a\left\{ {1 + \sigma g_{n} } \right\}} \right\rangle$ for $0 < \rho , \sigma \in {\mathcal{R}}$ and $f_{n} , g_{n}$ are two Cauchy sequences of functions having converging points $\frac{1}{{k_{1} }} \,{\text{and }}\,\frac{1}{{k_{2} }}$, $0 \ne k_{1} , k_{2} \in {\mathcal{R}}$ respectively then the fuzzy set $\tilde{A}$ is called Triangular dense fuzzy lock set with double keys $k_{1} , k_{2}$. The membership function along with its graphical representation is given by (3) and figure 2, respectively and they are stated below:

$$ \mu \left( {x,n} \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\;\;x < a\left\{ {1 - \rho f_{n} } \right\}\;{\text{and}}\;x > a\left\{ {1 + \sigma g_{n} } \right\}} \hfill \\ {\left\{ {\frac{{x - a\left\{ {1 - \rho f_{n} } \right\}}}{{a\rho f_{n} }}} \right\}} \hfill & {{\text{if}}\;\;a\left\{ {1 - \rho f_{n} } \right\} \le ~x \le a} \hfill \\ {\left\{ {\frac{{a\left\{ {1 + \sigma g_{n} } \right\} - x}}{{a\sigma g_{n} }}} \right\}} \hfill & {{\text{if}}\begin{array}{ll} {\begin{array}{ll} {~a \le ~x \le } \\ \end{array} a\left\{ {1 + \sigma g_{n} } \right\}} \\ \end{array} } \hfill \\ \end{array} } \right. $$

(3)

Figure 2

Membership function of TDFLS.

Example 2

Let us assume that the component functions of a TDFLS be $f_{n} = \frac{1}{{k_{1} }} - \frac{1}{n + 1}\; \text {and} \;g_{n} = \frac{1}{{k_{2} }} - \frac{1}{n + 1}$ then the TDFS can be put as $\tilde{A} = \left\langle {a\left\{ {1 - \rho \left( {\frac{1}{{k_{1} }} - \frac{1}{n + 1}} \right)} \right\}, a,a\left\{ {1 + \sigma \left( {\frac{1}{{k_{2} }} - \frac{1}{n + 1}} \right)} \right\}} \right\rangle$ for $0 < \rho ,\sigma \in {\mathcal{R}}$. Thus, constructing its membership function as per usual way and taking help of De and Beg [38], the index value of the fuzzy objective function reduces to

$$ \begin{aligned} I\left( {\tilde{A}} \right) = & \frac{1}{2N}\mathop \sum \limits_{n = 0}^{N} \mathop \int \limits_{0}^{1} \left\{ {L^{ - 1} \left( {\alpha ,n} \right) + R^{ - 1} \left( {\alpha ,n} \right)} \right\}d\alpha \\ = & a\left[ {1 + \frac{1}{4}\left( {\frac{\sigma }{{k_{2} }} - \frac{\rho }{{k_{1} }}} \right) + \frac{1}{4N}\left( {\frac{\sigma }{{k_{2} }} - \frac{\rho }{{k_{1} }}} \right)\left\{ {1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots + \frac{1}{N} + \frac{1}{{\left( {1 + N} \right)}}} \right\}} \right] \\ \end{aligned} $$

(4)

Now, (8) shows that, the series

$$ \frac{1}{N}\left\{ {1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots + \frac{1}{N} + \frac{1}{{\left( {1 + N} \right)}}} \right\} \to 0\;{\text{as}}\;N \to \infty ,{\text{so}}\;I\left( {\tilde{A}} \right) \to a\left\{ {1 + \frac{1}{4}\left( {\frac{\sigma }{{k_{2} }} - \frac{\rho }{{k_{1} }}} \right)} \right\} $$

(5)

2.3 Implication of triangular dense fuzzy lock sets (TDFLS)

The modern research on any kind of inventory management problem (IMP) basically deals with behavioral study. The behavior of an IMP is being modified with time through the application of learning experiences and periodic monitoring of the process itself. Also learning experiences is directly related to how frequent the review works have been performed within the entire cycle time of an inventory. Thus, for practical use, it is impossible to perform review works for infinite times because of several constraints like limitation on time, staff problem and monetary problem, etc. Moreover, it has been observed that, though the adequate number of reviews has been performed in due time but due to some other (existence of extraneous variables) reasons and hence the decision makers (DM) are unable to minimize their system cost as a whole. But it is natural that, the DM can do everything by means of taking cost effective measure (component-wise controlling system expenditures) of an inventory even in a supply chain also. To capture the situation no such methodology has been developed yet. In fuzzy environment, especially with the use of lock set the DM could definitely be able to minimize the system costs alone.

3 Case study and problem statement

In the capital city of West Bengal, India, we visited a toy producing company last month. After primary discussion with the manager the exact facts of the production – supply process has been noted. It is seen that raw materials are arriving from different suppliers and they are inspected batch-wise and if in any batch is found to be defective then the whole raw materials have been rejected instantly. Then to run the production process items are backordered partially until the good quality has been received. On the other hand, if it is found to be good quality then it is accepted and letting it ready to go for manufacturing system. Also, it is observed that, the occurrence of getting two successive positive inventories is a random variable. The goodwill loss during backorder period is considered. Thus, the problems of the manager of the company is defined in such a way that the good will loss as well as the average system cost will be controlled:

• (a) What will be the actual cycle time (between two defective or standard batch received) of the production process?

• (b) What will be the actual cycle time between two positive inventories?

• (c) What is the proportion when the inventory behaves positively?

• (d) What is the expected average inventory cost?

The information associated with the production process is given in table 2.

Table 2 Observed survey data for toy company.

4 Model description

Consider the three stages supply chain where the first level is the supplier of raw materials with random imperfect quality. The second level is the manufacturer who produces items with a constant production rate, and the third level involves some retailers/customers in which the demand rate is deterministic. The schematic structure of the supply chain is shown in figure 3.

Figure 3

Schematic 3-layer supply chain structure.

The essential primary suppositions have been used in this paper listed as follows:

• (1) The demand is constant.

• (2) The replenishment is ordered with a fixed rate.

• (3) Shortfalls are permitted and partially backordered.

• (4) The backorders are satisfied before the arriving orders (FIFO policy).

• (5) There is a fixed time interval T in the middle of two succeeding.

• (6) Imperfect deliveries happening with a definite probability, and they are independent of each other.

• (7) An “all or none” inspection plan is considered.

• (8) All cost components of the supply chain are assumed to be dense fuzzy lock set.

4.1 Mathematical model

Here we develop the exact EPQ model where the several possibilities on inventory situations may occur. Generally, two situations may occur within the inspection department: (a) either the batches of raw material have always the required quality (in the case for perfect supply quality, $\lambda = 0$), or (b) some batches with imperfect quality level ($\lambda > 0$). In both cases, we consider that the fraction of backordered demand is $\beta$ (in $\left[ {0, 1} \right]$). Therefore, the two extreme cases correspond to $X = 0$, in which the whole demand through the stock out period is fallen (full lost sales), and $X = 1$, in which all demands are willing to wait for the next production run (complete backorders) is possible in both situations.

For perfect quality situation ($\lambda = 0$), all production-inventory cycles have the same length $T^{{\prime }} = T$ and we get the deterministic EPQ with partial backordering. However, in the second situation the length of the production-inventory cycles is a random variable, whose probability distribution depends on the proportion ($\lambda$) that a supply batch is rejected.

In the case of imperfect supply quality items, the defective raw material batches have been rejected and the quantity of the next ordering (which would be received after $T$) should be enough to cover all the remaining demand. So all backordered demand from time $T$ until time $\left( {X + 1} \right)T$, should be supplied by producing during $\frac{\beta DXT}{P - \beta D}$ units of time (as shown in figure 4). In this way we can define, the duration of any inventory cycle $T^{\prime}$ relates to the random variable $X$ as: $T^{\prime} = \left( {X + 1} \right)T + \frac{\beta DXT}{P - \beta D}$. Additionally, $X$ is a geometric random variable with parameter $\uplambda$ (see Salehi et al. [22]) and probability mass function ${ \Pr }\left( {{\text{X}} = {\text{x}}} \right) =\uplambda^{\text{x}} \left( {1 -\uplambda} \right), {\text{x}} \ge 0$.

Figure 4

A typical cycle of length $T^{\prime}$ in EPQD-PBO.

A typical cycle ($T^{\prime} = 2T + \frac{\beta DT}{P - \beta D})$ is illustrated in figure 4 (where a faulty raw material delivery at time $T$ has been refused). As shown in figure 4, a regular production and inventory interval (the first-time interval of length $T$ in the inventory cycle) can be split into four time-intervals. The lengths of these intervals are (Pentico et al. [10]):

$$ t_{1} = \delta T\left( {\frac{D}{P}} \right),t_{2} = \delta T\left( {1 - \frac{D}{P}} \right),t_{3} = \left( {1 - \delta } \right)T\left( {1 - \frac{\beta D}{P}} \right)\;{\text{and}}\;t_{4} = \left( {1 - \delta } \right)T\left( {\frac{\beta D}{P}} \right). $$

We formulate the model with respect to two decision variables $\left( {\delta , T} \right)$. So, the inventory-related costs of the manufacturer $CC \left( {\delta , T, X} \right)$ in a cycle of length $T^{\prime}$ can be obtained as follows:

$$ \begin{aligned} CC\left( {\delta ,T,X} \right) = & \left( {X + 1} \right)C_{o} + \frac{{C_{h} DT^{2} \delta^{2} }}{2}\left( {1 - \frac{D}{P}} \right) + \frac{{\beta C_{b} DT^{2} \left( {1 - \delta } \right)^{2} }}{2}\left( {1 - \frac{\beta D}{P}} \right) \\ & \quad + \frac{{\beta C_{b} DT^{2} X^{2} }}{2}\left( {1 + \frac{\beta D}{P - \beta D}} \right) + C_{l} DT\left( {1 - \beta } \right)\left( {X + 1 - \delta } \right) + C_{l} DT\left( {1 - \beta } \right)\left( {\frac{\beta DX}{P - \beta D}} \right) \\ \end{aligned} $$

(6)

The expected value and the second moment of $X$ can be obtained from: ${\text{E}}\left( X \right) = \frac{\lambda }{1 - \lambda }$ and ${\text{E}}\left( {X^{2} } \right) = {\text{Var}}\left( X \right) + \left( {{\text{E}}\left( X \right)} \right)^{2} = \frac{\lambda }{{\left( {1 - \lambda } \right)^{2} }} + \frac{{\lambda^{2} }}{{\left( {1 - \lambda } \right)^{2} }} = \frac{{\lambda \left( {1 + \lambda } \right)}}{{\left( {1 - \lambda } \right)^{2} }}$. Therefore, the predictable value of $CC \left( {\delta , T, X} \right)$ in (6) is given by:

$$ \begin{aligned} C\left( {\delta ,T} \right) = & \frac{{C_{o} }}{1 - \lambda } + \frac{{C_{h} DT^{2} \delta^{2} }}{2}\left( {1 - \frac{D}{P}} \right) + \frac{{\beta C_{b} DT^{2} \left( {1 - \delta } \right)^{2} }}{2}\left( {1 - \frac{\beta D}{P}} \right) + \frac{{\beta C_{b} DT^{2} \left( {1 + \frac{\beta D}{P - \beta D}} \right)}}{2}\frac{{\lambda \left( {1 + \lambda } \right)}}{{\left( {1 - \lambda } \right)^{2} }} \\ & \quad + C_{l} DT\left( {1 - \beta } \right)\left( {\frac{1}{1 - \lambda } - \delta + \frac{\beta D\lambda }{{\left( {1 - \lambda } \right)\left( {P - \beta D} \right)}}} \right) \\ \end{aligned} $$

(7)

Again, $T^{\prime} = \left( {X + 1} \right)T + \frac{\beta DXT}{P - \beta D}$, so we have

$$ {\text{E}}(T^{'} ) = T\left( {E\left( X \right) + 1 + \frac{\beta DE\left( X \right)}{P - \beta D}} \right) = T\left( {\frac{P - \beta D + \beta D\lambda }{{\left( {1 - \lambda } \right)\left( {P - \beta D} \right)}}} \right) $$

(8)

To simplify the notation, we define $\eta = \left( {\frac{P - \beta D + \beta D\lambda }{{\left( {1 - \lambda } \right)\left( {P - \beta D} \right)}}} \right),$ consequently the every expected inventory cycle can be simplified as:

$$ {\text{E}}(T^{'} ) = \eta T $$

(9)

Hence, the total average expected inventory cost per unit time is obtained as:

$$ \begin{aligned} TC\left( {\delta ,T} \right) = & \frac{{C\left( {\delta ,T} \right)}}{{{\text{E}}({\text{T}}^{'} )}} = \frac{{C_{o} }}{{\eta T\left( {1 - \lambda } \right)}} + \frac{{C_{h} DT\delta^{2} }}{2\eta }\left( {1 - \frac{D}{P}} \right) + \frac{{\beta C_{b} DT\left( {1 - \delta } \right)^{2} }}{2\eta }\left( {1 - \frac{\beta D}{P}} \right) \\ & \quad + \frac{{\beta C_{b} DTP\lambda \left( {1 + \lambda } \right)}}{{2\eta \left( {P - \beta D} \right)\left( {1 - \lambda } \right)^{2} }} + \frac{{C_{l} D\left( {1 - \beta } \right)\left( {\eta - \delta } \right)}}{\eta } \\ \end{aligned} $$

(10)

4.1a Particular case Recalling (7), Let $P \to \infty \,and \,\beta \to 1$, then $C\left( {\delta ,T} \right) = \frac{{C_{o} }}{1 - \lambda } + \frac{{C_{h} D^{2} T^{2} \delta^{2} }}{2D} + \frac{{C_{b} D^{2} T^{2} \left( {1 - \delta } \right)^{2} }}{2D} + \frac{{C_{b} D^{2} T^{2} }}{2D}\frac{{\lambda \left( {1 + \lambda } \right)}}{{\left( {1 - \lambda } \right)^{2} }} \Rightarrow \frac{{C_{o} }}{1 - \lambda } + \frac{{C_{h} \left( {Q - J} \right)^{2} }}{2D} + \frac{{C_{b} J^{2} }}{2D} + \frac{{C_{b} }}{2D}\frac{{\left( {Q - J} \right)^{2} \lambda \left( {1 + \lambda } \right)}}{{\left( {1 - \lambda } \right)^{2} }}\, \text{Where},Q = \delta DT\, \text{and}\, J = \left( {1 - \delta } \right)DT$, which is very close to the results obtained by Skouri et al. [26].

4.2 Model optimization

To solve the objective function of the manufacturer; (${\text{Minimize }}TC\left( {\updelta,T} \right)$, subject to $T > 0$ and $0 \le \delta \le 1$) we can simplify the notation and rewritten Eq. (10) as follows:

$$ TC\left( {\delta ,T} \right) = \frac{{C_{o}^{'} }}{T} + C_{h}^{'} DT\delta^{2} + \beta C_{b}^{'} DT\left( {1 - \delta } \right)^{2} + \beta C_{b}^{''} DT + C_{l}^{'} D\left( {\eta - \delta } \right) $$

(11)

where

$$ C_{o}^{'} = \frac{{C_{o} }}{{\eta \left( {1 - \lambda } \right)}},C_{h}^{'} = \frac{{C_{h} }}{2\eta }\left( {1 - \frac{D}{P}} \right),C_{b}^{'} = \frac{{C_{b} }}{2\eta }\left( {1 - \frac{\beta D}{P}} \right),C_{b}^{''} = \frac{{C_{b} \left( {1 + \frac{\beta D}{P - \beta D}} \right)}}{2\eta }\frac{{\lambda \left( {1 + \lambda } \right)}}{{\left( {1 - \lambda } \right)^{2} }},C_{l}^{'} = \frac{{C_{l} \left( {1 - \beta } \right)}}{\eta }. $$

For a fixed value of $T$, Eq. (11) is a quadratic function in $\delta$ that attains its minimal at the point:

$$ \delta^{*} \left( T \right) = \left\{ {\begin{array}{*{20}c} {\frac{{C_{l}^{'} + 2\beta C_{b}^{'} T}}{{2T\left( {C_{h}^{'} + \beta C_{b}^{'} } \right)}}} & {{\text{if}}\,T \ge C_{l}^{'} /2C_{h}^{'} } \\ 1 & {{\text{if}}\,T < C_{l}^{'} /2C_{h}^{'} } \\ \end{array} } \right. $$

(12)

With the objective value

$$ TC\left( {\delta^{*} \left( T \right),T} \right) = \left\{ {\begin{array}{*{20}l} {W_{1} \left( T \right) = \frac{{C_{o}^{'} }}{T} + (C_{h}^{'} + \beta C_{b}^{''} )DT + C_{l}^{'} D\left( {\eta - 1} \right)} \hfill & {{\text{if}}\,T < C_{l}^{'} /2C_{h}^{'} } \hfill \\ {W_{2} \left( T \right) = \frac{{a_{o} }}{T} + a_{1} T + a_{2} } \hfill & {{\text{if}}\,T \ge C_{l}^{'} /2C_{h}^{'} } \hfill \\ \end{array} } \right. $$

(13)

where

$$ \begin{aligned} a_{o} = & \frac{{4C_{o}^{{\prime }} \left( {C_{h}^{{\prime }} + \beta C_{b}^{{\prime }} } \right) - C_{l}^{{{\prime }2}} D}}{{4\left( {C_{h}^{ '} + \beta C_{b}^{ '} } \right)}}, \\ a_{1} = & \frac{{\beta D\left[ {C_{h}^{{\prime }} \left( {C_{b}^{{\prime }} + C_{b}^{{\prime \prime }} } \right) + \beta C_{b}^{{\prime }} C_{b}^{{\prime \prime }} } \right]}}{{C_{h}^{{\prime }} + \beta C_{b}^{{\prime }} }} \ge 0, \\ a_{2} = & \frac{{C_{l}^{{\prime }} D\left( {\alpha C_{h}^{{\prime }} + \left( {\eta - 1} \right)\beta C_{b}^{{\prime }} } \right)}}{{C_{h}^{{\prime }} + \beta C_{b}^{{\prime }} }} \ge 0. \\ \end{aligned} $$

Next, we determine the optimal value T^*such that $TC\left( {\delta^{ * } \left( T \right),T} \right)$ is minimized. Notice that $TC\left( {\delta^{*} \left( T \right),T} \right)$ is a continuous function for all $T > 0$.The first derivative of TC($\delta$ ^*(T),T) is

$$ \frac{d}{dT}TC\left( {\delta^{*} \left( T \right),T} \right) = \left\{ {\begin{array}{*{20}l} {W_{1}^{'} \left( T \right) = \frac{{ - C_{o}^{'} }}{{T^{2} }} + (C_{h}^{'} + \beta C_{b}^{''} )D} \hfill & {{\text{if }}T < C_{l}^{'} /2C_{h}^{'} } \hfill \\ {W_{2}^{'} \left( T \right) = \frac{{ - a_{o} }}{{T^{2} }} + a_{1} } \hfill & {{\text{if }}T > C_{l}^{'} /2C_{h}^{'} } \hfill \\ \end{array} } \right. $$

(14)

Since $W_{1}^{'} \left( {C_{l}^{'} /2C_{h}^{'} } \right) = W_{2}^{'} \left( {C_{l}^{'} /2C_{h}^{'} } \right),$ the above derivative is a continuous function for $T > 0$.

We have the following cases:

• 1. If a_o < 0, after thatW₂(T) is a strictly growing function for $T > C_{l}^{'} /2C_{h}^{'} ,$ W₁(T) is a strictly reducing function for T∈(0,T_o) in addition a strictly increasing function for $T\left( {T_{o} ,C_{l}^{'} /2C_{h}^{'} } \right)$, where

$$ T_{o} = \sqrt {\frac{{C_{o}^{'} }}{{D\left( {C_{h}^{'} + \beta C_{b}^{''} } \right)}}} $$

(15)

Therefore, TC($\delta$ ^*(T),T) attains its minimal at $T_{o}$.

• 2. If a_o = 0, then two situations may occur:

  • (i) if β = 0 then W₂(T) is a constant function and W₁(T) is strictly decreasing function for $T\left( {0,C_{l}^{'} /2C_{h}^{'} } \right)$. In consequence, TC($\delta^*$ (T), T) attains minimal at any point of the interval [$C_{l}^{'} /2C_{h}^{'} ,\infty )$.

  • (ii) If $\beta > 0$ then it is immediate that TC($\delta^*$ (T), T) attains minimal at T_o.

• 3. If a_o > 0, we consider the following situations:

  • (i) if $\beta = 0$ then W₁(T) is a strictly reducing function for $T\left( {0,C_{l}^{'} /2C_{h}^{'} } \right)$ and W₂(T) is also strictly reducing in its domain. In consequence, TC($\delta$ ^*(T),T) attains its minimum at ∞.

  • (ii) If $\beta > 0$ then: (a) TC($\delta$ ^*(T),T) attains its minimal at T_o when $T_{o} \le C_{l}^{'} /2C_{h}^{'}$, (b) otherwise, TC($\delta$ ^*(T),T) obtains its minimal at T₁, where

$$ T_{1} = \sqrt {\frac{{a_{o} }}{{a_{ 1} }}} $$

(16)

4.3 Numerical experiments

Based on the data set obtained from Case study (table 2), we obtain the following optimal solution along with their partial backorder fractional and probabilistic variation (as shown in table 3).

Table 3 Average inventory cost variation due to various $\beta \,{\text{and}}\, \lambda .$

From the above table it is seen that, at $\lambda = 0.10$ (obtained from case study), for partial backorder fraction $\beta = 0.80$ the average inventory cost is minimum and for 1.2124 month cycle time with $\delta^{*} = 0.9549$. However, the results showing $\delta^{*} = 1.0$ for any other cases except $\beta = 0.80$ and these cases are not supporting the case study model (because of $\delta^{*} < 1.0$ in not satisfied). Thus the value of the crisp model is taken as $Z^{*} = 1162.573$ with $T^{*} = 0.5364$, $T^{/*} = 1.2124.$ Now if we consider the cost variation due to the variation of the production and demand rate then we observe that the system cost is increasing with them (table 4).

Table 4 Variation of inventory cost due to several demand and production rate.

5 Fuzzy mathematical model

Let us consider the cost coefficients associated in the three-layer supply chain production inventory model be flexible in nature. We assume these flexible values in such a way that the decision maker can perform a final decision according to his/her needs. Such situation can be handled through the proper use of Triangular dense fuzzy lock set over learning experiences to the specific cost vectors of the objective function alone. Therefore, we shall fuzzify the inventory costs all at a time. A schematic overview of the fuzzy model has been presented in figure 5.

Figure 5

Schematic overview of three-layer fuzzy lock SC model.

Now, recalling the average expected supply chain inventory cost (10) re-defined as:

$$ Z = \frac{{C_{o} }}{{\eta T\left( {1 - \lambda } \right)}} + \frac{{C_{h} DT\delta^{2} }}{2\eta }\left( {1 - \frac{D}{P}} \right) + \frac{{\beta C_{b} DT}}{2\eta }\left\{ {\left( {1 - \delta } \right)^{2} \left( {1 - \frac{\beta D}{P}} \right) + \frac{{P\lambda \left( {1 + \lambda } \right)}}{{\left( {P - \beta D} \right)\left( {1 - \lambda } \right)^{2} }}} \right\} + \frac{{C_{l} D\left( {1 - \beta } \right)\left( {\eta - \delta } \right)}}{\eta } $$

(17)

$$ \Rightarrow Z = \mathop \sum \limits_{i = 0}^{3} C_{i} f_{i} $$

(18)

where

$$ \left\{ {\begin{array}{*{20}c} {C_{0} = c_{0} ,C_{1} = c_{h} , C_{2} = c_{b} , C_{3} = c_{l} } \\ {f_{0} = \frac{P - \beta D}{{T\left( {P - \beta D + \beta D\lambda } \right)}}} \\ {f_{1} = \frac{{DT\delta^{2} \left( {1 - \lambda } \right)\left( {P - \beta D} \right)}}{{2\left( {P - \beta D + \beta D\lambda } \right)}}\left( {1 - \frac{D}{P}} \right)} \\ {f_{2} = \beta DT\left[ {\frac{{\left( {1 - \delta } \right)^{2} }}{2}\left( {1 - \frac{\beta D}{P}} \right) + \frac{{P\lambda \left( {1 + \lambda } \right)}}{{\left( {P - \beta D} \right)\left( {1 - \lambda } \right)^{2} }}} \right]\frac{{\left( {1 - \lambda } \right)\left( {P - \beta D} \right)}}{{\left( {P - \beta D + \beta D\lambda } \right)}}} \\ {f_{3} = \left( {1 - \beta } \right)D\left[ {\frac{{P\left( {1 - \delta } \right) - \beta D\left( {1 - \lambda } \right)\left( {1 - \delta } \right) + \lambda P\delta }}{P - \beta D + \beta D\lambda }} \right]} \\ \end{array} }\right.$$

(19)

Now we assume the cost vector moves towards a triangular dense fuzzy lock set and the corresponding average inventory cost is turned as

$$ \tilde{Z} = \mathop \sum \limits_{i = 0}^{3} \tilde{C}_{i} f_{i} $$

(20)

with $\tilde{C}_{i} = \left\langle {c_{i} \left\{ {1 - \rho_{i} \left( {\frac{1}{{k_{1i} }} - \frac{1}{n + 1}} \right)} \right\}, c_{i} ,c_{i} \left\{ {1 + \sigma_{i} \left( {\frac{1}{{k_{2i} }} - \frac{1}{n + 1}} \right)} \right\}} \right\rangle \quad {\text{for}}\ i = 0 , 1, 2 \ and \ 3$

Therefore, as per De [53], the index value of the fuzzy objective is given by

$$ I\left( {\tilde{Z}} \right) = W = \frac{1}{2N}\mathop \sum \limits_{n = 0}^{N} \mathop \sum \limits_{i = 0}^{3} I\left( {\tilde{C}_{i} } \right)f_{i} $$

$$ = \mathop \sum \limits_{i = 0}^{3} f_{i} c_{i} \left[ {1 + \frac{1}{4}\left( {\frac{{\sigma_{i} }}{{k_{2i} }} - \frac{{\rho_{i} }}{{k_{1i} }}} \right) + \frac{1}{4N}\left( {\frac{{\sigma_{i} }}{{k_{2i} }} - \frac{{\rho_{i} }}{{k_{1i} }}} \right)\left\{ {1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots + \frac{1}{N} + \frac{1}{{\left( {1 + N} \right)}}} \right\}} \right] $$

Thus, the crisp equivalent problem of the fuzzy objective (20) is

$$ \left\{ {\begin{array}{*{20}c} {{\text{Minimize}} W} \\ {{\text{Subject to the conditions }}\left( {19} \right) {\text{with}}} \\ {W = \mathop \sum \limits_{i = 0}^{3} f_{i} c_{i} \left[ {1 + \frac{1}{4}\left( {\frac{{\sigma_{i} }}{{k_{2i} }} - \frac{{\rho_{i} }}{{k_{1i} }}} \right) + \frac{1}{4N}\left( {\frac{{\sigma_{i} }}{{k_{2i} }} - \frac{{\rho_{i} }}{{k_{1i} }}} \right)\left\{ {1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots + \frac{1}{N} + \frac{1}{{\left( {1 + N} \right)}}} \right\}} \right]} \\ \end{array} } \right. $$

(21)

5.1 Particular cases

• (i) If we take $\frac{{\sigma_{i} }}{{k_{2i} }} = \frac{{\rho_{i} }}{{k_{1i} }}, {\text{for}} i = 0, 1, 2 \,{\text{and}}\, 3$ then $W = \mathop \sum \nolimits_{i = 0}^{3} f_{i} c_{i}$ gives the crisp problem.

• (ii) If we take $k_{2i} = k_{1i} = 1 \,{\text{and}}\, N \to \infty \quad \,{\text{for}}\,i = 0,1,2 \,{\text{and}}\, 3$ then $W = \mathop \sum \nolimits_{i = 0}^{3} f_{i} c_{i} \left[ {1 + \frac{1}{4}\left( {\sigma_{i} - \rho_{i} } \right)} \right]$ gives the general fuzzy problem

• (iii) If we take $k_{2i} = k_{1i} = 1 \,{\text{and}}\, N{ \nrightarrow }\infty$ for $i = 0, 1, 2 {\text{and}} 3$ then $W = \mathop \sum \nolimits_{i = 0}^{3} f_{i} c_{i} \left[ {1 + \frac{1}{4}\left( {\sigma_{i} - \rho_{i} } \right)\left\{ {1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots + \frac{1}{N} + \frac{1}{{\left( {1 + N} \right)}}} \right\}} \right]$ gives the problem of dense fuzzy model

• (iv) If we take $k_{2i} = k_{1i} = k_{i} \,{\text{and}}\, N{ \nrightarrow }\infty$ for $i = 0, 1, 2 \,{\text{and}}\, 3$ then $W = \mathop \sum \nolimits_{i = 0}^{3} f_{i} c_{i} \left[ {1 + \frac{1}{{4k_{i} }}\left( {\sigma_{i} - \rho_{i} } \right)\left\{ {1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots + \frac{1}{N} + \frac{1}{{\left( {1 + N} \right)}}} \right\}} \right]$ gives the problem of dense fuzzy lock model for single key.

• (v) If we take $k_{2i} \ne k_{1i} \,{\text{and}}\, N{ \nrightarrow }\infty$ for $i = 0, 1, 2 \,{\text{and}}\, 3$ then $W = \mathop \sum \nolimits_{i = 0}^{3} f_{i} c_{i} \left[ {1 + \frac{1}{4}\left( {\frac{{\sigma_{i} }}{{k_{2i} }} - \frac{{\rho_{i} }}{{k_{1i} }}} \right) + \frac{1}{4N}\left( {\frac{{\sigma_{i} }}{{k_{2i} }} - \frac{{\rho_{i} }}{{k_{1i} }}} \right)\left\{ {1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots + \frac{1}{N} + \frac{1}{{\left( {1 + N} \right)}}} \right\}} \right]$ gives the problem of dense fuzzy lock model for double keys.

5.2 Method of finding the keys of the fuzzy lock sets

Here we take the bounds of the fuzzy cost vectors for finding their corresponding keys. As per De [53], the keys can be found from the following: We already have, $I\left( {\tilde{C}_{i} } \right) = c_{i} \left[ {1 + \frac{1}{4}\left( {\frac{{\sigma_{i} }}{{k_{2i} }} - \frac{{\rho_{i} }}{{k_{1i} }}} \right)} \right]$ for $i = 0, 1, 2 \,{\text{and}}\, 3$ as $N \to \infty$ which is coming from the left and right α-cuts that splits into $\frac{1}{2}c_{i} \left[ {1 - \frac{{\rho_{i} }}{{2k_{1i} }}} \right]$ and $\frac{1}{2}c_{i} \left[ {1 + \frac{{\sigma_{i} }}{{2k_{2i} }}} \right]$ respectively. Let the lower and upper bounds of each cost parameters are $c_{i}^{L}$ and $c_{i}^{U}$ respectively. Thus, it is clear that $c_{i}^{L} \le \frac{1}{2}c_{i} \left[ {1 - \frac{{\rho_{i} }}{{2k_{1i} }}} \right]$ and $\frac{1}{2}c_{i} \left[ {1 + \frac{{\sigma_{i} }}{{2k_{2i} }}} \right] \le c_{i}^{U}$ giving $k_{1i} \ge \frac{{\rho_{i} c_{i} }}{{2c_{i} - 4c_{i}^{L} }}$ and $k_{2i} \ge \frac{{\sigma_{i} c_{i} }}{{4c_{i}^{U} - 2c_{i} }}$ for dolkeys and that fong y we always have $k_{2i} = k_{1i} = k_{i} = {\text{Maximum}}\left\{ {\frac{{\rho_{i} c_{i} }}{{2c_{i} - 4c_{i}^{L} }} , \frac{{\sigma_{i} c_{i} }}{{4c_{i}^{U} - 2c_{i} }}} \right\}$.

5.3 Numerical Example 2

For numerical illustration, we already have $c_{0} = 275, c_{1} = 2, c_{2} = 3.2 , c_{3} = 4$, $\beta = 0.8, D = 1100, P = 9200, \lambda = 0.1$. Here we shall keep the bounds of the different cost vectors stated as follows:$\left[ {c_{0}^{L} , c_{0}^{U} } \right] = \left[ {260, 290} \right], \left[ {c_{1}^{L} , c_{1}^{U} } \right] = \left[ {1.2, 2.6} \right], \left[ {c_{2}^{L} , c_{2}^{U} } \right] = \left[ {2.5, 4.2} \right], \left[ {c_{3}^{L} , c_{3}^{U} } \right] = \left[ {2.8, 5.6} \right], \rho_{0} = \rho_{1} = \rho_{2} = \rho_{3} = 0.3$ and $\sigma_{0} = \sigma_{1} = \sigma_{2} = \sigma_{3} = 0.4$. Using the above definition of finding the keys we write,

$$ \left[ {\begin{array}{*{20}c} {\left\{ {k_{10} ,k_{20} } \right\}} \\ {\left\{ {k_{11} ,k_{21} } \right\}} \\ {\begin{array}{*{20}c} {\left\{ {k_{12} ,k_{22} } \right\}} \\ {\left\{ {k_{13} ,k_{23} } \right\}} \\ \end{array} } \\ \end{array} } \right] \ge \left[ {\begin{array}{*{20}c} {\left\{ {\frac{{\rho_{0} c_{0} }}{{2c_{0} - 4c_{0}^{L} }} , \frac{{\sigma_{0} c_{0} }}{{4c_{0}^{U} - 2c_{0} }}} \right\}} \\ {\left\{ {\frac{{\rho_{1} c_{1} }}{{2c_{1} - 4c_{1}^{L} }} , \frac{{\sigma_{1} c_{1} }}{{4c_{1}^{U} - 2c_{1} }}} \right\}} \\ {\begin{array}{*{20}c} {\left\{ {\frac{{\rho_{2} c_{2} }}{{2c_{2} - 4c_{2}^{L} }} , \frac{{\sigma_{2} c_{2} }}{{4c_{2}^{U} - 2c_{2} }}} \right\}} \\ {\left\{ {\frac{{\rho_{3} c_{3} }}{{2c_{3} - 4c_{3}^{L} }} , \frac{{\sigma_{3} c_{3} }}{{4c_{3}^{U} - 2c_{3} }}} \right\}} \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left\{ {\frac{0.3 \times 275}{2 \times 275 - 4 \times 260} , \frac{0.4 \times 275}{4 \times 290 - 2 \times 275}} \right\}} \\ {\left\{ {\frac{0.3 \times 2}{2 \times 2 - 4 \times 1.2}, \frac{0.4 \times 2}{4 \times 2.6 - 2 \times 2}} \right\}} \\ {\begin{array}{*{20}c} {\left\{ {\frac{0.3 \times 3.2}{2 \times 3.2 - 4 \times 2.5}, \frac{0.4 \times 3.2}{4 \times 4.2 - 2 \times 3.2}} \right\}} \\ {\left\{ {\frac{0.3 \times 4}{2 \times 4 - 4 \times 2.8} , \frac{0.4 \times 4}{4 \times 5.6 - 2 \times 4}} \right\}} \\ \end{array} } \\ \end{array} } \right] $$

$= \left[ {\begin{array}{*{20}c} {\left\{ {\frac{82.5}{ - 490} , \frac{110}{610}} \right\}} \\ {\left\{ {\frac{0.6}{ - 0.8}, \frac{0.8}{6.4}} \right\}} \\ {\begin{array}{*{20}c} {\left\{ {\frac{9.6}{ - 3.6}, \frac{1.28}{10.4}} \right\}} \\ {\left\{ {\frac{1.2}{ - 3.2} , \frac{1.6}{14.4}} \right\}} \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left\{ { - 0.168,0.180 } \right\}} \\ {\left\{ { - 0.75, 1.25 } \right\}} \\ {\begin{array}{*{20}c} {\left\{ { - 2.667, 0.123 } \right\}} \\ {\left\{ { - 0.375, 0.111} \right\}} \\ \end{array} } \\ \end{array} } \right]$ and that for single key, $\left[ {\begin{array}{*{20}c} {k_{0} } \\ {k_{1} } \\ {\begin{array}{*{20}c} {k_{2} } \\ {k_{3} } \\ \end{array} } \\ \end{array} } \right] \ge \left[ {\begin{array}{*{20}c} {Max\left\{ {\frac{{\rho_{0} c_{0} }}{{2c_{0} - 4c_{0}^{L} }} , \frac{{\sigma_{0} c_{0} }}{{4c_{0}^{U} - 2c_{0} }}} \right\}} \\ {Max\left\{ {\frac{{\rho_{1} c_{1} }}{{2c_{1} - 4c_{1}^{L} }} , \frac{{\sigma_{1} c_{1} }}{{4c_{1}^{U} - 2c_{1} }}} \right\}} \\ {\begin{array}{*{20}c} {Max\left\{ {\frac{{\rho_{2} c_{2} }}{{2c_{2} - 4c_{2}^{L} }} , \frac{{\sigma_{2} c_{2} }}{{4c_{2}^{U} - 2c_{2} }}} \right\}} \\ {Max\left\{ {\frac{{\rho_{3} c_{3} }}{{2c_{3} - 4c_{3}^{L} }} , \frac{{\sigma_{3} c_{3} }}{{4c_{3}^{U} - 2c_{3} }}} \right\}} \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {Max\left\{ { - 0.168,0.180 } \right\}} \\ {Max \left\{ { - 0.75, 1.25 } \right\}} \\ {\begin{array}{*{20}c} {Max\left\{ { - 2.667, 0.123 } \right\}} \\ {Max\left\{ { - 0.375, 0.111 } \right\}} \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {0.180} \\ {1.250} \\ {\begin{array}{*{20}c} {0.123} \\ {0.111} \\ \end{array} } \\ \end{array} } \right]$. Now for practical purpose we assume for single key $\left[ {\begin{array}{*{20}c} {k_{0} } \\ {k_{1} } \\ {\begin{array}{*{20}c} {k_{2} } \\ {k_{3} } \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 2 \\ 3 \\ {\begin{array}{*{20}c} 4 \\ 5 \\ \end{array} } \\ \end{array} } \right]$ and that for double keys $\left[ {\begin{array}{*{20}c} {\left\{ {k_{10} ,k_{20} } \right\}} \\ {\left\{ {k_{11} ,k_{21} } \right\}} \\ {\begin{array}{*{20}c} {\left\{ {k_{12} ,k_{22} } \right\}} \\ {\left\{ {k_{13} ,k_{23} } \right\}} \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left\{ {2,3 } \right\}} \\ {\left\{ {2,4 } \right\}} \\ {\begin{array}{*{20}c} {\left\{ {2,5 } \right\}} \\ {\left\{ {2,6 } \right\}} \\ \end{array} } \\ \end{array} } \right]$ which must satisfy the above constraints.

Note that the smaller values of the keys will give the objective values that correspond the cases of weak fuzzy numbers. But in our study, we are only interested with strong fuzzy numbers. Thus, we obtain the optimum average inventory cost sated in table 5.

Table 5 Optimum Solution for EPQ model under fuzzy locks.

From the above table we see that, for the case of crisp environment, the expected average inventory cost is $1162.57 with respect to the 93.38% perfect order items over maximum cycle time 1.2027 months with 0.5365 month inventory exhaust time. However, the general fuzzy and dense fuzzy environment keeps the same time periods with inventory costs $1133.51 and $1118.98, respectively. Also, if we think of the case of single key under fuzzy lock then the maximum cycle time reduces to 1.1885 months for 94.15% perfect items costing $1134.78 alone. But the case of double keys assumes the expected average inventory cost of $1089.91 with respect to the 92% perfect items over 1.227 months cycle time with 0.5474 month inventory exhaust time.

6 Sensitivity analysis

Since, from table 5 we see the proposed model has been minimized for fuzzy locks of double keys approach so we shall take the sensitivity analysis of the double key parameters for the cost vector associated in the supply chain model itself. We made the changes from − 50% to +50% for each of the keys (single and double) taking one at a time and keeping others as constants and to get the table 6.

Table 6 Sensitivity analysis for EPQ model under several fuzzy environments.

6.1 Discussion on sensitivity analysis

Table 6 explores that all the key vectors have similar types of sensitivity over average inventory cost whenever we make a change any one of those parameters from − 50% to +50%. It is also observed that the changes for the keys of the fixed inventory cost and the holding cost assume almost same values of the objective function. The more reduction of the key parameters gives the more relative reduction of the average inventory cost with respect to the crisp optimum. Throughout the whole table we see, at − 50% change of the holding cost parameter the relative change of the cost becomes − 10.22% alone and at +50% change for the keys of the fixed cost as well as the holding cost, the relative change of the objective function itself reduces to − 6.54% of the crisp value. However, for the cases of perfect items, at − 50% change of the unit holding cost parameter of items gives minimum average inventory cost ($1043.75) with respect to the 95.11% perfectness of the ordered items in the process of supply chain alone.

7 Graphical illustrations

Figure 6 shows that the average inventory cost of the supply chain is maximum (near $1160) for the crisp model but it is minimum (near $1060) for the fuzzy lock model of double keys. The general fuzzy model gives finer result than crisp and fuzzy lock model of single key but only the dense fuzzy model keeps quite better result than those models. Figure 7 shows that if we make a sensitivity from − 50% to +50% of the double keys of the associated cost vectors then the average inventory cost curves meet near $1075 which comes at the change of keys of the cost vectors near − 30% explicitly. The graph also reveals that, the inventory holding cost and the set-up cost are highly sensitive and they are becoming overlapped through the changes of the keys parameters for the proposed model. Although, the backlogging cost and the cost for goodwill lost are moderately sensitive. Moreover, the trends of each cost curve are to meet near $1075 so that it is the minimum cost. Figure 8 indicates that the items under proper inspection assume more than 90% perfect whenever the inventory runs with backlog and the set-up cost and the holding cost get flexible values through fuzzy locks. However, for the variation of the goodwill loss cost, the standard items under inspection with maximum cycle time is reduced to nearly 90%; but for the variation of backlogging cost, few cases may arise where the good items reach to 95%. Also, it is seen that, the good items lie near 85% all the time whenever we look into the model backlog free. Figure 9 focuses the average inventory cost under several optimum cycle times. We notice that starting from a minimum value, the average inventory cost function gradually increases within the range of cycle time 1.21–1.22 months exclusively. Beyond this interval the objective function assumes zigzag values without attaining the model minima. Figure 10 explores an umbrella type curve which corresponds the good items under inspection that might affect the average inventory cost. At 91% perfectness the objective function gives maximum objective value but beyond that the average inventory cost gradually decreases to meet a model minimum. Moreover, our study reveals that under the fuzzy lock environment the bounds of good items lie within 95.11% as a whole.

Figure 6

Average Inventory cost under fuzzy Environments.

Figure 7

Cost Sensitive Objective Function.

Figure 8

Perfectness of items for several cycle times.

Figure 9

Average inventory cost vs maximum cycle time.

Figure 10

Average inventory function Vs Perfect items.

8 Conclusions

The aim of this research is to extend the criteria of decision making over the control of several cost components under fuzzy lock environment. Traditionally, in general fuzzy system, the role of decision maker was quite inactive and hence the economy (cost effectiveness) of an inventory process was not guaranteed there. However, the learning experiences (the case of dense fuzzy) of DM over inventory management process could help to minimize the system cost up to a certain extent. But, in fuzzy lock system, the DM’s participation is vital and the judgements are made with the consultation of other’s view (usually we assume an industrialist and his/her manager, the case of double keys) which might expedite the decision towards specific goal. Although, two related articles (Skouri et al. [26]) and Konstantaras et al. [27]) fall into this study but the major difference is that they consider the EOQ model with disruption for single -layer supply chain with fully backlogged demand in the shortage period. Moreover, the concept of goodwill loss cost, partial backordering, average inventory cost and the extension of supply chain (three-layer production inventory) was not considered by them which are the basic novelties of this model. So, with the numerical study our model is not comparable with their result but relaxing few parameters from our model it is possible to reach near Skouri’s model analytically. We have incorporated a production inventory problem in three stages chain with random disruption in delivery raw material batches at the supply side of the network under an “all or none” inspection policy, defective raw materials (due to quality problems) are rejected and excess demand of retailer is partially backordered by the manufacturer. Numerical experiments show that under industrialist-manager consultation the objective function of the three-layer supply chain model can be optimized.

The major findings of our proposed modes are:

• (i) More imperfectness of items (it may be raw materials or finished goods) does not mean to have a lower objective value.

• (ii) Higher cycle time duration does not mean more inventory cost but it attains a minimum value for a finite range of time.

• (iii) We always have minimum objective value for stochastic fuzzy lock model instead of deterministic model.

• (iv) Single view (Single key) of the decision maker is not able to optimize the fuzzy lock model fairly but with the consultation of others it is possible to optimize the system cost exclusively.

• (v) For single review policy (cases of dense fuzzy and lock fuzzy model) we always have model minima rather than crisp model.

• (vi) Fuzzy lock model is the latest extension of the dense fuzzy model which facilitates the decision maker to challenge any drastic situation of an inventory process in recent times.

The essential notation and the primary suppositions have been used in this paper listed are as follows:

9 Parameters

$D$ :

Demand rate of retailers (unit/time)

P :

Production rate (unit/time), $P > D$

$C_{o}$ :

Fixed Set-up cost per cycle

$C_{h}$ :

Storage cost (unit/time)

$C_{b}$ :

Backlog cost (unit/time)

${\text{C}}_{\text{l}}$ :

Cost for good will loss per unit item.

$\beta$ :

The fraction of stock outs that will be backlogged ($0 \le \beta \le 1$)

$\lambda$ :

Probability of supply batch faultiness ($0 \le \lambda < 1$)

10 Variables

• $X$ Number of successive defective supply raw materials batches deliveries (random variable)

• $T$ Time interval between two succeeding supply transfers of the same type (that is, the two batches are both standards or both defective which are decision variables)

• $T^{\prime}$ Time interval between two succeeding production intervals with positive inventory, that is, length of the inventory cycle (random variable)

• $\delta$ A fraction of inventory cycle with positive inventory level (decision variable)