1 Introduction

The economic order quantity (EOQ) model is an important technique/methodology to overcome some bottlenecks of the supply chain (Cárdenas-Barrón 2007; Cárdenas-Barrón et al. 2011, 2012a, 2012b, 2012c). Ioannou et al. (2004) proposed a novel, analytical and simple approach to determine the supply chain node in which inventory held in order to minimize inventory-holding costs under service level constraints. Gallego and Hu (2004) analyzed a discrete-time based production/inventory system with finite production capacity considering a single item, single-location, periodic-review model with finite capacity and Markov modulated demand and supply. Krieg and Kuhn (2004) presented an approximate evaluation procedure for stochastic single-stage multi-product kanban systems with state-dependent setups and lost sales, assuming the demand inter-arrival, setup, and container processing times as exponentially distributed. Arcelus et al. (2006) investigated the retailer’s response to temporary manufacturer’s trade dealt with a time interval of random length and uncertain duration. The uncertainty of termination date is handled through the creation of two decision variables: one is a reordering point, defined as a critical number, which determines the inventory level below which a special order is placed. The second measures the time at which the reordering point is activated. Kalpakam and Shanthi (2006) developed a lost sales (s,S) type perishable inventory system with varying ordering quantity under renewal demands while mean rate of replenishment is dependent on the order size. Ghosh and Chaudhuri (2006) investigated an economic order quantity model considering quadratic demand, time-proportional deterioration and shortages in all cycles. Sarkar and Sarkar (2013) extended an inventory model for deteriorating items with stock-dependent demand, considering time varying backlogging rate as well as time varying deterioration rate. Generally speaking, the demand rate of the end customers is quite sensitive with promotional effort and selling price, maintaining the standard quality of the products. The promotional effort includes free gift, price discount, better service, delay payments, advertising which results in cost factor. The customers are motivated or tempted to buy more for promotional effort although it generates costs. Also, lower selling price per unit item causes higher demand of the customers. Goyal and Gunasekaran (1995) extended a production-inventory model for advertising sensitive demand. In this direction, the works of Xie and Neyret (2009), Xie and Wei (2009), Sana and Chaudhuri (2008), Sana (2010, 2011a, 2011b, 2012) should be mentioned, among others.

In a competitive marketing system, the factors of the businesses are not fixed rather they are non-randomly uncertain in nature. Again, in many cases such as at the sales counter, the demand on spot, the selling price is quite flexible in nature. Consequently, we consider the selling prices and PE as fuzzy numbers. Zadeh (1965) first developed the concept of fuzzy set theory. Thereafter, Bellman and Zadeh (1970) made an application of fuzzy set theory in several decision making problems of operations research. Thereafter, several research papers have been published in fuzzy environment. Kaufmann and Gupta (1988) developed a fuzzy mathematical model in engineering and management science. Vojosevic et al. (1996) fuzzified the order cost into trapezoidal fuzzy number in the backorder model. Using these propositions, another authors Wu and Yao (2003) studied a fuzzy inventory with backorder for fuzzy order quantity and fuzzy shortage quantity. With the help of fuzzy extension principle, an economic order quantity in fuzzy sense for inventory without backorder model has been developed by Lee and Yao (1999). Yao et al. (2000) analyzed a fuzzy model without backorder for fuzzy order quantity and fuzzy demand quantity. A lot size reorder point inventory model with fuzzy demands was developed by Kao and Hsu (2002) considering the α-cut of the fuzzy numbers and they had used ranking index method to solve the model. De et al. (2003) developed an economic production quantity (EPQ) model for fuzzy demand rate and fuzzy deterioration rate using the α-cut of the membership function of the fuzzy parameters. Mishra and Ghosh (2006) established the bi-level quadratic fractional programming problem with the essentially cooperative decision makers (DMs) and proposed an interactive fuzzy programming for the problem. Ganesan and Veeramani (2006) proved fuzzy analogues of some important theorems of linear programming problem with trapezoidal fuzzy numbers. De et al. (2008) studied an economic ordering policy of deteriorated items with shortage and fuzzy cost coefficients for vendor and buyer. Recently Kumar et al. (2012) developed a fuzzy model with ramp type demand rate and partial backlogging.

In crisp sense, several optimization techniques have been used in inventory literature. Among these, golden region search method and analytic approach via eigen values are worth mentioning. Golden Region Search method in Simulation technique was developed by Kabiran and Olafsson (2011) and analytic approach via eigen values of the system Jacobian Matrix expressing from characteristic polynomial was analyzed by Saleh et al. (2010). The intuitionistic fuzzy (IF) set theory was independently developed by Takeuti and Titani (1984) and it has some terminological difficulties in fuzzy set theory. Dabois et al. (2005) observed that Takeuti and Titani’s IF logic is simply an extension of intuitionistic logic (Van D. Dalen 2002). i.e., all formulas in the intuitionistic logic can be proved in their logic. Takeuti and Titani’s approach is an absolutely legitimate which is absent in Atanassov’s (1986) IFS. To remove the misunderstanding, we may abbreviate Atanassov’s (1986) model as A-IFS. It may be treated as a classification model subject to a valuation space with three classes and defining specific structure (Montero et al. 2007). The basic concept of A-IFS is based on the simultaneous consideration of membership μ and non-membership γ of an element of a set in the set itself (Atanassov 1986) such that 0≤μ+ν≤1. Chen and Tan (1994) and Dymova and Sevastjanov (2011) proposed subsequently to use the so called score function S(x)=μ(x)−ν(x) where x is the IFS (Intuitionistic Fuzzy Set).

In this paper, we consider PE and unit selling price as intuitionistic fuzzy set. As far as our knowledge goes, such research paper has not yet been published in this direction. First, we have optimized the profit function under crisp environment. Then, we have constructed a General Fuzzy Optimization (GFO) problem and Intuitionistic Fuzzy Optimization (IFO) problem. Using the α-cuts of the membership functions and β-cuts of the non-membership functions for the objective function, we develop the score function (net membership) of the proposed fuzzy parameters. On the basis of area compensation, we use Yager’s (1981) ranking index method to achieve the best policy for GFO and IFO problems. To overcome the complexities on integration, the problem is solved with the help of Mathematica 5.2 software. Finally, a sensitivity analysis, graphical illustrations and a concluding remark are made to generalize the model.

2 Assumptions and notations

The following notations and assumptions are adopted to develop the model.

2.1 Assumptions

  1. 1.

    Replenishment rate is instantaneously infinite.

  2. 2.

    The time horizon is infinite.

  3. 3.

    Backlogging are allowed.

  4. 4.

    Demand rate is unit selling price (s p) and promotional effort/sales teams’ initiatives (ρ) dependent

where \(D=\eta ( \frac{s^{m} - s^{p}}{s^{p} - s_{m}} ) +\tau ( \frac{\rho}{1+\rho} )\), η and τ are constants.

2.2 Notation

q::

The order quantity per cycle.

D::

Demand rate per year.

s::

Shortage quantity per cycle.

ρ::

Promotional effort/sales teams’ initiatives.

ρ m ::

Lower bound of ρ.

ρ m::

Upper bound of ρ.

ρ ∗::

Optimal value of ρ for crisp model.

c 1::

Setup cost per cycle ($).

c 2::

Inventory holding cost per unit quantity per unit time ($).

c 3::

Shortage cost per unit quantity per unit time ($).

s p::

Selling price per unit item ($)

s m::

Upper bound of s p.

s m ::

Lower bound of s p.

p 1::

Purchasing price of unit item ($).

k::

Cost ($) of promotional effort/sales teams’ initiatives per unit effort, it is a positive scale parameter.

m::

A positive integer.

t 1::

Inventory run time (months).

t 2::

Shortage period (months).

T::

Cycle time in months.

Z::

Average profit ($) of the inventory.

3 Formulation of the model

3.1 Crisp model

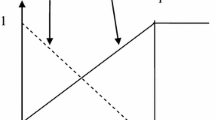
In our proposed model, the inventory starts with shortages and it continues up to time t 1. At time t 1, the shortage level (s) is adjusted from the order size q. Then, the rest amount (q−s) satisfies demand (D per unit time) of the customers for the time span [0,t 2]. The cycle length is T=t 1+t 2. Therefore, the average inventory and shortages (see Fig. 1) are \(\frac{ ( q-s )^{2}}{ 2q}\) and \(( \frac{s^{2}}{2q} )\) respectively. The cost of the effort for promotional activities/sales teams’ initiatives is kρ m where k(≥0) is scale and m(≥0) is elasticity parameters.Therefore, the average profit of the model, considering revenue from selling the items, purchasing cost, setup cost, inventory holding cost, penalty for stockout and cost of promotional effort, is

$$\begin{aligned} z =& \frac{1}{T} \textrm{Revenue from selling} - \textrm{Purchasing cost}- \textrm{Setup cost}- \textrm{Inventory cost} \\ &{}-\textrm{Penalty for Shortage} - \textrm{cost of Promotional effort} \\ =& \bigl( s^{p} - p_{1} \bigr) D- c_{1} \biggl( \frac{D}{q} \biggr) - c_{2} \biggl( \frac{ ( q-s )^{2}}{2q} \biggr) - c_{3} \biggl( \frac{s^{2}}{2q} \biggr) -k \rho^{m} \end{aligned}$$
(1)

subject to the conditions

$$ q=DT,\qquad s=D t_{1},\qquad q-s=D t_{2},\qquad T= t_{1} + t_{2} $$
(2)

Here, the demand rate of the customers is

$$ D = \eta \biggl( \frac{s^{m} - s^{p}}{s^{p} - s_{m}} \biggr) + \tau \biggl( \frac{\rho}{1+ \rho} \biggr) $$
(3)

where η, τ, s m, s m are positive constants and (s p,ρ) are variable parameters. The first part of the demand is selling price sensitive. It is rational that the demand of the customer decreases with increasing value of selling price (s p). The variable s p has lower bound (s m ) and upper bound (s m). When selling price s p tends to s m, the first part of D tends to zero, but it tends to infinity when s p tends to s m , i.e., the selling price is less than the purchasing price. In real situation both the cases are not required in any business organization in a given economy. Therefore, s p belongs to the open interval (s m ,s m). The 2nd part of D is an increasing function of the promotional effort (PE) which is measured by the promotional activities such as gift, better services, packaging advertising etc. In existing inventory literature, some authors considered the demand rate is an unbounded increasing function of ρ which is unrealistic assumption. In our formula, the promotional index sensitive part tends to τ when ρ→∞, i.e., the 2nd part varies from zero to τ for ρ∈[0,∞). This is quite realistic in any business organization.

Fig. 1
figure 1

Inventory versus time

Full size image

Now, our objective is to

$$ \left \{ \begin{array}{@{}l@{}} \mathrm{Maximize}\ Z\\ \mathrm{subject}\ \mathrm{to}\ \mathrm{the}\ \mathrm{conditions}\\ q\geq 0,\ s \geq 0,\ \rho \geq 0 \end{array} \right \} $$
(4)

For maximum value of Z, we always have

$$\begin{aligned} &\frac{\partial Z}{\partial q} = 0 = \frac{\partial Z}{\partial s}\quad \mbox{and}\quad \biggl( \frac{\partial^{2} Z}{\partial q^{2}} \biggr) =- \biggl( \frac{2 c_{1} D+ ( c_{2} + c_{3} ) s^{2}}{q^{3}} \biggr) <0, \\ & \biggl(\frac{\partial^{2} Z}{\partial s^{2}} \biggr) =- \biggl( \frac{c_{2} + c_{3}}{q} \biggr) <0, \\ &\biggl( \frac{\partial^{2} Z}{ \partial q^{2}} \biggr) \biggl( \frac{\partial^{2} Z}{\partial s^{2}} \biggr) - \biggl( \frac{\partial^{2} Z}{\partial q\partial s} \biggr)^{2} = \frac{2 c_{1} D ( c_{2} + c_{3} )}{q^{4}} >0\quad \forall q,\ s \in R^{+}. \end{aligned}$$

Now, \(\frac{\partial Z}{\partial q} =0= \frac{\partial Z}{\partial s}\) provide us as follows:

$$q^{*} = \sqrt{\frac{2 c_{1} ( c_{2} + c_{3} ) D}{c_{2} c_{3}}},\qquad s^{*} = \sqrt{ \frac{2 c_{1} c_{2} D}{c_{3} ( c_{2} + c_{3} )}}\quad \mbox{and}\quad q^{*} = \biggl( \frac{c_{2} + c_{3}}{c_{2}} \biggr) s^{*}. $$

Substituting the above values in Eq. (1), we have the optimized (maximum) value of the average profit function

$$ \varphi \bigl( s^{p},\rho \bigr) = Z^{*} \bigl(s^{p},\rho \bigr) = \bigl( s^{p} - p_{1} \bigr) D- \sqrt{2 c_{1} c_{2} c_{3} D/ ( c_{2} + c_{3} )} -k \rho^{m} $$
(5)

For maximum value of φ(s p,ρ), we should have a solution such that

$$\begin{aligned} &\frac{\partial\varphi}{\partial\rho} =0= \frac{\partial\varphi}{\partial s^{p}}\quad \mbox{and}\quad \biggl( \frac{\partial^{2} \varphi}{\partial \rho^{2}} \biggr) <0, \quad \biggl( \frac{\partial^{2} \varphi}{\partial s^{p2}} \biggr) <0, \\ &\biggl(\frac{\partial^{2} \varphi}{\partial \rho^{2}} \biggr) \biggl( \frac{\partial^{2} \varphi}{\partial s^{p2}} \biggr) - \biggl( \frac{\partial^{2} \varphi}{\partial\rho\partial s^{p}} \biggr)^{2} >0\quad \mbox{for } \rho\in R^{+} \mbox{ and } s^{p} \in \bigl( s_{m}, s^{m} \bigr). \end{aligned}$$

3.2 Fuzzy mathematical model

In the traditional EOQ model, we have seen that, the demand rate is constant but, in practice, it depends upon PE and selling price per unit which are flexible in nature. For this reason, we shall fuzzify these parameters.

Now using (2), (3) and (4), the fuzzy problem for (5) is given by

$$\begin{aligned} &\mathrm{Maximize}\quad \tilde{\phi} ( \tilde{s}^{p}, \tilde{\rho} ) = \bigl( \tilde{s}^{p} - p_{1} \bigr) \tilde{D} - \sqrt{2 c_{1} c_{2} c_{3} \tilde{D} / ( c_{2} + c_{3} )} -k \tilde{\rho}^{m} \end{aligned}$$
(6)
$$\begin{aligned} &\mbox{Subject to the conditions}\quad \tilde{q} = \sqrt{\frac{2 c_{1} ( c_{2} + c_{3} ) \tilde{D}}{c_{2} c_{3}}}\quad \mbox{and}\quad \tilde{s} = \sqrt{\frac{2 c_{1} c_{2} \tilde{D}}{c_{3} ( c_{2} + c_{3} )}} \end{aligned}$$
(7)

where

$$ \tilde{D} = \eta \biggl( \frac{s^{m} - \tilde{s}^{p}}{\tilde{s}^{p} - s_{m}} \biggr) + \tau \biggl( \frac{\tilde{\rho}}{1+ \tilde{\rho}} \biggr) $$
(8)

3.2.1 Cases of optimality

Now we seek to solve (6) for the following cases:

We may assume s p∈[s m ,s m] and ρ∈[ρ m ,ρ m]. From our proposed model, we see that at s p=s m the demand rate is infinite and at s p=s m the demand rate depends upon ρ only. Also from our observation the crisp optimality attained at ρ=ρ ∗ (say) and it attains its maximum value (when average profit reaches near zero) at ρ=ρ m (say). Thus we take the possible domain space for s p and ρ as under.

Case 1::

\(s_{m} < s^{p*} < s_{1} ' < s_{1} < s_{2} < s_{3} < s_{3} ' < s^{m}\)

Case 2::

\(s_{m} < s_{1} ' < s^{p*} < s_{1} < s_{2} < s_{3} < s_{3} ' < s^{m}\)

Case 3::

\(s_{m} < s_{1} ' < s_{1} < s^{p*} < s_{2} < s_{3} < s_{3} ' < s^{m}\)

Case 4::

\(s_{m} < s_{1} ' < s_{1} < s_{2} < s^{p*} < s_{3} < s_{3} ' < s^{m}\)

Case 5::

\(s_{m} < s_{1} ' < s_{1} < s_{2} < s_{3} < s^{p*} < s_{3} ' < s^{m}\)

Case 6::

\(s_{m} < s_{1} ' < s_{1} < s_{2} < s_{3} < s_{3} ' < s^{p*} < s^{m}\)

Case i::

\(\rho_{m} <\rho^{*} < \rho_{1} ' < \rho_{1} < \rho_{2} < \rho_{3} < \rho_{3} ' < \rho^{m}\)

Case ii::

\(\rho_{m} <\rho_{1} ' < \rho^{*} < \rho_{1} < \rho_{2} < \rho_{3} < \rho_{3} ' < \rho^{m}\)

Case iii::

\(\rho_{m} <\rho_{1} ' < \rho_{1} < \rho^{*} < \rho_{2} < \rho_{3} < \rho_{3} ' < \rho^{m}\)

Case iv::

\(\rho_{m} <\rho_{1} ' < \rho_{1} < \rho_{2} < \rho^{*} < \rho_{3} < \rho_{3} ' < \rho^{m}\)

Case v::

\(\rho_{m} <\rho_{1} ' < \rho_{1} < \rho_{2} < \rho_{3} < \rho^{*} < \rho_{3} ' < \rho^{m}\)

Case vi::

\(\rho_{m} <\rho_{1} ' < \rho_{1} < \rho_{2} < \rho_{3} < \rho_{3} ' < \rho^{*} < \rho^{m}\).

To obtain all solutions we have to compute a total of 36 different tables which is out of scope in this paper. We intend here to know the trend of the GFO and IFO solution near crisp optimal solution. Hence, we shall take the cases (4, iv) only.

Definition 1

Intuitionistic fuzzy set Let a set X be fixed. An Intuitionist fuzzy set A in X is an object having the form A={〈x,μ A (x),ν A (x)〉:x∈X} where the μ A (x):X→[0,1] and ν A (x):X→[0,1] define the degree of membership and degree of non-membership respectively. If the element x∈X to the set A, which is a subset of X, for every element of x∈X, 0≤μ A (x)+ν A (x)≤1.

Definition 2

(α,β) level intervals or (α,β)-cuts:

A set of (α,β)-cut, generated by IFS-A, where α and β∈[0,1] are fixed numbers such that (α+β)∈[0,1] that defined as

$$A_{\alpha,\beta} = \left \{ \begin{array}{@{}l@{}} ( x, \mu_{A} ( x ), \nu_{A} ( x ) ):x\in X\\ \mu_{A} ( x ) \geq\alpha, \nu_{A} ( x ) \leq\beta,\alpha,\beta\in [ 0, 1 ] \end{array} \right \}. $$

(α,β) level intervals or (α,β)-cut denoted by A α,β is defined as the crisp set of elements x which belongs to A at least to the degree α and which does belong to A at most to the degree β.

Definition 3

Triangular Intuitionistic Fuzzy Number (TIFN) (Fig. 2)

Fig. 2
figure 2

(Non) Membership function for TIFN

Full size image

A TIFN, A, is an Intuitionistic fuzzy set in R with following membership function μ A (x) and non-membership function ν A (x) (for more details see Mahapatra and Roy 2009):

$$ \mu_{A} ( x ) = \left \{ \begin{array}{@{}l@{\quad}l@{}} \frac{x- a_{1}}{a_{2} - a_{1}} & \mbox{for } a_{1} <x< a_{2}\\ \frac{a_{3} -x}{a_{3} - a_{2}} & \mbox{for } a_{2} <x\leq a_{3}\\ 0& \mbox{for elsewhere} \end{array} \right \}\quad \mbox{and}\quad \nu_{A} ( x ) = \left \{ \begin{array}{@{}l@{\quad}l@{}} \frac{a_{2} -x}{a_{2} - a_{1} '} & \mbox{for } a_{1} ' <x< a_{2}\\ \frac{x-a_{2}}{a_{3} ' - a_{2}} & \mbox{for } a_{2} <x\leq a_{3} '\\ 1& \mbox{for elsewhere} \end{array} \right \} $$
(9)

where \(a_{1} ' < a_{1} < a_{2} < a_{3} < a_{3} '\) and μ A (x), ν A (x)≤0.5.

For μ A (x)=ν A (x), the TIFN is denoted by \(A_{TIFN} = ( a_{1}, a_{2}, a_{3}: a_{1} ', a_{2}, a_{3} ' )\).

If we are interested to find a solution near the crisp optimality, then we shall choose the above case (4), for selling price s p and (iv) for ρ only.

Let the unit selling price s p and PE (ρ) are representing Triangular intuitionistic fuzzy numbers.

Therefore, the membership and non-membership functions for ρ and s p are obtained as follows:

$$ \mu_{\tilde{\rho}} ( \tilde{\rho} ) = \left \{ \begin{array}{@{}l@{\quad}l@{}} \frac{\rho- \rho_{1}}{\rho_{2} - \rho_{1}} & \mbox{for } \rho_{1} <x< \rho_{2}\\ \frac{\rho_{3} -\rho}{\rho_{3} - \rho_{2}} & \mbox{for } \rho_{2} <x\leq \rho_{3}\\ 0& \mbox{for elsewhere} \end{array} \right \} $$
(10)

and

$$ \nu_{\tilde{\rho}} ( \tilde{\rho} ) = \left \{ \begin{array}{@{}l@{\quad}l@{}} \frac{\rho_{2} -\rho}{\rho_{2} - \rho_{1} '} & \mbox{for } \rho_{1} ' <\rho< \rho_{2}\\ \frac{\rho-\rho_{2}}{\rho_{3} ' - \rho_{2}} & \mbox{for } \rho_{2} <\rho\leq \rho_{3} '\\ 1& \mbox{for elsewhere} \end{array} \right \} $$
(11)

As per Chen and Tan (1994), the score function (net membership) of ρ is given by

$$ \omega_{\tilde{\rho}} ( \tilde{\rho} ) = \left \{ \begin{array}{@{}l@{\quad}l@{}} \frac{\rho- \rho_{1}}{\rho_{2} - \rho_{1}} - \frac{\rho_{2-} \rho}{\rho_{2} - \rho_{1} '} & \mbox{for } \delta_{1} <x< \rho_{2}\\ \frac{\rho_{3} -\rho}{\rho_{3} - \rho_{2}} - \frac{\rho- \rho_{2}}{\rho_{3} ' - \rho_{2}} & \mbox{for } \rho_{2} <x\leq \delta_{3}\\ 0& \mbox{for elsewhere} \end{array} \right \} $$
(12)

where \(\delta_{1} = ( \frac{\rho_{2}^{2} - \rho_{1} \rho_{1} '}{2 \rho_{2} - \rho_{1} - \rho_{1} '} )\) and \(\delta_{3} = ( \frac{\rho_{3} \rho_{3} ' - \rho_{2}^{2}}{\rho_{3} + \rho_{3} ' -2 \rho_{2}} )\).

Putting the above score function in a compact form, we get

$$ \omega_{\tilde{\rho}} ( \tilde{\rho} ) = \left \{ \begin{array}{@{}l@{\quad}l@{}} \lambda_{1} ( \rho- \delta_{1} ) & \mbox{for } \delta_{1} <x< \rho_{2}\\ \lambda_{2} ( \delta_{3} -\rho ) & \mbox{for } \rho_{2} <x\leq \delta_{3}\\ 0& \mbox{for elsewhere} \end{array} \right \} $$
(13)

where \(\lambda_{1} = [ \frac{2 \rho_{2} - \rho_{1} - \rho_{1} '}{ ( \rho_{2} - \rho_{1} ) ( \rho_{2} - \rho_{1} ' )} ]\) and \(\lambda_{2} = [ \frac{\rho_{3} + \rho_{3} ' -2 \rho_{2}}{ ( \rho_{3} - \rho_{2} ) ( \rho_{3} ' -\rho_{2} )} ]\).

Now, the α-cut of the score function \(\omega_{\tilde{\rho}} ( \tilde{\rho} )\) is given by

$$ \bigl[ L_{\rho}^{-1} ( \alpha ),\ R_{\rho}^{-1} (\alpha) \bigr] = \biggl[ \frac{\alpha}{\lambda_{1}} + \delta_{1}, \delta_{3} - \frac{\alpha}{\lambda_{2}} \biggr] $$
(14)

The membership and non-membership functions for s p along with score function are respectively as follows:

$$\begin{aligned} \mu_{\tilde{s}^{p}} \bigl( \tilde{s}^{p} \bigr) =& \left \{ \begin{array}{@{}l@{\quad}l@{}} \frac{s^{p} - s_{1}}{s_{2} - s_{1}} & \mbox{for } s_{1} < s^{p} < s_{2}\\ \frac{s_{3} - s^{p}}{s_{3} - s_{2}} & \mbox{for } s_{2} < s^{p} < s_{3}\\ 0& \mbox{for elsewhere} \end{array} \right \} \end{aligned}$$
(15)
$$\begin{aligned} \nu_{\tilde{s}^{p}} \bigl( \tilde{s}^{p} \bigr) =& \left \{ \begin{array}{@{}l@{\quad}l@{}} \frac{s_{2} - s^{p}}{s_{2} - s_{1} '} & \mbox{for } s_{1} ' < s^{p} < s_{2}\\ \frac{s^{p} -s_{2}}{s_{3} ' - s_{2}} & \mbox{for } s_{2} < s^{p} < s_{3} '\\ 1& \mbox{for elsewhere} \end{array} \right \} \end{aligned}$$
(16)
$$\begin{aligned} \pi \bigl( s^{p} \bigr) =& \left \{ \begin{array}{@{}l@{\quad}l@{}} \lambda_{1} ' ( s^{p} - \delta_{1} ' ) & \mbox{for } \delta_{1} ' < s^{p} < s_{2}\\ \lambda_{2} ' ( \delta_{3} ' - s^{p} ) & \mbox{for } s_{2} < s^{p} \leq \delta_{3} '\\ 0 & \mbox{for elsewhere} \end{array} \right \} \end{aligned}$$
(17)

where

$$\begin{aligned} &\lambda_{1} ' = \biggl[ \frac{2 s_{2} - s_{1} - s_{1} '}{ ( s_{2} - s_{1} ) ( s_{2} - s_{1} ' )} \biggr], \qquad \lambda_{2} ' = \biggl[ \frac{s_{3} + s_{3} ' -2 s_{2}}{ ( s_{3} - s_{2} ) ( s_{3} ' -s_{2} )} \biggr],\\ & \delta_{1} ' = \biggl( \frac{s_{2}^{2} - s_{1} s_{1} '}{2 s_{2} - s_{1} - s_{1} '} \biggr) \quad \mbox{and}\quad \delta_{3} ' = \biggl( \frac{s_{3} s_{3} ' - s_{2}^{2}}{s_{3} + s_{3} ' -2 s_{2}} \biggr). \end{aligned}$$

Also, the α-cut of the score function π(s p) is given by

$$ \bigl[ L_{s^{p}}^{-1} ( \alpha ),\ R_{s^{p}}^{-1} (\alpha) \bigr] = \biggl[ \frac{\alpha}{\lambda_{1} '} + \delta_{1} ', \delta_{3} ' - \frac{\alpha}{\lambda_{2} '} \biggr] $$
(18)

Let, D=d 1+d 2 where \(d_{1} = \eta ( \frac{s^{m} - s^{p}}{ s^{p} - s_{m}} )\) and \(d_{2} =\tau ( \frac{\rho}{1+ \rho} )\).

Therefore, the membership and non-membership function of d 1 is as follows

$$\begin{aligned} &\mu_{d 1} ( \tilde{d}_{1} ) = \left \{ \begin{array}{@{}l@{\quad}l@{}} \frac{ [ s_{2} - s_{m} -\eta ( \frac{s^{m} - s_{m}}{d_{1} +\eta} ) ]}{s_{3} - s_{2}} & \mbox{for } \frac{\eta ( s^{m} - s_{3} )}{s_{3} - s_{m}} < d_{1} < \frac{\eta ( s^{m} - s_{2} )}{s_{2} - s_{m}}\\ \frac{ [ s_{m} - s_{1} +\eta ( \frac{s^{m} - s_{m}}{d_{1} +\eta} ) ]}{s_{2} - s_{1}} & \mbox{for } \frac{\eta ( s^{m} - s_{2} )}{s_{2} - s_{m}} < d_{1} < \frac{\eta ( s^{m} - s_{1} )}{s_{1} - s_{m}}\\ 0& \mbox{for elsewhere} \end{array} \right \} \end{aligned}$$
(19)
$$\begin{aligned} &\nu_{d 1} ( \tilde{d}_{1} ) = \left \{ \begin{array}{@{}l@{\quad}l@{}} \frac{ [ s_{m} - s_{2} +\eta ( \frac{s^{m} - s_{m}}{d_{1} +\eta} ) ]}{s_{3} ' - s_{2}} & \mbox{for } \frac{\eta ( s^{m} - s_{3} ' )}{s_{3} ' - s_{m}} < d_{1} < \frac{\eta ( s^{m} - s_{2} )}{s_{2} - s_{m}} \\ \frac{[ s_{m} - s_{1} ' -\eta ( \frac{s^{m} - s_{m}}{d_{1} +\eta} ) ]}{s_{2} - s_{1} '}& \mbox{for } \frac{\eta ( s^{m} - s_{2} )}{s_{2} - s_{m}} < d_{1} < \frac{\eta ( s^{m} - s_{1} ' )}{s_{1} ' - s_{m}}\\ 1& \mbox{for elsewhere} \end{array} \right \} \end{aligned}$$
(20)

Therefore, the net membership (score function) of d 1 is given by

$$\psi ( d_{1} ) = \left \{ \begin{array}{@{}l@{\quad}l@{}} \frac{ [ s_{m} + s_{2} -\eta ( \frac{s^{m} - s_{m}}{d_{1} +\eta} ) ]}{s_{3} - s_{2}} - \frac{ [ s_{m} - s_{2} +\eta (\frac{s^{m} - s_{m}}{d_{1} +\eta} ) ]}{s_{3} ' - s_{2}} & \mbox{for } d_{1} ' < d_{1} < d_{1}^{''}\\ \frac{ [ s_{m} + s_{1} -\eta ( \frac{s^{m} - s_{m}}{d_{1} +\eta} ) ]}{s_{2} - s_{1}} - \frac{ [ s_{m} - s_{1} +\eta ( \frac{s^{m} - s_{m}}{d_{1} +\eta} ) ]}{s_{2} ' - s_{1}} & \mbox{for } d_{1}^{''} < d_{1} < d_{1}^{'''}\\ 0& \mbox{for elsewhere} \end{array} \right \} $$

or,

$$ \psi ( d_{1} ) = \left \{ \begin{array}{@{}l@{\quad}l@{}} k_{1} - \frac{k_{2}}{d_{1} +\eta} & \mbox{for } d_{1} ' < d_{1} < d_{1}^{''}\\ \frac{k_{4}}{d_{1} +\eta} - k_{3} & \mbox{for } d_{1}^{''} < d_{1} < d_{1}^{'''}\\ 0& \mbox{for elsewhere} \end{array} \right \} $$
(21)

where

$$\begin{aligned} &k_{1} = ( s_{2} - s_{m} ) \biggl[\frac{1}{s_{3} - s_{2}} + \frac{1}{s_{3} ' - s_{2}} \biggr],\qquad k_{2} = \biggl[ \frac{\eta k_{1} ( s^{m} - s_{m} )}{ ( s_{2} - s_{m} )} \biggr], \\ &k_{3} = ( s_{1} - s_{m} ) \biggl[ \frac{1}{s_{2} - s_{1}} +\frac{1}{s_{2} - s_{1} '} \biggr],\qquad k_{4} = \biggl[\frac{\eta k_{3} ( s^{m} - s_{m} )}{ ( s_{1} - s_{m} )} \biggr] \end{aligned}$$

and \(d_{1} '\), \(d_{1}^{''}\), \(d_{1}^{'''}\) are to be calculated properly.

Therefore α-cut of the score function ψ(d 1) is given by

$$ \bigl[ L_{d 1}^{-1} ( \alpha ), R_{d 1}^{-1} ( \alpha ) \bigr] = \biggl[ \frac{k_{2}}{k_{1} -\alpha} -\eta, \frac{k_{4}}{ k_{3} +\alpha} -\eta \biggr] $$
(22)

The membership and non-membership function of d 2 are as follows

$$\begin{aligned} &\mu_{d 2} ( \tilde{d}_{2} ) = \left \{ \begin{array}{@{}l@{\quad}l@{}} [ \frac{\frac{\tau}{ ( \tau- d_{2} )} - ( 1+ \rho_{1} )}{\rho_{2} - \rho_{1}} ] & \mbox{for } ( \frac{\tau \rho_{1}}{1+ \rho_{1}} ) < d_{2} < ( \frac{\tau \rho_{2}}{1+ \rho_{2}} ) \\ {[} \frac{ ( 1+ \rho_{2} ) - \frac{\tau}{ ( \tau- d_{2} )}}{\rho_{3} - \rho_{2}} ] & \mbox{for } ( \frac{\tau \rho_{2}}{1+ \rho_{2}} ) < d_{2} < ( \frac{\tau \rho_{3}}{1+ \rho_{3}} ) \\ 0& \mbox{for elsewhere} \end{array} \right \} \end{aligned}$$
(23)
$$\begin{aligned} &\nu_{d 2} ( \tilde{d}_{2} ) = \left \{ \begin{array}{@{}l@{\quad}l@{}} [ \frac{ ( 1+ \rho_{1} ) - \frac{\tau}{ ( \tau- d_{2} )}}{\rho_{2} - \rho_{1} '} ] & \mbox{for } ( \frac{\tau \rho_{1}}{1+ \rho_{1}} ) < d_{2} < ( \frac{\tau \rho_{2}}{1+ \rho_{2}} )\\ {}[ \frac{\frac{\tau}{ ( \tau- d_{2} )} - ( 1+ \rho_{3} ' )}{\rho_{3} ' - \rho_{2}} ] &\mbox{for } ( \frac{\tau \rho_{2}}{1+ \rho_{2}} ) < d_{2} < ( \frac{\tau \rho_{3} '}{1+ \rho_{3} '} )\\ 1 & \mbox{for elsewhere} \end{array} \right \} \end{aligned}$$
(24)

Therefore the score function of d 2 is given by

$$ \zeta ( d_{2} ) = \left \{ \begin{array}{@{}l@{\quad}l@{}} \frac{ [ \frac{\tau}{ ( \tau- d_{2} )} - ( 1+ \rho_{1} ) ]}{\rho_{2} - \rho_{1}} - \frac{ [ ( 1+ \rho_{2} ) - \frac{\tau}{ ( \tau- d_{2} )} ]}{\rho_{2} - \rho_{1} '}& \mbox{for } d_{2} ' < d_{2} < d_{2}^{''} \\ \frac{ [ ( 1+ \rho_{2} ) - \frac{\tau}{ ( \tau- d_{2} )} ]}{\rho_{3} - \rho_{2}} - \frac{ [ \frac{\tau}{ ( \tau- d_{2} )} - ( 1+ \rho_{3} ' ) ]}{\rho_{3} ' - \rho_{2}}& \mbox{for } d_{2}^{''} < d_{2} < d_{2}^{'''} \\ 0& \mbox{for elsewhere} \end{array} \right \} $$
(25)

or,

$$ \zeta ( d_{2} ) = \left \{ \begin{array}{@{}l@{\quad}l@{}} ( \frac{u_{1}}{\tau- d_{2}} ) - u_{2} & \mbox{for } d_{2} ' < d_{2} < d_{2}^{''}\\ u_{3} - ( \frac{u_{4}}{\tau- d_{2}} ) & \mbox{for } d_{2}^{''} < d_{2} < d_{2}^{'''}\\ 0& \mbox{for elsewhere} \end{array} \right \} $$
(26)

where

$$\begin{aligned} &u_{1} =\tau \biggl[ \frac{1}{\rho_{2} - \rho_{1}} + \frac{1}{\rho_{2} - \rho_{1} '} \biggr], \qquad u_{2} = \biggl[ \frac{1+ \rho_{1}}{\rho_{2} - \rho_{1}} + \frac{1+ \rho_{2}}{\rho_{2} - \rho_{1} '} \biggr],\\ & u_{3} = \biggl[ \frac{1+ \rho_{3}}{\rho_{3} - \rho_{2}} + \frac{1+ \rho_{3} '}{ \rho_{3} ' - \rho_{2}} \biggr], \qquad u_{4} =\tau \biggl[ \frac{1}{\rho_{3} - \rho_{2}} + \frac{1}{\rho_{3} ' - \rho_{2}} \biggr] \end{aligned}$$

and \(d_{2} '\), \(d_{2}^{''}\), \(d_{2}^{'''}\) are to be calculated properly and consequently, the α-cut of the score function ζ is given by

$$ \zeta ( d_{2} ) \rfloor_{\alpha} = \bigl[ L_{d 2}^{-1} ( \alpha ), R_{d 2}^{-1} ( \alpha ) \bigr] = \biggl[ \tau- \biggl( \frac{u_{1}}{u_{2} +\alpha} \biggr),\tau- \biggl( \frac{u_{4}}{u_{3} -\alpha} \biggr) \biggr] $$
(27)

Now, using (22) and (27) the α-cuts of the score function of D=d 1+d 2 are as follows: S(D)| α =ψ(d 1)| α +ζ(d 2)| α that provides as

$$\begin{aligned} &\bigl[ L_{D}^{-1} ( \alpha ), R_{D}^{-1} ( \alpha ) \bigr] \\ &\quad = \biggl[ \biggl( \frac{k_{2}}{k_{1} -\alpha} \biggr) - \biggl( \frac{u_{1}}{u_{2} +\alpha} \biggr) -\eta+\tau, \biggl( \frac{k_{4}}{k_{3} +\alpha} \biggr) - \biggl( \frac{u_{4}}{u_{3} -\alpha} \biggr) -\eta+\tau \biggr] \end{aligned}$$
(28)

However, since the α-cut of the score function of the total demand D is monotonically increasing so the α-cut of \(\sqrt{D}\) is given by

$$\begin{aligned} &\bigl[ L_{\sqrt{D}}^{-1} ( \alpha ), R_{\sqrt{D}}^{-1} ( \alpha ) \bigr] \\ &\quad = \biggl[ \sqrt{ \biggl( \frac{k_{2}}{k_{1} -\alpha} \biggr) - \biggl( \frac{u_{1}}{u_{2} +\alpha} \biggr) -\eta+\tau}, \sqrt{ \biggl( \frac{k_{4}}{k_{3} +\alpha} \biggr) - \biggl( \frac{u_{4}}{ u_{3} -\alpha} \biggr) -\eta+\tau} \biggr] \end{aligned}$$
(29)

Also the α-cuts of the score function of (s p−p 1) is obtained by using (17) and is given by

$$ \bigl[ L_{s^{p} - p 1}^{-1} ( \alpha ), R_{s^{p} - p 1}^{-1} ( \alpha ) \bigr] = \biggl[ \frac{\alpha}{\lambda_{1} '} + p_{1} + \delta_{1} ', p_{1} + \delta_{3} ' - \frac{\alpha}{\lambda_{2} '} \biggr] $$
(30)

Now, we have from Eq. (5)

$$\varphi= Z^{*} \bigl( s^{p},\rho \bigr) = \bigl( s^{p} - p_{1} \bigr) D- \sqrt{\frac{2 c_{1} c_{2} c_{3} D}{c_{2} +c_{3}}} -k \rho^{m} $$

Using basic arithmetic on α-cut, the α-cut of the score function φ can be constructed with the help of Eqs. (14), (28), (29) and (30). Therefore,

$$\begin{aligned} L_{\varphi}^{-1} ( \alpha ) =& \biggl[ \biggl( p_{1} + \delta_{1} ' + \frac{\alpha}{\lambda_{1} '} \biggr) \biggl\{ \frac{k_{2}}{k_{1} -\alpha} - \frac{u_{1}}{u_{2} +\alpha} -\eta+\tau \biggr\} \\ &{} - \sqrt{\frac{2 c_{1} c_{2} c_{3}}{c_{2} + c_{3}} \biggl\{ \frac{k_{4}}{k_{3} +\alpha} - \frac{u_{4}}{u_{3} -\alpha} -\eta+\tau \biggr\}} -k \biggl( \delta_{3} - \frac{\alpha}{\lambda_{2}} \biggr)^{m} \biggr] \end{aligned}$$
(31)

and

$$\begin{aligned} R_{\varphi}^{-1} ( \alpha ) =& \biggl[ \biggl( p_{1} + \delta_{3} ' + \frac{\alpha}{\lambda_{2} '} \biggr) \biggl\{ \frac{k_{4}}{k_{3} +\alpha} - \frac{u_{4}}{u_{3} -\alpha} -\eta+\tau \biggr\} \\ &{}- \sqrt{ \frac{2 c_{1} c_{2} c_{3}}{c_{2} + c_{3}} \biggl\{ \frac{k_{2}}{k_{1} -\alpha} - \frac{u_{1}}{u_{2} +\alpha} -\eta+\tau \biggr\} } -k \biggl( \delta_{1} + \frac{\alpha}{\lambda_{1}} \biggr)^{m} \biggr] \end{aligned}$$
(32)

Let us construct the indexed values of the decision parameters s, q and ϕ.

To do this we shall use (31) and (32) and Yager’s (1981) ranking index method. Then, we have

$$\begin{aligned} I ( \varphi ) =& \frac{1}{2} \int_{0}^{1} \bigl\{ L_{\varphi}^{-1} ( \alpha ) + R_{\varphi}^{-1} ( \alpha ) \bigr\} d\alpha \\ =& \frac{1}{2} \bigl( p_{1} + \delta_{1} ' \bigr) \biggl[ k_{2} \operatorname{Log}\biggl( \frac{k_{1}}{k_{1} -1} \biggr) - u_{1} \operatorname{Log}\biggl( \frac{1+ u_{2}}{u_{2}} \biggr) - ( \eta-\tau ) \biggr] \\ &{}+ \frac{1}{2 \lambda_{1} '} \biggl[ u_{1} u_{2} \operatorname{Log}\biggl( \frac{1+ u_{2}}{ u_{2}} \biggr) + k_{1} k_{2} \operatorname{Log}\biggl( \frac{k_{1}}{k_{1} -1} \biggr) - u_{1} - k_{2} - \biggl( \frac{\eta-\tau}{2} \biggr) \biggr] \\ &{}+ \frac{1}{2} \bigl( p_{1} + \delta_{3} ' \bigr) \biggl[ k_{4} \operatorname{Log}\biggl( \frac{k_{3} +1}{k_{3}} \biggr) - u_{4} \operatorname{Log}\biggl( \frac{u_{3} -1}{u_{3}} \biggr) - ( \eta-\tau ) \biggr] \\ &{}+ \frac{1}{2 \lambda_{2} '} \biggl[ u_{3} u_{4} \operatorname{Log}\biggl( \frac{u_{3} -1}{ u_{3}} \biggr) + k_{3} k_{4} \operatorname{Log}\biggl( \frac{k_{3} +1}{k_{3}} \biggr) - u_{4} - k_{4} - \biggl( \frac{\eta-\tau}{2} \biggr) \biggr] \\ &{}- \frac{1}{2} \sqrt{ \biggl( \frac{2 c_{1} c_{2} c_{3}}{c_{2} +c_{3}} \biggr)} \int _{0}^{1} \biggl\{ \sqrt{\frac{k_{2}}{k_{1} -\alpha} - \frac{u_{1}}{u_{2} +\alpha} - ( \eta-\tau )} \\ &{} + \sqrt{\frac{k_{4}}{k_{3} +\alpha} - \frac{u_{4}}{u_{3} -\alpha} - ( \eta-\tau )} \biggr\} d\alpha \\ &{}- \biggl( \frac{k}{m+1} \biggr) \biggl[ \lambda_{1} \biggl( \delta_{1} + \frac{1}{\lambda_{1}} \biggr)^{m+1} - \lambda_{1} \delta_{1}^{m+1} + \lambda_{2} \delta_{3}^{m+1} - \lambda_{2} \biggl( \delta_{3} - \frac{1}{ \lambda_{2}} \biggr)^{m+1} \biggr] \end{aligned}$$
(33)

Further using (29), we have

$$\begin{aligned} I ( s ) =& \frac{1}{2} \sqrt{ \biggl( \frac{2 c_{1} c_{2}}{c_{3} ( c_{2} +c_{3} )} \biggr)} \int _{0}^{1} \biggl\{ \sqrt{\frac{k_{2}}{k_{1} -\alpha} - \frac{u_{1}}{u_{2} +\alpha} - ( \eta-\tau )} \\ &{}+ \sqrt{\frac{k_{4}}{k_{3} +\alpha} - \frac{u_{4}}{ u_{3} -\alpha} - ( \eta-\tau )} \biggr\} d\alpha \end{aligned}$$
(34)

and

$$ I ( q ) = \biggl( \frac{c_{2} + c_{3}}{c_{2}} \biggr) I(s) $$
(35)

Furthermore, using (14) and (18) the indexed value of s p and ρ are obtained respectively as under:

$$ I ( \rho ) = \frac{1}{2} \int_{0}^{1} \bigl\{ L_{\rho}^{-1} ( \alpha ) + R_{\rho}^{-1} ( \alpha ) \bigr\} d\alpha= \frac{1}{2} \biggl( \delta_{1} + \delta_{2} + \frac{1}{2 \lambda_{1}} - \frac{1}{2 \lambda_{2}} \biggr) $$
(36)

and

$$ I \bigl( s^{p} \bigr) = \frac{1}{2} \int_{0}^{1} \bigl\{ L_{s^{p}}^{-1} ( \alpha ) + R_{s^{p}}^{-1} ( \alpha ) \bigr\} d\alpha= \frac{1}{2} \biggl( \delta_{1} ' + \delta_{2} ' + \frac{1}{2 \lambda_{1} '} - \frac{1}{2 \lambda_{2} '} \biggr) $$
(37)

4 Numerical example

Example 1

For Crisp Model, let a seller started his/ her business with initial demand rate η=80 units, τ=50 units, setup cost c 1=100 ($), holding cost per unit item c 2=2.5 ($), Shortage cost c 3=8 ($), s m=30; s m =12; m=3, purchasing price p 1=12 ($), k=15 ($), the cycle time T=1 month then we get the following results in Table 1.

Table 1 Crisp optimal solution for fixed ρ and s p
Full size table

From Table 2, we see that the maximum profit will reach when ρ ∗=2.538 and m ∗=1; the inventory run time is 26 days and the shortage period is 4 days only. Also we further observe that the profit will be nominal for m=3 and ρ m=3.9.

Table 2 Crisp optimal solution for different ρ and m
Full size table

Example 2

As per Example 1, let a seller started his/her business with linear demand factor η=80 units and τ=50 units. If the set up cost c 1=$100.00, holding cost per unit item c 2=$2.5, shortage cost c 3=$8.0, selling price per unit item s m=$30.0, s m =$12.0, unit purchasing price p 1=$12.0, k=$15.0, m=3, the cycle time T=1 month then we have the solution in Table 3.

Table 3 GFO Solution for s m <s 1<s 2<s p∗<s 3<s m and ρ 1<ρ 2<ρ ∗<ρ 3<ρ m
Full size table

4.1 Interpretation on GFO and IFO solutions (Tables 3–4)

In Table 3, when ρ assumes value 0.925 and unit selling price s p be $15.25 with shortage quantity 28.442 unit and order quantity 119.453 unit then the average maximum profit be $218.41 under GFO policy. However, Table 3 shows that for minimum shortage time 5 days with ρ=1.025, little more order quantity (0.375 unit) than the above, the profit is decreased to $192.17. Throughout the whole table, we see within a specific selling price interval, the profit function follows a parabolic path. Also it is noticed that the order quantity is high with same selling price and follows the marginal profit. Table 4 shows, in IFO environment, for 6 days shortage time, the maximum order quantity be 106.765 units, shortage quantity 25.421 units, unit selling price $16.37, ρ=0.996 and maximum profit be $445.66. The whole table shows the profit function behaves linear increasing trend within specific limits of selling prices. It is also observed that,in all cases, shortage period is fixed to 6 days and it is getting better result than GFO policy.

Table 4 IFO Solution for \(s_{m} < s_{1} ' < s_{1} < s_{2} < s^{p*} < s_{3} < s_{3} ' < s^{m}\) and \(\rho_{1} ' < \rho_{1} < \rho_{2} < \rho^{*} < \rho_{3} < \rho_{3} ' < \rho^{m}\)
Full size table

4.2 Comments on Fig. 3

In Fig. 3, when s p lies in [15, 17] then IFO policy gives better result than the GFO policy for all cases. The upper straight line bar shows the optimal solutions for the IFO policy and the lower V-shaped bar shows the solutions for GFO policy. For GFO policy, when s p and ρ follows a straight path then the average maximum profit function follows a parabolic path whereas, in IFO policy, whenever follows a parabolic path then unit selling price and average maximum profit follows a straight path. The total graph shows IFO policy gives the better solution than GFO solution. Furthermore, it is undesirable to say that, the optimal solution involves in GFO or IFO policy has a large difference with respect to the crisp value.

Fig. 3
figure 3

GFO and IFO Solutions near Crisp Optimality

Full size image

5 Sensitivity analysis

We take a sensitivity for the crisp model of the parameters {c 1,c 2,c 3,k,τ,η,p 1} from (−50 % to +50 %) and this can be shown in the following table.

From Table 5, we observe that the parameters c 1, c 2 and τ have fair sensitivity whenever a change is made from (−50 % to +50 %) each separately. At +50 % and −50 % changes in demand parameter τ, the profit is increased to 5.36 % and it decreases to −3.89 % respectively. At +50 % and −50 % changes in c 2 the profit decreases to −6.26 % and it increases to 10.71 % respectively. The cost price parameter p 1 is tremendously high sensitive for changes from −50 % to +50 %. At −50 % and −30 % change of p 1 the solution is unbounded but at +50 % change, the average profit decreases to −72.57 %. The demand parameter η has moderately high and linear sensitivity within the changes from −50 % to +50 %. Throughout the table, the average total profit is maximum when the demand parameter η increases to +50 % and in that case the decision variables are the order quantity q ∗=258.772, the shortage quantity s ∗=61.613, the promotional effort ρ ∗=0.891 and the maximum average profit Z ∗=$1372.76.

Table 5 Sensitivity Analysis
Full size table

6 Conclusion

In this paper we have discussed the solutions of Crisp, GFO and IFO problems. The selling price and promotional effort/sales teams’ initiatives dependent demand rate is considered in well known classical backorder EOQ model. Considering profit function, we have solved the model under intuitionistic fuzzy environment. The score function (net membership) have been taken care of and a trend is studied for their optimal solutions. In this study, it is observed in fuzzy environment that the average profit would decrease always, but the use of A-IFS has restriction in the worst condition. In the appendix, it has been shown that the net membership function follows the ranking index rule. Neither high selling price nor low promotional effort would be able to give a considerable high average profit. The proposed model provides a proper direction to a manager of a business organization to achieve maximum profit while the decision variables are fuzzy variables in nature. The new major contribution of the paper is to consider the demand function as a function of selling price and promotional effort simultaneously in crisp model. The analysis of the model by GFO and IFO approach is also quite new, considering these decision variables as fuzzy variables.

7 Scope of future work

The proposed model can be extended further in many ways. One immediate extension can be done in a supply chain consisting of multiple members involving sharing cost of promotional effort among them and discount offer on whole sale prices in each stage to motivate the downstream members to buy more. Using several score functions, this model can be extended further so that any one may obtain a better solution. This may enrich the trend value also.