1 Introduction

The evolutionary dynamics of the expanded collective instability excitations in star-forming complex molecular clouds has attracted immense attraction among researchers in recent years. This is due to the not-well-understood active roles played by such waves and instabilities in various kinetic processes of the complex fluid material transports leading to superdense phases responsible for the initiation of gravitationally bounded non-homologous structure formation in varied astro-cosmo-plasmic circumstances [1,2,3,4,5]. An example in this milieu may be the formation of massive stars in the Orion molecular cloud – exhibiting a rich plethora of the excited active waves, collective oscillations and cooperative instabilities – mainly at the cloud surface boundary [6].

For exploring the complex dynamical processes prevalent in structuring the astroclouds tentatively, an ideal magnetohydrodynamic (MHD) mean-fluidic approach has extensively been applied for the stability analyses in the recent astrocosmic scenarios [7,8,9,10]. In this direction, it has been established in the past that a self-gravitating, partially ionised and magnetised cloud becomes gravitationally unstable on the grounds that the non-local self-gravity overcomes the conjoint action of the magneto-thermal pressure support on the spatial scales of the evolutionary cloud [11,12,13,14]. The presence of the wide-range MHD spectral waves and collective fluctuations provide stabilising stimuluses against the canonical self-gravitating cloud collapse triggering the formation mechanism of diverse non-homologous astrostructures in reality [11, 15].

It has been reported in another work (ideal, isothermal MHD) that, the critical Jeans length, \(\lambda _{\mathrm{JB}} \), and the critical Jeans mass, \(M_{\mathrm{JB}} \), increase drastically in the presence of a magnetic field relative to the field-free normal counterparts as

$$\begin{aligned} \lambda _{\mathrm{JB}} =10\lambda _{\mathrm{J}} \left( {1+M_{\mathrm{A}} } \right) ^{1 / 2}\hbox { and }M_{\mathrm{JB}} =M_{\mathrm{J}} \left( {1+M_{\mathrm{A}} } \right) ^{1 / 2}, \end{aligned}$$

where \(\lambda _{\mathrm{J}} \) is the usual Jeans length, \(M_{\mathrm{JB}} ={v_{\mathrm{A}} } / {c_{s} }\) is the Alfvenic Mach number and \(M_{\mathrm{J}} \) is the usual critical Jeans mass [13]. Apart from the above, it has also been shown that similar cloud collapse in the real astronomical situations gets triggered at the cost of slow waves [12]. It has been highlighted therein that, the non-local self-gravity could act as an alternate source for sustaining fluid turbulence needed for the antigravity pressure support, if the energy supply from giant structure formation is almost negligible, and so forth [12, 16]. Parallely, the main distinction between the traditional magnetically driven and gravitationally driven ambipolar diffusions in normal star-forming clouds has also been reported [16]. It has been demonstrated that the former acts as a cloud stabiliser and the latter as a cloud destabiliser against the collapse [17]. It is restricted on the grounds that the growth rate of the latter (gravitational diffusion) cannot exceed the free in-falling rate of the cloud matter against the former (magnetic diffusion).

We cannot ignore the fact that, in the case of magnetised partially ionised self-gravitating plasmas, concentration-induced diffusive drifts originate from the diversified collisional effects leading to momentum transports among the diversified constitutive species. It results in a significant number of unavoidable non-ideal effects in the involved MHD description. These non-idealities still remain to be well explored and well understood in the real domains of astronomical relevancy. In such a situation, the plasma inertia as well as the non-ideality effects are simultaneously important as far as the bulk fluid behaviour is concerned. In the mean-fluidic fabric, several researchers have studied the non-ideal MHD wave excitation, propagation and instability dynamics in different situations [18,19,20,21,22]. Based on such reports, it is noted that the coupling of the magnetic field lines with the constitutive neutral species is given by a specific parameter, known as the Hall parameter \(\beta _{j} ={\omega _{cj} } / {\upsilon _{j} }\), which is the ratio between the cyclotron frequency and the collision frequency of the constituents (plasma–plasma plus plasma–neutral). Such coupling phenomena are described with the help of the electromagnetic induction equation in a modified form involving ambipolar diffusion and Hall drift in addition to the usual Ohmic diffusion [19,20,21,22].

The Hall-induced MHD instability in normal magnetised fluids is indeed non-dissipative in nature playing an active role in the redistributive cascading processes of magnetic energy from large-to-small scales [23]. The structure-forming molecular cloud cores become gravitationally unstable in the presence of the Hall catalytic action leading thereby to the formation of stellar disks. In contrast, if the Ohmic, ambipolar and Hall diffusions are simultaneously included in a differentially rotating disk system (with weak ionisation \({\sim }10^{-4}{-}10^{-8}\)), new unstable modes may be excited [16,17,18]. As a direct consequence, the ambipolar diffusion and differential disk rotation couple together to amplify the intrinsic magnetic field in the disk [24, 25]. The self-gravitational fragmentation of the clouds into stars is enhanced because of the reduction in cloud magnetic energy due to weak neutral plasma coupling in the presence of ambipolar diffusion [26]. In fact, the ambipolar diffusion is more prominent in rarer clouds. It is due to the fact that the ambipolar dissipation time scale (\({\sim }10^{5}\) yr) is much lower than the Ohmic dissipation one (\({\sim }10^{15}\) yr). So, the plasma particles can drift along the field lines due to the action of the electromagnetic Maxwell stress [27].

Apart from the above, the fluid kinematic viscosity is another key parameter affecting such dynamics [28]. This damping agency helps in the relaxation process of the microscopic molecular motions in the fluid, and thus, usually acts as a fluid-cloud stabiliser against the non-local self-gravity. In parallel, another unavoidable factor to be considered in the star formation processes is the tidal force field effect [29,30,31,32]. The tidally generated waves participate in the overall redistribution of the transport properties, such as the angular momentum, mass, energy, and so on. In the case of a rotating fluid body, the dissipation of the waves is dependent on the tidal frequency, which increases with the size of the body, and vice versa [30]. As the tidal force is an external gravitational source arising from neighbouring objects [29,30,31,32], it helps in the growth of instability in a self-gravitating system, which, indeed, counteracts the effects of magnetic field, thereby, leading to halt the fragmentation. In other words, it is seen that [31], the action of a typical disruptive tidal field provides stability against the gravitational collapse. It results in the enhancement of the effective Jeans scale length (super-Jeans) relative to the usual Jeans case (critical-Jeans). Even a compressible tidal field can make such perturbations easily grow even when the cloud mass is sub-critical (sub-Jeans) relative to the usual picture [31].

The compressive tidal force is one of the responsible factors for the formation and evolution of stellar structures in the presence of a magnetic buoyancy force [32]. It may be pertinent to add here that the Coriolis force, which is another addition to stellar catalytic agencies, is an inertial force, acting as a rotational correction over the Newtonian fluid equation in a uniformly rotating frame of reference [10, 14, 30, 33]. Such Coriolis rotations of astroclouds change the properties of tidally generated waves substantially [33]. It seems that astrofluid stability analyses depicting the structure formation are inadequate in the absence of the Coriolis rotation effects.

The energetic cosmic rays \(({\sim }1\,\hbox {eV cm}^{-3})\) arise from supernova, hypernova remnants and other extraterrestrial sources [29,30,31,32,33,34]. The interaction between the extremely high energetic cosmic rays (\(\sim \)MeV–TeV) and the constitutive cold particles (\(\sim \)eV) of the ISM introduces the excitation of two-stream types of instability, or even beam-plasma microinstability, firehose instability, dynamo instability and so forth, where the particle velocities are locally different in different realistic astrospace situations [35,36,37,38,39,40,41,42,43,44,45]. Such instability patterns could even saturate in the nonlinear regime to form solitary pulses, double layers, oscillitons, and other coherent eigenmode structures [43]. The amplification of the cosmic magnetic field via the dynamo instability is noteworthy [1, 34, 35]. A self-consistent kinetic model has been developed to address the role of the cosmic rays on the marginal stability of the kinetic Alfven waves amid the interstellar (galactic) charged-neutral collisions [40]. It has recently been shown that the charge density and mass density fluctuations are coupled together to excite the gravitational instabilities towards the structure formation dynamics [38,39,40,41,42,43,44,45].

It can now clearly be seen here that a full portrayal simultaneously describing the real astronomic non-ideal MHD effects and cosmo-tidal phenomenological factors in rotating viscous star-forming clouds has rarely been addressed in the past. In other words, the existing reports have ignored a majority of the important astrofluidic factors for the sake of simplification, such as the tidal force field, cosmic ray pressure effects, Coriolis force, viscosity, etc. This is the main motivation and novelty of the proposed study aiming at the real cloud stability dynamics. In particular, we include synchronously, for the first time, the complex coupling dynamics between the non-ideal MHD factors and gyro-cosmo-tidal effects. A normal mode analysis results in a linear quartic dispersion relation with atypical variable dispersion coefficients. A numerical platform, which is based on a standard root finder [46], is sensibly built to identify and see the stabilising and destabilising agencies. It is established principally that the ambipolar diffusion is the only non-ideal MHD effect influencing the excitation and propagation of the magneto-acoustic waves. The reliability aspects of our non-trivial outcomes found herein are compared, correlated and validated with the diverse prior special cases and corollaries in varied realistic astronomic circumstances.

2 Non-ideal MHD model analysis

The main goal of our local analysis lies in the deep analysis of the self-gravitating non-ideal MHD fluctuations in the fabric of a single classical non-relativistic mean-fluid approach on the relevant astrophysical fluid scales of space and time. It is well-known that cosmic rays comprise \(10^{-9}\) of the interstellar kinetic particles in such situations. However, their energy density (\({\sim }1~\hbox {eV cm}^{-3})\) is that of the constituent thermal particles [34, 35]. The interaction of the energetic cosmic particles ionises the interstellar gaseous medium (ionisation rate \({\sim }10^{-16}{-}10^{-17}\,\hbox {s}^{-1})\). The cosmic rays, magnetic field and interstellar thermal constituents maintain a pressure equilibrium almost with no thermal energy gradient [34,35,36]. The main ionising source of the ISM sensibly is the local ionising source, such as stars, supernovae, etc. It ignores the dynamics of intergalactic medium (space between galaxies ionised by the energetic cosmic ray particles). So, in our case, the interstellar ionisation source is the most effective one.

The basic governing equations structuring the considered fluid consist of the equation of continuity for fluid net mass conservation, momentum equation for net force density conservation, electromagnetic induction equation in a modified (with non-ideality effects) form for magnetic field dynamics. The system closure finally comes from the self-gravitational Poisson equation for the potential distribution sourced in the local material density fields in the low-frequency approximation [9]. Thus, the equation of continuity for the non-ideal MHD with all the usual notations in an inertial frame of reference is given as

$$\begin{aligned} \partial _{t} \rho +{\vec {\nabla }}\cdot \left( {\rho \,{\vec {v}}} \right) =0, \end{aligned}$$
(1)

where \(\rho =\rho _{e} +\rho _{i} +\rho _{n} \) and \({ v}=({\rho _{e} { v}_{e} +\rho _{i} { v}_{i} +\rho _{n} { v}_{n}})\big /\rho \) are the mean-fluid material density and mean-fluid velocity contributed by all the constitutive species, respectively. The subscripts e, i and n signify the constitutive electrons, ions and neutrals, respectively. Thus, the generalised complex fluid is projected as a single mean-fluid subjected to all the possible dynamical key factors relevant to the astrophysical scales of space and time. A few remarks on the above are given as follows.

As mentioned, we study a partially ionised self-gravitating dense interstellar dark cold cloud having a number density of \({\sim }1\,\hbox {cm}^{-3}\). In this density scale range, the ionisation, recombination or heat conduction are not so significant on the astrophysical fluid scales of space and time. That is why we ignore the radiative effects, such as temperature fluctuations, radiative loss–gain processes and other photochemical actions in the evolutionary or growth dynamics of the constituent particles. Accordingly, the force density or momentum balance equation that includes concurrently the gravity, magnetic field and viscosity in the customary notations [17,18,19,20, 40] can be cast as

(2)

where \(d_{t} =( {\partial _{t} +{\vec {v}}\cdot \,{\vec {\nabla }}} )\) denotes the material derivative, or Lagrangian temporal derivative, or substantial derivative. B is the magnetic induction vector (field strength), \(\psi \) is the long-range self-gravitational potential contributed by the material density field associated with the heavier fluid constitutive elements in a non-local form, \(T_{\mathrm {tidal}}\) is the tidal force field originated collectively from the distant gravitating astro-objects, \(\omega _{r} \) is the uniform Coriolis rotational frequency and \(\eta _{v} \) denotes the kinematic viscosity coefficient of the astronomic mean-fluidic matter under investigation.

It may be pertinent to add that the physical significance of each of the terms appearing above is a generic one. As such, (1) indicates the fluid net influx–outflux balancing. The net force density balance (also, energy transport equation on its moment integration) is represented by (2). The term in the LHS in (2) is well-known to typify the inertial nature of the fluid parcel under consideration. The first term in the RHS represents the combined force–density effects stemming from the fluid thermal pressure, \(P_{\mathrm{Th}} \), and the cosmic ray pressure, \(P_{\mathrm{CR}} .\) The second term in the RHS represents the Lorentz force arising jointly from the magnetic tension force, \({( {{\vec {B}}\cdot {\vec {\nabla }}} )B} / {4\pi }\), and the magnetic pressure force, \({\vec {\nabla }}{\left( {B^{2}} \right) } / {8\pi }\). The third term gives the non-local cloud-centric self-gravitational force. The fourth term arises from the tidal force field action. Similarly, the fifth term originates from the uniform Coriolis inertial force. Lastly, the sixth term gives the dissipative effects sourced by the fluid kinematic viscosity.

Now, the electromagnetic induction equation, which is due to Faraday and Ohm in a generalised form, describing the spatiotemporal dynamics of the resultant evolutionary magnetic field lines in the non-ideal MHD framework [21] in the cloud can be given as

$$\begin{aligned} \partial _{t} {\vec {B}}= & {} {\vec {\nabla }}\times ( {{\vec {v}}\times {\vec {B}}} )-{\vec {\nabla }}\nonumber \\&\times \left[ {\begin{array}{l} \eta \,( {{\vec {\nabla }}\times {\vec {B}}} )+\eta _\mathrm{H} ( {{\vec {\nabla }}\times {\vec {B}}} )\times \hat{{B}} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\eta _\mathrm{A} ( {{\vec {\nabla }}\times {\vec {B}}} )_{\bot } \\ \end{array}} \right] . \end{aligned}$$
(3)

The term in the LHS in (3) portrays the temporal accumulation term giving the net field spatial evolution out of all the non-ideal effects present in the RHS depicting the non-steady processes. The first term in the RHS gives the advection of the magnetic field lines with the plasma flowing with velocity v. The second term depicts the magnetic field line diffusion through the flowing plasma as a summative effect of the Ohmic (due to the particle collisions), Hall (due to the heteropolar symmetry breaking in the magnetic field) and ambipolar magneto-diffusive processes (due to the particle concentration gradients). The symbols, \(\eta \), \(\eta _{\mathrm{H}}\) and \(\eta _{\mathrm{A}} \) denote the Ohmic, Hall and ambipolar diffusion coefficients, respectively.

For low density and relatively low degree of ionisation, the magnetic field lines are frozen into the plasma fluid and drift together with the neutrals. We can take \(\eta \), \(\eta _{\mathrm{H}} \sim 0\) , thereby, reducing (3) into a simpler inductive form [18, 21] as

$$\begin{aligned} \partial _{t} {\vec {B}}={\vec {\nabla }}\times [ {( {{\vec {v}}+{\vec {v}}_{B} } )\times {\vec {B}}} ], \end{aligned}$$
(4)

where \({\vec {v}}_{B} ={\eta _{\mathrm{A}}[ {( {{\vec {\nabla }}\times {\vec {B}}} )\times {\vec {B}}} ]} / {B^{2}}\) denotes the drift velocity of the field lines through the plasma due to the ambipolar magneto-diffusive activity. It is based on the fact that the electron-cyclotron and ion-cyclotron frequencies are now estimated as: \(\omega _{ce} =1750~\hbox {s}^{-1}\) and \(\omega _{ci} =3.2\times 10^{-2}~\hbox {s}^{-1}\). In such parametric windows, our estimation yields \(\beta _{e} =1.47\times 10^{6}\) and \(\beta _{i} =3.2\times 10^{-2}\), which develops the ambipolar diffusion in our partially ionised cloud plasma model.

As a closure of the fluid model, we apply the gravitational Poisson equation for the non-local long-range self-gravitational potential distribution created by the local density field [31] given as

$$\begin{aligned} \nabla ^{2}\psi =4\pi G\left( {\rho -\rho _{0} } \right) , \end{aligned}$$
(5)

where \(\rho _{0} \) denoting the global mean of the fluid material density, accounts for the so-called ‘Jeans swindle’ [3, 37]. We designate the Newtonian gravitational coupling constant as \(G=6.67\times 10^{-11}~\hbox {m}^{3}\,\hbox {kg}^{-1}\,\hbox {s}^{-2}\). It is perhaps needless to mention here that the swindle invoked herein acts as an analytic simplification tool in a judicious way with the help of which the zeroth-order force field effects arising from equilibrium inhomogeneities and non-uniformities in such media may be ignored and a ‘local normal mode analysis’ could be carried out with no loss of generality associated with the fundamental physical laws. We see that, it is not the material density, rather the material density fluctuations, which develop the gravitational potential in the inhomogeneous astroplasmas.

2.1 Perturbation analysis

In order to analyse cloud stability locally, we apply a standard technique of normal mode analysis over the perturbed cloud about its magnetohydrostatic homogeneous (local) equilibrium. We consider the linear perturbations (\(f_{1}\)) in all the relevant physical variables (f) in eqs (1)–(5) to undergo small-scale amplitude (linear) sinusoidal variation relative to the respective static equilibrium values (\(f_{0}\)) in the framework of homology transformations [1,2,3,4,5,6] given as

$$\begin{aligned}&f\left( {x,z\,;\,t} \right) =f_{0} +f_{1} \,\left( {x,z;\,t} \right) \text{ e}^{-i\left( {\omega \,t-k_{x} x-k_{z} z} \right) }, \end{aligned}$$
(6)
$$\begin{aligned}&f=\left[ {\rho \,\,\,\,\,\,{ v}\,\,\,\,\,\,P\,\,\,\,\,\,B\,\,\,\,\,\,\psi } \right] \,^{T}, \end{aligned}$$
(7)
$$\begin{aligned}&f_{0} =\left[ {\rho _{0} \,\,\,\,\,\,{ v}_{0} \,\,\,\,\,\,\,P_{0} \,\,\,\,\,\,B_{0} \,\,\,\,\,\,\psi _{0} } \right] \,^{T}, \end{aligned}$$
(8)
$$\begin{aligned}&f_{1} =\left[ {\rho _{1} \,\,\,\,\,{ v}_{1} \,\,\,\,\,\,P_{1} \,\,\,\,\,\,\,B_{1} \,\,\,\,\,\,\psi _{1} } \right] \,^{T}, \end{aligned}$$
(9)

where \(\omega \) is the radian frequency of the homologous fluctuations with the radian wave number and \({\vec {k}}\left( {=k_{x} \hat{{x}}+k_{z} \hat{{z}}} \right) \) is presumed to lie in the xz-plane at an angle \(\theta \) with the B-direction. It is evident that (8) represents plane-wave fluctuations on the ground that the assumed radius of geometrical curvature of the cloud is much larger than any other characteristic scale lengths of the system. In a broader sense, the plane-wave treatment here is justifiable due to a two-fold region: unbounded cloud and no geometrical edge effect realisable in the cloud.

Applying (6)–(9), the homologically transformed algebraic form of (1)–(5) in the defined wave space \(\left( {\omega ,\,k} \right) \) can respectively be derived and presented as

$$\begin{aligned}&\omega \rho _{1} -\rho _{0} \left( {k_{x} { v}_{1x} +k_{z} { v}_{1z} } \right) =0 \end{aligned}$$
(10)
$$\begin{aligned}&\omega ^{2}{} { v}_{1x} -\left( {1+\alpha } \right) \,c_{s}^{2} k_{x} \left( {k_{x} { v}_{1x} +k_{z} { v}_{1z} } \right) \nonumber \\&\quad -2i\omega \omega _{ry} { v}_{1z} +i\omega \eta _{\mathrm{eff}} k^{2}{} { v}_{1x} =0 \end{aligned}$$
(11)
$$\begin{aligned}&\omega \,{ v}_{1y} +\frac{\,B_{0x} }{4\pi \rho _{0} }\left( {k_{x} B_{1y} } \right) \nonumber \\&\quad -2i\left( {\omega _{ry} { v}_{1x} -\omega _{rx} { v}_{1z} } \right) =0 \end{aligned}$$
(12)
$$\begin{aligned}&\omega ^{2}{} { v}_{1z} -\left( {1+\alpha } \right) \,c_{s}^{2} k_{z} \left( {k_{x} { v}_{1x} +k_{z} { v}_{1z} } \right) \nonumber \\&\quad +\frac{\omega \,B_{0x} }{4\pi \rho _{0} }\left[ {k_{x} B_{1z} -k_{z} B_{1x} } \right] \nonumber \\&\quad -\omega \,k_{z} \psi _{1} -i\left( {k_{x} { v}_{1x} +k_{z} { v}_{1z} } \right) \,T_{z} \nonumber \\&\quad +2i\omega \omega _{ry} { v}_{1x} +i\omega \eta _{\mathrm{eff}} k^{2}{} { v}_{1z} =0\, \end{aligned}$$
(13)
$$\begin{aligned}&\omega \,B_{1x} =B_{0x} k_{z} { v}_{1z} \end{aligned}$$
(14)
$$\begin{aligned}&\omega \,B_{1y} =-B_{0x} k_{x} { v}_{1y} \end{aligned}$$
(15)
$$\begin{aligned}&\omega \,B_{1z} =-\left( {\frac{\omega \,k_{x} -i\eta _\mathrm{A} k_{x} k_{z}^{2} }{\omega +i\eta _\mathrm{A} k_{x}^{2} }} \right) B_{0x} { v}_{1z} \end{aligned}$$
(16)
$$\begin{aligned}&k_{z}^{2} \psi _{1} =-\frac{\omega _\mathrm{J}^{2} }{\omega }\left( {\frac{k_{x} { v}_{1x} +k_{z} { v}_{1z} }{k_{z}^{2} }} \right) . \end{aligned}$$
(17)

In the above equations, \(\eta _{\mathrm{eff}} ={\eta _{v} } / {\rho _{0}}\) represents the effective rescaled fluid kinematic viscosity coefficient, \(\alpha ={P_{\mathrm{CR0}} } / {P_{\mathrm{Th0}}}\) denotes the ratio between the cosmic ray pressure and plasma thermal pressure, \(T_{z}\) is the considered tidal force field in the z-direction, \(\eta _{\mathrm{A}} =\left( {{\rho _{n} } / {\rho _{i} }} \right) {{ v}_{\mathrm{A}}^{\mathrm{2}} } / {\nu _{ni} }\) denotes the ambipolar diffusion coefficient with neutral-ion collision frequency \(\nu _{ni} \) and \(\omega _{\mathrm{J}} =\sqrt{4\pi \!G\rho _{0} }\) is the Jeans angular frequency. Clearly, (11)–(13) represent the resolved components of (2) in the three independent spatial directions of x, y and z, respectively. Similarly, the components of (3) are shown by (14)–(16), respectively. In our proposed analysis, application of (12) and (15) is relaxed as per the non-ideal MHD model configuration.

2.2 Dispersion relation

As we are interested to investigate the magnetosonic wave propagation dynamics (transverse to the direction of the embedded magnetic field), we herewith ignore the y-directional components of the fluid momentum transfer and the y-directional contribution from the electromagnetic induction effects. As a consequence, the perturbation dynamics in our model takes place in the xz-plane of the configuration space. We now resolve the angular wave number k as \(k_{x} =k\cos \,\theta \) and \(k_{x} =k\sin \,\theta \), where \(\theta \) is the angle subtended between the direction of wave propagation and that of the magnetic field, B. An algebraic exercise of elimination and decomposition over (10)–(17) subsequently results in a linear generalised quartic dispersion relation with an atypical set of multiparametric coefficients given as

$$\begin{aligned}&\omega ^{4}+a_{3} \omega ^{3}+a_{2} \omega ^{2}+a_{1} \omega +a_{0} =0 \end{aligned}$$
(18)
$$\begin{aligned}&a_{3} =i\,\left( {\eta _{\mathrm{eff}} +2\eta _{\mathrm{A}} \cos ^{2}\theta } \right) \,k^{2} \end{aligned}$$
(19)
$$\begin{aligned}&a_{2} =\omega _{\mathrm{J}}^{\mathrm{2}} -ik\sin \theta T_{z} -\eta _{\mathrm{eff}} \left( {\eta _{\mathrm{eff}} +2\eta _{\mathrm{A}} \cos ^{2}\theta } \right) \,k^{4} \nonumber \\&\quad -\omega _{\mathrm{A}}^{\mathrm{2}} -\left( {1+\alpha } \right) \,\omega _{s}^{2} -4\omega _{ry}^{2} \end{aligned}$$
(20)
$$\begin{aligned}&a_{1} =\left[ {\begin{array}{l} \left( {\eta _{\mathrm{eff}} +2\eta _\mathrm{A} \cos ^{2}\theta } \right) \left\{ {k\sin \theta T_{z} +i\omega _{\mathrm{J}}^{\mathrm{2}} -i\left( {1+\alpha } \right) \omega _{s}^{2} } \right\} \, \\ +\,\eta _{\mathrm{eff}} k^{2}\left\{ {k\sin \theta T_{z} -i\omega _{\mathrm{A}}^{\mathrm{2}} -i\eta _{\mathrm{A}} \eta _{\mathrm{eff}} k^{4}\cos ^{2}\theta } \right\} \\ +\,2\omega _{ry} \cos \theta \left\{ {kT_{z} +i\left( {{\omega _{\mathrm{J}}^{\mathrm{2}} }/{\sin \theta }} \right) -2ik\eta _{\mathrm{A}} \omega _{ry} \cos \theta } \right\} \\ \end{array}} \right] \end{aligned}$$
(21)
$$\begin{aligned}&a_{0} =\left[ {\begin{array}{l} \left( {1+\alpha } \right) \omega _{s}^{2} \omega _{\mathrm{A}}^{\mathrm{2}} \cos ^{2}\theta +\eta _{\mathrm{A}} \eta _{\mathrm{eff}} k^{4}\cos ^{2}\theta \\ .\left\{ {ik\sin \theta T_{z} +\left( {1+\alpha } \right) \omega _{s}^{2} -\omega _\mathrm{J}^{2} } \right\} \\ \,+2\eta _{\mathrm{A}} \omega _{ry} k^{2}\cos ^{3}\theta \left( {ikT_{z} -{(\omega _\mathrm{J}^{2} }/{\sin \theta ) }} \right) \\ \end{array}} \right] \nonumber \\ \end{aligned}$$
(22)

where \({ v}_{\mathrm{A}} ={B_{0} } / {\sqrt{4\pi \rho _{0} } }\) is the Alfven (MHD) wave phase speed with \(\omega _{\mathrm{A}} =kv_{\mathrm{A}} \) as the Alfven radian frequency and \(\omega _{s} =kc_{s} \) as the magneto-acoustic radian frequency.

In order to explore the instability behaviours governed by the derived unique dispersion relation (18) in a scale-free (scale-invariant) form, we employ a standard astronomical normalisation scheme [23]. As per this organisation, \(\Omega =\omega / {\omega _{\mathrm{J}} }\) is the Jeans-normalised (by \(\omega _{\mathrm{J}}\)) fluctuation frequency and \(K=k / {k_{\mathrm{J}} }\) is the Jeans-normalised (by \(k_{\mathrm{J}}\)) fluctuation wave number. The normalised form of (20) with a modified set of dispersion coefficients thus reads as

$$\begin{aligned}&\Omega ^{4}+A_{3} \Omega ^{3}+A_{2} \Omega ^{2}+A_{1} \Omega +A_{0} =0 \end{aligned}$$
(23)
$$\begin{aligned}&A_{3} ={i}\left( {\eta _{\mathrm{eff}} +2\eta _{\mathrm{A}} \cos ^{2}\theta } \right) \,\omega _{\mathrm{J}}^{-\text{1 }} k_{\mathrm{J}}^{\mathrm{2}} K^{2} \end{aligned}$$
(24)
$$\begin{aligned}&A_{2} =1-\left[ {\begin{array}{l} iKk_{\mathrm{J}} \sin \theta T_{z} +\omega _{\mathrm{A}}^{\mathrm{2}} +\left( {1+\alpha } \right) \omega _{s}^{2} +4\omega _{ry}^{2} \\ +\eta _{\mathrm{eff}} \left( {\eta _{\mathrm{eff}} +2\eta _{\mathrm{A}} \cos ^{2}\theta } \right) {K}^{4}k_{\mathrm{J}}^{\mathrm{4}} \\ \end{array}} \right] \,\nonumber \\&\qquad \times \omega _{\mathrm{J}}^{-\text{2 }} \end{aligned}$$
(25)
$$\begin{aligned}&A_{1} =\left[ {\begin{array}{l} \left( {\eta _{\mathrm{eff}} +2\eta _{\mathrm{A}} \cos ^{2}\theta } \right) \left\{ {\begin{array}{l} Kk_{\mathrm{J}} \sin \theta T_{z} +i\omega _\mathrm{J}^{2} \\ -i\left( {1+\alpha } \right) \omega _{s}^{2} \\ \end{array}} \right\} \\ +\eta _{\mathrm{eff}} K^{2}k_{\mathrm{J}}^{\mathrm{2}} \left\{ {\begin{array}{l} Kk_\mathrm{J} \sin \theta T_{z} -i\omega _{\mathrm{A}}^{\mathrm{2}} \\ -i\eta _{\mathrm{A}} \eta _{\mathrm{eff}} K^{4}k_{\mathrm{J}}^{\mathrm{4}} \cos ^{2}\theta \\ \end{array}} \right\} \\ +2\omega _{ry} \cos \theta \left\{ {\begin{array}{l} Kk_{\mathrm{J}} T_{z} +i\left( {{\omega _{\mathrm{J}}^{\mathrm{2}} }/{\sin \theta }} \right) \\ -2iKk_{\mathrm{J}} \eta _{\mathrm{A}} \omega _{ry} \cos \theta \\ \end{array}} \right\} \\ \end{array}} \right] \nonumber \\&\qquad \times \omega _{\mathrm{J}}^{-\text{3 }} \end{aligned}$$
(26)
$$\begin{aligned}&A_{0} =\left[ {\begin{array}{l} \left( {1+\alpha } \right) \omega _{s}^{2} \omega _{\mathrm{A}}^{\mathrm{2}} \cos ^{2}\theta +\eta _{\mathrm{A}} \eta _{\mathrm{eff}} K^{4}k_{\mathrm{J}}^{\mathrm{4}} \cos ^{2}\theta \\ .\left\{ {\begin{array}{l} iKk_{\mathrm{J}} \sin \theta T_{z} \\ +\left( {1+\alpha } \right) \omega _{s}^{2} -\omega _{\mathrm{J}}^{\mathrm{2}} \\ \end{array}} \right\} \\ +2\eta _{\mathrm{A}} \omega _{ry} K^{2}k_{\mathrm{J}}^{\mathrm{2}} \cos ^{3}\theta \left( {iKk_{\mathrm{J}} T_{z} -{(\omega _{\mathrm{J}}^{\mathrm{2}} }/{\sin \theta ) }} \right) \\ \end{array}} \right] \nonumber \\&\qquad \times \omega _\mathrm{J}^{-4} . \end{aligned}$$
(27)

It is seen from (23) that this is a quartic equation. The roots of the equation are

$$\begin{aligned}&\Omega _{1} =\frac{-b_{1} +\left[ {b_{1}^{2} -4\left( {b_{0} -c_{0} p} \right) \left( {1-p} \right) } \right] ^{1 / 2}}{2\left( {1-p} \right) },\\&\Omega _{2} =\frac{-b_{1} -\left[ {b_{1}^{2} -4\left( {b_{0} -c_{0} p} \right) \left( {1-p} \right) } \right] ^{1 / 2}}{2\left( {1-p} \right) },\\&\Omega _{3} =\frac{-b_{1} +\left[ {b_{1}^{2} -4\left( {b_{0} +c_{0} p} \right) \left( {1-p} \right) } \right] ^{1 / 2}}{2\left( {1+p} \right) } \end{aligned}$$

and

$$\begin{aligned} \Omega _{4} =\frac{-b_{1} -\left[ {b_{1}^{2} -4\left( {b_{0} +c_{0} p} \right) \left( {1+p} \right) } \right] ^{1 / 2}}{2\left( {1+p} \right) }, \end{aligned}$$

where

$$\begin{aligned}&b_{1} =\left[ {-\beta +\sqrt{\beta ^{2}+\alpha ^{3}} } \right] ^{1 /3}+\left[ {-\beta -\sqrt{\beta ^{2}+\alpha ^{3}} } \right] ^{1/3}\\&\qquad +\frac{4}{3}\frac{A_{2} }{A_{3} },\\&c_{1} =\sqrt{\frac{A_{3} b_{0}^{2} }{A_{3} -2b_{1} -A_{0} }} ,\\&p=\sqrt{1-2\frac{b_{1} }{A_{3} }} ,\\&\alpha =\frac{12A_{1} A_{3} +8A_{2}^{2} -48A_{0} }{9A_{3}^{2} },\\&\beta =\frac{8A_{2}^{3} -36A_{1} A_{2} A_{3} -288A_{0} A_{2} +108A_{0} A_{1}^{2} A_{3}^{2} }{27A_{3}^{3} }. \end{aligned}$$

It can now be clearly seen (from (23)–(27)) that the fluctuation dynamics in the considered complex plasma fluid is significantly affected by the various realistic complications adopted afresh herein. Based on it, as such, a few analytic special cases are in order as follows:

Case I: In the absence of ambipolar diffusion (i.e., \(\eta _{\mathrm{A}} =0\)), (18) governing the evolution of the instability reduces to

$$\begin{aligned}&\omega ^{4}+2i\eta _{\mathrm{eff}} k^{2}\omega ^{3}+\left[ {\begin{array}{l} \omega _{\mathrm{J}}^{\mathrm{2}} -ikT_{z} \sin \theta -\eta _{\mathrm{eff}}^{\mathrm{2}} k^{4} \\ -\omega _{\mathrm{A}}^{\mathrm{2}} -\left( {1+\alpha } \right) \omega _{s}^{2} -4\omega _{ry}^{2} \\ \end{array}} \right] \,\omega ^{2}\nonumber \\&+\left[ {\begin{array}{l} \eta _{\mathrm{eff}} k^{2}\left\{ {2kT_{z} \sin \theta +i\left( {\omega _{\mathrm{J}}^{\mathrm{2}} -\omega _{\mathrm{A}}^{\mathrm{2}} } \right) -i\left( {1+\alpha } \right) \,\omega _{s}^{2} }\right\} \\ +2\omega _{ry} \cos \theta \left\{ {kT_{z} +\left( {{\omega _{\mathrm{J}}^{\mathrm{2}} }/{\sin \theta }} \right) } \right\} \\ \end{array}} \right] \omega \nonumber \\&+\omega _{s}^{2} \omega _{\mathrm{A}}^{\mathrm{2}} \left( {1+\alpha } \right) \cos ^{2}\theta =0. \end{aligned}$$
(28)

Clearly, (28) describes the damped gravito-magneto-acoustic wave modified by tidal force field and cosmic ray pressure in a rotating idealised incompressible cloud. The wave dispersion results match with the previous predictions in similar astronomical contexts [10, 21, 32].

Case II: If both the effective viscosity and ambipolar diffusion are switched off (i.e., \(\eta _{\mathrm{eff}} ,\,\eta _{\mathrm{A}} \sim 0)\), (18) simplifies to

$$\begin{aligned}&\omega ^{4}+\left[ {\omega _{\mathrm{J}}^{\mathrm{2}} -ikT_{z} \sin \theta -\omega _{\mathrm{A}}^{\mathrm{2}} -\left( {1+\alpha } \right) \omega _{s}^{2} -4\omega _{ry}^{2} } \right] \,\nonumber \\&\times \omega ^{2} +\left[ {2\omega _{ry} \cos \theta \left\{ {kT_{z} +\left( {\frac{\omega _{\mathrm{J}}^{\mathrm{2}} }{\sin \theta }} \right) } \right\} } \right] \omega \nonumber \\&\quad +\omega _{s}^{s2} \omega _{\mathrm{A}}^{\mathrm{2}} \left( {1+\alpha } \right) \cos ^{2}\theta =0 \end{aligned}$$
(29)

which gives the dispersive properties of a self-gravitating cosmic plasma system in the presence of the conjoint effects produced by the tidal force field and Coriolis rotation. Obviously, the instability properties with the non-local self-gravity here, especially in the presence of tidal force action, are in fair agreement with a previously reported prediction without self-gravity and without rotational effects [32]. It is worthwhile to tell that, in the present context, our (29) describes wave propagation dynamics in an ionised medium with a relatively higher degree of ionisation. As a consequence, the effects of non-ideal ambipolar diffusion are of less significance in contrast with the quasi-magneto-hydrostatic equilibrium and local ionisation equilibrium scenarios as predicted by others [2, 17].

Case III: In the absence of effective viscosity (i.e., \(\eta _{\mathrm{eff}} \sim 0\)), (18) for the inviscid fluid fluctuations reduces to

$$\begin{aligned}&\omega ^{4}+\left[ {2i\eta _{\mathrm{A}} \cos ^{2}\theta \,\,k^{2}} \right] \omega ^{3}+\left[ {\begin{array}{l} \omega _{\mathrm{J}}^{\mathrm{2}} -ik\sin \theta T_{z} -\omega _{\mathrm{A}}^{\mathrm{2}} \\ -\left( {1+\alpha } \right) \omega _{s}^{2} -4\omega _{ry}^{2} \, \\ \end{array}} \right] \omega ^{2} \nonumber \\&+\left[ {\begin{array}{l} \left( {2\eta _{\mathrm{A}} \cos ^{2}\theta } \right) \left\{ {k T_{z} +i\omega _{\mathrm{J}}^{\mathrm{2}} -i\left( {1+\alpha } \right) \omega _{s}^{2} } \right\} \\ +2\omega _{ry} \cos \theta \left\{ {\begin{array}{l} k T_{z} +i\left( {{\omega _{\mathrm{J}}^{\mathrm{2}} }/{\sin \theta }} \right) \\ -2ik\eta _{\mathrm{A}} \omega _{ry} \cos \theta \\ \end{array}} \right\} \\ \end{array}} \right] \omega \nonumber \\&+2\eta _{\mathrm{A}} \omega _{ry} K^{2}k_{\mathrm{J}}^{\mathrm{2}} \cos ^{3}\theta \,\left( {ikT_{z} -\frac{\omega _{\mathrm{J}}^{\mathrm{2}} }{\sin \theta }} \right) \nonumber \\&\quad +\left( {1+\alpha } \right) \omega _{s}^{2} \omega _{\mathrm{A}}^{\mathrm{2}} \cos ^{2}\theta =0. \end{aligned}$$
(30)

It represents the dispersion relation for the non-ideal MHD waves in cosmic, magnetised and rotating plasma fluids in the presence of ambipolar diffusion. One of the roots of (30) would depict the gyromagnetic Jeans instability in the non-ideal partially ionised inviscid MHD fluid.

Case IV: In the absence of all the non-ideal effects (ideal gravitating MHD), (18) algebraically reduces to

$$\begin{aligned} \omega ^{4}+\left( {\omega \,_{\mathrm{J}}^{2} -\omega \,_{\mathrm{A}}^{\mathrm{2}} -\omega \,_{s}^{2} } \right) \,\omega ^{2}+\omega \,_{s}^{2} \omega \,_{\mathrm{A}}^{\mathrm{2}} {\cos }^{2}\theta =0. \end{aligned}$$
(31)

This equation gives the dispersion relation for an ideal magnetohydrodynamic wave in a gravitating fluid [12].

Case V: In the absence of self-gravity effects, (30) becomes

$$\begin{aligned} \omega ^{4}-\left( {\omega \,_{\mathrm{A}}^{\mathrm{2}} +\omega \,_{s}^{2} } \right) \omega \,^{2}+\omega \,_{s}^{2} \omega \,_{\mathrm{A}}^{\mathrm{2}} \cos ^{2}\theta =0. \end{aligned}$$
(32)

Clearly, (32) agreeably describes the copious evolutionary dynamics of the normal magnetosonic waves and instabilities in a non-gravitating ideal MHD [9]. It may be speculated that, in all the special corollaries as indicated in (28)–(32), the plasma fluid medium exhibits a confirmatory plethora of excitation of collective waves and instabilities dictated piecewise by the generalised dispersion relation (as by (23)).

3 Results and discussions

The dynamics of instabilities existing in a complex partially ionised incompressible astronomical cloud fluid is analysed in the framework of a non-ideal mean-fluid (MHD) approach. It includes realistic significant complication factors, such as gyro-gravitation, tidal force field effect sourced by distant gravitating objects, kinematic viscosity arising from microscopic molecular agitations, cosmic ray pressure effects from extra-terrestrial sources and the relevant non-ideality effects (ambipolar diffusion). An explicit unique set of the cloud structuring equations is methodologically constructed and interpreted in the single-fluidic fabric. Assuming a magneto-hydrostatic homogeneous equilibrium, we apply a normal mode analysis treating all the relevant small-scale linear perturbations to evolve as sinusoidal homology waves. An algebraic exercise decouples the perturbed cloud equations into a unique form of quartic dispersion relation having a special set of multiparametric coefficients. The analytic reliability of our proposed calculation scheme is bolstered with the help of a number of special corollaries which confirmed that our results are in good agreement with the various earlier predictions reported in the literature. After the analytic reliability checkup, the derived dispersion relation is judiciously analysed in a numerical standpoint [46]. It is constructed on the well-known method of decomposition and factorisation numerically to show the results (figures 1–4).

Fig. 1
figure 1

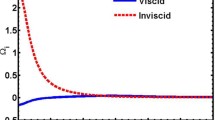
Profile of the normalised (a) real frequency (\(\Omega _{{r}}\)), (b) growth rate (\(\Omega _{{i}}\)) and (c) logarithmic growth per period (\(\Omega _{{i}}/\Omega _{{r}}\)) in the Jeans-normalised space of angular wave number (K) for different values of the ratio (\(\alpha \)) between the cosmic ray pressure and thermal pressure. The corresponding spectral profiles for the same in the inviscid (\(\eta _{{\mathrm {eff}}\,}\approx 0\)) condition to highlight viscosity effects relative to the former are depicted in the inset panels (a\(^{*})\), (b\(^{*})\) and (c\(^{*})\), respectively. The fine details on the numerics are presented in the text.

Full size image

In figure 1, we depict the profiles of the normalised (a) real frequency \(\left( {\Omega _{r} } \right) \), (b) growth rate \(\left( {\Omega _{i} } \right) \) and (c) logarithmic growth per period \(\left( {{\Omega _{i} } / {\Omega _{r} }} \right) \) with variation in the Jeans-normalised space of angular wave number (K) for different values of the ratio \(\left( {{\alpha =P_{\mathrm{CR}} } / {P_{\mathrm{Th}} }} \right) \) between the cosmic ray pressure \(\left( {P_{\mathrm{CR}} } \right) \) and thermal pressure \(\left( {P_{\mathrm{Th}} } \right) \). The corresponding spectral profiles for the same in the inviscid \(\left( {\eta _{\mathrm{eff}} \approx 0} \right) \) condition to highlight the specific viscosity effects relative to the former are depicted in the inset panels (\(\hbox {a}^{*}\)), (\(\hbox {b}^{*}\)) and (\(\hbox {c}^{*})\) respectively. The various fine inputs on the numerics are judiciously adopted from the literature [23, 39] as \(n_{0} =10^{6}\) \(\hbox {m}^{-3}\), magnetic field \({B=10^{-8}}\) T, ionisation fraction \(x_{p} =10^{-7}\), mass of electron \(m_{e} =9.1\times 10^{-31}~\hbox {kg}\), mass of ion \(m_{i} =30\,m_{p}\), mass of proton \(m_{p} =1.67\times 10^{-27}~\hbox {kg}\) and mass of neutral \(m_{n} =2.33\,m_{p}\), \(T=100~\hbox {K}\), \(T_{z} \approx 10~\hbox {km s}^{-1}\,\hbox {kpc}^{-1}\). It is seen that the fluctuation frequency significantly increases with the cosmic-to-thermal pressure ratio, and vice versa. For a fixed \(\alpha \)-value, the fluctuation frequency steeply increases (dispersive wave nature) in the K-space upto \(K=1.7\). Beyond that, the frequency becomes well-stabilised (non-dispersive wave nature) at the respective saturation levels (figure 1a). In contrast, only the quasidispersive wave nature of the evolutionary fluctuation dynamics is pronounced in the inviscid case (figure 1\(\hbox {a}^{*})\).

Fig. 2
figure 2

Same as figure 1, but for different values of magnetothermal pressure ratio (\(\beta ^{*}\)). The fine details on the numerics are in the text.

Full size image
Fig. 3
figure 3

Same as figure 1, but for different values of the rotation frequency (\(\omega _{ry})\).

Full size image
Fig. 4
figure 4

Same as figure 1, but for different values of the ratio (\(T_{{z}}/g_{\mathrm {self}}\)) between the compressive tidal force field and self-gravity.

Full size image

Correspondingly, the instability growth shows augmentation with the \(\alpha \)-value increment, and vice versa (figure 1b). It allows us to conjecture that \(\alpha \) plays a destabilising role in the instability dynamics. It happens because of coherent phase and amplitude coordination between the cloud-centric cosmic and self-gravitational forces against the counteracting randomising tidal pressure effects. It is further evident that the growth maxima (peaks) occur in the K-space only at \(K=1.7\). So, only the waves near the Jeansian critical wave number get significantly unstable. We further see that, beyond \(K=1.7\), the perturbations get gradually damped out at the asymptotic limit of \(K\rightarrow \infty .\) In contrast, no such damping features are speculated in the inviscid situation (figure 1\(\hbox {b}^{*})\). As a consequence, the damping mechanism of the perturbations beyond \(K=1.7\) (figure 1b), unlike those in the inviscid case (figure 1\(\hbox {b}^{*})\), are justifiably attributable to the kinematic viscosity arising because of the constitutive microscopic particle kinetics. Moreover, a corroborating test is presented to identify the instability as a slow one (figure 1c). It is also reflected that the linear approximation in our homology perturbation characterisation is well-validated \(\left( {{\Omega _{i} } / {\Omega _{r} <1}} \right) \). The effect of kinematic viscosity is realised only in the turning-out zone of the \({\Omega _{i} } / {\Omega _{r} }\) behaviour from a non-linear (figure 1c) into a quasilinear one (figure \(1\hbox {c}^{*})\), without upsetting the linear validity limits.

In figure 2, we show similar characteristic features as in figure 1, but for different situations dictated by the magnetothermal pressure ratio \(\left( \beta ^{*}={B^{2}} / {8\pi P_{\mathrm{Th}} }=1 / \beta \right) \). It is found that the phase velocity of the magnetoacoustic wave instability is not affected noticeably in the complex viscous fluid (figure 2a). In contrast, the phase velocity of the instability decreases with the \(\beta ^{*}\)-increment, and vice versa (figure 2\(\hbox {a}^{*})\). It happens because the magnetic field always tries to confine the particle gyrokinetic dynamics. As a result, the phase velocity of the associated waves decreases. It is further seen that the instability growth decreases with the \(\beta ^{*}\)-increment, and vice versa (figure 2b). As before, after \(K=1.7\), the cloud acquires a propensity towards stability. In the inviscid case (figure 2\(\hbox {b}^{*})\), there is no such damping tendency of the instability. In both the \(\beta ^{*}\)-dependent cases, we see that the \(\beta ^{*}\)-parameter introduces a stabilising influence on the perturbed cloud dynamics. The logarithmic growth per period shows the instability characteristic growth features (figures 2c, 2\(\hbox {c}^{*})\) in the viscous and inviscid circumstances as in figures 1c and 1\(\hbox {c}^{*}\), respectively.

The circumstantial conditions are dictated by the Coriolis rotation \(\left( {\omega _{ry} } \right) \). It is noteworthy that the phase velocity of the instability decreases upto a critical wave number \(K=3.4\) in magnitude with the \(\omega _{ry} \)-increment, and vice versa (figure 3a). Beyond the \(K=3.4\) limit, it is, however, interesting to see that the magneto-acoustic waves travel with a unified saturated frequency \(\left( {\Omega _{r} \approx 1.5} \right) \), irrespective of the \(\omega _{ry} \)-values. Thus, it is speculated that, both the non-dispersive and dispersive waves get excited in the regions in the K-space demarcated by \(K=3.4\). The dispersive features are, however, found to disappear under non-viscous conditions (figure 3\(\hbox {a}^{*})\). The growth of the instability is found to get reduced with the \(\omega _{ry} \)-increment, and vice versa (figure 3b). After the critical point \(K=3.4\), all the growths merge together immaterial of the \(\omega _{ry}\)-variation. The amalgamation of the growth lines is found to be absent in the inviscid cloud condition. In both the cases, the Coriolis rotation acts as a stabilising agency to the perturbed cloud dynamics. The respective logarithmic growths per period are shown in figures 3c and 3\(\hbox {c}^{*}\). The mechanism behind such dynamical behaviours is that the net inward pressure effect decreases with the cloud rotation because of the enhancement in the centrifugal cloud action. The cloud collapse propensity decreases owing to the Coriolis-induced centrifugal effects, thereby showing stabilising effect (decrement in growth).

Lastly, figure 4 illustrates similar spectral behaviours as in figure 1, but for different configurations depicted by the ratio of the tidal force field and self-gravity \(\left( {{T_{z} } / {g_{\mathrm{self}} }} \right) \). We see that the real frequency and hence, the phase velocity are not affected by the \({T_{z} } / {g_{s\mathrm{elf}} }\)-variation (figures 4a, 4\(\hbox {a}^{*})\). Moreover, the combined effect of the tidal interaction and cloud rotation generates oscillatory-like linear stable motions only beyond \(K=1.7\) in the viscous medium (figures 1a–4a). It is further investigated that the growth amplitude (figure 4b with viscosity and figure 4\(\hbox {b}^{*}\) without viscosity) increases with increase in the \({T_{z} } / {g_{\mathrm{self}} }\)-value. Thus, \({T_{z} } / {g_{\mathrm{self}} }\) acts as a destabilising factor to the perturbed cloud dynamics. The corresponding growth features per period for different situations, similar to the earlier cases, are shown in figures 4c and 4\(\hbox {c}^{*}\) in the viscous and inviscid configurations, respectively. It implies that the external gravitational source (the tidal force field) helps in destabilising the self-gravitating magnetised medium and strengthens the corresponding cloud collapse induced by the magnetoactive instability.

In this work, the value of the field-wave angle is taken as \({\theta =\pi } / 4\) to obtain the required growth rates numerically. For other values, no significant growth profiles depicting any sensible outcome on the canonical collapse cosmodynamics are found to exist. It is noteworthy that the theoretic formalism here is a single (mean) fluid (MHD) model for the collective cloud instability analysis. As a result, the instability growth rates cannot be depicted for the individual constituent species separately in the collective mean-fluidic fabric. Thus, all the individual constituent species of the partially ionised plasma medium contribute collectively to the overall growth dynamics of the mean-fluidic stability.

4 Conclusions

The complex instability dynamics excited in a realistic gyrogravitating magnetised tidally affected viscous partially ionised molecular cloud is analysed in the fabric of the non-ideal MHD (mean-fluid) formalism. The influential dynamical factors of the real astral relevancy are systematically included. We applied a standard homology perturbation method (plane wave, no geometric boundary effects and single common frequency) to derive a generalised local dispersion relation. It has a quartic vocality in the eigenmode frequency degree and contains a unique set of variable coefficients. Its analytic explicit consistency is examined positively in the panoptic light of a number of newly derived sensible special cases and corollaries of the real astrocosmic worth matching fairly with the prevailing archetypal reports in [11, 17].

A numerical illustrative platform is provided to identify and characterise the various stabilising (destabilising) factors. A graphical standpoint to test the validation of the linear theory approximation is also reinforced via the instability growths per cycle. It is specifically shown that the magnetothermal pressure ratio \(\left( {\beta ^{*}} \right) \) and the Coriolis rotation \(\left( {\omega _{ry} } \right) \) introduce stabilising effects (growth reduction) in the cloud gyro-magneto-acoustic mode dynamics. It is attributable to the fact that both the outward effects \(\left( {\beta ^{*},\,\,\omega _{ry} } \right) \) couple with the cloud inward self-gravity resulting in lower instability growths. In contrast, the cosmic-to-thermal pressure ratio \(\left( \alpha \right) \) and the tidal-to-gravitational field ratio \(\left( {{T_{z} } / {g_{\mathrm{self}} }} \right) \) trigger destabilising influences to the cloud instability. It is attributable to the fact that both the effects \(\left( {{\alpha ,\,T_{z} } / {g_{\mathrm{self}} }} \right) \) co-act along with the non-local self-gravity resulting in enhanced growth rates. A generalised conjecture is herewith drawn that the normal mode (gyrogravito-magneto-acoustic wave) is modified by the conjoint action of both the ambipolar diffusion (growth enhancer) and fluid viscosity (growth reducer). For ambipolar diffusion to operate in star-forming nurseries, we require at least two-fluid (ideal) MHD models: charged and neutral components. The ambipolar diffusion-triggered effects are sensationally speculated even in the single mean-fluid MHD model (non-ideal) formalism against the usual picture [11, 12].

The proposed investigation could reproduce a number of earlier well-established analytic predictions. Its marginal reliability checkup is progressively strengthened via numerical simulations and comparative analyses. The analytical techniques employed herein, despite some facts and faults on geometric issues, may extensively be applied to see the stability of diversified magneto-active fluids in the astrocosmic realms [9, 34]. It is remarkable that the enhanced gravitational instability growths are directly correlated with the boosted structure formation rate towards planetesimals, stellesimals and so forth [43]. Accordingly, our results presented here could be of vital significance broadly in various instability-triggered initiation dynamics of the bounded astrostructure formation [41,42,43,44,45], particularly, in the \(\hbox {H}_{\mathrm {II}}\) (also, RCW 38) regions compositionally dominated by the interstellar gaseous hydrogen in the collective ionised form.