Dynamics of gravoviscothermal instability in complex astrofluids amid cosmic radiative moderation effects

Abstract

The gravoviscothermal instability dynamics excitable in a spherical composite astrofluidic system (CAS) existent in dwarf satellite galaxies, which are mainly constituted of an admixture of neutral gas fluid (NGF) and cosmic ray fluid (CRF) coupled via a barotropic correlation in spherical geometry, is studied. A spherical normal mode analysis over the perturbed CAS yields a unique quartic dispersion relation having an atypical set of multiparametric coefficients. The growth behaviours of the instability are illustratively specified in two distinct situations: inviscid (ideal) and viscid (real). It is seen that the CAS kinematic viscosity and temperature play stabilizing roles to the CAS instability against the gravity. In contrast, the CRF diffusion destabilizes the instability. A faster rate of structure formation, which is sourced by the CRF moderation effects, is interestingly a formal picture in such astrosituations. It achieves a peaky growth in the acoustic domain at near the centre of the entire CAS mass distribution. The average instability pattern behaviours are fairly confirmed in two distinct pure fluctuation regimes: gravitational (low-frequency, Jeans-type) and the thermal (high-frequency, acoustic-type). The reliability of our results is marginally validated in the light of the prior reports. We lastly offer a tentative application of our main results in the real astrocosmic context of reorganizing and restructuring the astrocloud stability dynamics via the excitation of gravothermal supercritical catastrophic instability, pair-instability, etc.

1 Introduction

One of the most interesting phenomenological effects in self-gravitating complex conducting fluid media is the evolution of “gravoviscothermal instability” in different realistic astrocosmic circumstances. This type of instabilities is a hybrid relaxation mode of the complex fluids having a propensity to reach towards its macroscopic bulk equilibrium state (Balbus and Soker 1989; Gomez-Pelaez and Moreno-Insertis 2002). They are excited under the conjoint action of the non-zero thermal fluid currents, driven by the free-energy source stemming from the gravothermal interplay in the unperturbed inhomogeneous fluid configuration. Such instabilities are of a great importance in diversified real astronomical domains. It is because of their active roles played in a number of astrodynamic phenomena, such as the dwarf galactic structuring-clustering processes (Taruya and Sakagami 2002; Chavanis 2002; Sormani and Bertin 2013), cosmic pair-instability (Posch and Trirring 2005), gravothermal catastrophe (Taruya and Sakagami 2002), etc. They play a significant influence in the initiation processes of the cosmic evolutionary dynamics of diversified structures via non-uniform fluid material transport mechanisms still lying not fully well-understood from a non-planar gravothermal bifluidic viewpoint in the presence of cosmic radiative agencies.

The excitation dynamics of pure thermal instability and its saturation mechanism with no gravity have been pioneeringly worked out in gravity-free astroenvirons by Field (1965). A good number of researchers have studied it from different dynamical perspectives in the light of both planar (plane-parallel) geometric symmetry and non-planar (spherical) symmetric geometry (Drury and Falle 1986; Chavanis 2002). The same instability in a thermally conductive fluid medium, which consists of a neutral gas fluid (NGF) gravitationally decoupled from the cosmic ray fluid (CRF), has also been investigated (Gomez-Pelaez and Moreno-Insertis 2002). It has hereby revealed a critical scale-length, which is termed as the generalized Field length, demarcating the stable-unstable regions in the Fourier space (Field 1965). The influence of the combined action of the CRF diffusion and pressure effects on the instability criteria in different circumstances, dominated by convective-diffusive transport phenomena, has also been investigated (Drury and Falle 1986; Wagner et al. 2005, 2006, 2007, 2009). It has been found mainly that the cosmic diffusion acts as a neutral agency to the pure thermal instability; whereas, as a stabilizing agency to the impure magnetothermal counterpart. In addition, the energy transfer from the CRF to the NGF due to the CRF-driven acoustic instability is responsible for the suppression of the thermal overstability of radiative shocks (Drury and Falle 1986; Wagner et al. 2005, 2006).

It may now be clearly noticed that all the past stability analyses in the thermally conducting media, hitherto reported, have thoroughly ignored the long-sought goal of handling the combined influence of the astro-relevant key factors (Bellan 2008; Binney and Tremaine 2008; Shadmehri 2009; Kuwabara and Ko 2015; Tricco et al. 2017). This existing lacuna in the earlier studies of such instabilities forms the basic motivational foundation for the current investigation proposed here. As a result, the main motivation is driven herein from the diversified properties of the complex fluid dynamics composing dwarf satellite galaxies and the complex dynamics of the supported nonhomologous structure formation mechanisms.

We, herein, methodically develop a theoretic model to explore the gravoviscothermal instability dynamics, collectively excitable in a spherical viscous self-gravitating composite astrofluidic system ($\mbox{CAS}=\mbox{NGF}+\mbox{CRF}$). The principal stimulus behind the spherical geometry is that a spherically confined self-gravitating fluid is unstable against the perturbations of all wavelengths as the non-local self-gravity is always organizationally cloud-fluid-centric in action (Karmakar and Das 2018). The adopted CAS is subjected to all the key fluid dynamical complications previously remaining completely unaddressed. The focal goal is to include for the first time the astronomically relevant key dynamic factors in the instability analysis, such as the fluid kinematic viscosity (Shaikh et al. 2008), nonlocal self-gravity (Bellan 2008), CRF diffusion (Drury and Falle 1986; Wagner et al. 2005, 2006, 2007, 2009), polytropicity (Horedt 2004), geometrical curvature effects (Tomisaka and Ikeuchi 1983; Elmore and Heald 1969; Avinash et al. 2006; Karmakar and Borah 2016), and so forth. Another novelty is in the relaxation of the so-called Jeans swindle (Binney and Tremaine 2008)—an equilibrium homogenization assumption applicable at least initially—a conventional local approximation to avoid equilibrium gradient force fields. A spherical wave analysis over the perturbed inhomogeneous CAS results in a quartic linear dispersion relation involving an atypical set of multiparametric coefficients. A numerical illustrative platform is developed to explore the main instability characteristics, such as the resonant excitation regimes, stability factors, etc. It is seen that the CAS kinematic viscosity and temperature play stabilizing roles to the CAS instability against the gravity. In contrast the CRF diffusion destabilizes the said instability. The reliability of our analysis is bolstered from the fact that the mean instability behaviours and patterns found here go fairly well in accordance with the previously reported results in similar astroenvirons extensively. We, finally, present the scope of our findings in the real astrocosmic circumstantial perspectives.

2 Physical model and formalism

A composite fluid model system comprising of a two-fluid admixture (NGF plus CRF) is considered on the astrocosmic fluid evolutionary scales of space and time. The aim is to see the gravoviscothermal instability dynamics excitable in a spherically symmetric complex cloud. The considered spherical geometry is due to the fact that a spherical cloud is unstable against the perturbations of all wavelengths as the non-local self-gravity is always cloud-centric in nature. It concurrently considers the influential factors, such as the fluid thermal conductivity, cosmic ray diffusion, self-gravity, fluid kinematic viscosity, and so forth. In particular, the CRF diffusive factor is included herein because the cosmic ray moderation effects usually slow down the structure formation rate in complex astrofluids (Shadmehri 2009). It could actualize realistically the active mechanisms responsible for structuring and restructuring of dwarf and satellite galaxies filled up with complex neutral fluids and dark matter fluids (Papaderos et al. 2012; Karmakar and Das 2017a,b), such as DDO 154, NGC3741, etc.

The basic governing equations dictating the complex fluid in a standard normalized coupled form in the customary spherically symmetric symbolism (Wagner et al. 2005; Shadmehri 2009) respectively are cast as

$$\begin{aligned} &{\frac{\partial \rho ^{*}}{\partial \tau } + \biggl( \frac{\partial }{\partial \xi } + \frac{2}{\xi } \biggr)\rho ^{*} M = 0, } \end{aligned}$$

(1)

$$\begin{aligned} &{\rho ^{*} \biggl( \frac{\partial M}{\partial \tau } + M\frac{\partial M}{\partial \xi } \biggr) = - \frac{\partial }{\partial \xi } ( P + P_{cr} ) - \rho ^{*}\frac{\partial \varPsi }{\partial \xi }} \\ &{\phantom{\rho ^{*} \biggl( \frac{\partial M}{\partial \tau } + M\frac{\partial M}{\partial \xi } \biggr) =}{} + \eta _{eff}^{*} \biggl( \frac{\partial ^{2}}{\partial \xi ^{2}} + \frac{2}{\xi } \frac{\partial }{\partial \xi } \biggr)M,} \end{aligned}$$

(2)

$$\begin{aligned} &{\biggl( \frac{\partial P}{\partial \tau } + M\frac{\partial P}{\partial \xi } \biggr) + \gamma P \biggl( \frac{\partial }{\partial \xi } + \frac{2}{\xi } \biggr)M } \\ &{\qquad{}+ ( \gamma - 1 ) \rho ^{*} \bigl[ L \bigl( \rho ^{*}, T^{*} \bigr) \bigr]} \\ &{\quad = ( \gamma - 1 ) \biggl( \frac{\kappa _{T}T_{0}}{p_{0}\omega _{J}\lambda _{J}^{2}} \biggr) \biggl( \frac{\partial ^{2}}{\partial \xi ^{2}} + \frac{2}{\xi } \frac{\partial }{\partial \xi } \biggr)T^{*},} \end{aligned}$$

(3)

$$\begin{aligned} &{\biggl( \frac{\partial P_{cr}}{\partial \tau } + M\frac{\partial P_{cr}}{\partial \xi } \biggr) + \gamma _{cr}P_{cr} \biggl( \frac{\partial }{\partial \xi } + \frac{2}{\xi } \biggr)M } \\ &{\quad{}- ( \gamma _{cr} - 1 ) \biggl( \frac{\chi _{cr}}{\omega _{J}\lambda _{J}^{2}} \biggr) \biggl( \frac{\partial ^{2}}{\partial \xi ^{2}} + \frac{2}{\xi } \frac{\partial }{\partial \xi } \biggr)P_{cr} = 0,} \end{aligned}$$

(4)

$$\begin{aligned} &{\biggl( \frac{\partial ^{2}}{\partial \xi ^{2}} + \frac{2}{\xi } \frac{\partial }{\partial \xi } \biggr)\varPsi = \rho ^{*}.} \end{aligned}$$

(5)

Here, $\xi = r / \lambda _{J}$ is the Jeans-normalized radial distance relative to the cloud centre treated as the reference point; where, $\lambda _{J} = c_{s}\omega _{J}$ is the Jeans scale length as the spatial normalizing parameter and $\tau = \omega _{J}^{ - 1} = ( 4\pi G\rho _{0} )^{ - 1 / 2}$ is the Jeans time scale as the temporal normalizing factor. Then, $\rho ^{*} = \rho / \rho _{0}$ is the normalized (by equilibrium density, $\rho _{0}$) mass density, $M = v / c_{s}$ is the Mach number, and $P = p / p_{0}$ is the normalized (by equilibrium thermal pressure, $p_{0}$) NGF pressure. Likewise, $P_{cr} = p_{cr} / p_{cr0}$ is the normalized (by equilibrium cosmic ray pressure, $p_{cr0}$) cosmic ray pressure. The normalized total pressure is $P_{tot} = P + P_{cr}$. $\varPsi = \psi / c_{s}^{2}$ is the normalized (by acoustic phase speed squared, $c_{s}^{2} = \gamma p / \rho$) gravitational potential. $\kappa _{T}$ denotes the thermal conductivity of the astrofluid. $\chi _{cr}$ stands for the cosmic ray diffusivity. The cosmic ray diffusion time scale (Shadmehri 2009) now can be simply given as $t_{D} = \lambda _{J}^{2} / \chi _{cr}$. Then, the newly introduced symbolic notation $\eta _{eff}^{*} = [ 1 / ( \rho _{0}\omega _{J}\lambda _{J}^{2} ) ] [ \zeta + ( 4\eta / 3 ) ]$ represents the effective generalized NGF kinematic viscosity, contributed conjointly by both the bulk viscosity $( \zeta )$ and shear viscosity $( \eta )$. The entire fluid system is presumed to satisfy a polytropic equation of state, $p = k_{p}\rho ^{\varGamma }$; where, $k_{p}$ is the polytropic constant and $\varGamma$ is the polytropic exponent. Here, $\gamma ( = c_{p} / c_{v} )$ is the specific heat ratio for the NGF and $\gamma _{cr} ( = 4 / 3 )$ for the CRF. The modified Jeans wavenumber due to the polytropic index is $k_{J} = \sqrt{4\pi G\rho _{0} / \gamma c_{th}}$; where, $c_{th} = \sqrt{p / \rho }$ is the isothermal sound phase speed in the NGF. Lastly, $L = L ( \rho ^{*}, T^{*} )$ is the auto-normalized heat-loss function (heat loss due to all the sinks minus heat gain due to all the sources per unit fluid mass) that signifies the effective specific NGF thermal energy loss processes via the collective conjoint action of kinematic viscosity, radiative diffusion, heat conduction, and so on (Field 1965).

It is well understood that Eqs. (1)–(5) represent the material conservation law, force density conservation law, thermal energy transfer law, cosmic ray diffusion law and self-gravitational potential distribution law, respectively. The model is indeed devised for an incompressible fluid in the absence of any source or any sink (governed by Eqs. (1)–(5)). The hydrostatic and thermal equilibrium conditions (Field 1965; Binney and Tremaine 2008), which define the force density balance and specific heat energy balance on the Jeans scales, can respectively be given as

$$\begin{aligned} &{\frac{\partial }{\partial \xi } ( p + p_{cr} ) = - \rho _{0}g,} \end{aligned}$$

(6)

$$\begin{aligned} &{L_{0} ( \rho _{0}, T_{0} ) = 0,} \end{aligned}$$

(7)

where, $g = - \partial \varPsi / \partial \xi$ denotes the strength of the conservative cloud-centric non-local self-gravity, and $L_{0}$ is the equilibrium heat-loss function of the fluid system.

We slightly perturb the relevant physical CAS dynamic variables $F ( \xi , \tau )$ featuring the constituent fluid as $F_{1} ( \xi , \tau )$ in the fabric of a homologous collective spherical wave analysis around a hydrostatic homogeneous equilibrium $F_{0} ( 0, 0 )$ in the spherically symmetric geometry (Elmore and Heald 1969; Karmakar and Das 2018) in a form as given below

$$\begin{aligned} &{F ( \xi , \tau ) = F_{0} + F_{1} \biggl( \frac{1}{\xi } \biggr)\exp \bigl[ - i ( \varOmega \tau - K\xi ) \bigr],} \end{aligned}$$

(8)

$$\begin{aligned} &{F_{0} = [1\ 0\ 1\ 1\ 1\ 0]^{ T},} \end{aligned}$$

(9)

$$\begin{aligned} &{F_{1} = \bigl[ \rho_{1}^{*}\ M_{1}\ T_{1}^{*}\ P_{1}\ P_{cr1}\ \varPsi _{1} \bigr]^{ T}.} \end{aligned}$$

(10)

It may be worth mentioning that the $1 / \xi$-appearance in Eq. (8), is due to the consideration of nonplanar (spherical) geometry of the astroclouds. We clearly see that the geometrical curvature of the astrocloud thereby transforms a plane wave perturbation, $\exp [ - i ( \varOmega \tau - K\xi ) ]$, into a spherically symmetric radial wave, $( 1 / \xi )\exp [ - i ( \varOmega \tau - K\xi ) ]$. Here, $\varOmega$ and $K$ are the Jeans-normalized angular frequency and Jeans-normalized angular wavenumber of the homology cloud perturbations, respectively. The linear spatiotemporal differential operators now transform in the Jeans-normalized Fourier space $( \varOmega , K )$ as $\partial / \partial \xi \equiv ( iK - 1 / \xi )$ and $\partial / \partial \tau \equiv - i\varOmega$. As a consequence, we get the linearized forms of Eqs. (1)–(5), respectively, derived and given as

$$\begin{aligned} &{M_{1} = i\varOmega \biggl( iK + \frac{1}{\xi } \biggr)^{ - 1}\rho _{1}^{*},} \end{aligned}$$

(11)

$$\begin{aligned} &{\bigl( i\varOmega - \eta _{eff}^{*}K^{2} \bigr)M_{1}} \\ &{\quad = \biggl( iK - \frac{1}{\xi } \biggr) \bigl[ \bigl\{ \beta _{iso}T_{1}^{*} + ( \beta _{iso} + \varGamma \beta _{pol} )\rho _{1}^{*}+ \beta _{cr}P_{cr1} \bigr\} } \\ &{\qquad{} + K^{ - 2}\rho _{1}^{*} \bigr],} \end{aligned}$$

(12)

$$\begin{aligned} &{T_{1}^{*} = \biggl( iK + \frac{1}{\xi } \biggr) \biggl[ \frac{ ( i\varOmega b_{2} - \varLambda _{\rho }^{*} ) / ( i\varOmega - \gamma b_{1} )}{\varLambda _{T}^{*} + ( \gamma - 1 )\kappa _{{T}}^{*}K^{2} - i\varOmega } \biggr]M_{1},} \end{aligned}$$

(13)

$\kappa _{T}^{*}=(\kappa_{T}T_{0})/(p_{0}\omega_{J}\lambda^{2}_{J})$ stands for the normalized (effective) thermal conductivity.

$$\begin{aligned} &{P_{cr1} = \biggl[ \frac{\gamma _{cr} ( iK + 1 / \xi )}{i\varOmega - ( \gamma _{cr} - 1 )\chi _{cr}^{*}} \biggr]M_{1},} \end{aligned}$$

(14)

$\chi _{cr}^{*}=(\chi _{cr})/(\omega_{J}\lambda^{2}_{j})$ stands for the normalized cosmic ray diffusivity.

Applying Eqs. (11), (13)–(14) in Eq. (12), we after elimination and decomposition, finally get a linear quartic dispersion relation (biquadratic in degree) as

$$\begin{aligned} &{\varOmega ^{4} + A_{3}\varOmega ^{3} + A_{2}\varOmega ^{2} + A_{1}\varOmega + A_{0} = 0,} \end{aligned}$$

(15)

$$\begin{aligned} &{A_{3} ( K ) = i \bigl[ \varLambda _{T}^{*} + ( \gamma - 1 )\kappa _{T}^{*}K^{2} + ( \gamma _{cr} - 1 )\chi _{cr}^{*}} \\ &{\phantom{A_{3} ( K ) =}{} + \eta _{eff}^{*}K^{2} \bigr],} \end{aligned}$$

(16)

$$\begin{aligned} &{A_{2} ( K, \xi )} \\ &{\quad = \bigl\{ ( 1 - \gamma ) ( \gamma _{cr} - 1 ) \bigl( \varLambda _{T}^{*} + \kappa _{T}^{*} \bigr)\chi _{cr}^{*}K^{2} \bigr\} } \\ &{\qquad{} - \eta _{eff}^{*} \bigl\{ \varLambda _{T}^{*} + ( \gamma _{cr} - 1 )\chi _{cr}^{*} - ( \gamma - 1 )\kappa _{T}^{*}K^{2} \bigr\} K^{2}} \\ &{\qquad{} - \bigl[ ( \beta _{iso} + \varGamma \beta _{pol} ) - K^{2} + \beta _{iso} ( b_{2} + \gamma b_{1} ) } \\ &{\qquad{}- \beta _{iso}\chi _{cr}^{*} \bigr] \bigl( K^{2} + \xi ^{ - 2} \bigr),} \end{aligned}$$

(17)

$$\begin{aligned} &{A_{1} ( K, \xi ) = i \biggl[ \beta _{iso} \bigl\{ \varLambda _{T}^{*} + ( \gamma _{cr} - 1 )\chi _{cr}^{*} \bigr\} \bigl( K^{2} + \xi ^{ - 2} \bigr)} \\ &{\phantom{A_{1} ( K, \xi ) =}{}- \left \{ \textstyle\begin{array}{l} ( K^{2} + \xi ^{ - 2} )\chi _{cr}\beta _{cr} \{ \varLambda _{T}^{*} + ( \gamma - 1 )\kappa _{T}^{*}K^{2} \} \\ \quad{}+ ( \gamma - 1 ) ( \gamma _{cr} - 1 )\kappa _{T}^{*}\chi _{cr}^{*}\eta^{*} _{eff}K^{4} \end{array}\displaystyle \right \}} \\ &{\phantom{A_{1} ( K, \xi ) =}{} - \bigl( K^{2} + \xi ^{ - 2} \bigr) \bigl\{ ( \beta _{iso} + \varGamma \beta _{poly} ) - K^{ - 2} \bigr\} \varLambda _{T}^{*}} \\ &{\phantom{A_{1} ( K, \xi ) =}{} + \kappa _{T}^{*} ( \gamma _{cr} - 1 ) \kappa _{T}^{*}\chi _{cr}^{*}K^{4} \biggr],} \end{aligned}$$

(18)

$$\begin{aligned} &{A_{0} ( K, \xi )} \\ &{\quad = \chi _{cr}^{*} ( \gamma _{cr} - 1 ) \bigl( K^{2} + \xi ^{ - 2} \bigr) \bigl[ \bigl\{ ( \beta _{iso} + \varGamma \beta _{poly} )K^{2} - 1 \bigr\} } \\ &{\qquad{} + ( \gamma - 1 )\kappa _{T}^{*} - \beta _{iso}\varLambda _{\rho }^{*} \bigr].} \end{aligned}$$

(19)

The new notations are $\beta _{iso} = c_{th}^{2} / c_{s}^{2}$, $\beta _{pol} = p_{p0} / \rho _{0}c_{s}^{2}$, $\beta _{cr} = c_{cr}^{2} / c_{s}^{2}$, $b_{1} = 1 + p_{p0} / p_{iso}$ and $b_{2} = 1 + \varGamma ( p_{p0} / p_{iso} )$. Here, $p_{p0} ( = k_{p}\rho _{0}^{\varGamma } )$ and $p_{iso} ( = K_{B}\rho _{0}T_{0} / m )$ are the equilibrium polytropic pressure and isothermal equilibrium pressure, respectively. $c_{cr} ( = \sqrt{T_{0} / m} )$ is the cosmic fluid sound speed. Lastly, the symbolism includes $\varLambda _{\rho }^{*} = ( \partial L /\partial \rho )_{T} [ ( \gamma - 1 )\rho _{0}^{2} / p_{iso}\omega _{J} ]$ and $\varLambda _{T}^{*} = ( \partial L / \partial T )_{\rho } [ ( \gamma - 1 )\rho _{0}T_{0} / p_{iso}\omega _{J} ]$, giving the normalized radiative cooling functions with the explicit dependencies on the density and temperature of the NGF, respectively.

It is clearly seen that the linear stability dynamics of the considered astrofluid in the form of a hybrid mode is dictated by a generalized linear quartic dispersion relation as given by Eq. (15). In principle, Eq. (15) would simultaneously describe a gravitational instability in the long-wavelength regime ($K<1$) and a radiative instability in the short-wavelength regime ($K>1$). The dependency of the intermixed (gravoviscothermal) instability on the multiparametric fluid behaviours is revealed via the mathematical constructs of the involved dispersion coefficients $A_{0}$–$A_{3}$ (Eqs. (16)–(19)). Thus, the excitation dynamics of the mixed gravoviscothermal instability is appreciably affected by the various active factors of astronomical significance.

Clearly, Eq. (15) reveals various microphysical aspects of the instability excited in the presence of the CRF diffusion in an unmagnetized fluid situation. If we neglect the effects of kinematic viscosity, self-gravity and spherical symmetry, then our Eq. (15) gives the similar wave mode characteristics as per the previous results (quartic dispersion) in the light of the Hermite-Bieler theorem reported elsewhere (Wagner et al. 2005).

2.1 Radiative mode analysis

In the high-frequency regime (high-$K$ regime), which is the radiative domain of the instability, the canonical Jeans collapse is opposed by the thermal pressure. The instability growth rate from Eq. (15) is now given as

$$ \varOmega _{i} = ( 1 - \gamma ) \kappa _{T}^{*} - \varLambda _{T}^{*} + ( 1 - \gamma _{cr} ) \chi _{cr}^{*} - \eta _{eff}^{*}K^{2}. $$

(20)

It is clearly evident from Eq. (20) that the growth rate of the instability in the acoustic regime is significantly affected due to the NGF kinematic viscosity and CRF diffusion simultaneously.

2.2 Jeans mode analysis

The hydrodynamic (low-frequency) version of Eq. (15) in the gravitational regime (low-$K$ regime) is given as

$$\begin{aligned} \varOmega _{i} =& \bigl[ \epsilon \epsilon _{cr} ( \gamma - 1 ) \kappa _{T}^{*}d_{1}K^{2} - \epsilon \beta _{iso}\beta _{cr}\varLambda _{\rho }^{*} \bigr] \\ &{}\times\bigl[ ( 1 - \gamma ) \epsilon _{cr}\kappa _{T}^{*} \eta _{eff}K^{4} - d_{1}h_{1} \\ &{}+ \epsilon ( \beta _{iso}h_{2} - \beta _{cr}h_{3} ) \bigr]^{ - 1}. \end{aligned}$$

(21)

The notational symbolism involved in Eq. (21) is defined as $\epsilon = K^{2} + \xi ^{ - 2}$, $\epsilon _{cr} = ( \gamma _{cr} - 1 ) \chi_{cr}^{*}$, $d_{1} = \epsilon [ ( \beta _{iso} + \varGamma \beta _{poly} ) - K^{ - 2} ]$, $h_{1} = [ \varLambda _{T}^{*} + \epsilon _{cr} + ( \gamma - 1 ) \kappa _{T}^{*}K^{2} ]$, $h_{2} = [ \varLambda _{\rho }^{*} + \epsilon _{cr} + ( \gamma _{cr} - 1 )\chi _{cr}^{*} ]$, and $h_{3} = \chi _{cr}^{*} ( \varLambda _{T}^{*} + ( \gamma - 1 ) \kappa _{T}^{*}K^{2} )$. It is interestingly seen that Eq. (21) represents the gravoviscothermal instability growth rate in the low-$K$ regime. It unveils the self-gravitational collapse dynamics of the global cosmic fluid system sourced inherently by the local fragmentation instabilities.

3 Results and discussions

An evolutionary gravoviscothermal instability excitable in a spherically symmetric CAS, constituted of an NGF-CRF admixture coupled via barotropic correlation effects, is theoretically investigated on the relevant astrocosmic spatiotemporal scales. The hydrostatic homogenous model equilibrium is ruled by the time-stationary version $( \partial / \partial \xi \ne 0; \partial / \partial \tau = 0 )$ of the basic fluid governing equations (Eqs. (1)–(5)). The stability analysis is methodically executed with the help of a perturbatively derived unique quartic dispersion relation with atypical polyparametric coefficients. A numerical platform for the dispersion analysis (via Eq. (15)) yields many new results on the CAS stability features as illustrated pictorially in Figs. 1–7.

Fig. 1

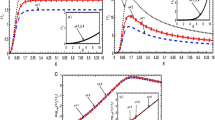
Evolution of the Jeans-normalized growth rate $( \varOmega _{i} )$ of the gravoviscothermal instability with variation in the Jeans-normalized wavenumber $( K )$ in the viscid (ideal, blue solid line) and inviscid (real, red dashed line) configurations distinctly. The fine details are in the text

In Fig. 1, we portray the Jeans-normalized growth rate $( \varOmega _{i} )$ characteristics of the gravoviscothermal instability mode with variation in the Jeans-normalized angular wavenumber ($K$). The distinct lines refer to the viscid (ideal, blue solid line) and inviscid (real, red dashed line) configurations, respectively. The input parameters used here are $T_{0} = 10~\mbox{K}$, $\eta^{*} _{eff} = 0.1$, $\chi _{cr}^{*} = 1$, $\varLambda _{\rho }^{*} = \varLambda _{T}^{*} = 0.1$, $\kappa _{T}^{*} = 0.2$ and, etc. It is seen that the instability growth rate is more pronounced in the inviscid regime than the viscid one. It is furthermore seen, herein, that the growth behaviours in the two distinct cases are quite different only up to the critical Jeans point ($K=1$); but, not so beyond. Thus, the composite fluid viscosity has no significant role to play in influencing the instability growth after this critical point. Such behaviours are attributable to the macroscopic presence of strong collective correlative coupling among the microscopic fluid elements.

In Fig. 2, we depict a similar $( K, \varOmega _{i} )$-evolution; but for the two distinct cases without (blue solid line) and with (red dashed line) radiative condensation. The astrophysical conditions are imposed here are the same as Fig. 1. It specially highlights the influence of the radiative cooling on the instability. We see that the CAS growth shows interesting behaviours in the two isolated cases only up to $K=1.5$; but, not so beyond. We infer that the radiative cooling acts as a boosting source of the cloud gravitational destabilization, thereby causing the complex cloud to undergo self-gravitational collapse dynamics. It is, conversely, quite in agreement with our usual astronomical perception that cooler the complex cloud (with the less thermal pressure outward), more unstable the cloud (with the more self-gravitational pressure inward) is; and vice-versa.

Fig. 2

Same as Fig. 1, but for a fixed Jeans-normalized viscosity $\eta^{*} _{eff} = 0.1$. It specifically refers to the two distinct cases without (blue solid line) and with (red dashed line) radiative condensation

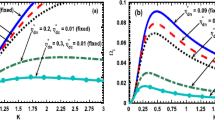
As in Fig. 3, we illustrate a graphical similarity as before (Fig. 2); but, for different conditions dictated by the normalized cosmic ray diffusion coefficient $( \chi _{cr}^{*} )$. The distinct lines refer to the isolated cases characterized by $\chi _{cr}^{*} = 0$ (blue solid line), $\chi _{cr}^{*} = 2$ (red dotted line) and $\chi _{cr}^{*} = 4$ (black dash-dotted line), respectively. It is found that there is no significant influential change on the growth up to $K= 0.2$. But, the growth increases sensibly with $\chi _{cr}^{*}$ only in a particular range of $K= 0.2\mbox{--}1.2$. After $K=1.5$, which features the radiative instability regime ($K >1$), the CAS remains stabilized irrespective of the $K$-domains. Thus, it may be inferred that $\chi _{cr}^{*}$ acts as a destabilizing agency to the cloud in the Jeansian domain ($K<1$) only. It is interestingly against the previous analysis depicting cosmic ray moderation effects slowing down the structure formation rate (Shadmehri 2009). The physical insight responsible behind it can be explained as in the following. The cosmic ray constituent particles are well-known to be highly energetic (on GeV scale) in nature (Somov 2000). However, if and when such particles penetrate optically thick layers of such cloud fluids, its thermal energy (temperature) slowly rises in comparison with the more dominant inward self-gravity counterpart. A stage is asymptotically reached when the enhanced inward self-gravitational pressure wins over the outward thermal pressure resulting in a propensity to destabilize the global cloud configuration to undergo non-local fragmentation processes and hence, causing faster structure formation rate.

Fig. 3

Same as Fig. 2, but for with a fixed Jeans-normalized kinematic viscosity $\eta^{*}_{eff} = 0.1$. Different lines link to $\chi _{cr}^{*} = 0$ (blue solid line), $\chi _{cr}^{*} = 2$ (red dotted line) and $\chi _{cr}^{*} = 4$ (black dash-dotted line), respectively

As in Fig. 4, we depict the same as Fig. 3, but for the different values of the equilibrium cloud temperature $( T_{0} )$. The distinct lines link to $T_{0} = 10~\mbox{K}$ (blue solid line), $T_{0} = 20~\mbox{K}$ (red dotted line) and $T_{0} = 30~\mbox{K}$ (black dash-dotted line), respectively. It is seen herein that the instability growth rate decreases with increase in the cloud temperature; and vice-versa. It is attributable to the fact that as the cloud becomes hotter and hotter, the strength of the thermal outward pressure increases to counteract with that of the gravitational inward pressure. A stage comes with the former dominating over the later. Thus, the cloud temperature acts as a stabilizing source against the nonlocal gravitational cloud collapse.

Fig. 4

Same as Fig. 3, but for a fixed Jeans-normalized cosmic diffusion coefficient $\chi _{cr}^{*} = 2$. Varied lines link to $T_{0} = 10~\mbox{K}$ (blue solid line), $T_{0} = 20~\mbox{K}$ (red dotted line) and $T_{0} = 30~\mbox{K}$ (black dash-dotted line), respectively

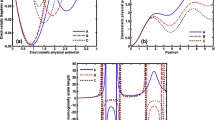
The spatiospectral evolution of the instability growth behaviour in a generalized comprehensive mode is depicted pictorially in Fig. 5. The fine details are the same as Fig. 4, but for a fixed $T_{0} = 10~\mbox{K}$. It is observed that the maximum instability growth occurs at $\xi = 3\mbox{--}4$ corresponding to $K = 3$. It implicates that only the acoustic-like fluctuations at near the off-central region of the cloud undergo a resonant growth peak, which is, indeed, attributable to the collective mutualistic phase-amplitude correlation of the instability spectral components in a coordinated fashion. It, contrastwise, implicates that the off-central spectral components undergo collective in-phase (coherent) coordination to form the resonant growth. The overall growth features gradually decrease to the asymptotic near-zero (cloud-centric) values in the ($\xi$–$K$)-plane elsewhere.

Fig. 5

Spatiospectral evolution of the generalized instability growth rate $( \varOmega _{i} )$ in the ($\xi$–$K$) space. The fine details are the same as Fig. 4, but for $T_{0} = 10~\mbox{K}$

Finally, Figs. 6–7 illustrate the spatiospectral growth characteristics for the two distinct special cases, purely gravitational (low-frequency) and purely thermal (high-frequency) instability regimes, respectively. The fine details are the same as Fig. 5. The inset panels, as both in Figs. 6–7, give the same growth features as the corresponding special cases of $\varOmega _{i} = f ( \xi)$. It is found that the negative instability growth (decay rate) increases with both radial distance and wavenumber in the former (Fig. 6). In contrast, the instability growth remains unchanged with radial distance, but increases with the wavenumber in the latter (Fig. 7). It enables us summarily to infer that the gravitational (nonthermal, low-frequency) fluctuations are sensitive to the radial dimension of the gravitating clouds relative to the critical Jeans size (Fig. 6); whereas, the thermal (acoustic-like, high-frequency) perturbations are not so pronounced (Fig. 7).

Fig. 6

Same as Fig. 5, but especially for the purely gravitational (low-frequency) instability regime. The inset panel specially shows the decay evolution as $\varOmega _{i} = f ( \xi )$

Fig. 7

Same as Fig. 6, but especially for the purely thermal (high-frequency) regime of the instability

4 Conclusions

In summary an astrohydrodynamic model formalism is constructed to study the excitation of hybrid gravoviscothermal instability dynamics in an inhomogeneous spherical CAS. The CAS is an admixture, composed of the NGF and CRF, coupled only via the non-local self-gravity action. A set of key parametric factors of astrocosmic importance are concurrently included, such as the fluid polytropicity, kinematic viscosity, CRF diffusion effects, etc. Application of spherical normal mode analysis over the perturbed CAS, allowing it to be unstable against all the perturbation wavelengths subject to the cloud-centric non-local self-gravity, results in a generalized quartic dispersion relation, containing a unique set of analytic coefficients, which are significantly modified by the canonical fluid characteristic features. A numerical illustrative platform is provided to analyze the varied stabilizing factors of the instability exactly. It is seen that the kinematic viscosity acts as an energy dissipative source to the CAS instability. It is further seen that the instability growth rate is more and more pronounced in the inviscid regime than the viscid one. Thus, the radiative cooling acts as a boosting source of the gravitational destabilization, thereby causing a faster CAS collapse dynamics. A faster rate of structure formation sourced by the CRF moderation effects is interestingly a new addition to such instability scenarios against the traditional picture in similar circumstances (Shadmehri 2009). It is, furthermore, confirmed that the hotter the CAS, the more stabilized it is against self-gravity; and vice-versa. The negative instability growth (decay) increases with both the radial cloud size and wavenumber in the gravitational case (low-frequency, Fig. 6). In contrast, the instability growth remains unchanged with the CAS-centric radial distance, but increases with the wavenumber in the radiative instability regime (high-frequency, Fig. 7). A few concluding remarks highlighting the non-trivial applicability of our analysis in the real astrocosmic environments are summarily given as:

• 1. The semi-analytic exploration of the gravoviscothermal instability in cloud fluids presented here could enable us to identify and characterize the key factors influencing the cloud stability behaviours accomplishable to realize the mechanism of structuring and restructuring of dwarf spheroidals, dwarf ellipticals, and other satellite galaxies filled up with complex neutral fluids and dark matter fluids (Papaderos et al. 2012; Karmakar and Das 2017a,b), such as DDO 154, NGC3741, etc.

• 2. This instability may couple with the pair-instability supernova excited by the conjugational processes of free electron-positron pair production in supermassive stars $( M\sim 30 M_{\varTheta } )$, which result in preventing the supermassive stars from being gravitationally collapsed by lowing the net internal pressure support as a unique stabilizing agency.

• 3. The large-scale self-gravitating astrophysical polytropic systems are considerably modified in the presence of non-extensive nonthermal effects treated in the light of the Tsallis non-extensive thermostatistical mechanics (Constantio 2009). As a result, the astrophysical polytropes are significantly modified with a non-extensive nonthermal polytropic equation of state (Taruya and Sakagami 2002; Shaikh et al. 2008), expressed in the customary notations as, $p = k_{p}\rho ^{ ( 5q - 3 ) / ( 3q - 1 )}$; where, $q$ is the nonextensivity parameter – an important point being considered in future directions.

• 4. It may be applied to understand the obscure gravothermal supercritical cloud-centric catastrophic instabilities, which are, in turn, responsible for exhibiting cloud negative specific heats (Posch and Trirring 2005; Binney and Tremaine 2008), and so forth.