1 Introduction

The natural existence of conjugational bimodal instability dynamics (pulsational type) in complex astrophysical plasma fluids under the conjoint gravito-electrostatic interplay is one of the most fundamental tenets in astrophysics for decades. The instability dynamics is triggered by the counteraction of long-range conjugational gravito-electrostatic force fields in partially ionised complex dusty astrofluids [1,2,3,4,5,6,7,8]. The threshold condition responsible for triggering such an instability leading to bounded structures to form is that the gravito-electrostatic forces should be nearly comparable [4]. In other words, bounded structures would result in the existence of an overlapping scale between the self-gravitational and electromagnetic interactions by the constitutive dust grains. Its relevance is primarily pronounced in various complex mechanisms of wave-induced fluid material redistribution leading to the phase dynamics initiation of astrophysical large-scale bounded structures, such as planetsimals, stellesimals, comets, etc. [1, 2].

A good number of researchers have carried out systematic investigations to explore the complex instability dynamics of pulsational source leading to structure formation in astrofluid media in the recent past. The conjugational instability dynamics in the presence of fluid viscoelasticity has recently been addressed by Dutta and Karmakar [7]. The most important point reported in their study is that the grain mass and the viscoelastic relaxation time associated with the charged dust fluid play stabilising roles on the fluctuations in the hydrodynamic regime. In contrast, in the kinetic regime, the stabilising effects are introduced by the equilibrium ionic population distribution, dust mass and dust equilibrium density. Again, they have studied the evolutional dynamics of the pulsational mode in non-thermal turbulent viscous astrofluids [5]. They have found that the non-thermal parameters (electron–ion non-extensivities) and kinematic viscosity of the dust fluids act as stabilising agents against the non-local gravity. In another configuration, Bhakta et al [9] have found that the dust viscosity has a stabilising influence on the cloud. The grain surface charge number \(Z_{d} \) has no role to play in the propagation dynamics [9]. As far as we know, nobody has so far addressed the instability dynamics in such complex media in the presence of the Boltzmann electrons–ions, polytropic bipolar dust fluids with partial ionisation, nonlinear log-barotropic effects stemming from fluid turbulence, collective correlative viscoelasticity and heterogeneous interspecies collisional momentum transfer simultaneously. Such intricate instability phenomena are unexplored despite their great importance in understanding bounded structure formation in real astronomical strongly correlated environments for years. It may, in other words, be clearly realised that the conjugational bimodal cloud instability dynamics of pulsational type in a strongly coupled self-gravitating complex plasma fluid in the presence of turbulent flow and interspecies collisional effects has still been an open challenge to be addressed in the context of galactic element formation and evolution for years.

The present work reports a theoretical instability analysis of conjugational turbo-viscoelastic pulsational mode in a strongly coupled multifluidic self-gravitating plasma fluid. It considers all the possible key factors responsible for structuring the cloud, but rarely addressed simultaneously in the past. It is motivated by the need evident from the current observational scenarios on diversified astro-cosmo-space cloud fluid dynamics in a generalised hydrodynamic framework [4, 10, 11]. Thus, a generalised polynomial dispersion relation (sextic in degree) with unique variable multiparametric coefficients is mathematically derived and numerically analysed herein. To distinguish and classify the mode fluctuations on the basis of the perturbation scaling, two extreme classes, hydrodynamic and kinetic regimes, are considered. It is seen that, in the hydrodynamic regime, the dust-charge ratio (negative-to-positive grains) plays a destabilising role whereas, the dust–mass ratio (negative-to-positive grains) plays a stabilising role in the wave-dynamic processes. In the kinetic regime however, the viscoelastic relaxation velocity plays a stabilising role for the positively charged grains, and a destabilising role for the negatively charged ones in the cloud dynamics. The propagatory and non-propagatory characteristics of the viscoelastic bimodal instability in reorganising the cloud are also explored.

The layout of the paper, apart from the introduction in §1, is as follows. In §2, we describe the formalism of the considered astrocloud. Section 3 contains mode analyses of the conjugational bimodal fluctuations. Section 4 describes the numerical results and discussions. And, finally, in §5, we present some important conclusive remarks together with a concise highlight on future relevant applicability.

2 Model and formalism

A strongly coupled self-gravitating multifluidic complex plasma system of illimitable spatial extension in the framework of generalised hydrodynamic model on the astrophysical spatiotemporal scales is considered. The viscoelastic plasma model is indeed a complex admixture of weakly correlated lighter electrons and less-light ions, and strongly coupled heavier positively (due to intense radiations) and negatively (due to contact electrification) charged dust grains with partial ionisation. It may be noted that the viscoelasticity of the complex admixture arises from the collective correlative interactions among the constituent macroscopic particles [10, 11]. In the case of charged (dust) fluids, the degree of sensitivity of viscoelasticity can be measured from the high electrothermal Coulomb coupling [10]. In contrast, the correlative interaction mechanism is sourced by the binary and frictional interfluidic couplings [7, 10]. The complex multifluidic turbulent effects are incorporated with the help of nonlinear logatropic barotropic equation of state arising due to the existence of multi-spatiotemporal irregular overlapping of the fluid chaotic vorticity [12,13,14,15,16]. The constitutive component fluids constitute a special type of polytropic (adiabatic) configuration with a polytropic exponent of \(\gamma _{+} =\gamma _{-} =\gamma _{n} =3\) in the customary notations [17]. This is because of the fact that the dimension along which the thermodynamic potential varies is \(D=1\), and hence, \(\gamma =(D+2)/D=3\) [18, 19]. The equilibrium macrostate is presupposed as a uniform quasi-neutral hydrostatic homogeneous gaseous phase. The fluid model is simplified by adopting identical non-Brownian dust microspheres in the absence of tidal, rotational and extra-galactic disturbance forces. The presence of asymmetric irregular grains is neglected for simplicity. Such model environs may be widely realisable in a number of star-forming dust–gas complexes in real astronomical situations [20,21,22,23,24].

In the generalised hydrodynamic viewpoint [7, 10, 22], the multifluidic complex model is framed with the help of continuity equation for fluid flux conservation, viscoelastic momentum equation for the force density conservation, nonlinear log-barotropic equation of state for the macroscopic thermodynamic characterisation and closing electrogravitational Poisson equations for the long-range potential distributions sourced by the density fields of the charged and massive species. The dynamics of the thermalised electrons and ions are respectively modelled with the Boltzmann distribution laws in the generic notations as

$$\begin{aligned} n_{e}= & {} n_{e0} \exp \left( {\frac{e\phi }{T_{e} }} \right) , \end{aligned}$$
(1)
$$\begin{aligned} n_{i}= & {} n_{i0} \exp \left( {-\frac{e\phi }{T_{i} }} \right) . \end{aligned}$$
(2)

Here, \(n_{e\left( i \right) } \) denotes the population density of electrons (ions) at temperature \(T_{e\left( i \right) } \) eV with the corresponding equilibrium density value \(n_{e\left( i \right) 0} \) and electric charge –e (\(+e)\), respectively. The dynamics of the neutral dust is described in a classical non-relativistic closed customary form [7, 10] in spatially-flat space–time (x, t) given respectively as

$$\begin{aligned}&\frac{\partial n_{n} }{\partial t}\,+\,\frac{\partial }{\partial x}\left( {n_{n} u_{n} } \right) =0, \end{aligned}$$
(3)
$$\begin{aligned}&\left[ {1+\tau _{n} \left( {\frac{\partial }{\partial t}+u_{n} \frac{\partial }{\partial x}} \right) } \right] \left[ \rho _{n} \left( {\frac{\partial }{\partial t}\,+\,u_{n\,} \frac{\partial }{\partial x}} \right) u_{n}\right. \nonumber \\&\qquad +\frac{\partial p_{n} }{\partial x} +\rho _{n} \frac{\partial \psi }{\partial x}\nonumber \\&\qquad +\rho _{n}\left. \left\{ {f_{n,+}} \left( {u_{n} -u_{+} } \right) +{{f_{n,-}} \left( {u_{n} -u_{-} } \right) } \right\} \right] \nonumber \\&\quad =\chi _{n} \frac{\partial ^{2}u_{n} }{\partial x^{2}}, \end{aligned}$$
(4)
$$\begin{aligned}&\frac{\partial p_{n} }{\partial t}\,+\,u_{n} \frac{\partial p_{n} }{\partial x}\,+\,\gamma _{n}p_{n} \frac{\partial u_{n} }{\partial x}\,=0. \end{aligned}$$
(5)

Similarly, the equilibrium dynamics of the positively (negatively) charged dust grains in the same customary notations are respectively modelled as

$$\begin{aligned}&\frac{\partial n_{+\left( - \right) } }{\partial t}\,+\,\frac{\partial }{\partial x}\left( {n_{+\left( - \right) } u_{+\left( - \right) } } \right) =0, \end{aligned}$$
(6)
$$\begin{aligned}&\left[ {1+\tau _{+\left( - \right) } \left( {\frac{\partial }{\partial t}+u_{+\left( - \right) } \frac{\partial }{\partial x}} \right) } \right] \nonumber \\&\quad \times \left[ \rho _{+\left( - \right) } \left( {\frac{\partial }{\partial t}\,+\,u_{+\left( - \right) } \frac{\partial }{\partial x}} \right) u_{+\left( - \right) } \right. \nonumber \\&\quad \left. -\,q_{+\left( - \right) } n_{+\left( -\right) } \frac{\partial \phi }{\partial x}+ \frac{\partial p_{+\left( - \right) } }{\partial x}+\rho _{+\left( - \right) } \frac{\partial \psi }{\partial x} \right. \nonumber \\&\quad \left. +\, \rho _{+\left( - \right) } \,\left\{ \,f_{+\left( - \right) ,-\left( + \right) } \left( {u_{+\left( - \right) } -u_{-\left( + \right) } } \right) \right. \right. \nonumber \\&\quad \left. \left. +\, {f_{+(n),-(n)} \left( {u_{+\left( - \right) } -u_{n\left( n \right) } } \right) } \right\} \right] =\chi _{+\left( - \right) } \frac{\partial ^{2}u_{+\left( - \right) } }{\partial x^{2}} , \end{aligned}$$
(7)
$$\begin{aligned}&\frac{\partial p_{+\left( - \right) } }{\partial t}\,+\,u_{+\left( - \right) } \frac{\partial p_{+\left( - \right) } }{\partial x}\,\nonumber \\&\quad +\,\gamma _{+\left( - \right) } \,p_{+\left( - \right) } \frac{\partial u_{+\left( - \right) } }{\partial x}\,=0. \end{aligned}$$
(8)

It may be noted that the momentum conservation equations (eqs (4) and (7)) are validated only if the lowest-order viscoelasticity of the constituent compressible fluids does not change in the adopted spatiotemporal domains [11]. It alternatively indicates that none of the bulk viscosity (\(\zeta _{j} )\) and shear viscosity (\(\eta _{j} )\) coefficients undergo any remarkable change either with the variation in fluid pressure or with the temperature. With all these basic reservations, the astrofluid model is finally closed by the electrogravitational Poisson potential distribution equations respectively given as

$$\begin{aligned}&\frac{\partial ^{2}\phi }{\partial x^{2}}=\,4\pi e\left[ {n_{e} \,-n_{i} +\,\,Z_{-} n_{-} -Z_{+} n_{+} } \right] , \end{aligned}$$
(9)
$$\begin{aligned}&\frac{\partial ^{2}\psi }{\partial x^{2}}=\,4\pi G\left[ {m_{-} n_{-} +m_{+} n_{+} \,+\,\,m_{n} n_{n} } \right] . \end{aligned}$$
(10)

The terms \(n_{j}\), \(u_{j}\) and \(m_{j} \) denote the population density, flow velocity and mass of the \(j\hbox {th}\) dust species, respectively. Here, the index \(j = +\) is for positively charged grains, − is for negatively charged grains and n stands for neutral grains. The notation, \(q_{j} = j\,Z_{j} \left| e \right| \), signifies the corresponding grain charge. The parameter, \(\chi _{j} =\left( {\zeta _{j} +{4\eta _{j} } / 3} \right) \), is the effective generalised viscosity, where \(\zeta _{j} \) and \(\eta _{j} \) are the bulk (first viscosity, resistance to longitudinal flow) and shear (second viscosity, resistance to lateral expansion) viscosity coefficients, respectively. The viscoelastic relaxation time (memory-parametric effect) is denoted as \(\tau _{+\left( - \right) } \) for charged dust and \(\tau _{n} \) for neutral dust. \(p_{j} =T_{j} \rho _{j}^{\gamma _{j} }+T_{j} n_{j0} \log \left( {{\rho _{j} } / {\rho _{j0} }} \right) \) is the net pressure in the nonlinear logatropic form in terms of the material density \(\rho _{j} \) at temperature \(T_{j} \) eV [11]. It is comprehensively composed of the adiabatic pressure (first term) and the turbulent pressure (second term) similar to the fluid equilibrium density \(\rho _{j0} \). Moreover, the notations \(f_{+(-)} \), \(f_{-(+)} \), \(f_{+(n)} \), \(f_{-(n)} \), \(f_{n,+} \) and \(f_{n,-} \) represent interspecies collisional frequencies of the \(j\hbox {th}\) species. \(G=6.67\times 10^{-11}\hbox { m}^{\mathrm {3}}\hbox { kg}^{\mathrm {-1}}\hbox { s}^{\mathrm {-2}}\) is the universal gravitational (Newtonian) coupling constant. Finally, \(\phi \) and \(\psi \) represent the electrostatic and gravitational potentials developed by charge–matter density fluids, respectively.

We are interested in a scale-invariant (normalised) standard formalism of the conjugational perturbation dynamics. A standard astrophysical normalisation scheme [7, 9] is accordingly adopted. The normalised set of eqs (1)–(10) is constructed respectively as

$$\begin{aligned}&N_{e} =\text{ e}^{\Phi }, \end{aligned}$$
(11)
$$\begin{aligned}&N_{i} =\text{ e}^{-\Phi }, \end{aligned}$$
(12)
$$\begin{aligned}&\frac{\partial N_{j} }{\partial T}\,+\,\frac{\partial }{\partial X}\left( {N_{j} M_{j} } \right) =0, \end{aligned}$$
(13)
$$\begin{aligned}&\left[ 1+\tau _{+} \omega _{J} \left( \frac{\partial }{\partial T}+M_{+} \frac{\partial }{\partial X} \right) \right] \nonumber \\&\quad \times \left[ N_{+} \left( {\frac{\partial }{\partial T}\,+\,M_{+\,} \frac{\partial }{\partial X}} \right) M_{+} \right. \nonumber \\&\quad \left. +Z_{+} \beta _{-,+} N_{+} \frac{\partial \Phi }{\partial X}\right. \nonumber \\&\quad \left. +\beta _{-,+} \left( {\frac{T_{+} }{T_{p} }} \right) \left\{ {\frac{\partial N_{+}^{\gamma }}{\partial X}+\frac{\partial }{\partial X}\left( {\log \,N_{+} } \right) } \right\} \right. \nonumber \\&\left. \quad +\,N_{+} \frac{\partial \Psi }{\partial X}+N_{+} \left. \left\{ {F_{+,-} \left( {M_{+} -M_{-} } \right) } \right. \,\,\right. \right. \nonumber \\&\quad \left. \left. +F_{+,n} \left( {M_{+} -M_{n} } \right) \right\} \right] \nonumber \\&\quad =\frac{1}{\kappa _{+} }\left( {\chi _{+} } \right) \frac{\partial ^{2}M_{+} }{\partial X^{2}}, \end{aligned}$$
(14)
$$\begin{aligned}&\left[ {1+\tau _{-} \omega _{J} \left( {\frac{\partial }{\partial T}+M_{-} \frac{\partial }{\partial X}} \right) } \right] \nonumber \\&\quad \times \left[ N_{-} \left( {\frac{\partial }{\partial T}\,+\,M_{-\,} \frac{\partial }{\partial X}} \right) M_{-} \right. \left. -Z_{-} N_{-} \frac{\partial \Phi }{\partial X}\right. \nonumber \\&\quad \left. +\left( {\frac{T_{-} }{T_{p} }} \right) \left\{ {\frac{\partial N_{-}^{\gamma }}{\partial X}+\frac{\partial }{\partial X}\left( {\log \,N_{-} } \right) } \right\} +N_{-} \frac{\partial \varPsi }{\partial X} \right. \nonumber \\&\left. \quad {+N_{-} \left. {\left\{ {F_{-,+} \left( {M_{-} -M_{+} } \right) } \right. +F_{-,n} \left( {M_{-} -M_{n} } \right) } \right\} } \right] \nonumber \\&\quad =\frac{1}{\kappa _{-} }\left( {\chi _{-} } \right) \frac{\partial ^{2}M_{-} }{\partial X^{2}}, \end{aligned}$$
(15)
$$\begin{aligned}&\left[ {1+\tau _{n} \omega _{J} \left( {\frac{\partial }{\partial T}+M_{n} \frac{\partial }{\partial X}} \right) } \right] \left[ N_{n} \left( {\frac{\partial }{\partial T}+M_{n\,} \frac{\partial }{\partial X}} \right) M_{n} \right. \nonumber \\&\left. \qquad +\beta _{-,n} \left( {\frac{T_{n} }{T_{p} }} \right) \left\{ {\frac{\partial N_{n}^{\gamma }}{\partial X}+\frac{\partial }{\partial X}\left( {\log \,N_{n} } \right) } \right\} +N_{n} \frac{\partial \varPsi }{\partial X}\right. \nonumber \\&\left. \qquad {+N_{n} \left. {\left\{ {F_{n,+} \left( {M_{n} -M_{+} } \right) } \right. +F_{n,-} \left( {M_{-} -M_{n} } \right) } \right\} } \right] \nonumber \\&\quad =\frac{1}{\kappa _{n} }\left( {\chi _{n} } \right) \frac{\partial ^{2}M_{n} }{\partial X^{2}}, \end{aligned}$$
(16)
$$\begin{aligned}&\frac{\partial ^{2}\varPhi }{\partial X^{2}}=\mu \left[ n_{e0} N_{e} \,-n_{i0} N_{i} \right. \nonumber \\&\qquad \qquad \left. +Z_{-} n_{-0} N_{-} -Z_{+} n_{+0} N_{+} \right] , \end{aligned}$$
(17)
$$\begin{aligned}&\frac{\partial ^{2}\varPsi }{\partial X^{2}}=\,\rho _{0}^{-1}\left[ m_{-} n_{-} \left( {N_{-} -1} \right) \right. \nonumber \\&\left. \qquad \qquad +m_{+} n_{+} \left( {N_{+} -1} \right) +\,\,m_{n} n_{n} \left( {N_{n} -1} \right) \right] . \end{aligned}$$
(18)

The independent parameters X for position and T for time are normalised by the Jeans wavelength \(\lambda _{J} ={c_{ss} } /{\omega _{J} }\) and Jeans time \(\omega _{J}^{-1}=\left( {{c_{ss} } /{\lambda _{J} }} \right) ^{-1}\), respectively. The dust-acoustic phase speed associated with the negatively charged dust fluid is \(c_{ss} =\left( {{T_{p} } /{m_{-} }} \right) ^{1 / 2}\). Next, the parameters \(N_{e} \), \(N_{i} \,\) and \(N_{j} \) are the normalised population densities of electrons, ions and the jth dust species, which are normalised by their respective equilibrium concentration values \(n_{e0} \), \(n_{i0} \) and \(n_{j0} \). The parameter \(M_{j} \) is the normalised dust fluid velocity associated with the \(j\hbox {th}\) dust species, normalised by \(c_{ss} \). A normal constitutional temperature scaling (in \(\mathrm{e}\hbox {V}\)) supposed the cloud such that \(T_{e} {\sim }T_{i} =T_{p}>>T_{j} \). Moreover, \(P_{j} ={p_{j} } /{p_{j0} =}N_{j}^{\gamma }+\log N_{j} \) denotes the normalised net pressure in the normalised logatropic form, where \(p_{j0} =n_{j} \,T_{j} \) is the equilibrium isothermal pressure of the rarefied cloud complex, which may be even of the polytropic form for denser cases [25]. The term, \(\kappa _{j} =\rho _{j0} \omega _{J} \lambda _{J} ^{2}\), denotes the Jeans dynamic viscosity associated with the jth species. The symbols \(\Phi \) and \(\Psi \) are the normalised electrostatic potential and self-gravitational potential, which are normalised by the cloud thermal potential, \({T_{p} } / e\) and the dust-acoustic phase speed squared, \(c_{ss}^{2}\), respectively. Moreover, the terms \(F_{+,-} \), \(F_{+,n} \), \(F_{-,+} \), \(F_{-,n} \), \(F_{n,+} \) and \(F_{n,-} \) are the normalised collisional frequencies of the constitutive dust species, each normalised by the Jeans frequency \(\omega _{J} \). In addition, \(\beta _{-,j} ={m_{-} } / {m_{j} }\) represents the grain–mass ratio of the negative to the \(j\hbox {th}\) dust species. Finally, the term \(\mu ={e^{2}} / {\left( {\rho _{0} m_{d-} G} \right) }\) denotes a new electrogravitational coupling parameter modelling the constitutive correlated grains in the composite astrocloud.

3 Mode analysis

It is well known that the equilibrium of any turbulent plasma system cannot be defined with the help of first principles [12,13,14,15,16]. In the present specific case, the effects of erratic fluid turbulence are strategically incorporated in the basic set up via a photospectroscopically derived nonlinear log-barotropic equation of state [16]. It is allowed to undergo a local small-scale perturbation around a defined homogeneous equilibrium. We seek the non-homology perturbation solutions (\(F_{1})\) for the relevant parameters (F) around their respective hydrostatic homogeneous equilibrium values (\(F_{\mathrm {0}})\) in a standard form [6] with the normalised angular wave number \(K= k/k_{J}\) and normalised angular frequency \(\Omega =\omega /\omega _{J} \) as

$$\begin{aligned} F\left( {X,\,T} \right)= & {} F_{0} +F_{1} \,\text{ e}^{-i\left( {\Omega T-KX} \right) }, \end{aligned}$$
(19)
$$\begin{aligned} F\left( {X,\,T} \right)= & {} \left[ N_{e}\,\,\,N_{i}\,\,\,N{ }_{+}\,\,\,N_{-} \,\,\, N_{n} \,\,\,M{ }_{+}\,\,\,M_{-} \,\right. \nonumber \\&\left. M_{n} \,\,\,\Phi \,\,\,\varPsi \right] ^{T}, \end{aligned}$$
(20)
$$\begin{aligned}&F_{0}=[1\,\,\,1\,\,\,1\,\,\,1\,\,\,1\,\,0\,\,\,0\,\,\,0\,\,\,0\,\,\,0]^{T}, \end{aligned}$$
(21)
$$\begin{aligned}&F_{1} =\left[ N_{e1}\,\,\,N_{i1}\,\,\,N{}_{+1}\,\,\, N_{-1}\,\,\,N_{n1}\,\,\,M{ }_{+1}\,\,\,M_{-1}\right. \nonumber \\&\qquad \qquad \left. M_{n1}\,\,\,\Phi _{1}\,\,\,\Psi _{1} \right] ^{T}. \end{aligned}$$
(22)

The algebraically transformed form of eqs (13)–(18) in the normalised Fourier space (\(K,\Omega \)) is respectively given as

$$\begin{aligned}&M_{+1} =\Omega K^{-1}N_{+1} , \\&\left[ \left( {1-i\tau _{+} \omega _{J} \Omega } \right) \left\{ -i\Omega ^{2}K^{-1}+i\beta _{-,+} \left( {1+\gamma } \right) \left( {\frac{T_{+} }{T_{p} }} \right) K\right. \right. \nonumber \\&\left. \left. +\left( {F_{+,-} \,+F_{+,n} } \right) \Omega K^{-1} \right\} +\frac{1}{\kappa _{+} }\left( {\chi _{+} } \right) \Omega K \right] N_{+1} \nonumber \end{aligned}$$
(23)
$$\begin{aligned}&-\left( {1-i\tau _{+} \omega _{J} \Omega } \right) \Omega K^{-1}\left( {F_{+,-} N_{-1} +F_{+,n} N_{n1} } \right) \nonumber \\&+\, i\left( {1-i\tau _{+} \omega _{J} \Omega } \right) K\left( {Z_{+} \beta _{-,+} \Phi _{1} +\Psi _{1} } \right) =0, \end{aligned}$$
(24)
$$\begin{aligned}&M_{-1} =\Omega K^{-1}N_{-1} , \\&\left[ \left( {1-i\tau _{-} \omega _{J} \Omega } \right) \left\{ -i\Omega ^{2}K^{-1}+i\left( {1+\gamma } \right) \left( {\frac{T_{-} }{T_{p} }} \right) K\right. \right. \nonumber \\&\left. \left. \quad +\left( {F_{-,+} \,+F_{-,n} } \right) \Omega K^{-1} \right\} +\frac{1}{\kappa _{-} }\left( {\chi _{-} } \right) \Omega K \right] N_{-1}\nonumber \end{aligned}$$
(25)
$$\begin{aligned}&\quad -\left( {1-i\tau _{-} \omega _{J} \Omega } \right) \Omega K^{-1}\left( {F_{-,+} N_{-1} +F_{+,n} N_{n1} } \right) \nonumber \\&\quad -i\left( {1-i\tau _{-} \omega _{J} \Omega } \right) K\left( {Z_{-} \Phi _{1} -\Psi _{1} } \right) =0, \end{aligned}$$
(26)
$$\begin{aligned}&M_{n1} =\Omega K^{-1}N_{n1} , \\&\left[ \left( {1-i\tau _{n} \omega _{J} \Omega } \right) \left\{ -i\Omega ^{2}K^{-1}+i\beta _{-,n} \left( {1+\gamma } \right) \left( {\frac{T_{n} }{T_{p} }} \right) K\right. \right. \nonumber \\&\left. \left. \quad +\left( {F_{n,+} \,+F_{n,-} } \right) \Omega K^{-1} \right\} +\frac{1}{\kappa _{n} }\left( {\chi _{n} } \right) \Omega K \right] N_{n1}\nonumber \end{aligned}$$
(27)
$$\begin{aligned}&\quad -\left( {1-i\tau _{n} \omega _{J} \Omega } \right) \left( {F_{n,+\,} N_{+1} +F_{n,-} N_{-1} } \right) \Omega K^{-1}\nonumber \\&\quad +i\left( {1-i\tau _{n} \omega _{J} \Omega } \right) K\Psi _{1} =0, \end{aligned}$$
(28)
$$\begin{aligned}&\Phi _{1} =\left\{ {(n_{i0} -n_{e0} )\mu -K^{2}} \right\} ^{-1}\left[ \mu \left( Z_{-} n_{-0} N_{-1} \right. \right. \nonumber \\&\left. \left. \quad \qquad -Z_{+} n_{+0} N_{+1} \right) \right] , \end{aligned}$$
(29)
$$\begin{aligned}&\Psi _{1} =\,-\rho _{0}^{-1}\left[ m_{-} n_{-0} N_{-1} \right. \nonumber \\&\left. \quad \qquad +m_{+} n_{+0} N_{+1} \,+\,\,m_{n} n_{n0} N_{n1} \right] K^{2}. \end{aligned}$$
(30)

After a systematic algebraic elimination and simplification, eqs (23)–(30) decouple into a linear generalised polynomial dispersion relation with multiparametric variable coefficients as

$$\begin{aligned}&\left[ \left( {1-i\tau _{+} \omega _{J} \Omega } \right) \left\{ {-i\,\Omega ^{2}K^{-1}+a_{1} \Omega \,+a_{2} } \right\} \,+a_{3} \Omega \right] \nonumber \\&\quad \times \left[ {\left[ {\left( {1-i\tau _{-} \omega _{J} \Omega } \right) \left\{ {-i\,\Omega ^{2}K^{-1}+a_{4} \Omega +a_{5} } \right\} +a_{6} \Omega } \right] } \right. \nonumber \\&\quad \times \left[ {\left( {1-i\tau _{n} \omega _{J} \Omega } \right) \left\{ {-i\,\Omega ^{2}K^{-1}+a_{7} \Omega +a_{8} } \right\} +a_{9} \Omega } \right] \nonumber \\&\quad -\left[ {\left( {1-i\tau _{n} \omega _{J} \Omega } \right) \left( {-F_{n,-} K^{-1}\Omega +a_{10} } \right) } \right] \left[ {\left( {1-} \right. } \right. \nonumber \\&\quad \left. {\left. {\left. {i\tau _{-} \omega _{J} \Omega } \right) \left( {-F_{-,n} \,K^{-1}\Omega +a_{11} } \right) } \right] } \right] \nonumber \\&\quad -\left[ {\left( {1-i\tau _{+} \omega _{J} \Omega } \right) \left( {-F_{+,-} \,K^{-1}\Omega +a_{12} } \right) } \right] \nonumber \\&\quad \times \left[ \left[ \left( 1-i\tau _{-} \omega _{J} \Omega \right) \left( -F_{+,-} \,K^{-1}\Omega +a_{13} \right) \right] \right. \nonumber \\&\quad \times \left[ {\left( {1-i\tau _{n} \omega _{J} \Omega } \right) \left\{ {-i\,\Omega ^{2}K^{-1}+a_{7} \Omega +a_{8} } \right\} +a_{9} \Omega } \right] \nonumber \\&\quad -\left[ {\left( {1-i\tau _{n} \omega _{J} \Omega } \right) \left( {-F_{n,+} K^{-1}\Omega +a_{14} } \right) } \right] \left[ {\left( {1-} \right. } \right. \nonumber \\&\quad \left. {\left. {\left. {i\tau _{-} \omega _{J} \Omega } \right) \left( {-F_{-,n} \,K^{-1}\Omega +a_{11} } \right) } \right] } \right] \nonumber \\&\quad +\left[ {\left( {1-i\tau _{+} \omega _{J} \Omega } \right) \left( {-F_{+,n} \Omega K^{-1}+a_{11} } \right) } \right] \nonumber \\&\quad \times \left[ \Big [ {\left( {1-i\tau _{-} \omega _{J} \Omega } \right) } \left( {-F_{+,-} \,K^{-1}\Omega } \right. \right. \nonumber \\&\quad \left. {+a_{13} } \right) \Big ]\left. {\left[ {\left( {1-i\tau _{n} \omega _{J} \Omega } \right) } \right. \left( {-F_{n,-} K^{-1}\Omega +a_{10} } \right) } \right] \nonumber \\&\quad -\left[ {\left( {1-i\tau _{n} \omega _{J} \Omega } \right) \left( {-F_{n,+} K^{-1}\Omega +a_{14} } \right) } \right] \nonumber \\&\quad \times \left. \left[ \left( {1-i\tau _{-} \omega _{J} \Omega } \right) \left\{ -i\,\Omega ^{2}K^{-1}+a_{4} \Omega +a_{5} \right\} +a_{6} \Omega \right] \right] \nonumber \\&\quad =0. \end{aligned}$$
(31)

The various multiparametric dispersion coefficients involved in eq. (31) are given in Appendix A. We see the mode features on the basis of the hydrokinetic perturbation scalings.

3.1 Hydrodynamic regime

In the hydrodynamic regime (\(\Omega \,\tau _{+\left( - \right) }<<1\), \(\Omega \,\tau _{n}<<1)\) [7], which admits the low-frequency fluctuations to evolve, the generalised dispersion relation (eq. (31)) reduces to a unique form of sextic polynomial dispersion relation given as

$$\begin{aligned} \Omega ^{6}+A_{5} \Omega ^{5}+A_{4} \Omega ^{4}+A_{3} \Omega ^{3}+A_{2} \Omega ^{2}+A_{1} \Omega +A_{0} =0. \end{aligned}$$
(32)

The new set of various multiparametric dispersion coefficients involved in eq. (32) are given in Appendix B. Now, to solve eq. (32) numerically, we use the decomposition method [26] to reduce eq. (32) into a pair of cubic form of dispersion relations, and then, the Cardan method [27, 28] to integrate these reduced cubic forms. Out of all the so obtained six roots, the considered root (sixth root, \(\Omega =\Omega _{6} )\) with positive real–imaginary parts (\(\Omega _{r} >0\), \(\Omega _{i} >0)\) is given as

$$\begin{aligned} \Omega _{6}= & {} -\frac{\left( {2g_{0} +2p_{2}^{2}h_{0} +p_{2} l_{1} } \right) }{2\left( {1+p_{2} +p_{2}^{2}} \right) }-\frac{\big [ {\left( {2g_{0} +2p_{2}^{2}h_{0} +p_{2} l_{1} } \right) ^{2}-4\left( {1+p_{2} +p_{2}^{2}} \right) \left( {g_{0}^{2}+p_{2}^{2}h_{0}^{2}+p_{2} l_{2} } \right) } \big ]^{1/2}}{2\left( {1+p_{2} +p_{2}^{2}} \right) }, \end{aligned}$$
(33)

where the different involved terms are given as

$$\begin{aligned} g_{0}= & {} \frac{l_{1} +\left( {l_{1}^{2}-4l_{2} } \right) ^{1/2}}{2}, \quad h_{0} =\frac{l_{1} -\left( {l_{1}^{2}-4l_{2} } \right) ^{1/2}}{2},\\ l_{1}= & {} \frac{e_{1} e_{2} -9e_{0} }{e_{2}^{2}-3e_{1} }, \quad l_{2} =\frac{e_{1}^{2}-3e_{0} e_{2} }{e_{2}^{2}-3e_{1} }, \\ p_{2}= & {} \left[ {\frac{e_{2} -3g_{0} }{e_{2} -3h_{0} }} \right] ^{1/3}, \\ e_{2}= & {} \frac{1}{2}A_{5} , \quad e_{1} =A_{6} -\frac{1}{8}A_{5}^{2}+\frac{1}{2}A_{4} , \\ e_{0}= & {} \frac{A_{7} }{A_{6} }+\frac{1}{16}A_{5}^{3}-\frac{1}{4}A_{5} A_{4} +\,\frac{1}{2}A_{3},\\ A_{7}= & {} b_{0} b_{1} -\frac{A_{1} }{2}, \\ A_{6}= & {} \left[ {\frac{5}{64}A_{5}^{4}-\frac{3}{8}A_{4} A_{5} ^{2}+\frac{1}{4}a_{4}^{2}+\frac{1}{2}A_{3} A_{5} -A_{2} } \right] ^{1/2}, \\ b_{1}= & {} \frac{1}{2}A_{4} -\frac{1}{8}A_{5}^{2}, \quad b_{0} =\frac{1}{2}A_{3} -\frac{1}{4}A_{4} A_{5} +\frac{1}{16}A_{5}^{3}. \end{aligned}$$

3.2 Kinetic regime

In the kinetic regime (\(\Omega \,\tau _{+\left( - \right) }>>1\), \(\Omega \,\tau _{n}>>1)\), which allows high-frequency fluctuations to evolve, the generalised dispersion relation (eq. (31)) reduces to a unique sextic form as

$$\begin{aligned} \Omega ^{6}+B_{5} \Omega ^{5}+B_{4} \Omega ^{4}+B_{3} \Omega ^{3}+B_{2} \Omega ^{2}+B_{1} \Omega +B_{0} =0. \end{aligned}$$
(34)

Likewise, as in the hydrodynamic regime, the various dispersion multiparametric coefficients involved in eq. (34) are given in Appendix C. We apply the same procedure for the exact solutions as previously described. The considered root of eq. (34) (first root, \(\Omega =\Omega _{1} )\) with real part \(\Omega _{r} >0\) and imaginary part \(\Omega _{i} <0\) is given as

$$\begin{aligned} \Omega _{1} =\frac{p_{3} r_{2} -r_{1} }{1-p_{3} }. \end{aligned}$$
(35)

Here, the diversified parameters involved are presented as

$$\begin{aligned} r_{1}= & {} \frac{s_{1} +\left( {s_{1}^{2}-4s_{2} } \right) ^{1/2}}{2}, \quad r_{2} =\frac{s_{1} -\left( {s_{1}^{2}-4s_{2} } \right) ^{1/2}}{2},\\ s_{1}= & {} \frac{q_{1} q_{2} -9q_{0} }{q_{2}^{2}-3q_{1} }, \quad s_{2} =\frac{q_{1}^{2}-3q_{0} q_{2} }{q_{2}^{2}-3q_{1} }, \\ p_{3}= & {} \left[ {\frac{q_{2} -3s_{1} }{q_{2} -3s_{2} }} \right] ^{1/3}, \\ q_{2}= & {} \frac{1}{2}B_{5} , \quad q_{1} =-B_{6} -\frac{1}{8}B_{5}^{2}+\frac{1}{2}B_{4} , \nonumber \\ q_{0}= & {} \frac{B_{7} }{B_{6} }+\frac{1}{16}B_{5}^{3}-\frac{1}{4}B_{5} B_{4} +\frac{1}{2}B_{3} , \nonumber \\ B_{7}= & {} n_{0} n_{1} -\frac{B_{1} }{2}, \\ B_{6}= & {} \left[ {\frac{5}{64}B_{5}^{4}-\frac{3}{8}B_{4} B_{5} ^{2}+\frac{1}{4}B_{4}^{2}+\frac{1}{2}B_{3} B_{5} -B_{2} } \right] ^{1/2}, \\ n_{1}= & {} \frac{1}{2}B_{4} -\frac{1}{8}B_{5}^{2}, \\ n_{0}= & {} \frac{1}{2}B_{3} -\frac{1}{4}B_{4} B_{5} +\frac{1}{16}B_{5}^{3}. \end{aligned}$$

The exact propagatory and stability features of the considered cloud dynamics in both the hydrokinetic perturbation regimes will be discussed in results and discussions.

4 Results and discussions

The stability behaviours of the turbo-viscoelastic pulsational mode excitable in a strongly coupled multifluidic self-gravitating turbulent dusty plasma having illimitable boundary are investigated on the astrophysical spatiotemporal scales. A generalised hydrodynamic model is methodologically constructed to derive a generalised linear dispersion relation (eq. (31)) followed by a numerical illustrative analysis in two extreme cases of perturbation scaling: the hydrodynamic (eq. (32)) and the kinetic (eq. (34)) regimes. The threshold condition for the onset of instability in trivial cases is \(K>1\) [1, 16, 17]. Various parametric inputs for the numerical analysis to proceed are adopted from the judicious plasma multiparametric windows relevant in the real astroscenarios [4, 7, 13, 29]. The obtained results are graphically displayed in figures 1 and 2 in the hydrodynamic limit and in figures 3 and 4 in the kinetic limit.

Fig. 1
figure 1

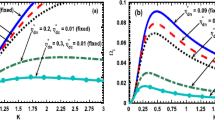
Profiles of the normalised (a) real frequency (\(\Omega _{r} \), lower curves) and imaginary frequency (\(\Omega _{i} \), upper curves) and (b) phase velocity (\(V_{p} \), lower curves) and group velocity (\(V_{g} \), upper curves) of the turbo-viscoelastic pulsational mode with variation in the Jeans-normalised wave number (K) for different values of the negative-to-positive grain–charge ratio (\(\sigma ={Z_{-} } / {Z_{+} })\) in the hydrodynamic limit. Various lines link to \(\sigma =1.30\) (a: blue solid line, A: black dash–dotted line), \(\sigma =1.40\) (b: red dashed line, B: magenta circle-marked solid line) and \(\sigma =1.50\) (c: green dotted line, C: brown square-marked solid line) respectively. Fine input details are discussed in the text.

Full size image

In figure 1, we show the profiles of the normalised (a) real frequency (\(\Omega _{r} \), lower curves) and imaginary frequency (\(\Omega _{i} \), upper curves) and (b) phase velocity (\(V_{p} \), lower curves) and group velocity (\(V_{g} \), upper curves) of the turbo-viscoelastic pulsational mode by varying the Jeans-normalised wave number (K) for different values of negative-to-positive grain-charge ratio (\(\sigma ={Z_{-} } / {Z_{+} })\) in the hydrodynamic limit. Various lines link to \(\sigma =1.30\), \(\sigma =1.40\) and \(\sigma =1.50\). The other parameters which are kept fixed are \(n_{e0} =6.00\times 10^{12}\,\hbox {m}^{\mathrm {-3}}\), \(n_{i0} =2.00\times 10^{13}\,\hbox { m}^{\mathrm {-3}}\), \(n_{-} =4.00\times 10^{10}\,\hbox {m}^{\mathrm {-3}}\), \(n_{+} =3.50\times 10^{10}\,\hbox {m}^{\mathrm {-3}}\), \(n_{n} =5.00\times 10^{10}\,\hbox {m}^{\mathrm {-3}}\), \(Z_{-} =1500\), \(m_{-} =1.00\times 10^{-14}\,\hbox {kg}\), \(m_{+} =9.00\times 10^{-15}\,\hbox {kg}\), \(m_{n} =9.00\times 10^{-15}\,\hbox {kg}\), \(\chi _{-} =1.00\times 10^{-1}\,\hbox {kg m}^{\mathrm {-1}}\hbox { s}^{\mathrm {-1}}\), \(\chi _{+} =1.00\times 10^{-1}\,\hbox {kg m}^{\mathrm {-1}}\hbox { s}^{\mathrm {-1}}\), \(\chi _{n} =1.00\times 10^{-1}\,\hbox {kg m}^{\mathrm {-1}}\hbox { s}^{\mathrm {-1}}\), \(\alpha _{1} \,= {T_{-} } / {T_{p} }=\) \(9\times 10^{-2}\), \(\alpha _{2} \,= {T_{+} } / {T_{p} }=\) \(5\times 10^{-2}\), \(\alpha _{3} \,= {T_{n} } / {T_{p} }=\) \(4\times 10^{-2}\), \(F_{-,+} \,=1.00\times 10^{-1}\), \(F_{-,n} \,=\) \(1.00\times 10^{-1}\), \(F_{+,-} \,= 1.00\times 10^{-1}\), \(F_{+,n} \,= 1.00\times 10^{-1}\), \(F_{n,-} \,= 1.00\times 10^{-1}\) and \(F_{n,+} \,= 1.00\times 10^{-1}\). It is seen that both \(\Omega _{r} \) and \(\Omega _{i} \) increase with increase in \(\sigma \) (figure 1a). There exists a critical point in the K-space, given as \({K}_{c} \approx \) 0.20 (figure 1a), beyond which we speculate both growth (figure 1a, upper curves) and propagatory (figure 1a, lower curves) characteristics of the instability. The maximum growth is found to occur at \({K}\approx 0.25\) (figure 1a, lower curves). Here, it is seen that the dust charge ratio (negative-to-positive grains) acts as a destabiliser against the conjugational fluctuations dynamics. Moreover, \(V_{p} \) and \(V_{g} \) increase with increase in \(\sigma \) (figure 1b). The \(V_{p} \)–\(V_{g} \) profiles in K-space confirm the dispersive nature of the fluctuations (figure 1b). In the \(V_{g}\) patterns, we see an explosive singularity behaviour at the critical wave number, \(K_{c} \approx 0.20\). It shows that no wave gets excited below this critical point, and wave propagation initiates only beyond it. Another interesting feature observed here is that \(V_{g}>0\), which means that the longer waves (gravitational) move faster than the shorter ones (acoustic), well bolstered in the light of spectral wave packet model [30]. It indicates that the wave dispersion caused is an anomalous type rather than a normal one. This happens physically due to the fluid turbulent effects in the presence of deviation from gravito-electrostatic neutrality in the considered fluid medium.

Fig. 2
figure 2

Same as figure 1, but for different values of the negative-to-positive grain–mass ratio (\(\beta _{-,+} ={m_{-} } /{m_{+} })\) for \(Z_{-} =1000\) and \(Z_{+} =1500\). Various lines correspond to \(\beta _{-,+} =1.10\) (a: blue solid line, A: black dash–dotted line), \(\beta _{-,+} =1.30\) (b: red dashed line, B: magenta circle-marked solid line) and \(\beta _{-,+} =1.50\) (c: green dotted line, C: brown square-marked solid line), respectively.

Full size image
Fig. 3
figure 3

Same as figure 1, but for different values of the viscoelastic relaxation mode velocity (\(V_{rx+} \), for positive grains) in the kinetic limit. Various lines correspond to \(V_{rx+} =7.96\times 10^{-2}\hbox { m s}^{\mathrm {-1}}\) (a: blue solid line, A: black dash–dotted line), \(V_{rx+} =8.45\times 10^{-2}\hbox { m s}^{\mathrm {-1}}\) (b: red dashed line, B: magenta circle-marked solid line) and \(V_{rx+} =9.03\times 10^{-2}\hbox { m s}^{\mathrm {-1}}\) (c: green dotted line, C: brown square-marked solid line); respectively. Further details of the inputs are given in the text.

Full size image

Figure 2 is depicted similar to figure 1, but now for different values of negative-to-positive grain–mass ratio (\(\beta _{-,+} ={m_{-} } / {m_{+} })\) for \(Z_{-} =1000\) and \(Z_{+} =1500\). Various lines correspond to \(\beta _{-,+} =1.10\), \(\beta _{-,+} =1.30\) and \(\beta _{-,+} =1.50\). We see that the \(\Omega _{r} \) and \(\Omega _{i} \) fluctuations decrease with increase in \(\beta _{-,+} \) (figure 2a). Clearly, the grain–mass acts as a dispersive stabilising source towards instability. In addition, we observe similar dispersive nature of fluctuations (figure 2b) as speculated in the previous case (figure 1b). The only difference found here is that the anomalous dispersion decreases with increase in \(\beta _{-,+} \), and vice versa (figure 2b).

Fig. 4
figure 4

Same as figure 3, but for different values of the viscoelastic relaxation mode velocity (\(V_{rx-} \), for negative grains). Various lines correspond to \(V_{rx-} =1.2\times 10^{-1}\hbox { m s}^{\mathrm {-1}}\) (a: blue solid line, A: black dash–dotted line), \(V_{rx-} =1.4\times 10^{-2}\hbox { m s}^{\mathrm {-1}}\) (b: red dashed line, B: magenta circle-marked solid line) and \(V_{rx-} =1.6\times 10^{-2}\hbox { m s}^{\mathrm {-1}}\) (c: green dotted line, C: brown square-marked solid line), respectively.

Full size image
Table 1 Our results in the present study vs. those in the literature.
Full size table

Figure 3 is displayed similar to figure 1, but for different values of viscoelastic relaxation mode velocity (\(V_{rx+} \), for positively charged grains) in the kinetic limit. Various lines correspond to \(V_{rx+} =7.96\times 10^{-2}\hbox { m s}^{\mathrm {-1}}\), \(V_{rx+} =8.45\times 10^{-2}\hbox { m s}^{\mathrm {-1}}\) and \(V_{rx+} =9.03\times 10^{-2}\hbox { m s}^{\mathrm {-1}}\). The other parameters which are kept fixed are: \(n_{e0} =6.00\times 10^{14}\,\hbox {m}^{\mathrm {-3}}\), \(n_{i0} =5.00\times 10^{14}\,\hbox {m}^{\mathrm {-3}}\), \(n_{-} =4.00\times 10^{11}\,\hbox {m}^{\mathrm {-3}}\), \(n_{+} =3.50\times 10^{11}\,\hbox {m}^{\mathrm {-3}}\), \(n_{n} =5.00\times 10^{11}\,\hbox {m}^{\mathrm {-3}}\), \(Z_{-} =1500\), \(Z_{+} =1000\), \(m_{-} =10.00\times 10^{-10}\,\) kg, \(m_{+} =7.00\times 10^{-10}\,\hbox {kg}, m_{n} =9.00\times 10^{-8}\,\hbox {kg}\), \(\chi _{-} =1.00\times 10^{-1}\,\hbox {kg m}^{\mathrm {-1}}\hbox { s}^{\mathrm {-1}}\), \(\chi _{+} =1.00\times 10^{-1}\,\hbox {kg m}^{\mathrm {-1}}\hbox { s}^{\mathrm {-1}}\), \(\chi _{n} =1.00\times 10^{-1}\,\hbox {kg m}^{\mathrm {-1}}\hbox { s}^{\mathrm {-1}}\), \({\alpha _{1} =T_{d-} } / {T_{p} }=5\times 10^{-2}\), \(\alpha _{2} \,=\) \({T_{+} } / {T_{p} }= 3\times 10^{-2}\), \(\alpha _{3} \,= {T_{n} } / {T_{p} }= 4\times 10^{-2}\), \(F_{-,+} \,=1.00\times 10^{-1}\,\), \(F_{-,n} \,= 1.00\times 10^{-1}\,\), \(F_{+,-} \,= 1.00\times 10^{-1}\), \(F_{+,n} \,= 1.00\times 10^{-1}\,\), \(F_{n,-} \,= 1.00\times 10^{-1}\) and \(F_{n,+} \,= 1.00\times 10^{-1}\). It is seen that \(\Omega _{r} \) and \(\Omega _{i} \) strengths of the fluctuations decrease with increase in \(V_{rx+} \) (figure 3a). This happens physically due to the strongly coupled impurity ions with more mass and less thermal velocity. It is now seen that \(V_{rx+} \) acts as a stabilising agent towards dynamical instability. It is further seen that, in the kinetic regime, the \(V_{p} \)–\(V_{g} \) variations (figure 3b) show the same dispersive characteristic features as previously described in figures 1b and 2b. The only difference seen here is that the anomalous dispersion decreases with increase in \(V_{rx+} \) with cloud-centric peak shifting, and vice versa (figure 3b).

Lastly, figure 4 is displayed similar to figure 3, but for different values of viscoelastic relaxation mode velocity (\(V_{rx-} \), for negatively charged grains). Various lines correspond to \(V_{rx-} =1.2\times 10^{-1}\hbox { m s}^{\mathrm {-1}}\), \(V_{rx-} =1.4\times 10^{-2}\hbox { m s}^{\mathrm {-1}}\) and \(V_{rx-} =1.6\times 10^{-2}\hbox { m s}^{\mathrm {-1}}\). Here, it is seen that \(\Omega _{r} \) and \(\Omega _{i} \) profiles of the fluctuations increase with increase in \(V_{rx-} \) (figure 4a). This is because the electrons are relatively weakly coupled due to their lesser mass. It acts as a destabilising source in the wave dynamics processes. Moreover, the \(V_{p} \)–\(V_{g} \) variations (figure 4b) depict the same dispersive characteristic features as previously described in figures 1b, 2b and 3b. The only difference seen here is that the anomalous dispersion exhibited by the conjugational instability increases with increase in \(V_{rx-} \) with anticloud-centric peak shifting (against the previous cloud-centric peak shifting as in figure 3b), and vice versa (figure 4b).

In summary, we can instantly say from our numerical analysis that the relevant wave features under the combined action of the conjugational gravitoelectrostatic interplay in the turbo-viscoelastic correlated astrocloud fluid in both the hydrokinetic regimes are illustrated. Various stabilising and destabilising sources against the cloud collapse are identified. The results on the current turbo-viscoelastic pulsational mode stability are in good agreement with the earlier viscoelastic pulsational mode features [7] as clearly highlighted in table 1. Various qualitative aspects between the complementary turbo-viscoelastic and viscoelastic pulsational modes for an instant perception are also concisely outlined in table 1.

5 Conclusions

The turbo-viscoelastic pulsational mode instability behaviours in a strongly coupled multifluidic self-gravitating plasma fluid of infinite spatial extension (\({>}{>}\) Jeans length) are theoretically investigated in the framework of a generalised hydrodynamic model configuration. The instability analysis is executed in two extreme cases of the hydrodynamic and kinetic regimes of paramount astronomical importance. A constructive numerical illustrative scheme is presented in detail. Various stabilising and destabilising key factors against the non-local naturalistic cloud collapse are identified judiciously. The main conclusive remarks drawn are as follows:

1. A theoretical model study of the turbo-viscoelstic pulsational mode instability in a strongly coupled multifluidic self-gravitating complex plasma fluid is constructed.

2. A detailed generalised dispersion relation (polynomial in nature) and its illustration on the fluctuations dynamics are numerically presented.

3. The turbo-viscoelstic (pulsational) instability shows both the propagatory and anomalous dispersive features in the cloud complex.

4. In the hydrodynamic regime, the dust-charge ratio (negatively-to-positively charged dust grains) acts as the destabiliser and the dust–mass ratio (negatively-to-positively charged dust grains) acts as the stabilising sources against the non-local gravitational collapse dynamics.

5. In the kinetic regime, the viscoelastic relaxation mode velocity of the positively (negatively) charged grains acts as a stabiliser (destabiliser).

6. The group dispersion of the pulsational instability interestingly exhibits a singular type of behaviour at a certain critical wave number on the Jeans scale length (\(K_{c} \approx 0.20)\).

7. Comparison of our results with the literature shows good agreement, thereby ensuring the reliability of the proposed bimodal analysis.

To sum up, we further concede that considering the effects of complex fluid turbulence via the nonlinear logatropic barotropic nonlinear law [13] in our presented investigation is physically not so justifiable. It is hereby suggested that a fully nonlinear spectral power-law treatment of both the wave kinetic energy and cloud material density [13] is indeed necessary. This important fluid aspect, however, is left now for our next investigations.

The presented analysis, despite some analytic simplifications in the basic fluid model set up without any loss of astrobasic generality, may be conveniently useful in understanding the physical insights responsible for the formation of complex astronomical environs and associated hydrowave instability phenomena of self-gravitational origin leading to wave-induced matter accretive–decretive processes and subsequent early phases of large-scale bounded structures via global cloud collapse in diversified astro-cosmo-plasmic circumstances.