1 Introduction

Bursting oscillations belong to the class of mixed-mode oscillations, which may occur in the slow–fast dynamical system [1]. This phenomenon is ubiquitous in physics [2], chemistry [3], biochemistry [4] and neuroscience [5,6,7]. The generation mechanism of bursting oscillations of slow–fast system has been understood thanks to the slow–fast analysis method introduced by Rinzel [8]. Subsequent to this pioneering work, Izhikevich [9] summarised the bifurcation mechanism of bursting oscillations and classified almost all the bursting oscillations in low-dimensional systems. Bursting oscillations may occur in a non-autonomous system with periodic external excitation under the condition that the external excitation has a low frequency. Such a system can be treated as a slow–fast system by regarding the whole excitation term as a slow-varying variable. In this case, a powerful tool, termed ‘transformed phase diagram’, is introduced to explain the dynamical mechanism of the bursting oscillations [10]. Up to now, most of the literatures on bursting oscillations are confined to smooth or piecewise smooth continuous dynamical systems (e.g. [11,12,13,14,15] and references therein).

A Filippov system is a piecewise discontinuous system. It usually has one or more discontinuity boundaries (switching manifolds) which may cause qualitative changes in a system’s dynamics, termed discontinuity-induced bifurcations or non-smooth bifurcations. They include boundary equilibrium bifurcations occurring when an equilibrium meets a switching manifold. They also include sliding bifurcations occurring when an attracting periodic orbit meets a switching manifold, thereby loses or gains a segment of sliding [16]. Bursting behaviours may occur when a Filippov system involves slow-varying and fast-varying variables. The existence of non-smooth bifurcations in the Filippov system may lead to complicated bursting patterns. Thus, investigating the bursting oscillations in the Filippov system and accounting for the dynamical mechanism have attracted many scholars’ attention [17, 18]. However, up to now, the effects of boundary homoclinic bifurcation, non-smooth fold limit cycle bifurcation and the sliding vector field on the bursting dynamics were rarely reported in the published papers we have read.

Chua’s circuit, which is a well-known generator of chaotic oscillations, has not only become one of the most common examples in research articles on nonlinear oscillation [19], but has also been used in secret communication [20] and voice encryption [21]. A very simple modification of a scheme can lead to substantial new results [22, 23].

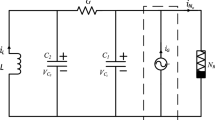
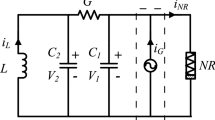
In this paper, we investigate the dynamical mechanism of bursting oscillations in three-dimensional Filippov system, focussing on the effects of boundary homoclinic bifurcation, non-smooth fold limit cycle bifurcation and the sliding vector field on the bursting dynamics. For this purpose, the typical Chua’s circuit is modified, which is shown in figure 1, where \(i_G\) is a periodically exciting current and NR is a non-linear resistor whose i–v characteristic curve is piecewise and cubic (see figure 2).

Fig. 1
figure 1

The modified Chua’s circuit.

Full size image
Fig. 2
figure 2

The i–v characteristic curve of the nonlinear resistor NR.

Full size image

2 Mathematical model and its bursting oscillations

The equations of the circuit are

$$\begin{aligned}&C_1\displaystyle \frac{\mathrm {d}V_1}{\mathrm {d}\tau }=G(V_2-V_1)-g(V_1)+I_G\,\text{ sin }(\omega \tau ),\nonumber \\&C_2\displaystyle \frac{\mathrm {d}V_2}{\mathrm {d}\tau }=G(V_1-V_2)+i_L, \nonumber \\&L\displaystyle \frac{\mathrm {d}i_L}{\mathrm {d}\tau }=-V_2, \end{aligned}$$
(1)

where

$$\begin{aligned} g(V_1)=\left\{ \begin{array}{l} -G_AV_1+G_BV_1^3+I_C, ~\text{ if }~V_1>0,\\ -G_AV_1+G_BV_1^3-I_C, ~\text{ if }~V_1<0, \end{array} \right. \end{aligned}$$
(2)

corresponding to figure 2, denotes the relationship between the current and voltage passing across NR, \(G_A\) and \(G_B\) are conductance and \(I_C\) is a direct current. We assume \(G\ne G_A\) in this paper. The system is governed by different differential equations when \(V_1>0\) or \(V_1<0\). Therefore, \(H(V_1,V_2,i_L)=V_1=0\) is a switching surface.

By applying the following changes of variables: \(V_1=({I_C}/{G})x,V_2=({I_C}/{G})y, i_L=I_Cz\) and \(\tau =({C_2}/{G})t\), (1) can be normalised and rewritten in the dimensionless form

$$\begin{aligned} \dot{\mathbf{x}}=\left\{ \begin{array}{l} f^+(\mathbf{x},w)=(f^+_1,f^+_2,f^+_3), \quad \text{ if }~ x>0,\\ f^-(\mathbf{x},w)=(f^-_1,f^-_2,f^-_3), \quad \text{ if }~ x<0, \end{array} \right. \end{aligned}$$
(3)

where

$$\begin{aligned} f^+(\mathbf{x},w)= & {} (\alpha (y+(a-1)x-bx^3-1)\nonumber \\&+w,x -y+z,-\beta y), \end{aligned}$$
(4)
$$\begin{aligned} f^-(\mathbf{x},w)= & {} (\alpha (y+(a-1)x-bx^3+1)\nonumber \\&+w,x-y+z,-\beta y), \end{aligned}$$
(5)

with

$$\begin{aligned} \mathbf{x}= & {} (x,y,z)\in R^3, \quad \alpha =\frac{C_2}{C_1},\quad \beta =\frac{C_2}{LG^2}, \quad \\ a= & {} \frac{G_A}{G},\quad b=\frac{G_B{{I}_{C}^{2}}}{G^3},\quad \gamma =\frac{C_2I_G}{C_1I_C},\quad \Omega =\frac{\omega C_2}{G} \end{aligned}$$

and

$$\begin{aligned} w=\gamma \sin (\Omega t), \end{aligned}$$

satisfying the conditions \(\alpha>0, \beta>0, \gamma>0, \omega>0, a>0, b>0\) and \(a\ne 1\).

The switching surface is redefined as \(h(x,y,z)=x=0\), and the switching manifold is written as \(\Sigma =\{\mathbf{x}|x=0\}\). \(\Sigma \) divides the phase space into two subregions, denoted by \(\Sigma _\pm \) with \(\Sigma _+=\{\mathbf{x}\in R^3|x>0\}\) and \(\Sigma _-=\{\mathbf{x}\in R^3|x<0\}\), respectively. Obviously, the dynamics of the system in \(\Sigma _{\pm }\) are governed by \(\dot{\mathbf{x}}=f^{\pm }(\mathbf{x},w)\), respectively.

If \(0<\Omega \ll 1\), there may exist an order gap between the excitation frequency \(\Omega \) and the natural one \(\Omega _N\), implying that system (3) is a slow–fast system and \(\Omega \) may satisfy \(0<\Omega \ll \Omega _N\), in which \(w=\gamma \sin {(\Omega t)}\) is the slow subsystem. In this case, during an arbitrary period \({2\pi }/{\Omega _N}\), i.e., \(t\in [t_0,t_0+({2\pi }/{\Omega _N})]\), the excitation term w varies between \(w_0=\gamma \, \text{ sin }(\Omega t_0)\) and \(w_N=\gamma \,\text{ sin }(\Omega t_0+2\pi ({\Omega }/{\Omega _N}))\), implying \(w_0 \approx w_N\). As state variables may oscillate mainly according to the natural frequency \(\Omega _N\), the analysis above means that w keeps almost a constant value during any arbitrary oscillating period [24]. Therefore, w can be regarded as a bifurcation parameter to explore the bifurcation mechanism of bursting oscillations.

When the parameters are fixed at \(a=0.95,~b=0.1,~\alpha =1.82,~\beta =0.23\) and \(\Omega =0.005\), two types of new bursting oscillations can be observed with the variation of the excitation amplitude. Here, the initial values of the state variables are set at \(x_0=0.1,~y_0=0.1\) and \(z_0=0.1\).

Numerical simulation shows that bursting oscillations do not occur if \(\gamma \) is less than some critical value \(\gamma _0\). If \(\gamma >\gamma _0\), bursting oscillations appear. For a typical case, when \(\gamma =3.0\), the bursting oscillations are shown in figures 3–6.

Fig. 3
figure 3

Three-dimensional phase portrait of the bursting oscillations for \(\gamma =3.0\), where the blue segments are in the regions \(\Sigma _{\pm }\) and the red segments are on the switching manifold \(\Sigma \).

Full size image
Fig. 4
figure 4

Phase portrait of the bursting oscillations on the (z, x) plane for \(\gamma =3.0\).

Full size image
Fig. 5
figure 5

Time history of the bursting oscillations on the (t, x) plane for \(\gamma =3.0\).

Full size image
Fig. 6
figure 6

Locally enlarged parts of figure 5.

Full size image

When \(\gamma \) is larger than \(\gamma _0\) and less than another critical value \(\gamma _1\), the system keeps similar bursting patterns as above. If \(\gamma >\gamma _1\), new bifurcations involve the bursting attractor, forming new bursting oscillations (see the representative ones in figure 7–10 for \(\gamma =3.8\).

Fig. 7
figure 7

Three-dimensional phase portrait of the bursting oscillations for \(\gamma =3.8\), where the blue segments are in the regions \(\Sigma _{\pm }\) and the red segments are on the switching manifold \(\Sigma \).

Full size image
Fig. 8
figure 8

Phase portrait of the bursting oscillations on the (z, x) plane for \(\gamma =3.8\).

Full size image
Fig. 9
figure 9

Time history of the bursting oscillations on the (t, x) plane for \(\gamma =3.8\).

Full size image
Fig. 10
figure 10

Locally enlarged parts of figure 9.

Full size image

Remark 1

According to §3.4, the critical value \(\gamma _0=\alpha =1.82\), and the critical value \(\gamma _1\approx 3.254\).

In order to explore the mechanism of the bursting oscillations, in the following section, we turn to the bifurcation analysis of the non-smooth vector field.

3 Bifurcation analysis

3.1 Pseudoequilibrium analysis and sliding solution on the switching manifold

The switching manifold \(\Sigma \) partitions the phase space into two subregions \(\Sigma _\pm \). The directional Lie derivatives

$$\begin{aligned} L_{f^{\pm }}h=\langle \nabla h,f^{\pm }(\mathbf{x},w)\rangle =f_1^{\pm } \end{aligned}$$
(6)

determine the kind of contact of smooth vectors \(f^{\pm }(\mathbf{x},w)\) with \(\Sigma \), where \(h=x\), \(\nabla h\) and \(\langle \cdot ,\cdot \rangle \) denote the gradient of smooth function h and the canonical inner product, respectively [25].

If \(L_{f^{\pm }}h=0\), we get two sets of tangential singularities \(S^{\pm }=\{\mathbf{x}\in \Sigma ~|f_1^{\pm }=0\}=\{\mathbf{x}\in \Sigma ~|\alpha (y\mp 1)+w=0\}\), which divide the switching manifold \(\Sigma \) into three subregions, denoted by \(\Sigma ^{c\pm }\) and \(\Sigma ^{s}\) with \(\Sigma ^{c+}=\{\mathbf{x}\in \Sigma |f_1^+>0,f_1^->0\}\), \(\Sigma ^{c-}=\{\mathbf{x}\in \Sigma |f_1^+<0,f_1^-<0\}\) and \(\Sigma ^{s}=\{\mathbf{x}\in \Sigma |f_1^+<0,f_1^->0\}\), respectively. \(\Sigma ^{c\pm }\) and \(\Sigma ^{s}\) are termed crossing regions and sliding region, respectively.

\(S^\pm \) are a pair of parallel lines with respect to w and y on \(\Sigma \) if the parameter \(\alpha \) is fixed, and the distance between \(S^+\) and \(S^-\) is 2. In other words, the shape of the sliding region \(\Sigma ^{s}\) remains unchanged during the variation of the parameter w, while their position changes on \(\Sigma \). A diagrammatic sketch of the three subregions and two sets of tangential singularities are shown in figure11.

Fig. 11
figure 11

Diagrammatic sketch of the three subregions and the two sets of tangent singularities for \(\alpha =1.82\).

Full size image

When \(\mathbf{x}\in \Sigma ^s\), following the Filippov convention (see [26]), the sliding vector field associated with \(f^+(\mathbf{x},w)\) and \(f^-(\mathbf{x},w)\) is the vector field \({\hat{f}}^s(\mathbf{x})\) which is tangent to \(\Sigma \) and expressed in coordinates as

$$\begin{aligned} \begin{array}{ll} {\hat{f}}^s(\mathbf{x})&{}=(1-\delta )f^+(\mathbf{x},w)+\delta f^-(\mathbf{x},w),\\ \end{array} \end{aligned}$$
(7)

where

$$\begin{aligned} \delta =\frac{L_{f^+}h}{L_{f^+}h-L_{f^-}h}. \end{aligned}$$

A straightforward calculation gives

$$\begin{aligned} \hat{f^s}(\mathbf{x})=(0,-y+z,-\beta y). \end{aligned}$$
(8)

Note that, in the region \(\Sigma ^s\), system \(\dot{\mathbf{x}}=\hat{f^s}(\mathbf{x})\) is topologically equivalent [25] to

$$\begin{aligned} {\dot{x}}^s={f^s}(y,z)=(-y+z,-\beta y), \end{aligned}$$
(9)

where \(x^s=(y,z)\in \Sigma \). We can take advantage of the invariance of \(\Sigma \) under the flow determined by \(f^s\) and reduce the dimension of the problem by one.

When \( \hat{f^s}(\mathbf{x})=0\), we get the pseudoequilibrium of (3) at \(E_s=(0,0,0)\). The stability of \(E_s\) is equivalent to that of \(E_0=(0,0)\) which is the equilibrium of (9). The stability of \(E_0\) can be determined by the eigenvalues of the associated Jacobian matrix \(({\mathrm {d}f^s(y,z)}/{\mathrm {d}x^s})|_{E_0}\), which are

$$\begin{aligned} \lambda _{1,2}=\frac{-1\pm \sqrt{1-4\beta }}{2}. \end{aligned}$$

This means that \(E_s\) is a stable pseudonode or a stable pseudofocus, and so there is no bifurcation associated with the pseudoequilibrium of the sliding vector field.

The analytical solution of (9) can be written as

$$\begin{aligned}&y=y(t)=c_1\,\exp {(\lambda _{1}t)}+c_2\,\exp {(\lambda _{2}t)}, \nonumber \\&z=z(t)=({\lambda _{1}}/{\beta }) c_1\,\exp {(\lambda _{2}t)}+({\lambda _{2}}/{\beta })c_2\,\exp {(\lambda _{1}t)},\nonumber \\ \end{aligned}$$
(10)

for \(\beta \ne \dfrac{1}{4}\) or

$$\begin{aligned}&y=y(t)=(c_1+c_2t)\exp {(-\frac{1}{2}t)},\nonumber \\&z=z(t)=(-2c_1t-c_2t^2)\exp {(-\frac{1}{2}t)}, \end{aligned}$$
(11)

for \(\beta =\frac{1}{4}\), where \(c_1\) and \(c_2\) are two constants which are determined by the initial conditions of (9). Equation (10) or (11) can describe the route from the point, which is the intersection of the trajectory and \(\Sigma \), to the stable pseudonode or stable pseudofocus.

3.2 Equilibrium analysis of the fast subsystem

Now we turn to the bifurcation analysis of the fast subsystems by regarding the whole excitation term \(\omega =\gamma \,\sin (\Omega t)\) as a bifurcation parameter.

The admissible equilibria of the subsystems \({\dot{x}}=f^{\pm }(\mathbf{x},w)\) can be computed at \(E_{\pm }=(X_{\pm }, 0, -X_{\pm })\), where sign(\(X_{\pm })=\pm 1\) and \(X_{\pm }\) satisfy

$$\begin{aligned} \alpha ((a-1)X_{\pm }-bX_{\pm }^3\mp 1)+w=0, \end{aligned}$$
(12)

respectively. The stability of the equilibria \(E_\pm \) can be determined by the associated characteristic equations, written in the form

$$\begin{aligned} \lambda ^3+Q_{1\pm }\lambda ^2+Q_{2\pm }\lambda +Q_{3\pm }=0, \end{aligned}$$
(13)

respectively, where \(Q_{1\pm }=3\alpha bX_{\pm }^2-a\alpha +\alpha +1\), \(Q_{2\pm }=3\alpha bX_{\pm }^2-a\alpha +\beta \), \(Q_{3\pm }=3\alpha b\beta X_{\pm }^2-a\alpha \beta +\alpha \beta \). Fold bifurcation of the equilibrium point may be observed if

$$\begin{aligned} 3\alpha b\beta X_{\pm }^2-a\alpha \beta +\alpha \beta =0, \end{aligned}$$
(14)

and \(Q_{1\pm }>0, Q_{1\pm }Q_{2\pm }-Q_{3\pm }>0\) while Hopf bifurcation may occur if

$$\begin{aligned} Q_{1\pm }Q_{2\pm }-Q_{3\pm }=0, \end{aligned}$$
(15)

and \(Q_{1\pm }>0, Q_{3\pm }>0\). These show that a pair of pure imaginary eigenvalues may be observed, leading to possible periodic movement.

3.3 Boundary equilibrium bifurcation

Equation (12) shows that if \(w=\pm \alpha \), the admissible equilibria \(E_\pm \) collide with the pseudoequilibrium \(E_s\) at the point \(E_{s\pm }(0,0,0)\) which are located on \(S^{\pm }\). Further calculation reveals that, \(f^{\pm }(E_{s\pm },\pm \alpha )=0\), but \(f^{\mp }(E_{s\pm },\pm \alpha )\ne 0\); \(h(E_{s\pm },\pm \alpha )=0\); det(\(f^{\pm }_\mathbf{x}(E_{s\pm },\pm \alpha ))=\alpha (a-1)\beta \ne 0\), i.e., \(f^{\pm }_\mathbf{x}(E_{s\pm },\pm \alpha )\) is invertible; \(h_w(E_{s\pm },\pm \alpha )-h_\mathbf{x}(E_{s\pm },\pm \alpha )\) \([(f^{\pm }_\mathbf{x})^{-1}f^{\pm }_w](E_{s\pm },\pm \alpha )=-({1}/{\alpha (a-1)})\ne 0\). Therefore, by following [27], system (3) undergoes boundary equilibrium bifurcations at \(w=\pm \alpha \), with respect to fields \(f^+\) and \(f^-\), respectively. The type of the boundary equilibrium bifurcation will be discussed in §3.4.

3.4 Equilibrium branches and related bifurcations

Now fix the parameters at \(a=0.95,~b=0.1,~\alpha =1.82,~\beta =0.23\). We explore the bifurcations of equilibrium and limit cycle by regarding w as a bifurcation parameter. One-parameter bifurcation diagram of (3) is computed numerically and projected on the (w, x) plane (see figure 12). The equilibrium branches as well as the bifurcation points with respect to w, y, x are plotted in figure 13. Meanwhile, the stability of the equilibria, the bifurcation points and the labels in the bifurcation diagram are summarised in tables 1 and 2.

Fig. 12
figure 12

One-parameter bifurcation diagram with respect to w on the (w, x) plane.

Full size image
Fig. 13
figure 13

Equilibrium branches and the bifurcation points with respect to w, y and x, in which \(BH_{\pm }\in S^{\pm }\).

Full size image

In figure 12, a branch of admissible equilibria of subsystem \(\dot{\mathbf{x}}=f^+(\mathbf{x},w)\), i.e., \(EB_{2+}\) turns into a branch of pseudonodes, i.e., PEB on \(\Sigma \) with the decrease of w, resulting in a persistence bifurcation at \(BH_+\) corresponding to \(w=1.82\). When \(w\in (1.82, 3.254)\), there exist stable limit cycles \(LC_{1+}\) with sliding segments, seeing the representative limit cycle for \(w=2.8\) in figures 14 and 15. The periods of the limit cycles \(LC_{1+}\) drastically increase as w approaches 1.82. When \(w=1.82\), an admissible saddle collides with the pseudonode at \(P_2\), resulting in an orbit with infinite period (see figures 16 and 17). In this case, the boundary equilibrium bifurcation can be termed boundary homoclinic bifurcation. Because of the symmetry, another boundary homoclinic bifurcation occurs at \(BH_-\) corresponding to \(w=-1.82\). Depending on the change of direction of w, the boundary homoclinic bifurcations can explain either the appearance or the disappearance of the limit cycle attractors \(LC_{1\pm }\).

Table 1 Bifurcations, labels and critical values.
Full size table
Table 2 Stability of the equilibria.
Full size table
Fig. 14
figure 14

Representative stable limit cycle for \(w=2.8\), where PN and Sa denote the pseudonode and saddle, respectively.

Full size image
Fig. 15
figure 15

Time history of the limit cycle on the (t, x) plane for \(w=2.8\).

Full size image
Fig. 16
figure 16

The boundary homoclinic orbit for \(w=1.82\).

Full size image
Fig. 17
figure 17

Time history of the boundary homoclinic orbit for \(w=1.82\).

Full size image
Fig. 18
figure 18

Rest and spiking areas: \(A_{r0}\) corresponding to a pseudoequilibrium attractor and \(A_{r\pm }\) corresponding to two equilibrium attractors are the rest areas; \(A_{s\pm }\) corresponding to two limit cycle attractors are the spiking areas.

Full size image

Subcritical Hopf bifurcations at \(HB_{\pm }\), corresponding to \(w=\pm 2.92966\), lead to the appearance of unstable limit cycles, denoted by \(LC_{2\pm }\) in figure 12. \(LC_{2\pm }\) are approached by the stable limit cycles \(LC_{1\pm }\) as w approaches \(LPC_{\pm }\) corresponding to \(w=\pm 3.254\). \(LC_{1\pm }\) and \(LC_{2\pm }\) coalesce and annihilate each other at \(w=\pm 3.254\), resulting in the occurrence of fold limit cycle bifurcations. Notice that limit cycles \(LC_{1\pm }\) involve sliding segments located on \(\Sigma \) (e.g., see figure 14), which means such fold limit cycle bifurcations are somewhat different from that of conventional ones, and we call them non-smooth fold limit cycle bifurcations.

4 Dynamical mechanism of bursting oscillations

In what follows, we study the dynamical mechanism of the bursting oscillations based on the bifurcation analysis in §3. In fact, the range of w can be divided into five areas by \(w=\pm \gamma _0\) and \(w=\pm \gamma _1\), i.e., rest areas \(A_{r-}=\{w|w<-\gamma _1\}\), \(A_{r0}=\{w|-\gamma _0<w<\gamma _0\}\) and \(A_{r+}=\{w|w>\gamma _1\}\), spiking areas \(A_{s-}=\{w|-\gamma _1<w<-\gamma _0\}\) and \(A_{s+}=\{w|\gamma _0<w<\gamma _1\}\) (see figure 18).

Bursting oscillations in figure 5 are formed as the external excitation slowly and periodically visits the rest area \(A_{r0}\) corresponding to a stable pseudoequilibrium attractor and the spiking areas \(A_{s\pm }\) corresponding to two limit cycle attractors, while the bursting oscillations in figure 9 are formed as the external excitation slowly and periodically visits the rest areas \(A_{r0}, A_{r\pm }\) and the spiking areas \(A_{s\pm }\), where \(A_{r\pm }\) correspond to two stable equilibrium attractors (see black and blue curves in figure 18).

We have revealed the rest and spiking areas in the range of the bifurcation parameter. Now we present the dynamical mechanism of the bursting oscillations for the two typical cases, \(\gamma =3.0\) and 3.8.

4.1 ‘Boundary homoclinic/boundary homoclinic’ bursting

To get a clear idea of the dynamical mechanism of the bursting oscillations shown in figure 5, the transformed phase diagram of the bursting oscillations and the bifurcation diagram are overlapped with each other, which are shown in figures 19–23.

Fig. 19
figure 19

The overlap of the transformed phase diagram and the bifurcation diagram on the (w, x) plane for \(\gamma =3.0.\)

Full size image
Fig. 20
figure 20

Locally enlarged part of figure 19.

Full size image
Fig. 21
figure 21

Locally enlarged part one of figure 20.

Full size image
Fig. 22
figure 22

Locally enlarged part two of figure 20.

Full size image
Fig. 23
figure 23

The transformed phase diagram and the equilibrium branch with respect to w, y and x for \(\gamma =3.0\).

Full size image

Assume that the trajectory starts at the point \(BH_+\) with \(w=1.82\), at which a boundary homoclinic bifurcation occurs (see figure 19). The system stays at the neighbourhood of the stable pseudonode of the sliding vector field in rest state until the slow-varying parameter w decreases to \(w=-1.82\), corresponding to the point \(BH_-\). Another boundary homoclinic bifurcation occurring at \(BH_-\) results in the disappearance of the rest state (see figure 20). Driven by the excitation term w, the trajectory jumps to the spiking attractor \(LC_{1-}\) and oscillates along \(LC_{1-}\) until it arrives at the minimum value of w with \(w=-3.0\) (see figures 21–22). With the increase of the slow-varying variable w, the trajectory moves backward along \(LC_-\) until it arrives at the neighbourhood of the point \(BH_-\) (see figure 21). Now half period of the bursting oscillations is finished. Further increase of w leads to the other half period of the symmetric movement, which is omitted here for simplicity.

From the above analysis, one may find that, boundary homoclinic bifurcations lead to the transitions between the rest states and the spiking states. Therefore, this type of bursting oscillations can be called ‘boundary homoclinic/boundary homoclinic’ bursting.

4.2 ‘Boundary homoclinic/non-smooth fold cycle/sub-Hopf/boundary homoclinic’ bursting

When \(\gamma =3.8\), the subcritical Hopf and non-smooth fold limit cycle bifurcations involve the bursting attractor. The transformed phase diagram and the bifurcation diagram are overlapped in figure 24.

Fig. 24
figure 24

The overlap of the transformed phase diagram and the bifurcation diagram on the (w, x) plane for \(\gamma =3.8\).

Full size image
Fig. 25
figure 25

Locally enlarged part one of figure 24.

Full size image
Fig. 26
figure 26

Locally enlarged part two of figure 24.

Full size image
Fig. 27
figure 27

Locally enlarged part three of figure 24.

Full size image
Fig. 28
figure 28

The transformed phase diagram and the equilibrium branch with respect to w, y and x for \(\gamma =3.8\).

Full size image
Fig. 29
figure 29

Numerical results of time interval between two adjacent spikes of bursting dynamics and the duration of the system staying at the stable pseudonode corresponding to figure 5 for the external excitation frequency \(\omega =0.0025, 0.005, 0.01\), respectively.

Full size image

Assume that the trajectory starts at point \(P_+\) corresponding to the maximum value of the slow-varying variable w with \(w=3.8\) (see figure 24). With the decrease of w, the trajectory moves along the stable focus-type equilibrium branch \(EB_{1+}\) until it arrives at the neighbourhood of the point \(HB_+\), at which a subcritical Hopf bifurcation occurs (see figure 25). The instability of the saddle points on the equilibrium branch \(EB_{2+}\) causes the trajectory to leave \(EB_{2+}\) gradually. Then the trajectory is captured by the basin of attraction of the limit cycle \(LC_{1+}\), forming a spiking state with only one peak (see figure 26). When the trajectory arrives at the neighbourhood of the point \(BH_+\) corresponding to \(w=1.82\), a boundary homoclinic bifurcation occurs. The spiking state disappears and the system resides at the stable pseudonode of the sliding vector field in rest state until \(w=-1.82\), corresponding to the point \(BH_-\), at which another boundary homoclimic bifurcation occurs (see figure 24). The trajectory jumps to the limitcycle \(LC_{1-}\) and oscillates along \(LC_{1-}\), until it arrives at the dash line \(LPC_-\), corresponding to \(w=-3.254\), at which a fold limit cycle bifurcation occurs (see figure 27). Attracted by the stable foci, the trajectory settles down to \(EB_{1-}\) abruptly and then moves along \(EB_{1-}\) until it arrives at point \(P_-\), corresponding to the minimum value of w with \(w=-3.8\) (see figure 27). Now half period of the bursting oscillations is finished. Further increase of w leads to the other half period of the symmetric movement, which is omitted here. This type of bursting oscillations can be called ‘boundary homoclinic/non-smooth fold cycle/sub-Hopf/boundary homoclinic’ bursting.

Remark 2

Once the trajectory arrives at the discontinuity boundary \(\Sigma \), it will be governed by (10) and moves along the sliding region \(\Sigma ^s\), forming sliding solution of system (3) (see the red segments in figures 3 and 7). The sliding solution terminates at one of the sliding boundaries \(S^{\pm }\) or at the neighbourhood of \(E_0\), which is determined by the initial point where the trajectory intersects with \(\Sigma ^s\) (see figures 23 and 28).

5 Effects of excitation amplitude and frequency on bursting oscillations

We have investigated the dynamical mechanism of bursting oscillations. In this section, we focus on the effects of external excitation amplitude and frequency on such bursting oscillations.

First, the effect of external excitation amplitude on bursting oscillations is considered. As described earlier, bursting oscillations are formed because external excitation term passes through boundary homoclinic bifurcation values \(w=\gamma _0\) periodically. So, when the excitation amplitude \(\gamma \) satisfies \(\gamma <\gamma _0\), bursting oscillations do not occur because the external excitation term is not able to pass through the boundary homoclinic bifurcation. If \(\gamma >\gamma _0\), bursting oscillations may be formed. When \(\gamma \) is between \(\gamma _0\) and \(\gamma _1\), the dynamical mechanism of the bursting oscillations are similar to that in figures 3–5. If \(\gamma >\gamma _1\), the dynamical mechanism of the bursting oscillations are similar to that in figures 7–9.

Secondly, the effect of external excitation frequency on bursting oscillations is considered. As a kind of coupling oscillator, the bursting dynamics of the whole slow–fast coupling system has the frequency of \(\Omega \). The time intervals between two symmetric adjacent spikes of bursting oscillations can be calculated, which is \(\Delta T={\pi }/{\Omega }\). Furthermore, the duration of the system staying at the stable pseudonode is concluded at \(\Delta T_1=({2}/{\Omega })\arcsin ({\alpha }/{\gamma })\). When \(\Omega =0.0025,0.005\) and 0.01, we have \(\Delta T=400\pi , 200\pi \) and \(100\pi \), respectively. Take the waveforms in figure 5 as an example, when \(\Omega =0.0025,0.005\) and 0.01 respectively, the corresponding time intervals \(\Delta T_1\) and \(\Delta T\) are measured and shown in figure 29, where the numerical results agree well with the analytical ones.

6 Conclusion

Because of non-smoothness, a Chua’s circuit of Filippov-type may exhibit bursting oscillations with new patterns under certain external excitation conditions. Uncovering the essence of the bursting oscillations is an important issue in non-smooth bursting dynamics. We first consider the external excitation term as a bifurcation parameter and study its influence on the generalised autonomous system, and at the same time, we explore the sliding solution of the Filippov system and pseudoequilibrium bifurcation of the sliding vector field on the switching manifold. Then employ the transformed phase diagram to account for the bursting oscillations. Boundary homoclinic bifurcation, non-smooth fold limit cycle bifurcation and subcritical Hopf bifurcation may result in the system’s switching between different attractors, forming complicated bursting oscillations, which shows that the transitions between rest states and spiking states may be caused by not only the conventional bifurcations but also the non-smooth bifurcations. Here, we would like to suggest that the dynamical behaviours of the system on the switching manifold should be considered, as the sliding vector field on the switching manifold may influence the bursting attractor of a Filippov systems. Our research enriches the non-smooth dynamics of the bursting oscillations in the Filippov system.