Novel bursting patterns and the bifurcation mechanism in a piecewise smooth Chua’s circuit with two scales

Abstract

The aim of this paper is to investigate the influence of the coupling of two scales on the dynamics of a piecewise smooth dynamical system. A relatively simple model with two switching boundaries is taken as an example by introducing a nonlinear piecewise smooth resistor and a harmonically changed electric source into a typical Chua’s circuit. Taking suitable values of the parameters, four different types of bursting oscillations are observed corresponding to different values of the exciting amplitude. Regarding the periodic excitation as a slow-varying parameter, equilibrium branches of the fast subsystem as well as the related bifurcations, such as fold bifurcation, Hopf bifurcation, period doubling bifurcation, nonsmooth Hopf bifurcation and nonsmooth fold limit cycle bifurcation, are explored with theoretical and numerical methods. With the help of the overlap of the transformed phase portrait and the equilibrium branches, the mechanism of the bursting oscillations can be analyzed in detail. It is found that for relatively small exciting amplitude, since the trajectory is governed by a smooth subsystem, only conventional bifurcations take place, leading to the transitions between the spiking states and quiescent states. However, with an increase of the exciting amplitude so that the trajectory passes across the switching boundaries, nonsmooth bifurcations occurring at the boundaries may involve the structures of attractors, leading to complicated bursting oscillations. Further increasing the exciting amplitude, the number of the spiking states decreases although more bifurcations take place, which can be explained by the delay effect of bifurcation.

1 Introduction

Multi-scale coupling systems, charactered by the significant magnitude differences between change rates of state variables, have striking advantage to reveal the nonlinearity essence of many complex phenomena. Meanwhile, they have been widely used as models in various fields of science and engineering, such as chemical reactions [1, 2], electrical activity of neurons [3,4,5], mechanical systems [6,7,8], electrical circuits [9,10,11], population dynamics [12, 13]. Compared with general nonlinear systems, systems with multiple scales may display more complex dynamical behaviors, such as bursting oscillations [14], mixed-mode oscillations [15] and canard explosion phenomena [16]. Due to lack of valid analytical method, most of the early results related to those systems are obtained based on the approximated approaches as well as the numerical simulations [17, 18]. Fortunately, as the slow-fast analysis method first proposed by Rinzel [19] was introduced, researchers turned to the triggering mechanism of the dynamics under multiple scales. Generally, the slow-fast systems are presented in two forms during practical applications, i.e., the autonomous one with state variables of different time scale and the non-autonomous one containing slow excitations [20]. A typical autonomous slow-fast dynamical system with two scales can be divided into two subsystems, i.e., the fast subsystems(FS) and the slow subsystems(SS), expressed in the standard form [21]

$$\begin{aligned} \begin{aligned} \dot{{\mathbf {x}}}&={\mathbf {f}}({\mathbf {x}},{\mathbf {y}},\varvec{\mu }),\ \ \ \qquad (\text {Fast Subsystem}) \\ \dot{{\mathbf {y}}}&=\epsilon {\mathbf {g}}({\mathbf {x}},{\mathbf {y}},\varvec{\mu }),\qquad (\text {Slow Subsystem}) \end{aligned} \end{aligned}$$

(1)

where ${\mathbf {x}} \in {\mathbb {R}}^M$, ${\mathbf {y}} \in {\mathbb {R}}^N$, $\varvec{\mu } \in {\mathbb {R}}^K$, while $0< \epsilon \ll 1$ describes the ratio between the fast and slow scales. The state variables ${\mathbf {y}}$ are treated as slow-varying parameters so that the equilibrium branches as well as the bifurcations of the fast subsystem can be derived, which can be used to reveal the mechanism of the dynamics [22]. This method has been manifested to be a powerful tool in the study of bursting dynamics, and a mass of research focusing on bursting oscillations as well as the bifurcation mechanisms have been reported [3, 23,24,25]. For the non-autonomous systems, such as periodic exciting systems with an order gap between the exciting frequency and the natural frequency, i.e., two scales in frequency domain, bursting oscillations can also be observed, while the bursting mechanism can’t be obtained directly by the traditional slow-fast analysis method. In recent years, Bi et al. [7, 26,27,28] presented a modified slow-fast method with the conceptions of generalized autonomous system and transformed phase portrait, which have been demonstrated to be an effective tool to analyze the generation mechanism of bursting oscillations in dynamical systems with a single slow excitation. The one periodic excitation dynamical systems can be expressed in the form

$$\begin{aligned} \dot{{\mathbf {x}}}={\mathbf {f}}[{\mathbf {x}},\varvec{\mu },Acos(\omega t)], \end{aligned}$$

(2)

where A and $\omega$ represent the amplitude and the frequency of the excitation, respectively. When the exciting frequency is far less than the natural frequency, system (2) can be converted to the form

$$\begin{aligned} \begin{aligned} \dot{{\mathbf {x}}}&={\mathbf {f}}({\mathbf {x}},\varvec{\mu },w),\ \qquad (\text {Fast Subsystem}) \\ w&=Acos(\omega t),\qquad (\text {Slow Subsystem}) \end{aligned} \end{aligned}$$

(3)

in which the whole exciting term w is considered as a generalized slow-varying state variable and the fast subsystem can be called the generalized autonomous system. Subsequently, one may obtain the equilibrium branches and the related bifurcations of the generalized fast subsystem, which can be used to investigate the spiking and quiescent states as well as the switching mechanism between the two states of the bursting oscillations.

On the other hand, the study of nonsmooth dynamical systems has attracted a rapidly increasing interest in the last decades. In fact, different types of nonsmooth factors may be involved in many science and engineering problems. For example, switches in electrical circuits and traffic management [29, 30], dry friction and impact in mechanical systems [31, 32], threshold strategy in ecological economic dynamics [33], etc. Besides, due to the nonsmooth property, the systems may display many special dynamical behaviors, such as grazing, sliding and chattering [34, 35], which can’t be investigated through traditional nonlinear theory of smooth systems. Generally, nonsmooth dynamical systems can be distinguished into three types, i.e., nonsmooth continuous systems, Filippov systems, and systems which expose discontinuities in time of the state [36]. A nonsmooth system usually has one or more switching boundaries, at which nonsmooth bifurcations may take place, leading to qualitative changes on the dynamics of the system [37]. Bursting behaviors may occur when a nonsmooth dynamical system involves two scales. Many patterns of bursting oscillations as well as different types of nonsmooth bifurcations have been obtained, such as symmetric focus/focus-fold/fold bursting attractors with nonsmooth fold bifurcations in a piecewise linear system [38], periodic movements and quasi-periodic oscillations with generalized Hopf bifurcation in switched dynamical systems [39], periodic symmetric Hopf/Hopf-fold-sliding and fold/fold-fold-sliding bursting oscillations with sliding bifurcations in Filippov systems [40], asymmetric and symmetric nonsmooth bursting oscillations with nonsmooth Hopf bifurcations in a piecewise smooth system [41]. Recently, Wang et al. [42] have investigated the C-bifurcation as well as its effects on the bursting oscillations. Though much work has been done, it remains a challenge to study the generation mechanism of bursting oscillations in nonsmooth systems with two scales. A case that the transition behaviors between the spiking and quiescent states are triggered by the nonsmooth fold limit cycle bifurcation, at which a nonsmooth limit cycle and a smooth limit cycle coalesce and annihilate each other on the switching boundary, has barely been reported and needs to be further explored.

In this paper, we try to investigate the bursting oscillations as well as the mechanism in a piecewise smooth Chua’s circuit with a periodically slow-varying external excitation, focusing on the effects of the nonsmooth Hopf bifurcation and nonsmooth fold limit cycle bifurcation on bursting dynamics. In addition, we will show that slow-varying external excitation and the delay effect of bifurcation play an important role in the evolution processes of the system. The rest of this paper is organized as follows. In Section 2, a piecewise smooth mathematical model with two scales in frequency domain is established based on a typical Chua’s circuit. In Section 3, the stability of the generalized autonomous fast subsystem is derived and different types of equilibrium branches as well as the bifurcations are obtained with theoretical and numerical methods. In Section 4, the evolution of the bursting oscillations and the related bifurcation mechanism corresponding to different excitation amplitudes are presented in detail. Finally, the conclusion of the research is summarized.

2 Mathematical model

Fig. 1

A modified Chua’s circuit with a piecewise nonlinear resistor and a periodic excitation

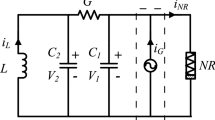
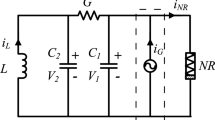
The Chua’s circuit, presented by Chua et al. [43] in 1986, has become one of the most simplest models exhibiting abundant nonlinear dynamic phenomena such as bifurcations and chaos [44, 45]. When a periodically slowly varying electric current source is applied on the circuit, implying an order gap exists between the exciting frequency and the natural frequency, bursting oscillations can be observed [26]. To reveal the influence of nonsmoothness on the dynamics with two scales, a modified Chua’s circuit is established by introducing a nonlinear resistor $N_R$ with piecewise smooth characteristics as well as a periodically changed electrical current source into the typical Chua’s circuit, shown in Fig. 1, and the mathematical model can be given by the following set of equations

$$\begin{aligned} \frac{dv_{C_1}}{d\tau }&=\frac{1}{C_1}[G(v_{C_2}-v_{C_1})-g(v_{C_1})+I_{G} cos(\omega \tau )],\nonumber \\ \frac{dv_{C_2}}{d\tau }&=\frac{1}{C_2}[G(v_{C_1}-v_{C_2})+i_{L}],\nonumber \\ \frac{di_L}{d\tau }&=-\frac{1}{L} v_{C_2}, \end{aligned}$$

(4)

where $G=\frac{1}{R}$, and $g(v_{C_1})$ denotes the relationship between the current and voltage passing through the nonlinear resistor $N_R$, described by

$$\begin{aligned} g(v_{C_1})= {\left\{ \begin{array}{ll} K_1 v_{C_1} \tanh (K_2 v_{C_1})+K_3 v_{C_1}+K_0,&{} \\ \quad \text {if } v_{C_1} > V_0,\\ {A_1}v_{C_1}^3+{B_1}v_{C_1},&{} \\ \quad \text {if } |v_{C_1}|\le V_0,\\ -K_1 v_{C_1} \tanh (K_2 v_{C_1})+K_3 v_{C_1}-K_0,&{} \\ \quad \text {if } v_{C_1}< -V_0, \end{array}\right. } \end{aligned}$$

(5)

with $K_0={A_1}V_{0}^3+({B_1}-K_3)V_0-K_1 V_{0} \tanh (K_2 V_{0})$. After the rescaling, $v_{C_1}= \frac{I_C}{G}x$, $v_{C_2}= \frac{I_C}{G}y$, $i_L= I_Cz$, $\tau = \frac{C_2}{G}t$, where $I_C$ is a variable direct current constant, system (4) is transformed into the following simpler dimensionless form

$$\begin{aligned} \frac{dx}{dt}&=\alpha (y-x-f(x))+w,\nonumber \\ \frac{dy}{dt}&=x-y+z,\nonumber \\ \frac{dz}{dt}&=-\beta y, \end{aligned}$$

(6)

where $\alpha =\frac{C_2}{C_1}$, $\beta =\frac{C_2}{LG^2}$ and $w={A} \cos (\varOmega t)$, in which ${A}=\frac{I_GC_2}{I_CC_1}$ and $\varOmega =\frac{\omega C_2}{G}$ correspond to the amplitude and frequency respectively, while f(x) can be expressed by

$$\begin{aligned} f(x)= {\left\{ \begin{array}{ll} \gamma x \tanh (\delta x)+\eta x+\sigma ,&{} \text {if } x > x_0,\\ ax^3+bx,&{} \text {if } |x|\le x_0,\\ -\gamma x \tanh (\delta x)+\eta x-\sigma ,&{} \text {if } x < -x_0, \end{array}\right. } \end{aligned}$$

(7)

with $\gamma =\frac{K_1}{G}$, $\delta =\frac{K_2I_C}{G}$, $\eta =\frac{K_3}{G}$, $a=\frac{{A_1}I_C^2}{G^3}$, $b=\frac{{B_1}}{G}$ and $x_0=\frac{G}{I_C}V_0$.

Because of the piecewise smooth characteristics of the nonlinear resistor $N_R$, two switching boundaries $\varSigma _{\pm }=\left\{ (x,y,z)|x=\pm x_0\right\}$ exist, which divide the phase space into three regions, denoted by $D_{+}=\left\{ (x,y,z)|x>x_0\right\}$, $D_{0}=\left\{ (x,y,z)||x|\le x_0\right\}$ and $D_{-}=\left\{ (x,y,z)|x<-x_0\right\}$, respectively. Obviously, the dynamics of the system in these regions are governed by three different subsystems, denoted by $S_{+}$, $S_{0}$ and $S_{-}$, respectively. With the variation of the parameters, bifurcations may occur not only in the three regions, but also at the switching boundaries, which may lead to complicated behaviors of the dynamical system. In this paper, we consider the case that the exciting frequency $\varOmega$ is far less than the natural frequency $\varOmega _N$, i.e., $\varOmega \ll \varOmega _N$, implying the effect of two time scales which often represents bursting oscillations may appear in the system. Obviously, the exciting term w oscillates periodically according to the exciting frequency, i.e., $O(dw/dt)\approx O(\varOmega ) \equiv T_1$, while the state variables x, y, z may oscillate mainly according to another much larger scale, i.e., $O(dx/dt, dy/dt, dz/dt)\approx O(\varOmega _N) \equiv T_2$, leading to a coupling between the two scales $T_1$ and $T_2$. Consequently, the whole exciting term w and the state variables x, y, z are regarded as the slow and fast variables, respectively.

3 Bifurcation analyses of the FS

As has been argued, if the exciting frequency $\varOmega$ is sufficiently small, the effect of two scales in frequency domain may appear, which often behaves in bursting oscillations. Such dynamical behaviors, characterized by the periodic alternation between rapid oscillations, denoted by the spiking states (SPs), and near steady-state behaviors, represented by the quiescent states (QSs), can be well understood by bifurcation analysis of a frozen or fast subsystem. Now we turn to the bifurcation analysis of the generalized fast subsystem by regarding the whole excitation term $w={A}cos(\varOmega t)$ as a bifurcation parameter.

3.1 Conventional bifurcation analysis of the three subsystems

The equilibrium of the subsystem $S_0$ can be computed at $E_0=(X_0,0,-X_0)$, where $X_0$ satisfies the equation

$$\begin{aligned} \alpha (aX_0^3+(1+b)X_0)-w=0. \end{aligned}$$

(8)

The stability of $E_0$ can be determined by the associated characteristic equation, expressed as

$$\begin{aligned} \lambda ^3+d_1\lambda ^2+d_2\lambda +d_3=0, \end{aligned}$$

(9)

where

$$\begin{aligned} d_1&=3\alpha aX_0^2+\alpha b+\alpha +\beta +1,\nonumber \\ d_2&=3\alpha a(\beta +1)X_0^2+\alpha \beta b+\alpha b+\alpha \beta +\beta ,\nonumber \\ d_3&=3\alpha \beta aX_0^2+\alpha \beta b. \end{aligned}$$

(10)

According to the Routh–Hurwitz criterion, the equilibrium point $E_0$ is stable for the conditions

$$\begin{aligned}&3\alpha aX_0^2+\alpha b+\alpha +\beta +1>0,\nonumber \\&\quad 3\alpha \beta aX_0^2+\alpha \beta b>0,\nonumber \\&\quad 9\alpha ^2a^2(\beta +1)X_0^4+3\alpha a[2\alpha (b\beta +\beta +b)\nonumber \\&\qquad +(\beta +1)^2+\alpha ]X_0^2 \nonumber \\&\qquad +(b+1)(\beta b+\beta +b)\alpha ^2\nonumber \\&\qquad +[(b+1)(\beta +1)^2-1]\alpha +\beta (\beta +1)>0. \end{aligned}$$

(11)

When the eigenvalues pass the imaginary axis, codimension-1 bifurcations such as fold bifurcation and Hopf bifurcation may occur. Fold bifurcation of the equilibrium point may be observed at

$$\begin{aligned} FB:3\alpha \beta aX_0^2+\alpha \beta b=0, \end{aligned}$$

(12)

with $d_1>0$ and $d_2>0$, at which a zero eigenvalue can be obtained, leading to the phenomena of jumping between different equilibrium points. Hopf bifurcation may take place at

$$\begin{aligned}&HB: 9\alpha ^2a^2(\beta +1)X_0^4+3\alpha a[2\alpha (b\beta +\beta +b)\nonumber \\&\quad +(\beta +1)^2+\alpha ]X_0^2 \nonumber \\&\quad +(b+1)(\beta b+\beta +b)\alpha ^2\nonumber \\&\quad +[(b+1)(\beta +1)^2-1]\alpha +\beta (\beta +1)=0, \end{aligned}$$

(13)

with $d_1>0$ and $d_3>0$, at which a pair of pure imaginary eigenvalues exists, causing periodic oscillation with the frequency $\varOmega _H=\sqrt{d_2}$.

For the two subsystems $S_{\pm }$, the equilibria can be computed at $E_*^{\pm }=(\pm X_*,0,{\mp } X_*)$, where $X_*$ satisfies the equation

$$\begin{aligned} \alpha [\gamma X_* \tanh (\delta X_*)+(1+\eta ) X_*+\sigma ]-w=0. \end{aligned}$$

(14)

The stability of $E_*^{\pm }$ can be determined by the associated characteristic equation, written as

$$\begin{aligned} \lambda ^3+e_1\lambda ^2+e_2\lambda +e_3=0, \end{aligned}$$

(15)

in which the coefficients are

$$\begin{aligned} e_1&=\alpha \gamma [\delta X_* {{\,\mathrm{sech}\,}}^2(\delta X_*)+ \tanh (\delta X_*)]\nonumber \\&\quad +\alpha \eta +\alpha +\beta +1,\nonumber \\ e_2&=\alpha (\beta +1)\gamma [\delta X_* {{\,\mathrm{sech}\,}}^2(\delta X_*)+\tanh (\delta X_*)]\nonumber \\&\quad +\alpha \eta (\beta +1) +(\alpha +1) \beta ,\nonumber \\ e_3&=\alpha \beta \gamma [\delta X_*{{\,\mathrm{sech}\,}}^2(\delta X_*)+\tanh (\delta X_*)]+\alpha \beta \eta . \end{aligned}$$

(16)

For simplicity, we denote $g(X_*)\triangleq \delta X_* {{\,\mathrm{sech}\,}}^2(\delta X_*)+ \tanh (\delta X_*)$. Thus, the equilibria $E_*^{\pm }$ are stable when

$$\begin{aligned}&\alpha \gamma g(X_*)+\alpha \eta +\alpha +\beta +1>0,\nonumber \\&\quad \alpha \beta \gamma g(X_*)+\alpha \beta \eta>0,\nonumber \\&\quad (\alpha \gamma g(X_*)+\alpha \eta +\alpha +\beta +1)[\alpha (\beta +1)\gamma g(X_*)\nonumber \\&\qquad +\alpha \eta (\beta +1)+\alpha \beta ]+\beta (\alpha +\beta +1)>0. \end{aligned}$$

(17)

Consequently, the fold bifurcation conditions for $E_*^{\pm }$ can be described as

$$\begin{aligned} FB:\alpha \beta \gamma g(X_*)+\alpha \beta \eta =0, \end{aligned}$$

(18)

with $e_1>0$ and $e_2>0$, while the Hopf bifurcation conditions can be expressed as

$$\begin{aligned}&HB:(\alpha \gamma g(X_*)+\alpha \eta +\alpha +\beta +1)[\alpha (\beta +1)\gamma g(X_*)\nonumber \\&\quad +\alpha \eta (\beta +1)+\alpha \beta ]+\beta (\alpha +\beta +1)=0,\nonumber \\ \end{aligned}$$

(19)

with $e_1>0$ and $e_3>0$, the frequency of which can be computed by $\varOmega _H=\sqrt{e_2}$.

3.2 Non-smooth bifurcation analysis on the switching boundaries

When the trajectory passes across the switching boundaries, the behavior can be affected by both states on two sides of the boundaries, while nonsmooth bifurcations may take place, which can be explored by the differential inclusion theory [36]. The characteristic equation, related to the generalized matrix ${\mathbf {J}}=(1-q){\mathbf {J}}_0+q{\mathbf {J}}_{\pm }$ at the equilibrium points located on the switching boundaries, can be written as

$$\begin{aligned}&\lambda ^3+[(1-q)d_1+qe_1]\lambda ^2\nonumber \\&\quad +[(1-q)d_2+qe_2]\lambda +[(1-q)d_3+qe_3]=0,\nonumber \\ \end{aligned}$$

(20)

where $q(q\in [0, 1])$ is introduced as an auxiliary parameter. With the variation of the auxiliary parameter, the associated eigenvalues may pass across the real or the pure imaginary axes, resulting in possible nonsmooth bifurcations. For the conditions

$$\begin{aligned}&NFB:(1-q)d_3+qe_3=0, \nonumber \\&\quad ((1-q)d_1+qe_1>0,(1-q)d_2+qe_2>0) \end{aligned}$$

(21)

nonsmooth fold bifurcation may be observed at the switching boundaries, while nonsmooth Hopf bifurcation may take place when

$$\begin{aligned}&NHB:[(1-q)d_1+qe_1][(1-q)d_2+qe_2]\nonumber \\&\quad -[(1-q)d_3+qe_3]=0,\nonumber \\&\quad ((1-q)d_1+qe_1>0,(1-q)d_3+qe_3>0) \end{aligned}$$

(22)

with the frequency $\varOmega _H=\sqrt{(1-q)d_2+qe_2}$.

Fig. 2

Distribution of eigenvalues with the variation of q: a eigenvalue-path of $\lambda _1$, b eigenvalue-path of $\lambda _{2,3}$ with locally enlarged part in (c)

Fig. 3

Equilibrium branches and bifurcation diagram of FS in (a) with locally enlarged parts in (b), (c) and (d)

Table 1 Equilibria as well as the stability

Table 2 Bifurcations as well as the abbreviations in Fig. 3

For example, we fix the parameters in system(6) at

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha =5.0, \beta =7.0, \gamma =0.76, \delta =0.5,\\ \eta =-1.2, a=0.4, b=-1.2, x_0=1.4, \end{array}\right. } \end{aligned}$$

(23)

while $\sigma$ can be computed by $\gamma x_0 \tanh (\delta x_0)+\eta x_0-ax_0^3-bx_0$. When $w=4.088$, the equilibrium point located on the switching boundary $\varSigma _{+}=\left\{ (x,y,z)|x=1.4\right\}$ can be computed, namely, $E_N^{+}=(1.4,0,-1.4)$, at which the generalized Jacobian can be expressed as the set-valued matrix ${\mathbf {J}}=\{{\mathbf {J}}_q,q\in [0,1]\}$ with

$$\begin{aligned} \begin{array}{c} {\mathbf {J}}_q \end{array}= & {} (1-q)\left[ \begin{array}{ccc} -10.76 &{} 5 &{} 0 \\ 1 &{} -1 &{} 1 \\ 0 &{} 0 &{} -7 \end{array} \right] \nonumber \\&+q\left[ \begin{array}{ccc} 1-3.8g(0.7) &{} 5 &{} 0 \\ 1 &{} -1 &{} 1 \\ 0 &{} 0 &{} -7 \end{array} \right] , \end{aligned}$$

(24)

and the corresponding characteristic equation is written as

$$\begin{aligned} \begin{aligned}&\lambda ^3+[18.76(1-q)+(3.8g(1.4)\\&\quad +7)q]\lambda ^2+[88.08(1-q) \\&\quad +(30.4g(1.4)-6)q]\lambda \\&\quad +[40.32(1-q)+(26.6g(1.4)-42)q]=0. \end{aligned} \end{aligned}$$

(25)

With the variation of the auxiliary parameter from $q=0$ to $q=1$, the path of the eigenvalues is depicted in Fig. 2. A pair of pure imaginary eigenvalues can be observed at $q = 0.9941$, leading to a nonsmooth Hopf bifurcation(see Fig. 3c).

3.3 Bifurcations for specific parameters

In order to explain the bifurcations in more detail, now we take the parameters in the system as in (23). By regarding the slow-varying parameter w as a bifurcation parameter, there are different numbers of equilibrium points, which form a set of equilibrium branches. The equilibrium branches as well as the bifurcations are computed numerically and plotted in Fig. 3, in which the black solid and dotted lines denote the stable and unstable equilibrium branches, the red solid and dotted lines correspond to the stable and unstable limit cycles, while the green points refer to the bifurcation points. To sum up, the branches of stable and unstable equilibria as well as the abbreviations are listed in Table 1, while the bifurcations as well as the labels are presented in Table 2.

As shown in Fig. 3b, we can observe two fold bifurcation points at $FB_{\pm }$, at which jumping phenomenon may occur. Two supercritical Hopf bifurcations, leading to the stable limit cycles $LC_{\pm 1}^{(1)}$, appear at $HB_{\pm 1}$, while two subcritical Hopf bifurcations, causing the unstable limit cycles $LC_{\pm 2}$, occur at $HB_{\pm 2}$. Specially, two period doubling bifurcations take place at $PD_{\pm 1}$, giving rise to the emergence of stable period-2 limit cycles $LC_{\pm }^d$ and the evolution of $LC_{\pm 1}^{(1)}$ into unstable limit cycles $LC_{\pm 1}^{(2)}$, while another two period doubling bifurcations happen at $PD_{\pm 2}$, leading to the disappearance of $LC_{\pm }^d$ and the evolution of $LC_{\pm 1}^{(2)}$ into stable limit cycles $LC_{\pm 1}^{(3)}$. $LC_{\pm 1}^{(3)}$ meet with $LC_{\pm 2}$ as w approaches $LPC_{\pm 1}$, corresponding to $w = \pm 0.566757$, where the two pairs of limit cycles coalesce and annihilate each other, resulting in the occurrence of fold limit cycle bifurcations.

In Fig. 3c, there exists a nonsmooth Hopf bifurcation at the point $NH_{+}$, leading to stable limit cycle $LC_{+3}$, which crosses the switching boundary $\varSigma _{+}$ continuously but non-smoothly. The stable limit cycle $LC_{+3}$ connects with unstable limit cycle $LC_{+4}$ which bifurcates from subcritical Hopf bifurcation at $HB_{+3}$, forming fold limit cycle bifurcation at $NLPC_{+1}$, corresponding to $w=5.566318$. It is noteworthy that when w approaches $NLPC_{+1}$ from the left, the two limit cycles $LC_{+3}$ and $LC_{+4}$ coalesce and annihilate each other on the switching boundary $\varSigma _{+}$, which implies such fold limit cycle bifurcation is somewhat different from that of conventional one. Thus, we call it nonsmooth fold limit cycle bifurcation. Similarly, as illustrated in Fig. 3d, stable limit cycle $LC_{+5}$ meets with unstable limit cycle $LC_{+6}$ which bifurcates from subcritical Hopf bifurcation at $HB_{+4}$, leading to nonsmooth fold limit cycle bifurcation at $NLPC_{+2}$, referring to $w=9.555126$. Because of the symmetry, another two nonsmooth fold limit cycle bifurcations, i.e., $NLPC_{-1}$ and $NLPC_{-2}$, occur at $w=-5.566318$ and $w=-9.555126$, respectively(see Fig. 3a).

The equilibrium branches and the related bifurcations with the variation of the slow-varying parameter w can be used to investigate the mechanism of the bursting oscillations, which will be presented in the following.

4 Evolution of the Bursting Oscillations

In this section, we take the excitation frequency at $\varOmega =0.0001$ to study the bursting dynamics as well as the mechanism and the evolution of nonsmooth behaviors, while the other parameters of the system are fixed in (23). Note that system(6) remains unchanged under the transformations $x\rightarrow -x$, $y\rightarrow -y$, $z\rightarrow -z$, $t\rightarrow \pi /\varOmega +t$, indicating there exists a type of $Z_2$ symmetry in the vector field. Thus, symmetric dynamical behaviors of periodic bursting oscillations may be observed with the increase of the exciting amplitude. The evolution of the bursting oscillations as well as the corresponding bifurcation mechanism will be investigated by the time histories, the corresponding phase portraits, the equilibrium bifurcation diagram and the transformed phase portraits. For convenience, the orbit of periodic bursting oscillations in the transformed phase portraits is divided into two parts, denoted by $T_-$ and $T_+$. Here, $T_-$ represents the part for $\varOmega t(mod2 \pi )\in [-\pi ,0]$ and is highlighted with blue, while $T_+$ describes the part for $\varOmega t(mod2 \pi )\in [0,\pi ]$ and is highlighted with dark gray.

4.1 Symmetric fold/supHopf bursting oscillations

For the excitation amplitude fixed at $A=0.4$, we can find two fold bifurcation points $FB_{\pm }$, two supercritical Hopf bifurcation points $HB_{\pm 1}$ and four period doubling bifurcation points $PD_{\pm i}$($i=1,2$), which are symmetrically distributed with respect to $w= 0$. With the parameter w varying between $-0.4$ and 0.4, symmetric bursting oscillations of system(6) can be observed in Fig. 4 through numerical simulation, which can be roughly divided into four stages, i.e., two spiking states $SP_i$ and two quiescent states $QS_i$($i=1,2$). Figure 4a presents the time history of variable x, while Fig. 4b depicts the corresponding phase portrait on (x, y) plane.

Fig. 4

Symmetric fold/supHopf bursting oscillations for A=0.4: a time history of x, b phase portrait on (x, y) plane, c overlap of the transformed phase portrait and the equilibrium branches on (w, x) plane with locally enlarged part in (d) and (e), (f) a period-2 cycle corresponding to $w=0.031$

To reveal the generation mechanism of the oscillations, we turn to the overlap of the transformed phase portrait and the equilibrium branches on (w, x) plane, exhibited in Fig. 4c–e. Assuming the trajectory of $T_-$ starts at the point $P_1$, corresponding to the minimum value $w=-0.4$, large-amplitude oscillations appear due to the attracting of the stable limit cycle $LC_{-1}^{(3)}$, manifesting the system as spiking state $SP_1$. When the parameter w increases to the point $PD_{-2}$, period doubling bifurcation takes place, giving rise to the attracting period-2 limit cycle $LC_{-1}^{d}$ and the repelling limit cycle $LC_{-1}^{(2)}$. However, the trajectory still oscillates along $LC_{-1}^{(2)}$ for a short time and then starts to oscillate around $LC_{-1}^{d}$(see Fig. 4c and Fig. 4e). As w further increases to the point $PD_{-1}$, another period doubling bifurcation occurs, resulting in the disappearance of $LC_{-1}^{d}$ and the emergence of stable limit cycle $LC_{-1}^{(1)}$. After that, the trajectory starts to oscillate along the stable limit cycle $LC_{-1}^{(1)}$. It is worth noting that the period doubling bifurcations do not cause the transition between quiescent state and spiking state, indicating that system(6) remains in spiking state $SP_1$ at this stage. Supercritical Hopf bifurcation occurs at the point $HB_{-1}$, causing the disappearance of stable limit cycle $LC_{-1}^{(1)}$ and appearance of stable equilibrium branch $EB_{-1}$, leading to the transition from $SP_1$ to $QS_1$. The trajectory will move along equilibrium branch $EB_{-1}$ for a while until it arrives at the fold bifurcation point $FB_-$, where jumping phenomenon to stable limit cycle $LC_{+1}^{(3)}$ takes place, resulting in repetitive spiking oscillations $SP_2$. The amplitudes of the oscillations increase gradually and the trajectory finally arrives at the point $P_2$ with the maximum value $w=0.4$, at which the first half period of the bursting oscillations $T_-$ is completed. With further increase of time, the trajectory moves back from $P_2$ to $P_1$, forming the other half period of the movement, i.e., $T_+$, which we have omitted here for simplicity as a result of the symmetry.

Since the transitions between the quiescent states and the spiking states are caused by fold bifurcations and supercritical Hopf bifurcations, and the two spiking states show a symmetric relationship. Therefore, this type of bursting oscillations can be called symmetric fold/supHopf bursting oscillations.

4.2 Symmetric compound subHopf/supHopf-fold/fold limit cycle bursting oscillations

When the excitation amplitude increases to $A= 0.8$, the parameter w varies between $-0.8$ and 0.8, aside from two fold bifurcation points $FB_{\pm }$, two supercritical Hopf bifurcation points $HB_{\pm 1}$ and four period doubling bifurcation points $PD_{\pm i}$($i=1,2$), two subcritical Hopf bifurcation points $HB_{\pm 2}$ and two fold limit cycle bifurcations $LPC_{\pm 1}$ are also found. Thus, a dynamical phenomenon of symmetric compound bursting oscillations may be observed when the parameter w traverses all the bifurcation points. Figure 5a–b exhibits the time history of variable x and the corresponding phase portrait on (x, y) plane, respectively, from which one may find that a period of bursting oscillations consists of four spiking states $SP_i$ and four quiescent states $QS_i$($i=1,2,3,4$). Meanwhile, Fig. 5c–d demonstrates the overlap of the transformed phase portrait and the equilibrium branches on (w, x) plane.

Starting at the point $P_1$, located in stable equilibrium branch $EB_{-3}$, corresponding to the minimum value $w=-0.8$, the trajectory of $T_-$ moves almost strictly along $EB_{-3}$ and passes across the point $HB_{-2}$, at which subcritical Hopf bifurcation takes place and the unstable equilibrium branch $EB_{-2}$ appears. However, nearly straight movement of the trajectory will last a short time until it reaches the point $P_2$. At this stage, system(6) stays in quiescent state $QS_1$. Attracted by the stable limit cycle $LC_{-1}^{(3)}$, small-amplitude oscillations emerge, the amplitudes of which develop rapidly with the increase of w, resulting in the spiking state $SP_1$, as shown in Fig. 5d. Because of the influence of the supercritical Hopf bifurcation at $HB_{-1}$, the trajectory then settles down to stable equilibrium branch $EB_{-1}$, leading to the quiescent state $QS_2$. Fold bifurcation occurs at the point $FB_{-}$, causing the trajectory to jump to the stable limit cycle $LC_{+1}^{(3)}$ and behave in large-amplitude oscillations, implying the transition from $QS_2$ to $SP_2$. When w increases to $w=0.566757$, fold limit cycle bifurcation occurs, the amplitudes of repetitive spiking oscillations $SP_2$ decrease quickly and finally the trajectory settles down to $EB_{+3}$, appearing in the quiescent state $QS_3$. As the trajectory along $EB_{+3}$ arrives at the point $P_3$, corresponding to the maximum value $w=0.8$, the first half period of the compound bursting oscillations $T_-$ is completed.

In this case, there are four spiking states in one excitation cycle, two of them are ignited by subcritical Hopf bifurcations and quit by supercritical Hopf bifurcations, while the other two are ignited by fold bifurcations and quit by fold limit cycle bifurcations. So, this type of bursting pattern can be called symmetric compound subHopf/supHopf-fold/fold limit cycle bursting oscillations.

Fig. 5

Symmetric compound subHopf/supHopf-fold/fold limit cycle bursting oscillations for A=0.8: a time history of x, b phase portrait on (x, y) plane, c overlap of the transformed phase portrait and the equilibrium branches on (w, x) plane with locally enlarged part in (d)

Remark 1

When the slow-varying parameter travels across a bifurcation point from one equilibrium branch to another, the corresponding bifurcation behavior of the trajectory may not occur immediately. Further change of the slow-varying parameter may lead to the bifurcation behavior, the example of which can be observed in Fig. 5c. This phenomenon is called the delay of bifurcation, which has been explained by the slow passage effect in reference [46].

4.3 Symmetric compound subHopf/nonsmooth Hopf-subHopf/supHopf-fold/fold limit cycle-nonsmooth Hopf/nonsmooth fold limit cycle bursting oscillations

With the exciting amplitude increasing to $A= 6.0$, more bifurcations such as nonsmooth Hopf bifurcations occurring at the points $NH_{\pm }$ and nonsmooth fold limit cycle bifurcations corresponding to $w=\pm 5.566318$ may involve the attractors, which will possibly lead to new patterns of the bursting oscillations. As can be observed in Fig. 6a, there exists eight spiking states $SP_i$ and eight quiescent states $QS_i$ in one period of bursting oscillations($i=1,2,...,8$), and some of the trajectories of the spiking states travel across the switching boundary $\varSigma _{\pm }$, implying nonsmooth bifurcations of limit cycle may involve in the spiking attractors. In the following, we focus on the bursting oscillation mechanism with the help of the overlap of the transformed phase portrait and the equilibrium branches on (w, x), illustrated in Fig. 6c–f.

Fig. 6

Symmetric compound subHopf/nonsmooth Hopf-subHopf/supHopf-fold/fold limit cycle-nonsmooth Hopf/nonsmooth fold limit cycle bursting oscillations for A=6.0: a time history of x, b phase portrait on (x, y) plane, c overlap of the transformed phase portrait and the equilibrium branches on (w, x) plane with locally enlarged part in (d), (e) and (f)

Taking $P_1$ as the initial point with $w=-6.0$, the trajectory of $T_-$ runs strictly along stable equilibrium branch $EB_{-5}$ and passes across the point $HB_{-3}$, at which subcritical Hopf bifurcation takes place. Because of the delay effect, the trajectory does not oscillate immediately but moves along unstable equilibrium branch $EB_{-4}$ for a while until it arrives at point $P_2$, shown in Fig. 6d. At this stage, system(6) stays in quiescent state $QS_1$. Affected by stable limit cycle $LC_{-3}$, small-amplitude oscillations can be observed, the amplitudes of which increase quickly, leading to spiking state $SP_1$. The repetitive spiking keeps until the trajectory meets the point $NH_-$, at which nonsmooth Hopf bifurcation occurs, causing the spiking state settle down to quiescent state $QS_2$. The $QS_2$ continues before the trajectory arrives at the point $P_3$. After that, the trajectory begins to oscillate around $EB_{-2}$ due to the attraction of the stable period-2 limit cycle $LC_{-1}^{d}$, resulting in spiking state $SP_2$. The effect of supercritical Hopf bifurcation at the point $HB_{-1}$ appears, which causes the trajectory gradually settle down to stable equilibrium branch $EB_{-1}$, yielding quiescent state $QS_3$, the time window of which seems a bit short, shown in Fig. 6a. With the increase of time, the trajectory jumps to oscillate according to the stable limit cycle $LC_{+1}^{(3)}$ via fold bifurcation at the point $FB_{-1}$, appearing in spiking state $SP_3$. As w increases to $w=0.566757$, fold limit cycle bifurcation occurs, leading to rapid decrease in the oscillating amplitude, resulting in transition to quiescent state $QS_4$. When the trajectory along $EB_{+3}$ arrives at the point $NH_+$, the oscillations caused by nonsmooth Hopf bifurcation do not appear immediately due to the delay effect. After a short straightly movement of the trajectory, small-amplitude oscillations emerge, the amplitude of which increases gradually to begin the spiking oscillations $SP_4$, as shown in Fig. 6f. The repetitive spiking keeps until w increases to $w=5.566318$, at which nonsmooth fold limit cycle bifurcation occurs, causing the trajectory to settle down to $EB_{+3}$, yielding the quiescent state $QS_5$. When the trajectory moves almost strictly along $EB_{+3}$ to the point $P_4$ with the maximum value $w=6.0$, the half period of the bursting oscillations $T_-$ is finished.

According to the bifurcations at the transitions between the quiescent states and the spiking states, this pattern of bursting oscillations can be called symmetric compound subHopf/nonsmooth Hopf-subHopf/supHopf-fold/fold limit cycle-nonsmooth Hopf/nonsmooth fold limit cycle bursting oscillations.

Remark 2

When the trajectory passes across the switching boundaries, nonsmooth bifurcations, such as nonsmooth Hopf bifurcation and nonsmooth fold limit cycle bifurcation, may take place, which will possibly involve the bursting attractors and change the bursting pattern.

4.4 Symmetric compound subHopf/nonsmooth fold limit cycle-fold/fold limit cycle-nonsmooth Hopf/nonsmooth fold limit cycle bursting oscillations

Further increase in the exciting amplitude to $A=12.0$, although another four bifurcations can be found, namely subcritical Hopf bifurcations emerging at $HB_{\pm 3}$ and nonsmooth fold limit cycle bifurcations with $w=\pm 9.555126$, which may change the structure of the bursting attractor. The time history of variable x and the corresponding phase portrait on (x, y) plane are plotted in Fig. 7a–b, from which we may find that the number of the spiking states doesn’t increase but decreases to 6 compared with the case with $A=6.0$. The principal reason for this phenomenon is that not only the bifurcations but also the delay effect of bifurcation may lead to different bursting attractors. To investigate the mechanism of the oscillations, we also turn to the overlap of the transformed phase portrait and the equilibrium branches on (w, x), shown in Fig. 7c–f.

Fig. 7

Symmetric compound subHopf/nonsmooth fold limit cycle-fold/fold limit cycle-nonsmooth Hopf/nonsmooth fold limit cycle bursting oscillations for A=12.0: a time history of x, b phase portrait on (x, y) plane, c overlap of the transformed phase portrait and the equilibrium branches on (w, x) plane with locally enlarged part in (d), (e) and (f)

Starting from the point $P_1$ with $w=-12.0$, the trajectory of $T_-$ behaves in spiking state $SP_1$, the amplitude of which increases rapidly due to the attraction of stable limit cycle $LC_{-5}$, shown in Fig. 7d. After undergoing a period of large amplitude oscillations, the trajectory tries to settle down to stable equilibrium branch $EB_{-5}$ via nonsmooth fold limit cycle bifurcation, corresponding to $w=-9.555126$. Then the trajectory moves almost strictly along $EB_{-5}$, $EB_{-4}$, $EB_{-3}$, $EB_{-2}$ and $EB_{-1}$ until it arrives at the neighborhood of the point $FB_-$, behaving in quiescent state $QS_1$. Fold bifurcation takes place, causing the trajectory to jump rather abruptly to stable limit cycle $LC_{+1}^{(3)}$, yielding repetitive spiking oscillations $SP_2$, as shown in Fig. 7e. Because of the fold limit cycle bifurcation, corresponding to $w=0.566757$, the trajectory gradually settles down to $EB_{+3}$ to begin the quiescent state $QS_2$ until it arrives at the boundary $\varSigma _{+}$. Attracted by stable limit cycle $LC_{+3}$ via nonsmooth Hopf bifurcation at $NH_+$, small-amplitude oscillations appear, the amplitude of which increases gradually to start spiking oscillations $SP_3$, shown in Fig. 7f. When w increases to $w=5.566318$, nonsmooth fold limit cycle bifurcation causes the trajectory to settle down to stable equilibrium branch $EB_{+5}$, yielding the quiescent state $QS_3$. As the trajectory moving along $EB_{+5}$ and $EB_{+6}$ and arriving at the point $P_2$ with $w=12.0$, the half period of the bursting oscillations $T_-$ is finished.

Fig. 8

The trajectory between the two Hopf bifurcation points $HB_{-1}$ and $HB_{-2}$: a locally enlarged overlap of the transformed phase portrait and the equilibrium branches on (w, x) plane, b time history of w

Here, we call this bursting pattern as symmetric compound subHopf/nonsmooth limit cycle-fold/fold limit cycle-nonsmooth Hopf/nonsmooth fold limit cycle bursting oscillations

Remark 3

It is noteworthy that the trajectory between the two Hopf bifurcation points $HB_{-1}$ and $HB_{-2}$ doesn’t appear spiking behavior in the case with $A=12.0$. The main reason for this phenomenon can be accounted for by the fact that an increase in the exciting amplitude A may lead to a shorter travel time between the two Hopf bifurcation points, leading to more delay effect of bifurcation, shown in Fig. 8. Thus, the trajectory keeps always in quiescent state along the unstable equilibrium branch $EB_{-2}$.

5 Conclusions

Nonsmooth dynamical systems, usually possessing one or more switching manifolds, may exhibit complex dynamics and have become an interesting topic in the study of nonlinear dynamics. In this research, bursting oscillations, characterized by large-amplitude oscillations that alternate with small-amplitude oscillations or rest, have been investigated in a piecewise smooth Chua’s circuit with a slow-varying external excitation. By using the modified slow-fast analysis method, the evolutionary mechanism of the equilibrium branches as well as the related bifurcations of the generalized fast subsystem are obtained. As a result, two novel bursting patterns, i.e., bursting of “subHopf/nonsmooth Hopf-subHopf/supHopf-fold/fold limit cycle-nonsmooth Hopf/nonsmooth fold limit cycle” type and bursting of “subHopf/nonsmooth fold limit cycle-fold/fold limit cycle-nonsmooth Hopf/nonsmooth fold limit cycle” type, have been revealed aside from another two common ones. With the increase of the slow-varying parameter, not only the conventional bifurcations, such as fold and Hopf bifurcations, but also the nonsmooth bifurcations, such as nonsmooth Hopf and nonsmooth fold limit cycle bifurcations, can lead to transitions between different attractors. Furthermore, it can be found that the delay effect of bifurcation can be observed near the conventional and nonsmooth bifurcations, which may change the structure of bursting attractors, resulting in different types of bursting oscillations. Our research enriches the nonsmooth dynamics of bursting oscillations in the nonsmooth continuous dynamical system.