Bursting oscillations with delayed C-bifurcations in a modified Chua’s circuit

Abstract

In this research, a typical Chua’s circuit with a piecewise nonlinear resistor and a slow-varying periodic excitation is considered to investigate the dynamical mechanisms of bursting oscillations in the piecewise-smooth dynamical system. A set of new bursting oscillations is observed when the amplitude of the excitation is changed. By regarding the excitation term as a bifurcation parameter, the codimension-1 conventional bifurcations and non-smooth bifurcations of the fast subsystem are explored. Fold bifurcation, supercritical Hopf (sup-Hopf) bifurcation, non-smooth Hopf bifurcation, grazing bifurcation, and C-bifurcation are discovered via theoretical and numerical methods. The C-bifurcation connects the stable limited cycle bifurcated from non-smooth Hopf bifurcation with the stable limited cycle bifurcated from the sup-Hopf bifurcation. When the fast subsystem driven by the slow subsystem passes through the bifurcation points, slow passage effect near the non-smooth Hopf bifurcation and delay of the C-bifurcation take place. The delayed C-bifurcation may lead to multiple transition patterns between different attractors, including two transition patterns of reverse direction near the fold and sup-Hopf bifurcations. The delayed transition to other attractor creates a non-smooth hysteresis loop and enables the generation of bursting oscillations.

1 Introduction

Bursting oscillations, as a typical representative behavior of the slow–fast dynamical system, characterized by a combination of large amplitude oscillation and relatively small amplitude oscillation during each evolution period, are ubiquitous in various fields of science and engineering, such as chemical experiments [1], electromechanical engineering [2], neuroscience [3], and physics [4]. The generation mechanisms of bursting oscillations of slow–fast system have been understood thanks to the slow–fast analysis method introduced by Rinzel [5]. Subsequent to this pioneering work, the investigation of bursting in dynamical systems has received much attention in both theory and practical applications. However, most of the research in this area is made for smooth systems (e.g., [6,7,8,9,10,11,12] and the references therein).

Piecewise-smooth system can be observed widely in many fields of science and engineering. A piecewise-smooth system always has one or more switching manifolds, which can cause qualitative changes in the system’s dynamics, termed discontinuity-induced bifurcations or non-smooth bifurcations, including boundary equilibrium bifurcations and non-smooth limit cycle bifurcations [13]. For the low-dimensional piecewise-smooth system, different types of the non-smooth bifurcations as well as the conditions have been reported [14], which may lead to non-smooth dynamical behaviors [15]. When the coupling of multi time scales involves the vector field, bursting oscillations may occur. For example, Simpson et al. analyzed a piecewise linear FitzHugh–Nagumo model and found the addition of small noise induces mixed-mode oscillations in the vicinity of the canard point [16]; Zhang et al. investigated the influence of non-smooth fold bifurcations on the bursting oscillations in a piecewise linear system [17]; Fernández et al. showed the dynamical mechanisms of mixed-mode oscillations of three different amplitudes and frequencies in a piecewise linear system with three time scale coupling [18]; Li et al. studied the existence condition and generation mechanisms of bursting oscillations in a piecewise mechanical system with different time scales and proposed focus-type periodic bursting oscillations [19]; Singla et al. studied the relationship of the frequency of the perturbation and that of the antiperiodic oscillations in a Chua’s circuit with periodic forcing [20]; Qu et al. investigated bursting oscillations with sliding bifurcation in a Filippov system [21]. Recently, Wang et al. have investigated the non-smooth Hopf bifurcation on the discontinuity boundary and its effect on the bursting oscillations [22]. Even so, up to now, few results have been published recently on the effect of delayed non-smooth limit cycle bifurcation on the bursting oscillations.

The present paper investigates the bursting dynamics in the piecewise nonlinear system, focusing on the effects of the delayed C-bifurcation on bursting dynamics. For this purpose, a modified Chua’s circuit, possessing a slow-varying periodic excitation and a nonlinear resistor, is considered, in which the characteristics of the resistor can be described by a continuous piecewise nonlinear function.

2 Mathematical model

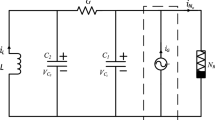
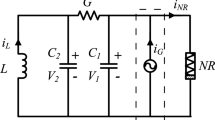
The modified Chua’s circuit is shown in Fig. 1, in which NR is a piecewise nonlinear resistor and $i_G$ is a periodically exciting electric current.

Fig. 1

A Chua’s circuit with a piecewise nonlinear resistor and a slow-varying periodic excitation

The model’s equations are

$$\begin{aligned} \begin{array}{l} C_1\displaystyle \frac{\mathrm{d}V_1}{\mathrm{d}\tau }=G(V_2-V_1)-g(V_1)+I_G\text{ sin }(\omega \tau ),\\ C_2\displaystyle \frac{\mathrm{d}V_2}{\mathrm{d}\tau }=G(V_1-V_2)+i_L,\\ L\displaystyle \frac{\mathrm{d}i_L}{\mathrm{d}\tau }=-V_2, \end{array} \end{aligned}$$

(1)

where $g(V_1)$ denotes the relationship between the current and voltage passing across the nonlinear resistor, NR, described by

Fig. 2

Bursting oscillations for $\gamma =0.16$: a time history on the (t, x) plane; b time history on the (t, y) plane

$$\begin{aligned} g(V_1)=\left\{ \begin{array}{ll} G_KV_1+(G_K+G_A)V_0-G_BV_0^3,&{}~\text{ if }~V_1<-V_0,\\ -G_AV_1+G_BV_1^3, &{}~\text{ if }~|V_1|{\le }V_0,\\ G_KV_1-(G_K+G_A)V_0+G_BV_0^3,&{}~\text{ if }~V_1>V_0, \end{array} \right. \end{aligned}$$

(2)

with $G_K$, $G_A$, and $G_B$ being conductances. Equation (1) can be normalized by applying the following change of variables: $V_1=\frac{I_C}{G}x,V_2=\frac{I_C}{G}y, i_L=I_Cz$, and time $\tau =\frac{C_2}{G}t$, where $I_C$ is a variable direct current constant. Defining the new parameters: $\alpha =\frac{C_2}{C_1}, \beta =\frac{C_2}{LG^2}, a=\frac{G_A}{G}, b=\frac{G_B{I_C}^2}{G^3}, k=\frac{G_K}{G}, d=\frac{G_K+G_A}{I_C}V_0-\frac{G_B}{I_C}V_0^3, x_0=\frac{GV_0}{I_C}, \gamma =\frac{I_GC_2}{I_CC_1}$, and $\Omega =\frac{\omega C_2}{G}$, the dimensionless model of (1) is given by

$$\begin{aligned} \begin{array}{l} \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}=\alpha (y-x-f(x))+w,\\ \displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}=x-y+z,\\ \displaystyle \frac{\mathrm{d}z}{\mathrm{d}t}=-\beta y, \end{array} \end{aligned}$$

(3)

where

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} kx+d, &{}\text{ if }~x<-x_0,\\ -ax+bx^3, &{}\text{ if }~|x|{\le } x_0,\\ kx-d, &{}\text{ if }~x>x_0, \end{array} \right. \end{aligned}$$

(4)

and $w=\gamma \sin (\Omega t)$.

The discontinuity boundaries $\Sigma _{\pm }=\{\mathbf{x}|x=\pm x_0\}$, where $\mathbf{x}=(x,y,z)\in R^3$, partition the phase space into three regions, denoted by $D_-=\{\mathbf{x}|x<-x_0\}$, $D_0=\{\mathbf{x}||x|{\le }x_0\}$, and $D_+=\{\mathbf{x}|x>x_0\}$, in which the dynamics of the system are governed by three different subsystems in (3), denoted by $S_-, S_0$, and $S_+$, respectively. When the frequency of the excitation satisfies $0<\Omega \ll 1$, the effect of two scales in frequency domain may appear, yielding complicated dynamical behaviors.

Fig. 3

Bursting oscillations for $\gamma =0.35$: a time history on the (t, x) plane; b time history on the (t, y) plane; c, d the local enlargements of (a)

3 Evolution of the bursting oscillations

Now we turn to the evolution of the dynamical behaviors of the system (3). When the parameters are fixed at $a=1.05, b=0.5, \alpha =2.75, \beta =3.0, k=2.0, x_0=0.645$, and $\Omega =0.001$, the coupling effect of two scales may influence the dynamics of the system. With the variation in the excitation amplitude, a set of bursting oscillations can be observed. Notice that the parameter d in the system can be computed by $d=(k+a)x_0-bx_0^3$. For convenience, in what follows, we use SP and QS to denote the spiking state and quiescent state of the bursting oscillations, respectively.

Fig. 4

Bursting oscillations for $\gamma =0.5$: a time history on the (t, x) plane; b time history on the (t, y) plane

Fig. 5

Bursting oscillations for $\gamma =0.84$: a time history on the (t, x) plane; b time history on the (t, y) plane; c, d the local enlargements of (a)

Fig. 6

Bursting oscillations for $\gamma =0.93$: a time history on the (t, x) plane; b time history on the (t, y) plane; c, d the local enlargements of (a)

Symmetric bursting oscillations can be observed when $\gamma =0.16$ (Fig. 2), which can be roughly divided into two stages corresponding to two spiking states, denoted by $SP_1$ and $SP_2$, respectively. One may find that some of the trajectories of the spiking states are located in region $D_0$, and the rest of the trajectories pass through the discontinuous boundary $\Sigma _+$ or $\Sigma _-$, implying non-smooth bifurcations of the limit cycle may involve the spiking attractor.

With the increase in the excitation amplitude $\gamma$, the structure of the bursting attractor may change. Boundary equilibrium bifurcations may involve the bursting attractor when $\gamma$ is larger than some critical value $\gamma _0$, which may cause each of the spiking states in Fig. 2 to be divided into two asymmetric spiking states, see the bursting oscillations in Fig. 3 for $\gamma =0.35$. In this case, the spiking state $SP_1$ in Fig. 2 is divided into $SP_2$ and $SP_3$ in Fig. 3, while the spiking state $SP_2$ in Fig. 2 is divided into $SP_4$ and $SP_1$ in Fig. 3.

A new limit cycle bifurcation occurring on the discontinuity boundary may involve bursting attractor when the excitation amplitude $\gamma$ is larger than some critical value $\gamma _1$, leading to new bursting oscillations, see Fig. 4 for $\gamma =0.5$, in which the spiking state $SP_1$ comes from the combination of $SP_1$ and $SP_2$ in Fig. 3, while the spiking state $SP_2$ comes from the combination of $SP_3$ and $SP_4$ in Fig. 3.

When the excitation amplitude $\gamma$ is larger than some critical value $\gamma _2$, the new limit cycle bifurcation mentioned above may no longer affect the structure of the bursting attractor, and the spiking states in Fig. 4 exhibit division behaviors again. A typical pattern of bursting oscillations is shown in Fig. 5 for $\gamma =0.84$. Notice that the bursting oscillations in this case are different from that in Fig. 3.

With the increase in the excitation amplitude $\gamma$, the number of the spiking states remains unchanged in one period of bursting oscillations, but the structure of the bursting attractor may change. A typical pattern of bursting oscillations is shown in Fig. 6 for $\gamma =0.93$. Compared with Fig. 5, one may find that there exists a quiescent state not only between $SP_1$ and $SP_2$, but also between $SP_3$ and $SP_4$ in Fig. 6.

Remark 1

According to the “Bifurcation analysis” discussed in Sect. 4, the critical value $\gamma _0$ can be proved to be $\gamma _0=\alpha \,\left( \left( 1-a\right) {x_0}+b{x_0}^{3} \right) \approx 0.2803$, while the critical values $\gamma _1$ and $\gamma _2$ can be approximated numerically, which are $\gamma _1\approx 0.4778$ and $\gamma _2\approx 0.7288$, respectively.

It can be found that, with the increase in the amplitude of the excitation, the spiking attractors undergo several times of division and combination, resulting in complicated bursting oscillations, in which the non-smooth bifurcations on the discontinuity boundaries and traditional bifurcations may play important roles. To explore the mechanisms of the bursting oscillations, we have presented above, in the following section, we will turn to the bifurcation analysis of the non-smooth vector field.

Fig. 7

One-parameter bifurcation diagram: a one-parameter bifurcation diagram with respect to w on the (w, x) plane; b the local enlargement of (a)

4 Bifurcation analysis

Note that the discontinuity boundaries $\Sigma _{\pm }$ divide the phase space into three regions. In the regions $D_{\pm }$ and $D_0$, the behaviors of the system are governed by the subsystems $S_{\pm }$ and $S_0$, respectively. The equilibrium state of the generalized autonomous system (3) can be defined by $\frac{\mathrm{d}x}{\mathrm{d}t}=0, \frac{\mathrm{d}y}{\mathrm{d}t}=0, \frac{\mathrm{d}z}{\mathrm{d}t}=0$, in which the slow-varying excitation term $w=\gamma \sin (\Omega t)$ is regarded as a bifurcation parameter.

4.1 Equilibrium analysis of the subsystems $\mathbf{S_{\pm }}$

For the two linear subsystems $S_{\pm }$, the equilibria can be computed at $E_{\pm }=({\pm }\frac{\alpha d{\pm } w}{\alpha (1+k)},0,{\mp }\frac{\alpha d{\pm } w}{\alpha (1+k)})$, respectively. The stability of $E_{\pm }$ can be determined by the associated characteristic equations, written in the same form

$$\begin{aligned} \lambda ^3+P_2\lambda ^2+P_1\lambda +P_0=0, \end{aligned}$$

(5)

where $P_0=\alpha \beta +\alpha k\beta , P_1=\beta +\alpha k, P_2=1+\alpha k+\alpha$. It is easy to check that $P_i>0,{i=0,1,2}$, and $P_1P_2-P_0=\beta +\alpha k+\alpha ^2k^2+\alpha ^2k>0$ under the assumptions $\alpha>0, \beta>0, a>0, b>0$ and $k>0$, implying the equilibria $E_{\pm }$ are stable hyperbolic equilibrium points. In other words, there are no bifurcation phenomena associated with the equilibria in the two linear subsystems $S_{\pm }$.

4.2 Bifurcation of the subsystem ${\mathbf{S}_0}$

The equilibrium of the subsystem $S_0$ can be computed at $E_0=(X_0,0,-X_0)$, where $X_0$ satisfies the equation

$$\begin{aligned} \alpha \big ((a-1)X_0-bX_0^3\big )+w=0. \end{aligned}$$

(6)

The stability of $E_0$ can be determined by the associated characteristic equation, expressed as

$$\begin{aligned} \lambda ^3+Q_2\lambda ^2+Q_1\lambda +Q_0=0, \end{aligned}$$

(7)

where $Q_0=3\alpha b\beta X_0^2-\alpha a\beta +\alpha \beta , Q_1=3\alpha bX_0^2+\beta -\alpha a$, $Q_2=3\alpha bX_0^2+1+\alpha -\alpha a$. Fold bifurcation of the equilibrium point may be observed if

$$\begin{aligned} 3\alpha b\beta X_0^2-a\alpha \beta +\alpha \beta =0. \end{aligned}$$

(8)

This shows that fold bifurcations may occur for

$$\begin{aligned} w=\pm \frac{2\sqrt{3b}\alpha (a-1)^{\frac{3}{2}}}{9b}, \end{aligned}$$

(9)

at each of which there exists one zero eigenvalue, leading to possible jumping behavior. These two loci meet and disappear in a cusp catastrophe for $a=1$. The Hopf bifurcation may occur if

$$\begin{aligned} Q_1Q_2-Q_0=0, \end{aligned}$$

(10)

and $Q_0>0, Q_2>0$. These show that Hopf bifurcations may take place for

$$\begin{aligned} w=\pm \,{\frac{\sqrt{6\alpha \,b\left( M_1+ M_2\right) }\left( M_3+M_2\right) }{36 \alpha \,b}}, \end{aligned}$$

(11)

or

$$\begin{aligned} w=\pm \,{\frac{\sqrt{6\,\alpha \,b\left( M_1- M_2\right) }\left( M_3-M_2\right) }{36 \alpha \,b}}, \end{aligned}$$

(12)

where $M_1=2\alpha \,a-\alpha -1, M_2{=}\sqrt{{\alpha }^{2}+2\,\alpha {+}1{-}4\,\beta }{,} M_3= 5\,\alpha -4\,\alpha \,a-1$. A pair of pure imaginary eigenvalues of Eq. (7) may be observed at each of the critical values in (11)–(12), leading to possible periodic movement.

4.3 Non-smooth bifurcations on the discontinuity boundaries

If the equilibrium branches of the subsystems intersect the discontinuity boundaries $\Sigma _{\pm }$, boundary equilibrium bifurcations may appear at the intersections. When the bifurcation parameter $w=\alpha \big ((1-a)x_0+bx_0^3\big )$, the boundary equilibria can be computed at $E_{\pm }^*=(\pm x_0,0,{\mp } x_0)$, respectively, and the characteristic equation related to the generalized matrix upon the differential inclusion theory [23] can be written as

$$\begin{aligned} \lambda ^3+N_2\lambda ^2+N_1\lambda +N_0=0, \end{aligned}$$

(13)

where $q(q\in [0,1])$ is introduced as an auxiliary parameter, $N_i=qQ_i+(1-q)P_i, i=0,1,2$. With the variation in the auxiliary parameter q, the associated eigenvalues may pass across the real or the pure imaginary axes, resulting in possible non-smooth bifurcations. Non-smooth fold bifurcation may appear if

$$\begin{aligned} qQ_0+(1-q)P_0=0, \end{aligned}$$

(14)

and $N_2>0, N_1N_2-N_0>0$, which shows that if

$$\begin{aligned} q={\frac{1+k}{-3\,b{x_0}^{2}+a+k}}\in (0,~1), \end{aligned}$$

(15)

the non-smooth fold bifurcation may take place, while the non-smooth Hopf bifurcation may occur if

$$\begin{aligned} N_1N_2-N_0=0 \end{aligned}$$

(16)

and $N_0>0, N_2>0$, which shows that if

$$\begin{aligned} q={\frac{\alpha +1+2\alpha \,k+\sqrt{{\alpha }^{2}+2\,\alpha +1 -4\,\beta }}{2\alpha \,\left( -3\,b{x_0}^{2}+a+k \right) }}\in (0,~1),\nonumber \\ \end{aligned}$$

(17)

or

$$\begin{aligned} q={\frac{\alpha +1+2\alpha \,k-\sqrt{{\alpha }^{2}+2\,\alpha +1 -4\,\beta }}{2\alpha \,\left( -3\,b{x_0}^{2}+a+k \right) }}\in (0,~1),\nonumber \\ \end{aligned}$$

(18)

the non-smooth Hopf bifurcation may take place, leading to possible periodic movement.

Table 1 Bifurcations as well as the abbreviations in Fig. 7

Table 2 Equilibria as well as the stability

Fig. 8

C-bifurcation occurring at $CB_+$: a representative phase portrait for $w<0.0543$, which is obtained when $w=0.05$; b critical phase portrait for $w=0.0543$; c representative phase portrait for $w>0.0543$, which is obtained when $w=0.07$

Fig. 9

Grazing bifurcation occurring at $GB_+$: a representative phase portrait for $w<0.1036$, which is obtained when $w=0.1$; b critical phase portrait for $w=0.1036$; c representative phase portrait for $w>0.1036$, which is obtained when $w=0.104$

4.4 Bifurcation diagram

The one-parameter bifurcation diagram of system (3) with respect to w for the parameter conditions: $a=1.05, b=0.5$, $\alpha =2.75, \beta =3.0, k=2.0$, and $x_0=0.645$, is computed numerically and shown in Fig. 7. The bifurcations as well as the abbreviations in Fig. 7 are summarized in Table 1. The branches of stable and unstable equilibria as well as the labels in Fig. 7 are summarized in Table 2.

In Fig. 7a, the limit cycles $LC_{\pm 1}$ connect with the limit cycles $LC_{\pm 2}$ by $CB_{\pm }$, in which $LC_{\pm 1}$ are bifurcated from the non-smooth Hopf bifurcations occurring at $NH_{\pm }$, while $LC_{\pm 2}$ are bifurcated from the supercritical Hopf bifurcations occurring at $HB_{\pm 1}$. When the bifurcation parameter w passes through $CB_{\pm }$, the stability of limit cycles $LC_{\pm 1}$ and $LC_{\pm 2}$ does not change, but the topological structures of which change. Let’s focus on the system dynamical behaviors near the $CB_+$, corresponding to $w=0.0543$ (Fig. 8). There exists a limit cycle governed only by the subsystem $S_0$ when the bifurcation parameter $w<0.0543$ (Fig. 8a). A part of the limit cycle crosses the boundary $\Sigma _+$ continuously but non-smoothly when the bifurcation parameter w passes through the value 0.0543, forming another limit cycle which is governed by subsystems $S_0$ and $S_+$ (Fig. 8c). Figure 8b depicts the critical orbit which is tangent to the boundary $\Sigma _+$, corresponding to $w=0.0543$. Based on the analysis above, there exists a C-bifurcation at $w=0.0543$ [24]. Because of the symmetry, another C-bifurcation occurs at $w=-0.0543$. C-bifurcation can cause the system to switch from one periodic state to another. However, the limit cycle $LC_0$ may approach $\Sigma _-$ or $\Sigma _+$ and then disappear after being tangent to $\Sigma _-$ or $\Sigma _+$, implying the grazing bifurcations occur at $GB_{\pm }$, corresponding to $w=\pm 0.1036$, respectively, when the bifurcation parameter w passes through $GB_+$ from the left to the right or passes through $GB_-$ from the right to the left. The behaviors of the system near $GB_+$, corresponding to $w=0.1036$, can illustrate this point (Fig. 9). There exists a limit cycle crossing the discontinuity boundaries $\Sigma _{\pm }$ when $w<0.1036$ (Fig. 9a). Once the limit cycle is tangent to the boundary $\Sigma _-$, corresponding to $w=0.1036$, it will disappear and the trajectory will be attracted by other attractor (Fig. 9b), implying that a bifurcation of limit cycle takes place at $w=0.1036$. Figure 9c gives a limit cycle for $w>0.1036$, which is not bifurcated from the bifurcation occurring at $w=0.1036$ but bifurcated from the non-smooth Hopf bifurcation occurring at point $NH_+$. Thus, there is a grazing bifurcation occurring at $w=0.1036$. Because of the symmetry, another grazing bifurcation takes place at $w=-0.1036$. Grazing bifurcation can cause a periodic state of the system to disappear or emerge.

The bifurcation diagram can be used to investigate the mechanisms of the bursting oscillations, which will be presented in the following section.

5 Mechanisms of the bursting oscillations

Now we turn to the transformed phase diagrams of the bursting oscillations shown in Figs. 2, 3, 4, 5, and 6 and overlay them with the bifurcation diagram shown in Fig. 7 to detect the associated bifurcation mechanisms. In order to give a clear view of the dynamical mechanism, the bursting is divided into two bursting parts, i.e., $B_-$ and $B_+$. Here, $B_-$ denotes the bursting part for $\Omega t (\text{ mod } 2\pi )\in [-\frac{\pi }{2},\frac{\pi }{2}]$ and $B_+$ means the part for $\Omega t(\text{ mod } 2\pi )\in [\frac{\pi }{2},\frac{3\pi }{2}]$. The bursting $B_-$ and bursting $B_+$ are highlighted with dark cyan and black, respectively.

Fig. 10

Slow–fast analysis of the bursting pattern for $\gamma =0.16$. The bursting $B_-$ and bursting $B_+$ are highlighted with dark cyan and black, respectively. a overlap of the bifurcation diagram and the transformed phase portrait on the (w, x) plane; b–d the local enlargements of (a)

Fig. 11

Slow–fast analysis of the bursting pattern for $\gamma =0.35$: a overlap of the bifurcation diagram and the transformed phase portrait on the (w, x) plane; b–e the local enlargements of (a)

Fig. 12

Slow–fast analysis of the bursting pattern for $\gamma =0.5$: a overlap of the bifurcation diagram and the transformed phase portrait on the (w, x) plane; b–f the local enlargements of (a)

5.1 Delayed C-bursting of point/cycle type

Figure 10a gives the overlap of the transformed phase portrait and the bifurcation diagram on the (w, x) plane for $\gamma =0.16$. From the point $P_-$, corresponding to the minimum value of the slow-varying parameter w($=-0.16$) (Fig. 10a, b), the trajectory of $B_-$ oscillates along $LC_{-1}$ until it arrives at $CB_-$, where a C-bifurcation takes place. After passing through $CB_-$, the trajectory still remains the oscillating state of crossing the discontinuity boundary $\Sigma _-$ for some time (delay interval in Fig. 10c), resulting in the increase in the oscillation amplitude. Attraction of the limit cycle $LC_{-2}$ causes the trajectory to settle down to $LC_{-2}$ gradually, and the trajectory oscillates along $LC_{-2}$ until it arrives at the neighborhood of the point $HB_-$ (Fig. 10d). The trajectory begins to approach the stable equilibrium branch $EB_{-3}$ with gradually decreasing amplitude until it arrives at the neighborhood of $FB_-$. Fold bifurcation at $FB_-$ causes the trajectory to jump to the stable limit cycle $LC_{+2}$ (Fig. 10d), and the trajectory oscillates along $LC_{+2}$ until it arrives at $CB_+$, at which another C-bifurcation occurs. The trajectory turns to and oscillates along the stable limit cycle $LC_{+1}$ until it arrives at the point $P_+$, corresponding to the maximum value of w at $w=0.16$ (Fig. 10a). Now half period of the bursting oscillations is finished. Further increase in the time leads to the other half period of the bursting, i.e., $B_+$. When the trajectory goes back to the point $P_-$, a non-smooth hysteresis loop is closed, forming the bursting oscillations in Fig. 2.

Considering the attractor type involved, the bursting pattern can be called “delayed C-bursting of point/cycle type”

Remark 2

When the slow-varying parameter moves to the bifurcation point, the related bifurcations may not occur. Further change of the slow-varying parameter may lead to the bifurcations, the phenomenon of which is called the delay of the bifurcation. In the case of $\gamma =0.16$, after the slow-varying parameter w passes through the C-bifurcation point, the trajectory still remains the oscillating state of crossing the discontinuity boundary $\Sigma _-$ for some time. After a while, the trajectory does not cross the boundary $\Sigma _-$ again and begins to turn to other attractors, i.e., a delayed C-bifurcation behavior is created. One may find that, with the increase in the amplitude of the excitation, the delayed C-bifurcation may cause the oscillating amplitude of the trajectory to increase before it transfers to other attractors, which may result in other complicated bursting oscillations.

5.2 Delayed C-bursting of point/cycle/point/cycle/point type

When the excitation amplitude $\gamma >\gamma _0 (0.2083)$, the non-smooth Hopf bifurcations on the discontinuity boundaries $\Sigma _{\pm }$ involve the bursting attractor, resulting in new pattern of bursting oscillations, e.g., the bursting oscillations in Fig. 3 for $\gamma =0.35$. The overlap of the transformed phase portrait and the bifurcation diagram is shown in Fig. 11a.

From the point $P_-$ with $w=-0.35$, the trajectory of $B_-$ moves along the stable equilibrium branch $EB_{-1}$ until it arrives at the neighborhood of the point $NH_-$, at which a non-smooth Hopf bifurcation occurs. Because of the slow passage effect, the trajectory moves along the unstable equilibrium branch $EB_{-2}$ and exhibits oscillation in small amplitude for quite some time after it passes through the point $NH_-$ (Fig. 11b); then, it jumps rather abruptly to the limit cycle $LC_{-1}$ (Fig. 11c) and oscillates along $LC_{-1}$ until it arrives at $CB_-$, where a C-bifurcation occurs and delayed C-bifurcation can be observed. After undergoing a period of large amplitude oscillations, the trajectory settles down to the limit cycle $LC_{-2}$ and oscillates around $LC_{-2}$ until it arrives at the neighborhood of the supercritical Hopf bifurcation point $HB_-$ (Fig. 11d). The trajectory begins to approach the stable equilibrium branch $EB_{-3}$ with gradually decreasing amplitude until it arrives at the neighborhood of the fold bifurcation point $FB_-$. With the increase in the slow-varying parameter w, the trajectory jumps to and oscillates around the limit cycle $LC_{+2}$ until it arrives at another C-bifurcation point $CB_+$; then, the trajectory passes through $CB_+$ and begins to oscillate along the stable limit cycle $LC_{+1}$ until it arrives at the neighborhood of the point $NH_+$, at which another non-smooth Hopf bifurcation occurs (Fig. 11e). After that, the trajectory settles down to the stable equilibrium branch $EB_{+1}$ and moves along it until the trajectory arrives at the point $P_+$ with $w=0.35$. Half period of the bursting oscillations is finished. Further increase in the time leads to bursting $B_+$. When the trajectory goes back to the point $P_-$, a non-smooth hysteresis loop is closed, forming the bursting oscillations in Fig. 3. The bursting pattern is termed “delayed C-bursting of point/cycle/point/cycle/point type.”

Remark 3

Similar to the conventional Hopf bifurcation, the slow passage effect can also be observed near non-smooth Hopf bifurcation.

5.3 Delayed C-bursting of point/cycle/point type

Because of the effect of the delay of C-bifurcation, the amplitude of spiking states $SP_1$ and $SP_3$ further increases with the increase in excitation amplitude $\gamma$. When $\gamma >\gamma _1 (0.4778)$, the trajectory begins to enter the attraction basin of limit cycle $LC_0$ before it settles down to $LC_{\pm 2}$, which results in the combination of the spiking state $SP_1$ and $SP_2$ as well as the combination of the spiking state $SP_3$ and $SP_4$, forming the bursting oscillations in Fig. 4. Here $SP_i, i=1,2,3,4$ are the spiking states in Fig. 3.

Figure 12a gives the overlap of the transformed phase portrait and the bifurcation diagram for $\gamma =0.5$. Starting at the point $P_-$ with $w=-0.5$, the trajectory of $B_-$ moves along the stable equilibrium branch $EB_{-1}$ (Fig. 12a) until it arrives at the neighborhood of the point $NH_-$. The slow passage effect near the non-smooth Hopf bifurcation causes the trajectory to oscillate around the unstable equilibrium branch $EB_{-2}$ in small amplitude for some time after it passes through the point $NH_-$ (Fig. 12b). Then, the trajectory jumps rather abruptly to the limit cycle $LC_{-1}$ and oscillates along $LC_{-1}$ (Fig. 12c) until it arrives at $CB_-$, where the C-bifurcation occurs. With the increase in the slow-varying parameter w, the amplitudes of the oscillations increase gradually and the trajectory tends to the stable limit cycle $LC_0$ (Fig. 12d). After that, the trajectory oscillates along $LC_0$ until it arrives at $GB_+$, where the grazing bifurcation occurs. The amplitudes of the oscillations decrease gradually, and then, the trajectory oscillates along the stable limit cycle $LC_{+1}$ until it arrives at the neighborhood of the non-smooth Hopf bifurcation point $NH_+$,(Fig. 12e,f). The trajectory settles down to the stable equilibrium branch $EB_{+1}$ and moves along $EB_{+1}$ until it arrives at the point $P_+$ with $w=0.5$. Half period of the bursting oscillations is finished. Further increase in the time leads to the bursting $B_+$. When the trajectory goes back to the point $P_-$, a non-smooth hysteresis loop is closed, forming the bursting oscillations in Fig. 4. The bursting pattern is termed “delayed C-bursting of point/cycle/point type.”

Fig. 13

Slow–fast analysis of the bursting pattern for $\gamma =0.84$: a Overlap of the bifurcation diagram and the transformed phase portrait on the (w, x) plane; b–d the local enlargements of (a)

Fig. 14

Slow–fast analysis of the bursting pattern for $\gamma =0.93$: a overlap of the bifurcation diagram and the transformed phase portrait on the (w, x) plane; b–d the local enlargements of (a)

5.4 Delayed C-bursting of point/cycle/cycle/point type with reverse transition

When the excitation amplitude $\gamma$ is larger than $\gamma _2 (0.7288)$, the grazing bifurcations do not involve bursting attractor again, resulting in the divisions of spiking states in Fig. 4, forming the bursting oscillations in Fig. 5. The transformed phase portrait of Fig. 5a and the bifurcation diagram is overlapped in Fig. 13a.

The trajectory of $B_-$, starting at the point $P_-$ with $w=-0.84$, moves along the stable equilibrium branch $EB_{-1}$ with the increase in the slow-varying parameter w until it reaches the non-smooth bifurcation point $NH_-$ (Fig. 13a). After a relatively long period of small amplitude oscillation, the trajectory jumps rather abruptly to the limit cycle $LC_{-1}$ until it arrives at $CB_-$ (Fig. 13b,c). The delay of the C-bifurcation causes the trajectory to begin to oscillate along $LC_{-2}$ in large amplitude. Before settling down to $LC_{-2}$ , the trajectory arrives at the neighborhood of the sup-Hopf bifurcation point $HB_+$ and then enters into the basin of attraction of the stable limit cycle $LC_{+2}$ bifurcated from $HB_+$. The slow passage effect near the sup-Hopf bifurcation causes the trajectory to oscillate around $EB_{+2}$ in small amplitude for a while (Fig. 13d). Then, the trajectory jumps to and oscillates along $LC_{+2}$ until it arrives at $CB_+$. The trajectory turns to and oscillates around $LC_{+1}$ until it arrives at $NH_+$. After that, the trajectory settles down to the stable equilibrium branch $EB_{+1}$ until it reaches the point $P_+$ with $w=0.84$, corresponding to the maximum of the slow-varying parameter w (Fig. 13a). Half period of the bursting oscillations is finished. Further increase in the time leads to the other half period of the bursting, i.e., $B_+$. When the trajectory goes back to the point $P_-$, a non-smooth hysteresis loop is closed, forming the bursting oscillations in Fig. 5. The bursting pattern is termed “delayed C-bursting of point/cycle/cycle/point type with reverse transition.”

5.5 Delayed C-bursting of point/cycle/point/cycle/point type with reverse transition

Further increase in the excitation amplitude $\gamma$ does not change the numbers of the spiking and quiescent attractors in one period, but the structure of bursting attractor changes. Figure 14a gives the overlap of the transformed phase portrait and the bifurcation diagram for $\gamma =0.93$. The trajectory of $B_-$, starting at the point $P_-$ with $w=-0.93$ (Fig. 14a), moves along the stable equilibrium branch $EB_{-1}$ until it arrives at the neighborhood of $NH_-$ (Fig. 14b). The slow passage effect causes the trajectory to oscillate in small amplitude along the unstable equilibrium branch $EB_{-2}$ (Fig. 14c) for a long period of time. Then, the amplitude increases abruptly, and the trajectory oscillates along the limit cycle $LC_{-1}$ until it passes through the C-bifurcation point. The delay of C-bifurcation causes the trajectory to oscillate around $LC_{-2}$ in large amplitude until it arrives at the neighborhood of the fold bifurcation point $FB_+$. The trajectory moves along the stable equilibrium branch $EB_{+3}$ with the increase in w in quiescent state until it passes through the Hopf bifurcation point $HB_+$. Slow passage effect near the Hopf bifurcation causes the trajectory to oscillate around the unstable equilibrium branch $EB_{+2}$ in small amplitude for a long period of time, resulting in the occurrence of delayed C-bifurcation after the trajectory passes through $CB_+$. Then, the trajectory jumps rather abruptly to the limit cycle $LC_{+1}$ and oscillates along the limit cycle $LC_{+1}$ gradually until it arrives at the neighborhood of $NH_+$ (Fig. 14c, d, b). The trajectory moves along the stable equilibrium branch $EB_{+1}$ in quiescent state until it arrives at $P_+$ (Fig. 14a). Half period of the bursting oscillations is finished. Further increase in the time leads to the bursting $B_+$. When the trajectory goes back to the point $P_-$, a non-smooth hysteresis loop is closed, forming the bursting oscillations in Fig. 6. The bursting pattern is termed “delayed C-bursting of point/cycle/point/cycle/point type with reverse transition.”

Remark 4

The delayed C-bifurcation may lead to a transition pattern from spiking state to quiescent state by jumping behavior in reverse direction near the fold bifurcation, or from spiking state to spiking state by jumping behavior in reverse direction near the supercritical Hopf bifurcation.

6 Conclusion

A slow–fast piecewise-smooth system may exhibit complicated bursting oscillations. Not only the conventional bifurcations, such as fold and Hopf bifurcations, but also the non-smooth bifurcations, such as C-bifurcation, non-smooth Hopf and grazing bifurcations, can lead to transitions between different attractors. Slow passage effect, being frequently observed near the conventional Hopf bifurcation, can be observed near the non-smooth Hopf bifurcation as well. Delayed C-bifurcation can lead to multiple behaviors of transitions, such as from cycle to cycle or from cycle to stable equilibrium, resulting in different bursting patterns. The non-smooth hysteresis loop caused by the delayed transition to other attractor is responsible for the generation of bursting oscillations.