1 Introduction

A chaotic system is a complex nonlinear system, which is highly sensitive to initial conditions and parameter variations. In comparison with the integer-order systems, fractional-order systems have received considerable attention in describing the real-world physical phenomena [1]. Recently, the applications of fractional calculus in such cases are investigated. For example, in physics, engineering and especially in secure communication, fractional calculus has attracted much attention [2, 3]. In secure communication, complex variables can increase the security of information signals and additionally carry more transmitted information [4,5,6]. Several fractional-order complex chaotic systems such as the Lorenz system [7], Chen system [8], T system [9] and Lü system [10] have been proposed and designed till now. In [8], chaotic secure communication of the coupled fractional-order complex chaotic Chen systems based on hybrid synchronisation is investigated.

Since Pecora and Carroll studied synchronisation of chaotic systems with different initial conditions [11], many synchronisation methods, such as complete synchronisation, phase projective synchronisation, lag projective synchronisation, modified complex projective synchronisation (MCPS) [12,13,14,15] and modified generalised projective synchronisation [3], have been proposed. Due to the potential applications of chaos synchronisation in different fields such as physics [16], chemistry [17] and secure communications [18], several control techniques such as feedback control [19], adaptive control [20], adaptive fuzzy control [21], sliding mode control [22, 23] and passive control [5, 6, 24] have been proposed to achieve chaos synchronisation. In the last few decades, the passive control technique plays an important role in the stabilisation of nonlinear systems such as unified chaotic system [25]. The main advantage of this control method is that internal stability of the system is guaranteed.

Secure communication based on synchronisation of chaotic dynamical systems has been developed in the past decades; but there was little work for secure communication based on synchronisation of fractional-order chaotic systems [2, 3]. Fractional-order real and complex systems have memory and nonlinearity which make them different from the integer-order one. The complex variables in the fractional-order complex systems can be double the number of variables to increase the transmission capacity [8].

In the usual chaotic communications scheme, the message to be transmitted is carried from the transmitter to the receiver by a chaotic signal, may be destroyed by such noises, and then reconstructed by the receiver system [26]. Some of the important approaches of chaotic communications include chaos masking [27, 28], chaos modulation [5, 6, 28, 29], chaos shift keying [30, 31] and chaos switching.

Recently, the application of complex function projective synchronisation of two coupled complex chaotic systems in secure communication is investigated in the presence of channel noise by Liu and Zhang [4]. Mahmoud et al [5] introduced projective synchronisation of hyperchaotic complex systems using the passive control technique and its application in secure communication without the effect of channel noise is studied. Wu et al [6] investigated the chaotic secure communication in the presence of channel noise via the synchronisation of two hyperchaotic complex systems realised by passive control technique. However, this research attempts to develop a special case of synchronisation of two identical fractional-order complex chaotic systems that are exposed to bounded noise. The complex scaling factors, manipulated by complex states of the transmitter system, are sent to the public channel. We employ parameter modulation method to build a secure communication scheme so that security of the information signal can be improved. Moreover, a simple filter is used in the receiver module to assure the accuracy of the recovered message signal. The details of the proposed secure communication scheme are explained in §4.

Some contributions of this paper can be considered as: (i) the proposed new scheme is achieved for fractional-order complex chaotic systems, pertaining to which there are only a few investigations. (ii) The designed controller is based on a passive control technique using the fractional Lyapunov function which can provide wide applicability for the synchronisation of fractional-order systems. (iii) The problem for chaotic secure communication via the passive synchronisation of fractional-order complex chaotic systems is resolved. (iv) The effects of different kinds of noises are investigated.

The lay-out of this paper is as follows. In §2, some preliminaries of fractional calculus are reviewed. The principle of the passive control technique for the fractional-order complex nonlinear systems is given in §3. In §4, a secure communication scheme via the MCPS of fractional-order complex chaotic systems is investigated. Numerical simulations are employed in §5, and finally, concluding remarks are drawn in §6.

2 Mathematical preliminaries

The fractional integration of a function \(g(t)\!:R^{+}\rightarrow R\) is given by [32, 33]

$$\begin{aligned} {}_{t_0}D_t^{-q} g(t)=\frac{1}{\Gamma (q)} \int _{t_0}^t (t-\tau )^{q-1}g(\tau ) \hbox {d}\tau , \end{aligned}$$
(1)

where \(\Gamma (\cdot )\) is the well-known Euler’s gamma function, defined by \(\Gamma (z)=\int _{t_0}^{\infty } t^{z-1}\hbox {e}^{-t} \hbox {d}t\).

There are many definitions for fractional differential operators [32, 33]. The most well-known definition is the Riemann–Liouville definition. The Riemann–Liouville fractional derivative of the function \(g(t)\!\!:\, R^{+}\rightarrow R\) is given as follows:

$$\begin{aligned} { }_a D_t^q g(t)= \frac{1}{\Gamma (k-q)}\frac{\hbox {d}^{k}}{\hbox {d}t^{k}} \int _0^t \frac{g(\tau )}{(t-\tau )^{q+1-k}}\hbox {d}\tau , \end{aligned}$$
(2)

where k is the first integer larger than q, i.e. \(k-1\le q<k\).

The Caputo fractional derivative of the function \(g(t)\!\!: R^{+}\rightarrow R\) is defined by

$$\begin{aligned}&D^{q}g(t)\nonumber \\&\quad {=}\,\left\{ \begin{array}{ll} \dfrac{1}{\Gamma (k-q)}\int _0^t \dfrac{g^{(k)}(\tau )}{(t-\tau )^{q+1-k}} \hbox {d}\tau , &{} \quad k-1{<}q{<}k, \\ \dfrac{\hbox {d}^{k}g(t)}{\hbox {d}t^{k}}, &{} \quad q=k. \end{array}\right. \end{aligned}$$
(3)

In our theoretical analysis, we used the Caputo definition. Also, in order to solve fractional-order differential equations, we recall the Adams–Bashforth–Moulton algorithm [34].

3 The theory of passive control

The fractional-order complex nonlinear system with uncertain parameters can be considered in the following general form:

$$\begin{aligned} \left\{ {{\begin{array}{l} D^{q}x=f(x,\theta )+g({x,\theta })\Xi ,\\ y=h({x,\theta }),\\ \end{array} }} \right. \end{aligned}$$
(4)

where \(x\in C^{n}\) is the state complex vector, \(x=x^{\mathrm{r}}+\hbox {j}x^{\mathrm{i}}\), \(x^{\mathrm{r}}=( {u_1 ,u_3 ,\ldots ,u_{2n-1} } )^{\mathrm{T}}\), \(x^{\mathrm{i}}=( {u_2 ,u_4 ,\ldots ,u_{2n} } )^{\mathrm{T}}\). \(\Xi \in C^{\kappa }\) is the control complex vector, \(\Xi =\Xi ^{\mathrm{r}}+\hbox {j}\Xi ^{\mathrm{i}}, \quad \Xi ^{\mathrm{r}}=( {\nu _1 ,\nu _3 ,\ldots ,\nu _{2\kappa -1} } )^{\mathrm{T}}\), \(\Xi ^{\mathrm{i}}=( \nu _2 ,\nu _4 ,\ldots ,\nu _{2\kappa } )^{\mathrm{T}}\) and the output \(y\in C^{\kappa }\), \(y=y^{\mathrm{r}}+\hbox {j}y^{\mathrm{i}}\), \(y^{\mathrm{r}}=( {\iota _1 ,\iota _3 ,\ldots ,\iota _{2\kappa -1} } )^{\mathrm{T}}\) and \(y^{\mathrm{i}}=( {\iota _2 ,\iota _4 ,\ldots ,\iota _{2\kappa } } )^{\mathrm{T}}\); \(\kappa <n,\hbox {j}=\sqrt{-1}\). f and \(\kappa \) columns of g are smooth vector fields, h is a mapping that is smooth. \(\theta \in R^{p}\) is an uncertain parameters vector.

The real form of system (4) can be rewritten as

$$\begin{aligned} \left\{ {{\begin{array}{l} D^{q}W=F({W,\theta })+G({W,\theta })\chi , \\ \Upsilon =H({W,\theta }), \\ \end{array} }} \right. \end{aligned}$$
(5)

where \(W\in R^{2n}\) is the state real vector, \(W=( {u_1 ,u_2 ,\ldots ,u_{2n} } )^{\mathrm{T}}\). \(\chi \in R^{2\kappa }\) is the real external input, \(\chi =( {\nu _1 ,\nu _2 ,\ldots ,\nu _{2\kappa } } )^{\mathrm{T}}\) and \(\Upsilon \in R^{2\kappa }\) is the output, \(\Upsilon =( {\Upsilon _1 ,\Upsilon _2 ,\ldots ,\Upsilon _{2\kappa }})^{\mathrm{T}}\). The functions F and G are locally Lipschitz with \(F( 0 )=0\) and \(G( 0 )=0\). The vector field F has at least one equilibrium point and we assume that it is at the origin.

DEFINITION 1

[5, 6, 24, 35]

System (5) is said to have a relative degree \([ {1,1,\ldots ,1} ]\) at the origin if the matrix \(L_G H( 0 )=( {\partial H/\partial W} )G( {W,\theta } )\) is non-singular.

DEFINITION 2

System (5) is a minimum phase system if \(L_G H(0)\) is non-singular and \(W=0\) is one of the symptotically stabilised equilibrium points of F(W).

DEFINITION 3

System (5) is said to be passive if the following two conditions are satisfied:

  1. 1.

    There should be two smooth vector fields \(F(W)\) and \(G(W)\) and also a smooth mapping \(H(W)\).

  2. 2.

    There should be a continuous differentiable positive semidefinite function \(V(u)\), a real-valued constant \(\varepsilon \), a positive constant \(\delta \) and fractional-order operator \(q\in (0, 1]\) such that \(\forall t\ge 0\), and the following inequality holds:

$$\begin{aligned} \int _0^t \chi ^{\mathrm{T}}(\tau )\Upsilon (\tau )\hbox {d}\tau +\frac{t^{(1-q)}\varepsilon }{\Gamma (2-q)}\ge \delta \int _0^t \Upsilon ^{\mathrm{T}}(\tau )\Upsilon (\tau )\hbox {d}\tau . \end{aligned}$$
(6)

Remark 1

For \(q=1\), inequality (6) becomes the well-known definition for integer-order counterpart, where the constant parameter \(\varepsilon \) is the initial value of the function V(u). In inequality (6), t and q are positive real constants. Therefore, \(( {t^{( {1-q} )}\varepsilon })/( {\Gamma ( {2-q} )} )\) is a real positive constant, which satisfies the necessary condition for the passivity of system (5).

If system (5) has the relative degree \([ {1,1,\ldots ,1} ]\) at \(W=0\) and the distribution defined by the vector field \(G_1 (W), G_2 ( W),\ldots ,G_{2\kappa }( W )\), then we can describe the following parametric normal form:

$$\begin{aligned} \left\{ {{\begin{array}{l} D^{q}\omega =\varphi (\omega ,\theta )+\rho (\omega ,\Upsilon ,\theta )\Upsilon , \\ D^{q}\Upsilon =\Psi ({\omega ,\Upsilon ,\theta }) +\phi ({\omega ,\Upsilon ,\theta }t)\chi . \\ \end{array} }} \right. \end{aligned}$$
(7)

Based on (5) and (7), the new coordinate of system (5) is \(( {\omega ,\Upsilon })\), locally defined close to the origin. Suppose that \(\phi ( {\omega ,\Upsilon ,\theta } )\) in system (7) is parameter-independent, i.e. \(\phi ( {\omega ,\Upsilon ,\theta } )=\phi ( {\omega ,\Upsilon })\), and so system (7) becomes

$$\begin{aligned} \left\{ {{\begin{array}{l} D^{q}\omega =\varphi ({\omega ,\theta }) +\rho (\omega ,\Upsilon ,\theta )\Upsilon . \\ D^{q}\Upsilon =\Psi ({\omega ,\Upsilon ,\theta }) +\phi ({\omega ,\Upsilon })\chi . \\ \end{array} }} \right. \end{aligned}$$
(8)

If an appropriate controller \(\chi \) is designed, the passivity of (8) may be satisfied. Assume that system (8) represents the dynamics of the error system. So the equilibrium point of system (8) by the controller \(\chi \) can be asymptotically stabilised [36].

Lemma 1

[37]. Let \(g(t)\in R\) be continuous differentiable. Then, for any time instant \(t\ge t_0\) and fractional-order differential equations, which are defined by Caputo fractional derivatives, the following inequality is obtained:

$$\begin{aligned} D^{q}g^{2}(t)\le 2 g(t)D^{q}\!g(t), \quad \forall \,q\in (0,1). \end{aligned}$$
(9)
Fig. 1
figure 1

Block diagram of the chaotic communication system.

Full size image

Remark 2

[37]. When \(g(t)\in R^{n}\), Lemma 1 is still valid. That is, \(\forall \,q\in (0, 1)\) and \(\forall \,t\ge t_0 \)

$$\begin{aligned} D^{q}\!g^{\mathrm{T}}\!(t)g(t)\le 2\!g^{\mathrm{T}}\!(t)D^{q}\!g(t). \end{aligned}$$
(10)

The proof is straightforward and is based on [37]. Hence the proof is omitted here.

4 Secure communication based on MCPS

In figure 1, a secure communication based on MCPS of two identical fractional-order complex chaotic Lorenz systems is shown. The information signal is modulated into one parameter of the fractional-order complex system in the transmitter after being transformed by an invertible transformation function \(\gamma (\cdot )\) and the resulting system still exhibits a chaotic behaviour. Since this system is chaotic, it is hard to detect the information signal by detectors from the transmitted signals in the noisy public channel. In the receiver end, with the help of controller \(\Xi (X^{\prime }_1,X_2)\), MCPS between the transmitter and the receiver systems using the passive control technique can be realised. Thus, by using the output of the adaptive controllers and the invertible transformation function, the information signal can be identified, asymptotically. Based on figure 1, in the transmitter, the new parameter \(\beta (t)\) is defined as a function of the information signal s(t).  \({\mathcal {N}}(t)\) is the noise of the channel. The weighted state signals \(\Phi X_1 \) that may be influenced by channel noises are the complex signals received in the receiver module. When MCPS is achieved, the receiver system can estimate the unknown parameter \(\hat{\beta } (t)\). Finally, as depicted in the receiver module, using the states of the receiver system and the designed controller, the weighted states of the transmitter system and the receiver system will synchronise and the corresponding information signal can be recovered through an appropriate adaption law and some simple operations.

The chaotic transmitter system is in the following form [7]:

$$\begin{aligned} \left\{ {{\begin{array}{l} D^{q}x_1 =10({x_2 -x_1 }), \\ D^{q}x_2 =a_2 x_1 - x_2 -x_1 x_{3,} \\ D^{q}x_3 =1/2({\bar{x}_1 x_2 +x_1 \bar{x}_2})-x_3 , \\ \end{array} }} \right. \end{aligned}$$
(11)

where \(x_1 =u_{11} +\hbox {j}u_{12} \), \(x_2 =u_{13} +\hbox {j}u_{14}\), \(x_3 =u_{15} \).

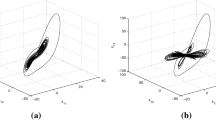
As the results in [7], system (11) with \(a_2 =180\) and \(q=0.95\) is chaotic with the largest Lyapunov exponent of 0.0148. The chaotic behaviour of (11) with \(a_2 =180\) and different values of fractional-order (q) are plotted in figure 2. The chaotic behaviour of the system decreases when the fractional-order (q) decreases from 0.95 to 0.8 and the behaviour of the system changes to a periodic case. The largest Lyapunov exponents of (11) with \(q=0.9\) and 0.8 are 0.0124 and 0.0027, respectively.

Fig. 2
figure 2

(a, b) Projections of chaotic attractors of (11) when \(q=0.8\); (c, d) projections of chaotic attractors of (11) when \(q=0.9\) and (e, f) projections of chaotic attractors of (11) when \(q=0.95\).

Full size image

A new parameter \(\beta (t)\) is defined in system (11) to exhibit the chaotic behaviour.

Hence, according to (11), one obtains

$$\begin{aligned} \left\{ {{\begin{array}{l} D^{q}x_1 =10({x_2 -x_1 }),\\ D^{q}x_2 =\beta (t)x_1 - x_2 -x_1 x_3 ,\\ D^{q}x_3 =1/2({\bar{x}_1 x_2 +x_1 \bar{x}_2 })-x_3 .\\ \end{array} }} \right. \end{aligned}$$
(12)

In the receiver end, the receiver system is constructed as follows:

$$\begin{aligned} \left\{ {{\begin{array}{l} D^{q}y_1 =10( {y_2 -y_1 } ), \\ D^{q}y_2 =\hat{\beta } (t)y_1 - y_2 -y_1 y_3 +\Xi _1 ,\\ D^{q}y_3 =1/2({\bar{y}_1 y_2 +y_1 \bar{y}_2} )-y_3 +\Xi _2 ,\\ \end{array} }} \right. \end{aligned}$$
(13)

where \(y_1 =u_{21} +\hbox {j}u_{22} \), \(y_2 =u_{23} +\hbox {j}u_{24}\), \(y_3 =u_{25} \), \(\Xi _1 =\nu _1 +\hbox {j}\nu _2 \), \(\Xi _2 =\nu _3 \). \(\hat{\beta } (t)\) is the unknown parameter of the receiver system which needs to be estimated.

Define the MCPS error variables as \(E=Y-\Phi X\), where \(E=({E_1 , E_2 , E_3})^{\mathrm{T}}=({e_1 +\hbox {j}e_2 , e_3+\hbox {j}e_4 , e_5})^{\mathrm{T}}\) and suppose \(\Phi =\hbox {diag}({1-\hbox {j}, 1-\hbox {j}, 1})\).

Thus, one can obtain

$$\begin{aligned}&\Phi X =((u_{11} +u_{12})+\hbox {j}(u_{12} -u_{11}),(u_{13} +u_{14})\nonumber \\&\qquad \,\, +\,\hbox {j}(u_{14} -u_{13}),u_{15})^{\mathrm{T}} \nonumber \\&\quad \quad =({s_{11} +\hbox {j}\ s_{12} ,s_{13} +\hbox {j}\ s_{14} ,s_{15}})^{\mathrm{T}} \nonumber \\&\left\{ {{\begin{array}{lll} E_1 &{}=e_1 +\hbox {j}e_2 =y_1 -({1-\hbox {j}})x_1\\ &{}=({u_{21} -s_{11}})+\hbox {j}({u_{22} -s_{12}}), \\ E_2 &{}=e_3 +\hbox {j}e_4 =y_2 -({1-\hbox {j}} )x_2\\ &{}=({u_{23}-s_{13}})+\hbox {j}({u_{24} -s_{14}}), \\ E_3 &{}=e_5 =y_3 -x_3 =u_{25} -s_{15} \\ \end{array}}}\right. \end{aligned}$$
(14)

and consider the parameter estimate error as \(e_\beta (t)=\beta (t)-\hat{\beta } (t)\).

Using (12)–(14), the error dynamical system can be written as follows:

$$\begin{aligned} \left\{ {\begin{array}{lll} D^{q}E_1 =10({e_3 -e_1})+\hbox {j}({10({e_4 -e_2})}), \\ D^{q}E_2 =-e_\beta ({s_{11}})+\hat{\beta } (t)e_1 -e_3 -u_{21} u_{25} \\ \qquad \qquad \ \ \, +\, s_{11} s_{15} +\hbox {j}( -e_\beta s_{12} +\hat{\beta } (t)e_2 -e_4\\ \qquad \qquad \ \ \,-\,u_{22} u_{25} +s_{12} s_{15})+\Xi _1 , \\ D^{q}E_3 =u_{21} u_{23} +u_{22} u_{24}\\ \ \quad \qquad \quad \ -1/2({s_{11} s_{13} +s_{12} s_{14}})-e_5 +\Xi _2 . \\ \end{array}}\right. \end{aligned}$$
(15)

By designing suitable controllers \(\Xi _k (t), k=1,2\), and the parameter update rule, the error dynamical system (15) can be asymptotically stabilised at the origin, i.e. \(\lim _{t\rightarrow \infty }\Vert E\Vert =0\), \(\lim _{t\rightarrow \infty }|{e_\beta }|=0\). That is, MCPS between the transmitter system (12) and the receiver system (13) is globally achieved and the uncertain parameter can be estimated asymptotically.

Theorem 1

The error dynamical system (15) is a minimum phase system with the control laws as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} \nu _1 =10\omega _1 -\hat{\beta } (t)\omega _1 +\Upsilon _1 +u_{21} u_{25}\\ \quad \qquad - s_{11} s_{15} -\delta \Upsilon _1 +\eta _1 , \\ \nu _2 =10\omega _2 -\hat{\beta } (t)\omega _2 +\Upsilon _2 +u_{22} u_{25}\\ \qquad \quad -s_{12} s_{15} -\delta \Upsilon _2 +\eta _2 , \\ \nu _3 =-u_{21} u_{23} -u_{22} u_{24} +1/2({s_{11} s_{13} +s_{12} s_{14} })\\ \qquad \quad +\Upsilon _3 -\delta \Upsilon _3 +\eta _3\\ \end{array}\right. \end{aligned}$$
(16)

and the uncertain parameter update law is as follows:

$$\begin{aligned} \dot{\hat{\beta }}(t)=\dot{\beta }(t)-D^{1-q}(\Upsilon _{1}s_{11} +\Upsilon _{2}s_{12}), \end{aligned}$$
(17)

where \(\delta >0\) is the feedback control gain, and \(\eta =(\eta _1, \eta _2 , \eta _3)^\mathrm{T}\) are the external input signals that are connected with the reference inputs.

Proof

First, it is necessary to compute \(L_G H(0)\). Obviously, \(L_G H(0)\) is non-singular. Then, based on Definition 1, system (15) has a relative degree \([1,1,\ldots , 1]\). So, consider the parametric version of the normal form of system (15) and let \(\Upsilon =({\Upsilon _1 , \Upsilon _2 ,\Upsilon _3})^{\mathrm{T}} =({e_3 , e_4 ,e_5})^{\mathrm{T}}\) as the system outputs and \(\omega =({\omega _1 , \omega _2})^{\mathrm{T}}=({e_1 , e_2})^{\mathrm{T}}\), then system (15) can be written as

$$\begin{aligned} \left\{ {\begin{array}{l} D^{q}( {\omega _1 +\hbox {j}\omega _2 } )=10( {\Upsilon _1 -\omega _1 } )+\hbox {j}({10( {\Upsilon _2 -\omega _2 })}), \\ D^{q}({\Upsilon _1 +\hbox {j} \Upsilon _2})=-e_\beta s_{11} +\hat{\beta } (t)\omega _1 \\ \qquad \quad \qquad \qquad \qquad -\,\Upsilon _1 -u_{21} u_{25} +s_{11} s_{15}\\ \qquad \qquad \qquad \qquad \quad +\,\hbox {j}(-e_\beta s_{12} +\hat{\beta } (t)\omega _2 -\Upsilon _2\\ \qquad \qquad \qquad \qquad \quad -\,u_{22} u_{25} +s_{12} s_{15})+\Xi _1 , \\ D^{q}\Upsilon _3 =u_{21} u_{23} +u_{22} u_{24}\\ \qquad \qquad -1/2({s_{11} s_{13} +s_{12} s_{14}})-\Upsilon _3 +\Xi _2 . \\ \end{array}} \right. \end{aligned}$$
(18)

According to (8) and (18), we have

$$\begin{aligned}&\chi =({\nu _1 ,\nu _2 ,\nu _3})^{\mathrm{T}},\quad \varphi (\omega , \theta ) =\left( \begin{array}{l} -10\omega _1 \\ -10\omega _2 \\ \end{array}\right) , \nonumber \\&\rho ({\omega ,\Upsilon ,\theta })=\left( \begin{array}{lll} 10&{}\quad 0&{}\quad 0 \\ 0&{}\quad 10&{}\quad 0 \\ \end{array}\right) ,\nonumber \\&\phi (\omega ,\Upsilon )=\left( \begin{array}{lll} 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1 \\ \end{array}\right) ,\nonumber \\&\Psi ({\omega ,\Upsilon ,\theta })\nonumber \\&\quad =\left( \begin{array}{c} -e_\beta s_{11} +\hat{\beta } (t)\omega _1 -\Upsilon _1 -u_{21} u_{25} +s_{11} s_{15} \\ -e_\beta s_{12} +\hat{\beta } (t)\omega _2 {-}\Upsilon _2 {-}u_{22} u_{25} {+}s_{12} s_{15} \\ u_{21} u_{23} +u_{22} u_{24} {-}1/2({s_{11} s_{13} {+}s_{12}s_{14}}) {-}\Upsilon _3 \\ \end{array}\right) .\nonumber \\ \end{aligned}$$
(19)

Let the positive storage function candidate be defined as

$$\begin{aligned} V(\omega , \Upsilon ,\theta )=X(\omega , \theta ) +(\Upsilon ^{\mathrm{T}}\Upsilon +e_\beta ^{2})/2, \end{aligned}$$
(20)

where

$$\begin{aligned} X(\omega , \theta )=1/2(\omega ^{\mathrm{T}}\omega ) =1/2(\omega _1 ^{2}+\omega _2 ^{2}),\ \ X(0)=~0. \end{aligned}$$

The zero dynamics of system (8) describes the internal dynamics and it occurs when \(\Upsilon =0\), i.e. \(D^{q}\omega =\varphi (\omega ,\theta )\).

By taking the fractional derivative from \(W(\omega , \theta )\) and using Remark 2, one obtains

$$\begin{aligned} D^{q}X(\omega ,\theta )\le & {} \omega ^{\mathrm{T}}D^{q}\omega \le \left( {{\begin{array}{l} {\omega _1 } \\ {\omega _2 } \\ \end{array} }} \right) ^{\mathrm{T}}\left( {{\begin{array}{l} {-10\omega _1 } \\ {-10\omega _2 } \\ \end{array} }} \right) \nonumber \\= & {} -20 X(\omega ,\theta )\le 0. \end{aligned}$$
(21)

As \(D^{q}X({\omega ,\theta })\le 0\) and \(X({\omega ,\theta })\) is a positive Lyapunov function of \(\varphi ({\omega ,\theta })\), according to Definition 2, system (15) is a minimum phase system.

Taking the fractional derivative from (20) along the trajectory of the error system (18) yields

$$\begin{aligned} D^{q}V({\omega ,\Upsilon ,\theta })\le \omega ^{\mathrm{T}}D^{q}\omega +\Upsilon ^{\mathrm{T}}D^{q}\Upsilon +e_\beta D^{q}e_{\beta } . \end{aligned}$$
(22)

Inserting (8) into (22), we have

$$\begin{aligned} D^{q}V({\omega ,\Upsilon ,\theta })\le & {} \omega ^{\mathrm{T}} ({\varphi ({\omega ,\theta })+\rho ({\omega ,\Upsilon ,\theta })\Upsilon })\nonumber \\&+\Upsilon ^{\mathrm{T}}({\varPsi ({\omega ,\Upsilon ,\theta }) +\phi ({\omega ,\Upsilon })\chi })\nonumber \\&+e_\beta D^{q}e_\beta . \end{aligned}$$
(23)

Substituting (19) into (23), one gets

$$\begin{aligned}&D^{q}V({\omega ,\Upsilon ,\theta })\nonumber \\&\quad \le \left( {{\begin{array}{l} {\omega _1 } \\ {\omega _2 } \\ \end{array}}}\right) ^{\mathrm{T}}\left( {{\begin{array}{l} {-10\omega _1 } \\ {-10\omega _2 } \\ \end{array}}}\right) +\left( {{\begin{array}{l} {\Upsilon _1 } \\ {\Upsilon _2 } \\ {\Upsilon _3 } \\ \end{array} }} \right) ^{\mathrm{T}} \left( {{\begin{array}{l} {10\omega _1 -e_\beta s_{11} +\hat{\beta } (t)\omega _1 -\Upsilon _1 -u_{21} u_{25} +s_{11} s_{15} +v_1} \\ {10\omega _2 -e_\beta s_{12} +\hat{\beta } (t)\omega _2 -\Upsilon _2 -u_{22} u_{25} +s_{12} s_{15} +v_2} \\ {u_{21} u_{23} +u_{22} u_{24} -1/2({s_{11} s_{13} +s_{12} s_{14}})-\Upsilon _3 +v_3 } \\ \end{array} }} \right) \nonumber \\&\qquad +e_\beta D^{q}({\beta (t)-\hat{\beta }(t)}). \end{aligned}$$
(24)

Because system (15) is a minimum phase system, i.e. \(D^{q}({\omega ^{\mathrm{T}}\varphi ({\omega , \theta })} )\le 0\), inequality (24) can be obtained as

$$\begin{aligned} D^{q}V({\omega ,\Upsilon ,\theta })\le & {} \left( {{\begin{array}{l} \Upsilon _1 \\ \Upsilon _2 \\ \Upsilon _3 \\ \end{array} }}\right) ^\mathrm{T} \left( {{\begin{array}{lll} 10\omega _1 -e_\beta s_{11} +\hat{\beta } (t)\omega _1 -\Upsilon _1 -u_{21} u_{25} +s_{11} s_{15} +v_1 \\ 10\omega _2 -e_\beta s_{12} +\hat{\beta } (t)\omega _2 -\Upsilon _2 -u_{22} u_{25} +s_{12} s_{15} +v_2 \\ u_{21} u_{23} +u_{22} u_{24} -1/2({s_{11} s_{13} +s_{12} s_{14} } )-\Upsilon _3 +v_3 \\ \end{array} }} \right) \nonumber \\&+\,e_\beta D^{q}({\beta (t)-\hat{\beta }(t)}). \end{aligned}$$
(25)

Substituting (16) and (17) into (25), leads to

$$\begin{aligned} D^{q}V({\omega ,\Upsilon ,\theta })\le \eta ^{\mathrm{T}}\Upsilon -\delta \Upsilon ^{\mathrm{T}}\Upsilon . \end{aligned}$$
(26)

As is well known, inequality (26) is equivalent to a Volterra integral inequality [25]

$$\begin{aligned}&V({\omega ,\Upsilon ,\theta })-\sum \limits _{k=0}^{\lceil q \rceil -1} V({{\omega _0} ,\Upsilon _0 ,\theta _0})^{(k)}\frac{t^{k}}{k!}\nonumber \\&\quad \le \frac{1}{\Gamma (q)}\int _0^t ({t-\tau })^{q-1}({\eta ^{\mathrm{T}} (\tau )\Upsilon }(\tau ))\hbox {d}\tau \nonumber \\&\qquad -\frac{\delta }{\Gamma (q)}\int _0^t ({t-\tau })^{q-1} (\Upsilon ^{\mathrm{T}}(\tau )\Upsilon (\tau ))\hbox {d}\tau . \end{aligned}$$
(27)

For \(V({\omega ,\Upsilon ,\theta })\ge 0\), let \(\sum \nolimits _{k=0}^{\lceil q \rceil -1} V({\omega _0 ,\Upsilon _0 ,\theta _0})^{(k)}({t^{k}/k!})=\varepsilon \), inequality (27) can be rewritten as

$$\begin{aligned}&\frac{\delta }{\Gamma (q)}\int _0^t ({t-\tau })^{q-1} ({\Upsilon ^{\mathrm{T}}(\tau )\Upsilon (\tau )})\hbox {d}\tau \nonumber \\&\quad \le V({\omega ,\Upsilon ,\theta }) {+}\frac{\delta }{\Gamma (q)}\int _0^t ({t{-}\tau })^{q-1} ({\Upsilon ^{\mathrm{T}}(\tau )\Upsilon (\tau )})\hbox {d}\tau \nonumber \\&\quad \le \frac{1}{\Gamma (q)}\int _0^t ({t-\tau })^{q-1} ({\eta ^{\mathrm{T}}(\tau )\Upsilon (\tau )})\hbox {d}\tau +\varepsilon . \end{aligned}$$
(28)

Using the convolution definition, the convolution of two continuous functions f(t) and g(t) is as \(f(t)*g (t)=\int _0^t f({t-\tau })g(\tau )\hbox {d}\tau \), where t is the upper limit of the integral, \(0<\tau <t\).

Hence, inequality (28) is obtained as

$$\begin{aligned}&\frac{1}{\Gamma (q)}(t)^{q-1}*({\eta ^{\mathrm{T}}(t) \Upsilon (t)})+\varepsilon \nonumber \\&\quad \ge \frac{\delta }{\Gamma (q)} (t)^{q-1}*({\Upsilon ^{\mathrm{T}} (t)\Upsilon (t)}). \end{aligned}$$
(29)

Taking the Laplace transform from both sides of (29) yields

$$\begin{aligned} \frac{1}{s^{q}}({\eta ^{\mathrm{T}}(s)\Upsilon (s)}) +\frac{\varepsilon }{s}\ge \frac{\delta }{s^{q}}({\Upsilon ^{\mathrm{T}} (s)\Upsilon (s)}). \end{aligned}$$
(30)
Fig. 3
figure 3

The synchronised states of two identical fractional-order complex chaotic systems.

Full size image

Inequality (30) can be converted in the time domain as follows:

$$\begin{aligned}&\int _0^t u({t-\tau } )({\eta ^{\mathrm{T}}(\tau )\Upsilon (\tau )}) \hbox {d}\tau +\frac{t^{({1-q})}\,\varepsilon }{({1-q})!}\nonumber \\&\quad \ge \delta \int _0^t u({t-\tau })({\Upsilon ^{\mathrm{T}}(\tau ) \Upsilon (\tau )})\hbox {d}\tau . \end{aligned}$$
(31)

Inequality (31) satisfies Definition 3. Therefore, system (15) is a passive system by the control laws (16) and the parameter update rule (17).

In the receiver, when synchronisation between the transmitter system (12) and the receiver system (13) under the control laws (17) is achieved, the uncertain parameter \(\beta (t)\) can be estimated asymptotically according to Theorem 1. Using the invertible transformation function, \(\hat{s}(t)=\gamma ^{-1} ({\hat{\beta } (t)})\). \(\square \)

5 Numerical simulation and experimental results

To verify and demonstrate the effectiveness and applicability of the proposed method, two computer simulations are considered. To solve the fractional-order differential systems with a step size \(h=0.001\), the fourth-order Runge–Kutta method is used.

An arbitrary information signal is considered as follows:

$$\begin{aligned} s(t)=0.5\ \hbox {sin}({1.5t})+1.5. \end{aligned}$$
(32)

Based on the control laws (16) and the parameter update rule (17), the MCPS between the transmitter system (12) and the receiver system (13) is achieved and the unknown parameter \(\hat{\beta } (t)\) is identified. Assume that the initial conditions \(({x_1 (0),\,x_2 (0),\,x_3 (0)})^{\mathrm{T}}=({1.5+\hbox {j}0.5, \,2+\hbox {j},\,2.5} )^{\mathrm{T}}\) and \(({y_1(0), \,y_2 (0), \,y_3 (0)})^{\mathrm{T}}=({0.5+\hbox {j}2,\,1+\hbox {j}2, \,1.5})^{\mathrm{T}}\) are employed. Also, the initial value of the unknown parameter is arbitrarily chosen as \(\hat{\beta } (0)=0.001\), the external signals \(\eta _k = 0, k=1, 2, 3\) and we select \(\delta =200\).

5.1 Secure communication without channel noise

Based on (32), the new parameter of the proposed chaotic system is \(\beta (t)=5\,({2s(t)+3} )+150,\) where the new chaotic system (12) exhibits chaotic behaviour. The synchronised states of two systems (12) and (13) with transmission matrix \(\Phi =\hbox {diag}( {1-\hbox {j}, 1-\hbox {j}, 1})\) are plotted in figure 3. The synchronisation errors between two mentioned systems are depicted in figure 4, which indicates that the synchronisation between two systems is realised.

Fig. 4
figure 4

The synchronisation errors between systems (12) and (13).

Full size image
Fig. 5
figure 5

The synchronisation error \(e_2(t)\) vs. different fractional-order (q).

Full size image
Fig. 6
figure 6

(a) The recovered information signal \(s(t)=0.5\,\hbox {sin}({1.5t})+1.5\) without channel noise and (b) the error between the information signal and the recovered information signal.

Full size image
Fig. 7
figure 7

(a) The recovered information signal \(s(t)=0.5\,\hbox {sin}({1.5t})+1.5\) with white channel noise and (b) the error between the information signal and the recovered information signal.

Full size image
Fig. 8
figure 8

(a) The recovered information signal \(s(t)=0.5\,\hbox {sin}({1.5\,t})+1.5\) with colour channel noise and (b) the error between the information signal and the recovered information signal.

Full size image
Fig. 9
figure 9

(a) The recovered information signal \(s(t)=0.5\,\hbox {sin}({1.5\,t})+1.5\) with sinusoidal channel noise and (b) the error between the information signal and the recovered information signal.

Full size image

In order to investigate the effect of fractional-order (q) on the synchronisation time, we apply the synchronisation error \(e_2 ( t)\). As one can see from figure 5, when \(q=0.8\), \(e_2 ( t)\) converges to zero faster than \(e_2 (t)\) when \(q=0.9\) and 0.95. It is clear because the chaotic behaviour of the system decreases and so convergence to zero is faster.

Figure 6a shows that the information signal is successfully recovered as

$$\begin{aligned} \hat{s}(t) =0.5({({\hat{\beta } (t)-150})/5-3}). \end{aligned}$$
(33)

From figure 6b, we can see that the error between the original and the recovered information signals converges to zero after a short transient time.

5.2 Secure communication with channel noise

Here, the proposed chaotic secure communication scheme will study with the effect of additive noise in the channel. The white channel noise (e(t)) is Gaussian with a variance of 1. Also, the colour noise \(({e(t) + 0.5e({t-1})+0.3e({t-2})})\) is considered in the communication channel. In this communication system, signal-to-noise ratio is 0.05. The information signal is as (32). The new parameter of the proposed chaotic system (12) is \(\beta (t)=5({2s(t)+3})+150\), where the new chaotic system exhibits chaotic behaviour. Figures 7a and 8a show that the information signals successfully recovered as (33) when the scaling matrix is chosen as \(\Phi =\hbox {diag}({1-\hbox {j}, 1-\hbox {j}, 1})\). From figures 7b and 8b, one can see that the errors between the information signal and the recovered information signal with the channel noise converge to zero after a short transient. Also, when an external noise is supposed to be \((0.2\,\hbox {sin}(t)+\hbox {j}\,0.25\,\hbox {cos} ({2t}), 0.15\,\hbox {cos}(t)+\hbox {j}\,0.1\,\hbox {sin}(t), 0.15\,\hbox {cos}({3t}))\), then the recovered information signal and its error are depicted in figures 9a and 9b, respectively.

6 Conclusion

Chaotic secure communications via the synchronisation of fractional-order complex chaotic systems just appeared in recent years, since the fractional-order system possesses memory and also doubling the number of variables in the complex chaotic system may be used to increase the security of the transmitted information. The information signal can be recovered accurately at the receiver end by applying robust controllers and fractional update law of uncertain parameter when additive noise such as white noise and colour noise as high-frequency disturbances as well as low-frequency disturbances such as sinusoidal signal exist in the transmission channel. For high-frequency disturbances, a simple filter in the receiver end is used to recover the information signal accurately.